A comprehensive investigation into the performance, robustness, scalability and convergence of chaos-enhanced evolutionary algorithms with boundary constraints

Abstract

The purpose of this research is to investigate the effects of different chaotic maps on the exploration/exploitation capabilities of evolutionary algorithms (EAs). To do so, some well-known chaotic maps are embedded into a self-organizing version of EAs. This combination is implemented through using chaotic sequences instead of random parameters of optimization algorithm. However, using a chaos system may result in exceeding of the optimization variables beyond their practical boundaries. In order to cope with such a deficiency, the evolutionary method is equipped with a recent spotlighted technique, known as the boundary constraint handling method, which controls the movements of chromosomes within the feasible solution domain. Such a technique aids the heuristic agents towards the feasible solutions, and thus, abates the undesired effects of the chaotic diversification. In this study, 9 different variants of chaotic maps are considered to precisely investigate different aspects of coupling the chaos phenomenon with the baseline EA, i.e. the convergence, scalability, robustness, performance and complexity. The simulation results reveal that some of the maps (chaotic number generators) are more successful than the others, and thus, can be used to enhance the performance of the standard EA.

1 Introduction

So far, extensive studies have been carried out to embed the concept of chaos into the structure of metaheuristic optimization algorithms. Intensification (exploitation capability) and diversification (exploration capability) are the main properties of such algorithms. Intensification incurs more effective search around local minima, and diversification leads to more covering of the search space which in turn reduces the probability of trapping into local minima and missing the most qualified solutions. Generally, the development of metaheuristic optimization algorithms is performed within two main frames, i.e. introducing novel algorithms and improvement of the existing methods (Goldberg 1989; Yang 2008). Although proposing novel metaheuristics is still welcome according to no free lunch theorem (Wolpert and Macready 1997; Karaboga and Basturk 2007; Mozaffari et al. 2012c; Abdechiri et al. 2013), the second field of investigation, i.e. improving intensification/diversification capabilities of the well-established metaheuristics, such as evolutionary algorithms (EAs) and swarm based methods, is of higher importance. The urge for improving the exploration/exploitation capabilities of well-established metaheuristics has come to the mind of many researchers of the both basic and practical science societies, and thus numerous related research papers can be found in literature [see for example Mozaffari et al. (2012a, 2013a), Karaboga and Akay (2009), Civicioglu and Besdok (2013) and references therein].

In the recent years, researchers have been looking for some techniques to replace the stochastic nature of the randomization with a purposeful process (Caponetto et al. 2003; Mozaffari et al. 2015). This is done through embedding orderliness into the stochastic operators (responsible for exploration of metaheuristics) while retaining their unpredictability characteristic.

Fascinating trait of nonlinear dynamical systems (Huaguang and Yongbing 2001), in particular chaotic dynamics, has drawn an increasing attention of researchers. Chaos is mathematically defined as a deterministic nonlinear system which produces randomness (Alatas and Akin 2009; Emami et al. 2016). Some main properties of chaos dynamic systems include ergodicity, semi-stochastic nature and dependence on the initial conditions (Schuster 1988). Promising reports on the successful applications of chaotic systems to a wide spectrum of scientific fields such as mathematics, physics, biology, chemistry and economics have provoked researchers of the engineering community to find out whether it can be of use for other practical tasks. For this purpose, researchers have tried to substitute deterministic chaos-based signals with stochastic ones. The mentioned strategy has been employed in various practical domains such as telecommunication and secure transmissions (Wong et al. 2005), signal, image and video processing (Gao et al. 2006; Abdechiri et al. 2017a, b, c), nonlinear circuits (Arena et al. 2000), DNA computing (Manganaro and Pine dade Gyvez 1997), control (Ott et al. 1990; Kapitniak 1995; Zhang et al. 2014), information decryption (Zelinka and Jasek 2010) and synchronization (Pecora and Carroll 1990; Zhang et al. 2010).

Along with the above-mentioned applications, the concept of substituting chaos sequences with stochastic signals has been used by researchers of the metaheuristic community to improve the randomness of metaheuristic algorithms (Zelinka et al. 2010). As mentioned, chaotic maps improve the exploration/exploitation capabilities of metaheuristics by replacing their stochastic randomness with a deterministic disordered repetitive pattern (Gao et al. 2010). Actually, most of the exerted simulations indicate an obvious enhancement in the accuracy of metaheuristics when they use bounded chaotic based explorative operators instead of pure stochastic processes (Zelinka et al. 2010).

In this work, the impact of combining chaotic maps with EAs, as one of the most popular types of swarm and evolutionary optimizers is empirically analyzed. In particular: (1) different chaotic maps are adopted to select the most compatible one for EAs, (2) the performance improvement and time complexity associated with replacing chaotic sequences with conventional stochastic random procedure is rigorously studied, (3) the robustness of chaos-enhanced methods are evaluated using statistical metrics, and (4) the scalability of the chaotic methods are tested using numerous scalable benchmarks of different properties considering three different dimensions (50D, 100D and 200D). To the authors’ best knowledge, this is the first time that a comprehensive numerical study is carried out which simultaneously verifies the impact of different types of chaotic maps on the algorithmic complexity, robustness, convergence behavior, scalability and performance of EAs. Therefore, it is believed that the findings of the current study can be a good guide which provides a vision for the researchers of metaheuristic computing regarding the efficacy of specific types of chaotic maps for real-life optimization tasks.

The rest of the paper is organized as follows. Section 2 presents the literature review of the advances on chaotic evolutionary computing. Section 3 is devoted to the definition and analysis of chaotic evolutionary algorithms. In Sect. 4, the performances of CEAs are investigated experimentally, and the most efficient chaotic maps are presented. Finally, the paper is concluded in Sect. 5.

2 A review of the theoretical advances and applications of chaotic evolutionary computing

So far, the use of chaotic embedded operators has been examined in different evolutionary algorithms for a wide range of real-life and numerical optimization problems. Table 1 lists the important research papers together with their application and findings.

Table 1 Chronological progress of the conducted researches on chaos-enhanced evolutionary computing

As can be inferred from the given information, chaos-enhanced EAs have successfully been applied to a wide range of applications, and seem to be used even more in near future for handling complicated optimization problems.

3 The proposed chaotic evolutionary algorithms

3.1 A concise review on the background of evolutionary algorithms

By the middle of twentieth century, the promising reports on using nature-inspired methods for handling complicated problems has drawn an increasing attention from computer scientists. In particular, the use of algorithms mimicking the theory of evolution and survival of the fittest has been found to be very effective for solving complex optimization problems. Investigation on the potentials of evolutionary algorithms (EAs) for optimization has been incepted by a number of independent research groups in 1960s. In 1962, the studies of Holland’s research group in Ann Arbor (Holland 1975) and Fogel’s research group in San Diego (Fogel et al. 1966) led to the proposition of GA and evolutionary programming (EP), respectively. In 1965, Schwefel and Rechenberg’s research in Berlin led to the development of evolutionary strategies (ES) (Beyer and Schwefel 2002). Such pioneering investigations have played a key role in the formation of the field today known as evolutionary computation. There exists an extensive literature regarding the variants of EAs, from which genetic programming (GP) (Brameier and Banzhaf 2007) and differential evolution (DE) (Storn and Price 1997) have gained a remarkable reputation. In spite of the structural differences of the abovementioned algorithms, all of them follow the same concepts for solving a problem, namely the laws of natural competition and survival of the fittest. This is done by executing a series of coupled mathematical operators in the form of selection, crossover and mutation on individuals (chromosomes) to balance the exploitation and exploration rate of search.

In the next sub-section, the authors explain the steps required for implementing the considered EA.

3.2 Implementation of evolutionary algorithm

To conduct the current experiments, the authors went through the literature to extract some powerful operators suited for developing an accurate and robust EA. Over the past decades, numerous investigations have been carried out to develop powerful operators for EAs (Zhou et al. 2011). In general, the efficacy of each EA depends on the optimality/efficiency of its operators, i.e. the selection, crossover and mutation operators. As the aim of the current study is to investigate the effects of chaotic maps on the performance of EAs, it is crucial to select operators which can be easily combined with chaotic maps. On the other hand, to derive firm conclusions regarding the performance of chaotic maps, we have to ensure that the basic operators of the considered EA are quite efficient. Such facts have motivated us to search the existing literature to find acceptable types of selection, crossover and mutation operators. In what follows the section, the authors scrutinize the operators constructing the algorithmic structure of the considered EA.

3.2.1 Tournament selection

Proposed by Goldberg (1989), tournament selection is one of the most well-known and applicable types of selection mechanisms. In this approach, a pre-defined number of chromosomes are selected randomly and participate in a tournament. The winner of the tournament which is an individual with higher fitness value (as compared to the other rival individuals) is selected for the crossover operation. This can be mathematically expressed as below:

$$\begin{aligned} T\left( {X_1 ,\ldots ,X_u ,\ldots ,X_r } \right) =X_u \;\leftrightarrow \;\max \left( {{ fit}\left( {X_1 } \right) ,\ldots ,{ fit}\left( {X_u } \right) ,\ldots ,{ fit}\left( {X_r } \right) } \right) ={ fit}\left( {X_u } \right) \end{aligned}$$

(1)

where T is a function indicating the output of the tournament, X represents an individual, r indicates the maximum number of chromosomes participating in the tournament mechanism, and fit shows the fitness function of the individuals.

In general, the tournament selection can be enumerated as a flexible technique as the selection rate can be easily tuned by changing the number of individuals participating in the tournament (r). Obviously, the more the number of individuals participating in the tournament, the higher the probability of exploitation. To be more to the point, when the number of participating individuals is large, the weak chromosomes have smaller chance to be selected as the outputs of the tournament. Consequently, the chromosomes selected for the crossover selection have lots of similar characteristics which in turn foster the exploitation (intensification) capability of EAs. The flexibility of tournament selection provides us with an opportunity to easily tune a rational balance between exploration/exploitation capabilities of the considered EA.

3.2.2 Heuristic crossover

Generally, crossover operators can be considered as a mean for increasing the intensification of EAs. In this phase, two or more chromosomes (depends on the type of crossover mechanism) exchange their information through a phenomenon called intersection. The outputs of such a procedure are the chromosomes known as off-springs. Proposed by Wright (1991), heuristic crossovers (HX) can be considered as one of the most applicable types of crossover operators. Based on empirical experiments, it has been demonstrated that heuristic crossover can be used for solving nonlinear constraint and unconstraint problems (Michalewicz 1995; Thakur 2013). HX uses two parent chromosomes for generating off-springs. Consider that two parent chromosomes $X_{1}$ and $X_{2}$ are selected for the process. Then, the off-spring produced by HX can be determined as:

$$\begin{aligned} \xi =X_1 +\alpha \left( {X_1 -X_2 } \right) \end{aligned}$$

(2)

Provided that:

$$\begin{aligned} { fitness}\left( {X_1 } \right) >{ fitness}\left( {X_2 } \right) \end{aligned}$$

(3)

where $\xi =\left\{ {\varsigma _1 ,\varsigma _2 ,\ldots ,\varsigma _D } \right\}$ represents the resulted off-spring, $X=\left\{ {x_1 ,x_2 ,\ldots ,x_D } \right\}$ delegates the vector of parent solutions and $\alpha$ is a random number with uniform distribution spanning the unity [0,1].

In spite of the numerical efficacies provided by HX, it has a remarkable deficiency. Indeed, there is a possibility that the produced solution exceeds the feasible ranges of the solution domain (i.e. $\varsigma _i >x_i^U$ or $\varsigma _i <x_i^L$). In such a situation, it is mandatory to devise a technique which can guide the exceeding solutions towards the feasible domain. The salient asset of HX lies in its simplicity. As it can be inferred, the mathematical steps and criteria required for implementing HX are not demanding in comparison with the other types of crossover operators such as Laplace crossover (Deep and Thakur 2007) and simulated binary crossover (Deb and Agrawal 1995).

3.2.3 Arithmetic graphical search mutation

Goldberg’s arithmetic graphical search (AGS) mutation is a self-adaptive mutation operator which has found its place in the realm of evolutionary computation (Goldberg 1989). The adaptive instinct of AGS helps EA to dynamically set a proper balance between exploitation/exploration capabilities. In this regard, at the very beginning of the procedure, AGS fosters the diversification capability of EA and gradually abates the probability of mutation (which in turn decreases the diversification rate) to help the optimizer focus on specific regions to find the most optimum solution. In practice, such mutation operators have been proven to be very effective for optimizing multimodal problems (Mozaffari et al. 2012a; Fathi and Mozaffari 2014). The mathematical formulation of AGS is as follows:

$$\begin{aligned} \xi =\left\{ \begin{array}{ll} \left\{ \begin{array}{l} X+\delta \left( {t,\left( {X^{{ ub}}-X} \right) } \right) \\ or \\ X+\delta \left( {t,\left( {X-X^{{ lb}}} \right) } \right) \\ \end{array}\right. &{}\quad { if\;rand}<\lambda \\ X&{} \quad { if\;rand}\ge \lambda \\ \end{array} \right. \end{aligned}$$

(4)

where $\lambda$ is a pre-defined value which verifies the chance of mutation, t is the current generation number, $\xi$ shows the resulted chromosome (mutant solution), X shows the chromosome selected for mutation, and $\delta (x,y)$ is calculated as:

$$\begin{aligned} \delta \left( {t,y} \right) =y\times \phi \times \left( 1-\frac{t}{T}\right) ^{b} \end{aligned}$$

(5)

where T is the number of the maximum iteration, b is a random number larger than 1, and $\phi$ is a random number within the range of [0,1].

As it can be seen, two alternative equations are considered for the mutation operator (${ rand}<\lambda$). We implement the operator in a fashion that EA can randomly choose one of them for the exploration. Therefore, each time AGS could select the first equation to conduct the exploration considering the upper bound, or select the second term and explore the solution domain with respect to lower bound values of the optimization variables.

3.2.4 The proposed boundary constraint handling strategy

As it was mentioned, there is a possibility that the solutions produced by HX and AGS operators exceed from the feasible range of the solution domain. In such cases, the optimization algorithms loose the valid trajectory over the procedure. This may result in finding invalid/impractical solutions and incurring miss-judgments. Hence, it is really necessary to devise a technique capable of controlling/correcting the movements of heuristic agents (chromosomes) over the optimization procedure. In general, such techniques are known as boundary constraint handling strategies (BCHSs).

BCHSs control the positions obtained by the produced chromosomes, and correct them when they are exceeding the admissible solution domain. Indeed, when using BCHSs, we are seeking for a controlling formulation which can detect and modify the position of the violated solutions. The modification is done by using a map which transfers the violated solutions within the admissible range of solution domain. This issue has been clearly addressed by many researchers of the swarm and evolutionary computing society, and there exist several types of such maps in the literature (Gandomi and Yang 2012; Mozaffari et al. 2013b). A previous research by the authors’ research group revealed that the following formulation can result in a really powerful BCHS (Mozaffari et al. 2012a):

$$\begin{aligned} X=\left\{ {\begin{array}{ll} 2\times X^{{ lb}} -X &{} \quad { if}\;X<X^{{ lb}} \\ 2\times X^{{ ub}} -X &{} \quad { if}\;X>X^{{ ub}} \\ X &{} \quad { otherwise} \\ \end{array}} \right. \end{aligned}$$

(6)

where $X^{{ lb}}$ and $X^{{ ub}}$ are the lower and upper bound of the solution domain, respectively. As it can be inferred, after updating each position, the validity of new chromosome is checked using the above map and necessary modifications are inflicted on the chromosome, if required. Based on rigor experimental studies, it has been observed that the above map prevents the optimizer from trapping into local optima, and therefore deters premature convergence of EAs (Tessema 2006). The 2D graphical representation of the considered BCHS is shown in Fig. 1. As seen, by using the considered BCHS, the solutions which violate the constraints (red squares) are mapped into the feasible domain (light green region).

Fig. 1

Performance of the proposed boundary constraint handling technique. (Colour figure online)

3.2.5 Other parameters and steps

To run the EA, some controlling parameters should be taken into account. As an evolutionary based metaheuristic, the performance of the considered EA is controlled by a set of pre-defined elements such as: crossover probability ($P_C )$, mutation probability ($P_m )$, population size ($P_S )$, number of generations (t), number of elite chromosomes (e), number of chromosomes participating in the tournament (r), the diversification factor of AGS mutation operator (b) and etc. To set the values of the mentioned controlling parameters, we have no choice but to conduct an experimental analysis. To encode the considered EA, the procedure given in Algorithm 1 should be fulfilled.

Algorithm 1. Pseudo-code of the considered EA
Step 1: Set the controlling parameters, i.e. $P_C,P_m,P_S,t,e,t$, and b.
Step 2: Initialize the population of chromosomes $P_S$ randomly.
Step 3: Evaluate the fitness of the generated population.
Step 4: Generation $\hbox {Number}=1$.
Step 5: Perform the tournament selection to select a set of chromosomes for crossover operation.
Step 6: Perform the HX to produce off-springs ($\xi$) from parent chromosomes X (based on the value of $P_C$).
Step 7: Archive the elite solution (e) and send the other chromosomes for mutation procedure
Step 8: Apply AGS mutation to produce mutant chromosomes ($\xi$)
Step 9: Simulate the law of survival of the fittest by sorting the choromosomes and discarding the weak ones from the population (based on their fitness values). Obviously, at this stage, the population is updated.
Step 10:$\hbox {Iteration Number}=\hbox {Iteration Number}+1$.
Step 11: If the Iteration Number is equal to Max-Iteration, stop the process, else go to Step 5.

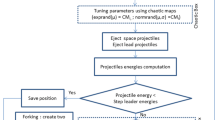
Now, it is important to find the most optimum values of the controlling parameters. To do so, an empirical analysis is taken into account. Table 2 indicates a set of potential values for the controlling parameters. As it can be seen, 16 different sets of the controlling parameters are considered to find out which of them can yield better results.

Table 2 Considered sets of the controlling parameters for the standard EA

These 16 different EAs are used for optimizing 27 different benchmark optimization problems given in “Appendix A”. The performance and convergence behavior of the selected cases are considered as the evaluation metrics. The performance metric indicates the capability of the considered EAs in optimizing the benchmark problems (this is done by considering the values of objective value of the chromosomes). The convergence metric indicates the capability of considered EAs in balancing the exploration/exploitation characteristics over the optimization procedure (Mozaffari et al. 2013b). In this research, the numerical analysis is utilized to verify the impact of the considered controlling parameters on the convergence rate of the standard EAs. Obviously, the convergence rate of the chromosomes cannot be evaluated directly by using their fitness functions. Therefore, a proper formulation should be taken into account. Based on the results of a recent study by the authors, the following formulation is used to calculate the convergence rate of EA:

$$\begin{aligned} { fitness~(ObjVal)}= & {} \left\{ {\begin{array}{ll} \frac{1}{ObjVal+1}&{} \quad ObjVal>0 \\ 1+\left| {ObjVal} \right| &{} \quad ObjVal<0 \\ \end{array}} \right. \end{aligned}$$

(7)

$$\begin{aligned} { Mean\;fitness}= & {} \frac{\sum \nolimits _{i=1}^{P_S } {{ fitness}(ObjVal(X_i ))} }{P_S } \end{aligned}$$

(8)

$$\begin{aligned} { Best\;fitness}= & {} \max \left\{ {{ fit}(ObjVal(X_i ))|\;i=1,\ldots ,P_S } \right\} \end{aligned}$$

(9)

$$\begin{aligned} { Convergence\;rate}= & {} \frac{{ Mean\;fitness}}{{ Best\;fitness}} \end{aligned}$$

(10)

As it can be inferred, the algorithm converges to a specific region when the value of convergence rate (CR) approaches to the proximity of 1. Therefore, the algorithm performs a diverse stochastic search when the value of CR is less than 0.3. It is expected that an efficient EA neatly balances the exploration/exploitation capabilities.

To capture the undesired effects of randomness, all of the experiments are conducted for 30 independent runs with random initial seeds, and the mean values of the considered performance evaluation metrics are reported. Initially, all of the algorithms execute the optimization with $P_S = 40$ (this value has been obtained through a complexity analysis which will be shown later in this section). The generation number (t) is set to be 1000. As the main goal of this experiment is to extract the optimum values of controlling parameters, there is no need for exposing the simple EAs to a scalable optimization framework. Hence, the experiments are conducted by considering the 50D version of the benchmark functions.

Table 3 indicates the mean performances of the standard EAs for the benchmark problems. From the results, it can be realized which sets of the controlling parameters can neatly tune the exploration/exploitation capabilities of EA. The best results are shown in bold. As seen, the best performance belongs to the 6${\mathrm{th}}$ set of the controlling parameters. In this case, the related EA outperforms the rival techniques for 10 benchmark functions. Along with the mentioned EA, the 14${\mathrm{th}}$ set of the controlling parameters show promising results, as it outperforms the rival techniques 8 times.

Table 3 Mean performances of the standard EAs for benchmark problems

To ensure the authenticity of the 6${\mathrm{th}}$ scenario and also avoid any miss-judgment, the second performance evaluation criterion, i.e. convergence analysis, should be taken into account. We claim that the 6${\mathrm{th}}$ set of the controlling parameters is most optimal if and only if it can show acceptable convergence behavior. To be more to the point, if the exploration/exploitation of chromosomes of the population is deliberate, without any doubt, the 6${\mathrm{th}}$ scenario yields the most efficient values of the controlling parameters for the EA. Given the mathematical formulations provided, the authors visualize the real-time convergence behavior of the selected EAs in Fig. 2. From the figure, it can be easily inferred that in most of the cases, the selected EA is able to balance its exploration/exploitation capabilities over the optimization procedure. Apparently, at the very beginning of the optimization process, the heuristic agents are diffused over the solution domain and thus, the convergence of EA is really low. However, after a number of iterations, the heuristic agents concentrate on a specific region to exploit for the global optimum solution, and finally the convergence rate approaches the value of 1. This implies that the heuristic agents successfully converge to a unique solution. An interesting observation pertains to the amplitude of the convergence during the process. By checking the benchmark problems, it can be interpreted that when the problem is multimodal, the heuristic agents have an attitude towards exploring a larger domain to avoid trapping into local pitfalls. In the case of uni-modal benchmark problems, a direct ascending behavior can be seen. In such a case, the heuristic agents of EA gradually decrease their distances and converge to a unique solution. As a general remark, it can be expressed that the selected values of the controlling parameters (the 6${\mathrm{th}}$ set) are not only able to show an acceptable performance, but also can manage the exploration/exploitation capabilities of the chromosomes in order to find the global optimum solutions.

Fig. 2

Convergence behavior of the standard EA with 6${\mathrm{th}}$ set of controlling parameters for the benchmark problems

After verifying the optimum values of the controlling parameters, we have to check whether the population size of 40 is the best choice for the experiments. To this aim the both computational complexity and performance should be taken into account. This lets us obtain a logical trade-off between the accuracy and complexity of the EA. In this research, time complexity is used as a mean for evaluating the computational complexity of EAs of different population sizes. The mathematical equations required for implementing the time complexity criterion is given below (Fathi and Mozaffari 2013):

$$\begin{aligned} Time\_Complexity=\frac{\hat{{\tau }}_2 -\tau _1 }{\tau _0 } \end{aligned}$$

(11)

where $\tau _0$ is the code execution time for 200,000 evaluations of the programming operators, i.e. %, $\times$, +, $-, \hat{\,}$, /, exp, and ln, on a simple 2 dimensional vector, $\tau _1$ is the required time for 200,000 function evaluations and $\hat{{\tau }}_2$ is the mean of 30 execution times.

This time, the experiments are carried out by the population sizes of 20, 40, 60, 80 and 100. Note that for all of the cases, the 6${\mathrm{th}}$ set of the controlling parameters is used. As in this case, the difference of EAs only refers to the population size, there is no need for a rigor experimental study. For the sake of brevity, the analysis is conducted using $f_{{1}}, f_{{6}}, f_{{12}}$, $f_{{19}}$ and $f_{{27}}$ benchmarks. Table 4 lists the obtained results. As it can be seen, for the most of the benchmark problems, the performance of EA with 40 chromosomes is better than the other cases. It seems that the interactions of this amount of heuristic agents through different operators of EA can be really useful for the function optimizations. By taking the results of time complexity into account, one interesting point can be observed. As it can be seen, for most of the cases, the time complexity of EA with a population size of 20 is higher than the other cases. The reason to this phenomenon should be sought within the algorithmic functioning of EA. Obviously, when the number of chromosomes is low, EA should activate the operators much more than that required for larger number of heuristic agents. To be more to the point, for example, in our case, we have to continue the optimization for 200,000 function evaluations. For a convenient interpretation, let us consider that EA works with HX crossover operator (a pure crossover based metaheuristic). In such a condition, when the number of chromosomes is large (e.g. 100), we can comply with that number of function evaluations by activating the operators for 2000 times. However, for the lower numbers of chromosomes (e.g. 20), the same procedure requires at least 10,000 times of HX activation. Therefore, the computational time of the EA is higher when the number of chromosomes is low. Based on the results obtained, it can be seen that the time complexity of EA with 20 chromosomes is remarkably higher than other scenarios. But, for the other cases, the time complexities are really close. Considering the results of complexity and performance in tandem, it can be seen that the EA with a population size of 40 yields the most promising results (the best performance at the cost of logical computational complexity). Therefore, this number of heuristic agents is considered for the rest of the experiments.

Table 4 Performance and complexity of the EAs of different population sizes

Based on the conducted experiments, the following remarks can be reported regarding the effect of the controlling parameters on the performance of EA:

• (1) The results indicated that for the crossover probability of 0.9, the mutation probability of 0.01, and the tournament selection with 7 participants, the EA can show really acceptable results in terms of the both accuracy and convergence behavior. As the number of chromosomes participating in the tournament is relatively high, the EA tends to perform exploitive search over the procedure. It is also worth noting that the AGS mutation guarantees the exploration of the EA, as well.

• (2) It was observed that the selected set of controlling parameters enables EA to efficiently balance its exploration/exploitation capabilities over the procedure. As it can be seen from Fig. 2, based on the characteristics of the problem, the heuristic agents show explorative behavior to effectively search the solution space, and finally perform an intensive exploitation to find the global optimum solution.

• (3) Through conducting a deliberate trade-off among the computational complexity and the computational capability of the EA, the authors have been enabled to find the most optimum number of heuristic agents (chromosomes). The results indicated that by using the optimum values of the controlling parameters and a relatively low number of chromosomes, we are able to effectively execute the optimization without consuming a remarkable amount of the computational budget.

• (4) By finding the most efficient characteristics of the standard EA, we are now able to reliably investigate the effects of chaotic maps, and find out whether they can be useful for improving the exploration/exploitation capabilities of EA.

3.3 Embedding chaos into the structure of EA

In our implementation, the chaotic maps are replaced with a random parameter ($\alpha )$ in the HX crossover and rand AGS mutation operators. This allows us evaluate the performances of crossover and mutation operators based on the laws of chaotic sequences, and also, find out whether devising such a policy can improve the searching capabilities of the resulting algorithm. As it was mentioned, the main purpose of using chaotic maps instead of the stochastic random parameter is to find out whether deterministic nonlinear systems capable of producing randomness have positive impacts on the exploration/exploitation capability of EAs. As a dynamic system, the output of chaotic maps ($\psi$) at generation $t + 1$ depends on its value at the current generation t. Let us embed chaos into the structure of HX and AGS operators.

• (a) Modified chaotic crossover operator: the mathematical formulation of the modified crossover operator combined with chaotic sequences is given by:

  $$\begin{aligned} \xi =X_1 +\psi (t).\left( {X_1 -X_2 } \right) \end{aligned}$$

  (12)

  where $\psi$ represents a chaotic sequence, and there is a nonlinear map ($\Psi )$ which produces chaos as:

  $$\begin{aligned} \psi (t+1)=\Psi \left( {\psi (t)} \right) \end{aligned}$$

  (13)

• (b) Modified chaotic mutation operator: to modify the mutation operator, the chaotic sequence should be embedded into Eq. (5) to derive the following formulation:

  $$\begin{aligned} \delta \left( {t,y} \right) =y\times \psi (t)\times \left( 1-\frac{t}{T}\right) ^{b} \end{aligned}$$

  (14)

  where, the chaotic sequence $\psi$ can be produced based on the formulation given in Eq. (13).

Through the above steps, the chaotic versions of EA can be easily implemented. The exploitation characteristics of the CEA depend on the behavior of the embedded chaos. The mathematical formulation of chaotic maps used in the current study are given in Table 5.

Table 5 Mathematical formulation of the considered chaotic maps

As it can be seen, for each of the above maps, there exists a specific function $\Psi$ which produces chaotic sequences. As an example, for the logistic map, this function can be written as $\Psi (\psi (t))=\alpha \psi (t)(1-\psi (t))$. In our study, the output of $\Psi$ function is confined within the range of unity. The shape of this iterative function for Chebyshev, logistic, sine and sinusoidal maps are shown in Fig. 3. The salient asset of using the considered maps lies in the bifurcation they are able to produce. In general, the chaotic behavior enables the considered maps to create deterministic randomness suited for evolutionary computation.

Fig. 3

Iterative chaotic sequences of the Chebyshev, logistic, sine and sinusoidal chaotic maps

4 Results and discussion

4.1 Experimental setup

Before describing the results, some parameters required for experimental procedures should be discussed. For the experiments, the standard EA and 18 chaotic CEAs (9 CEAs with chaotic crossovers and 9 CEAs with chaotic mutations) are taken into account. The selected test bed consists of 27 numerical benchmarks of different landscapes, difficulties and multimodalities. As the characteristics of the selected test bed is really exhaustive, the derived conclusions can be reliably extended for other applications. The selected benchmarks can be found in “Appendix A”.

To evaluate the scalability of the considered chaotic maps, three different dimensions, namely 50, 100 and 200, are taken into account. The rival optimization techniques are compared in terms of the performance, robustness, success and complexity. As the algorithmic functioning of the basic EA is constant, the results of time complexity let us discern the most computationally efficient CEAs. The population size ($P_S )$ of all of the rival algorithms is set to be 40, and the concept of elitism is applied to all of the rival algorithms. The crossover and mutation probabilities are equal to 0.9 and 0.01, respectively. In the tournament selection phase, 7 chromosomes are randomly chosen to participate in the competition, and the diversification factor of AGS mutation (b) is set to be 2.

All of the optimizations are conducted for 1000 iterations. To capture the undesired effects of stochastic optimizations, all of the identification scenarios are conducted for 30 independent runs and the mean, best, worth and standard deviation values are reported. Also, to make sure that the obtained results are unbiased, for each of the optimization scenarios, the starting point (initialization) is taken the same. Thus, all of the algorithms start searching the solution landscape with the same initial condition. All of the algorithms are implemented in the MATLAB software, and the computational procedures are conducted on a PC with a Pentium IV, Intel Dual core 2.2 GHz and 2 GBs RAM.

4.2 Experimental results

The experimental procedures can be divided into two main parts. Most of the experiments are performed in the first sub-section which is devoted to numerical problems. To attest the authenticity of the obtained results for the real-life problems, a demanding optimization problem, i.e. optimizing the controlling parameters of a power system, is considered which is discussed in the second part of the experiment.

4.2.1 Numerical experiments

In this subsection, the effects of the CEAs with the proposed boundary constraint handling technique are investigated. Through an exhaustive study, the authors will draw some conclusions regarding the impact of the chaotically encoded HX and AGS operators on the performance of the algorithm. The first three stages of the experiment are devoted to the evaluation of the robustness and accuracy of the rival methods for medium scale, semi large-scale, and large-scale benchmark optimization problems. Thus, the results will examine the robustness and accuracy of the algorithms as well as their potentials to be used for the optimization problems of different scales (scalability). Then, based on the results obtained in the previous stags, in the fourth stage of the experiment, the real-time evolution and scalability of the rival methods are tested. The last two stages of the experiment are devoted to analyzing the convergence and time complexity of the rival techniques.

4.2.1.1. Chaotic crossover and mutation: medium scale benchmarks

Tables 6 and 7 indicate the statistical results obtained by the rival techniques with chaotically encoded HX operators for the 50D version of the considered benchmark problems. For convenience, in the rest of the section, the best obtained results among the rival algorithms are shown in a bold format. From these two tables, one can easily see that the sinusoidal version of CEA outperforms the other optimizers. Along with the sinusoidal CEA, the logistic and sine versions of CEA show acceptable results too. The success of the other versions of CEAs is not remarkable for the 50D version of the benchmark problems.

Table 6 Statistical results of the optimizations for 50D version of benchmarks ($f_{{1}}-f_{{14}})$

Table 7 Statistical results of the optimizations for 50D version of benchmarks ($f_{{15}}-f_{{27}})$

Table 8 Statistical results of the optimizations for 50D version of benchmarks ($f_{{1}}-f_{{ 14}}$)

Table 9 Statistical results of the optimizations for 50D version of benchmarks ($f_{{15}}-f_{{ 27}}$)

Tables 8 and 9 list the statistical results obtained by the rival techniques with chaotically encoded AGS mutation operators for the 50D version of the considered benchmark problems. One of the general observations is that embedding the chaotic maps into the structure of AGS mutation further improves the performance of CEAs as compared to those using the chaotic maps in their HX crossover operator. Indeed, for most of the benchmarks, the obtained mean values are less than those reported in Tables 6 and 7. It can be also observed that for this case, the best performance belongs to the Gauss–Mouse and logistic maps. The piecewise and Liebovitch maps also have acceptable performances as compared to the other maps.

By comparing the results of mutation and crossover experiments, it can be realized that the sinusoidal map which worked well for the crossover operator cannot provide promising results for the mutation operator. This brings us to the conclusion that, at least for the medium scale benchmarks, the logistic map can afford relatively better solutions for the both mutation and crossover experiments. The robustness criterion is the other important element which should be analyzed. Taking the std. values into account, it can be seen that in most of the cases for both mutation and crossover experiments, the robustness of all versions of CEAs is really close. However, it sounds that the circle, Gauss–Mouse and sinusoidal versions of CEAs can afford much more promising outcomes in terms of the robustness metric. By taking the characteristics of the chaotic maps into account, it can be inferred that the logistic, sinusoidal, and Gauss–Mouse chaotic maps are not only able to effectively improve the performance of the standard EA, but also can generate random deterministic chaotic sequences with a low computational budget (as their mathematical formulation is really straight forward).

By comparing the results of CEAs with those obtained by the standard EAs, it can be seen that embedding chaotic sequences into the structure of EA can effectively improve its accuracy and robustness. This fact can be concluded by taking the mean performance into account. As seen, it is just for $f_{{24}}$ benchmark problem that the EA outperforms its chaotic embedded counterpart. Besides, for the most of the benchmark problems, the robustness of CEAs is really higher than the standard EA. Such observations augur the remarkable improvements afforded by embedding chaos into the structure of the baseline EA, at least for the 50D benchmark problems.

4.2.1.2. Chaotic crossover and mutation: semi large scale benchmarks

At the second step of the experiment, the 100D versions of the benchmark problems are considered for evaluating the performance of EAs with chaotic crossover and mutation operators. This allows us realize whether the same observations are valid when the dimensionalities of the landscapes of benchmark functions are increased. To be more to the point, considering a higher dimension of benchmark problems yield some results regarding the scalability of CEAs.

Tables 10 and 11 summarize the statistical results of numerical experiments for the rival techniques with chaotically encoded HX operators. Interestingly, for the 100D problems, the best performance belongs to the sinusoidal version of CEA. It seems that the sinusoidal map can be neatly combined with the EA so that the exploration/exploitation features remain qualified for solving semi large-scale optimization problems.

Table 10 Statistical results of the optimizations for 100D version of benchmarks ($f_{{1}}-f_{{14}})$

Table 11 Statistical results of the optimizations for 100D version of benchmarks ($f_{{15}}-f_{{ 27}})$

Tables 12 and 13 list the obtained statistical results for the rival techniques with chaotically encoded AGS operators. Once more, it can be seen that the solutions obtained by the EAs with chaotically encoded AGS operators are more qualified than those of the crossover experiments. This, in turn, endorses the fact that the EAs with chaotic mutation operator can outperform the EAs with chaotically encoded crossovers even when the dimensionality of the benchmarks increases. It is interesting that for most of the cases, the best performance belongs to the mutation operator with Gauss–Mouse chaotic map. It can be also seen that for some of the benchmarks, the Chebyshev, circle and piecewise maps show acceptable performances. Once more, the results indicate that the sinusoidal map is best suited to be combined with the crossover operator and the Gauss–Mouse map is the fittest one for the mutation operator.

Table 12 Statistical results of the optimizations for 100D version of benchmarks ($f_{{1}}-f_{{14}})$

Table 13 Statistical results of the optimizations for 100D version of benchmarks ($f_{{15}}-f_{{ 27}})$

As a general remark, it can be inferred that the results of the other CEAs are not as promising as those obtained in the 50D experiments. Apparently, except the sinusoidal and Gauss–Mouse CEAs, the other CEAs can outperform the other optimizers at most for one time. However, the standard EA outperforms its chaotic counterparts for the $f_{{7}}$ and $f_{{23}}$ benchmark problems for the crossover experiments and the $f_{{21}}$ benchmark for the mutation experiment. This spontaneously implies that the chaotic maps (except the sinusoidal for crossover and the Gauss–Mouse for mutation) could not retain their acceptable performance when the dimensionality of the benchmarks increases. However, it is worth mentioning that their performance is still fine as compared to the standard EA. By considering the results of the standard deviation, it can be concluded that the robustness of the standard EA, sinusoidal, tent, circle and Leibovitch CEAs is acceptable for this experiment. Once more, it has been observed that the chaotic maps are not only able to improve the accuracy of the standard EA, but also can retain their robustness at a standard level.

4.2.1.3. Chaotic crossover and mutation: large scale benchmarks

As a final experiment, the rival methods are exposed to a very demanding and large-scale version of the considered benchmark problems (200D version). This final numerical test helps us to make some firm decisions regarding the scalability of CEAs as well as their accuracy when facing to large-scale multimodal problems. The results of the experiment for the CEAs with chaotically encoded crossover operators are presented in Tables 14 and 15. Once more, the sinusoidal CEA shows an explicit domination over the other optimizers. Such a fact demonstrates the high potential of the sinusoidal CEA for handling large-scale optimization problems. However, it seems that for some of the problems, other versions of the CEAs, i.e. Leibovitch, and sine CEAs, can yield acceptable results as well. This is while such an observation was not valid for 100D benchmarks. This brings us to the conclusion that the performance of CEA with sinusoidal crossover shows a slight degeneration for the 200D problems.

Table 14 Statistical results of the optimizations for 200D version of benchmarks ($f_{{1}}-f_{{14}})$

Table 15 Statistical results of the optimizations for 200D version of benchmarks ($f_{{15}}-f_{{27}}$)

Tables 16 and 17 list the simulation results for the CEAs with chaotically encoded mutation operators. An interesting observation pertaining to this set of the experiments is that most of the rival techniques could show acceptable results, at least, for one of the benchmark problems. However, the Gauss–Mouse map is still the most dominant chaotic sequence at the heart of mutation operator. For this experiment, the relatively same observation is valid. It can be seen that the standard EA preserves its acceptable performance while the EAs with chaotic mutation could not keep their performance by increasing the dimensionality of benchmark problems. For this set of the experiments, the standard EA retains its quality as it outperforms its chaotic counterparts for two of the benchmark problems. Based on such facts, it can be concluded that embedding the chaotic maps within the algorithmic functioning of EAs makes them very sensible.

Table 16 Statistical results of the optimizations for 200D version of benchmarks ($f_{{1}}-f_{{14}})$

Table 17 Statistical results of the optimizations for 200D version of benchmarks ($f_{{15}}-f_{{27}})$

Obviously, some types of chaotic maps improve the performance of the standard EA while some other types undermine its performance significantly. Hence, the selection of a suitable chaotic map is really important. The same conclusion is valid in view of the robustness capability of the rival techniques. Among the 27 problems, for both of the experiments, the standard EA shows a very acceptable rate of the robustness for 18 problems. For these cases, only a few types of CEAs can show comparative robustness. However, in the case of $f_{{11}}, f_{{12}}, f_{{16}}, f_{{ 17}}, f_{{18}}, f_{{19}}, f_{{20}}, f_{{23}}$ and $f_{{26}}$ benchmarks, the robustness of the most of the CEAs are really higher than the standard EA.

4.2.1.4. Real-time evolution and scalability results

Figures 4 and 5 indicate the real-time mean performance of the rival techniques for optimizations of the 200D benchmarks over 1000 iterations, for crossover tests. This figure lets us evaluate the both real-time evolution and accuracy of the algorithms. As it can be seen, for most of the cases, the sinusoidal CEA shows a fast convergence behavior. Besides, except $f_{{3}}, f_{{13}}, f_{{14}}, f_{{23}}, f_{{24}}$ benchmarks, the dominancy/eligibility of the sinusoidal CEA over the other techniques is really obvious. On contrary to some types of metaheuristics which focus on the exploration at the early iterations and then shift to the exploitation, the implemented CEAs try to have a balance between the exploration and exploitation capabilities. Apparently, for most of the benchmark problems, a permanent gradual evolution is observed for the whole optimization period, and also, a smooth evolution towards the global solution can be recognized. Such trait of the designed CEAs is very advantageous as the gradual evolution ensures that the optimizer does not trap into a local pitfall, and thus, an unacceptable premature convergence is prevented.

Fig. 4

Real-time mean performances of the rival techniques for optimization of 200D benchmark problems over 1000 iterations ($f_{{1}}-f_{{12}})$

Fig. 5

Real-time mean performances of the rival techniques for optimization of 200D benchmark problems over 1000 iterations ($f_{{13}}-f_{{27}})$

To evaluate the overall performance of the rival techniques, the bar diagrams of the mean performances for all of the conducted experiments, including the both crossover and mutation tests, are provided in Figs. 6 and 7. As it can be seen, for the crossover tests, the sinusoidal CEA preserves its dominancy for the benchmarks of different dimensionalities (medium scale, semi large scale and large scale). This, in turn, endorses the scalability of this type of chaotic map. For the mutation tests, the results are a little bit different. It can be seen that the logistic CEA yields the superior performance for the medium scale version of benchmarks while the Gauss/mouse CEA surpasses the other rival methods for the semi large scale and large scale benchmarks. Furthermore, the results show that, for the large scale benchmarks, it is impossible to discriminate one of the approaches as the superior method. To be more to the point, it seems that the circle, logistic, and Gauss/mouse maps closely follow each other. For the mutation experiments, it can be interpreted that the performance of the methods are very sensible to the dimensionality (scale) of the benchmarks.

Fig. 6

Number of success of the standard EAs for crossover tests, a Chebyshev CEA, b circle CEA, c Gauss/mouse CEA, d Liebovitch CEA, e logistic CEA, f piecewise CEA, g sine CEA, h sinusoidal CEA, i tent CEA, j standard EA

Fig. 7

Number of success of the standard EAs for mutation tests, a Chebyshev CEA, b circle CEA, c Gauss/mouse CEA, d Liebovitch CEA, e logistic CEA, f piecewise CEA, g sine CEA, h sinusoidal CEA, i tent CEA, j standard EA

4.2.1.5. Time complexity analysis At this point, it can be concluded that the CEAs with sinusoidal crossover and Gauss–Mouse mutation can show very promising outcomes with respect to the accuracy, robustness and scalability. However, these features are not enough to substantiate the applicability of the mentioned CEAs for practical applications. Maybe, the computational power of those algorithms is guaranteed at the cost of a higher computational complexity. To be more to the point, without performing a time complexity analysis, we cannot claim that the CEAs with sinusoidal crossover and Gauss–Mouse mutation are the best choices among the existing rival methods. Thus, here, a time complexity analysis is performed to check whether the CEAs with sinusoidal crossover and Gauss–Mouse mutation are computationally efficient as well.

Table 18 lists the results of a time complexity analysis for $f_{{4}}$ benchmark problem in 3 different dimensions using both chaotic mutation and crossover operators. As it can be observed, the algorithmic complexities of the CEAs with sinusoidal map and the embedded crossover and the Gauss–Mouse mutation operators are quite acceptable. In most of the cases, the CEAs with sinusoidal crossover and Gauss–Mouse mutation operators are among the algorithms with the lowest computational complexities. The results of the complexity experiments confirm the high potential of the CEAs with sinusoidal crossover and Gauss–Mouse mutation operators for the optimization tasks.

Table 18 Time complexity analysis of the rival algorithms for $f_{{4}}$ benchmark function

4.2.1.6. Convergence analysis

At the final stage of the numerical experiments, the authors are to investigate the convergence behavior of the sinusoidal CEA. This helps the readers to discern whether embedding the sinusoidal chaos into the EA does not undermine its ability in balancing the exploration/exploitation over the optimization process. Previously, through a tentative experiment, it was indicated that the basic EA has the power of balancing the exploration/exploitation of the chromosomes. Here, the same experiment is conducted for sinusoidal CEA.

The convergence test is done for the 50D version of the benchmark problems with chaotic crossover operators to avoid any miss-judgment. Figure 8 reveals the convergence behavior of sinusoidal CEA for the considered problems. As it is obvious, the convergence behaviors of CEAs are very acceptable. It seems that the chaotic agents of the CEA are really capable of balancing their exploration/exploitation characteristics which results in a correct convergence at the end of the optimization procedure.

Fig. 8

Convergence behavior of the sinusoidal CEA for the benchmark problems

Fig. 9

Performances of the rival techniques for optimizing the operating parameters of Damavand power plant

4.2.2 Optimizing the operating parameters of Damavand power plant

At the second stage, the experiments are continued by applying the rival algorithms to a demanding real-life problem. In general, optimizing the operating parameters of a power plant can be really demanding. This is because of the steps required for implementing a proper objective function. The optimization of power plants is not possible unless several constraints and decision variables are taken into account. Besides, the objective function should be formulated by coupling several non-linear mathematical equations. This in turn produces a non-convex, highly multimodal and nonlinear objective function. Therefore, exposing the rival algorithms to such a problem can provide us with reliable feed-back regarding their potentials in handling demanding practical problems. In a recent study by the authors’ research group, a very large-scale power plant known as Damavand power plant has been analyzed based on different laws of thermodynamics (Mozaffari et al. 2012b). Damavand power plant is the biggest power plant in the middle-east sited in Iran consisting of 12 symmetric phases which work in parallel, and each phase hosts one steam turbine (ST) and two gas turbine (GT) power systems. This power plant plays an important role by supplying over 2300 MW electricity for industrial, agricultural, civil and domestic regions for various provinces of Iran. The stepwise and detailed procedures required for implementing the constraints and objective functions of the power plant are presented in (Mozaffari et al. 2012b). Therefore, here, for the sake of brevity, the detailed formulations required for simulating the power plant are not provided. To optimize the Damavand power plant, 9 decision variables, i.e. compressor pressure ratio ($r_{p}$), isentropic efficiency of compressor ($\eta _C$), isentropic efficiency of gas turbine ($\eta _T$), temperature of combustion products ($T_{{5}}$, $T_{{14}}$), temperatures of air preheater products entering the combustion engines ($T_{{3}}$, $T_{{12}}$), temperatures of compression products ($T_{{ 2}}$, $T_{{11}}$) air temperature ($T_{{1}}$, $T_{{ 10}}$), air mass flow rate ($m_{a}$) and fuel mass flow rate ($m_{f}$), should be considered. Besides, to obtain practical results, a set of nonlinear constraints should be devised [for more information please see (Mozaffari et al. 2012b)]. The optimal design of operating parameters is not possible unless two conflicting objective functions, i.e. maximizing the power output (energetic efficiency) and minimizing the total cost, are taken into account. The mathematical formulation required for implementing these two objective functions are given in the online supplementary file. Here, the concept of self-adaptive penalty function (SAPF) is used to equalize the impact of constraints in the objective function (Tessema 2006). Therefore, all of the rival techniques should optimize a single objective function which always yields the normalized objective values within the range of unity. Considering the SAPF strategy, the objective function can be formulated as:

Table 19 Obtained results of the power plant optimization problem

$$\begin{aligned} F_{\textit{SAPF}} (X)=-f_1 (X)+10^{-6}f_2 (X)+\frac{1}{23}\sum _{j=1}^{23} {\frac{c_j (X)}{c\;\max _j }} \end{aligned}$$

(15)

The mathematical procedures which yield the above function are given in the online supplementary file. Figure 9 indicates the performance of the rival techniques for optimizing the operating parameters of Damavand power plant. To avoid any miss-judgment, all of the rival metaheuristics start the optimization with the same initial population. As it can be seen, sinusoidal CEA converges to a more qualified solution. It is worth noting that the sinusoidal CEA is the only algorithm which can neatly balance its exploration/exploitation capabilities. Apparently, after the iteration of 560, this algorithm fosters its exploitation capability and therefore, escapes from the local pitfalls and finally converges to the most optimum solution. The numerical results including the values of the decision variables and the corresponding objective values are listed in Table 19. Obviously, the sinusoidal CEA suggests a vector of parameters which can consequently suggest an acceptable rate of energetic efficiency at a logical amount of cost.

5 Conclusions

In this research, the authors proposed a rigor test bed to effectively study the impact of chaotic maps into the algorithmic functioning of evolutionary algorithms (EAs). The experiments were composed of two different phases. At the first stage, several benchmark problems in medium, semi-large and large scale dimensions were utilized to investigate the convergence, scalability, accuracy and robustness of different versions of chaotic EAs (CEAs). Besides, the exploration/exploitation characteristics of the most successful CEA were evaluated empirically. At the next stage, a constraint real-life engineering problem was used to find out whether the derived conclusions are valid for practical problems. Based on the experiments, the following remarks were concluded:

• (1) It was observed that the proposed boundary constraint handling technique (BCHT) can be reliably used within the structure of CEAs to direct the infeasible solutions towards feasible regions in the solution domain.

• (2) By exposing the rival techniques to the various types of benchmarks with different scales, it was inferred that the CEAs with sinusoidal crossover and with Gauss–Mouse mutation can show very acceptable results in terms of the robustness, convergence and accuracy. Besides, it was observed that this approach could retain its acceptable quality during the optimization, and also, its performance did not degrade by increasing the dimensionality of the problems.

• (3) Another important observation is that CEAs are not only capable of improving the accuracy of standard EA (because of their chaotic exploitation instinct) but also can retain an acceptable amount of robustness over the process. This fact was demonstrated in the both stages of the experiments.

• (4) Through the conducted complexity analysis, it was revealed that embedding the chaos into the algorithmic functioning of EAs does not increase their computational complexity. Also, it was observed that the CEAs with sinusoidal crossover and with the Gauss–Mouse mutation (the most successful CEA) can show a similar convergence behavior as compared to the standard EA.

In the future, the authors will design an ensemble optimization frame based on the integration of different chaotic CEAs to find out whether it can improve the performance of single chaotic based metaheuristics.

Appendix A: Benchmark problems

See Table 20.

Table 20 Characteristics of the benchmark problems