1 Introduction

Fluoride is an important constituent in groundwater because, among other things, it is required ..... for the healthy growth of bones and teeth in human beings (Asghari Moghaddam and Fijani 2008; Rafique et al. 2008). However, long-term intake of high doses of fluoride can have adverse effects on human health and result in fluorosis, a bone disorder (Cerklewski 1997; Barbier et al. 2010; Patel et al. 2014). The permissible limit for fluoride concentration in water is 1.5 mg/L according to the World Health Organization guidelines (WHO 2008). Groundwater contamination with fluoride is a serious worldwide problem that has negative effects on public health; globally, around 200 million people from 25 nations are exposed to grave health risks because of high amounts of fluoride in groundwater (Ayoob and Gupta 2006).

Fluoride occurs in almost all natural waters from trace concentrations to as high as 15,000 mg/L in mine water from the Kola Peninsula (Kraynov et al. 1969; Valenzuela-Vasquez et al. 2006). The natural concentration of fluoride in groundwater is governed principally by climate, composition of the host rock, and hydrogeology (Gupta et al. 2006; Valenzuela-Vasquez et al. 2006). High concentrations of fluoride in the groundwater are also contributed by anthropogenic activities such as the use of phosphatic fertilizers, pesticides, sewage and sludge, as well as depletion of the groundwater table (EPA 1997; Ramanaiah et al. 2006; Kundu and Mandal 2009). Many factors can control the release of fluoride to groundwater, including the mineralogy of the rock (e.g. granite rocks), hydrogeological conditions, groundwater chemistry (e.g. presence or absence of ion complexes, precipitation of ions and colloids, and anion exchange capacity of aquifer materials), the interaction period of groundwater with a particular formation, and the dissolution kinetics of fluoride-bearing minerals (Patel et al. 2014).

Groundwater quality modeling enables the identification of groundwater quality trends and their influencing variables, which are important components of water resources management. In the last decades, numerically and physically based groundwater models were the most common groundwater modeling tools (Javadi and Al-Najjar 2007). However, the performance of these models depends on an adequate understanding of the hydrological behavior of the process in question, and the availability of detailed data on groundwater system properties. These two conditions are often absent, especially in developing regions, resulting in unsatisfactory model performance (Coppola et al. 2005; Alagha et al. 2014).

Numerical models are employed to simulate hydrological and hydrogeological problems, but these models are less user-friendly and lack knowledge transfer in model interpretation, which is leading to a large gap between model developers and practitioners. The advancement in Artificial Intelligence (AI) over the past two decades makes it possible to integrate these technologies into numerical modeling systems in order to bridge the gaps (Chau 2006). Also, AI techniques have rendered it possible to simulate human problem—solving expertise in this narrowly—defined domain by integrating descriptive knowledge, procedural knowledge and reasoning knowledge (Mirabbasi 2015; Chau 2006).

Recently, AI models have been used to predict groundwater contamination. For instance, Chowdhury et al. (2010) developed artificial neural network (ANN) models for spatial mapping of arsenic contamination of groundwater in Bangladesh. Alagha et al. (2014) applied AI models such as ANN and support vector machine (SVM) to predict nitrate contamination of the Gaza coastal aquifer. Cho et al. (2011) developed an ANN model for prediction of contamination potential of groundwater arsenic in Cambodia, Laos and Thailand. Al-Mahallawi et al. (2012) used neural networks for the prediction of nitrate groundwater contamination in rural and agricultural areas. Sahoo et al. (2006) applied ANN to assess pesticide contamination of shallow groundwater in Illinois, USA. Sirat (2013) applied backpropagation neural networks (BP-NN) to data taken from 1302 domestic and rural hydraulic wells in the Mid-continent of the USA, including Illinois, Iowa and 12 other states to predict contamination of groundwater with pesticides.

Some researchers have used AI models for fluoride contamination of groundwater. For example, Dar et al. (2012) applied ANNs for fluoride contamination of the Mamundiyar basin, India. Amini et al. (2009) used several hybrid methods by combining two classification techniques, classification tree and knowledge based clustering, and three predictive techniques (multiple regression, logistic regression and adaptive neuro-fuzzy inference system) for groundwater fluoride modeling using a global fluoride database. Nadiri et al. (2013) used a supervised committee machine artificial intelligence model for predicting groundwater fluoride concentrations of the Maku area. Chitsazan et al. (2016) applied hierarchical Bayesian model averaging to combine the predictions of multiple artificial neural networks (ANNs) for fluoride contamination of the Maku area. As can be seen, AI models are generally able to predict the contamination of groundwater. However, to date, no research has been published that uses an extreme learning machine (ELM) model to predict groundwater quality, especially groundwater contamination. For other applications, Zhang et al. (2015) proposed a self-adaptive differential evolution extreme learning machine (SADE-ELM) model for classification of water quality parameters in the Huaihe River, China. Imen (2015) applied artificial neural network, ELM and genetic programming for the long-term observation of total organic carbon (TOC) concentrations throughout Lake Mead in the United States. Dongwen (2013) used ELM to forecast total phosphorous and total nitrogen of a reservoir in Yunnan province, China.

Earlier studies in the Maku area (Asghari Moghaddam and Fijani 2008, 2009; Asghari Moghaddam et al. 2005, 2007) have indicated high concentrations of fluoride in the groundwater. The main objective of the present study is to investigate the ability of an extreme learning machine to predict the fluoride contamination of groundwater in the Maku area of northwest Iran. The usefulness of the ELM model was verified against the multilayer perceptron and support vector machine (SVM) models.

2 Methodology

2.1 Multilayer perceptron

A detailed description of ANN models is given in Haykin (Haykin 1999). However, in brief, ANNs consist of an input layer of source nodes, one or more hidden layers of computation nodes or neurons and one output layer. The input layer nodes distribute the input information to the next layer (i.e. the first hidden layer). The hidden and output layer nodes process all incoming signals by applying factors to them (termed weights). Each layer also has an additional element called a bias node. Bias nodes simply output a signal to the nodes of the current layer. All inputs to a node are weighted, combined and then processed through a transfer function that controls the strength of the signal released through the node’s output connections. Some of the most popular transfer (activation) functions are Sigmoid, Gaussian, Hyperbolic, Tangent and Hyperbolic Secant (Malekmohammadi et al. 2011; Barzegar et al. 2016c).

The proposed method for the ANN to be used in this study was the Multilayer Perceptron, in which the neurons are disposed in successive layers (feed-forward). Backpropagation is the most popular algorithm used for training a feed-forward ANN (Jain and Srinivasulu 2004; Fernando and Shamseldin 2009; Goyal et al. 2014). The structure of the MLP neural network model is shown in Fig. 1. In this figure, i, j and k denote input layer, hidden layer and output layer neurons, respectively, and w is the applied weight by the neuron. The explicit expression for an output value of a three-layered MLP is given by Belayneh and Adamowski (2012), Nourani et al. (2013), Barzegar and Asghari Moghaddam (2016) and Barzegar et al. (2016b, c):

Fig. 1
figure 1

The structure of the MLP model

Full size image
$$y_{k} = f_{^\circ } \left[ {\mathop \sum \limits_{i = 1}^{{M_{N} }} W_{kj} \cdot f_{h} \left( {\mathop \sum \limits_{i = 1}^{{N_{N} }} W_{ji} X_{i} + W_{j0} } \right) + W_{k0} } \right]$$
(1)

where W ji is a weight in the hidden layer connecting the ith neuron in the input layer and the jth neuron in the hidden layer, W j0 is the bias for the jth hidden neuron, f h is the activation function of the hidden neuron, W kj is a weight in the output layer connecting the jth neuron in the hidden layer and the kth neuron in the output layer, W k0 is the bias for the kth output neuron, f o is the activation function for the output neuron, X i is the ith input variable for the input layer and y j is the computed output variable. N N and M N are the number of the neurons in the input and hidden layers, respectively. The gradient descent, conjugate gradient, Levenberg–Marquardt, and other learning algorithms can be used for training the MLP model (Kisi et al. 2015; Barzegar and Asghari Moghaddam 2016).

2.2 Support vector machine

The support vector machine (SVM) is a popular estimator introduced by Vapnik (1995). Based on Vapnik’s theory, the SVM functions are offered by Eqs. (2–6), where R = {x i , d i } n i is used for assuming a set of data points, the input space vector of the data sample is shown by x i , and the desired value and data size are defined as d i and n, respectively. The procedure of an SVM regression estimator (f) is written as (Zaji et al. 2016; Amirmojahedi et al. 2016; Mojumder et al. 2016; Ebtehaj et al. 2016; Al-Shammari et al. Al-Shammari et al. 2016; Shamshirband et al. 2016):

$$f\left( x \right) = w\varphi \left( x \right) + b$$
(2)
$$R_{\text{SVMs}} \left( C \right) = \frac{1}{2}||w^{2} || + C\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} L\left( {x_{i} ,d_{i} } \right)$$
(3)

where φ(x) is a high dimensional space feature that maps the input space vector x, w is a weight vector, b is a bias and \(C\frac{1}{n}\sum\nolimits_{i = 1}^{n} {L\left( {x_{i} ,d_{i} } \right)}\) represents the empirical error. The parameters w and b can be estimated with a regularized risk minimization function after introducing positive slack variables \(\xi_{i }\) and \(\xi_{i}^{{^{*} }}\), which represent upper and lower excess deviation, respectively.

$${\text{Minimize}} \quad R_{{{\text{SVM}}s}} \left( {w,\xi^{*} } \right) = \frac{1}{2}||w^{2} || + C\mathop \sum \limits_{i = 1}^{n} \left( {\xi_{i } - \xi_{i}^{*} } \right)$$
(4)
$${\text{Subject to }}\left\{ {\begin{array}{l} {d_{i} - w\varphi \left( {x_{i} } \right) + b_{i} \le \varepsilon + \xi_{i } } \\ {w\varphi \left( {x_{i} } \right) + b_{i} - d_{i} \le \varepsilon + \xi_{i}^{*} } \\ {\xi_{i } , \xi_{i}^{*} \ge 0,\quad i = 1, \ldots ,l } \\ \end{array} } \right.$$
(5)

where \(\frac{1}{2}||w^{2} ||\) is the regularization term, C is the error penalty factor used to regulate the difference between the regularization term and empirical error, ε is the loss function, which equates to the approximation accuracy of the training data point and l is the number of elements in the training data set.

Equation (2) can be resolved by proposing a Lagrange multiplier and optimality constraints, therefore obtaining a generic function given by Eq. (6):

$$f\left( {x, \beta_{i} \beta_{i}^{*} } \right) = \mathop \sum \limits_{i = 1}^{n} \left( {\beta_{i} - \beta_{i}^{*} } \right)K\left( {x_{i} ,x_{j} } \right) + b$$
(6)

where K(x i , x j ) is recognized as the kernel function and it is equal to \(K\left( {x_{i} ,x_{j} } \right) = \varphi \left( {x_{i} } \right)\varphi \left( {x_{j} } \right)\). The latter term is an inner product of the two vectors, x i and x j , in the feature space φ(x i ) and φ(x j ), respectively. This inner product space is a vector space that has an additional structure termed as the inner product. This relates each pair of vectors with a scalar quantity known as the inner product of the vectors. The structure of the SVM model is shown in Fig. 2.

Fig. 2
figure 2

The structure of the SVM model

Full size image

In this study, a radial basis function (RBF) \(K\left( {x_{i} ,x_{j} } \right) = exp\left( { - \gamma ||x_{i} - x_{j} ||} \right), \gamma > 0, \gamma = 1/(2\sigma^{2} )\), linear function \(K\left( {x_{i} ,x_{j} } \right) = x_{i} x_{j}\), polynomial basis function \(K\left( {x_{i} ,x_{j} } \right) = \left[ {\left( {x_{i} x_{j} } \right) + c} \right]^{d}\)(c ≥ 0, d is the degree of the polynomial kernel), and sigmoid function \(K\left( {x_{i} ,x_{j} } \right) = tanh\left( {\gamma x_{i} x_{j} + c} \right) \left( {\gamma > 0, c \ge 0 } \right)\) were applied as the kernel functions.

2.3 Extreme learning machine

Extreme learning machine (ELM) was first proposed by Huang et al. (2004) as a fast learning technique with high generalization performance that uses single-hidden layer (feature mapping) feed-forward neural networks (SLFNs) (Huang et al. 2004, 2006; Abdullah et al. 2015). The ELM chooses the input weights randomly and determines the output weights of the SLFN analytically (Aghbashlo et al. 2016). It is capable of determining all the network parameters analytically, which prevents trivial human intervention (Shamshirband et al. 2016). The main objectives of the ELM are to reach the smallest training errors, the smallest norm of output weights, and good generalization performance (Huang et al. 2006).

The network structure of the ELM model is shown in Fig. 3. For N different training samples \(\left( {x_{i} ,y_{i} } \right) \in R^{n} \times R^{m} \left( {i = 1,2,3, \ldots ,n} \right)\), the number of hidden nodes is L. The SLFN model, which has the activation function f(x), can be expressed as (Ding et al. 2016; Liu et al. 2016; Aghbashlo et al. 2016):

$$\mathop \sum \limits_{i = 1}^{L} \beta_{i} f_{i} \left( {x_{j} } \right) = \sum\limits_{i = 1}^{{\widetilde{L}}} {\beta_{i} f} \left( {a_{i} \cdot b_{i} \cdot x} \right),\quad j = 1, \ldots ,N$$
(7)

where \(a_{i} = \left[ {a_{i1} , a_{i2} , \ldots , a_{in} } \right]^{T}\) is the input weight vector connected to the hidden layer node, i, b i is the bias value of hidden layer nodes, \(\beta_{i} = \left[ {\beta_{i1} , \beta_{i2} , \ldots , \beta_{im} } \right]^{T}\) are the output weight vectors connected to the hidden layer node, and i, a i , x j is the inner product of a i · x j ,.

Fig. 3
figure 3

The structure of the ELM model

Full size image

Equation (7) can be rewritten compactly as follows:

$$\mathop \sum \limits_{i = 1}^{L} \beta_{i} f_{i} \left( {x_{j} } \right) = H\beta$$
(8)
$$H = \left[ {\begin{array}{*{20}c} {f\left( {a_{1} \cdot x_{1} \cdot b_{1} } \right)} & \ldots & {f\left( {a_{L} \cdot x_{1} \cdot b_{L} } \right)} \\ \vdots & \ldots & \vdots \\ {f\left( {a_{1} \cdot x_{N} \cdot b_{1} } \right)} & \ldots & {f\left( {a_{L} \cdot x_{N} \cdot b_{L} } \right)} \\ \end{array} } \right]_{N \times \,\,L}$$
(9)
$$\beta = \left[ {\begin{array}{*{20}c} {\beta_{1}^{T} } \\ \vdots \\ {\beta_{L}^{T} } \\ \end{array} } \right]_{L \times m} T = \left[ {\begin{array}{*{20}c} {y_{1}^{T} } \\ \vdots \\ {y_{L}^{T} } \\ \end{array} } \right]_{N \times m}$$
(10)

where H is the output matrix of the hidden layer,\(\beta\) is the output weight matrix, and T is the label matrix.

Not all parameters need to be adjusted when the excitation function f(x) is infinitely differentiable at any interval. At the start of the training process, SLFNs are assigned random values to the input weight a and hidden layer node bias b. When input weights and hidden layer node biases are determined by random assignment methods, the hidden layer output matrix H from the input samples can be obtained. Thus, training SLFNs are transformed into solving least square solutions.

By introducing regularization theory into the ELM model, the cost function can be expressed as:

$$\hbox{min} L_{\text{ELM}} = \frac{1}{2}||\beta ||^{2} + \frac{C}{2}||T - H\beta ||^{2}$$
(11)

The least squares solution of Eq. (11) is:

$$V - CH^{T} \left( {T - H\beta } \right) = 0$$
(12)

When the number of training samples is more than the number of hidden layer nodes,

$$\beta = \left( {\frac{1}{C} + H^{T} H} \right)^{ - 1} H^{T} T$$
(13)

When the number of training samples is less than the number of hidden layer nodes,

$$\beta = H^{T} \left( {\frac{1}{C} + HH^{T} } \right)^{ - 1} T$$
(14)

When the number of hidden layer units is large enough in the ELM algorithm, the regression accuracy of the algorithm is always stable.

In this study, the activation functions were defined by sine (f sin ), sig (f sig ), hard-limit (f hardlim ), radial basis (f radbas ) and triangular basis (f tribas ), as in the following equations:

$$f_{sin} = \left( {a,b,x} \right) = \sin \left( {ax + b} \right)$$
(15)
$$f_{sig} = \left( {a,b,x} \right) = \frac{1}{{1 + { \exp }( - \left( {ax + b} \right))}}$$
(16)
$$f_{hardlim} \left( {a,b,x} \right) = \left\{ {\frac{1, \,if\,\,ax + b < 0}{0,\quad otherwise}} \right.$$
(17)
$$f_{radbas} \left( {a,b,x} \right) = exp\left( { - \left( {ax + b} \right)^{2} } \right)$$
(18)
$$f_{tribas} \left( {a,b,x} \right) = \left\{ {\frac{{1 - \left| {ax + b} \right|, if - 1 \le (ax + b) \le 1}}{0,\quad otherwise}} \right.$$
(19)

2.4 Performance evaluation of the models

The performance of the developed models for training and testing sets was evaluated by following measures of goodness-of-fit: the coefficient of determination (R 2), Nash–Sutcliffe efficiency coefficient (NSC), root mean squared error (RMSE) and mean absolute bias error (MABE), shown in Eqs. (20–23), respectively. R 2 expresses the degree of the relation when two variables are linearly related. If R 2 is close to 1, there is good correlation between the observed and predicted values. The Nash–Sutcliffe coefficient of efficiency (NSC), an indicator of the model fit, is a normalized measure (−∞ to 1) that compares the mean square error generated by a particular model simulation to the variance of the target output sequence. An NSC value of 1 indicates perfect model performance, an NSC value of zero indicates that the model is, on average, performing only as well as the use of the mean target value as prediction, and an NSC < 0 indicates an altogether questionable choice of the model (Nash and Sutcliffe 1970). A perfect fit between observed and predicted values would have an RMSE of 0.

$$R^{2} = \left[ {\mathop \sum \limits_{i = 1}^{N} \left( {P_{i} - \bar{P}} \right)\left( {O_{i} - \bar{O}} \right)} \right]^{2} \left[ {\mathop \sum \limits_{i = 1}^{N} \left( {P_{i} - \bar{P}} \right)^{2} \left( {O_{i} - \bar{O}} \right)^{2} } \right]^{ - 1}$$
(20)
$${\text{NSC}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - P_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - \bar{O}} \right)^{2} }}$$
(21)
$${\text{RMSE}} = \left[ {N^{ - 1} \mathop \sum \limits_{i = 1}^{N} \left( {P_{i} - O_{i} } \right)^{2} } \right]^{0.5}$$
(22)
$${\text{MABE}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {P_{i} - O_{i} } \right|$$
(23)

where N is the number of observations, P i is the predicted value, O i is the observed data, and \(\bar{P}\) and \(\bar{O}\) are the mean values for P i and O i , respectively.

3 Study area and data

3.1 Study area

The Maku area is located in the north of West Azerbaijan province in the northwest of Iran. It lies between 44°21′ and 45°10′ east longitude and 35°10′ and 39°34′ north latitude, covering an area of approximately 1600 km2. The study area is covered up to 400 km2 by basaltic lavas. It is bounded in the west by Turkey and in the east by the Aras River, as shown in Fig. 4. The most important cities in the area are Maku, Poldasht and Bazargan. The climate of the area is cold and arid. The annual average precipitation is about 300 mm and the maximum and minimum precipitation occur in May and September, respectively (Asghari Moghaddam and Fijani 2009). Mean daily temperatures at the Maku Synoptic Station (1411 m amsl) vary from −7.4 °C in January up to 17.2 °C in July, with an annual average of 10.4 °C (Asghari Moghaddam and Fijani 2009). The main rivers in the study area are Sari Su and Zangmar, which flow from west to east.

Fig. 4
figure 4

Location of the study area and sampling points

Full size image

The Maku area includes formations of Precambrian to Quaternary ages. The major formation in the area is lava, which mainly consists of basaltic rocks. The great extent of young lava in the extreme northwest of Iran is attributable to the volcanic activity of Ararat in Turkey (Asghari Moghaddam and Fijani 2008). Young alluvium clay to gravel sheets, spreading as fan deposits from the mountain flanks and flood plains, are the recent unconsolidated materials filling the lowlands and river beds (Asghari Moghaddam and Fijani 2007, 2008). The Maku area aquifers have a range of lithologies, including basaltic-alluvium, alluvium and karstified limestone. However, the basaltic-alluvium aquifer forms the main water-bearing layers of the area (Asghari Moghaddam and Fijani 2009). Detailed discussion regarding the geology, hydrogeology and hydrochemistry of the Maku area is presented in Asghari Moghaddam et al. (2005), Fijani (2007) and Asghari Moghaddam and Fijani (2007, 2008, 2009).

Groundwater is the main water source used for various purposes such as drinking, agriculture and industry in the study area. Fluoride contamination is considered to be the main water quality problem in the Maku area, where the average concentration of fluoride is 2.85 mg/L (Asghari Moghaddam and Fijani 2008, 2009). The volcanic rocks in the study area contain silicate minerals, apatite and fluorapatite, and the weathering of these minerals is likely to be the main source of fluoride in the groundwater of the study area (Asghari Moghaddam et al. 2005; Fijani 2007).

3.2 Data collection and pre-processing

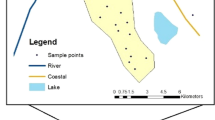
In this study, the chemical analyses of 143 water samples were used. Water was collected from 39 sampling sites over water sources (wells, springs, qanats, etc.) in a 5-year period, from 2004 to 2008. The locations of the sampling sites are shown in Fig. 4. The largest and smallest data sets were in August 2006 (38 samples) and July 2004 (8 samples), respectively. The water samples were analyzed in the Hydrogeology Laboratory of the University of Tabriz. The electrical conductivity (EC) and pH were measured in situ in the field. Fluoride concentration in water samples was determined using the method of SPADNS—using a Spectro 40 spectrophotometer at 570 nm—and the other ions (Ca2+, Mg2+, Na+, K+, HCO3 −, CO3 2−, SO4 2− and Cl−) were determined by standard methods (American Public Health Association 1998). The accuracy of the water analysis was within the limit of ±5% according to the cation–anion balance (Domenico and Schwartz 1990). In this study complete hydrological data sets (e.g. groundwater flow and stream flow) were not available, except groundwater level, and there was no correlation between groundwater level and fluoride contamination. Therefore, this study may indicate the suitability of certain AI models for hydrological modeling, particularly in regions where detailed and complete data sets about hydrological processes are usually unavailable. For example, in this case study, there are many data sets of major ions, but the fluoride concentrations are not available for such data sets. Therefore, AI models can be used for prediction of the unavailable fluoride concentrations.

One of the most important steps in developing a prediction model is the selection of the input variables. For the selection of input variables, certain fluoride-related variables were chosen. For this purpose, principal component analysis (PCA) was used. PCA can be used to reduce the complexity of input variables when there are large volumes of information and better interpretation of variables is recommended (Noori et al. 2010, 2011). It can be seen from Table 1 that Na+, K+, Ca2+ and HCO3 − concentrations have the greatest effect on the first component (PC1). Therefore, these four variables were selected as inputs of the developed models. The high positive loading of the HCO3 − in PC1 could be due to the release of hydroxyl and bicarbonate ions simultaneously during the leaching and dissolution process of fluoride bearing minerals into the groundwater. Groundwater with high K+ and Na+ concentrations likely occurs as a result of silicate mineral hydrolysis of volcanic rocks as a source of fluoride in the study area. High concentrations of Na+ increase the solubility of the fluoride bearing minerals. Also, the presence of Na+, K+ and HCO3 − variables in PC1 could be an indication of ion-exchange and carbonate weathering. The negative loading of the Ca2+ reflects precipitation of fluorite (CaF2) mineral, due to the high solubility product of fluoride (Rafique et al. 2008).

Table 1 Principal component analysis (PCA) to determine the input variables
Full size table

Before developing the models, the data set values were normalized between 0.2 and 0.8, using Eq. (24):

$$Normalized\,X = C_{1} \frac{{X_{i} - X_{min} }}{{X_{max} - X_{min} }} + C_{2}$$
(24)

in which X max and X min are the maximum and minimum of the data sets. In the current study, the C 1and C 2 values were assigned as 0.6 and 0.2, respectively. Therefore, the data were normalized into the range [0.2, 0.8]. This normalization was employed following the suggestion of Cigizoglu (2003), who showed that scaling input data between 0.2 and 0.8 gives ANNs the flexibility to estimate beyond the training range.

To develop the MLP, SVM and ELM models, the cross-validation technique (Chang et al. 2013; Fijani et al. 2013; Barzegar et al. 2016b) was used to divide the data sets into training and testing sub sets. The data sets were divided into a training/validation set (80% of the data) and a testing set (the remaining 20% of the data). Statistical analysis of the training/validation and testing data sets are listed in Table 2.

Table 2 Statistical analysis of the training/validation and testing data sets
Full size table

4 Development of the models

4.1 MLP model

As previously mentioned, 80% of the data set was considered for training/validation and the remaining 20% for testing. For the MLP model, the training/validation set was further divided into 80% training and 20% validation, so overall, 64% of the data were used for training, 16% were used for validation, and 20% were used for testing.

The neural network training was implemented through the MATLAB Neural Network toolbox. In this study, the three-layered feed-forward neural network was trained with the Levenberg–Marquardt algorithm (TrainLM). This algorithm is a variation of Newton’s method and is designed to second-order training speed without having to compute the Hessian matrix (Adamowski and Sun 2010). Traditionally, the trial and error method is used to select the optimal number of hidden neurons (Belayneh et al. 2014, 2016; Adamowski and Sun 2010; Barzegar et al. 2016a, b). However, Wanas et al. (1998) and Mishra and Desai (2006) empirically considered equations log(N), where N is the number of training samples, and 2n + 1, where n is the number of input neurons to determine the number of hidden neurons. In this study, the optimal number of hidden neurons was determined to be between log (N) and (2n + 1). Two hidden neurons and nine hidden neurons were determined by using the Wanas et al. (1998) and Mishra and Desai (2006) methods, respectively; thereafter, the optimal number was chosen via trial and error. The number of neurons in the hidden layer was seven. The transfer function between layer one and layer two was TANSIG, while PURELIN was used for the last layer. Learning rates and momentum factors of 0.1 and 0.2, respectively, were chosen by trial and error. The magnitude of the gradient and the number of validation checks used to terminate network training are presented in Fig. 5a. At an epoch of 16 iterations, the gradient was 7.069 × 10−4, barely above the 1 × 10−4 threshold below which training will stop, and at six, the validation checks also indicated training should stop. The performance plot (Fig. 5b) shows the value of the function in terms of training, validation, and testing behaviors, versus the iteration number. The best validation performance was at epoch 10, based on a mean square error equal to 1.743 × 10−3. The MLP model was trained in 0.45 s. When the training of the model was completed, the testing data served as model input and fluoride concentration values were predicted.

Fig. 5
figure 5

Training state and performance of the developed MLP neural network model

Full size image

4.2 SVM model

In this study, DTREG (Data Regression) was utilized for the SVM modeling. The models were created by using the Epsilon-SVR kernel type. Both grid and pattern search—as well as tenfold cross-validation re-sampling methods—were employed to find optimal parameter values. During grid search, the program (DTREG) evaluates values of each parameter within the predefined search area. On the other hand, a pattern search (also known as a line search or compass search) starts from the centre of the search area and tries steps in both directions for each parameter. The centre of the search area is then moved to the new point if a better model fit is obtained. The process is repeated until the specified tolerance rate is reached (Sonebi et al. 2016; Al-Anazi and Gates 2010).

Model parameters such as C have a search range of 0.1–5000, kernel parameter γ of 0.001–50, and ε (Epsilon) of 0.001–100. By selecting the pattern search technique using 10 search intervals which would require 1000 model evaluations and 1e-008 tolerance for stopping the iterative optimization process and the optimal values through the grid search, we could create a fluoride prediction model with higher stability and lower RMSE. The optimal calibration constants and kernel parameters for developing SVM models are shown in Table 3. After constructing the SVM models, the testing data set was used for testing the models.

Table 3 Optimal training constants and kernel parameters for developing SVM models
Full size table

4.3 ELM model

The ELM models were developed in a MATLAB environment. Three layers were used to build the architecture for fluoride contamination prediction in designing the ELM. The number of neurons was 4 (input) for each of the developed ELM models. The ELM output layer had one neuron representing the predicted fluoride. The number of hidden nodes is changeable for better accuracy, and the number of hidden neurons was selected via a trial and error method. The number of neurons between 1 and 50 were tested in hidden layers of the ELM models. In each trial, the number of nodes in the hidden layer was increased gradually until the optimal nodes were reached. A taxonomy of activation functions was tried one-by-one, which included "sigmoid", "sine", "radial basis", "triangular basis" and "hard-limit". The optimal hidden neurons for different activation functions are listed in Table 4. After training the models, the testing data set was used to test the developed models.

Table 4 Optimal hidden neurons for developing ELM models
Full size table

5 Results

The performance of the MLP, SVM and ELM models for prediction of fluoride contamination in both training and testing stages is presented in Tables 5, 6 and 7, respectively. The statistical evaluation criteria revealed that all the models for the prediction of fluoride concentration yielded satisfactory results. Therefore, these models are acceptable—due to high R 2 and NSC values and low RMSE values—for predicting fluoride contamination in the Maku area. The values of R 2 and NSC which were close to unity, and fairly low RMSE and MABE in all the models—for both the training and testing sets—emphasized good generalization and predictive abilities of the three modeling approaches for the given data set. However, relatively lower prediction errors obtained by models in the training set as compared to the testing set indicated that these models exhibited relatively better generalization as compared to the predictions.

Table 5 Results of MLP model during training and testing
Full size table
Table 6 Results of SVM models for training and testing stages
Full size table
Table 7 Results of ELM models for training and testing stages
Full size table

Table 5 shows the statistical evaluation criteria of training and testing for the MLP model. The R 2, NSC, RMSE and MABE of the MLP model for the training data were 0.9191, 0.9179, 0.4914 (mg/L) and 0.3607 (mg/L), respectively; those for the testing data were 0.8152, 0.8019, 0.8232 (mg/L) and 0.6131 (mg/L), respectively. Figure 6a shows the comparison between the measured and predicted values of fluoride for the MLP model in the testing stage.

Fig. 6
figure 6

The performance of the a MLP, b SVM and c ELM models developed for prediction of fluoride concentration in the testing stage

Full size image

Table 6 shows a performance comparison of the different kernel functions used for SVM model development. The RBF and linear kernel functions showed the best and worst performance, respectively, among the utilized kernel functions for the SVM models. The R 2, NSC, RMSE and MABE for the linear-based SVM model for training data were 0.8721, 0.8885, 0.5925 (mg/L) and 0.4316 (mg/L), respectively, whereas those for the testing data were 0.8521, 0.7774, 0.8727 (mg/L) and 0.7124 (mg/L), respectively. In the training stage, the SVM model with the RBF kernel function resulted in an R2 of 0.9014, an NSC of 0.9122, an RMSE of 0.5082 (mg/L), and an MABE of 0.3146 (mg/L). However, for the testing data, the corresponding values were 0.8833, 0.8658, 0.6775 (mg/L) and 0.5596 (mg/L), respectively. The RBF kernel function significantly reduced the overall prediction errors. It was demonstrated that the radial basis kernel function (RBF) performed better than linear, sigmoid and polynomial kernel functions in terms of performance criteria. This result was confirmed by Rajasekaran et al. (2008), Yang et al. (2009), Wu and Wang (2009) and Amirmojahedi et al. (Amirmojahedi et al. 2016). Figure 6 shows a comparison between the measured and predicted values of the fluoride concentration for the SVM model with the RBF kernel function in the testing stage. The results show that the use of nonlinear kernel functions achieved better performance than the linear kernel.

Table 7 shows a comparison of the performance of the different activation functions utilized for ELM model development. The radial basis and hard-limit functions showed the best and worst performance among the activation functions used for ELM models, respectively. The R 2, NSC, RMSE and MABE for the hard-limit-based ELM model for training data were 0.913, 0.9126, 0.5069 and 0.3907 (mg/L), respectively, whereas those for the testing data were 0.901, 0.8863, 0.6236 and 0.4925 (mg/L), respectively. The radial basis-based ELM model resulted in an R 2 of 0.9453, NSC of 0.9449, RMSE of 0.4024 (mg/L), and MABE of 0.3157 (mg/L) for the training data and in an R 2 of 0.921, NSC of 0.9071, RMSE of 0.5638 (mg/L) and MABE of 0.4635 (mg/L) for the testing data. The performance of the ELM with the radial basis function for fluoride contamination prediction in the testing stage is shown in Fig. 6c. The results show that the ELM models performed better than MLP and SVM models for prediction of fluoride contamination. Empirical studies have shown that the generalization ability of ELM is better than that of SVM models (Huang et al. 2006, 2012; Fernandez-Delgado et al. 2014; Huang et al. 2014, 2015).

The ELM models had advantages in computation time in comparison with MLP and SVM models. It was observed that ELM models learned faster than the other models during model development trials while the SVM models had the highest computation time. As analyzed by Huang et al. (2015), the training of SVM is a quadratic programming problem, and thus, it requires high computational costs. In contrast, the parameters of the ELM hidden layer need not be adjusted and can be independent of the training data. Hence, the ELM model only computes the output weights analytically, and it has a much faster learning speed and lower computational complexity than SVM (Wang et al. 2015). The grid search was another reason for the high computation times of the SVM models because, by using this method, the model must be evaluated at many points within the grid for each parameter (Al-Anazi and Gates 2010).

6 Conclusions

This study investigated the ability of three different machine learning algorithms including MLP, SVM and ELM to predict the fluoride contamination of groundwater in the Maku area of northwest Iran. The results demonstrated that the ELM models outperformed the MLP and SVM models for prediction of fluoride contamination. This study found that the SVM model with the RBF kernel function outperformed the linear-, sigmoid- and polynomial kernel function-based models. The radial basis and hard-limit functions, among the utilized activation functions, showed the best and worst performance for ELM models, respectively. During model development trials, it was observed that ELM models learned faster than the other models while the SVM models had the highest computation time.