1 Introduction

Fire risk can be defined as a product of fire occurrence probability and expected impacts (Bachmann and Allgower 2001). An area can be considered to have high wildfire risk if the probability of fire is high and the expected impacts of fire are large. Furthermore, fires are getting larger, more destructive, and more economically expensive due to fuel accumulations, shifting land management practices, and climate change. Wildfires have negative effects on human life and health, human property and wellbeing, cultural and natural heritage, employment, recreation, economic and social infrastructures and activities. It is worth noting that some fire episodes have caused catastrophic damages including, loss of human lives and significant economic and environmental losses.

The European Mediterranean is a highly populated region. Approximately 65,000 fires occur in the European Mediterranean region every year. Wildfires destroy around 500,000 ha every year in the European Union, 0.7–1 million ha in the Mediterranean basin. This has a serious impact on the environment and on socio-economic activities, especially in southern Europe. Over 95 % of the fires in Europe are due to human causes. An analysis of fire causes show that the most common cause of fires comes from agricultural practices, followed by negligence and arson (Reus Dolz and Irastorza 2003). These wildfires are relatively frequent events with recurrence time of 23 years (Serra et al. 2012).

Wildfires also destroy biodiversity, increase desertification, affect air quality, the balance of greenhouse gases and water resources. During recent years the increasing extension of urban areas mixed with rural or forest areas associated with a marked increase of fire activity make this impact even greater. The intense urbanization of our societies, the abandonment of rural lands and rural activities such as forest management along with the rapid expansion of urban/forest interface are key drivers for wildfires in Europe and in the Mediterranean region.

Weather is a fundamental component of the fire environment. The prolonged drought and high temperatures of the summer period in the Mediterranean climate are the typical drivers that demarcate the temporal and spatial boundaries of the main fire season. Future trends of wildfire risks in the Mediterranean region, as a consequence of climate change, will lead to the increase of temperature in the East and West of the Mediterranean, with more frequent dryness periods and heat waves facilitating the development of very large fires. Future scenarios of climate change should affect local fire regimes, and therefore local analyses need to be performed by adapting global climatic models to regional conditions. Many factors have been considered to explain the temporal variation in fire regime in recent decades in Spain: climate change is one factor which involves an increasing relationship between the number of days of extreme fire hazard weather and the number and size of fires in the Mediterranean coast of Spain.

Earlier detection often leads to smaller fire size, and therefore reduces the probability of fire escape (Fernandes and Botelho 2003), final fire size, cost and risks to fire response crews. Wildfire prevention should be considered as an important part of sustainable forest management and should integrate a landscape approach taking into account different land uses. Knowledge of short and long-term impacts of wildfire is essential for effective risk assessment, policy formulation, and wildfire management.

Spain is one of the most affected countries in Europe, both considering number of fires and area burned. Between 1980 and 2004 nearly 380,000 fires have occurred in Spain, and more than 4.7 millions ha have been burned (roughly 10 % of the country). Extreme fires (>500 ha) are relatively frequent events with recurrence time of 2–3 years, causing large human, economic and environmental damage altogether. Their ignition and spread occur under favorable weather conditions, often following drought periods, in areas where fuel accumulation helps quick fire spread and high fire intensity, they usually burn out of control and can only be stopped when meteorological conditions support aerial and ground fire fighting (San-Miguel-Ayanza et al. 2012, 2013). In Catalonia these fires only represent 1.4 % of all fires and 79 % of burned area. In this study we have included wildfires larger than 50 ha because in the Mediterranean region they represent more than 75 % of the area burned, although they represent only 2.6 % of the total number of wildfires (Gonzalez and Pukkala 2007; Piñol et al. 1998). Over the last few years, the occurrence of large wildfire episodes with extreme fire behavior has affected different regions of Europe: Portugal, south-eastern France, Spain and Greece.

Wildfires have been studied in many ways, for instance as a spatial point pattern (Comas et al. 2009; Comas and Mateu 2011; Juan et al. 2012; Serra et al. 2012; Turner 2009) or through modeling the size of fires (Amaral-Turkman et al. 2011) or the relative risk of the big fires (Wang et al. 2012; Wisdom and Dlamini 2010). Lately a large variety of complex statistical models can be fitted routinely to complex data sets, in particular wildfires, as a result of widely accessible high-level statistical software, such as R (R Development Core 2011). Researchers from many different disciplines are now able to analyze their data with sufficiently complex methods rather than resorting to simpler yet non-appropriate methods. In this case, the objective in this paper is to model the occurrence of big wildfires, and to determine those factors which are significative in helping any fire to become a big wildfire.

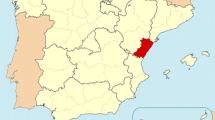
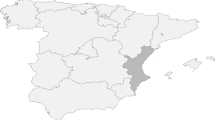
We analyze the occurrence of big wildfires in Catalonia between 1994 and 2011, and consider a big wildfire to be a fire that burns areas larger than a fixed extension of hectares. Specifically we consider three sizes of areas; 50, 100 and 150 ha. Moreover, we distinguish between the numerous potential causes of wildfire ignition. In particular, we consider: (i) natural causes; (ii) negligence and accidents; (iii) intentional fires or arson; and (iv) unknown causes and rekindled. The study area encompasses 32,000 km2 and represents about 6.4 % of the total Spanish national territory (Fig. 1).

Fig. 1
figure 1

Catalonia location in Europe

Full size image

In addition to the locations of the fire centroids, several marks and covariates are considered. The year the wildfire occurred is the unique mark considered. The spatial covariates are also considered, specifically, eight continuous covariates (i.e. topographic variables—slope, aspect, hill shade and altitude; proximity to anthropic areas—roads, urban areas and railways; and meteorological variables—maximum and minimum temperatures) and one categorical variable (land use).

The methodology for fitting spatial point process models to complex data sets has seen previous advances in facilitating routine model fitting for spatial point processes (Cressie 1993; Diggle 2003; Møller and Díaz-Avalos 2010). For instance, the work by Baddeley and Turner (2005) has facilitated the routine fitting of point processes based on an approximation of the pseudolikelihood to avoid the issue of intractable normalizing constants (Berman and Turner 1992) through the use of the library spatstat for R (Baddeley and Turner 2005). In the same way, (Illian and Hendrichsen 2010) consider hierarchical models able to analyze a wide variety of point process models, for example those appearing in fire problems.

In our case, spatio-temporal data can be idealized as realizations of a stochastic process indexed by spatial and temporal coordinates. Spatio-temporal clustering of wildfires might indicate the presence of risk factors which are not evenly distributed in space and time. In fact, what is usually of interest is to assess the association of clustering of wildfires to spatial and seasonal covariates (Serra et al. 2012). Covariate information usually comes in the form of spatial patterns in regular lattices or as regular vector polygons that may be rasterized into lattice images using GIS (Simpson et al. 2011). The right methodological context able to deal with these pieces of information comes from spatio-temporal point processes. To bypass the problem of inefficiency in the estimation under a general integrated nested Laplace approximation (INLA) (Rue et al. 2009), we have tried a computationally tractable approach based on stochastic partial differential equation (SPDE) models (Lindgren et al. 2011). On one hand, we use SPDE to transform the initial Gaussian Field (GF) to a Gaussian Markov Random Field (GMRF). GMRFs are defined by sparse matrices that allow for computationally effective numerical methods. Furthermore, by using Bayesian inference for GMRFs in combination to the INLA algorithm, we take advantage of the many significant computational improvements (Rue et al. 2009). If, in addition, we follow the approach suggested by Simpson et al. (2011), in which the specification of the Gaussian random field is completely separated from the approximation of the Cox process likelihood, we gain far greater flexibility.

The proposed method in this paper is an adapted two-part econometric model, specifically a Hurdle model. It consists of two stages and it is specified in such a way as to gather together the two processes theoretically involved in the presence of wildfires, that is, the fact to be a big wildfire (greater than a given extension of hectares) and the frequency of big wildfires per spatial unit. Specifically, the Poisson hurdle model consists of a point mass at zero followed by a truncated Poisson distribution for the non-zero observations.

This paper addresses two issues. We develop complex joint models for big wildfires and, at the same time, we provide methods facilitating the routine for the fitting of these models, using a Bayesian approach. The approach is based on the INLA, which speeds up parameter estimation substantially so that particular models can be fitted within feasible time.

This paper is organized as follows: the following section describes the data. Section 3 presents the methodology used, including the statistical framework, the description of the Poisson Hurdle model and the statistical inference explanation. Section 4 presents the results. Finally, the paper ends with a discussion and future coming steps.

2 Data setting

In this paper we analyze the occurrence of big wildfires in Catalonia between 1994 and 2011. The total number of fires recorded in the analysis is 3,283, which are distributed as follows: 206 wildfires bigger than 50 ha, 141 wildfires bigger than 100 ha, and 112 wildfires bigger than 150 ha. In Fig. 2, on the left, we can see all wildfires and wildfires bigger that 50 ha.

In Catalonia, the agency responsible for identifying the coordinates of the origin of the fire, the starting time and the cause of the fire is the Forest Fire Prevention Service (Government of Catalonia). In addition, they record the ending time of the fire, the hectares (and their type) affected, and the perimeter of the fire. The data used in this article are provided directly by the Service, and have been tested and polished before handling.

We distinguish between the numerous potential causes of wildfire ignition. In particular, we consider: (i) natural causes; (ii) negligence and accidents; (iii) intentional fires or arson; and (iv) unknown causes and rekindled. The first category includes lightning strikes or heat from the sun. The second takes into account that human carelessness can also start a wildfire, for instance, with campfires, smoking, fireworks or improper burning of trash. Negligence and accidents also includes those wildfires caused purely by chance. The third cause considers those wildfires that are started deliberately. Finally, the fourth set includes unknown causes and rekindled fires. In Fig. 3 we can understand the nature of the entire population of fires by the histogram of area burnt by fires and in Fig. 2, on the right, we show the spatial distribution of wildfires bigger than 50 ha distinguishing by causes.

Fig. 2
figure 2

Left All wildfires (1994–2011) and big wildfires. Right big wildfires distinguishing by causes

Full size image
Fig. 3
figure 3

Histogram of area burnt by fires

Full size image

In addition to the locations of the fire centroids, measured in Cartesian coordinates (Mercator transversal projections, UTM, Datum ETRS89, zone 31-N), several covariates are considered. Specifically, eight continuous covariates (i.e. topographic variables—slope, aspect, hill shade and altitude; proximity to anthropic areas—roads, urban areas and railways; and meteorological variables—maximum and minimum temperatures) and one categorical variable (land use).

Land use will obviously affect fire incidence, but moreover, topographic variables (slope, aspect and hill shade) affect not only fuel and its availability for combustion (Ordóñez et al. 2012), but also the weather, inducing diverse local wind conditions, which include slope and valley winds. In fact, Dillon et al. (2011) point out that those topographic variables are relatively more important predictors of severe fire occurrence, than either climate or weather variables. The proximity to anthropic areas can be considered a factor explaining not only the incidence of fires in the intentional fires and arson category, but also why natural cause fires do not occur. As climatic variables are feasibly important for natural cause fires and perhaps rekindled fires, we use the maximum and minimum temperatures (further details can be found in Serra et al. 2012).

In this paper, slope is the steepness or degree of incline of a surface. Slope cannot be directly computed from elevation points; one must first create either a raster or a TIN surface. In this article, the slope for a particular location is computed as the maximum rate of change in elevation between the location and its surroundings. Slope is expressed in degrees. Aspect is the orientation of the slope and it is measured clockwise in degrees from 0 to 360, where 0 is north-facing, 90 is east-facing, 180 is south-facing, and 270 is west-facing. Hill shading is a technique used to visualize terrain as shaded relief by illuminating it with a hypothetical light source. Here, the illumination value for each raster cell is determined by its orientation to the light source, which, in turn, is also measured in degrees, from 0 to 360. Finally, altitude is considered as elevation above sea level and it is expressed in meters. To obtain topographic variables (DTM) we use the MET-15 model, which is a regular grid containing orthometric heights distributed according to a metricconverterProductID15 m15 m grid side, and is created for the Cartographic Institute of Catalonia (ICC). We also use the surface analysis tools included in the ArcGis10 application Spatial Analyst (Serra et al. 2012).

The distances, in meters, from the location of the wildfire to urban areas, roads and railroads, are constructed by considering a geographical layer in each case. The urban area and road layers are obtained from the Department of Territory and Sustainability of the Catalan Government, through the ICC (http://www.icc.cat). To obtain the two new raster layers we use the Euclidean distance function, included in the ArcGis10 application Spatial Analyst. Then, we use the merge function of ArcGis10 Geoprocessing module, to combine those two layers (urban areas and roads and railroads) into one single layer. The layers are continuous and defined as a raster layer (details can be found in Serra et al. 2012).

We also use the land use in Catalonia maps (1:250,000), with classification techniques applied on existing LANDSAT MSS images for 1992, 1997 and 2002 (Chuvieco 2009; García et al. 2008; Røder et al. 2008). Additionally, we use orthophotomaps (1:5,000) 2005–2007, to create the land use map for 2010. Specifically, we assign the land use map just before the date of each wildfire. We assign, as the land use, only the percentage value corresponding to the principal land use of the spatial units. In this paper, we transform the 22 categories, obtained from the ICC cover map of Catalonia, into 8 categories: coniferous forests; dense forests; fruit trees and berries; artificial non-agricultural vegetated areas; transitional woodland scrub; natural grassland; mixed forests; and urban, i.e., beaches, sand, bare rocks, burnt areas, and water bodies.

We also consider the temperatures (maximum and minimum) and up to 7 days before the occurrence of the fire, at the location of the wildfire (note that meteorological data are provided by the Area of Climatology and Meteorological Service of Catalonia). The temperatures at the point of the occurrence of the wildfire, along with the temperatures from the previous day and up to a week before, are estimated by means of a two-step Bayesian model. Further details can be found in Saez et al. (2012).

3 Methods

3.1 Statistical framework

Spatio-temporal data can be idealized as realizations of a stochastic process indexed by a spatial and a temporal dimension

$$ {\rm Y}\left({\rm s,t}\right)\equiv \{{\rm y(s,t)|(s,t)}\in {\rm D}\times {\rm T}\in {{\mathbb R}}^{2} \times {\mathbb R}\} $$
(1)

where D is a (fixed) subset of \({{\mathbb R}}^{2}\) and T is a temporal subset of \({\mathbb R}. \) The data can then be represented by a collection of observations \({\rm y}= \{{\rm y}\left({{\rm s}}_{1},{{\rm t}}_{1}\right),\dots ,{\rm y}\left({{\rm s}}_{{\rm n}},{{\rm t}}_{{\rm n}}\right)\},\) where the set (s 1, ..., s n ) indicates the spatial locations, at which the measurements are taken, and (t 1, ..., t n ) the temporal instants.

The mathematical theory of point processes on a general space is now well-established (Bremaud 1981; Daley and Vere-Jones 2003). However, most models for specific applications are restricted either to point processes in time or to the two-dimensional space. Cox processes are widely used as models for point patterns which are thought to reflect underlying environmental heterogeneity.

A spatio-temporal correlation structure is a complicated mathematical entity and its practical estimation is very difficult. We thus assume separability in the sense that we model the spatial correlation by the Matérn spatial covariance function defined in Eq. 4 and the temporal correlation is modeled using a Random Walk model of order 1 (RW1). We introduce also the interaction effect between the space and time using another RW1 structure. Nevertheless, this inclusion of the interaction does not change the separability structure. The Random Walk structure for the temporal dependence is justified by the apparent randomness of the wildfires distribution among time, as shown in Fig. 4. In fact, the dispersion of big wildfires varies between the periods considered. In particular, there is a reduction considering the number of them, specifically in the period 2008–2011.

Fig. 4
figure 4

Big wildfires in Catalonia in 1994–2011. Left-up 1994–1997; right-up 1998–2002; left-down 2003–2007 and right-down 2008–2011

Full size image

3.2 The Poisson hurdle model

The model used in this paper is an adapted two-stage econometric model proposed by Deb and Trivedi (2002), specifically a hurdle model. It consists of two stages and specified in a way to gather together the two processes theoretically involved in the presence of wildfires, that is, the occurrence of being a big wildfire (greater than a given extension of hectares) and the frequency of big wildfires per spatial unit (Neelon et al. 2013). Specifically, the Poisson hurdle model consists of a point mass at zero followed by a truncated Poisson distribution for the non-zero observations.

In the first stage, we predict the probability that any wildfire becomes larger than 50, 100 and 150 ha. In the second stage, we model the number of these big wildfires per spatial unit.

The first part of the process can be modeled using a logistic regression, that models the probability that any wildfire becomes larger than a fixed area following the expression

$$ \begin{aligned} p_{itk}&=Prob\left(y_{itk}>A | Z,\beta \right)\\ log {\left(\frac{p_{itk}}{1-p_{itk}}\right)\ }&=\beta_{0i}+Z'\beta +S_i+{\tau }_t+{\upsilon }_{it} \end{aligned} $$
(2)

where A denotes one of the fixed area’s values (50, 100 or 150 ha), y is the response variable (in this case, each wildfire), Z a matrix of explanatory spatial covariates (containing the intercept), β 0i represents the heterogeneity as a random effect, β is the vector of unknown parameters associated with the covariates, the subscript i denotes the wildfire, the subscript t (t = 1994,\(\ldots\), 2011) the year of occurrence of the wildfire, and the subscript k (\(k =1,\ldots 4\)) the cause of occurrence. We also introduced three additional random effects: (i) spatial dependence, S i , (ii) temporal dependence, τ t and (iii) spatio–temporal interaction, \({\upsilon }_{{\rm it}}.\)

In accordance with that proposed by Mullahy (1986), in the second stage of the model the distribution of being a big wildfire follows a truncated Poisson that models the number of big wildfires per spatial unit, introducing covariates and spatial random effects (Neelon et al. 2013). The model in this stage is

$$ \begin{aligned} p\left( {y_{{jtk}} |S_{j} } \right) & = \left( {1 - p_{{jtk}} } \right)1_{{(y_{{jtk}} < A)}} + p_{{jtk}} Tpois(y_{{jtk}} ;\mu _{{jtk}} )1_{{(y_{{jtk}} > A)}} \\ \log \left( {\mu _{{jtk}} } \right) & = \eta \left( {p_{{jtk}} } \right) \\ \eta \left( {p_{{jtk}} } \right) & = \beta _{{0j}} + \sum\limits_{m} {\beta _{m} Z_{{m,jt}} } + S_{j} + \tau _{t} + \upsilon _{{jt}} \\ \end{aligned} $$
(3)

where Tpois(y jtk ;μ jtk ) denotes a truncated Poisson distribution with parameter μ jtk , η denotes a link function such as the logit link, Z m,jt represents the same spatial covariates used in the first stage, β 0j stands for the environmental heterogeneity and β m denotes the parameters associated with the covariates. The random effects are as in Eq. 2.

The particular estimation process has two steps. In the first step we use a binomial link in order to estimate the occurrence of a big wildfire. The probabilities of occurrence obtained from this first step are used in the second step as interim priors. In the second step the link is a truncated Poisson distribution. In any case, the likelihood of each part is introduced multiplicatively in only one equation.

To analyze and estimate the number of zeros in a dataset there exists different statistical alternatives. On one hand we have the ZIP model, which is employed to estimate event count models in which the data result in a larger number of zero counts than would be expected. The hurdle Poisson model (Mullahy 1986) is a modified count model with two processes, one generating the zeros and one generating the positive values. The two models are not constrained to be the same.

The concept underlying the hurdle model is that a binomial probability model governs the binary outcome of whether a count variable has a zero or a positive value. If the value is positive, the “hurdle is crossed,” and the conditional distribution of the positive values is governed by a zero-truncated count model. In the ZIP models, unlike the hurdle model, there are thought to be two kinds of zeros, “true zeros” and “excess zeros”.

3.3 Statistical inference

3.3.1 SPDE approach

The SPDE approach allows to represent a GF with the Matérn covariance function defined in Eq. 4 as a discretely indexed spatial random process which produces significant computational advantages (Lindgren et al. 2011). GFs are defined directly by their first and second order moments and their implementation is highly time consuming and provokes the so-called “big n problem”. This is due to the computational costs of \({\mathcal O}(n^3)\) to perform a matrix algebra operation with n × n dense covariance matrices, which is notably bigger when the data increases in space and time. To solve this problem, we analyze an approximation that relates a continuously indexed GF with Matérn covariance functions, to a discretely indexed spatial random process, i.e., a GMRF. The idea is to construct a finite representation of a Matérn field by using a linear combination of basis functions defined in a triangulation of a given domain D. This representation gives rise to the SPDE approach given by Eq. 5, which is a link between the GF and the GMRF. This link allows replacement of the spatio-temporal covariance function and the dense covariance matrix of a GF with a neighbourhood structure and a sparse precision matrix, respectively, typical elements that define a GMRF. This, in turn, produces substantial computational advantages (Harvill 2010; Lindgren et al. 2011; R-INLA project 2012).

Assuming separability we need to define the Matérn spatial covariance function which controls the spatial correlation at distance \(\left\|h\right\|=\left\|s_i-s_j\right\|,\) and this covariance is given by

$$ M\left(h | \nu ,\kappa \right)=\frac{2^{1-\nu }}{\Upgamma \left(\nu \right)}{\left(\kappa \left\|h\right\|\right)}^{\nu }{{\rm K}}_{\nu }(\kappa \left\|h\right\|) $$
(4)

where Kν is a modified Bessel function of the second kind and κ > 0 is a spatial scale parameter whose inverse, 1/κ, is sometimes referred to as a correlation length. The smoothness parameter ν > 0 defines the Hausdorff dimension and the differentiability of the sample paths (Gneiting et al. 2010). Specifically, we tried ν = 1,2,3 (Plummer and Penalized 2008).

Using the expression defined in Eq. 4, when ν + d/2 is an integer, a computationally efficient piecewise linear representation can be constructed by using a different representation of the Matérn field x(s), namely as the stationary solution to the SPDE (Simpson et al. 2011).

$$ {{(\kappa }^2-\Delta )}^{\alpha /2}x\left(s\right)=W(s) $$
(5)

where α = ν + d/2 is an integer, \( \Delta = \sum\nolimits_{{i = 1}}^{d} {\frac{{\partial ^{2} }}{{\partial s_{i}^{2} }}} \) is the Laplacian operator and W(s) is spatial white noise.

In the general spatial point process context, the intensity stands for the number of events (fires in our case) per unit area. When considering the total intensity in each cell, we refer to the number of fires per cell area. A particular problem in our wildfire dataset is that the total intensity in each cell, \({\Uplambda }_{jt}\) is difficult to compute, and so we use instead the approximation, \({\Uplambda }_{jt}\approx \left|s_j\right|{\rm exp}({\eta}_{jt}(s_j)),\) where η jt (s j ) is a ‘representative value’ (i.e., it represents the intensity or number of fires in a particular cell given by a linear predictor of covariates and other terms) (Simpson et al. 2011), within the cell and |s j | is the area of the cell s j . To treat this kind of problems, Cox processes are widely used. In particular, Log Gaussian Cox processes (LGCP), which define a class of flexible models are particularly useful in the context of modeling aggregation relative to some underlying unobserved environmental field (Illian and Hendrichsen 2010; Simpson et al. 2011) and they are characterized by their intensity surface being modeled as

$$ {\log \left(\lambda \left(s\right)\right)\ }=Z\left(s\right) $$
(6)

where Z(s) is a Gaussian random field.

3.3.2 LGCP

Conditional on a realization of Z(s), a log-Gaussian Cox process is an inhomogeneous Poisson process. Considering a bounded region \(\Upomega \subset{{\mathbb R}}^2\) and given the intensity surface and a point pattern Y, the likelihood for a LGCP is of the form

$$ \pi \left(Y | \lambda \right)={\rm exp}\left(|\Upomega |-\int\limits_{\Upomega }{\lambda \left(s\right)ds})\prod_{s_i\in Y}{\lambda \left(s_i\right)}\right) $$
(7)

where the integral is complicated by the stochastic nature of λ (s). We note that, the log-Gaussian Cox process fits naturally within the Bayesian hierarchical modeling framework. Furthermore, it is a latent Gaussian model, which allows to embed it within the INLA framework. This embedding paves the way for extending the LGCP to include covariates, marks and non-standard observation processes, while still allowing for computationally efficient inference (Illian et al. 2012).

The basic idea is that, as we have explained in previous paragraphs, from a GF with a Matérn covariance function, we use a SPDE approach to transform the initial GF to a GMRF, which, in turn, has very good computational properties. In fact, GMRFs are defined by sparse matrices that allow for computationally effective numerical methods. Furthermore, by using Bayesian inference for GMRFs, it is possible to adopt the INLA algorithm which, subsequently, provides significant computational advantages.

Because our data is potentially zero inflated, as not all our events will become big fires, in this paper we present a spatial Poisson hurdle model to address these particular aspects of the data.

3.3.3 Bayesian computation

In a statistical analysis, to estimate a general model it is useful to model the mean for the i-th unit by means of an additive linear predictor, defined on a suitable scale

$$ {\eta }_j=\beta_{0j} +\sum^M_{m=1}{{\beta }_mz_{mj}+\sum^L_{l=1}{f_l(v_{lj})}} $$
(8)

where β 0j is a scalar which represents the intercept, β = (β 1, .., β M ) are the coefficients which quantify the effect of some covariates z j  = (z 1j , .., z Mj ) on the response, and f = {f 1(.), .., f L (.)} is a collection of functions defined in terms of a set of covariates v = (v 1, .., v L ). From this definition, varying the form of the functions f l (.) we can estimate different kind of models, from standard and hierarchical regression, to spatial and spatio-temporal models (Rue et al. 2009).

Given the specification in Eq. 8, the vector of parameters is represented by θ = {β 0, β, f}.

In our case, assuming that the subscript i denotes the wildfire, the subscript j the municipal district and the subscript t (t = 1994\(\ldots\) 2011) the year of occurrence of the wildfire, for each cause, we specify the log-intensity of the Poisson process by a linear predictor (Illian et al. 2012) of the form

$$ {\eta }_{ijt}\left(s_j\right)={\beta}_{0j}+{\beta }_1X_{ijt}+{\beta }_2Z_{jt}+{\beta }_3W_j+S_j+{\tau }_t+{\upsilon }_{jt} $$
(9)

where β 0j represents the heterogeneity accounting for variation in relative risk across different municipals districts, S j is the spatial dependence; τ t is the temporal dependence; and \({\upsilon }_{ijt}\) is the spatio-temporal interaction.

Note that, we assume separability between spatial and temporal patterns and allow interaction between the two components.

Following the Bayesian paradigm we can obtain the marginal posterior distributions for each of the elements of the parameters vector

$$ p\left({\theta }_i|y\right)=\int{p\left(\psi |y\right)p\left({\theta }_i|\psi ,y\right)d\psi } $$
(10)

and (possibly) for each element of the hyper-parameters vector

$$ p\left({\psi }_k|y\right)=\int{p\left(\psi |y\right)pd{\psi }_{-k}} $$
(11)

Thus, we need to compute: (i) p(ψ|y), from which all the relevant marginals p(ψ k |y) can be obtained, and (ii) p(θ i |ψ, y), which is needed to compute the marginal posterior for the parameters. The INLA approach exploits the assumptions of the model to produce a numerical approximation to the posteriors of interest, based on the Laplace approximation (Tiernery and Kadane 1986).

Operationally, INLA proceeds by first exploring the marginal joint posterior for the hyper-parameters \(\hat{p}(\psi |y)\) in order to locate the mode; a grid search is then performed and produces a set G of “relevant” points{ψ *} together with a corresponding set of weights, {w * ψ } to give the approximation to this distribution. Each marginal posterior \(\hat{p}({\psi }^*|y)\) can be obtained using interpolation based on the computed values and correcting for (probable) skewness, e.g. by using log-splines. For each ψ *, the conditional posteriors \(\hat{p}({\theta }_i|{\psi }^*,y)\) are then evaluated on a grid of selected values for θ i and the marginal posteriors \(\hat{p}({\theta }_i|y\)) are obtained by numerical integration (Blangiardo et al. 2013)

$$ \hat{p}({\theta }_i|y)\approx \sum_{{\psi }^*\in G}{\hat{p}({\theta }_i|{\psi }^*,y)\hat{p}({\psi }^*|y)}w_{{\psi }^*} $$
(12)

Given the specification in Eq. 12, the vector of parameters is represented by \({\theta }_j=\{\beta_0 ,{\beta },S,{\tau }_t,\ {\upsilon }_{jt}\}\) where we can consider \(X_j=(S,{\tau }_t,\ {\upsilon }_{jt})\) as the j-th realization of the latent GF X(s) with the Matérn spatial covariance function defined in Eq. 4. We can assume a GMRF prior on θ, with mean 0 and a precision matrix Q. In addition, because of the conditional independence relationship implied by the GMRF, the vector of the hyper-parameters \(\psi =({\psi }_S,{\psi }_{\tau },{\psi }_{\upsilon })\) will typically have a dimension of order 4 and thus will be much smaller than θ. The heterogeneity was specified as a vector of independent and Gaussian distributed random variables on j, with constant precision (R-INLA project 2012).

Note that in both parts of the model we control for heterogeneity, spatial dependence and spatio-temporal extra variability. Models are estimated using Bayesian inference for GMRF through the INLA. All analyses are carried out using the R freeware statistical package (version 2.15.2) (R Development Core 2011) and the R-INLA package (R-INLA project 2012).

We have used the conjugate prior to the Poisson likelihood which is a Gamma distribution function. Indeed, with the aim of checking the robustness of our methodological choice we have used several other (non-conjugate) priors for the precision parameters (in particular Gaussian and flat priors) and the posterior distribution for the precision hyper-parameters has not changed significantly. We have thus preferred using in the paper the corresponding Gamma conjugate priors. Clearly, as used generically in INLA for the hyper-parameters, the distribution of the fixed parameters is normal for the intercept.

4 Results

We note that, in general, wildfires caused by natural causes are not larger than 50 ha. The same happens for those fires caused by unknown causes or for those rekindled. For this reason, even if we have analyzed the forth causes we focus our results only on big wildfires caused by negligence and accidents and on those caused intentionally or arson.

4.1 First stage results

We first consider a logistic regression to model the probability of a wildfire becoming larger than a particular area. Table 1 shows the significative factors of the logistic model distinguishing by the three sizes (50, 100 and 150 ha) and considering wildfires occurred by negligence and accidents (cause 2) and those caused by intention or arson (cause 3). The main factors that have an influence in the presence of wildfires (larger than a given extension of hectares) are the aspect and the land use. Taking into account the rest of the covariates considered we can see that the hill shade, the distance to anthropic areas and the maximum temperature have no influence in the probability of a fire to become larger than a specific area. Table 2 shows the means of the posterior distributions for the hyper-parameters of the first stage considering the three sizes of area analyzed. The heterogeneity, the time and the interaction have a small impact, their values, around 0.00005 are smaller than the spatial values, 0.246, and moreover, their values decrease when the extension of the wildfires increases, for instance for the heterogeneity effect they go from 0.000054 to 5.24E−09. We can also appreciate that there are not big differences between the two causes. On the other hand, the values of the spatial component show that there is an important spatial dependence with values from 0.01 to 0.246, especially for wildfires occurred by negligence and accidents. In Figs. 5 and 6, show the marginal distribution of hyper-parameters for causes 2 and 3: (a) κ which is a scaling parameter related to the range ρ; (b) ψ τ the precision parameter; (c) ρ which comes from the empirically derived equation (8ν)1/2/κ and represents the distance at which the spatial correlation becomes almost null; (d) the heterogeneity random effect; (e) the temporal random effect; and (f) the spatio-temporal interaction random effect. In all of them, the distribution is Gamma and the distributions are similar for both causes. Finally, Fig. 7 shows the prediction of the probability of a fire to become larger than 50 ha as well as the standard deviation of this prediction. Looking at the wildfires occurred by negligence and accidents we can see that higher probabilities are concentrated around the main urban areas of Catalonia: Girona (in the north-east), Barcelona (in the middle of the coast), Tarragona (in the south along the coast) and Lleida (in the center west). There are also high probabilities in the north-west, corresponding to a large forest area. With respect to intentional and arson wildfires the probabilities are less concentrated than in wildfires occurred by negligence and accidents but are also higher in the same areas. Regarding the standard deviation we do not appreciate alarming values. On the second cause higher values are found where the probabilities are also higher. The third cause presents lower values of deviation than wildfires occurred by negligence and accidents meaning that the model works better with wildfires occurred by intention or arson.

Table 1 Significative factors for the logistic model in the first stage of the analysis
Full size table
Table 2 Means of the posterior distributions for the hyper-parameters of the first stage
Full size table
Fig. 5
figure 5

From top-left to bottom-right: marginal posterior distribution for κ, ψ τ , ρ, heterogeneity, time and interaction, respectively, for cause 2

Full size image
Fig. 6
figure 6

From top-left to bottom-right: marginal posterior distribution for κ, ψ τ , ρ, heterogeneity, time and interaction, respectively for cause 3

Full size image
Fig. 7
figure 7

Top prediction maps for cause 2 and cause 3. Bottom standard deviation for the prediction under cause 2 and cause 3

Full size image

4.2 Second stage results

In the second stage we model the frequencies of wildfires (larger than a specific area) per spatial unit. Table 3 shows the values of the hyper-parameters. It is important to note that in this second stage the spatial values are not included. The reason is because there is a too high correlation between the spatial dependence component, S j , and the spatio-temporal interaction, \({\upsilon}_{jt},\) that prevents the model from working properly. Therefore, we introduce the spatial random effect through the interaction. The heterogeneity is quite much significant than in the first stage (values of 0.000054 in the first stage to values of 0.116 in this second stage), especially for intentional wildfires and arson. Something similar happens with the interaction (values of 0.000043 in the first stage to values of 0.0001 in this second stage). It is much larger than in the first stage and it is also more representative for wildfires occurred by intention and arson. This comes reflected in a significative spatial variability among the districts when counts of large fires come into effect. Finally, with respect to the temporal dependence, this is also larger than in the first stage but it has almost no variation between the two causes, around 0.00005. In addition there are not relevant differences between the three extensions of hectares in any of the three hyper-parameters analyzed. In Fig. 8, we show the marginal posterior distribution of hyper-parameters for heterogeneity, time and interaction for causes 2 and 3. In all of them, the distribution is Gamma. Finally, Fig. 9 shows the predicted number of wildfires larger than 50 ha per spatial unit. Wildfires occurred by negligence and accidents and those caused by intention or arson present the same pattern of distribution according to the probabilities obtained in the first stage of the model. In general, big wildfires are concentrated along the coast being denser around the metropolitan area of Barcelona. Looking at the standard deviations we point out that intention wildfires and arson have very low values so, again, we note that the model correctly fits wildfires occurred intentionally or arson.

Table 3 Hyper-parameters for the model in the second stage
Full size table
Fig. 8
figure 8

Posterior distribution of the hyper-parameters for the second stage. Left heterogeneity, Middle time and Right interaction. First line: cause 2, second line: cause 3

Full size image
Fig. 9
figure 9

Number of fires expected maps: On the top cause 2 and cause 3 and on the bottom cause 2-sd and cause 3-sd

Full size image

5 Discussion

The main finding of this study is that big wildfires are mostly caused by human actions either by negligence and accidents or by intention or arson. These results make sense with what the bibliography shows and what we have commented in the introduction; over 95 % of the fires in Europe are due to human causes. Normally a natural wildfire does not spread as much as an intentional wildfire and so, the number of wildfires which are larger than a big extension, is not enough to obtain results. Analyzing the forth causes separately we noticed no significant results for wildfires caused by natural causes and for those caused by unknown causes or rekindled. In fact separating wildfires by cause and by its extension we almost did not have wildfires caused by natural causes nor unknown causes or rekindled. In particular in our data there are only 15 wildfires bigger than 50 ha occurred by natural causes compared to 180 caused by negligence or accidents. Our model does not work properly with such a limited small number of data so, even if we have studied the forth causes, we have restricted the study to the second and the third causes. Although the practical results are very similar in both approaches, ZIP models and Hurdle models, the second one is more appropriate in our case, since every wildfire can turn into a big wildfire and therefore, every point is susceptible to become larger than a specific number of hectares.