1 Introduction

Fire is an ubiquitous ecological disturbance. Since the first plant communities were established on land, lightning and other ignition sources have started forest fires. In Mediterranean landscapes, fire is one of the main ecological disturbances, as it can affect forests severely enough to induce changes in forest dynamics and geohydrology. (Miguel et al. 2011; Shakesby 2011). Through time, living beings in most terrestrial ecosystems have adapted to the presence and effects of fire, turning it into a natural component in all forest ecosystems (Agee 1993). Despite this, fire represents a hazard to human life and property, encouraging society and policy makers to take measures that mitigate its effects. In European forests, wildfire incidence has increased in recent years, apparently associated to climate change and global warming (Aragó et al. 2016). Unlike other natural hazards, wildfire risk is predictable to some extent (Birot 2009), and thus models able to explain and predict the space and time variability of their incidence, as well as their variability in time to extinction, are of great importance (Faivre et al. 2018). Modeling forest fire dynamics helps to increase the structured knowledge about terrestrial ecosystems, to establish better management of them, and consequently, to set a sustainable use of forest resources (Ager et al. 2006; Lindner et al. 2010). Modeling the spatial variation of fires is important as their burning time is directly associated to the final size of the burned area and the amount of gasses and particulate matter emissions (van der Werf et al. 2009). Such association is also affected by local factors, like vegetation and lithology (Miranda et al. 1994).

Stochastic models for forest fire incidences have been in the literature since the pioneering modeling made by Dayananda (1977). With the advent of Geographic Information Systems (GIS), various attempts to model and screen out risk factors for forest fires have been developed (Amatulli et al. 2007). Though useful, some of these approaches lack necessary key components for adequate spatial modeling, e.g., the classical raster approach based on GIS assumes independence among pixels. In fact, most of the models based on GIS do not include a random component (Mandallaz and Ye 1997; Ager et al. 2006).

Ignition time and location of forest fires constitute a complex process, difficult to predict. However, historical data can be used to construct predictive maps for fire risk. In this sense, some authors have proposed models based on standard generalized linear models (Padilla and Garcia 2011; Vilar et al. 2010) and weighted generalized linear models (Marques et al. 2011). Other authors have proposed more elaborate models based on Markov random fields (Díaz-Avalos et al. 2001), maximum entropy models (Duane et al. 2015) (Duane et al., 2015), kernel density adaptive models (Amatulli et al. 2007), fire growth models (Bar Massada et al. 2009), quantile regression (Barros and Pereira 2014) and spatial point processes (e.g. Juan et al. 2012; Møller and Díaz-Avalos 2010; Turner 2009; Serra et al. 2014; Aragó et al. 2016; Díaz-Avalos et al. 2016), among others.

From an ecological viewpoint, characteristics such as ignition time, ignition location and fire duration, are relevant components for wildfire modeling. Indeed, these features are important as they are closely associated to fire dynamics, in the sense that they are amongst the main variables that control hazards and are also related to burning area and recurrence rate (McKenzie et al. 2011).

The observed sites and ignition times constitute a space-time point pattern and a natural framework to model this type of data is via marked point processes (see e.g. Daley and Vere-Jones 2008; Baddeley et al. 2015). These models have been used in fields such as biology, ecology, agronomy and physics, among others (Møller and Waagepetersen 2004; Illian et al. 2008; Diggle 2013). Within the forest fire modeling literature, various approaches have been proposed (see for example Møller and Díaz-Avalos 2010; Serra et al. 2014; Díaz-Avalos et al. 2016). While the theory and application of point processes is vast, in many cases their estimation remains a challenge. In this regard, the approach by Taddy and Kottas (2012), which models the intensity of a Poisson point process via weighted mixtures of Dirichlet processes, results in a flexible alternative to intensity modeling, as it borrows the practicality of Bayesian nonparametric inference techniques.

The complete randomness property inherent to Poisson point processes may be inadequate to model point patterns that exhibit regularity or clustering features. However, this effect is diminished when the intensity measure is modelled by another random measure, such as in the case of Cox processes. In fact, there are some intersections between non-homogeneous Poisson processes and renewal processes that fall within Cox processes theory (Yannaros 1994; Daley and Vere-Jones 2008).

In this work, we propose a marked Poisson point process for wildfire ignition times and locations as events, marked with durations. The central idea is to use a particular joint intensity function for events and marks, which adapts to the context at issue. Specifically, we apply the model to infer the intensity functions for ignition times and locations, the survival and hazard functions for durations, and the conditional survival function for durations given starting times and locations, for fires occurring in the Valencian Community, Spain, between January 1st, 2010, and December 31st, 2015. Wildfire ignitions may be intentional, accidental, or caused by natural forces such as lightning. In our study, we will only consider wildfires caused by lightning strikes.

2 Methodology

2.1 Study area

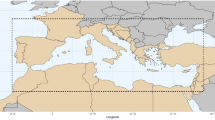
The Valencian Community is located in the east and southeast (SE) part of Spain, neighbouring the communities of Castilla - La Mancha, Cataluña, Aragón and Murcia (Fig. 1). The inland part of the territory is craggy, with the highest peaks in the Valencia and Castellón provinces forming part of the Iberian mountain range. The mountains in the Province of Alicante form part of the Subbaetic range. The coastal zone is mostly a fertile farming zone with some wetlands. According to the Agencia Estatal de Meteorología of Spain (2013), the climate in the study area is diverse, with Mediterranean climate in the coastal areas, continental Mediterranean climate in the continental zones and some zones with hot semi-arid climate.

Fig. 1
figure 1

Political division map showing the location of the Valencian Community in the Iberic Penninsula

Full size image

The vegetation of the Valencian community is diverse as well due to the topography in the community. According to the Coordination for the Information on the Environment (CORINE), there are more than forty-four vegetation types in the Valencian Community.

2.2 Data set

The data set used in our case study consists of \(m=337\) wildfires reported for the Valencian Community during the years 2010 to 2015 by the “Comité de Lucha contra Incendios Forestales” in the Valencian Community. The time span is 2191 days, starting from January 1st, 2010, 00:00:01 GTM. Wildfires are originated by several causes, but here we will analyze only those originated by natural causes. The information used in our analysis considers starting time (days since January 1st, 2010, 00:00:01 GTM), duration (days) and geographic location of the ignition site in UTM. Figure 2 shows nonparametric kernel estimates (Diggle 2013) of the intensity function for the five years considered in this study, using the observed point pattern of wildfires in space and time. The incidence of wildfire ignitions shows variability among the six years, but the levels of the intensity estimates have similar maxima except for 2010, where the overall intensity was low, and 2013, which shows an intensity peak in the SE part of the study area.

Fig. 2
figure 2

Estimated spatial incidence of wildfires in the Valencian Community, Spain, for years 2010 to 2015, obtained by using a space-time kernel estimator with border correction

Full size image
Fig. 3
figure 3

Spatial incidence of wildfires in the Valencian Community, Spain, between January 1st, 2010, and December 31st, 2015 (a), and temporal incidence along time in 30 day bins (b)

Full size image

To better highlight the areas where wildfires are more common, Fig. 3 presents the marginal spatial distribution of the wildfires in the Valencian Community, as well as the variation in 30 day bins of the number of wildfires between January 1st, 2010, and December 31st, 2015. The spatial incidence of the wildfires (Fig. 3a) shows only some areas where wildfires apparently form clusters. These areas are located in the western part of the study area, where forest zones and higher elevations are common. Wildfires at the north, south and coast zones of the Valencian Community were scarce during the study period. Figure 3b shows the seasonality of wildfire incidence in the study area, with high incidences during the warm and dry summer months, and lower incidence during winter. Due to the weather conditions, as well as to the closeness to firefight centers and accessibility, wildfire control times are random, analogous to survival analysis (Daley and Vere-Jones 2003). Thus, the observed spatial point pattern of wildfire ignition sites, ignition times, and survival times can be considered as a realization of a space-time marked Poisson process. Hence, our goal here is to propose and fit a model for the joint intensity function of the point pattern of wildfires occurring in the Valencian Community during the time span mentioned above. Note that the areas where the nonparametric estimate of the intensity function in Figs. 2 and 3 is high suggest the presence of some degree of clustering. However, when the events are spread along the five years of the study, the observed groupings are a consequence of a static projection of all events during that period rather than a true clustering effect.

3 Modeling the spatio-temporal incidence of wildfires using Dirichlet process mixture models

We assume that the observed point pattern is a realization of a space-time marked point process and denote the point configuration of fire i by \({\varvec{y}}_{i}=(s_{i},{\varvec{x}}_{i},l_{i})\), where \(s_{i}\in [0,\infty )\) and \({\varvec{x}}_{i}=(x_{1i},x_{2i}) \in \mathbb {R}^{2}\) are the wildfire starting times and locations, respectively, each attached with its duration \(l_{i}\in [0, \infty )\), say the marks. Specifically, we assume that \(\{{\varvec{y}}_{i}:i=1,\ldots ,m\}\) are \(m\in \mathbb {N}\) points generated from a marked space-time Poisson process (MPP) with a continuous intensity function \(\lambda :[0,\infty )\times \mathbb {R}^{2}\times [0, \infty )\rightarrow [0,\infty )\), such that

$$\begin{aligned} 0<\int _{[0,\infty )}\left\{ \int _{W_{0}}\lambda (s,{\varvec{x}},l)\mathrm {d}s\,\mathrm {d}{\varvec{x}}\right\} \mathrm {d}l<\infty \end{aligned}$$
(1)

for all bounded subsets \(W_{0}\) of \([0,\infty )\times \mathbb {R}^{2}\). Hence, in some \(W:=W_{0}\times [0,\infty )\), we observe m wildfire starting times \(\{s_{1},\ldots ,s_{m}\}\), their corresponding locations \(\{{\varvec{x}}_{1},\ldots ,{\varvec{x}}_{m}\}\) and durations \(\{l_{1},\ldots ,l_{m}\}\). Using (1) we can estimate features of the MPP through its likelihood function, which is proportional to

$$\begin{aligned}&\exp (-\rho )\rho ^{m}\prod _{i=1}^{m}\pi (s_{i},{\varvec{x}}_{i},l_{i}),\quad \mathrm {with}\quad \pi (\,\cdot \,):= \frac{\lambda (\,\cdot \,)}{\rho }\quad \mathrm {and}\nonumber \\&\quad \rho :=\int _{W}\lambda (s,{\varvec{x}},l)\mathrm {d}s\,\mathrm {d}{\varvec{x}}\, \mathrm {d}l. \end{aligned}$$
(2)

In (2), \(\pi :W\rightarrow [0,\infty )\) is a continuous probability density function by construction. As \(\exp (-\rho )\rho ^{m}\) depends on the data only through the sample size m, \(\{{\varvec{y}}_{i}:i=1,\ldots ,m\}\) can be considered as a random sample coming from \(\pi \), independent from \(\rho \). Thus, modeling \(\lambda \) flexibly is equivalent to modeling \(\pi \). This technique has been previously used by Taddy and Kottas (2012), who proposed modeling \(\pi \) as as Dirichlet process mixture (DPM) model (Antoniak 1974; MacEachern 1994; Escobar and West 1995), and a Jeffreys prior for \(\rho \), supported on \((0,\infty )\), with functional form \(\rho ^{-1}\). Under such framework, each \({\varvec{y}}_{i}\) is generated from a random probability density function \(\pi ({\varvec{y}}\mid H):=\int _{\Theta }\mathcal {K}({\varvec{y}}\mid \varvec{\theta })\mathrm {d}H(\varvec{\theta })\), which admits the hierarchical representation

$$\begin{aligned}&{\varvec{y}}_{i}\mid \varvec{\theta }_{i}{\mathop {\sim }\limits ^{\mathrm {ind.}}}\mathcal {K}(\,\cdot \mid \varvec{\theta }_{i}):i=1,\ldots ,m \nonumber \\&\quad \varvec{\theta }_{1},\ldots ,\varvec{\theta }_{m}\mid H{\mathop {\sim }\limits ^{\mathrm {i.i.d.}}}H \nonumber \\&\quad H\mid \alpha ,H_{0}{\mathop {\sim }\limits ^{}}\mathrm {DP}(\alpha ,H_{0}). \end{aligned}$$
(3)

Here, \(\mathrm {DP}(\alpha ,H_{0})\) represents a Dirichlet process (DP) with centering probability measure \(H_{0}\) and concentration parameter \(\alpha \) (Ferguson 1973; Blackwell and MacQueen 1973), and \(\mathcal {K}(\,\cdot \mid \varvec{\theta })\) is a suitable probability kernel indexed by a latent parameter \(\varvec{\theta }\in \Theta \). Model (3) can be enriched by assigning prior distributions to \(\alpha \) and (possible) hyper-parameters associated with \(H_{0}\).

Many theoretical properties regarding DPM models can be found in the specialized literature. Here, we highlight one that is important for model specification. Sethuraman (1994) shows that

$$\begin{aligned} H(\,\cdot \,)=V_{1}\delta _{\varvec{\theta }_{1}}(\,\cdot \,)+\sum _{r=2}^{\infty }\Bigg \{V_{r}\prod _{t=1}^{r-1}(1-V_{t})\Bigg \} \delta _{\varvec{\theta }_{r}}(\,\cdot \,), \end{aligned}$$
(4)

where \(\delta _{{\varvec{a}}}(\,\cdot \,)\) is the Dirac measure centred on \({\varvec{a}}\in \Theta \) and \(\{(\varvec{\theta }_{r},V_{r}):r\in \mathbb {N}\}\) is a sequence of independent random vectors \((\varvec{\theta }_{r},V_{r})\) whose coordinates are mutually independent with common distributions \(\varvec{\theta }_{r}\sim H_{0}\) and \(V_{r}\sim \mathrm {Beta}(1,\alpha )\). Equation (4) says that H is a discrete probability measure with probability one. Thus, \(\pi ({\varvec{y}}\mid H)\) given by (3) is a countably infinite random mixture centered at the parametric model \(\pi ({\varvec{y}}\mid H_{0}) :=\int _{\Theta }\mathcal {K}({\varvec{y}}\mid \varvec{\theta })\mathrm {d}H_{0}(\varvec{\theta })\). This feature can help in choosing \(\mathcal {K}\) by analyzing the marginal behaviour of s, \({\varvec{x}}\) and l, or some transformations on them. Also, (4) implies that the induced random intensity function \(\lambda ({\varvec{y}}\mid \rho ,H):=\rho \,\pi ({\varvec{y}}\mid H)\) is not separable in terms of s, \({\varvec{x}}\) and l, even when \(\mathcal {K}\) and \(H_{0}\) are factorizable.

A full specification of model (3) requires selecting \(\mathcal {K}\) and \(H_{0}\). Within a similar context, various choices have been studied, e.g., a Beta distribution for s (Kottas 2006a); a Sarmanov bivariate distribution with Beta marginals for \({\varvec{x}}\) (Kottas and Sansó 2007); a Weibull distribution (Kottas 2006b) or Gamma distribution (Fúquene 2015) for l. Implementing such choices for our context, we observed poor estimates for the corresponding parameters, which in turn affected every other posterior inference related to (3). After analysing our data, we found that working under transformations of the form \(z\mapsto \log (\frac{z-l_{b}}{u_{b}-z}):z\in [l_{b},u_{b}]\), wildfire starting times and locations can be captured by mixtures of Normal distributions. The choice of \(l_{b}\) and \(u_{b}\) were selected according to the range of data. Specifically, we applied the following data transformation

$$\begin{aligned} \textstyle f(s)= & {} \log \left( \frac{s}{2191-s}\right) \quad \mathrm {and}\quad \nonumber \\ {\varvec{G}}({\varvec{x}})= & {} (g_{1}(x_{1}),g_{2}(x))\nonumber \\= & {} \left( \log \left( \frac{x_{1}-591{,}685.7}{823{,}584.3-x_{1}}\right) ,\log \left( \frac{x_{2}-4{,}157{,}261}{4{,}578{,}246-x_{2}} \right) \right) \end{aligned}$$
(5)

for starting times and locations, respectively. For wildfire durations, we applied Cheng and Yuan (2013)’s approach. Hence,

$$\begin{aligned}&\mathcal {K}({\varvec{y}}\mid \varvec{\theta })=\{\mathrm {Normal}(f(s)\mid \eta ,\kappa )f'(s)\}\{\mathrm {Normal}({\varvec{G}}({\varvec{x}})\mid \varvec{\mu },\varvec{\Sigma }){\varvec{J}}({\varvec{x}})\}\nonumber \\&\quad \{\mathrm {Normal}(\log (l)\mid \xi , \phi )l^{-1}\}, \end{aligned}$$
(6)

where \(\varvec{\theta }=(\eta ,\kappa ,\varvec{\mu },\varvec{\Sigma },\xi ,\phi )\) and \({\varvec{J}}({\varvec{x}})=g_{1}'(x_{1})g_{2}'(x_{2})\). Here, \(\mathrm {Normal}(\, \cdot \mid {\varvec{m}},\mathbf {V})\) is the Normal probability density function with (scalar or vector) mean \({\varvec{m}}\) and (scalar or matrix) variance \(\mathbf {V}\), \((\eta ,\kappa )\in \mathbb {R}\times (0,\infty )\), \((\varvec{\mu },\varvec{\Sigma })\in \mathbb {R}^{2}\times \mathbb {S}^{2}\) and \((\xi ,\phi ) \in \mathbb {R}\times (0,\infty )\). The set \(\mathbb {S}^{2}\) is the space of positive-definite matrices of dimension \(2\times 2\). As for \(H_{0}\), we use the following distribution

$$\begin{aligned} \mathrm {d}H_{0}(\varvec{\theta })=\mathrm {d}H_{01}(\eta ,\kappa )\mathrm {d}H_{02}(\varvec{\mu },\varvec{\Sigma })\mathrm {d}H_{03}(\xi ,\phi ), \end{aligned}$$
(7)

where

$$\begin{aligned} \mathrm {d}H_{01}(\eta ,\kappa )&=\mathrm {Normal}(\eta \mid m_{s},c_{s}^{-1}\kappa )\mathrm {Inv}\text {-}\mathrm {Gamma}(\kappa \mid 0.5a_{s},0.5b_{s})\mathrm {d}\eta \, \mathrm {d}\kappa \\ \mathrm {d}H_{02}(\varvec{\mu },\varvec{\Sigma })&=\mathrm {Normal}(\varvec{\mu }\mid {\varvec{m}}_{{\varvec{x}}},c_{{\varvec{x}}}^{-1}\varvec{\Sigma })\mathrm {Inv}\text {-}\mathrm {Wishart}(\varvec{\Sigma }\mid a_{{\varvec{x}}},\mathbf {B}_{{\varvec{x}}})\mathrm {d}\varvec{\mu }\, \mathrm {d}\varvec{\Sigma }\\ \mathrm {d}H_{03}(\xi ,\phi )&=\mathrm {Normal}(\xi \mid m_{l},c_{l}^{-1}\phi )\mathrm {Inv}\text {-}\mathrm {Gamma}(\phi \mid 0.5a_{l},0.5b_{l})\mathrm {d}\xi \,\mathrm {d}\phi . \end{aligned}$$

Here, \(\mathrm {Inv}\text {-}\mathrm {Gamma}(\,\cdot \mid a,b)\) is the inverse-Gamma probability density function with shape a and scale b, \(\mathrm {Inv}\text {-}\mathrm {Wishart}(\,\cdot \mid d,\mathbf {S})\) is the inverse-Wishart probability density function with degrees of freedom d and scale matrix \(\mathbf {S}\), \((m_{s},c_{s},a_{s},b_{s})\in \mathbb {R}\times (0,\infty )^{3}\), \(({\varvec{m}}_{{\varvec{x}}},c_{{\varvec{x}}},a_{{\varvec{x}}},\mathbf {B}_{{\varvec{x}}})\in \mathbb {R}^{2} \times (0,\infty )^{2}\times \mathbb {S}^{2}\) and \((m_{l},c_{l},a_{l},b_{l})\in \mathbb {R}\times (0,\infty )^{3}\). Equation (7) is an appealing choice in that it is a conjugate distribution for (6), with hyperparameters that are easy to calibrate using the data in the transformed scale. With the idea of having posterior inference on weakly informative priors, we first set \(a_{s}=a_{l}=3\) and \(a_{{\varvec{x}}}=4\), which are the least integer values such that \(\kappa \), \(\varvec{\Sigma }\) and \(\phi \) have finite means and infinite variances. Next, we choose prior guesses for \((m_{s},c_{s},b_{s})\), \(({\varvec{m}}_{{\varvec{x}}},c_{{\varvec{x}}},\mathbf {B}_{{\varvec{x}}})\) and \((m_{l},c_{l},b_{l})\) which determine the first two moments of \(H_{01}\), \(H_{02}\) and \(H_{03}\), through the relations

$$\begin{aligned} \begin{array}{lll} \mathrm {E}[\eta ]=m_{s}, &{} \mathrm {Var}[\eta ]=c_{s}^{-1}b_{s}, &{} \mathrm {E}[\kappa ]=b_{s}, \\ \mathrm {E}[\varvec{\mu }]={\varvec{m}}_{{\varvec{x}}}, &{} \mathrm {Var}[\varvec{\mu }]=c_{{\varvec{x}}}^{-1}\mathbf {B}_{{\varvec{x}}}, &{} \mathrm {E}[\varvec{\Sigma }]=\mathbf {B}_{{\varvec{x}}}, \\ \mathrm {E}[\xi ]=m_{l}, &{} \mathrm {Var}[\xi ]=c_{l}^{-1}b_{l}, &{} \mathrm {E}[\phi ]=b_{l}. \end{array} \end{aligned}$$

These specifications ensure good coverage of the data along with a user-friendly specification.

Here is worth emphasizing that, besides the application at issue, the main difference between the approach by Kottas et al. (2005) and the one here proposed is the marked feature of our spatio-temporal model plus the choices for kernel and prior guess at the shape, (6) and (7), respectively. These variations allow us to capture the duration and the data-based spatio-temporal features under the transformations (5).

4 Posterior Inference

We adapt Algorithm 8 (see Algorithm 1 below), proposed by Neal (2000), which relies on (4). This characteristic implies ties among the latent parameters \(\varvec{\theta }_{1},\ldots , \varvec{\theta }_{m}\) in (3), thus forming a set of \(k\le m\) unique latent values \(\varvec{\theta }^{\star }_{1},\ldots , \varvec{\theta }^{\star }_{k}\). A convenient way for updating \(\varvec{\theta }\)s in terms of \(\varvec{\theta }^{\star }\)s, is by introducing a collection of auxiliary variables \(e_{1},\ldots ,e_{m}\in \{1,\ldots ,k\}\), such that \(e_{i}=j\) if \(\varvec{\theta }_{i} =\varvec{\theta }^{\star }_{j}\). As for the concentration parameter \(\alpha \), we use a \(\mathrm {Gamma}(a_{0},b_{0})\) prior distribution with shape \(a_{0}\) and rate \(b_{0}\) (see, e.g., Escobar and West 1995; Kottas et al. 2005), independent of all hyperparameters indexed in the centering measure \(H_{0}\). Parameters \(a_{0},b_{0}\in (0,\infty )\) can be fixed by exploring the prior distribution of k given \(\alpha \), whose mean and variance are equal to \(\sum _{r=1}^{m}\frac{\alpha }{\alpha +r-1}\) and \(\sum _{r=1}^{m}\frac{\alpha (r-1)}{(\alpha +r-1)^{2}}\), respectively. Details about all full conditionals and steps in this pseudo-algorithm are given in Sections A–C of the online Supplementary Material.

figure a

Although there are numerical features that can be estimated directly from the MCMC samples, several quantities necessarily require posterior samples from the mixing measure H in (3), a topic that is not addressed by Neal (2000). To fix ideas, let \(\mathcal {F}(\rho ,H):=\mathcal {F}(\lambda (\,\cdot \mid \rho ,H))\) be a generic function of the the intensity function \(\lambda (\,\cdot \mid \rho ,H)=\rho \,\pi (\,\cdot \mid H)\). Recall that \(\pi (\, \cdot \mid H)\) is given by (3), and \(\rho \) is independent of H, following a Jeffreys prior supported on \((0,\infty )\) with functional form \(\rho ^{-1}\). Given the observed data \(\{{\varvec{y}}_{1},\ldots ,{\varvec{y}}_{m}\}\), we use a method that allows reporting posterior point and interval estimates for \(\mathcal {F}(\rho ,H)\). This inferential problem requires to deal with the posterior distribution of H. To address this issue, Ishwaran and Zarepour (2002) proposed a clever method which combines the MCMC posterior samples

$$\begin{aligned}&\{(e_{1}(t),\ldots ,e_{m}(t)):t=1,\ldots ,T\},\quad \{\alpha (t):t=1,\ldots ,T\},\quad {\{\rho (t):t=1,\ldots ,T\}}\quad \mathrm {and} \\&\quad \{\{(\eta ^{\star }_{j}(t),\kappa ^{\star }_{j}(t),\varvec{\mu }^{\star }_{j}(t),\varvec{\Sigma }^{\star }_{j}(t),\xi ^{\star }_{j}(t), \phi ^{\star }_{j}(t)):j=1,\ldots ,k(t)\}:t=1,\ldots ,T\} \end{aligned}$$

with a “truncated” stick-breaking representation of the Dirichlet process (Sethuraman 1994). Algorithm 2 below provides a pseudo-code applying their technique in our context. Details can be found in Section D of the online Supplementary Material.

figure b

5 Results and discussion

Using the data set described in Section 2 and the algorithms described in the previous section, we fitted the model described in Section 3. Parameter elicitation suggested in Sections 3 and 4 is provided below.

  • Concentration parameter: \(a_{0}=2.5\) and \(b_{0}=0.2\). These values induce a priori \(\mathrm {E}[k] \approx 41\) and \(\mathrm {Var}[k]\approx 361\).

  • Unique latent parameters: \(m_{s}=0\), \(c_{s}=0.004\), \(b_{s}=0.04\), \({\varvec{m}}_{{\varvec{x}}} =(0,0)^{\top }\), \(c_{{\varvec{x}}}=0.02\), \(\mathbf {B}_{{\varvec{x}}}=\mathrm {diag}(0.1,0.1)\), \(m_{l}=-1\), \(c_{l}=0.1\) and \(b_{l}=1\). These values induce a priori \(\mathrm {E}[\eta ]=0\), \(\mathrm {Var}[\eta ]=10\), \(\mathrm {E}[\kappa ]=0.04\), \(\mathrm {E}[\varvec{\mu }]=(0,0)^{\top }\), \(\mathrm {Var}[\varvec{\mu }]=\mathrm {diag}(5,5)\), \(\mathrm {E}[\varvec{\Sigma }]=\mathrm {diag}(0.1,0.1)\), \(\mathrm {E}[\xi ]=-1\), \(\mathrm {Var}[\xi ]=10\) and \(\mathrm {E}[\phi ]=1\).

We collected 5,000 MCMC iterations after discarding the first 100,000. The estimation of the posterior survival function for durations given starting times and locations was done using a truncation index \(G=30\).

Given that the proposed model for the intensity function is based on a random distribution, under the assumption of an underlying Poisson point process, our model falls in the class of Cox point processes with random density (3). In order to check the validity of the Poisson assumption, we computed envelopes for the inhomogeneous L-function for a non-homogeneous Poisson process with density proportional to the intensity function shown in Fig. 3a (Møller and Waagepetersen 2004). Figure 4 shows the observed L-function computed from the observations and the \(95\%\) confidence bands. The observed non-homogeneous L-function lies inside the confidence bands, showing that there is no strong evidence against the Poisson assumption. Although one would expect some level of interaction between wildfires as areas burned by one fire become less prone to have another ignition, one should also consider that only a small proportion of wildfires burn large areas, and that the random origin of the ignition source for naturally caused wildfires—mostly lightning strikes—is likely to start wildfires in other areas. Further, the spread of the small number of fires observed in this study explains the lack of evidence of interactions.

Fig. 4
figure 4

Confidence band for the \((L(r)-r)\) function in terms of distance r (in meters), computed for the observed spatial marginal point pattern of wildfires in the Valencian Community between January 1st, 2010, and December 31st, 2015. Dotted lines represent the upper and lower band limits and the solid black line represents the observed non-homogeneous \((L(r)-r)\) function

Full size image

Figure 5 shows the estimated posterior intensity function for starting times. The flexibility of the model captures quite accurately the trend and local varying cycles across time. The figure also reveals that ignition times due to lightning strikes are highly concentrated in spring/summer, which is consistent with climatic factors in the region. In addition, the intensity function shows a positive trend over time in the number of outbreaking wildfires in the study area, a phenomenon that is probably associated to the change from agricultural to industrial society in Spain (Moreira et al. 2011). Land abandonment is a social factor related to wildfire increase in size, severity and risk in Europe (McLauchlan et al. 2020; Perpiña Castillo et al. 2021). Abandonment of agricultural lands results in shrub growth, increasing at a slow pace of highly flammable fuels (Jaber et al. 2001). The abandonment of farm lands induces an ecological succession process known as “old field succession”, which has been related to increased fire risk in Spain (Santana et al. 2010) as the abandoned farm lands represent an adequate habitat for grasses, weeds and other highly combustible pioneering vegetal species. The effect of the change from agricultural to industrial society on the incidence of forest fires in Spain has been discussed by Velez (1998), and for other Mediterranean countries by Rego (1992); Alexandrian and Esnault (1998); Pérez B. (2003). A detailed treatment of the subject is beyond the scope of this paper and the reader can find further details in the literature in ecology and ecological succession.

Fig. 5
figure 5

Estimated posterior intensity function (solid blue curve) for wildfire starting times. Shaded gray area represents the 95% credible interval. The symbols “\(\,\shortmid \,\)” below the x-axis are the observed starting times

Full size image

Figure 6a shows the estimated posterior intensity function for locations through a heat map. Notice that high-intensity zones are concentrated in the north-central portion of the Iberian System (Mira, Martés and Aledua mountain chains), where the type of flora that abounds corresponds to bushes, pastures, conifers and mountainous forests. The high risk of wildfires is possibly explained by the presence of these rapid combustion elements, together with the difficult access due to the altitude. Figure 6b displays the posterior mean absolute deviation as a measure of dispersion around the estimated intensity function.

Fig. 6
figure 6

Estimated posterior intensity function and mean absolute deviation for wildfire locations. Solid gray dots represent the observed data

Full size image

Wildfire duration data can be seen as lifetimes generated by a heavy-tailed survival distribution (Xi et al. 2019). In fact, the hazard function is also useful for understanding the severity and impact of wildfires on human communities and ecosystems. Indeed, for duration data, proportional hazard and frailty models (Kalbfleisch and Prentice 2002) are frequently used to assess how durations vary in space through a collection of fire compartments (Martell and Sun 2008). See also Morin (2014); Morin et al. (2015); Bayham (2015) for nice discussions and modeling details about fire durations. Here, we use the outcome of the Bayesian nonparametric estimation to estimate the posterior survival function. Figure 7a shows such a posterior estimate, revealing a right-asymmetric shape with heavy tail. For display purposes, we truncated the x-axis at 1.5 days. It should be noted that the estimated probability that a wildfire lasts more than 1.5 days lies between 0.044 and 0.087, with probability 0.95. Figure 7b shows the corresponding estimated posterior hazard function. There is little association between the pattern of lightning strikes and fire ignitions. Wildfires triggered by lightning strikes occur at random despite the existence of zones with high lightning-strike intensity (Agee 1993).

Fig. 7
figure 7

Estimated posterior survival and hazard functions for wildfire durations. Solid blue curves represent point-wise posterior means, and shaded gray areas, the corresponding 95% credible intervals. The symbols “\(\,\shortmid \,\)” below the x-axis indicate the observed durations

Full size image

To illustrate the versatility of the proposed model in estimating functions of the duration, Figs. 8a and b show estimated posterior survival curves for durations given two different space-time observed events, selected at random. Notice the difference on the decay of the curves. In Fig. 8a, the selected event has an associated duration \(l=0.0729\) days (1.75 h), whereas for Fig. 8b, \(l=1.1458\) days (27.5 h). Notice that Fig. 8a corresponds to a low fire incidence area, while Fig. 8b to a high incidence area. Clearly, the corresponding survival function shows a shorter duration for low incidence areas, whereas for high fire incidence zones, the survival times are longer. This could be due to the different fuel availability (Agee 1993).

Fig. 8
figure 8

Estimated posterior survival function for wildfire durations given two events \((s,{\varvec{x}})\). Solid blue curves represent point-wise posterior means and shaded gray areas, the corresponding 95% credible intervals

Full size image

6 Conclusions

Wildfires are becoming a common event in the European Mediterranean zone. Their impact in landscape change, \(\mathrm {CO}_{2}\) emissions to the atmosphere and the hazard they pose to human life and property make the study of the factors associated to their presence and the development of predicting models an important task. Here we have presented a model that considers the spatio-temporal variability and duration of wildfires, three of the most important properties for prevention, risk assessment and management. The case study is representative of a significant part of the European Mediterranean zone. Our proposal represents a good tradeoff between model generality and implementation feasibility.

Weighted DPM models are a rich class of stochastic processes that provide great flexibility in terms of modeling prior beliefs, avoiding the sometimes restrictive parametric assumptions about conditional intensity functions used in classical space-time modeling.

The approach undertaken here can potentially be explored in several directions. For example, other marks, such as the area burned by a wildfire, can be incorporated in the joint intensity function. Space-time covariates \({\varvec{z}}(s,{\varvec{x}})\in \mathbb {R}^{p}\), such as weather conditions, wind speed, etc., could potentially be introduced in the joint intensity function, at the expense of adding more complexity.