A recourse-based nonlinear programming model for stream water quality management

Abstract

A recourse-based nonlinear programming (RBNP) method is developed for stream water quality management under uncertainty. It can not only reflect uncertainties expressed as interval values and probability distributions but also address nonlinearity in the objective function. A 0-1 piecewise linearization approach and an interactive algorithm are advanced for solving the RBNP model. The RBNP is applied to a case of planning stream water quality management. The RBNP modeling system can provide an effective linkage between environmental regulations and economic implications expressed as penalties or opportunity losses caused by improper policies. The solutions can be used for generating a variety of alternatives under different combinations of pre-regulated targets, which are also associated with different water-quality-violation risk levels and varied potential economic penalty or loss values.

1 Introduction

Effective planning of water quality management is important for facilitating socio-economic development and eco-environmental sustainability in watershed systems. Over the past decades, a wide range of mathematical techniques have been developed to examine the temporal and spatial economic, environmental and ecological impacts of alternative pollution-control actions, and thus aid the planners or decision-makers in formulating and adopting cost–effective water-quality management plans and policies (Lung et al. 1999; Bakar and Hossain 2010; Lv et al. 2010). However, water-quality management requires not only the reinforcement of established principles and technologies but also their extension to much wider, higher and freer scope for the realization of sustainability (Huang and Xia 2001). The system objectives are often associated with a number of socio-economic and eco-environmental factors such as economic return, environmental protection, and ecological sustainability, while the constraints are related to stream flow, pollutant discharge, soil loss, resources availability, environmental requirement, and policy regulation. Furthermore, in water quality management problems, various uncertainties exist in a number of system components as well as their interrelationships; the uncertainties can be further amplified by not only interactions among various uncertain and dynamic impact factors, but also their associations with economic implications of satisfied or violated environmental requirements.

In the past decades, a great many efforts were undertaken in addressing uncertainties in water quality management through stochastic programming approaches (e.g., dynamical programming, chance-constrained programming, and recourse model) (Anderson et al. 2000; Kentel and Aral 2004; Maqsood et al. 2005; Qin and Huang 2009; Huang et al. 2010; Sivakumar and Elango 2010). For example, Fujiwara et al. (1988) proposed a chance-constrained programming method for identifying optimal waste removal strategies that could mitigate the impacts of the waste discharges on the dissolved oxygen (DO) concentration in a water body, where probability of violating the DO deficit standard was investigated. Masliev and Somlyody (1994) advanced a probabilistic method for uncertainty analysis and parameter estimation for dissolved oxygen models. Edirisinghe et al. (2000) advanced a chance-constrained programming model for the capacity planning of a multipurpose reservoir under random stream flows. Revelli and Ridolfi (2004) proposed a stochastic dynamic model for the evolution of the biological oxygen demand (BOD) probability distribution for a river system. Chaves and Kojiri (2007) advanced a stochastic fuzzy neural network model for identification of reservoir operational strategies through considering water quantity and water quality objectives. Kerachian and Karamouz (2007) combined a water quality simulation model and a stochastic GA-based conflict resolution technique to identify optimal operating rules for water quality management in reservoir-river systems. Li and Huang (2009) proposed an inexact two-stage stochastic quadratic programming method for water-quality management, where uncertainties expressed as probability distributions and interval values could be reflected. Stochastic dynamic programming and chance-constrained programming approaches could reflect coefficients that are not certainly known but can be represented as chances or probabilities; however, they were incapable of examining economic consequences of violating some overriding policies that were considered out of the scope of the planning exercise. In comparison, recourse model is effective for decision problems where analysis of policy scenarios is desired and the related data are mostly uncertain. In recourse models, a decision is often first undertaken before values of random variables are disclosed and, then, after the random events have occurred and their values are known, a recourse action is made in order to minimize “penalties” that may appear due to any infeasibility (Huang and Loucks 2000; Lund 2002; Li et al. 2009). Generally, although stochastic programming can deal with uncertainties expressed as random variables with known probability distributions, the increased data requirements for specifying the parameters’ probability distributions can affect their practical applicability.

Another attractive approach for water quality management under uncertainty is based on interval analysis technique, which can tackle uncertainties that generally cannot be quantified as either distribution functions or membership functions because interval numbers are acceptable as its uncertain inputs. Previously, a number of applications of interval (or grey) programming or coupled interval and other programming methods (e.g. fuzzy or stochastic) in water-quality management were reported. For example, Huang (1996) formulated an interval parameter water quality model for planning water pollution control within an agricultural system, which allowed uncertain information presented as interval numbers to be effectively communicated into the optimization processes and resulting solutions. Karmakar and Mujumdar (2006) developed a grey fuzzy optimization approach for river-water-quality management to address uncertainties expressed as interval grey numbers. Qin et al. (2007) proposed an interval-parameter programming model for water quality management, where the nonlinear objective function was linearized through piecewise conversion technique. Generally, the above stochastic and interval programming methods have advantages in their effectiveness in dealing with uncertainties. However, when applying these approaches to water quality management problems, difficulties arise due to system nonlinearities. For example, the economies of scale may affect the cost coefficients in a mathematical programming problem and make the relevant objective function nonlinear (e.g. in water quality management problems, treatment cost parameters are often presented as functions of wastewater-discharge levels).

Therefore, the objective of this study is to develop a recourse-based nonlinear programming (RBNP) method, where interval-parameter nonlinear programming will be incorporated within the stochastic recourse modeling framework. The developed RBNP will be used for handling uncertainties expressed as probability distributions and interval values, and also for dealing with nonlinearities in the objective function. An 0-1 piecewise linearization approach will be advanced for solving the RBNP model. Such an approach has advantages in identifying a global optimum and is associated with a relatively low computational requirement. Then, the developed RBNP model will be applied to a case study of stream water quality management and planning. The results obtained can help decision makers to not only manage stream water quality but also gain insight into the tradeoffs between environmental and economic objectives under uncertainty.

2 Methodology

Consider an interval-parameter nonlinear programming problem without x _j x _k (j ≠ k) terms as follows:

$$ {\text{Max}}\;f^{ \pm } = \sum\limits_{j = 1}^{n} {\left[ {c_{j}^{ \pm } x_{j}^{ \pm } + d_{j}^{ \pm } \left( {x_{j}^{ \pm } } \right)^{{\theta_{j} }} } \right]} $$

(1a)

subject to:

$$ \sum\limits_{j = 1}^{n} {a_{ij}^{ \pm } x_{j}^{ \pm } \le b_{i}^{ \pm } } , \quad i = 1,2, \ldots ,m $$

(1b)

$$ x_{j}^{ \pm } \ge 0, \quad j = 1,2, \ldots ,n $$

(1c)

where a ^± _ij , b ^± _i , c ^± _j , d ^± _j and x ^± _j are interval parameters/variables; the ‘−’ and ‘+’ superscripts represent lower and upper bounds of an interval parameter/variable, respectively; θ _j is exponent index, and θ _j  ≠ 1; f ^± is referred to as a nonlinear objective function with interval parameters and variables. An interval can be defined as a number with known lower and upper bounds but unknown distribution information (Huang 1996).

Model (1a–1c) is effective for addressing both nonlinearities in objective function and uncertainties presented as intervals in the modeling parameters. However, it has difficulties in reflecting uncertainties expressed as probabilistic distributions; it is also lack of linkage to economic consequences of violated policies pre-regulated by the authorities. For example, assume that b ^± _i of model (1a–1c) is not precisely known and only its distribution, with finite mean E(b ^± _i ), is given. We can then assume that there exists a penalty for any difference (a random variable) between $\sum\nolimits_{j = 1}^{n} {a_{ij}^{ \pm } x_{j}^{ \pm } }$ and b ^± _i .

Thus, when uncertainties of the model’s right-hand sides are expressed as random variables and decisions need to be made periodically over time, the problem can be formulated as a stochastic recourse model. A two-stage stochastic recourse model can be formulated as follows:

$$ {\text{Max}}\;f = cx - E\left[ {Q\left( {x,\omega } \right)} \right] $$

(2a)

subject to:

$$ Ax \le b $$

(2b)

$$ x \le 0 $$

(2c)

where x is the first-stage anticipated decisions made before the random variables are observed, and Q(x, ω) is the optimal value (for any given Ω) of the following nonlinear program:

$$ \min q\left( {y,\;\omega } \right) $$

(3a)

subject to:

$$ W\left( \omega \right)y = h\left( \omega \right) - T\left( \omega \right)x $$

(3b)

$$ y \ge 0 $$

(3c)

where y is the second-stage decision variables (i.e. recourse variables) that depends on the realization of the first-stage random vector; q(y, ω) denotes the second-stage cost function; $\left\{ {T(\omega ), \, W(\omega ), \, h(\omega )|\omega \in \Upomega } \right\}$ are model parameters with reasonable dimensions, and are functions of the random vector (ω). For given values of the first-stage variables (x), the second-stage problem can be decomposed into independent linear sub-problems, with one sub-problem for each realization of the uncertain parameters. Assume that the random vector ω has a discrete and finite distribution, with support $\Upomega = \left\{ {\omega_{1} ,\omega_{2} , \ldots ,\omega_{v} } \right\}$. Denote p _h as the probability of realization of scenario ω _h , with p _h  > 0 and $\sum\nolimits_{h = 1}^{v} {p_{h} = 1} .$ The expected value of the second-stage optimization problem can be expressed as:

$$ E\left[ {Q\left( {x,\;\omega } \right)} \right] = \sum\limits_{h = 1}^{v} {p_{h} Q\left( {x,\;\omega_{h} } \right)} $$

(4)

Then, based on the assumption of discrete distributions for the uncertain parameters, model (2a–2c) can be equivalently formulated as a linear program as follows:

$$ {\text{Max}}\; \, f = cx - \sum\limits_{h = 1}^{v} {p_{h} q\left( {y_{h} ,\;\xi_{h} } \right)} $$

(5a)

subject to:

$$ Ax \le b $$

(5b)

$$ T\left( {\omega_{h} } \right)x + W\left( {\omega_{h} } \right)y_{{\omega_{h} }} = h\left( {\omega_{h} } \right), \, \xi_{h} \in \Upomega $$

(5c)

$$ x \ge 0 $$

(5d)

$$ y_{h} \ge 0 $$

(5e)

Obviously, stochastic programming with recourse model can effectively deal with uncertainties presented as random variables with known probability distributions. However, in real-world optimization problems, the quality of available information about the uncertainties is often not satisfactory enough for establishing probability distributions; Even if the probability distributions are available, it could be difficult to reflect them in large-scale stochastic models (Li et al. 2006). Thus, one potential approach for handling such uncertainties presented as different formats is to couple the interval-parameter nonlinear programming with the stochastic programming, leading to a recourse-based nonlinear programming (RBNP) model as follows:

$$ {\text{Max}}\; \, f^{ \pm } = \sum\limits_{j = 1}^{{n_{1} }} {\left[ {c_{j}^{ \pm } x_{j}^{ \pm } + d_{j}^{ \pm } \left( {x_{j}^{ \pm } } \right)^{{\theta_{j} }} } \right]} - \sum\limits_{j = 1}^{{n_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ \pm } y_{jh}^{ \pm } + g_{j}^{ \pm } \left( {y_{jh}^{ \pm } } \right)^{{\delta_{j} }} } \right]} } $$

(6a)

subject to:

$$ \sum\limits_{j = 1}^{{n_{1} }} {a_{rj}^{ \pm } x_{j}^{ \pm } \le b_{r}^{ \pm } } , \quad r = 1,2, \ldots ,m_{1} $$

(6b)

$$ \sum\limits_{j = 1}^{{n_{1} }} {a_{tj}^{ \pm } x_{j}^{ \pm } } + \sum\limits_{j = 1}^{{n_{2} }} {a_{tjh}^{ \pm } y_{jh}^{ \pm } } \ge \widetilde{{w_{h}^{ \pm } }}, \quad t = 1,2, \ldots ,m_{2} ; \, h = 1,2, \ldots ,v $$

(6c)

$$ x_{j}^{ \pm } \ge 0, \quad j = 1,2, \ldots ,n_{1} $$

(6d)

$$ y_{jh}^{ \pm } \ge 0, \quad j = 1,2, \ldots ,n_{2} ; \, h = 1,2, \ldots ,v $$

(6e)

where θ _j and δ _j are exponent index (θ _j , δ _j  ≠ 1); $\widetilde{{w_{h}^{ \pm } }}$ is defined as interval-random variable, which is expressed in terms of random variables but, at the same time, some random events can only be quantified as discrete intervals, leading to dual uncertainties. An interval-stochastic linear programming model can be directly transformed into two deterministic submodels, which correspond to the lower and upper bounds of the objective function value.

Since nonlinearity exists in the objective function, one of the main challenges in solving model (6a–6e) is the identification of uncertain relationships between the objective function and the related decision variables during the transform processes (Chen and Huang 2001). Even if model (6a–6e) can be transformed into two deterministic nonlinear programming submodels, there are still difficulties in identifying global optimal solution, particularly for highly nonlinear and uncertain problems. Therefore, when problems strictly require globally optimal solutions, enhanced techniques (i.e. global optimization methods) should be employed. Linearization of a nonlinear problem into a piecewise linear one is a useful approach for handling nonlinearities in the objective function. The basic idea of the linearization is to cut the nonlinear function into several segments, and then use linear formulations to approximate them. Therefore, a 0-1 piecewise linearization approach is proposed to identify a global optimal solution for such a nonlinear program, where a number of binary variables will be introduced into model (6a–6e). Thus, the RBNP model can be converted into a linear one as follows:

$$ {\text{Max}}\;f^{ \pm } = \sum\limits_{j = 1}^{{n_{1} }} {\left[ {c_{j}^{ \pm } x_{j}^{ \pm } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\gamma_{jk}^{ \pm } x_{jk}^{\prime \pm } + \varphi_{jk}^{ \pm } x_{jk}^{ \pm } } \right)} } \right]} - \sum\limits_{j = 1}^{{n_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ \pm } y_{jh}^{ \pm } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\alpha_{jk}^{ \pm } y_{jhk}^{\prime \pm } + \beta_{jk}^{ \pm } y_{jhk}^{ \pm } } \right)} } \right]} } $$

(7a)

subject to:

$$ \sum\limits_{j = 1}^{{n_{1} }} {a_{rj}^{ \pm } x_{j}^{ \pm } } + \sum\limits_{j = 1}^{{n_{1} }} {a_{rj}^{\prime \pm } \left( {\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ \pm } } } \right)} \le b_{r}^{ \pm } , \quad r = 1,2, \ldots ,m_{1} $$

(7b)

$$ \sum\limits_{j = 1}^{{n_{1} }} {a_{tj}^{ \pm } x_{j}^{ \pm } } + \sum\limits_{j = 1}^{{n_{1} }} {a_{tj}^{\prime \pm } \left( {\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ \pm } } } \right)} + \sum\limits_{j = 1}^{{n_{2} }} {a_{tjh}^{ \pm } y_{jh}^{ \pm } } + \sum\limits_{j = 1}^{{n_{2} }} {a_{tjh}^{\prime \pm } \left( {\sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ \pm } } } \right)} \ge \widetilde{{w_{h}^{ \pm } }},\;\;\;\;t = 1,2, \ldots ,m_{2} ; \, h = 1,2, \ldots ,v $$

(7c)

$$ x_{jk}^{\prime \pm } = \left\{ \begin{array}{ll} 1, & {\text{ if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} < x_{jk}^{ \pm } \le \bar{M}_{k} \\ 0, & {\text{ if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots ,n_{1} ; \, \forall k $$

(7d)

$$ \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{\prime \pm } } = 1, \quad j = 1,2, \ldots ,n_{1} ; \, \forall k $$

(7e)

$$ x_{jk}^{ \pm } - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} x_{jk}^{\prime \pm } \ge 0,\quad j = 1,2, \ldots ,n_{1} ; \, \forall k $$

(7f)

$$ x_{jk}^{ \pm } - \bar{M}_{k} x_{jk}^{\prime \pm } \le 0,\quad j = 1,2, \ldots ,n_{1} ;\forall k $$

(7g)

$$ y_{jhk}^{\prime \pm } = \left\{ \begin{array}{ll} 1, & {\text{ if }}\underline{N}_{k} < y_{jhk}^{ \pm } \le \bar{N}_{k} \\ 0, & {\text{ if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots ,n_{2} ; \, \forall h, \, k $$

(7h)

$$ \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{\prime \pm } } = 1, \quad j = 1,2, \ldots ,n_{2} ; \, \forall h, \, k $$

(7i)

$$ y_{jhk}^{ \pm } - \underline{N}_{k} y_{jhk}^{\prime \pm } \ge 0,\quad j = 1,2, \ldots ,n_{2} ; \, \forall h, \, k $$

(7j)

$$ y_{jhk}^{ \pm } - \bar{N}_{k} y_{jhk}^{\prime \pm } \le 0,\quad j = 1,2, \ldots ,n_{2} ; \, \forall h, \, k $$

(7k)

$$ x_{j}^{ \pm } \ge 0, \quad j = 1,2, \ldots ,n_{1} $$

(7l)

$$ y_{jh}^{ \pm } \ge 0, \quad j = 1,2, \ldots ,n_{2} ; \, \forall h $$

(7m)

where $x_{jk}^{\prime \pm }$ is 0-1 binary variable for identifying which segment of x ^± _jk ; $y_{jhk}^{\prime \pm }$ is 0-1 binary variable for identifying which segment of y ^± _jhk ; k denotes segment for nonlinear decision variables; $\gamma_{jk}^{ \pm }$ and φ ^± _jk are Y-intersect and slope of the first-stage cost curve in segment k, respectively; α ^± _jk and β ^± _jk are Y-intersect and slope of the second-stage cost curve in segment k, respectively; $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k}$ and $\bar{M}_{k}$ are lower and upper bounds of segment k for x ^± _jk , respectively; $\underline{N}_{k}$ and $\bar{N}_{k}$ are lower and upper bounds of segment k for y ^± _jhk , respectively. Obviously, model (7a–7m) is an interval-stochastic mixed integer linear programming model, where decision variables can be sorted into two categories: continuous and binary. Based on the interactive algorithm, model (7a–7m) can be directly transformed into two deterministic submodels that correspond to the lower and upper bounds of the objective-function value, such that global optimum can be obtained. The detailed solution method for solving model (7a–7m) is provided in Appendix to this paper.

3 Application to water quality management

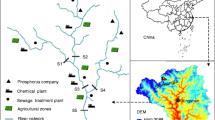
A city discharges wastewater into a nearby stream. One municipal wastewater treatment plant, three major industrial units (i.e. a paper mill, a tannery, and a tobacco factory) are the main pollutant dischargers. Figure 1 shows the schematic diagram of the study system. Uncertainties may exist in a variety of impact factors and pollution-related processes such as effluent characteristics, treatment measures, pollutant-discharge levels, deoxygenation and reaeration rates, and pollution-caused damages. For example, the volume and concentration of wastewater flows may vary with the industrial units, the generated products, and product amounts; the efficiency for mitigating biochemical oxygen demand (BOD) may also vary with operating conditions at the wastewater treatment plants (e.g., reagent ratio, temperature, pH level, and inlet BOD concentration). Since multiple wastewater discharge outlets scatter along the stream with temporal and spatial variations of their pollutant loadings, dynamic interactions exist between the pollutant loadings and the receiving water quality. Their activities are not only responsible for the pollution problems but also related to each other. Any change in one activity may lead to a series of environmental effects. Furthermore, from a long-term planning point of view, population growth and economic development within the studied region can result in increased demands for water resources and industrial products. These may lead to a continuous increase of wastewater discharge from each source. Challenges exist in satisfying the water quality requirement while facilitating the regional development.

Fig. 1

Schematic diagram of the study system

This study will focus on both maximization of economic benefit and mitigation of BOD discharges from multiple sources to the stream. For the industrial sector, the amount of wastewater can be defined in terms of units of production (e.g., gallons of wastewater per ton of pulp produced) (Eckenfelder Jr 2000). A returning wastewater flow for municipality can be estimated based on 1990 USGS water use data (Viessman and Hammer 1998). In this study, a minimum DO level for aquatic life throughout the stream water is required. The Streeter-Phelps model is used for supporting quantification of water quality constraints related to BOD and DO discharges as well as reflecting deoxygenation and reaeration dynamics within the stream. Table 1 provides the relationships among the activities (products), discharge flows, and BOD concentrations at different sources. There are significant differences in terms of the amounts and characteristics of wastewater discharged from different sectors. To guarantee water quality, wastewater treatment measures have to be adopted at point sources such as industrial discharge outlets. Table 2 shows the treatment efficiencies at different discharge sources. Table 3 provides the allowable BOD loading level for each pollution source as regulated by the local authority as well as the lower- and upper-bound levels of municipal water supply and industrial productions. The water quality requirements for BOD and DO deficit are not exceeded 6 and 3 mg/l, respectively (Viessman and Hammer 1998).

Table 1 Wastewater discharge rates and the associated probabilities

Table 2 BOD concentrations and treatment efficiencies

Table 3 Allowable BOD loading and market demand

When uncertainties of wastewater discharge rates are presented as intervals, the cost function for wastewater treatment can be estimated as follows (Loucks et al. 1981; Haith 1982):

$$ C^{ \pm } = k_{1}^{ \pm } Q^{{ \pm k_{2} }} + k_{3}^{ \pm } Q^{{ \pm k_{4} }} $$

(8)

where C ^± is the treatment cost for wastewater under a specific technology, including construction, operation and maintenance costs ($10³/year); Q ^± is the average wastewater flow treated by the process (10³ m³/day), k ^±₁ and k ^±₃ are the cost-function coefficients (k ^±₁ , k ^±₃  > 0); k ₂ and k ₄ are the economies of scale indexes for the capital and treatment costs (0 < k ₂ and k ₄ < 1), and different wastewater treatment processes (with different efficiencies) may lead to varied k ₂ and k ₄ values. Table 4 presents the related economic data of net benefits and costs. The costs are expressed as nonlinear functions of wastewater flows; they may vary along with the economy-of-scale indexes.

Table 4 Benefits and costs

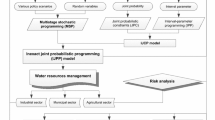
In the study problem, the associated complexities include that (i) uncertainties present in terms of random variables and/or interval values, (ii) nonlinearities exist in the wastewater treatment cost, and (iii) dynamic interactions exist among pollutant loadings, stream conditions, and water quality. The proposed RBNP method is suitable for tackling these complexities. Figure 2 presents the general framework of RBNP for water quality management. The objective is to maximize the system benefit subject to water quality requirements under various stream conditions. The decision variables are related to municipal water supply, industrial production, and recreation land use. The constraints include BOD loading allowance for each discharge source and allowable BOD and DO-deficit levels at each stream reach. Thus, we have

Fig. 2

Framework of RBNP for water quality management

Objective:

$$ \begin{aligned} {\text{Max}}\;f^{ \pm } & = L_{t} \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {NB_{it}^{ \pm } T_{it} } } + L_{t} \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {\sum\limits_{h = 1}^{v} {p_{ih} NB_{it}^{ \pm } \left( {X_{ith}^{ \pm } - T_{it} } \right)} } } \\ - L_{t}^{\prime } \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {\sum\limits_{h = 1}^{v} {p_{ih} \left[ {k_{1,i}^{ \pm } \left( {Q_{ith}^{ \pm } } \right)^{{k_{2,i} }} + k_{3,i}^{ \pm } \left( {Q_{ith}^{ \pm } } \right)^{{k_{4,i} }} } \right]} } } \\ \end{aligned} $$

(9a)

where $X_{ith}^{ \pm } = Q_{ith}^{ \pm } /w_{ith}^{ \pm } , \, \forall i,\;t,h$.

Constraints:

• (1) BOD discharge constraints:

  $$ \left( {1 - \eta_{i}^{ \pm } } \right)X_{ith}^{ \pm } w_{ith}^{ \pm } C_{it}^{ \pm } \le S_{it}^{ \pm } , \quad \forall i,\;t,h $$

  (9b)

• (2) Maximum allowable BOD discharge constraints:

  $$ U_{1} + \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RB_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 1 $$

  (9c)
  $$ U_{2} + m_{12} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + \left( {1 - \eta_{2}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RB_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 2 $$

  (9d)
  $$ U_{3} + m_{13} \left( {1 - \eta_{1t}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + m_{23} \left( {1 - \eta_{2}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + \left( {1 - \eta_{3}^{ \pm } } \right){{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RB_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 3 $$

  (9e)
  $$ U_{4} + m_{14} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + m_{24} \left( {1 - \eta_{2}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + m_{34} \left( {1 - \eta_{3}^{ \pm } } \right){{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + \left( {1 - \eta_{4}^{ \pm } } \right){{X_{4th}^{ \pm } w_{4th}^{ \pm } C_{4t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{4th}^{ \pm } w_{4th}^{ \pm } C_{4t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RB_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 4 $$

  (9f)

• (3) Maximum allowable DO-deficit constraints:

  $$ V_{2} + n_{12} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RD_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 2 $$

  (9g)
  $$ V_{3} + n_{13} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{23} \left( {1 - \eta_{2}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RD_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 3 $$

  (9h)
  $$ V_{4} + n_{14} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{24} \left( {1 - \eta_{2}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{34} \left( {1 - \eta_{3t}^{ \pm } } \right){{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RD_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 4 $$

  (9i)
  $$ V_{5} + n_{15} \left( {1 - \eta_{1}^{ \pm } } \right){{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{1th}^{ \pm } w_{1th}^{ \pm } C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{25} \left( {1 - \eta_{2t}^{ \pm } } \right){{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{2th}^{ \pm } w_{2th}^{ \pm } C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{35} \left( {1 - \eta_{3}^{ \pm } } \right){{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{3th}^{ \pm } w_{3th}^{ \pm } C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + n_{45} \left( {1 - \eta_{4}^{ \pm } } \right){{X_{4th}^{ \pm } w_{4th}^{ \pm } C_{4t}^{ \pm } } \mathord{\left/ {\vphantom {{X_{4th}^{ \pm } w_{4th}^{ \pm } C_{4t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le RD_{jt}^{ \pm } , \quad \forall t,h,{\text{ j}} = 5 $$

  (9j)

• (4) Product demand constraints:

  $$ T_{it}^{L} \le T_{it} \le T_{it}^{U} , \quad \forall i,\;t $$

  (9k)

• (5) Non-negative constraints:

  $$ X_{ith}^{ \pm } \ge 0, \quad \forall i,\;t,h $$

  (9l)

where j is name of reach (j = 1, 2, …, 5), where j = 1 for the upstream end, and j = 5 for the downstream end; i denotes wastewater discharge source (i.e., municipal wastewater treatment plant, paper mill, tannery plant, and tobacco facility); wastewater from these sources would enter into the stream at the beginnings of reaches 2 to 5; f ^± is net system benefit over the planning horizon ($); L _t  = length of period t (day); $L_{t}^{\prime }$ = length of period t (year); p _ih denotes probability of random wastewater-discharge rate at discharger i with level h (%); h denotes level of wastewater discharge rate at each source; t is planning period; NB ^± _it is net benefit per unit product from source i ($/unit product); C ^± _it is BOD concentration of raw wastewater generated at source i in period k (kg/m³); k ^±_1,i and k ^±_3,i are the cost-function coefficients for source i; k _2,i and k _4,i are the economies of scale indexes for the capital and treatment costs (0 < k _2,i and k _4,i  < 1); Q ^± _ith is the amount of discharged wastewater from source i during period t with level h (10³ m³/day); Q_r is stream flow (10³ m³/day), with $Q_{r} \gg \sum\nolimits_{i = 1}^{5} {Q_{ith}^{ \pm } }$; $\eta_{i}^{ \pm }$ is BOD treatment efficiency at source i (%); RB ^± _jt is designated BOD concentration at the beginning of reach j (mg/l); RD ^± _jt is allowable DO deficit at the end of reach j (mg/l); S ^± _it is BOD discharge allowance for source i during period t (tonne/day); T ^L _it and T ^U _it are lower- and upper-bound demands for product i during period t (unit/day), respectively; T _it is product target pre-regulated by source i during period k (the first-stage decision variable) (m³/day or tonne/day); w ^± _ith is random wastewater discharge rate at source i in period t with level h (m³/unit product); X ^± _ith means production level of source i during period t with level h, which is affected by the random BOD generation rates and the environmental requirements (the second-stage decision variable) (m³/day or tonne/day).

In model (9a–9l), m _ij is transfer factor of BOD from source i to reach j; U _j is relational constant of BOD (mg/l), and j = 1, 2, …, 4; n _ij is transfer factor of DO from source i to reach j; V _j is relational constant of DO (mg/l), and j = 2, 3, …, 5. In this study, the Streeter-Phelps model is used for supporting quantification of water quality constraints related to BOD and DO discharges as well as reflecting deoxygenation and reaeration dynamics within the stream. The total BOD loading and DO deficit at the beginning of each reach can be calculated as follows (Viessman and Hammer 1998):

$$ L_{j} = L_{j - 1} e^{{ - k_{d} t_{j - 1} }} + \left( {1 - \eta_{i} } \right)BOD_{i} $$

(10a)

$$ D_{j} = {\frac{{k_{d} L_{j - 1} }}{{k_{a} - k_{d} }}}\left( {e^{{ - k_{d} t_{j - 1} }} - e^{{ - k_{a} t_{j - 1} }} } \right) + D_{j - 1} e^{{ - k_{a} t_{j - 1} }} $$

(10b)

where L _j−1 and L _j are respectively BOD loads at the beginnings of reaches j − 1 and j; D _j is the oxygen deficit at the beginning of reach j; t _j−1 is the length of reach j − 1 expressed in time units; η _i is the wastewater treatment efficiency at source i; k _d is the first-order deoxygenation rate constant (day⁻¹); k _a is the first-order reaeration rate constant (day⁻¹); BOD _i is the total amount of BOD to be disposed of at source i (kg/day). Let $\alpha_{j} = e^{{ - k_{d} t_{j} }} ,$ $\beta_{j} = e^{{ - k_{a} t_{j} }} ,$, and $\gamma = {{k_{d} } \mathord{\left/ {\vphantom {{k_{d} } {\left( {k_{a} - k_{d} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {k_{a} - k_{d} } \right)}}$. Substituting the related items in Eqs. 10a and 10b with α _j−1 and β _j−1, the BOD load and DO deficit at the beginning of reach j can be calculated:

$$ L_{j} = \alpha_{j - 1} L_{j - 1} + \left( {1 - \eta_{i} } \right)BOD_{i} $$

(11a)

$$ D_{j} = \gamma L_{j - 1} \left( {\alpha_{j - 1} - \beta_{j - 1} } \right) + D_{j - 1} \beta_{j - 1} $$

(11b)

The BOD load and DO deficit at the downstream associated with m wastewater discharge sources can be formulated as follows:

$$ L_{n} = \prod\limits_{j = 1}^{n} {\alpha_{j} L_{0} } + \prod\limits_{j = 2}^{n} {\alpha_{j} \left( {1 - \eta_{1} } \right)BOD_{1} } + \cdots + \alpha_{n} \left( {1 - \eta_{m - 1} } \right)BOD_{m - 1} + \left( {1 - \eta_{m} } \right)BOD_{m} $$

(12a)

$$ D_{n} = \gamma L_{n - 1} \left( {\alpha_{n - 1} - \beta_{n - 1} } \right) + D_{n - 1} \beta_{n - 1} $$

(12b)

When uncertainties expressed as interval values that exist in the BOD discharge level and removal efficiency, Eqs. 12a and 12b can be converted into:

$$ L_{n}^{ \pm } = \prod\limits_{j = 1}^{n} {e^{{ - k_{d} t_{j} }} } L_{0}^{ \pm } + \prod\limits_{j = 2}^{n} {e^{{ - k_{d} t_{j} }} } \left( {1 - \eta_{1}^{ \pm } } \right)BOD_{1}^{ \pm } + \cdots + e^{{ - k_{d} t_{n} }} \left( {1 - \eta_{m - 1}^{ \pm } } \right)BOD_{m - 1}^{ \pm } + \left( {1 - \eta_{m}^{ \pm } } \right)BOD_{m}^{ \pm } $$

(13a)

$$ D_{n}^{ \pm } = {\frac{{k_{d} }}{{k_{a} - k_{d} }}}L_{n - 1}^{ \pm } \left( {e^{{ - k_{d} t_{n - 1} }} - e^{{ - k_{a} t_{n - 1} }} } \right) + D_{n - 1}^{ \pm } e^{{ - k_{a} t_{n - 1} }} $$

(13b)

According to the descriptions in Sect. 2, an 0-1 piecewise linearization approach is used to convert model (9a–9l) into a linear one. Through using a number of binary variables (i.e. 0-1 variables), the piecewise linearization can cut the nonlinear treatment cost function into several segments. Thus, we have:

$$ \begin{aligned} {\text{Max}}\;f^{ \pm } & = 1825 \times \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {NB_{it}^{ \pm } T_{it} } } + 1825 \times \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {\sum\limits_{h = 1}^{v} {p_{ih} NB_{it}^{ \pm } \left( {X_{ith}^{ \pm } - T_{it} } \right)} } } - 5 \times \sum\limits_{i = 1}^{4} {\sum\limits_{t = 1}^{3} {\sum\limits_{h = 1}^{v} {\sum\limits_{k = 1}^{{s_{i} }} {p_{ih} \left( {\beta_{itk}^{ \pm } z_{ithk}^{ \pm } + \alpha_{itk}^{ \pm } q_{ithk}^{ \pm } } \right)} } } } \\ \\ \end{aligned} $$

(14a)

where $Q_{ith}^{ \pm } = \sum\nolimits_{k = 1}^{{s_{i} }} {q_{ithk}^{ \pm } }$ and $X_{ith}^{ \pm } = \sum\nolimits_{k = 1}^{{s_{i} }} {q_{ithk}^{ \pm } /w_{ith}^{ \pm } }$

$$ \begin{aligned} & {\text{subject to:}} \\ & \quad \sum\limits_{k = 1}^{{s_{i} }} {q_{ithk}^{ \pm } } \left( {1 - \eta_{i}^{ \pm } } \right)C_{it}^{ \pm } \le S_{it}^{ \pm } , \quad \forall i,\;t,h \\ \end{aligned} $$

(14b)

$$ 1.558 + \sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{BOD}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 1 $$

(14c)

$$ 1.252 + 0.803\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + \sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{BOD}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 2 $$

(14d)

$$ 1.105 + 0.709\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.883\sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \\ + \sum\limits_{k = 1}^{{s_{3} }} {q_{3thk}^{ \pm } } {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{BOD}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 3 \\ $$

(14e)

$$ 0.975 + 0.626\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.779\sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \\ + 0.883\sum\limits_{k = 1}^{{s_{3} }} {q_{3thk}^{ \pm } } {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + \sum\limits_{k = 1}^{{s_{4} }} {q_{4thk}^{ \pm } } {{\left( {1 - \eta_{4}^{ \pm } } \right)C_{4t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{4}^{ \pm } } \right)C_{4t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{BOD}}}}^{ \pm } , \quad \forall t,h,\, j = 4 $$

(14f)

$$ 0.552 + 0.171\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{D}}}}^{ \pm } , \quad \forall t,h,{\text{j}} = 2 $$

(14g)

$$ 0.607 + 0.233\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.108\sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{D}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 3 $$

(14h)

$$ 0.638 + 0.276\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.188\sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \\ + 0.108\sum\limits_{k = 1}^{{s_{3} }} {q_{3thk}^{ \pm } } {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{D}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 4 $$

(14i)

$$ 0.647 + 0.322\sum\limits_{k = 1}^{{s_{1} }} {q_{1thk}^{ \pm } } {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{1}^{ \pm } } \right)C_{1t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.291\sum\limits_{k = 1}^{{s_{2} }} {q_{2thk}^{ \pm } } {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{2}^{ \pm } } \right)C_{2t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \\ + 0.256\sum\limits_{k = 1}^{{s_{3} }} {q_{3thk}^{ \pm } } {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{3}^{ \pm } } \right)C_{3t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} + 0.205\sum\limits_{k = 1}^{{s_{4} }} {q_{4thk}^{ \pm } } {{\left( {1 - \eta_{4}^{ \pm } } \right)C_{4t}^{ \pm } } \mathord{\left/ {\vphantom {{\left( {1 - \eta_{4}^{ \pm } } \right)C_{4t}^{ \pm } } {Q_{r} }}} \right. \kern-\nulldelimiterspace} {Q_{r} }} \le R_{{jt{\text{D}}}}^{ \pm } , \quad \forall t,h,{\text{ j}} = 5 $$

(14j)

$$ T_{it}^{L} \le T_{it} \le T_{it}^{U} , \quad \forall i,\;t $$

(14k)

$$ z_{ithk}^{ \pm } = \left\{ \begin{array}{ll} 1, & {\text{if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{ik} < q_{ithk}^{ \pm } \le \bar{M}_{ik} \\ 0, & {\text{if otherwise}} \\ \end{array} \right., \quad \forall i,\;t,\;h,\;k $$

(14l)

$$ \sum\limits_{k = 1}^{{s_{i} }} {z_{ithk}^{ \pm } } = 1, \quad \forall i, \, t, \, h, \, k $$

(14m)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{ik} z_{ithk}^{ \pm } \le q_{ithk}^{ \pm } \le \bar{M}_{ik} z_{ithk}^{ \pm } \quad \forall i, \, t, \, h, \, k $$

(14n)

$$ q_{ithk}^{ \pm } \ge 0, \quad \forall i, \, t, \, h, \, k $$

(14o)

where k is the segment for decision variables, where k = 1, 2, …, s _i for wastewater flow generated in source i; α ^± _itk is the slope of treatment-cost curve for wastewater flow at source i during period t in segment k ($/10³ m³ year), β ^± _itk  = Y-intersect of transportation-cost curve for wastewater flow at source i during period t in segment k ($/year); $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k}$ is the lower bound of segment k for wastewater flow (10³ m³); $\bar{M}_{k}$is the upper bound of segment k for wastewater flow (10³ m³); q ^± _ithk is wastewater amount at source i during period t in segment k (10³ m³/day) (continuous variable), and $\sum\nolimits_{k = 1}^{{s_{i} }} {q_{ithk}^{ \pm } } = Q_{ith}^{ \pm }$; z ^± _ithk is binary variable for identifying which segment is for treatment cost of wastewater flows.

Obviously, model (14a–14o) is an interval-stochastic two-stage mixed integer linear programming model, where decision variables can be sorted into two categories: continuous and binary. The continuous variables represent wastewater flows discharged by source i, while the binary ones help identify correct segments for treatment costs of different wastewater amounts. Through solving two deterministic submodels that correspond to the lower and upper bounds of the objective-function value [of model (14a–14o)], the final solutions can be obtained as follows:

$$ X_{{ith\,{\text{opt}}}}^{ \pm } = \left[ {X_{{ith\,{\text{opt}}}}^{ - } ,X_{{ith\,{\text{opt}}}}^{ + } } \right],\quad \forall i,t,h $$

(15a)

with $X_{ith}^{ - } = \sum\limits_{k = 1}^{{s_{i} }} {q_{ithk}^{ - } /w_{ith}^{ + } }$ and $X_{ith}^{ + } = \sum\limits_{k = 1}^{{s_{i} }} {q_{ithk}^{ + } /w_{ith}^{ - } }$

$$ PD_{{ith\,{\text{opt}}}}^{ \pm } /PS_{{ith\,{\text{opt}}}}^{ \pm } = X_{{ith\,{\text{opt}}}}^{ \pm } - T_{{it\,{\text{opt}}}} \quad \forall i, \, t, \, h $$

(15b)

$$ f_{\text{opt}}^{ \pm } = \left[ {f_{\text{opt}}^{ - } ,f_{\text{opt}}^{ + } } \right] $$

(15c)

The PD ^± _ith or PS ^± _ith means the probabilistic deficit or surplus under different BOD-generation levels. Probabilistic deficit or surplus will occur if the pre-regulated targets are different from the planned levels (i.e. probabilistic deficit/surplus = planned level − pre-regulated target). When the pre-regulated target exceeds the planned level, a probabilistic deficit (with negative sign) may exist; conversely, a surplus (with positive sign) will occur when the target is lower than the planned level. Correspondingly, the probabilistic deficit can lead to excess wastewater discharge and economic penalty due to violating environmental requirements; in comparison, the probabilistic surplus corresponds to a low target value and a low wastewater discharge level, and thus could result in opportunity loss due to a too conservative strategy for economic activities.

4 Result analysis

Figure 3 presents the targeted and planned values for the municipal wastewater treatment plant over the planning horizon. The optimized target value would be 70,000 m³/day in period 1. The planned levels would be [46.2, 78.0] × 10³ m³/day if the wastewater-discharge rate is low with a probability of 20%, [44.1, 74.5] × 10³ m³/day under medium discharge rate (probability = 60%), and [41.6, 70.0] × 10³ m³/day under high discharge rate (probability = 20%). In period 2, the optimized target would be 75,000 m³/day, and the planned values would be [50.8, 85.1] × 10³, [48.4, 81.2] × 10³ and [45.6, 81.2] × 10³ m³/day under the low, medium and high discharge rates, respectively. In period 3, the optimized target would be 72,000 m³/day, and the planned values would be [54.7, 91.5] × 10³, [52.2, 87.3] × 10³ and [49.2, 82.2] × 10³ m³/day under the low, medium and high discharge rates, respectively. The solutions for the planned level are presented as combinations of interval and distributional information. Their upper bounds correspond to a higher system benefit under advantageous conditions, while their lower bounds are related to a more conservative strategy under demanding conditions.

Fig. 3

Targeted and planned values for wastewater treatment plant

Probabilistic deficit or surplus would occur if the pre-regulated targets are different from the planned levels (i.e. probabilistic deficit/surplus = planned level − regulated target). Figure 4 provides the probabilistic deficit and surplus for the wastewater treatment plant over the planning horizon. Under low discharge rate, the probabilistic deficit (or surplus) levels would be [−23.8, 8.0] × 10³, [−24.2, 10.1] × 10³ and [−17.3, 19.5] × 10³ m³/day in periods 1, 2 and 3; under medium discharge rate, the probabilistic deficit (or surplus) levels would be [−25.9, 4.4] × 10³, [−26.6, 6.2] × 10³ and [−19.8, 15.3] × 10³ m³/day in periods 1, 2 and 3; when discharge rate is high, the probabilistic deficit (or surplus) levels would be [−28.4, 0.05] × 10³, [−29.4, 1.5] × 10³ and [−22.8, 10.2] × 10³ m³/day in periods 1, 2 and 3, respectively. The negative values represent probabilistic deficits under demanding conditions. They imply that, if the actual wastewater treatment activities are planned based on the target levels, untreated wastewater would then be 28.4 × 10³ m³/day (in period 1), 29.4 × 10³ m³/day (in period 2) and 22.8 × 10³ m³/day (in period 3) under high discharge rate. The untreated wastewater (i.e. deficit) would be subject to penalties (i.e. a reduced system benefit). In comparison, the positive values denote probabilistic surpluses. For example, when wastewater discharge rate is low over the planning horizon, there would be 8.0 × 10³, 10.1 × 10³ and 19.5 × 10³ m³/day of surplus flows can be treated within the environmental requirement. The results indicate that, under advantageous conditions, opportunity losses would occur due to a too conservative strategy (i.e. with a low target value).

Fig. 4

Probabilistic deficit or surplus values for wastewater treatment plant

Figures 5 and 6 show the optimized production plan and the probabilistic deficit (or surplus) for the paper mill over the planning horizon. The results indicate that, in period 1, the production target would be 22.0 tonne/day, and the planned production levels would be [19.4, 31.1], [18.4, 29.7] and [17.6, 28.2] tonne/day when the wastewater discharge rates are low, medium and high; correspondingly, the probabilistic deficit (or surplus) would be [−2.6, 9.1], [−3.6, 7.7] and [−4.4, 6.2] tonne/day with probabilities of 20, 60 and 20%, respectively. In period 2, the target value would be 25.0 tonne/day, and the planned levels would be [20.6, 33.2], [19.6, 31.6] and [18.7, 30.1] tonne/day under low, medium and high discharge rates; the probabilistic deficit (or surplus) would thus be [−4.4, 8.2], [−5.4, 6.6] and [−6.3, 5.1] tonne/day, respectively. In period 3, the targeted value would be 27.0 tonne/day, and the planned levels would be [21.7, 35.0], [20.6, 33.3] and [19.6, 31.7] tonne/day under low, medium and high discharge rates; the probabilistic deficit (or surplus) would thus be [−5.3, 8.0], [−6.4, 6.3] and [−7.4, 4.7] tonne/day, respectively.

Fig. 5

Targeted and planned values for paper mill

Fig. 6

Probabilistic deficit or surplus values for paper mill

Figures 7 and 8 show the targeted and planned values as well as the probabilistic deficit and surplus for the tannery plant over the planning horizon. For example, in period 1, the targeted value would be 14.5 tonne/day; the planned values would be [10.9, 16.9], [10.4, 16.1], [9.9, 15.4] and [9.4, 14.6] tonne/day when the wastewater discharge rates are low, low-medium, medium and high; correspondingly, the probabilistic deficit (or surplus) would be [−3.6, 2.4], [−4.1, 1.6], [−4.6, 0.9] and [−5.1, 0.1] tonne/day (with probabilities of 15, 25, 45 and 15% respectively). Figures 9 and 10 provide the results for the tobacco factory. For the tobacco factory, in period 1, the optimized target would be 4.5 tonne/day, and the planned values would be [2.1, 5.3], [2.0, 5.1], [1.9, 4.8], and [1.8, 4.6] tonne/day under low, low-medium, medium and high discharge rates; correspondingly, the probabilistic deficit (or surplus) would be [−2.4, 0.8], [−2.5, 0.6], [−2.6, 0.3] and [−2.7, 0.1] tonne/day, respectively. The results for the tannery plant and tobacco factory in periods 2 and 3 can be similarly interpreted based on the results presented in Fig. 7, 8, 9, and 10.

Fig. 7

Targeted and planned values for tannery plant

Fig. 8

Probabilistic deficit or surplus values for tannery plant

Fig. 9

Targeted and planned values for tobacco factory

Fig. 10

Probabilistic deficit or surplus values for tobacco factory

5 Discussion and conclusion

Various alternatives could be generated through adjustment of the decision variables between their lower and upper bounds (i.e. X ^± _ith ). The intervals for X ^± _ith are also useful for decision makers to justify the generated alternatives directly, or to adjust the planned activity levels when the stream water quality is violated under uncertainty. Table 5 presents sixteen decision alternatives generated under different combinations of planned levels (X ^± _ith ) at lower and upper levels through a 2⁴ (i.e. two-level with four variables) factorial design approach (Box et al. 1978). The results indicate the economic impacts of variations in planned level (i.e. probabilistic deficit or surplus). The alternatives were produced by adjusting the planned levels and thus probabilistic deficit or surplus values between lower and upper bounds of X ^± _ith . The results indicate that alternatives 2, 4, 6, 8, 10, 12, 14 and 16 (where X ^±_1th  = X ⁺_1th ) would lead to significantly higher system benefits than alternatives 1, 3, 5, 7, 9, 11, 13 and 15 (where X ^±_1th  = X ⁻_1th ). The effects of X ^±_1th , X ^±_2th , X ^±_3th and X ^±_4th on the system benefit are 918.5, 28.9, 39.9 and 167.6, respectively; the positive values mean that the system benefit would increase as the planned level increases. The interaction effects of X ^±_1th X ^±_2th X ^±_4th and X ^±_1th X ^±_3th X ^±_4th were 0.11 and −0.06, respectively, implying that the effects of X ^±_2th and X ^±_3th were mainly from interactions of X ^±_1th and X ^±_4th where X ^±_1th had a high effect level. Furthermore, the difference between the interaction effect of X ^±_1th X ^±_4th (i.e. −0.04) and the main effect of X ^±_1th (i.e. 918.5) was large, implying that the effect of X ^±_4th might be mainly due to itself. In summary, (i) X ^±_1th (i.e. the planned level for municipal wastewater treatment plant) has the most significant effect on the expected system benefit; (ii) X ^±_4th (the planned level for tobacco factory) has the second largest effect on the system benefit; (iii) X ^±_2th and X ^±_3th (the planned levels for paper mill and tannery plant) has considerable effects. Therefore, effective planning for municipal wastewater treatment plant under varying discharge rates is more important for improving the system’s performance than that of the industrial sector. Among the industrial dischargers, planning for the tobacco facility is more important than planning for the paper mill and tannery plant. Similar post-optimality analyses can also be conducted for solutions under other scenarios of economic targets.

Table 5 Alternatives obtained from solutions under the optimized targets

The expected net system benefit over the planning horizon would be $[1431.5, 3037.0] × 10⁶ under the optimized target levels, where the lower-bound value (i.e. $1431.5 × 10⁶) corresponds to demanding conditions while the upper-bound value (i.e. $3037.0 × 10⁶) is associated with advantageous conditions. Under demanding conditions, the first-stage benefit would be $2225.6 × 10⁶; the expected second-stage benefit would be −$783.7 × 10⁶; the probabilistic cost for wastewater treatment would be $10.4 × 10⁶. The negative second-stage benefit denotes penalties due to excess wastewater discharges under demanding conditions. In comparison, under advantageous conditions, the first-stage benefit would be $2738.5 × 10⁶; the expected second-stage benefit would be $311.7 × 10⁶; the probabilistic cost for wastewater treatment would be $13.3 × 10⁶. The positive second-stage benefit denotes opportunity losses would generate due to a too conservative strategy. Generally, solutions of the objective function value (i.e. $[1431.5, 3037.0] × 10⁶) provide two extremes of the expected net system benefit over the planning horizon, which correspond to conservative and optimistic strategies. As the actual value of each decision variable varies within its lower and upper bounds, the system benefit would change correspondingly between f ⁻_opt and f ⁺_opt with varying reliability levels. The lower-bound system benefit would range from $1431.5 × 10⁶ to $2466.3 × 10⁶ while the upper-bound system benefit would vary from $1761.8 × 10⁶ to $3037.0 × 10⁶ (as shown in Fig. 11). Planning with a lower system benefit represents a risk-averse attitude, which is associated with a higher system reliability. Conversely, a strong desire to acquire a higher system benefit is associated with a raised risk for violating the environmental criteria (particularly under demanding conditions).

Fig. 11

System benefits under different combinations of decision variables

The RBNP modeling formulation can provide a linkage between the pre-regulated targets and the associated economic penalties caused by improper policies. Different policies in regulating the municipal and industrial activities are associated with different options in handling the tradeoffs among system benefit and environment-violation risk. For example, when the regulated target (T _itopt) reaches the lower-bound demand for each source (i.e. T _itopt = T ^L _it ), the expected net system benefit would be $[1428.7, 3033.3] × 10⁶. Under demanding conditions, the first-stage benefit and second-stage probabilistic penalty would respectively be $2079.8 × 10⁶ and −$640.7 × 10⁶, both lower than values under the optimized target (i.e. $2738.5 × 10⁶ and −$783.7 × 10⁶). Under advantageous conditions, the first-stage benefit would be $2556.1 × 10⁶ (lower than that under the optimized target) and second-stage probabilistic loss would be $490.4 × 10⁶ (higher than that under the optimized target). Therefore, the results demonstrated that, when the regulated targets reach their lower bounds, there would then be less wastewater discharge and thus lower penalty; however, potentially more economic loss would be generated when wastewater discharge level is low.

In summary, a recourse-based nonlinear programming (RBNP) method has been developed for stream water quality management under uncertainty. The RBNP integrates stochastic programming with recourse and interval-parameter nonlinear programming techniques into a general framework. It can not only reflect uncertainties expressed as interval values and probability distributions but also address nonlinearity in the objective function. An 0-1 piecewise linearization approach and an interactive algorithm have been proposed for solving the RBNP model, which have advantages in identifying a global optimum and are associated with a relatively low computational requirement. The developed method has been applied to a case of planning stream water quality management. The modeling formulation can provide an effective linkage between environmental regulations and economic implications expressed as penalties or opportunity losses caused by improper policies. The results have demonstrated that the RBNP could effectively communicate different form uncertainties into the optimization process, and generate solutions presented as combinations of interval and distributional information. Decision alternatives could then be obtained by adjusting different combinations of the decision variables within their solution intervals. Willingness to accept a lower system benefit will guarantee a lower risk of violating the environmental regulations but, at the same time, may result in opportunity losses under advantageous conditions. A strong desire to acquire a higher system benefit will be associated with a raised risk of constraint violation under demanding conditions.

Although this study is the first attempt for planning a stream water-quality management system through the developed RBNP approach, a number of research extensions still exist. Firstly, different linearization levels could have significant influences on model solutions due to varied exponent. In a certain range, solution errors will decrease with the rising segmentation numbers. However, this inevitably results in increased number of decision variables for the optimization models. Consequently, system errors will accumulate due to the increased scale of calculations. Thus, it is critical that a proper linearization level be selected. Secondly, the study system was based on a hypothetical case of stream water-quality management, where BOD and DO were considered as the main water quality indicators. This situation is suitable to point-source pollution controls for water bodies in the vicinity of urban area with both residential sewage and industrial wastewater being the main pollution sources. Nutrients and pesticides from agricultural land are becoming water quality concerns when they move off target to surface water. Future work is desired to further account for non-point sources pollutions from agricultural sectors.

Appendix: Solution method

A two-step method is proposed for solving the RBNP model (i.e. model 7a–7l). The submodel corresponding to f ⁺ can be formulated in the first step when the system objective is to be maximized; the second submodel (corresponding to f ⁻) can then be formulated based on the solution of the first submodel. Thus, the first submodel can be formulated (assume that B ^± > 0 and f ^± > 0) as follows:

$$ \begin{aligned} {\text{Max }}f^{ + } = \sum\limits_{j = 1}^{{j_{1} }} {\left[ {c_{j}^{ + } x_{j}^{ + } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\gamma_{j}^{ + } x_{jk}^{\prime + } + \varphi_{j}^{ + } x_{jk}^{ + } } \right)} } \right]} + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left[ {c_{j}^{ + } x_{j}^{ - } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\gamma_{j}^{ + } x_{jk}^{\prime - } + \varphi_{j}^{ + } x_{jk}^{ - } } \right)} } \right]} \\ - \sum\limits_{j = 1}^{{j_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ - } y_{jh}^{ - } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\alpha_{j}^{ - } y_{jhk}^{\prime - } + \beta_{j}^{ - } y_{jhk}^{ - } } \right)} } \right]} } - \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ - } y_{jh}^{ + } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\alpha_{j}^{ - } y_{jhk}^{\prime + } + \beta_{j}^{ - } y_{jhk}^{ + } } \right)} } \right]} } \\ \end{aligned} $$

(16)

subject to:

$$ \sum\limits_{j = 1}^{{j_{1} }} {\left[ {\left| {a_{rj} } \right|^{ - } {\text{Sign}}\left( {a_{rj}^{ - } } \right)x_{j}^{ + } + \left| {a_{rj}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{rj}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ + } } } \right]} + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left[ {\left| {a_{rj} } \right|^{ + } {\text{Sign}}\left( {a_{rj}^{ + } } \right)x_{j}^{ - } + \left| {a_{rj}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{rj}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ - } } } \right] \le b_{r}^{ + } , \, \forall r} $$

(17)

$$ \begin{aligned} \sum\limits_{j = 1}^{{j_{1} }} {\left[ {\left| {a_{tj} } \right|^{ - } {\text{Sign}}\left( {a_{tj}^{ - } } \right)x_{j}^{ + } + \left| {a_{tj}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{tj}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ + } } } \right]} + \sum\limits_{{j = k_{1} + 1}}^{{j_{1} }} {\left[ {\left| {a_{tj} } \right|^{ + } {\text{Sign}}\left( {a_{tj}^{ + } } \right)x_{j}^{ - } + \left| {a_{tj}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{tj}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ - } } } \right]} \\ + \sum\limits_{j = 1}^{{j_{2} }} {\left[ {\left| {a_{tjh} } \right|^{ + } {\text{Sign}}\left( {a_{tjh}^{ + } } \right)y_{jhk}^{ - } + \left| {a_{tjh}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{tjh}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ - } } } \right]} \\ + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\left[ {\left| {a_{tjh} } \right|^{ - } {\text{Sign}}\left( {a_{tjh}^{ - } } \right)y_{jhk}^{ + } + \left| {a_{tjh}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{tjh}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ + } } } \right]} \, \ge \widetilde{{w_{h}^{ - } }}, \quad \forall t, \, h, \, k \\ \end{aligned} $$

(18)

$$ x_{jk}^{\prime + } = \left\{ \begin{array} {ll} 1, & {\text{if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} < x_{jk}^{ + } \le \bar{M}_{k} \\ 0, & {\text{if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots , \, j_{1} ; \, \forall k $$

(19)

$$ x_{jk}^{\prime - } = \left\{ \begin{array} {ll} 1,& {\text{if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} < x_{jk}^{ - } \le \bar{M}_{k} \\ 0, & {\text{if otherwise}} \\ \end{array} \right., \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} ; \, \forall k $$

(20)

$$ \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{\prime + } } = 1, \quad j = 1,2, \ldots , \, j_{1} ; \, \forall k $$

(21)

$$ \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{\prime - } } = 1, \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} ; \, \forall k $$

(22)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} x_{jk}^{\prime + } \le x_{jk}^{ + } \le \bar{M}_{k} x_{jk}^{\prime + } , \quad j = 1,2, \ldots ,j_{1} ; \, \forall k $$

(23)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} x_{jk}^{ - } \le x_{jk}^{ - } \le \bar{M}_{k} x_{jk}^{\prime - } , \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} ; \, \forall k $$

(24)

$$ y_{jhk}^{ - } = \left\{ \begin{array}{ll} 1,& {\text{ if }}\underline{N}_{k} < y_{jhk}^{ - } \le \bar{N}_{k} \\ 0,& {\text{ if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots ,j_{2} ; \, \forall h, \, k $$

(25)

$$ y_{jhk}^{\prime + } = \left\{ \begin{array}{ll} 1, & {\text{ if }}\underline{N}_{k} < y_{jhk}^{ + } \le \bar{N}_{k} \\ 0, & {\text{ if otherwise}} \\ \end{array} \right., \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(26)

$$ \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{\prime - } } = 1, \quad j = 1, \, 2, \ldots ,j_{2} ; \, \forall h, \, k $$

(27)

$$ \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{\prime + } } = 1, \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(28)

$$ \underline{N}_{k} y_{jhk}^{\prime - } \le y_{jhk}^{ - } \le \bar{N}_{k} y_{jhk}^{\prime - } , \quad j = 1,2, \ldots ,j_{2} ; \, \forall h, \, k $$

(29)

$$ \underline{N}_{k} y_{jhk}^{\prime + } \le y_{jhk}^{ + } \le \bar{N}_{k} y_{jhk}^{\prime + } , \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(30)

$$ x_{j}^{ + } , \, x_{jk}^{ + } \ge 0, \quad j = 1,2, \ldots ,j_{1} $$

(31)

$$ x_{j}^{ - } , \, x_{jk}^{ - } \ge 0, \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} $$

(32)

$$ y_{jh}^{ - } , \, y_{jhk}^{ - } \ge 0, \quad j = 1,2, \ldots ,j_{2} $$

(33)

$$ y_{jh}^{ + } , \, y_{jhk}^{ + } \ge 0, \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} $$

(34)

where x ⁺ _j and x ⁺ _jk (j = 1, 2, …, j ₁) are upper bounds of the first-stage variables with positive coefficients in the objective function; x ⁻ _j and x ⁻ _jk (j = j ₁ + 1, j ₁ + 2, …, n ₁) are lower bounds of the first-stage variables with negative coefficients; y ⁻ _jh and y ⁻ _jhk (j = 1, 2, …, j ₂) are the second-stage variables with positive coefficients in the objective function; y ⁺ _jh and y ⁺ _jhk (j = j ₂ + 1, j ₂ + 2, …, n ₂) are the second-stage variables with negative coefficients. Then, based on solutions of the first submodel (16–34), the second submodel (corresponding to f ⁻) can be formulated as:

$$ \begin{aligned} {\text{Max }}f^{ - } & = \sum\limits_{j = 1}^{{j_{1} }} {\left[ {c_{j}^{ - } x_{j}^{ - } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\gamma_{j}^{ - } x_{jk}^{\prime - } + \varphi_{j}^{ - } x_{jk}^{ - } } \right)} } \right]} + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left[ {c_{j}^{ - } x_{j}^{ + } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\gamma_{j}^{ - } x_{jk}^{\prime + } + \varphi_{j}^{ - } x_{jk}^{ + } } \right)} } \right]} \\ - \sum\limits_{j = 1}^{{j_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ + } y_{jh}^{ + } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\alpha_{j}^{ + } y_{jhk}^{\prime + } + \beta_{j}^{ + } y_{jhk}^{ + } } \right)} } \right]} } - \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\sum\limits_{h = 1}^{v} {p_{h} \left[ {e_{j}^{ + } y_{jh}^{ - } + \sum\limits_{k = 1}^{{s_{j} }} {\left( {\alpha_{j}^{ + } y_{jhk}^{\prime - } + \beta_{j}^{ + } y_{jhk}^{ - } } \right)} } \right]} } \\ \end{aligned} $$

(35)

subject to:

$$ \begin{aligned} \sum\limits_{j = 1}^{{j_{1} }} {\left[ {\left| {a_{rj} } \right|^{ + } {\text{Sign}}\left( {a_{rj}^{ + } } \right)x_{j}^{ - } + \left| {a_{rj}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{rj}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ - } } } \right]} \\ + \sum\limits_{{j = j_{1} + 1}}^{{n_{1} }} {\left[ {\left| {a_{rj} } \right|^{ - } {\text{Sign}}\left( {a_{rj}^{ - } } \right)x_{j}^{ + } + \left| {a_{rj}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{rj}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ + } } } \right] \le b_{r}^{ - } , \, \forall r} \\ \end{aligned} $$

(36)

$$ \begin{aligned} \sum\limits_{j = 1}^{{j_{1} }} {\left[ {\left| {a_{tj} } \right|^{ + } {\text{Sign}}\left( {a_{tj}^{ + } } \right)x_{j}^{ - } + \left| {a_{tj}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{tj}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ - } } } \right]} + \sum\limits_{{j = k_{1} + 1}}^{{j_{1} }} {\left[ {\left| {a_{tj} } \right|^{ - } {\text{Sign}}\left( {a_{tj}^{ - } } \right)x_{j}^{ + } + \left| {a_{tj}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{tj}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ + } } } \right]} \\ + \sum\limits_{j = 1}^{{j_{2} }} {\left[ {\left| {a_{tjh} } \right|^{ - } {\text{Sign}}\left( {a_{tjh}^{ - } } \right)y_{jhk}^{ + } + \left| {a_{tjh}^{\prime } } \right|^{ - } {\text{Sign}}\left( {a_{tjh}^{\prime - } } \right)\sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ + } } } \right]} \\ + \sum\limits_{{j = j_{2} + 1}}^{{n_{2} }} {\left[ {\left| {a_{tjh} } \right|^{ + } {\text{Sign}}\left( {a_{tjh}^{ + } } \right)y_{jhk}^{ - } + \left| {a_{tjh}^{\prime } } \right|^{ + } {\text{Sign}}\left( {a_{tjh}^{\prime + } } \right)\sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ - } } } \right]} \ge \widetilde{{w_{h}^{ + } }}, \, \forall t,h,k \\ \end{aligned} $$

(37)

$$ x_{jk}^{\prime - } = \left\{ \begin{array}{ll} 1,& {\text{ if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} < x_{jk}^{ - } \le \bar{M}_{k} \\ 0,& {\text{ if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots ,j_{1} ; \, \forall k $$

(38)

$$ x_{jk}^{\prime + }= \left\{ \begin{array}{ll} 1, & {\text{ if }}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} < x_{jk}^{ + } \le \bar{M}_{k}^{{}} \\ 0, & {\text{ if otherwise}} \\ \end{array} \right., \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} ; \, \forall k $$

(39)

$$ \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{\prime - } } = 1, \quad j = 1,2, \ldots ,j_{1} ; \, \forall k $$

(40)

$$ \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{\prime + } } = 1, \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} ; \, \forall k $$

(41)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} x_{jk}^{\prime - } \le x_{jk}^{ - } \le \bar{M}_{k} x_{jk}^{\prime - } , \quad j = 1,2, \ldots ,j_{1} ; \, \forall k $$

(42)

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{M}_{k} x_{jk}^{ + } \le x_{jk}^{ + } \le \bar{M}_{k} x_{jk}^{\prime + } , \quad j = j_{1} + 1,j_{1} + 2, \ldots , \, n_{1} ; \, \forall k $$

(43)

$$ y_{jhk}^{ + } = \left\{ \begin{array}{ll} 1,& {\text{if }}\underline{N}_{k} < y_{jhk}^{ + } \le \bar{N}_{k} \\ 0, & {\text{if otherwise}} \\ \end{array} \right., \quad j = 1,2, \ldots , \, j_{2} ; \, \forall h, \, k $$

(44)

$$ y_{jhk}^{\prime - } = \left\{ \begin{array}{ll} 1,& {\text{ if }}\underline{N}_{k} < y_{jhk}^{ - } \le \bar{N}_{k} \\ 0, & {\text{ if otherwise}} \\ \end{array} \right., \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(45)

$$ \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{\prime + } } = 1, \quad j = 1,2, \ldots , \, j_{2} ; \, \forall h, \, k $$

(46)

$$ \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{\prime - } } = 1, \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(47)

$$ \underline{N}_{k} y_{jhk}^{\prime + } \le y_{jhk}^{ + } \le \bar{N}_{k} y_{jhk}^{\prime + } , \quad j = 1,2, \ldots ,j_{2} ; \, \forall h, \, k $$

(48)

$$ \underline{N}_{k} y_{jhk}^{\prime - } \le y_{jhk}^{ - } \le \bar{N}_{k} y_{jhk}^{\prime - } , \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h, \, k $$

(49)

$$ 0 \le x_{j}^{ - } \le x_{{j\,{\text{opt}}}}^{ + } , \, 0 \le \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ - } } \le \sum\limits_{k = 1}^{{s_{j} }} {x_{{jk\,{\text{opt}}}}^{ + } } , \quad j = 1,2, \ldots ,j_{1} $$

(50)

$$ x_{j}^{ + } \ge x_{{j{\text{opt}}}}^{ - } , \, \sum\limits_{k = 1}^{{s_{j} }} {x_{jk}^{ + } } \ge \sum\limits_{k = 1}^{{s_{j} }} {x_{{jk\,{\text{opt}}}}^{ - } } , \quad j = j_{1} + 1, \, j_{1} + 2, \ldots ,n_{1} $$

(51)

$$ y_{jh}^{ + } \ge y_{{jh\,{\text{opt}}}}^{ - } , \, \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ + } } \ge \sum\limits_{k = 1}^{{s_{j} }} {y_{{jhk\,{\text{opt}}}}^{ - } } , \quad j = 1,2, \ldots ,j_{2} ; \, \forall h $$

(52)

$$ 0 \le y_{jh}^{ - } \le y_{{jh\,{\text{opt}}}}^{ + } , \, 0 \le \sum\limits_{k = 1}^{{s_{j} }} {y_{jhk}^{ - } } \le \sum\limits_{k = 1}^{{s_{j} }} {y_{{jhk\,{\text{opt}}}}^{ + } } , \quad j = j_{2} + 1, \, j_{2} + 2, \ldots ,n_{2} ; \, \forall h $$

(53)

where x ⁺ _j opt , x ⁺ _jk opt (j = 1, 2, …, j ₁), x ⁻ _j opt , x ⁻ _jk opt (j = j ₁ + 1, j ₁ + 2, …, n₁), y ⁻ _jh opt , y ⁻ _jhk opt (j = 1, 2, …, j ₂), y ⁺ _jh opt and y ⁺ _jhk opt (j = j ₂ + 1, j ₂ + 2, …, n₂) are solutions of submodel (1). Solutions of x ⁻ _j opt , x ⁻ _jk opt (j = 1, 2, …, j ₁), x ⁺ _j opt , x ⁺ _jk opt (j = j ₁ + 1, j₁ + 2, …, n₁), y ⁺ _jh opt , y ⁺ _jhk opt (j = 1, 2, …, j ₂), y ⁻ _jh opt and y ⁻ _jhk opt (j = j ₂ + 1, j ₂ + 2, …, n₂) can be obtained through solving submodel (35–53). Then, through integrating solutions of submodels (16–34) and (35–53), final solutions for the RBNP model can be obtained as follows:

$$ x_{{j\,{\text{opt}}}}^{ \pm } = \left[ {x_{{j\,{\text{opt}}}}^{ - } , \, x_{{j\,{\text{opt}}}}^{ + } } \right]{\text{ or }}\left[ {\sum\limits_{k = 1}^{{s_{j} }} {x_{{jk\,{\text{opt}}}}^{ - } } , \, \sum\limits_{k = 1}^{{s_{j} }} {x_{{jk\,{\text{opt}}}}^{ + } } } \right], \quad j = 1,2, \ldots ,n_{1} $$

(54)

$$ y_{{jh\,{\text{opt}}}}^{ \pm } = \left[ {y_{{jh\,{\text{opt}}}}^{ - } ,y_{{jh\,{\text{opt}}}}^{ + } } \right]{\text{ or }}\left[ {\sum\limits_{k = 1}^{{s_{j} }} {y_{{jhk\,{\text{opt}}}}^{ - } } , \, \sum\limits_{k = 1}^{{s_{j} }} {y_{{jhk\,{\text{opt}}}}^{ + } } } \right], \, j = 1,2, \ldots ,n_{2} ; \, \forall h $$

(55)

$$ f_{\text{opt}}^{ \pm } = \left[ {f_{\text{opt}}^{ - } , \, f_{\text{opt}}^{ + } } \right] $$

(56)