Multistage scenario-based interval-stochastic programming for planning water resources allocation

Abstract

In this study, a multistage scenario-based interval-stochastic programming (MSISP) method is developed for water-resources allocation under uncertainty. MSISP improves upon the existing multistage optimization methods with advantages in uncertainty reflection, dynamics facilitation, and risk analysis. It can directly handle uncertainties presented as both interval numbers and probability distributions, and can support the assessment of the reliability of satisfying (or the risk of violating) system constraints within a multistage context. It can also reflect the dynamics of system uncertainties and decision processes under a representative set of scenarios. The developed MSISP method is then applied to a case of water resources management planning within a multi-reservoir system associated with joint probabilities. A range of violation levels for capacity and environment constraints are analyzed under uncertainty. Solutions associated different risk levels of constraint violation have been obtained. They can be used for generating decision alternatives and thus help water managers to identify desired policies under various economic, environmental and system-reliability conditions. Besides, sensitivity analyses demonstrate that the violation of the environmental constraint has a significant effect on the system benefit.

1 Introduction

Previously, a large number of optimization methods were undertaken for allocating and managing water resources in efficient and environmentally benign ways (Bazaare and Bouzaher 1981; Jacovkis et al. 1989; Paudyal and Manguerra 1990; Basağaoğlu et al. 1999; Srinivasan et al. 1999; Sethi et al. 2002; Gang et al. 2003). In detail, Jacovkis et al. (1989) proposed a multi-objective linear programming model for planning water resources systems; the system consisted of reservoirs, hydropower stations, irrigated lands, and navigation channels over a river basin. Sylla (1995) proposed a large-scale nonlinear programming model for planning the operations of interconnected facilities equipped at hydroelectric power stations; the decision variables involved the monthly reservoir releases as well as the canal and pipeline flows through turbines, and the reduced gradient techniques were used to solve the problem. Srinivasan et al. (1999) proposed a mixed integer linear programming model for supporting water-supply planning and reservoir-performance optimization. Sethi et al. (2002) proposed a linear programming model based on a water balance formulation for water resources systems planning in the Coastal River Basin, India, where optimal cropping patterns under various scenarios of river-flow availability were identified.

However, in water resources management problems, many system parameters and their interrelationships are often associated with uncertainties presented in terms of multiple formats. Consequently, in the past decades, many inexact optimization methods were advanced for addressing uncertainties presented as different formats in water resources management systems (Slowinski 1986; Camacho et al. 1987; Morgan et al. 1993; Srinivasan and Simonovic 1994; Curi et al. 1995; Rangarajan 1995; Chang et al. 1996a, b; Dupačová et al. 1991; Russell and Campbell 1996; Huang 1996, 1998; ReVelle 1999; Anderson et al. 2000; Jairaj and Vedula 2000; Edirisinghe et al. 2000; Watkins et al. 2000; Seifi and Hipel 2001; Ji and Chang 2005; Maqsood et al. 2005; Li et al. 2007a; Guo and Huang 2008; Zarghami and Szidarovszky 2008). Among them, a number of chance-constrained programming (CCP) and multistage stochastic programming (MSP) methods were developed for decision problems whose coefficients (input data) are uncertain but can be represented as chances or probabilities. CCP was effectively reflect the reliability of satisfying (or risk of violating) system constraints under uncertainty (Charnes and Cooper 1983; Huang 1998; Li et al. 2007b). For example, Huang (1998) developed an inexact chance-constrained programming (ICCP) method for water resources management, where interval-parameter programming (IPP) was introduced into the CCP framework for examining risk of violating system constraints and for dealing with uncertainties expressed as probabilities and intervals. Edirisinghe et al. (2000) proposed a mathematical programming model for the planning of reservoir capacity under random stream flows, based on the CCP method with a special target-priority policy being considered according to given system reliabilities. Guo and Huang (2008) proposed a two-stage fuzzy chance-constrained programming approach for dealing with uncertainties expressed as fuzzy sets and probabilities in the water resources management systems.

In comparison, MSP is effective in handling uncertainties expressed as probability distributions as well as permitting revised decisions in each time stage based on the information of sequentially realized uncertain events (Birge and Louveaux 1997; Dupačová 2002; Li et al. 2008). The fundamental idea behind MSP is the concept of recourse, which is the ability to take corrective actions after a random event has taken place. For example, Pereira and Pinto (1991) proposed a multistage stochastic optimization approach and applied it to the planning of a hydroelectric energy system, based on the L-shaped method that allowed the large-scale problem to be decomposed by scenarios. Watkins et al. (2000) proposed a multistage stochastic programming model for planning water supplies from highland lakes, where dynamics and uncertainties of water availability (and thus water allocation) could be taken into account through generation of multiple representative scenarios. Li et al. (2006a) proposed an interval-parameter multistage stochastic programming method for supporting water resources decision making, where uncertainties expressed as random variables and interval numbers could be reflected. However, the above MSP methods were incapable of accounting for the risk of violating system constraints under multiple uncertainties; moreover, they had difficulties in tackling a system with multiple reservoirs where joint uncertainties existed in water availabilities and their allocations. Such uncertainties could lead to complexities in terms of water allocation that are of interactive and dynamic relationships within a multistage context.

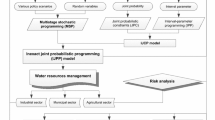
Therefore, the objective of this study is to develop a multistage scenario-based interval-stochastic programming (MSISP) method in responses to the above challenges. The developed MSISP will incorporate multistage stochastic programming (MSP) and inexact chance-constrained programming (ICCP) within a general framework for better accounting for uncertainties, dynamics and system reliabilities. The detailed tasks entail: (1) handling uncertainties presented as interval values and probability distributions, (2) reflecting the dynamics of system uncertainties and decision processes under a complete set of scenarios, (3) examining the reliability of satisfying (or risk of violating) system constraints under uncertainty, (4) applying the developed method to a case study of water-resources allocation within a multi-reservoir system, and (5) undertaking sensitivity analyses to reflect the constraint-violation effects on system benefit under different probability levels.

2 Methodology

Firstly, a multistage scenario-based stochastic linear programming model with recourse can be formulated as follows:

$$ {\text{Max}}\,f = \sum\limits_{t = 1}^{T} {C_{t} {\bf X}_{t} } - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{tk} Y_{tk} } } $$

(1a)

subject to:

$$ A_{rt} {\bf X}_{t} \le B_{rt} ,\quad r = 1,2, \ldots ,m_{1} ;\;t = 1,2, \ldots ,T $$

(1b)

$$ A_{it} {\bf X}_{t} + A^{\prime}_{itk} Y_{tk} \le w_{itk} ,\quad i = 1,2, \ldots ,m_{2} ;\;t = 1, 2, \ldots ,T;\;k = 1, 2 ,\ldots ,K_{t} $$

(1c)

$$ x_{jt} \ge 0,\quad x_{jt} \in {\bf X}_{t} ,\;j = 1,2, \ldots ,n_{1} ;\;t = 1,2, \ldots ,T $$

(1d)

$$ y_{jtk} \ge 0,\quad y_{jtk} \in Y_{tk} ,\;j = 1,2, \ldots ,n_{2} ;\;t = 1,2, \ldots ,T;\;k = 1, 2 ,\ldots ,K_{t} $$

(1e)

where p _tk is probability of occurrence for scenario k in period t, with p _tk  > 0 and $\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} } = 1;\;D_{tk}$ are coefficients of recourse variables (Y _tk ) in the objective function; $A^{\prime}_{itk}$ are coefficients of Y _tk in constraint i; w _itk is random variable of constraint i, which is associated with probability level p _tk ; K _t is number of scenarios in period t, with the total being $K = \sum\limits_{t = 1}^{T} {K_{t} } .$ In model (1), the decision variables are divided into two subsets: those that must be determined before the realizations of random variables are disclosed (i.e. x _jt ), and those (recourse variables) that can be determined after the realized random-variable values are available (i.e. y _jtk ).

Obviously, model (1) can deal with uncertainties in the right-hand sides presented as random variables when coefficients in the left-hand sides and in the objective function are deterministic. However, in a real-world water resources management problem, randomness in other right-hand-side parameters (e.g., available reservoir-storage capacities), also needs to be reflected. The chance-constrained programming (CCP) method can be used for dealing with this type of uncertainty and analyzing the risk of violating the uncertain constraints (Charnes et al. 1972; Charnes and Cooper 1983). Consider a general probabilistic stochastic linear problem as follows:

$$ {\text{Max}}\,C(t){\bf X} $$

(2a)

subject to:

$$ A(t){\bf X} \le B(t) $$

(2b)

$$ {\bf X} \ge 0 $$

(2c)

where X is a vector of decision variables, and A(t), B(t), and C(t) are sets with random elements defined on a probability space T, t ∈ T (Charnes et al. 1972; Infanger and Morton 1996). The CCP approach solves the above model by converting it into a deterministic version through: (1) fixing a certain level of probability q _i (q _i  ∈ [0, 1]) for uncertain constraint i, which represents the admissible risk of violating constraint i, and (2) imposing the condition that the constraint should be satisfied with at least a probability level of 1 − q _i . The feasible solution set is thus subject to the following constraints (Huang 1998; Li et al. 2006b):

$$ {\text{Pr}}[\{ A_{i} (t){\bf X} \le b_{i} (t)\} ] \ge 1 - q_{i} ,\quad A_{i} (t) \in A(t),\;i = 1,2, \ldots ,m $$

(3a)

Constraint (3a) is generally nonlinear, and the set of feasible constraints is convex only for some particular cases, one of which is when elements of A _i (t) are deterministic and b _i (t) are random (for all q _i values). Constraint (3a) can be converted into a linear one as follows:

$$ A_{i} (t){\bf X} \le b_{i} (t)^{{q_{i} }} ,\quad \forall i $$

(3b)

where $b_{i} (t)^{{q_{i} }} = F_{i}^{ - 1} (q_{i} )$, given the cumulative distribution function (CDF) of b_i [i.e. F _i (b _i )] and the probability of violating constraint i (i.e. q _i ). The problem with (3b) is that linear constraints can only reflect the case when the left-hand-side coefficients (A) are deterministic. If both left- and right-hand sides (A and B) are uncertain, the set of feasible constraints may become more complicated (Ellis 1991; Infanger 1993; Huang 1998; Li et al. 2007b).

In general, although the CCP can deal with left-hand-side uncertainties presented as probability distributions, three limitations exist: (1) the resulting nonlinear model would be associated with a number of difficulties in global-optimum acquisition; (2) it is unable to handle independent uncertainties in objective coefficients (Infanger 1993; Zare and Daneshmand 1995); (3) for many practical problems, the quality of information that can be obtained for these uncertainties is mostly not satisfactory enough to be presented as probability distributions (Huang 1998). Therefore, for uncertainties in left-hand sides and cost/revenue parameters in the objective function, an extended consideration would be the introduction of interval-parameter programming (IPP) technique into the CCP framework. This leads to an interval-parameter chance-constrained programming (ICCP) model as follows:

$$ {\text{Max}}\, f^{ \pm } = C^{ \pm } {\bf X}^{ \pm } $$

(4a)

subject to:

$$ {\text{Pr}}[\{ A_{i}^{ \pm } (t){\bf X}^{ \pm } \le b_{i}^{ \pm } (t)\} ] \ge 1 - q_{i} ,\quad A_{i}^{ \pm } (t) \in A^{ \pm } (t),\;i = 1,2, \ldots ,m $$

(4b)

$$ x_{j}^{ \pm } \ge 0,\quad x_{j}^{ \pm } \in {\bf X}^{ \pm } ,\;j = 1,2, \ldots ,n $$

(4c)

where A ^± ∈ {R ^±}^m × n, C ^± ∈ {R ^±}^1 × n, X ^± ∈ {R ^±}^n × 1, and R ^± denotes a set of interval numbers. An interval value can be defined as a number with known lower and upper bounds but unknown distribution information (Huang 1998). Then, model (4) can be converted into an equivalent deterministic version as follows:

$$ {\text{Max}}\, f^{ \pm } = C^{ \pm } {\bf X}^{ \pm } $$

(5a)

subject to:

$$ A_{i}^{ \pm } (t){\bf X}^{ \pm } \le B^{ \pm } (t)^{q} ,\quad A_{i}^{ \pm } (t) \in A^{ \pm } (t),\;i = 1,2, \ldots ,m $$

(5b)

$$ x_{j}^{ \pm } \ge 0,\quad x_{j}^{ \pm } \in {\bf X}^{ \pm } ,\;j = 1,2, \ldots ,n $$

(5c)

where $B^{ \pm } (t)^{q} = \{ b_{i}^{ \pm } (t)^{{q_{i} }} \left| i \right. = 1,2, \ldots ,m\} .$ The ICCP can be introduced into the above MSP framework to deal with randomness in the constraints of reservoir capacity and reserved storage requirement, as well as interval values in cost/revenue parameters in the objective function. This will lead to a multistage scenario-based interval-stochastic programming (MSISP) model as follows:

$$ {\text{Max}}\,f^{ \pm } = \sum\limits_{t = 1}^{T} {C_{t}^{ \pm } {\bf X}_{t}^{ \pm } } - \sum\limits_{t = 1}^{T} {\sum\limits_{k = 1}^{{K_{t} }} {p_{tk} D_{tk}^{ \pm } Y_{tk}^{ \pm } } } $$

(6a)

subject to:

$$ A_{rt}^{ \pm } {\bf X}_{t}^{ \pm } \le B_{rt}^{ \pm } ,\quad r = 1,2, \ldots ,m_{1} ;\;t = 1,2, \ldots ,T $$

(6b)

$$ A_{it}^{ \pm } {\bf X}_{t}^{ \pm } + A_{itk}^{' \pm } Y_{tk}^{ \pm } \le w_{itk}^{ \pm } ,\quad i = 1,2, \ldots ,m_{2} ;\;t = 1,2, \ldots ,T;\;k = 1,2, \ldots ,K_{t} $$

(6c)

$$ A_{st}^{ \pm } {\bf X}_{t}^{ \pm } + A_{st}^{' \pm } Y_{tk}^{ \pm } \le B_{s}^{ \pm } (t)^{{(q_{s} )}} ,\quad s = 1, 2, \ldots ,m_{3} ;\;t = 1,2, \ldots ,T;\;k = 1, 2 ,\ldots ,K_{t} $$

(6d)

$$ x_{jt}^{ \pm } \ge 0,\quad x_{jt}^{ \pm } \in {\bf X}_{t}^{ \pm } ,\;j = 1,2, \ldots ,n_{1} ;\;t = 1,2, \ldots ,T $$

(6e)

$$ y_{jtk}^{ \pm } \ge 0,\quad y_{jtk}^{ \pm } \in Y_{tk}^{ \pm } ,\;j = 1,2, \ldots ,n_{2} ;\;t = 1,2, \ldots ,T;\;k = 1, 2, \ldots ,K_{t} $$

(6f)

Generally, the MSISP method has three special characteristics that make it unique compared with the other optimization approaches that deal with uncertainties. Firstly, through a multilayer scenario tree, MSISP can deal with uncertainties presented in terms of probabilities and intervals, as well as their combinations. Secondly, the MSISP can reflect dynamics of not only the uncertainties but also the relevant decisions. For all scenarios under consideration, a decision must be made at each stage based on information about the actual realizations of the random variables as well as the earlier decisions; this allows corrective actions to be taken dynamically for the related policies and can thus help maximize the system benefit. Thirdly, it can be used for examining the reliability of satisfying (or the risk of violating) the system constraints under uncertainty; a range of violations for constraints are allowed, which are related to tradeoffs between the system benefit and the constraint-violation risk. Then, a case study of water resources allocation will be provided for demonstrating applicability of the developed MSISP method.

3 Case study

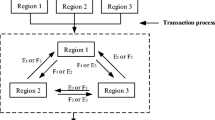
Consider a water resources management system consisting of two streams and two reservoirs, where an authority is responsible for allocating water to a municipality over a multi-period planning horizon (Fig. 1). The water supplies during the planning horizon are random variables, and the relevant water allocation plan would be of dynamic feature. Moreover, such uncertainties could lead to further complexities in terms of water allocation that are of interactive and dynamic relationships within a multistage context. Because of the spatial and temporal variations of the relationships between water demand and supply, the desired water-allocation patterns may also vary among different time periods. If the promised water is delivered, it will result in net benefits to the local economy; however, if the promised water is not delivered, either the water must be obtained from alternative and more expensive sources or the demand must be curtailed, resulting in penalties to the local economy. Uncertainties exist in many system components (provided as intervals for water-allocation demands and economic data, as well as distribution information for the total water availability, storage capacity, and reserve requirement). The problems under consideration are how to identify desired water-allocation patterns with a maximized net benefit and a minimized system-failure risk under uncertainties.

Fig. 1

Schematic of water resources allocation system

Therefore, the developed MSISP is considered to be a suitable approach for supporting the relevant decisions of water resources allocation within a multi-reservoir system. Uncertainties in the MSISP can be conceptualized into a multi-layer scenario tree, with a one-to-one correspondence between the previous random variable and one of the nodes (states of the system) in each time stage (Birge 1985; Li et al. 2006a). The first-stage variables (denoted as ${\bf X}_{t}^{ \pm }$) represent the allocation target that will be promised to the municipality, which should be determined before the random stream flows are disclosed. The recourse variables (denoted as $Y_{{tk_{1} k_{2} }}^{ \pm }$) involve probabilistic shortages if the allocation targets are not delivered to the municipality, which are related to the random water availabilities of the two streams ($Q_{{tk_{1} }}^{ \pm }$ and $Q_{{tk_{2} }}^{ \pm }$). Thus we have:

$$ {\text{Max}}\,f^{ \pm } = \sum\limits_{t = 1}^{T} {NB_{t}^{ \pm } } {\bf X}_{t} - \sum\limits_{t = 1}^{T} {\sum\limits_{{k_{1} = 1}}^{{K_{1}^{t} }} {\sum\limits_{{k_{2} = 1}}^{{K_{2}^{t} }} {p_{{tk_{1} }} p_{{tk_{2} }} } } } PE_{t}^{ \pm } Y_{{tk_{1} k_{2} }}^{ \pm } $$

(7a)

subject to:

• (1) Constraints of water-mass balance

$$ R_{{tk_{1} }}^{ \pm } = S_{tk1} + Q_{{tk_{1} }}^{ \pm } - E_{1t} - S_{{(t + 1)k_{1} }} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(7b)

$$ E_{1t} = A_{1}^{a} e_{1t}^{ \pm } \left( {\frac{{S_{{tk_{1} }} + S_{{(t + 1)k_{1} }}^{{}} }}{2}} \right) + A_{1}^{0} e_{1t}^{ \pm } $$

(7c)

$$ S_{{(t + 1)k_{1} k_{2} }} = S_{{tk_{1} k_{2} }} + (Q_{{tk_{2} }}^{ \pm } + R_{{tk_{1} }}^{ \pm } ) - E_{2t} - R_{{tk_{1} k_{2} }}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\cdots ,K_{2}^{t} $$

(7d)

$$ E_{2t} = A_{2}^{a} e_{2t}^{ \pm } \left( {\frac{{S_{{tk_{1} k_{2} }} + S_{{(t + 1)k_{1} k_{2} }} }}{2}} \right) + A_{2}^{0} e_{2t}^{ \pm } $$

(7e)

• (2) Constraint of available water

$$ {\bf X}_{t}^{ \pm } - Y_{{tk_{1} k_{2} }}^{ \pm } \le R_{{tk_{1} k_{2} }}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(7f)

• (3) Constraints of reservoir capacity

$$ \Pr \{ S_{{tk_{1} }} \le RSC_{1}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} \} \ge 1 - q $$

(7g)

$$ \Pr \{ S_{{tk_{1} k_{2} }} \le RSC_{2}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} \} \ge 1 - q $$

(7h)

• (4) Constraints of reserved storage requirement

$$ \Pr \{ S_{{tk_{1} }} \ge RSV_{1}^{ \pm } ,\quad \forall t;\;k_{1} = 1,2, \ldots ,K_{1}^{t} \} \ge 1 - q $$

(7i)

$$ \Pr \{ S_{{tk_{1} k_{2} }} \ge RSV_{2}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} \} \ge 1 - q $$

(7j)

• (5) Constraints of water allocation target

$$ De_{t}^{\min } \le {\bf X}_{t} \le De_{t}^{\max } ,\quad \forall t $$

(7k)

• (6) Non-negative constraint

$$ {\bf X}_{t} \ge Y_{{tk_{1} k_{2} }}^{ \pm } \ge 0,\quad \forall t ;\;k_{1} = 1, 2 ,\ldots , K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(7l)

The detailed nomenclatures for the variables and parameters are provided in Appendix 1. In Model (7), the objective is to maximize the expected net system benefit through allocating the water resources to the municipality from multi-reservoir over a multistage context. The constraints will help define the interrelationships among the decision variables and the water-allocation conditions. Constraints (7b)–(7e) present the mass balance for water resources in each time period (i.e., the change in storage equals inflows minus releases and evaporation losses), where the evaporation loss is assumed to be a linear function of the average storage of reservoir. Constraint (7f) means that the actual water allocated to the users must not exceed the amount of water released from the reservoirs, and this constraint also allows the spill of surplus water (i.e. issue of flood management is not considered in the study problem). Constraints (7g) and (7h) specify that the storage amount must not exceed each reservoir capacity under all scenarios. Constraints (7i) and (7j) require that the storage in each reservoir will not lower a reserve level under all scenarios. Constraint (7k) indicates that the allocated water must satisfy the user’s minimum necessity but not exceed its maximum requirement.

There are three assumptions for the above modeling formulation. Firstly, the random variables ($Q_{{tk_{1} }}^{ \pm }$and $Q_{{tk_{2} }}^{ \pm }$) are assumed to take on discrete distributions, such that the MSISP model can be solved through linear programming method; secondly, the two random variables are assumed to be mutually independent, such that the probabilistic shortages $(Y_{{tk_{1} k_{2} }}^{ \pm } )$ correspond to joint probabilities $(p_{{tk_{1} }} p_{{tk_{2} }} )$; thirdly, issue of flood management is not considered.

The above MSISP model can then be solved through a two-step method. The submodel corresponding to f ⁺ can be formulated in the first step when the system objective is to be maximized; the other submodel (corresponding to f ⁻) can then be formulated based on the solution of the first submodel. Thus, the first submodel is:

$$ {\text{Max}}\,f^{ + } = \sum\limits_{t = 1}^{T} {NB_{t}^{ + } } {\bf X}_{t} - \sum\limits_{t = 1}^{T} {\sum\limits_{{k_{1} = 1}}^{{K_{1}^{t} }} {\sum\limits_{{k_{2} = 1}}^{{K_{2}^{t} }} {p_{{tk_{1} }} p_{{tk_{2} }} } } } PE_{t}^{ - } Y_{{tk_{1} k_{2} }}^{ - } $$

(8a)

subject to:

$$ R_{{tk_{1} }}^{ + } = S_{{tk_{1} }} + Q_{{tk_{1} }}^{ + } - E_{1t}^{ - } - S_{{(t + 1)k_{1} }} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(8b)

$$ R_{{tk_{1} k_{2} }}^{ + } = S_{{tk_{1} k_{2} }} + (Q_{{tk_{2} }}^{ + } + R_{{tk_{1} }}^{ + } ) - E_{2t}^{ - } - S_{{(t + 1)k_{1} k_{2} }} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(8c)

$$ {\bf X}_{t} - Y_{{tk_{1} k_{2} }}^{ - } \le R_{{tk_{1} k_{2} }}^{ + } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(8d)

$$ S_{{tk_{1} }} \le (RSC_{1}^{ + } )^{q} ,\quad \forall t;\;k_{1} = 1,2, \ldots ,K_{1}^{t} $$

(8e)

$$ S_{{tk_{1} k_{2} }} \le (RSC_{2}^{ + } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots , K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(8f)

$$ S_{{tk_{1} }} \ge (RSV_{1}^{ - } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(8g)

$$ S_{{tk_{1} k_{2} }} \ge (RSV_{2}^{ - } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(8h)

$$ De_{t}^{\min } \le {\bf X}_{t} \le De_{t}^{\max } ,\quad \forall t $$

(8i)

$$ {\bf X}_{t} \ge Y_{{tk_{1} k_{2} }}^{ - } \ge 0,\quad \forall t ;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(8j)

where X _t and $Y_{{tk_{1} k_{2} }}^{ - }$ are decision variables; q is probability of violating the constraints of reservoirs’ capacities and reserved storage requirements, and q ∈ [0, 1]. Let X _{t opt} and $Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ - }$ be the solutions of model (8). Then, the second submodel corresponding to f ⁻ can be formulated as follows:

$$ {\text{Max}}\;f^{ - } = \sum\limits_{t = 1}^{T} {NB_{t}^{ - } } {\bf X}_{{t\,{\text{opt}}}} - \sum\limits_{t = 1}^{T} {\sum\limits_{{k_{1} = 1}}^{{K_{1}^{t} }} {\sum\limits_{{k_{2} = 1}}^{{K_{2}^{t} }} {p_{{tk_{1} }} p_{{tk_{2} }} } } } PE_{t}^{ + } Y_{{tk_{1} k_{2} }}^{ + } $$

(9a)

subject to:

$$ R_{{tk_{1} }}^{ - } = S_{{tk_{1} }} + Q_{{tk_{1} }}^{ - } - E_{1t}^{ + } - S_{{(t + 1)k_{1} }} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(9b)

$$ R_{{tk_{1} k_{2} }}^{ - } = S_{{tk_{1} k_{2} }} + (Q_{{tk_{2} }}^{ - } + R_{{tk_{1} }}^{ - } ) - E_{2t}^{ + } - S_{{(t + 1)k_{1} k_{2} }} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(9c)

$$ {\bf X}_{{t\,{\text{opt}}}} - Y_{{tk_{1} k_{2} }}^{ + } \le R_{{tk_{1} k_{2} }}^{ - } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(9d)

$$ S_{{tk_{1} }} \le (RSC_{1}^{ - } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(9e)

$$ S_{{tk_{1} k_{2} }} \le (RSC_{2}^{ - } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(9f)

$$ S_{{tk_{1} }} \ge (RSV_{1}^{ + } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} $$

(9g)

$$ S_{{tk_{1} k_{2} }} \ge (RSV_{2}^{ + } )^{q} ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(9h)

$$ Y_{{tk_{1} k_{2} }}^{ + } \ge Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ - } ,\quad \forall t ;\;k_{1} = 1, 2 ,\ldots , K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(9i)

where $Y_{{tk_{1} k_{2} }}^{ + }$are decision variables. Let $Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ + }$ be the solutions of model (9). Thus, we have solutions for the MSISP model as follows:

$$ Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ \pm } = [Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ - } , Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ + } ] $$

(10a)

$$ f_{\text{opt}}^{ \pm } = [f_{\text{opt}}^{ - } , f_{\text{opt}}^{ + } ] $$

(10b)

The optimized water-allocation scheme over the planning horizon would then be:

$$ A_{{tk_{1} k_{2} \,{\text{opt}}}}^{ \pm } = {\bf X}_{{t\;{\text{opt}}}} - Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ \pm } ,\quad \forall t;\;k_{1} = 1, 2 ,\ldots ,K_{1}^{t} ;\;k_{2} = 1, 2 ,\ldots ,K_{2}^{t} $$

(10c)

The MSISP modeling results will be used for answering questions such as (a) how to identify a desired water allocation plan that balances various conflicting water supply goals while appropriately hedging against the effects of drought (i.e. water shortage)? (b) how to achieve a maximized system benefit through effectively allocating water resources under uncertainty? and (c) how to examine the reliability of satisfying the system constraints? Table 1 provides the water-flow levels and associated probabilities, water allocation demands, as well as economic data. Obviously, the water availabilities will fluctuate dynamically due to the varying river flows. In general, the economic penalties are associated with the acquisition of water from higher-priced alternatives and/or the negative consequences generated from the curbing of regional development plans when the promised water is not delivered (Loucks et al. 1981; Howe et al. 2003). Table 2 shows the distributional information for the storage capacities of the two reservoirs and the regulations of the reserve water. It is indicated that the capacity availabilities and the environmental regulations vary with different q_i levels. Besides, the initial storages in reservoirs 1 and 2 are [19.5, 21.9] × 10⁶ and [27.3, 30.1] × 10⁶ m³, respectively.

Table 1 Technical and economic data

Table 2 Probabilistic information of storage capacities and reserve requirements

4 Result and discussion

4.1 Result analysis

In this study, a set of chance constraints on storage capacities and reserve requirements are considered, which can help investigate the risk of violating the capacity and environment constraints, and thus generate desired water-allocation patterns under uncertainty. The results indicate that, under q = 0.01, 0.05 and 0.10, the optimized water-allocation targets would be 124.50 × 10⁶ m³ in period 1 and 130.3 × 10⁶ m³ in period 2. However, in period 3, the optimized water-allocation would be different from each other with varied q levels. In period 3, the optimized water-allocation target would be 163.9 × 10⁶ m³ when q = 0.01, 169.5 × 10⁶ m³ when q = 0.05, 172.3 × 10⁶ m³ when q = 0.10, respectively. Deficits would occur if the available flows do not meet the regulated water-allocation targets over the planning horizon. The solutions of water shortage under the given targets are combinations of interval and probability information. This reflects the variations of system conditions caused by uncertain inputs of economic data, storage capacities, reserve water requirements, and stream flows. In general, under advantageous conditions (e.g., stream flows and storage capacities approach their upper bounds), the shortage levels may be low; however, under demanding conditions, the shortages may be raised. Moreover, the lower bound of water shortage (i.e. $Y_{{tk_{1} k_{2} }}^{ - }$) corresponds to a higher system benefit, and vice versa.

Figures 2, 3 and 4 present the probabilistic water shortages over the planning horizon under q = 0.01, 0.05 and 0.10, respectively. In this study, random variables (available water supplies) with probabilities can be handled through constructing two scenario trees. For example, for stream 1, a three-period (four-stage) scenario tree can be generated with having a branching structure of 1-3-3-3. Consequently, there would generate 258 scenarios for the two streams associated with different joint probabilities over the planning horizon. The results indicate that, when q = 0.01, the amount of shortage scenarios would be 94 under advantageous conditions; under demanding conditions, the amount of shortage scenarios would increase to 207, occupying approximately 80.2% of total water-allocation scenarios. When q = 0.05 and 0.1, under demanding conditions, the amount of shortage scenarios would be 198 and 194 (occupying approximately 76.7 and 75.2% of total scenarios, respectively). The results demonstrate that, under all of the three q levels, the region would be subject to water shortages in most of the scenarios under demanding conditions.

Fig. 2

Optimized water shortage pattern under q = 0.01

Fig. 3

Optimized water shortage pattern under q = 0.05

Fig. 4

Optimized water shortage pattern under q = 0.10

Figures 5, 6 and 7 presents the desired allocation plans under q = 0.01, 0.05 and 0.10. Each allocated flow is the difference between the promised target and the probabilistic shortage under a given stream condition with an associated probability level (i.e. $A_{{tk_{1} k_{2} \,{\text{opt}}}}^{ \pm } = {\bf X}_{{t\;{\text{opt}}}} - Y_{{tk_{1} k_{2} \,{\text{opt}}}}^{ \pm }$). The results indicate that the water-allocation patterns would be different under varied q levels. Analyses of the solutions for water allocation under scenario 1 are provided below. The solutions under the other scenarios can be similarly interpreted based on the results presented in Figs. 6, 7 and 8. In detail, when flows of the two streams in the three periods are all low with a joint probability of 0.128% (i.e. scenario 1), we have:

Fig. 5

Optimized water allocation pattern under q = 0.01

Fig. 6

Optimized water allocation pattern under q = 0.05

Fig. 7

Optimized water allocation pattern under q = 0.10

Fig. 8

Penalties under different q levels

• (a) when q = 0.01, the shortages would be [15.1, 56.7] × 10⁶ m³ in period 1, [15.8, 41.8] × 10⁶ m³ in period 2, and [66.7, 69.5] × 10⁶ m³ in period 3; the corresponding water allocations would be [67.8, 109.4] × 10⁶, [88.5, 114.5] × 10⁶ and [94.4, 97.2] × 10⁶ m³ in periods 1, 2 and 3, respectively; the total amount of water allocation over the planning horizon would thus be [250.7, 321.1] × 10⁶ m³;

• (b) when q = 0.05, shortages would be [9.7, 56.2] × 10⁶ m³ in period 1, [15.8, 39.0] × 10⁶ m³ in period 2, and 72.3 × 10⁶ m³ in period 3; the corresponding water allocations would be [68.3, 114.8] × 10⁶, [91.3, 114.5] × 10⁶ and 97.2 × 10⁶ m³ in periods 1, 2 and 3, respectively; the total amount of water allocation over the planning horizon would thus be [256.8, 326.5] × 10⁶ m³;

• (c) when q = 0.10, the shortages would be [6.9, 55.8] × 10⁶ m³ in period 1, [15.8, 36.2] × 10⁶ m³ in period 2, and 75.1 × 10⁶ m³ in period 3; the corresponding water allocations would be [68.7, 117.6] × 10⁶, [94.1, 114.5] × 10⁶ and 97.2 × 10⁶ m³ in periods 1, 2 and 3, respectively; the total amount of water allocation over the planning horizon would thus be [260.0, 329.3] × 10⁶ m³.

In this study, an increased q level could lead to not only an increased looseness for the storage capacities but also a decreased strictness for the environment requirements. Increased storage capacities would allow reservoirs retaining more surplus water when the flows of streams are high in periods 1 and 2, leading to less shortage when water flow is low in period 3. Meanwhile, decreased reserve requirements would allow less water being retained in the reservoirs when the flows are low over the planning horizon. These two facts could both result in a reduced water shortage and an increased water-allocation amount as q level increases. Figure 8 shows the trend of penalty variations with the q level. Penalties caused by water shortages would be $[961.3, 9971.0] × 10⁶ under q = 0.01, $[919.2, 9675.0] × 10⁶ under q = 0.05, and $[891.7, 9549.2] × 10⁶ under q = 0.10, demonstrating that a raised q level would lead to a reduced penalty interval. Moreover, Fig. 9 shows the trend of system-benefit variations with the q level. The solutions of system benefit $(f_{\text{opt}}^{ \pm } )$ would be $[3836.5, 15665.5] × 10⁶, $[4343.1, 15961.3] × 10⁶ and $[4574.2, 16115.6] × 10⁶ under q = 0.01, 0.05 and 0.10, respectively. A lower q level would result in a lower system benefit and a lower constraint-violation risk; conversely, a higher q level would sacrifice system safety and violate environment requirement in order to achieve a higher benefit. Therefore, there is a tradeoff among the water-allocation benefit, system safety, and environment constraint.

Fig. 9

System benefits under different q levels

4.2 Sensitivity analysis

By considering the constraints of both reservoir capacities and reserve requirements as a set of deterministic values under q = 0, the study problem can be solved through an interval multistage stochastic linear programming (IMSLP) method (Li et al. 2006a). The results indicate that the system benefit obtained through the IMSLP ($(f_{\text{opt}}^{ \pm } = \$ [3498.4,15331.2] \times 10^{6} )$ is lower than those through the MSISP under a range of q levels. Meanwhile, the penalties would be $[1032.6, 10090.9] × 10⁶, higher than those from the MSISP model. This is attributed to the fact that no violation (or relaxation) on the capacity and environment constraints is allowed in the IMSLP, leading to stricter capacity availability and environmental requirement, and thus result in more shortage and less water allocation. Figure 10 presents the solutions for the optimized water-allocation pattern when q = 0, demonstrating the fact. For example, when the flows of the two streams in the three periods are all low, the shortages would be [19.5, 56.9] × 10⁶ m³ in period 1, [21.5, 41.8] × 10⁶ m³ in period 2, and [56.0, 69.5] × 10⁶ m³ in period 3; the corresponding water allocations would be [67.6, 105.0] × 10⁶, [94.2, 114.5] × 10⁶, and [83.7, 97.2] × 10⁶ m³ in periods 1, 2 and 3, respectively. The total amount of water allocation would be [245.5, 316.7] × 10⁶ m³, lower than those under q = 0.01, 0.05 and 0.10. Moreover, without the chance constraints, the IMSLP method can hardly support in-depth analyses of the interrelationship between system benefit and constraint-violation risk. It only provides decision support under an extreme scenario of water-resources allocation conditions.

Fig. 10

Optimized water allocation pattern under q = 0

Figure 11 shows results of the effects of reserved storage variation on the system benefit under a range of q levels, through considering the constraints of reservoir capacities as a set of deterministic values under q = 0. The results of system benefits would be $[3831.1, 15587.2] × 10⁶ when q = 0.01, $[4260.9, 15872.9] × 10⁶ when q = 0.05, and $[4441.8, 16010.1] × 10⁶ when q = 0.10, respectively. The corresponding mid-values would be $9709.2 × 10⁶, $10066.9 × 10⁶ and $10226.0 × 10⁶ when q = 0.10, 0.05 and 0.10, respectively [i.e.$f^{\text{mid}} = (f^{ - } + f^{ + } )/2$]. The mid-value of system benefit is $9414.8 × 10⁶ under q = 0. Consequently, variation values would be $294.4 × 10⁶ (q = 0.01), $652.1 × 10⁶ (q = 0.05) and $811.2 × 10⁶ (q = 0.10) (i.e. 3.13, 6.93 and 8.62% of the mid system benefit under q = 0, respectively). In comparison, when a set of chance constraints on both storage capacities and reserve requirements are considered, the total variation would be 3.57% (q = 0.01), 7.83% (q = 0.05) and 9.88% (q = 0.10) of the mid system benefit under q = 0. The results of the sensitivity analysis thus demonstrate that violation of the environmental constraint (i.e. reserved water constraint) has a significant effect on the system benefit.

Fig. 11

Effect of environmental requirement variations on system benefits

5 Conclusions

A multistage scenario-based interval-stochastic programming (MSISP) method has been developed for water-resources allocation under uncertainty. This method extends upon the existing multistage stochastic programming (MSP) by allowing uncertainties expressed as probability distributions and interval values to be effectively incorporated within the optimization framework. It can reflect the dynamics of system uncertainties and decision processes under a representative set of scenarios, and can also help examine the reliability of satisfying (or risk of violating) system constraints under uncertainty. Moreover, penalties are exercised with recourse against any infeasibility, which permits in-depth analyses of various policy scenarios that are associated with different levels of economic consequences when the promised water-allocation targets are violated.

The developed method has then been applied to a case of water resources management planning within a multi-reservoir system associated with joint probabilities. A range of violation levels for capacity and environment constraints are examined under uncertainty. Solutions associated different risk levels of constraint violation have been obtained. They can be used for generating decision alternatives and thus help water managers to identify desired policies under various economic, environmental and system-reliability conditions. Sensitivity analyses have also been undertaken to demonstrate that the violation of the environmental constraint has a significant effect on the system benefit. Decisions at a lower risk level would lead to an increased reliability in fulfilling system requirements but with a lower system benefit; conversely, a desire for a higher system benefit could result in an increased risk of violating the system constraints.

In general, the MSISP method can not only handle uncertainties through constructing a set of scenarios that is representative for the universe of possible outcomes, but also reflect dynamic features of the system conditions and risk levels of violating system constraints within a multistage context. However, with such a multistage scenario-based interval-stochastic approach, issue of flood management is not considered. Moreover, the problem under study may be complicated by the need to take adequate account of hydrological records; this may lead to a too large-scale MSISP model when all water-availability scenarios are considered. Therefore, compilation of a larger hydrologic database, consideration of flood management, and development of a more advanced decomposition technique are desired for further enhancing the developed MSISP method.

Appendix 1 Nomenclatures for variables and parameters

f ^± :

net system benefit over the planning horizon ($)

t :

time period, and t = 1, 2,…,T

$A_{1}^{0}$ :

storage-area coefficient for reservoir 1

$A_{2}^{0}$ :

storage-area coefficient for reservoir 2

$A_{1}^{a}$ :

area (per unit of active storage volume) above $A_{1}^{0} ;$

$A_{2}^{a}$ :

area (per unit of active storage volume) above $A_{2}^{0} ;$

$De_{t}^{ \min }$ :

minimum amount of water demand for the municipality in period t (m³)

$De_{t}^{ \max }$ :

maximum water demand for the municipality in period t (m³)

e_1t :

average evaporation rate for reservoir 1 in period t

e_2t :

average evaporation rate for reservoir 2 in period t

$E_{1t}^{ \pm }$ :

evaporation loss of reservoir 1 in period t (m³)

$E_{2t}^{ \pm }$ :

evaporation loss of reservoir 2 in period t (m³)

$K_{1}^{t}$ :

number of possible scenarios for stream 1 in period t

$K_{2}^{t}$ :

number of possible scenarios for stream 2 in period t

$NB_{t}^{ \pm }$ :

net benefit per unit of water allocated in period t ($/m³)

$PE_{t}^{ \pm }$ :

penalty per unit of water not delivered in period t ($/m³), and PE _t  > NB _t

$p_{{tk_{1} }}$ :

probability of occurrence of scenario k ₁ (for stream 1) in period t, with $p_{{tk_{1} }} > 0$ and $\sum\limits_{{k_{1} = 1}}^{{K_{1}^{t} }} {p_{{tk_{1} }} = 1}$

$p_{{tk_{2} }}$ :

probability of occurrence of scenario k ₂ (for stream 2) in period t, with $p_{{tk_{2} }} > 0$ and $\sum\limits_{{k_{2} = 1}}^{{K_{2}^{t} }} {p_{{tk_{2} }} = 1}$

$Q_{{tk_{1} }}^{ \pm }$ :

random inflow into stream 1 in period t under scenario k ₁ (m³)

$Q_{{tk_{2} }}^{ \pm }$ :

random inflow into stream 2 in period t under scenario k ₂ (m³)

$R_{{tk_{1} }}^{ \pm }$ :

release flow from reservoir 1 in period t under scenario k ₁ (m³)

$R_{{tk_{1} k_{2} }}^{ \pm }$ :

release flow from reservoir 2 in period t under scenarios k ₁ and k ₂ associated with joint probabilities of $p_{{tk_{1} }} p_{{tk_{2} }}$ (m³)

$RSC_{1}^{ \pm }$ :

storage capacity of reservoir 1 (m³)

$RSC_{2}^{ \pm }$ :

storage capacity of reservoir 2 (m³)

$RSV_{1}^{ \pm }$ :

reserved storage level for reservoir 1 (m³)

$RSV_{2}^{ \pm }$ :

reserved storage level for reservoir 2 (m³)

$S_{{tk_{1} }}$ :

storage level in reservoir 1 in period t under scenario k ₁ (m³)

$S_{{tk_{1} k_{2} }}$ :

storage level in reservoir 2 in period t under scenarios k ₁ and k ₂ (m³)

X _t :

water allocation target that is promised to the municipality in period t (m³)

$Y_{{tk_{1} k_{2} }}^{ \pm }$ :

shortage level by which the water-allocation target is not met under scenarios k ₁ and k ₂ which is associated with joint probabilities of $p_{{tk_{1} }} p_{{tk_{2} }}$(m³)