ITOM: an interval-parameter two-stage optimization model for stochastic planning of water resources systems

Abstract

Planning of water resources systems is often associated with many uncertain parameters and their interrelationships are complicated. Stochastic planning of water resources systems is vital under changing climate and increasing water scarcity. This study proposes an interval-parameter two-stage optimization model (ITOM) for water resources planning in an agricultural system under uncertainty. Compared with other optimization techniques, the proposed modeling approach offers two advantages: first, it provides a linkage to pre-defined water policies, and; second, it reflects uncertainties expressed as probability distributions and discrete intervals. The ITOM is applied to a case study of irrigation planning. Reasonable solutions are obtained, and a variety of decision alternatives are generated under different combinations of water shortages. It provides desired water-allocation patterns with respect to maximum system benefits and highest feasibility. Moreover, the modeling results indicate that an optimistic water policy corresponding to higher agricultural income may be subject to a higher risk of system-failure penalties; while, a too conservative policy may lead to wastage of irrigation supplies.

Introduction

Inadequate supplies of fresh water are threatening human health, impairing prospects for agriculture and industry, and jeopardizing survival of ecosystems (CDDC 2004). Agricultural sector being one of the major water users is also facing water scarcity challenges associated with increasing pollution and changing climate. Efficient water allocations are vital for the planning and management of irrigated agriculture due to the competing needs of crops for limited supplies and cost of water. However, irrigation planning is coupled with many uncertain parameters. For instance, spatial and temporal variations exist in stream flows, and system costs and benefits are related to a number of uncertain impact factors. Moreover, irrigation policies in terms of water-allocation targets may comprise uncertainties and lead to economic implications. In addition, these complexities may be further increased by interactions among the uncertain parameters. Therefore, it is desired that parameter uncertainties and predefined policies be incorporated within irrigation planning problems so that water could efficiently be allocated among cropping farms to bring maximum possible benefits to the local economy.

Previously, several system analysis approaches were proposed to support decision-making in water resources planning under uncertainty (Rohde and Naparaxawong 1981; Gupta and Paudyal 1990; Eiger and Shamir 1991; Wagner et al. 1994; Russell and Campbell 1997; Mylopoulos et al. 1999; Teegavarapu and Simonovic 1999; Van Duc and Gupta 2000; Guo et al. 2001; Sahoo et al. 2001; Seifi and Hipel 2001; Carey and Zilberman 2002). For example, Mobasheri and Harboe (1970) developed a two-stage optimization model for the design and operation of a multi-purpose reservoir system. On-farm design and water management planning through a two-stage programming approach was undertaken by Sritharan et al. (1988). Paudyal and Gupta (1990) studied irrigation management by multilevel optimization. Abrishamchi (1991) carried out reservoir planning for irrigation districts using a chance-constrained optimization model. Recently, Bender and Simonovic (2000) proposed a fuzzy compromise approach for water resource systems planning. A robust modeling approach for water resources system planning under uncertainty was presented by Escudero (2000). Huang and Loucks (2000) introduced inexact two-stage stochastic programming for water resources management. Jairaj and Vedula (2000) performed optimization of a multireservoir system using fuzzy programming.

The above literature review reveals that the previous inexact modeling approaches for water resources planning were based on chance-constraint programming (CCP), fuzzy programming (FP), interval-parameter programming (IPP), or two-stage stochastic programming (TSP) techniques. However, CPP and FP methods cannot handle independent uncertainties of the model’s left-hand sides and cost coefficients; moreover, they are lack of linkage to economic consequences of violating system constraints that are essential for the related policy analyses. In contrast to CCP and FP, IPP can deal with uncertainties of the model’s left- and right-hand sides, and TSP can effectively reflect pre-defined policies and probability distributions. Thus, one potential approach for better accounting for policies as well as uncertainties is to incorporate IPP within a TSP frame. This leads to an interval-parameter two-stage optimization model (ITOM). The ITOM can directly incorporate uncertainties expressed as probability density functions and discrete intervals. More importantly, it can be employed for quantitatively analyzing a variety of policy scenarios that are associated with different levels of economic penalties when the promised policy targets are violated. No previous study has been reported on the application of ITOM to irrigation planning.

As an extension of the previous efforts, the objective of this study is to develop an ITOM and apply it to a case study of irrigation planning within an agricultural system under uncertainty. This study will help develop efficient water allocation plans under predefined policies and extensive uncertainties. A variety of decision alternatives will be generated and post-optimality analysis will be performed under different combinations of water shortages through a factorial design approach. These alternatives will be useful for the decision makers to adjust the allocation plan when they are not satisfied with the recommended alternatives. Moreover, economic impacts due to variations in water supply and demand will be investigated, and the performance of the proposed modeling approach will be compared with the conventional TSP method.

Inexact optimization techniques

For many practical problems, the data cannot be known accurately for a variety of reasons. This could be due to simple measurement error or data represent information about the future (e.g., stream flows, costs, and benefits) and simply cannot be known with certainty (Li 2003; Wang et al. 2003; Hoppe et al. 2004). To tackle such uncertainties, inexact optimization techniques can be employed. These inexact techniques try to determine the best solution under uncertainties while considering all options, actions, economics, and consequences. These can be classified into three main types including stochastic programming (SP), fuzzy programming (FP), and interval-parameter programming (IPP). Table 1 summarizes a comparison among inexact optimization techniques with details being presented in the following subsections.

Table 1 Comparison of inexact optimization approaches

SP deals with situations when some random parameters or variables appear in the modeling formulation of a program. Such random parameters are expressed as probability density functions. This implies that SP technique can be employed when the quality of uncertain information is comprehensive. The results can be interpreted under different level of probabilities (or risks). However, SP have higher computational efforts. This is because stochastic linear program need to be converted into an equivalent deterministic problem at the expense of increasing the size of the problem. SP can be further divided into its two well know types: (1) multistage stochastic programming (or two-stage stochastic programming known as TSP) or stochastic programming with resource, and (2) chance-constraint programming (CCP).

Two-stage stochastic programming proves effective for the analysis of medium- to long-term planning problems in which the system data is characterized by uncertainties and an examination of policy scenarios is desired. In TSP, such uncertain data are represented as probability density functions. For example, when TSP is employed for water resources planning problems, river and/or reservoir flows being stochastic parameters can be expressed as probability distributions. Thus, TSP can handle stochastic planning problems. In addition, TSP can help develop a sustainable development policy. Different policies for water resources management can be reflected though variations in the first-stage decision variables. Solutions under various policy scenarios can represent different options for trading off among system benefit and system-failure risk. Thus, TSP can also help analyze and develop sustainable policies.

The fundamental idea behind TSP is the concept of recourse, which refers to the ability to take corrective action after a random event has taken place. In TSP, an initial decision is made based on uncertain future events. When these future uncertainties are later resolved, a recourse or corrective action is taken. The initial decision is called the first-stage decision, and the corrective action is called the second-stage decision. The first-stage decisions are generally associated with planning issues, while the second stage decisions are often related to operating decisions. The objective function for such a two-stage recourse example would be to minimize (or maximize) the expected costs (or benefits) of all applicable decisions taken over the two periods.

The CCP can incorporate uncertainties in terms of probabilities, while FP is effective in handling imprecise information. Both FP and CCP methods cannot be effectively linked to the economic consequences of violating predefined system constraints, which is an essential feature for related policy analyses. Moreover, while CCP and FP can effectively express the stochastic aspects of a model’s right-hand-sides; however, they cannot capture independent uncertainties in the parameters of either the left-hand-sides or the cost coefficients.

In comparison, IPP deals with uncertain parameters with a known upper and lower bound but with unknown distribution information. IPP proves to be an effective procedure to deal with uncertainties in a model’s left-hand-sides, but encounters difficulties when the right-hand-sides are highly uncertain. IPP has a number of advantages such as (a) direct incorporation of uncertainties, (b) flexibility of results interpretation, (c) generation of decision alternatives, (d) reasonable computational requirements, (e) reflection of different uncertainties in solution outputs, and (f) application to practical problems (Huang 1996).

In short, each technique has advantages as well as shortcomings in terms of handling uncertainties. However, selection of a desired technique for a given problem depends on a number of factors. These factors may include (a) type of uncertain information accessible, (b) quality of information available, (c) complexity of solution method, (d) requirement of computational efforts, (e) flexibility of results interpretation, and (f) applicability to real-world problems. Moreover, selection of a suitable optimization modeling technique is highly associated with a modeler’s knowledge about the particular technique and ease to successfully apply this approach.

Modeling formulation

Water scarcity is one of many problems in agricultural irrigation facing today and will be a critical issue in the future. Growing population and economy associated with rising demand for water has led to increased competition of water resources. In a multicrop environment, competition for water exists among crops when available water is less than the demands. In such circumstances, it is wise to ensure that farmers know where they stand by providing foreseen information that is needed to make decisions for various activities and investments. For example, farmers’ knowledge about the fact that it is unwise to make a major investment in irrigation infrastructure for a small chance of receiving sufficient water in a dry season might happen all the time. Under inadequate water supplies, if the promised water is not delivered, farmers may not be able to conduct irrigation as planned. They will have to either obtain water from more expensive sources or curtail their development plans. In either case, this will result in decreased benefits (because of reduced crop yield) or increased costs (due to increased water price) leading to a decline in agricultural production (i.e., decreased benefits). It is thus desired that the available irrigation-water be effectively allocated to minimize possible penalties.

The problem can be formulated as maximizing the expected value of net system benefit using the inexact two-stage programming optimization model. Based on the local water management policies, a prescribed quantity of water can be defined to each crop. If this quantity is delivered, it will result in net benefits; however, if not delivered, the system will then be subject to penalties. Since the quantity of stream flows are uncertain, and uncertainties may also exist in system benefits and costs, as well as water policies need to be incorporated; thus, the problem under consideration can be formulated as an ITOM as follows (Loucks et al. 1981):

$$ {\text{Max}}\,f^ \pm = \sum\limits_{i = 1}^m {B_i^ \pm W_i^ \pm } - \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {p_j C_i^ \pm S_{ij}^ \pm } } $$

(1a)

$$ \sum\limits_{i = 1}^m {\left( {W_i^ \pm - S_{ij}^ \pm } \right)} \leqslant q_j^ \pm ,\quad \forall j $$

(1b)

$$ S_{ij}^ \pm \leqslant W_i^ \pm \leqslant W_{i\max }^ \pm ,\quad \forall j $$

(1c)

$$ S_{ij}^ \pm \geqslant 0,\quad \forall i,j $$

(1d)

where f^± is net system benefit ($/m³); B ^± _i is net benefit to farm i per m³ of water allocated ($);W ^± _i represents water policy in terms of fixed allocation amount of water that is promised to farm i (m³), (first stage decision variable); W ^±_imax is maximum allowable allocation amount for farm i (m³); C ^± _i is loss to farm i per m³ of water not delivered, C _i > B _i ($);S ^± _ij is shortage of water, which is the amount by which W _i is not met when the seasonal flow is q _j (m³) (second stage decision variable); q ^± _j is reservoir flow quantity with probability p _j of occurrence under flow level j (m³); p _j is probability of occurrence of flow level j (%); i is cropping farm index; i=1, 2, 3 where i=1 represents alfalfa farm, 2 represents wheat farm, and 3 represents potato farm; j is flow level index, j=1, 2, ..., 5 where j=1 for very low flows, 2 for low flows, 3 for medium flows, 4 for high flows, and 5 for very high flows; m is total number of farms; n is total number of flow levels. In model (1), the superscripts “±” represent lower and upper bounds of the parameters and variables. For example, B ^± _i are interval-parameters where B ^± _i =[B ⁻ _i , B _i +]; here, B ⁻ _i and B _i + correspond to lower and upper bounds of benefit. The model (1) can deal with uncertainties described as not only intervals but also probability distributions, as well as reflect water management policies.

Model (1) is an ITOM. In ITOM, a decision of water allocation target (W ^± _i ) needs to be made at the beginning facing future uncertainties of river flow (q ^± _j ); at a future time, when the uncertainties of water flow are quantified, a recourse action can then be taken (S ^± _ij ). Thus, decision of water allocation made at the beginning is called the first-stage decision (W ^± _i ), and the recourse decision is called the second-stage decision (S ^± _ij ). This leads to two-stage optimization model.

Solution method

The solution of ITOM cannot be obtained when W ^± _i are considered as uncertain inputs in model (1) because the existing methods for solving linear programming problems cannot be used directly (Huang 1996). However, an optimized set of target values can be obtained by having z _i in model (1) as decision variables. Let W ^± _i =W ⁻ _i +ΔW _i z _i have a deterministic value, where ΔW _i =W _i +− W ⁻ _i and z _i ∈[0,  1] (Huang and Loucks 2000). When W ^± _i approach their upper bounds (i.e. when z _i =1), the system benefit will be the highest as long as the water demands are well satisfied; however, this is associated with a higher risk of penalty when the promised amount is not delivered. Conversely, when W ^± _i reach their lower bounds (i.e. when z _i =0), the system may have a lower benefit; however, at the same time, the system may have a lower risk of violating the promised amounts and thus lower risk of system-failure penalties. Therefore, it is difficult to determine whether W _i + or W ⁻ _i will correspond to the desired lower bound of system benefit. Thus, by incorporating values of W ^± _i , Δf, ΔW_{i max}, and Δq ^± _j within the model (1), we have:

$$ {\text{Max}}\;f^ \pm = \sum\limits_{i = 1}^m {B_i^ \pm } \left( {W_i^ - + \Delta W_i z_i } \right) - \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {p_j C_i^ \pm S_{ij}^ \pm } } $$

(2a)

$$ \sum\limits_{i = 1}^m {\left( {W_i^ - + \Delta W_i z_i - S_{ij}^ \pm } \right)} \leqslant q_j^ \pm ,\forall j $$

(2b)

$$ W_i^ - + \Delta W_i z_i \leqslant W_{i\,\max }^ + ,\quad \forall j $$

(2c)

$$ - \Delta W_i z_i + S_{ij}^ \pm \leqslant W_i^ - ,\quad \forall i,j $$

(2d)

$$ S_{ij}^ \pm \geqslant 0,\quad \forall i,j $$

(2e)

$$ 0 \leqslant z_i \leqslant 1,\quad \forall i $$

(2f)

Model (2) can be transformed into two sets of deterministic submodels, which correspond to the lower and upper bounds of the desired objective. This transformation process is based on an interactive algorithm, which is different from normal interval analysis and best/worst case analysis (Huang et al. 1994). The resulting solutions provide stable intervals for the objective function and decision variables with different levels of risk in violating the constraints. They can be easily interpreted for generating decision alternatives. Since the objective is to maximize net system benefit, the objective-function value corresponding to f⁺ is desired first. A combination of the upper bounds for benefit coefficients and decision variables and the lower bounds for cost terms would correspond to f⁺. The submodel corresponding to f⁺ is (Huang 1996, 1998):

$$ {\text{Max}}\;f^ + = \sum\limits_{i = 1}^m {B_i^ + } \left( {W_i^ - + \Delta W_i z_i } \right) - \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {p_j C_i^ - S_{ij}^ - } } $$

(3a)

$$ \sum\limits_{i = 1}^m {\left( {\Delta W_i z_i - S_{ij}^ - } \right)} \leqslant q_j^ + \overline - \sum\limits_{i = 1}^m {W_i^ - } ,\quad \forall j $$

(3b)

$$ \Delta W_i z_i \leqslant W_{i\max }^ + - W_i^ - ,\quad \forall i $$

(3c)

$$ - \Delta W_i z_i + S_{ij}^ - \leqslant W_i^ - ,\quad \forall i,j $$

(3d)

$$ S_{ij}^ - \geqslant 0,\quad \forall i,j $$

(3e)

$$ 0 \leqslant z_i \leqslant 1,\quad \forall i $$

(3f)

where S ⁻ _ij and z _i are decision variables. Let S ⁻_{ij opt} and z_{i opt} be the solutions of model (3). The optimized water-allocation can be performed by calculating W ^±_{i opt} =W ⁻ _i +ΔW _i z_{i opt}, which corresponds to the extreme upper bound of system benefit under uncertain inputs of water-allocation amounts. According to Huang (1996, 1998), the submodel corresponding to f⁻ can be formulated as follows:

$$ {\text{Max}}\;f^ - = \sum\limits_{i = 1}^m {B_i^ - } \left( {W_i^ - + \Delta W_i z_{i\;{\text{opt}}} } \right) - \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {p_j C_i^ + S_{ij}^ + } } $$

(4a)

$$ \sum\limits_{i = 1}^m {\left( {\Delta W_i z_{i\;{\text{opt}}} - S_{ij}^ + } \right)} \leqslant q_j^ - - \sum\limits_{i = 1}^m {W_i^ - } ,\quad \forall j $$

(4b)

$$ - \Delta W_i z_{i\;{\text{opt}}} + S_{ij}^ + \leqslant W_i^ - ,\quad \forall i,j $$

(4c)

$$ S_{ij}^ + \geqslant S_{ij\;{\text{opt}}}^ - ,\quad \forall i,j $$

(4d)

where S _ij + are decision variables. Submodels (3) and (4) are deterministic linear programs. Thus, solutions for model (2) under the optimized water-allocation are (Huang 1996):

$$ f_{{\text{opt}}}^ \pm = [f_{{\text{opt}}}^ - ,{\text{ }}f_{{\text{opt}}}^ + ] $$

(5)

$$ S_{ij\;{\text{opt}}}^ \pm = [S_{ij\;{\text{opt}}}^ - ,{\text{ }}S_{ij\;{\text{opt}}}^ + ]{\text{ }},\quad \forall {\text{ }}i,j $$

(6)

where f_opt⁺ and S ⁻_{ij opt} are from solution of submodel (3), and f ⁻_opt and S_{ij opt}⁺ are from submodel (4). Thus, the optimum allocation of water to the given farms is:

$$ A_{ij\;{\text{opt}}}^ \pm = W_{i\;{\text{opt}}}^ \pm - {\text{ }}S_{ij\;{\text{opt}}}^ \pm ,\quad \forall {\text{ }}i,j $$

(7)

Case study

Overview of the study system

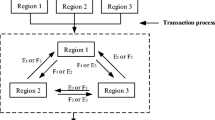
The proposed modeling approach is applied to a hypothetical case study of water resources allocation planning among a set of end-users within an agricultural sector. Consider an agricultural system in which a water manager is responsible for allocating water in a dry season from a reservoir to three farms cropped with alfalfa, wheat, and potato (Fig. 1). Allowable water-allocations and the related economic data are presented in Table 2. It is shown that the water allocation targets and the associated benefits and penalties vary among the farms. Table 3 provides reservoir flows and their associated probabilities of occurrence. In this case study, the “pre-defined water policies” are reflected though water-allocation targets (Table 2). These targets are prescribed quantities of water those have been promised to each end-user in advance before the outcomes of actual flows in the reservoir are known. Thus, if the promised water is delivered, it will result in net benefits to the agricultural economy owing to suitable water-allocation policies; and if not, it will lead to penalties to the agricultural system due to improper water-allocation policies.

Fig. 1

Schematic of water-allocation to multiple farms

Table 2 Allowable water-allocations (10⁶ m³) and related economic data ($/ m³)

Table 3 Reservoir flow distribution (10⁶ m³) and the associated probabilities (%)

Therefore, the problems under consideration are (a) how to effectively allocate the limited water supplies to the three farms in order to achieve maximum benefit, and (b) how to incorporate policies in terms of regulated water supplies within this planning problem with the least risk of system disruption. Since uncertainties exist in terms of intervals and probability distributions, and a link to a predefined policy is desired, the ITOM is considered to be a feasible approach for addressing this type of planning problem.

Result analysis

Table 4 shows results obtained through the ITOM. It is indicated that solutions for the objective-function value and of the non-zero decision variables related to the alfalfa, wheat, and potato farms are combinations of deterministic values and intervals. In case of insufficient water, allocation should be decreased firstly to the alfalfa farm, secondly to the wheat farm, and lastly to the potato farm. This is because the potato farm brings the highest benefit when water demand is satisfied and, likewise, is subject to the highest penalty if the promised water is not delivered. In comparison, the alfalfa and wheat farms correspond to lower benefits and penalties.

Table 4 Solution of the ITOM under optimized water-allocation targets (10⁶ m³)

Figure 2 and Table 4 present optimized water flow pattern and the associated allocation targets. The solutions of S ^±₁₁ = S ^±₁₂ =5 × S ^±₁₃ =[0, 4]×10⁶, and S ^±₁₄ =S ^±₁₅ =0 m³ indicate that, for alfalfa farm, some water shortages of 5×10⁶ and [0, 4]×10⁶ m³ may exist (in reference to the optimized water-allocation target of 5×10⁶ m³) under very low to medium flows, with the probability of occurrence being 10 to 40%; however, there will be no shortages of water under high to very high flows. Similarly, the results of S ^±₂₁ =5×10⁶, S ^±₂₂ =[1, 3]×10⁶, and S ^±₂₃ =S ^±₂₄ =S ^±₂₅ =0 m³ show that, for wheat farm, some shortages of 5×10⁶ and [1, 3]×10⁶ m³ may exist (in reference to the optimized water-allocation target of 5×10⁶ m³) under very low to low flows, with the probability of occurrence being 10 to 20%; however, there will be zero shortages of water under medium to very high flows. Likewise, the solutions of S ^±₃₁ =[0, 2]×10⁶ and S ^±₃₂ =S ^±₃₃ =S ^±₃₄ =S ^±₃₅ =0 m³ indicate that, for potato farm, there may be zero shortage of water under low to very high flows, and thus water will be fully allocated to the potato farm. However, under very low flow conditions the situation is more ambiguous for potato farm. There may be no water shortage under advantageous conditions when the other farms do not consume the full amounts of the allocated demands and/or the actual q ^±₁ value approaches its upper level; however, under demanding conditions, the shortage may become as high as 2×10⁶ m³ (in reference to the optimized water-allocation target of 3×10⁶ m³) with a probability of 10%.

Fig. 2

Optimized water-allocation patterns under very low (VL), low (L), medium (M), high (H) and very high (VH) flow levels

Alternatives evaluation and post-optimality analysis

Table 5 presents eight decision alternatives generated under different combinations of water shortages using a 2³ (two levels with three factors) factorial design approach. The alternatives were produced by adjusting the shortage values and thus allocation values between the upper and lower bounds of non-zero S ^±_{ij opt} . The intervals for S ^±_{ij opt} are useful for decision makers to justify the generated alternatives directly, or to adjust the allocation scheme when they are not satisfied with the recommended alternatives. Despite variations in S ^±₃₁ and S ^±₂₂ , alternatives 1 to 4 (where S ^±₁₃ =S ⁻₁₃ ) will lead to significantly higher system benefits than alternatives 5 to 8 (where S ^±₁₃ =S ⁺₁₃ ). The individual effects of S ^±₃₁ , S ^±₂₂ , and S ^±₁₃ are −45, −34, −112, respectively; and the combined effects of S ^±₃₁ S ^±₂₂ , S ^±₃₁ S ^±₁₃ , S ^±₂₂ S ^±₁₃ , and S ^±₃₁ S ^±₂₂ S ^±₁₃ are zero. It means that S ^±₁₃ (i.e. water-shortage to the alfalfa farm under medium flows) have a more significant effect on the system benefit than S ^±₃₁ (i.e. water-shortage to the potato farm under very low flows), S ^±₂₂ (i.e. water-shortage to the wheat farm under low flows), S ^±₃₁ S ^±₂₂ (i.e. combined shortage to the potato and wheat farms under very low to low flows), S ^±₃₁ S ^±₁₃ (i.e. combined shortage to the potato and alfalfa farms under very low to medium flows), S ^±₂₂ S ^±₁₃ (i.e. combined shortage to the wheat and alfalfa farms under low to medium flows), and S ^±₃₁ S ^±₂₂ S ^±₁₃ (i.e. combined shortage to the potato, wheat, and alfalfa farms under very low to medium flows). The negative sign for S ^±₃₁ , S ^±₂₂ S ^±₁₃ indicates that the system benefit will decrease as the water-shortage increases. Therefore, effective planning for water allocation to the alfalfa farm at medium seasonal flow is more important for improving the system’s performance than that of the wheat and potato farms. Similar post-optimality analyses can also be conducted for solutions under other scenarios of water-allocation targets.

Table 5 Alternatives generated from the ITOM solutions using a factorial design approach

Economic impacts of variations in water supply and demand are also determined by letting W ^± _i reach their upper bounds (Table 5). Generally, for each ITOM solution under a given scenario of water-allocation targets, lower shortage values correspond to more advantageous conditions. For example, alternative 1 (where S ^±₃₁ =S ⁻₃₁ , S ^±₂₂ =S ⁻₂₂ , and S ^±₁₃ =S ⁻₁₃ ) corresponds to a condition when water shortage values reach their lower bounds, which is advantageous (with the upper bound system benefit). In comparison, alternative 8 (where S ^±₃₁ =S₃₁+, S ^±₂₂ =S₂₂+, and S ^±₁₃ =S₁₃+) is based on a more demanding condition under which water shortage values reach their upper bounds, leading to a lower-bound system benefit. These alternatives reflect relationships between economic consideration and resources availability.

Policy analysis

Solutions of the ITOM provide desired water allocation patterns with maximized system benefit and feasibility. The complexities associated with the water-allocation amounts are mainly due to limited supply and increasing demand. Therefore, variations in the values of W ^± _i could reflect different policies for water resources management. An optimistic policy corresponding to the upper-bound system benefit may be subject to a high risk of system-failure penalties; while a too conservative policy may lead to waste of resources. Solutions under other policy scenarios can also be obtained by having W ^± _i equal different deterministic values. They represent different options for trading off among system benefit, reliability, and safety.

Comparison with the conventional TSP method

Model (1) can also be solved through a conventional TSP method by making all interval parameters be equal to their mean values. The obtained solution is a set of deterministic values and is indeed one of many alternatives from the ITOM. Although further sensitivity analysis can be undertaken, each TSP solution can only provide an individual response to variations of the uncertain inputs. Therefore, sensitivity analysis can hardly reflect interactions among various uncertainties (Huang and Loucks 2000; Lou et al. 2003 ).

The proposed modeling approach has an advantage in providing an effective linkage between the pre-defined water policies and the associated economic implications. Besides, the quality of information available for system modeling is often not good enough to be presented as either deterministic numbers or probability distributions. Instead, some uncertainties can only be quantified as intervals. The ITOM can handle various uncertainties described as probability distributions as well as discrete intervals.

The ITOM can directly incorporate uncertainties within its optimization framework. Its solutions are presented by combinations of deterministic values, intervals, and distributions; thus, offer flexibility in result interpretation and decision-alternative generation. Outputs of the ITOM can reflect fluctuations in system benefit (or cost) due to implementing different water-management policies. Moreover, its solutions contain information of system-failure risk under varying water-management conditions. Thus, ITOM solutions can provide bases for selecting desired irrigation-management policies and plans with reasonable benefits and minimized risk levels.

The proposed technique could also be applied to other areas of systems planning with pre-defined policies associated with uncertainties in related parameters. For example, in water-quality management, uncertainties and policies in pollutant loading associated with random river flows could be reflected through ITOM.

Conclusions

An ITOM was developed for irrigation planning of an agricultural system under uncertainty. Through this modeling study, a number of water allocation plans under predefined policies and extensive uncertainties were developed though a factorial design approach. The obtained solutions were reasonable and provided desired water-allocation patterns with maximized system benefits and feasibility. Further post-optimality analyses revealed that an optimistic water policy corresponding to higher agricultural income may be subject to a higher risk of system-failure penalties; while, a too conservative policy may lead to wastage of irrigation supplies.

The proposed model improves the existing two-stage stochastic and interval-parameter programming approaches. The ITOM allows predefined policies as well as uncertainties presented as random distributions and discrete intervals to be effectively incorporated within the optimization frame. An optimal allocation process was incorporated within the ITOM to determine the irrigation supplies to the cropping farms when a competition for water existed among them.

Although this study is the first attempt at the planning of an irrigated agricultural system through the ITOM, the results suggest that this hybrid technique is applicable and can be extended to other problems that involve policies with multi-objective and multi-stage concerns, as well as uncertainties that present in different formats.

Appendix

List of symbols

The following symbols are used in this paper:

f ^± :

Net system benefit ($/m³)

f ^±_opt :

Optimized net system benefit ($/m³)

B ^± _i :

Net benefit to farm i per m³ of water allocated ($)

W ^± _i :

Water policy in terms of fixed allocation amount of water that is promised to farm i (m³)

W ^±_imax :

Maximum allowable allocation amount for farm i (m³)

C ^± _i :

Loss to farm i per m³ of water not delivered, C _i > B _i ($)

S ^± _ij :

Decision variable representing shortage of water, which is the amount by which W _i is not met when the seasonal flow is q _j (m³)

S ^±_{ij opt} :

Optimized solution of S ^± _ij decision variable

q ^± _j :

Reservoir flow quantity with probability p _j of occurrence under flow level j (m³)

p _j :

Probability of occurrence of flow level j (%)

i :

Cropping farm index; i=1, 2, 3 where i=1 represents alfalfa farm, 2 represents wheat farm, and 3 represents potato farm

j :

Flow level index, j = 1, 2, ..., 5 where j = 1 for very low flows, 2 for low flows, 3 for medium flows, 4 for high flows, and 5 for very high flows

m :

Total number of farms

n :

Total number of flow levels

z _i :

Binary decision variable