1 Introduction

With rapid socio-economic development and urbanization, all sectors have become increasingly dependent on water resources (Bonaccorso et al. 2003; He et al. 2008; Maqsood et al. 2005). The practice of using agricultural water to meet the water needs of the industry, society and the environment has become increasingly serious, and the conflict between water resources supply and demand has become increasingly prominent. In the future, agriculture will likely face the problem of reduced water availability and the need to produce more food (Dogra et al. 2014). Therefore, it is increasingly important to improve the efficiency of agricultural water use. Optimal allocation of agricultural water is an important non-engineering measure that can achieve high water-use efficiency and meet the growing demand for food through efficient allocation of the limited water resources (Chen et al. 2008). This approach can promote sustainable socio-economic development and is one of the effective measures for realizing the sustainable utilization of agricultural water resources, which has been given considerable attention of scholars worldwide.

Numerous uncertainties and complexities exist in the agricultural irrigation management system (Li and Huang 2009). For example, there are uncertainties regarding regional water supply and demand situations, rainfall, runoff, crop water demand in the growth period, the fluctuation of the cost and benefit coefficient, different water supply ratios, etc. (Maqsood et al. 2005 and Liu et al. 2014). The previous certainty theory is no longer suitable for optimal allocation in an uncertainty system. To address the uncertainty, complexity and multi-water sources in the agricultural irrigation water allocation system, an increasing number of uncertainty theories and coupled methods can be used for optimal agricultural water allocation. These methods include interval programming, stochastic programming, fuzzy programming, and interval two-stage stochastic programming. (Zou et al. 2010), especially interval two-stage stochastic programming (TSP) models.

For example, Li and Huang (2008) combined an interval model with two-stage stochastic nonlinear programming (TSP) to solve the joint allocation of water resources among multi-reservoirs, multi-areas and multi-users. Lu et al. (2009) applied two-stage stochastic programming to optimize the allocation of agricultural water resources, coupling surface water and groundwater processes. Zhang and Li (2014) applied an interval two-stage planning model to optimize the water resource allocation between multi-water sources and multi-users in the Sanjiang plain, providing a reference for analyzing the uncertainty in the water resource system. Li and Zhang (2016) combined two-stage programming with fuzzy random programming to perform an optimization analysis of multi-water sources based on joint water distribution for each crop. Fu et al. (2014) combined interval two-stage stochastic programming (TSP) with a water production function to perform optimal water resources allocation among multi-sources, multi-regions and multi-crops under uncertainty. The TSP model can handle uncertainty to a certain degree (Lu et al. 2009 and Li and Huang 2009). However, the allocation process of agricultural water resources is random, and random factors can produce risk. Additionally, an interval two-stage stochastic programming(TSP) model regards the expectation value as the objective function. The average processing method may ignore some extreme cases (Mulvey et al. 1995 and Ahmed and Sahinidis 1998) and fail to capture the risk in stochastic programming processes associated with random information (Bai et al. 1997). Thus, this approach is not applicable for planning highly complex and dynamic systems, and the potential risk is high when decision makers exploit the system for greater economic benefit. Agricultural multi-water sources allocation risk is the possibility that multi-water source allocation will not realize the expected effect under the influence of the supply and demand of water, engineering and management strategies, and other uncertain factors (Gu et al. 2008). Stochastic robust optimization is an improved method of stochastic programming that combines the risk with a target function, using goal programming and scenario analysis methods to address uncertain parameters (Leung et al. 2007). Thus, this approach can help decision makers to balance the risk and the economic benefits in the agricultural irrigation water allocation system.

This study combines interval TSP with stochastic robust optimization to manage the agricultural irrigation water allocation in Jiamusi City of Heilongjiang Province, China. An allocation model based on robust interval TSP is established to analyze agricultural irrigation water allocation under uncertain conditions, and the model can allocate the agricultural water resources under multi-water source and multi-crop conditions according to the actual water resources in the study area. Then, the net benefits of the agricultural irrigation system at different robustness levels can be analyzed to maintain fairness in agricultural water distribution and promote sustainable development. Thus, the results can provide a theoretical basis for the efficient use of agricultural water resources and planting structure adjustment in the study area.

2 Methodology

2.1 Model Establishment

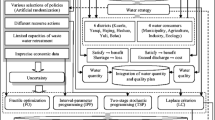
Due to the complexity and uncertainty that exists in the supply and demand of water in agricultural irrigation planning, water resources allocation in the agricultural sector is highly variable and complex, potentially resulting in a high-risk state of agricultural water distribution (e.g., water shortages in the critical period of crop growth, water supply unfairness, etc.). Robust planning can effectively capture the expected values of the two planning phases and the deviations of different scenarios, reducing the risks associated with water resource planning. In this study, two-stage stochastic optimization and robust optimization are coupled, and the maximum net benefit of agricultural irrigation is taken as the objective function. Water supply and demand and crop water requirements are the constraints. In the first stage, the goal is the expected water distribution under the full irrigation condition. In the second stage, the goal is crop production loss when the expected water supply amount is less than the expected demand. Finally, the optimal schemes of water allocation for different crops can be determined.

The model is as follows:

$$ \operatorname{Max}{f}^{\pm }=\sum \limits_{i=1}^m\sum \limits_{j=1}^n{NB}_{ij}^{\pm }{W}_{ij}^{\pm }-\sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm }-\omega \sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k\mid {C}_{ij}^{\pm }{S}_{ij k}^{\pm }-\sum \limits_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm}\mid $$
(1a)

where f is the net economic benefit in the agricultural irrigation area (RMB, yuan); i denotes water sources (surface water and groundwater); j denotes the main crops (rice, soybean and corn); \( {W}_{ij}^{\pm } \) represents the expected water allocation objectives of different water sources for different crops (planned water supply), which is the decision variables in the first phase (108 m3), i.e., when the water supply does not meet the expected target, the value will be punished; \( {NB}_{ij}^{\pm } \) is the net income of distribution when water source i distributes water to crop j (yuan/m3); \( {C}_{ij}^{\pm } \)is the water shortage penalty coefficient of crop j when the expected water distribution target is not satisfied (\( {C}_{ij}^{\pm } \)>\( {NB}_{ij}^{\pm } \)), i.e., the water supply deficit when the actual water supply is less than the expected amount (yuan/m3); and \( {S}_{ijk}^{\pm } \) is the water shortage when the water supply of source i does not meet the expected of water resource i distributes to demand of crop j, which is the decision variables in the second stage (108 m3). \( {S}_{ijk}^{\pm } \)is highly correlated with the water demand and rainfall; thus, it is difficult to determine. The variable p k  is the probability of the occurrence of incoming water level k (k = 1, 2,... r). When k = 1, the net inflow is the lowest in the forecast year, and it is deemed a low flow level. When k = 2, the net inflow is moderate in the forecast year. This situation is deemed a middle flow level and the water shortage is less severe. When k = r, the net inflow is the largest in the forecast year. This situation is deemed a high flow level, and the water shortage is the least severe. Additionally, p k  = p 1, p2 , p 3 \( , \kern0.5em \sum \limits_{k=1}^r{p}_k=1 \). ω is the target planning coefficient. Adjusting ω will produce a series of risk values in different scenarios of the model, providing a thorough and comprehensive analysis of the risk in the agricultural irrigation water allocation system. \( \mid {C}_{ij}^{\pm }{S}_{ij k}^{\pm }-\sum \limits_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm}\mid \) presents a measurement of the penalty function variation in the second stage. After introduction of the objective function, the model not only effectively reflects the multi-uncertainties but also ensures that the solution is more stable and reliable (Laguna 1998). The goal programming method (Yu and Li 2000) is used to simplify the relationship as follows:

$$ \operatorname{Max}{f}^{\pm }=\sum \limits_{i=1}^m\sum \limits_{j=1}^n{NB}_{ij}^{\pm }{W}_{ij}^{\pm }-\sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm }-\omega \sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k\left({C}_{ij}^{\pm }{S}_{ij k}^{\pm }-\sum \limits_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm }+2{\theta}_{ij k}^{\pm}\right) $$
(1b)

Constraint conditions:

  1. (1)

    The water supply capacity constraint is as follows:

$$ \sum \limits_{i=1}^m\sum \limits_{j=1}^n\left({W}_{ij}^{\pm }-{S}_{ij k}^{\pm}\right)\le \sum \limits_{i=1}^m\left({Q}_{ij}^{\pm }+{q}_{ij k}^{\pm}\right)\forall i,j,k $$
(1c)

where \( {Q}_{ij}^{\pm } \)is the available water quantity from different water sources in Jiamusi City at the beginning of planning period (108 m3) and \( {q}_{ijk}^{\pm } \) is the available water quantity from different water sources in the planning period (108 m3), where only rainfall is considered. Here \( {q}_{ijk}^{\pm } \)have obvious probability characteristics. The probability of the inflow quantity \( {q}_{ijk}^{\pm } \) is assumed to be p k , and water loss is not considered.

  1. (2)

    The maximum water supply constraint is as follows:

$$ {\sum}_{j=1}^n{W}_{ij}^{\pm}\le {W}_{i\mathit{\max}},\forall i,j $$
(1d)

where W imax is the maximum water supply of water source i (108 m3).

  1. (3)

    The constraint of the crop water requirement is as follows:

$$ {W}_{jmin}^{\pm}\le \sum \limits_{i=1}^m\sum \limits_{j=1}^n{W}_{ij}^{\pm}\le {W}_{jmax}^{\pm },\forall i,j,k $$
(1e)

where \( {W}_{jmin}^{\pm } \)and \( {W}_{jmax}^{\pm } \) of crop j under full irrigation conditions in the administrative area express the minimum water requirement and maximum water demand, respectively (108 m3).

  1. (4)

    The risk recourse constraints are as follows:

$$ {C}_{ij}^{\pm }{S}_{ij k}^{\pm }-{\sum}_{k=1}^r{p}_k{C}_{ij}^{\pm }{S}_{ij k}^{\pm }+{\theta}_{ij k}^{\pm}\ge 0,\forall i,j,k $$
(1f)
$$ {\theta}_{ijk}^{\pm}\ge 0,\forall i,j,k $$
(1g)
  1. (5)

    The variable non-negativity constraint is as follows.

$$ {W}_{ij}^{\pm}\ge {S}_{ij k}^{\pm}\ge 0,\forall i,j,k $$
(1h)

2.2 Model Solution

According to the characteristics of the model, \( {W}_{ij}^{\pm } \) is an uncertain variable expressed in the form of an interval number, and it is difficult to determine the system net irrigation maximum economic benefit when it takes that value; therefore methods for solving this problem have been proposed (Huang and Loucks 2000). Next, the decision variable z ij is introduced in the order of \( {W}_{ij}^{\pm }={W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij} \), where \( \varDelta {W}_{ij}={W}_{ij}^{+}-{W}_{ij}^{-} \) and ∆W ij is a constant value. If the crop water demand is met when \( {W}_{ij}^{\pm } \) approaches its upper limit (when z ij  = 1), the economic efficiency of the system will increase. Conversely, if the crop water requirements are not met, the system will be the greater punishment. Similarly, the economic benefits of the system will be reduced when \( {W}_{ij}^{\pm } \) is close to its lower limit (when z ij  = 0). If the water target is not reached, the risk of system water shortage will be low, and the consequences will be minimal. Through the introduction of z ij , the model can obtain the optimal value of z ijopt and the optimal value of \( {W}_{ij}^{\pm } \) using \( {W}_{ij}^{\pm }={W}^{-}+\varDelta {W}_{ij}{z}_{ij opt} \). This equation can determine W ij when the net benefit of the irrigation system is at its maximum, using the value as a known condition to solve it. Thus, the limit values of the model can be determined and \( {f}_{opt}^{+} \) and \( {S}_{ijopt}^{+} \) can be obtained. In this way, different water allocation schemes for crops can eventually be determined for a multi-water source. According to the above solution and interactive algorithm (Xu and Diwekar 2007), the model can be divided into two definite sub-models representing the upper and lower bounds. The sub-model of the upper limit of the objective function is as follows:

$$ \operatorname{Max}{f}^{+}=\sum \limits_{i=1}^m\sum \limits_{j=1}^n{NB}_{ij}^{+}\left({W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\right)-\sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k{C}_{ij}^{-}{S}_{ij k}^{-}-\omega \sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k\left({C}_{ij}^{-}{S}_{ij k}^{-}-\sum \limits_{k=1}^r{p}_k{C}_{ij}^{-}{S}_{ij k}^{-}+2{\theta}_{ij k}^{-}\right) $$
(2a)

The constraint conditions of eq. (2a) are as follows:

$$ {\sum}_{i=1}^m{\sum}_{j=1}^n\left({W}_{ij}^{-}+\Delta {W}_{ij}{z}_{ij}-{S}_{ij k}^{-}\right)\le {\sum}_{i=1}^m\left({Q}_{ij}^{+}+{q}_{ij k}^{+}\right),\forall i,j,k $$
(2b)
$$ {\sum}_{j=1}^n{W}_{ij}^{-}+\Delta {W}_{ij}{z}_{ij}\le {W}_{i\mathit{\max}},\forall i,j $$
(2c)
$$ {W}_{jmin}^{-}\le \sum \limits_{i=1}^m\sum \limits_{j=1}^n{W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\le {W}_{jmax}^{+},\forall i,j,k $$
(2d)
$$ {W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\ge {S}_{ij k}^{-}\ge 0,\forall i,j,k $$
(2e)
$$ {C}_{ij}^{-}{S}_{ij k}^{-}-{\sum}_{k=1}^r{p}_k{C}_{ij}^{-}{S}_{ij k}^{-}+{\theta}_{ij k}^{-}\ge 0,\forall i,j,k $$
(2f)
$$ {\theta}_{ijk}^{-}\ge 0,\forall i,j,k $$
(2g)

where z ij and \( {S}_{ijk}^{-} \) are decision variables, and z ijopt and \( {S}_{ijopt}^{-} \) are the solutions of the model and \( {f}_{opt}^{+} \) is the maximum value. The optimal target of water allocation \( {W}_{ij}^{\pm } \) can be calculated by introducing z ijopt into \( {W}_{ij}^{\pm }={W}_{ij}^{-}+\Delta {W}_{ij}{z}_{ij} \). In the same manner, z ijopt is introduced into the lower bound of the model, and the sub-model of the lower limit of the objective function is as follows:

$$ \operatorname{Max}{f}^{-}=\sum \limits_{i=1}^m\sum \limits_{j=1}^n{NB}_{ij}^{-}\left({W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\right)-\sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k{C}_{ij}^{+}{S}_{ij k}^{+}-\omega \sum \limits_{i=1}^m\sum \limits_{j=1}^n\sum \limits_{k=1}^r{p}_k\left({C}_{ij}^{+}{S}_{ij k}^{+}-\sum \limits_{k=1}^r{p}_k{C}_{ij}^{+}{S}_{ij k}^{+}+2{\theta}_{ij k}^{+}\right) $$
(3a)

The constraint conditions of eq. (3a) are as follows:

$$ \sum \limits_{i=1}^m\sum \limits_{j=1}^n\left({W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}-{S}_{ij k}^{+}\right)\le \sum \limits_{i=1}^m\sum \limits_{j=1}^n\left({Q}_{ij}^{-}+{q}_{ij k}^{-}\right),\forall i,j,k $$
(3b)
$$ {W}_{jmin}^{+}\le \sum \limits_{i=1}^m\sum \limits_{j=1}^n{W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\le {W}_{jmax}^{-},\forall i,j,k $$
(3c)
$$ \left({W}_{ij}^{-}+\varDelta {W}_{ij}{z}_{ij}\right)\ge {S}_{ij k}^{+}\ge 0,\forall i,j,k $$
(3d)
$$ {S}_{ijk}^{+}\ge {S}_{ijk}^{-},\forall i,j,k $$
(3e)
$$ {C}_{ij}^{+}{S}_{ij k}^{+}-{\sum}_{k=1}^r{p}_k{C}_{ij}^{+}{S}_{ij k}^{+}+{\theta}_{ij k}^{+}\ge 0,\forall i,j,k $$
(3f)
$$ {\theta}_{ijk}^{+}\ge 0,\forall i,j,k $$
(3g)

After solving for \( {S}_{ijopt}^{+} \)and \( {f}_{opt}^{-} \), the two sub-models are combined to obtain the solution of the robust, interval programming TSP model. The solution is as follows: \( {f}_{opt}^{\pm }=\left[{f}_{opt}^{-},{f}_{opt}^{+}\right],{S}_{ijopt}^{\pm }=\left[{S}_{ijopt}^{-},{S}_{ijopt}^{+}\right] \) and z ij  = z ijopt . The optimal water distribution scheme is as follows: \( {OPT}_{ij}^{\pm }={W}_{ij opt}^{\pm }-{S}_{ij opt}^{\pm },\forall i,j \) .

3 Application

3.1 Area Description

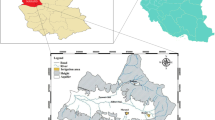
Jiamusi City (45° 56′-48° 28’ N, 129° 29′-135° 5′ E), is located at the site where the Songhua River, Heilongjiang River and Wusuli River converge. Jiamusi City is located in the Sanjiang Plain hinterland, in the northeastern Heilongjiang Province in northeast China (see Fig. 1). With an area of 3.27 × 104 km2 and population of 254 million, it is one of the most important grain commodity producers in Heilongjiang Province. The average volume of water resources per unit area is 1.2 × 105 m3/hm2, which is below the provincial average value (1.51 × 105 m3/hm2) and less than half of the national average level (3.0 × 105 m3/hm2). Thus, the city is considered a water-scarce region. According to statistics, there are various water supply projects in Jiamusi City, of which 62.07% are electromechanical wells. Compared with the exploitation of groundwater, the exploration capacity of transient water and surface water is poor under the current development conditions. In recent years, increased consumption of agricultural irrigation water (Ma et al. 2015) has led to more serious groundwater overdraft in Jiamusi City. Therefore, this paper optimally allocates the limited quantity of agricultural irrigation water among different crops and evaluates the economics and risks of the system in the context of the serious imbalance between the surface water and groundwater supplies.

Fig. 1
figure 1

Regional profile of the study area

Full size image

3.2 Data Sources

Field survey data were obtained from the “Heilongjiang Yearbook”, “Heilongjiang Statistical Yearbook” and other sources. According to historical rainfall and runoff data from Jiamusi City, the historical inflow can be divided into low, middle and high water levels. We know that the probability associated with a middle flow rate is higher than that of high flow and low flow rates, and the probabilities of high flow and low flow rates are similar based on a normal distribution. Thus, we assume that the predicted annual probabilities of the three levels of inflow are 0.2, 0.6 and 0.2. Table 1 lists the estimated upper and lower limits of forecast water availability in Jiamusi City at different water levels.

Table 1 Available water resources at different water levels
Full size table

In this paper, 2014 represents a typical year according to the "Heilongjiang Province local standards (water quota (2009))". Table 2 presents the typical quotas of crop irrigation and the expected supplies \( {W}_{ij}^{\pm } \) from different water sources for different crops in Jiamusi City. Based on available information and local research, 60% of the water supplied for agricultural irrigation in Jiamusi is groundwater, and 40% is surface water. Additionally, the coefficient of irrigation water use is 0.8 for paddy and 0.65 for upland.

Table 2 Crop irrigation quotas and supply water targets of each water source
Full size table

Based on relevant studies (Li and Zhang 2015), Table 3 provides the net benefit coefficient\( \kern0.5em {NB}_{ij}^{\pm } \) and punishment coefficient \( {C}_{ij}^{\pm } \) values corresponding to different water resources and different crops.

Table 3 Net system benefits and water shortage penalty coefficient per unit water (yuan·m−3)
Full size table

In a system of water resource management, the water resource allocation pattern should ensure the feasibility and reliability of the system. However, a water distribution pattern may occasionally lead to lower economic benefits in the system (Xu et al. 2009). The feasibility of the pattern is related to the water shortage amount, which indicates whether a water distribution pattern can be implemented. The reliability of the system is expressed as the degree of considering the the objective function value at different probability levels. The higher the feasibility of the water distribution pattern, the less severe the water shortage. Additionally, the higher the system reliability, the smaller the change of the objective function value.

4 Results and Analysis

4.1 Analysis of the Optimal Scheme of Water Distribution

Matlab 2013a software and Lingo 11 programming were used to solve the robust TSP model of multi-water source allocation in Jiamusi City. The results are presented in Table 4.

Table 4 Crop water distribution at different ω levels (108 m3)
Full size table

Table 4 illustrates that when ω equaled zero, different degrees of water shortage existed at different water inflow levels. The water shortage quantity decreased as the water inflow levels increased. This relationship is due to an increase in net natural water inflow and the quantity of water available, which reduced the water shortage. At different levels of water inflow, the largest water shortage is associated with rice. This shortage is mainly attributed to the fact that the rice irrigation quota and planting area are both too large; thus, the available quantity of water cannot meet the optimal allocation demand. For rice, the value of surface water decision variable z11 was 0.792, and the optimal water distribution target was 15.3 × 108 m3. The groundwater decision variable z21 equaled zero, and the optimal water allocation goal is 20 × 108 m3, which is the lower limit of the expected target. Regarding corn, the decision variables z12 and z22 were both equal to one, and the water shortage was less due to an ample water supply. Thus, the penalty punish risk was very low, and the net income per unit water was increased. Therefore, the upper limit value of water distribution was expected to be the optimal target. For soybean, the decision variables z23 and z13 were both equal to zero, because the crop irrigation quota and planting area are all small and the water demand was low. Therefore, the lower limit of the expected target was set as the optimal distribution target. From the crop water allocation scheme illustrated in Table 4, the surface water shortages associated with the three crops were always larger than the groundwater shortages at different inflow levels, indicating that the degree of surface water exploitation in the Jiamusi City was low. If this state continued, the groundwater exploitation amount would increase and more surface water would be wasted.

Decision variable Z is affected by numerous factors, such as variable water supplies, crop water requirements, and crop irrigation periods. The groundwater will increase under the low level of water inflow. Then, the surface water decision variable Z will decrease, and the groundwater decision variable Z will increase. When the water requirement decreases, Z also decreases. Additionally, if the crop irrigation period changes, a more adequate water supply is available in each period. Compared with irrigation at the same time, the Z value is relatively large, and which increases the system net economic efficiency.

4.2 Robust Optimization Analysis

The robust optimization of Table 4 can be analyzed. The water supply amount of different water sources to different crops varies with ω. As ω varies from zero to five at the low inflow level, the surface water supply amount is [8.8, 12.7] × 108 m3, [10.1, 12.8] × 108 m3, [10.4, 12.9] × 108 m3 and [10.7, 13.4] × 108 m3, and the groundwater supply amount is [17.5, 20.5] × 108 m3, [17.7, 20.6] × 108 m3, [18.1, 20.9] × 108 m3 and [18.6, 21.3] × 108 m3. As ω increases, the crop water supply amount increases and the water shortage decreases. Additionally, the upper and lower limits of water shortage change with the robust optimization coefficient ω. Thus, the risk of water shortage will decrease as ω increases, and the system reliability will improve.

The water shortage and water supply amount associated with different crops are different at different values of ω, which is also shown in Table 4. For rice, when ω ranges from 0 to 5 at three inflow levels, the total shortage of surface water is [10.1, 15.3] × 108 m3, [10.0, 14.1] × 108 m3, [9.4, 13.4] × 108 m3 and [8.5, 12.7] × 108 m3, and the total shortage of groundwater is [8.4, 15.2] × 108 m3, [8.1, 14.5] × 108 m3, [7.7, 13.7] × 108 m3 and [7.2, 13.0] × 108 m3. As the robust optimization coefficient ω increases, the total water quantity of rice decreases, which indicates that the reliability of the water supply system is enhanced. At the three levels of water inflow, rice always has a larger water shortage than corn and soybean. When ω = 0.5 and at a middle inflow level, the surface water shortage of rice, corn and soybean is [3.7, 4.9] × 108 m3, [0, 0.4] × 108 m3 and zero, respectively, and the groundwater shortages are [3.1, 5.1] × 108 m3, [0, 0.3] × 108 m3 and zero, respectively. The main reasons for these trends are as follows: (1) the irrigation quota and planting area of rice are both larger, requiring more water than other crops; (2) the net incomes of corn and soybean are both increased per unit water; (3) the total water requirements of corn and soybean are both relatively small and can generally be met by the water supply (Table 5).

Table 5 Water supply targets at different ω levels
Full size table

Figures 2 and 3 present the risk of recourse values and net economic benefits of the system at different ω levels. As ω increases, the risk of recourse value gradually increases. In addition, the net economic benefit of the system decreases and the difference between the upper and lower bounds of the net economic benefit narrows. When ω ranges from zero to five, the differences between the upper and lower bounds of the net economic benefit of the system are 70.65, 60.9, 59.61, 58.76, 55.15, 51.73 and 48.09. These results indicate that the robustness of the system is enhanced and the system eventually becomes reliable and stable. If the decision makers seek to maximize the net economic benefit, they will face increased risks of water shortage and reduced system reliability. Thus, interval TSP can help decision makers perform comprehensive assessments of system economics and reliability. In reality, decision makers must to choose between a stable and highly feasible scheme with low economic benefit and a high risk scheme, that may provide more economic benefit. Therefore, our approach can help decision makers thoroughly understand the characteristics of the multi-water source composite system, allowing them to make reasonable decisions.

Fig. 2
figure 2

Recourse costs at different robustness levels

Full size image
Fig. 3
figure 3

Net system benefit at different robustness levels

Full size image

In Jiamusi City, the water requirements, unit yields, income per unit water and penalty coefficients differ across crops, and these differences are large. Corn and soybean are dry land crops and the income per unit water is larger. Rice requires more water, and the income per unit water is less. If the agricultural water demand is too large, the crop cannot be fully irrigated, which reduces the water supply amount of some crops. However, the regional economic benefits of agriculture cannot be considerably reduced; a tradeoff must occur between economic benefit and risk. This study demonstrates that most of the crops lack water at different levels of water inflow, mainly because the irrigation quota and planting area of rice are both too large, reducing the water supply amount to other crops. At a low inflow level, rice is associated with a serious lack of water, and the water shortage risk is large, reducing the system benefit. Therefore, managers should appropriately adjust the crop planting structure.

5 Conclusions

Combining two-stage stochastic programming with robust optimization under uncertain conditions, this paper optimized agricultural water allocation of multi-water sources in Jiamusi City. The model linked the economic benefit and the system risk to remedy the shortcomings of the traditional interval two-stage stochastic programming (TSP) method. The model introduced a variability measurement to determine the water distribution that maximized the system net economic benefit. The results are provided in interval form and may provide a reasonable solution for decision makers to balance economic benefit and risk. The model can effectively manage the interval and random uncertainty information. Compared with the traditional two-stage model, the interval two-stage stochastic robust programming optimization model can effectively search for the risk associated with the stochastic programming process, improving the robustness of the model and the stability of the multi-water source system. The results revealed that the traditional model is improved and optimized. The ω = 0.5 decision scheme, which considered not only the system risk but also the net economic benefit of the system, was a reasonable risk-reward option at the middle inflow level. In addition, this paper considered the relationship between net economic benefit and risk at different levels of water inflow. Thus, this method can be used to solve actual problems associated with water resource allocation.

However, the annual distribution of the crop water demand is not based on the growing periods of crops. In the future, the water distribution for different crops will be based on their growing periods, combing the actual scenario and water distribution theory. According to the water allocation schemes, Jiamusi City should increase the surface water exploitation quantity and decrease the groundwater exploitation quantity to enhance the reliability of and reduce the risks to the water supply system in the future, which will be important way to solving the crop water shortage.