1 Introduction

Water resource is associated with a variety of activities with complicated supply–demand contradiction (Li et al. 2009). As a foundation of natural resources, the rational exploitation and utilization of water resources are closely related with the harmonious development of society, economy and environment. With the rapid development of socio-economic and continuous population growth, the conflict between increased water demand and decreased available water resources becomes particularly evident in most of the regions (Lu et al. 2008). While the demand for water reaches the upper limit of what the natural resources system can provide, water shortage will become a major obstacle to social-economic development and bring a series of troubles (Bronstert et al. 2000; Li et al. 2009).

Over the past decades, conflict-laden and controversial water allocation issues related to the interests which have challenged water resource managers have been intensified (Huang and Chang 2003; Wang et al. 2003; Maqsood et al. 2005; Fan et al. 2012). Particularly, the rapid growth of the population, shrinking water availabilities and deteriorating water environment have still further strengthened such competitions (Li and Huang 2008). To better solve above problems, a method of effective allocation of water resources is desired to be established.

In the water-resource system, uncertainties may exist in its internal relationship and have effect on the system analysis to some extend (Fan et al. 2012; Li et al. 2013). Such uncertainties may come from the randomness of rainfall events in temporal and spatial, the change in strategies and the instability of water supply–demand in various period of time (Thompson and Tanapat 2005; Guo and Huang 2009a; Zhang and Li 2014); The complexities among parameters can also strengthen the contractions in allocation, and then cause the confusion of uncertain information. The existing uncertainties and complexities increase difficulties for water managers to make proper decisions. Most planning methods are difficult to achieve optimal management of water resources. Therefore, it is desired to address more effective approaches to deal with the uncertainties and complexities in water resources system (Li et al. 2010).

Previously, aiming at dealing with the uncertainties existing in water resources planning system, a number of optimization approaches had been put forward (Stedinger et al. 1984; Kindler 1992; Huang 1996; Luo et al. 2003; Abdelaziz and Masri 2005; Guo and Huang 2009b; Guo et al. 2009; Ping et al. 2010). For example, in order to simplify reservoir operation, Stedinger et al. (1984) applied the stochastic dynamic programming models. Huang (1996) developed an internal parameter water quantity management (IPWM) model for an agricultural system to control water pollution. Li et al. (2008a, b) developed an interval-fuzzy multistage programming (IFMP) model in water resources management to solve uncertainties presented ass discrete intervals, fuzzy sets and probability distributions. Gu et al. (2013) proposed an interval multistage joint-probabilistic integer programming (IMJIP) to address uncertain problems existed water resource regulation.

Among the mathematical analysis approaches, as a representative stochastic programming method, two-stage stochastic programming (TSP) is effective for problems where an analysis of policy scenarios is desired and the uncertainties existing in the system can be expressed as random variables with known probability distributions (Li and Huang 2008; Li and Huang 2009). The substance of TSP is the concept of recourse, who has a distinctive capability to take corrective actions after a random event has taken place (Birge and Louveaux 1997); in TSP, a decision is firstly undertaken (named the first-stage) before values of random variables are known; then, after the random events have occurred and their values are known, a recourse action (named the second-stage) can be made in order to minimize “penalties” that may appear due to any infeasibility (Loucks et al. 1981; Birge and Louveaux 1988; Ruszczynski and Swietanowski 1997; Dupačová 2002; Li et al. 2008b).

Therefore, the TSP modeling formulation can be an effective tradeoff between the policies and the associated economic penalties caused by unreasonable plans (Seifi and Hipel 2001; Li and Huang 2006). Over the past decades, TSP was widely applied in all kinds of fields, including the field of water resources allocation management (Mobasheri and Harboe 1970; Kall 1979; Pereira and Pinto 1985; Wang and Adams 1986; Ferrero et al. 1998; Dai et al. 2000; Luo et al. 2003). For example, Pereira and Pinto (1985) proposed a stochastic optimization approach and applied in a 37 reservoirs hydroelectric system, and the dealing results was used in the weekly or monthly generation scheduling activities in real-time operation. Wang and Adams (1986) used a two-stage optimization framework, consisting of a real time model and a steady state model, in which reservoir inflows are described as periodic Markov processes because of hydrologic uncertainty and seasonality. Eiger and Shamir (1991) proposed a model for optimizing the multi-period operation in a multi-reservoir system, where uncertain inflows and water demands are formulated and uncertainties are considered in chance constraints. Ferrero et al. (1998) developed a new two-stage dynamic programming method and used it in a long-term hydrothermal scheduling in multi-reservoir systems. Nevertheless, TSP methods have some problems in handing vague information that may exist in the objective function and constraints.

Although the method can deal with the uncertainties existing in the process of water resources allocation, the TSP still has limitations. The TSP approaches needs all of the uncertain parameters to be presented as probability distributions, while the information presented as non-probability distribution can’t be reflected directly. In other words, not all of the uncertain information can be presented as probability distributions in the real-world. Even if such distributions are available, reflecting them in large-scale optimization models can be extremely challenged (Huang and Loucks 2000).

As another typical mathematical programming method, interval mathematical programming (IMP) is effective in tackling uncertainties presented as intervals with known lower and upper bounds but unknown distribution functions (Huang et al. 1992). IMP approach had shown a strong ability to deal with the uncertainties in the objective function as well as the left-hand side and right-hand side of the constraints. Order to improve TSP and take the advantage of IMP, integrating internal parameter programming with two-stage stochastic programming within a general optimization framework will be a perfect action. Therefore, Huang and Loucks (2000) made a hybrid between two-stage stochastic programming and inexact optimization and applied it to water resources decisions. Maqsood et al. (2005) developed an interval-parameter two-stage stochastic programming for water resources management under uncertainty. Li and Huang (2008) proposed an interval-parameter two-stage stochastic nonlinear programming (ITNP) method and applied to supporting the decisions of water-resources allocation when appearing the contradictions of water allocation and economic interests. Fan et al. (2012) advanced an inexact two-stage stochastic partial programming model to tackle uncertainties presenting as interval and partial probability distribution water resources management system. Xie et al. (2013) used the similar method for planning multi-regional water resources allocation plan in the Nansihu lake Basin, China. Although the integrated model has developed greatly and improved the allocation of water resources in different degrees, there is nearly no relevant studies considering about dividing the whole process into extraction process and distribution process.

Therefore, the study develops an inexact two-stage water allocation (ITWA) model for water resources planning and management and aims to allocate the mined water (surface water and groundwater) to multi-water supply subareas reasonably, and supplying water for multi-using sectors, as well as obtaining multi-planning goals. This proposed model combines interval parameters programming (IPP) with two-stage stochastic programming (TSP) as a general optimization framework and has been applies in an assumed area. The above model not only can handle the uncertainties and complexities presented as interval values and probability densities, but also can help decision makers obtain a tradeoff between the desirable water resources allocation and net system benefit. When the pre-allocating water quantity is set much higher, that is, it reaches the upper level, more net income and punishing risk will be generated if the established targets can be realized, otherwise higher amount of economic penalty will be generated if the promised targets are not reached. On the contrary, lower pre-allocating water quantity causes fewer economic penalties as well as fewer net incomes. The results from the ITWA can help decision makers to identify a desirable water resources planning. An assumed case will be presented to just demonstrate how the proposed method helps water resources managers identify the desirable system designs faced with the water shortage, and decides which is the most efficient design and can lead to the optimized system objectives.

2 Methodology

Consider a case wherein an authority is responsible for allocation scare water resources from multi-water sources to multi-water users. Water resources managers need to make a proper decision to allocate enough water to each sector user, and the most important point thing they concern is how to the balance the water allocation quantity and the net benefit. In general, the economic penalties are associated with the acquisition of water from higher-priced alternatives and/or the negative consequences generated from the curbing of regional development plans when the promised water is not delivered (Howe et al. 2003). Given a water quantity that is promised to using departments, if the promised water is delivered, it will generate larger net benefit; and vice versa, if the water is not delivered, a larger cost will be generated, for the reason is that the water shortage quantity should be got in other ways with more expensive spending (Loucks et al. 1981). Because of the high water requirement in different water using sectors, the allocated water quantity during planning becomes uncertain. It can be represented as random variables with known probabilities, and the relevant water allocation plan will be dynamic features.

Two-stage stochastic programming (TSP) reflects a tradeoff between predefined strategies and the associated adaptive adjustments. The model can be written as follows (Mance 2007)

$$ f= \min \left\{cx+E\left[Q\left(x,w\right)\right]\right\} $$
(1a)

Subject to

$$ Ax\le b $$
(1b)
$$ x\ge 0 $$
(1c)

Where A ∈ R m×n, b ∈ R m×l, c ∈ R l×n(R denotes a set of real numbers). w is the random variable (w ∈ Ω), x is the first-stage decision before the random variable is observed. E[Q(x, w)] is the expected value of a random variable. Let the random variable w take discrete values of w k with a probability level of p k , where k = 1, 2, …, K, and p k is the probability of occurrence, with p k  > 0 and ∑ k k = 1 p k  = 1. The expected value can be replaced in another kind of form as follows:

$$ E\left[Q\left(x,w\right)\right]={\displaystyle \sum_{k=1}^K{p}_kQ\left(x,{w}_k\right)} $$
(2a)

The occurrence of the second-stage decision depends on the realization of random variable w k . The second-stage penalty function can be denoted with q(y k , w k ) and y k is the second-stage adaptive decision. Therefore, the second-stage optimization problem can be then written as this:

$$ \mathrm{M}\mathrm{i}\mathrm{n}\kern1em q\left({y}_k,{w}_k\right) $$
(3a)

Subject to

$$ W(w)y=h(w)-T(w)x $$
(3b)
$$ y\ge 0 $$
(3c)

W(w), h(w) and T(w) (w ∈ Ω) are the relevant functions of random variable w with reasonable dimensions; T(w)x is the pre-decision value; h(w) is the actual value. When the random variable is observed, the discrepancy that exists between h(w) and T(w)x can be corrected by recourse action, and thus a minimized value of q(y k , w k ) can be got.

Combing models (1–3), a new model can be formulated as follows:

$$ f= \min \left\{cx+{\displaystyle \sum_{k=1}^K{p}_kq\left({y}_k,{w}_k\right)}\right\} $$
(4a)

Subject to

$$ Ax\le b $$
(4b)
$$ \begin{array}{ll}W\left({w}_k\right){y}_k=h\left({w}_k\right)-T\left({w}_k\right)x,\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(4c)
$$ x\ge 0,{y}_w\ge 0 $$
(4d)

Although the above model is effective to reflect the uncertainties existing in the system, and the uncertainties are formed as random variables of known probability distributions in the right-hand sides of constraints, uncertain parameters may still exist in the objective functions and the left-hand sides. Moreover, not all of the uncertain information can be presented as probability distributions in the real-world. Sometimes, the quality of information is mostly not enough to be presented as probability distributions (Huang and Loucks 2000). Based on the above analysis, interval parameter is brought up to the study.

Let x denote a bounded and closed set of real numbers. x ± denotes the upper bound and lower bound of interval value (Huang 1996).

$$ {x}^{\pm }=\left[{x}^{-},{x}^{+}\right]=\left\{t/{x}^{-}\le t\le {x}^{+}\right\} $$
(5a)

When x − = x +, t becomes a real number.

After integrating interval-parameter programming (IPP) and a two-stage stochastic programming (TSP), another model named inexact two-stage stochastic programming (ITSP) model is formed and described as this:

$$ {f}^{\pm }= \min \left\{{c}^{\pm }{x}^{\pm }+{\displaystyle \sum_{k=1}^K{p}_kq\left({y}_k^{\pm },{w}_k^{\pm}\right)}\right\} $$
(6a)

Subject to

$$ {A}^{\pm }{x}^{\pm}\le {b}^{\pm } $$
(6b)
$$ \begin{array}{ll}W\left({w}_k^{\pm}\right){y}_k^{\pm }=h\left({w}_k^{\pm}\right)-T\left({w}_k^{\pm}\right){x}^{\pm },\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(6c)
$$ {x}^{\pm}\ge 0,{y}_k^{\pm}\ge 0 $$
(6d)

If x ± is considered as uncertain input parameter, the above model can be solved directly. Therefore, in order to simplify the uncertain parameter, a decision variable z must be introduced into the inexact interval parameter two-stage stochastic allocation model. Accordingly, let x ± = x − + Δx ⋅ z, where Δx = x + − x − and z ∈ [0, 1]. Thus, model (6) can be reformulated as follows:

$$ {f}^{\pm }= \min \left\{{c}^{\pm}\left({x}^{-}+\varDelta x\cdot z\right)+{\displaystyle \sum_{k=1}^K{p}_kq\left({y}_k^{\pm },{w}_k^{\pm}\right)}\right\} $$
(7a)

Subject to

$$ {A}^{\pm }{c}^{\pm}\le {b}^{\pm } $$
(7b)
$$ \begin{array}{ll}W\left({w}_k^{\pm}\right){y}_k^{\pm }=h\left({w}_k^{\pm}\right)-T\left({w}_k^{\pm}\right){x}^{\pm },\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(7c)
$$ {x}^{\pm}\ge 0,{y}_k^{\pm}\ge 0 $$
(7d)
$$ \varDelta x={x}^{+}-{x}^{-} $$
(7e)
$$ 0\le z\le 1 $$
(7f)

Based on the interactive algorithm (Huang et al. 1994), model (7) can be transformed into two deterministic submodels, which correspond to the lower and upper bounds of the desired objective function value. Then we have (assumes c ± > 0, A ± > 0 and b ± > 0):

The lower bound value of objective function: f −

$$ {f}^{-}= \min \left\{{c}^{-}\left({x}^{-}+\varDelta x\cdot z\right)+{\displaystyle \sum_{k=1}^K{p}_kq\left({y}_k^{-},{w}_k^{-}\right)}\right\} $$
(8a)

Subject to

$$ {A}^{+}\left({x}^{-}+\varDelta xz\right)\le {b}^{-} $$
(8b)
$$ \begin{array}{ll}T\left({w}_k^{+}\right)\left({x}^{-}+\varDelta xz\right)+W\left({w}_k^{+}\right){y}_k^{+}=h\left({w}_k^{+}\right),\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(8c)
$$ \varDelta x={x}^{+}-{x}^{-} $$
(8d)
$$ {y}_k^{-}\ge 0 $$
(8e)
$$ 0\le z\le 1 $$
(8f)

Where z and y − k are decision variables. Let z opt , y − kopt , and f − opt be the solutions of the submodel (8). The optimized first-stage variable can be got by x ± opt  = x − + Δx ⋅ z opt , which may correspond to optimized lower bound objective function value.

The upper bound value of objective function: f +

$$ {f}^{+}= \min \left\{{c}^{+}\left({x}^{-}+\varDelta x\cdot z\right)+{\displaystyle \sum_{k=1}^K{p}_kq\left({y}_k^{+},{w}_k^{+}\right)}\right\} $$
(9a)

Subject to

$$ {A}^{-}\left({x}^{-}+\varDelta xz\right)\le {b}^{+} $$
(9b)
$$ \begin{array}{ll}T\left({w}_k^{-}\right)\left({x}^{-}+\varDelta xz\right)+W\left({w}_k^{-}\right){y}_k^{+}=h\left({w}_k^{-}\right),\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(9c)
$$ \varDelta x={x}^{+}-{x}^{-} $$
(9d)
$$ {y}_k^{+}\ge 0 $$
(9e)
$$ 0\le z\le 1 $$
(9f)

Where y + k is decision variable. Suppose y + kopt and f + opt are solutions of the submodel (9).

Thus, solutions of model (7) under the optimized first stage decision can be obtained as this:

$$ {f}_{opt}^{\pm }=\left[{f}_{opt}^{-},{f}_{opt}^{+}\right] $$
(10a)
$$ {x}_{opt}^{\pm }={x}^{-}+\varDelta x\cdot {z}_{opt} $$
(10b)
$$ \begin{array}{ll}{y}_{kopt}^{\pm }=\left[{y}_{kopt}^{-},{y}_{kopt}^{+}\right],\hfill & \forall k=1,2,\dots, K\hfill \end{array} $$
(10c)

3 Case Study

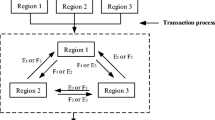
The proposed method is applied to a hypothetical water resources allocation case for the planning and management of water resources, which aims to allocate multi-water source (surface water and groundwater) by exploiting to multi-subarea and supply water for multi-using sectors. The whole study system is divided into two processes, namely extraction process and distribution process, containing six supplying water subareas and three water using sectors. And the water using sectors contain domestic sector (municipal and rural), productive sector (industrial and agricultural) and ecological sector (forest, grass and so on). The water availabilities are characterized as different levels with interval probabilities. The authority should make a promise to allocate water resources to each sector in advance. If the promised water quantity can satisfy the using of water sectors, it will bring a high net benefit; on the contrary, recourse action will happen and they must be obtain enough water from other areas with more expensive price (Huang and Loucks 2000; Li and Huang 2006). The purpose of second-stage decision is to adjust the first-stage decision and minimize the penalties due to any infeasibility. In addition, obtaining possible water resources need a process called extraction process. Detailed flow diagram is shown in Fig. 1.

Fig. 1
figure 1

Water resources allocation process diagram

Full size image

These processes can be reformulated as an inexact two-stage water allocation model. And they can be written like this:

$$ {f}^{\pm }= \min \left\{{\displaystyle \sum_{i=1}^I{\displaystyle \sum_{j=1}^JN{C}_{ij}^{\pm }{W}_{ij}^{\pm }+{\displaystyle \sum_{j=1}^J{\displaystyle \sum_{h=1}^HN{C}_{jh}^{\pm}\left({W}_{jh}^{-}+\varDelta {W}_{jh}\cdot {z}_j\right)}}}}\right.+\left.{\displaystyle \sum_{i=1}^I{\displaystyle \sum_{j=1}^J{\displaystyle \sum_{k=1}^KN{C^{\prime}}_{ij}^{\pm }{p}_k\varDelta {Q}_j^{\pm }}}}\right\} $$
(11a)

Subject to

$$ \begin{array}{ll}{W}_{jh \max}\ge {\displaystyle \sum_{j=1}^J{\displaystyle \sum_{h=1}^H\left({W}_{jh}^{-}+\varDelta {W}_{jh}\cdot {z}_j\right)}}\ge {W}_{jh \min },\hfill & \forall j,h\hfill \end{array} $$
(11b)
$$ \begin{array}{ll}{\displaystyle \sum_{j=1}^J{\displaystyle \sum_{h=1}^H\left[\left({W}_{jh}^{-}+\varDelta {W}_{jh}\cdot {z}_j\right)-{q}_k\right]}}\le Q,\hfill & \forall j,h,k\hfill \end{array} $$
(11c)
$$ \begin{array}{ll}{W}_{jh}^{-}+\varDelta {W}_{jh}\cdot {z}_j\ge {W}_{jh}^{-}+\varDelta {W}_{jh}\cdot {z}_j-{q}_k\ge 0,\hfill & \forall j,h,k\hfill \end{array} $$
(11d)
$$ \begin{array}{ll}{W}_{jh}^{-}\ge 0,\hfill & \forall j,h\hfill \end{array} $$
(11e)
$$ \begin{array}{ll}0\le {p}_k\le 1,\hfill & \forall k\hfill \end{array} $$
(11f)
$$ \begin{array}{ll}0\le {z}_j\le 1,\hfill & \forall j\hfill \end{array} $$
(11g)

Where f ± is the interval value of net cost (RMB, ¥); i denotes water sources for supplying, as i = 1, 2, with i = 1 representing surface water, and i = 2 representing groundwater, respectively; j denotes subareas for supplying water to water using sectors, as j = 1, 2 ⋯, 6; h denotes water using sector with h = 1 for domestic sector, h = 2 for the productive sector and h = 3 for the ecological sector, respectively; NC ± ij is the interval value of cost per unit in extraction process; NC ± jh is the interval value of cost per unit in distribution process (in the first-stage); NC ′ ± ij is the interval value of penalty per unit where the practical water supply quantity fails to satisfy expectations (in the second-stage); W ± ij is the interval value of exploitation water quantity; W ± jh is the lower bound of promised allocation quantity; ΔQ ± j is the supplying quantity difference between the actual and the expected when the total water amount is Q.

Table 1 shows the extraction water quantity, water availabilities under the associated probabilities of occurrence and water allocation targets to three water using sectors (domestic, productive and ecological). Table 2 lists a series of economic date of water allocation system. The penalty means a negative consequence when the promised water quantity is not delivered (Loucks et al. 1981).

Table 1 Water quantity in each subarea (108  m 3)
Full size table
Table 2 Economic data of water allocation (RMB¥/m 3)
Full size table

In practice, the maximum water extracting quantity is affected by not only the water supply capacity of engineering, and the current water availability. That is Min {Water supply capacity of engineering, Water availability}. At this point, the extracting water quantity was influenced by the flow condition with specific probability which the same as the water availabilities. Thus Table 1 is identified as the water quantity in the high inflow level with the probability at 0.2. In the same way, the exploiting water quantity under medium level can be listed in Table 3 with the probability at 0.6, as well as the supplying water quantity and the associated probabilities of occurrence; Table 4 lists the date of exploiting water quantity under low level with the probability at 0.2.

Table 3 Water quantity under medium level of extracting water quantity (p ′ = 0.6) (108 m 3)
Full size table
Table 4 Water quantity under low level of extracting water quantity (p ′ = 0.2) (108 m 3)
Full size table

4 Results Analysis

Table 5 presents the results obtained from the ITWA model. The optimized water allocation target, the optimized shortage water quantity and the optimized water allocation quantity are listed in this table. The optimized water allocation targets for water using sectors can be obtained as W ± jhopt  = W − jh  + ΔW jh  ⋅ z jopt . The optimized solutions can help managers spend the least under the uncertain water targets and water availabilities. In this table, we can find that the optimized target quantity allocation in the productive sector is the most in each subarea. For example, for productive sector, optimized target allocation of subarea1-6 is 25.36 × 108 m 3, 16.16 × 108 m 3, 28.12 × 108 m 3, 7.36 × 108 m 3, 13.94 × 108 m 3 and 26.87 × 108 m 3 in turn, while for domestic and ecological sectors, they are only 0.76 × 108 m 3, 0.14 × 108 m 3; 0.43 × 108 m 3, 0.11 × 108 m 3; 1.08 × 108 m 3, 0.09 × 108 m 3; 0.27 × 108 m 3, 0.05 × 108 m 3; 0.58 × 108 m 3, 0.11 × 108 m 3 and 1.16 × 108 m 3, 0.28 × 108 m 3, respectively. The reason is that productive department needs a lot of water. In order to meet the daily life, the allocation water quantity for domestic sector is administratively guaranteed, while water for productive and ecological sectors will be delivered later. Thus there is nearly no shortage for domestic sector. Due to the greater water demand, water shortage exists in supplying for the productive department. For example, in subarea 1, when the level of water availability is low, the shortage is [2.5, 3.6] × 108 m 3, while in medium and high levels, the shortage is [1.5, 1.8] × 108 m 3 and [0.5, 1.0] × 108 m 3, respectively. In the same way, in low, medium and high levels, the shortage of subarea 2 for productive sector is [1.7, 2.2] × 108 m 3, [1.0, 1.3] × 108 m 3 and [0.5, 0.7] × 108 m 3 respectively. The value difference between the optimized target and optimized shortage is the value of the optimized allocation water quantity. The detailed situations of other subareas are all similar as the description above. By contrast, water demand in ecological sectors is much lower, the shortage in different degrees still exists, especially under low and medium levels, for the reason is that humans have ignored the ecological environment to hunt for higher net income.

Table 5 Solutions obtained from the ITWR model
Full size table

Figures 2, 3, and 4 presents the water shortage quantity of each subarea in different exploiting probability levels under the same level of water availabilities. Each graph contains six subareas, and each subarea shows a comparison of water shortage quantity under three kinds of exploiting probability levels, namely high inflow level with the probability at 0.2, medium inflow level with the probability at 0.6 and low inflow level with a probability at 0.2. In general, the supply quantity and shortage quantity have been presented inverse proportion. Shown in these figures, in the same subarea, the higher the extracted water quantity is, the lower the water shortage quantity is, and thus shows a growth trend. Taken Fig. 2 as an example and the details can be described as follows: the results of Fig. 2 show that, in subarea 3, the shortage quantity will be [0.24, 18.61] × 108 m 3 when the extracting water quantity reaches a high inflow level; under low inflow, the shortage quantity reaches up to [6.64, 20.01] × 108 m 3; obviously, the shortage quantity in the medium level is in the middle position, and the relevant value is [4.44, 19.21] × 108 m 3. In this way, under high, medium and low inflow levels of extraction quantity, the shortage quantity are [2.19, 10.9] × 108 m 3, [5.59, 11.6] × 108 m 3 and [7.39, 12.5] × 108 m 3 respectively in subarea 5; in subarea 6, they are [0, 17.52] × 108 m 3, [1, 20.22] × 108 m 3 and [9.32, 21.22] × 108 m 3, respectively.

Fig. 2
figure 2

Water shortage when the water available level is low (p = 0.2)

Full size image
Fig. 3
figure 3

Water shortage when the water available level is medium (p = 0.6)

Full size image
Fig. 4
figure 4

Water shortage when the water available level is high (p = 0.2)

Full size image

Figure 2 presents the water shortage quantity when the level of water available is low with the probability at 0.2; Fig. 3 is the water shortage figure when the water available is in the medium level with the probability at 0.6; Fig. 4 represents the water shortage quantity when the water available is higher with the probability at 0.2. Compared with the three figures, the water shortage quantity reduces gradually with the increasing of water available under the same level of water exploitation. For example, in subarea 1, when the level of exploitation is high, the water shortage quantity under three levels of available water is [0, 12.26] × 108 m 3, [0, 3.16] × 108 m 3 and 0 m3; when the level of exploitation is 0.6, it is [0, 14.76] × 108 m 3, [0, 8.86] × 108 m 3 and 0 m3; when exploitation quantity is lower, the water shortage quantity under three levels of available water is [0, 12.76] × 108 m 3, [0, 7.86] × 108 m 3 and [0, 2.16] × 108 m 3 in turn. In subarea 2, the water shortage quantity under different water available levels changes from [1.08, 11.53] × 108 m 3, [3.48, 12.13] × 108 m 3 and [2.48, 11.03] × 108 m 3 to [0, 3.13] × 108 m 3, [0, 5.63] × 108 m 3 and [0, 8.73] × 108 m 3. Other subareas also appear in the same trend. On the other side, observing the Fig. 4, most of the lower bound values tend to 0. It manifests that no shortage arises and the pre-allocating water resources are enough to supply water for using departments. Then in this situation, there is no penalty.

Table 6 shows the costs of each process and the cumulative net costs under different levels of exploiting water quantity. From high level to low level of exploiting water quantity, the total net costs are [579.5, 946.3] × 108 RMB, [577.3, 969.9] × 108 RMB and [571.9, 964.9] × 108 RMB in turn. Observed this table, the exploiting cost in extraction process is [162.5, 303.7] × 108 RMB when the level of exploiting water quantity is high with the probability at 0.2; under the medium and low levels, the exploitation costs are [138.0, 252.6] × 108 RMB and [111.1, 214.5] × 108 RMB, respectively. In this way, the penalty costs in the second-stage of distribution process are [9.0, 181.1] × 108 RMB, [31.3, 255.8] × 108 RMB and [52.8, 288.9] × 108 RMB, respectively. The trend of the dates of the exploitation costs and the second-stage costs under different levels of exploitation water quantity are opposite. That is to say, the costs value gained by exploiting water resources declines gradually with the decreasing of water resources, while the penalties value show an increasing. A conclusion can be made by comparing with the values in three levels: when the exploiting water quantity is enough or nearly enough to satisfy the demand of water using departments, no penalties or punishment will emerge; on the contrary, if the exploiting water quantity is little, the available water quantity will be too little to supply water using areas. Under this circumstance, managers have to make decisions to obtain water from other districts in higher price, and then additional net costs will cause.

Table 6 Optimized net cost and the associated probability level. (× 108 RMB)
Full size table

5 Conclusions

There are a lot of uncertain factors existing in practical water resources system, and these uncertain factors affect the water resources optimization process and decision scheme generated. The uncertainties and complexities can be simplified via the inexact optimization model by integrating interval parameters programming (IPP) with two-stage stochastic programming (TSP) as a general optimization framework. And it can form an effective link between water resources allocation and net system benefit. The proposed model is applied into a case study of water resources planning and management. The whole allocation system is divided into two processes (extraction process and distribution process) and three phases (exploitation stage, pre-decision stage and recourse stage), and thus the objective function is composed by exploitation cost, the first-stage cost and the second-stage cost. Managers hope to minimize the economic penalty and satisfy each sector’s the water demand in maximum. The solutions can be used to demonstrate a proper policy that mitigating the penalty and reducing the waste of water resources. Although the study process is the first attempt for planning a water-resource management system through the ITWA approach, the results suggest that the hybrid method is applicable to many other management and planning problems, and can also be incorporated within other optimization frameworks to handle problems under uncertainty.