Iterative Universal Rigidity

Abstract

A bar framework determined by a finite graph $G$ and a configuration $\mathbf{p =(p_1,\ldots , p_n) }$ in $\mathbb {R}^d$ is universally rigid if it is rigid in any $\mathbb {R}^D \supset \mathbb {R}^d$. We provide a characterization of universal rigidity for any graph $G$ and any configuration $\mathbf{p}$ in terms of a sequence of affine subsets of the space of configurations. This corresponds to a facial reduction process for closed finite-dimensional convex cones.

1 Introduction

1.1 Basic Definitions

Given a configuration $\mathbf{p =(p_1,\ldots , p_n) }$ of $n$ points in $\mathbb {R}^d$, and a finite graph $G$, without loops or multiple edges, on those $n$ points one can ask the natural and fundamental question: is there another configuration $\mathbf{q =(q_1,\ldots , q_n) }$ in $\mathbb {R}^d$, where the distance between $\mathbf{p}_i$ and $\mathbf{p}_j$ is the same as the distance between $\mathbf{q}_i$ and $\mathbf{q}_j$ when $\{i,j\}$ is an edge of $G$? When this happens we say that $(G, \mathbf{p})$ is equivalent to $(G, \mathbf{q})$. (Traditionally $G(\mathbf{p})$ and $G(\mathbf{q})$ is the notation used for $(G, \mathbf{p})$ and $(G, \mathbf{q})$ respectively, which are called (bar) frameworks, but we break that tradition here.) Of course, if there is a congruence between $\mathbf{p}$ and $\mathbf{q}$, they are called trivially equivalent or congruent, since all pairs of distances are the same.

The following is a sequence of ever stronger rigidity properties of frameworks, where $(G,\mathbf{p})$ is a framework on $n$ vertices in $\mathbb {R}^d$.

• If all the frameworks $(G, \mathbf{q})$ in $\mathbb {R}^d$ equivalent to $(G, \mathbf{p})$ and sufficiently close to $(G, \mathbf{p})$ are trivially equivalent to $(G, \mathbf{p})$, we say that $(G, \mathbf{p})$ is locally rigid in $\mathbb {R}^d$ (or just rigid in $\mathbb {R}^d$).

• If all the frameworks $(G, \mathbf{q})$ in $\mathbb {R}^d$ equivalent to $(G, \mathbf{p})$ are congruent to $(G, \mathbf{p})$, we say that $(G, \mathbf{p})$ is globally rigid in $\mathbb {R}^d$.

• If all the frameworks $(G, \mathbf{q})$ in any $\mathbb {R}^D \supset \mathbb {R}^d$ equivalent to $(G, \mathbf{p})$ are trivially equivalent to $(G, \mathbf{p})$, we say that $(G, \mathbf{p})$ is universally rigid.

1.2 Main Result

It is well known that the existence of a certain kind of “stress” matrix associated with a specific framework is sufficient to prove its universal rigidity [10]. It is also known that when a “generic” framework is universally rigid, it is also necessary for it to have this type of associated stress matrix [20]. But there do exist special frameworks that are universally rigid while not possessing such a matrix. In this paper, we propose a new criterion in terms of a certain “sequence of stress matrices” which gives a complete (necessary and sufficient) characterization of universal rigidity for any specific framework in any dimension of any graph.

The validity of this certificate can be checked efficiently and deterministically in the real computational mode of [8]. We need to use a real model, since even if $\mathbf{p}$ is described using rational numbers, the stress matrix might have irrational entries. As such, this means that universal rigidity is in the class NP under this real computational model. Note that universal rigidity is clearly in CO-NP under real-valued computation since the non-universal rigidity of a framework $\mathbf{p}$ can always be certified by providing an equivalent non-congruent framework $\mathbf{q}$.

The main result will be explained in Sect. 8 and Theorem 8.1. We will derive our results in a self-contained manner, but note that technically, what we have is really a thinly disguised version of a known technique called “facial reduction” which is used to analyze convex cone programs [9]. The connection is explained explicitly in Sect. 10.

1.3 Relation to Other Forms of Rigidity

Given $(G, \mathbf{p})$, testing for local or global rigidity is known to be a hard computational problem [1, 39]. Fortunately, this is not the end of the story. For local and for global rigidity, the problems become much easier if we assume that $\mathbf{p}$ is generic. (We say that a configuration $\mathbf{p}$ is generic in $\mathbb {R}^d$ if all the coordinates of all the points of $\mathbf{p}$ are algebraically independent over the rationals. This means, in particular, there can be no symmetries in the configuration, no three points are collinear for $d \ge 2$, etc.) Local rigidity and global rigidity have efficient randomized algorithms under the assumption that the configuration is generic (and for $d=1$ or $d=2$, there are even purely combinatorial polynomial-time algorithms). See [11, 12, 21, 46] for information about all of these concepts. In particular, both local and global rigidity in $\mathbb {R}^d$ are generic properties of a graph $G$. That is, either all generic frameworks are rigid, or none of them are, and so these properties only depend on the graph $G$ and not on the configuration $\mathbf{p}$.

One justification for assuming that a configuration is generic is that, in any region, the generic configurations form a set of full measure. In other words, if a configuration is chosen from a continuous distribution, with probability one, it will be generic, and with any physical system, there will always be some indeterminacy with respect to the coordinates. But the problem is that special features of a particular configuration, such as symmetry, collinearity, overlapping vertices, etc, may be of interest and they are necessarily non-generic. In this paper we do not want to restrict ourselves to generic frameworks.

In order to test for local rigidity of a specific non-generic framework, there is a natural sufficient condition to use, namely infinitesimal rigidity. This says that in $\mathbb {R}^d$ (for $n \ge d$) the rank of the rigidity matrix $R(\mathbf{p})$ is $nd-d(d+1)/2$, where $R(\mathbf{p})$ is an $m$-by-$nd$ (sparse) matrix with integer linear entries, where $m$ is the number of members (another name for the bars) as defined in Sect. 6. See also [46], for example. Infinitesimal rigidity of $(G,\mathbf{p})$ can be computed efficiently [46].

Infinitesimal rigidity is simply a linearized form of local rigidity and thus is a very natural sufficient condition to use for testing the local rigidity of $(G,\mathbf{p})$. In fact, the matrix test for infinitesimal rigidity is central to the determination of generic local rigidity for $G$ just described. In contrast, we do not have such a natural sufficient condition to use for global rigidity. Indeed, the particular matrix test used to compute generic global rigidity for the graph $G$ does not give us information about the global rigidity of any specific framework $(G,\mathbf{p})$ [12].

Thus, in order to test for global rigidity of a specific non-generic framework, we often resort to “stronger” conditions; perhaps the most usable sufficient condition is universal rigidity. In this context, one can choose the ambient dimension $D$ to be, say, $n-1$ with no loss in generality. As such, understanding universal rigidity can be essential to determining global rigidity, and it is the focus of this paper.

1.4 Complexity Issues

The theoretical complexity of testing universal rigidity for $(G,\mathbf{p})$ (even when $\mathbf{p}$ is given by integer-valued input) is technically unknown. There are no known hardness results, nor are there any provably correct efficient algorithms. One can pose the problem of universal rigidity in the language of semi-definite programing (SDP) [49]. Unfortunately, the complexity for conclusively deciding an SDP feasibility problem is itself unknown [36].

In practice, one can use a numerical (say interior point) SDP solver for these problems. Roughly speaking, this can efficiently find a framework with an affine span of dimension $n-1$ (the highest possible dimension) that is within $\varepsilon$ of being equivalent to the given framework. If this framework appears to “almost” have an affine span of dimension $d$, and appears to be “very close” to the input $\mathbf{p}$, then we have strong “evidence” for universal rigidity. In effect, this means, in the case with imprecise input, that the problem to determine whether the framework is universally rigid cannot be solved because there is not enough information in the input to be able to solve it.

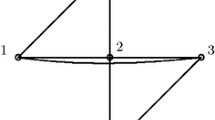
An exasperating issue is that there can be great sensitivity between errors in achieving desired edge lengths (which are what we get when using an SDP solver) and errors in the resulting configuration. Figure 1 shows a framework (with pinned vertices) that is universally rigid in $\mathbb {R}^2$. We will see that this can be verified using methods described in this paper. If the lengths in Fig. 1 are all increased by 0.5 %, this results in the realization in the plane shown in Fig. 2. Note that this slightly perturbed framework is far from being universally rigid. Here we see that a very small error in the numerical calculation of the lengths of the members can lead to a very large perturbation of the resulting configuration, and, indeed, the decision as to universal rigidity may be incorrect.

Fig. 1

The large black vertices are pinned to the plane, and the whole framework is universally rigid as in Corollary 8.2

Fig. 2

This is the same framework as in Fig. 1 but with the lengths of the bars increased by less than $0.5\,\%$

1.5 Certificates

The lack of conclusive algorithms for universal rigidity brings us, finally, to the topic of “sufficient certificates” for universal rigidity. In this paper, we show that there is a kind of sufficient certificate that must exist for any universally rigid framework. This certificate is described by a sequence of real-valued matrices and can be verified efficiently using real computation.

Note that we do not claim that, given a universally rigid framework, this certificate can always be found efficiently. But, as we describe in Sect. 15, there are many cases where we can systematically find the appropriate certificates for the universal rigidity of $(G,\mathbf{p})$. We also discuss other cases where we have at least a positive probability of finding the certificate.

Looking again at the situation of Figs. 1 and 2, we see that universal rigidity itself can be a fragile property, which is destroyed (along with its sufficient certificates) by any errors in the description of $\mathbf{p}$. Given our new characterization of universal rigidity, we suggest that when exploring and designing frameworks that we wish to be universally rigid, it may be best to explicitly maintain the appropriate certificates as part of the representation and description of $(G,\mathbf{p})$.

2 Stress

The central tool we will use to analyze universal rigidity is the concept of a stress.

Definition 2.1

A stress associated to a graph $G$ is a scalar $\omega _{ij}=\omega _{ji}$ assigned to each edge $\{i,j\}$ of $G$. Call the vector $\mathbf{\omega } = (\ldots , \omega _{ij}, \ldots )$, the stress vector.

We can suppress the role of $G$ here by simply requiring that $\omega _{ij}=0$ for any non-edge $\{i,j\}$ of $G$. (One should also be careful not to confuse the notion of stress here with that used in structure analysis, in physics or in engineering. There, stress is defined as a force per cross-sectional area. In the setup here, there are no cross sections; the scalar $\omega _{ij}$ is better interpreted as a force per unit length.)

Since we will be concerned with configurations in an arbitrarily high dimension, we will fix a large dimension $D$, which can effectively be taken to be $n$ if our framework has $n$ vertices. When we are given a particular configuration, we generally will assume that it is realized in $\mathbb {R}^D$. We can describe a configuration $\mathbf{p}$ in $\mathbb {R}^D$ using coordinates using a single vector in $\mathbb {R}^{Dn}$. Of course, for the purposes of deciding universal rigidity and some of the other concepts defined here, there is no reason to restrict the configurations to lie in some particular Euclidean space $\mathbb {R}^D$. But it is clear that once the ambient dimension $D$ is greater than $n$, any configuration in any higher dimension is congruent to one in $\mathbb {R}^D$, and it will be convenient to consider configurations in dimensions larger than $n$. In order to define a finite-dimensional space of configurations appropriate for universal rigidity, though, it is useful to restrict just to those configurations in $\mathbb {R}^D$, and if a construction pops out of $\mathbb {R}^D$, we can always rotate it back into $\mathbb {R}^D$.

Given a stress, we can measure the energy of a configuration: Let $\omega =(\ldots , \omega _{ij}, \ldots )$ be a stress for a graph $G$ and let $\mathbf{p =(p_1,\ldots , p_n) }$ be a configuration in $\mathbb {R}^D$.

Definition 2.2

We define the stress energy associated to $\omega$ as

$$\begin{aligned} E_{\omega }(\mathbf{p}):=\sum _{i<j} \omega _{ij} (\mathbf{p}_i-\mathbf{p}_j)^2, \end{aligned}$$

(2.1)

where the product of vectors is the ordinary dot product, and the square of a vector is the square of its Euclidean length.

Regarding the stress $\omega$ as fixed constants, $E_{\omega }$ is a quadratic form defined on vectors in $\mathbb {R}^{Dn}$, and it is easy to calculate that the configuration $\mathbf{p}$ is a critical point for $E_{\omega }$ when, for each vertex $i$ of $G$,

$$\begin{aligned} \sum _j \omega _{ij} (\mathbf{p}_j-\mathbf{p}_i) = 0. \end{aligned}$$

(2.2)

Definition 2.3

When (2.2) holds, we say that the stress $\omega$ is an equilibrium stress for the configuration $\mathbf{p}$. We also say that $\mathbf{p}$ is in equilibrium with respect to $\omega$.

It is useful to represent a stress in matrix form: The $n$-by-$n$ stress matrix $\Omega$ associated to the stress $\omega$ is defined by making the $\{i,j\}$ entry of $\Omega$ to be $-\omega _{ij}$ when $i \ne j$, and the diagonal entries of $\Omega$ are such that the row and column sums of $\Omega$ are zero.

It is easy to see that with respect to the standard basis of $\mathbb {R}^{Dn}$, the matrix of $E_{\omega }$ is $\Omega \otimes I^D$, where $I^D$ is the $D$-by-$D$ identity matrix and $\otimes$ is the matrix Kronecker product. Note that although $E_{\omega }$ is defined over the high-dimensional space $\mathbb {R}^{nD}$, its being PSD only depends on $\Omega$ and its rank only depends on the rank of $\Omega$ and $D$.

If $\mathbf{p}$ is a configuration in $\mathbb {R}^d$ with an equilibrium stress $\omega$, it is easy to check that, for any affine map of $a: \mathbb {R}^d \rightarrow \mathbb {R}^D$, the configuration $a(\mathbf{p})$ defined by $\mathbf{p}_i \rightarrow a(\mathbf{p}_i)$, for all $i$, is also an equilibrium configuration with respect to $\omega$.

Definition 2.4

We say that a configuration $\mathbf{p}$ is universal with respect to the stress $\omega$ if $\mathbf{p}$ is in equilibrium with respect to $\omega$, and any other configuration $\mathbf{q}$ in $\mathbb {R}^D$, which is also in equilibrium with respect to $\omega$, is such that $\mathbf{q}$ is an affine image of $\mathbf{p}$.

Definition 2.5

For a configuration $\mathbf{p =(p_1,\ldots , p_n) }$ we regard each $\mathbf{p}_i$ as a column vector in $\mathbb {R}^D$, as we define the $D$-by-$n$ configuration matrix of $\mathbf{p}$ as

$$\begin{aligned} P = \begin{bmatrix} \mathbf{p}_1&\mathbf{p}_2&\dots&\mathbf{p}_n \end{bmatrix}. \end{aligned}$$

Then it is easy to check that the equilibrium condition for a given stress is

$$\begin{aligned} P\,\Omega = 0, \end{aligned}$$

where $\Omega$ is the stress matrix for the stress $\omega$.

The following is easy to check and is already given in [10]. See also Lemma 7.1 for a general universal construction.

Proposition 2.1

Given a stress $\omega$, let $\mathbf{p}$ be any configuration that is in equilibrium with respect to $\omega$ and whose affine span is of maximal dimension over all such configurations. Let this affine span have dimension $d$. Then $\mathbf{p}$ is universal with respect to $\omega$ and the rank of $\Omega$ is $n-d-1$.

3 The Conic at Infinity

In a sense, an equilibrium stress can only make distinctions “up to affine motions” as seen in Proposition 2.1. For rigidity questions, we would like to know when the affine motions can be restricted to Euclidean congruences.

Definition 3.1

We say that $\mathbf{v}= \{\mathbf{v}_1, \ldots , \mathbf{v}_m\}$, a finite collection of non-zero vectors in $\mathbb {R}^d$, lie on a conic at infinity; if when regarded as points in real projective $(d-1)$ space $\mathbb {R} \mathbb {P}^{d-1}$, they lie on a conic.

This means that there is a non-zero $d$-by-$d$ symmetric matrix $A$ such that for all $i = 1, \ldots , m$, $\mathbf{v}_i^tA\mathbf{v}_i=0$, where $()^t$ is the transpose operation. The following shows how affine motions can be non-trivial flexes of a framework.

Definition 3.2

A flex of a framework $(G,\mathbf{p})$ is a continuous motion $\mathbf{p}(s)$, $0 \le s \le 1, \mathbf{p}(0)=\mathbf{p}$, where $\mathbf{p}(s)$ is equivalent to $\mathbf{p}$. It is non-trivial if $\mathbf{p}(s)$ is not congruent to $\mathbf{p}$ for all $s>0$. If $\mathbf{p}(s)=A(s)\mathbf{p}(0)$, where $A(s)$ is an affine function of Euclidean space, then we say $\mathbf{p}(s)$ is an affine flex.

Proposition 3.1

A framework $(G,\mathbf{p})$ in $\mathbb {R}^d$, with $d$-dimensional affine span, has a non-trivial affine flex if and only if it has an equivalent non-congruent affine image in $\mathbb {R}^d$ if and only if the member directions $\{\mathbf{p}_i-\mathbf{p}_j\}_{\{i,j\}\in E(G)}$ lie on a conic at infinity, where $E(G)$ are the edges of $G$.

See [10, 14] for a simple proof of this property. Note that, in the plane, the conic lies in $\mathbb {R} \mathbb {P}^1$, which consists of two points or one point. So affine motions of a framework can only occur when the edge directions lie in two possible directions.

4 The Fundamental Theorem

The major tool used for proving universal rigidity is the following. (See [10].)

Theorem 4.1

Let $(G,\mathbf{p})$ be a framework whose affine span of $\mathbf{p}$ is all of $\mathbb {R}^d$, with an equilibrium stress $\omega$ and stress matrix $\Omega$. Suppose further

• 1. $\Omega$ is positive semi-definite (PSD).

• 2. The configuration $\mathbf{p}$ is universal with respect to the stress $\omega$. (In other words, the rank of $\Omega$ is $n - d - 1$.)

• 3. The member directions of $(G,\mathbf{p})$ do not lie on a conic at infinity.

Then $(G,\mathbf{p})$ is universally rigid.

The idea is that $E_\omega (\mathbf{p})$ only depends on the edge lengths of $\mathbf{p}$, and so any configuration $\mathbf{q}$ equivalent to $\mathbf{q}$ must have zero energy. Since $E_\omega$ is PSD, this forces such a $\mathbf{q}$ to have coordinates in the kernel of $\Omega$ and thus $\mathbf{q}$ to be an affine image of $\mathbf{p}$. Thus by Proposition 3.1, their member directions must lie on a conic at infinity. So Condition 3 implies that $(G,\mathbf{p})$ is universally rigid.

Definition 4.1

If all three conditions of Theorem 4.1 are met, we say that the framework $(G,\mathbf{p})$ is super stable.

There are many instances of such frameworks. For example, the rigid tensegrities of [18] are super stable in $\mathbb {R}^3$, where the number of edges of $G$ is $m =2n$, and $n$ is the number of vertices. Theorem 4.1 is the starting point for most of our results in this paper, where this result will be generalized significantly.

Given such a matrix $\Omega$ and $(G,\mathbf{p})$ as real-valued input, one can efficiently verify (under, say a real model of computation) that $\Omega$ is PSD and that it is an equilibrium stress matrix for $(G,\mathbf{p})$.

We note, in passing, the following result in [4] in which the conic condition is replaced with a more natural one.

Definition 4.2

A configuration $\mathbf{p =(p_1,\ldots , p_n) }$ in $\mathbb {R}^d$ is in general position if no $k$ points lie in a $(k-1)$-dimensional affine space for $1 \le k \le d$.

Theorem 4.2

If Conditions 1 and 2 hold in Theorem 4.1 and Condition 3 is replaced by the assumption that the configuration $\mathbf{p}$ is in general position, then Condition 3 still holds and $(G,\mathbf{p})$ is super stable.

This natural question is whether the conditions of Theorem 4.1 are necessary for universal rigidity. The answer in the generic case is in the affirmative. The following is from [20]:

Theorem 4.3

A universally rigid framework $(G, \mathbf{p})$, with $\mathbf{p}$ generic in $E^d$ and having $n \ge d+2$ vertices, has a PSD equilibrium stress matrix with rank $n -d- 1$.

This result does not hold for non-generic frameworks (even in general position). For example, see the universally rigid framework in Fig. 3. In this paper, we will describe a (weaker) sufficient condition that is also necessary for universal rigidity for all frameworks.

Fig. 3

This is a framework where the vertices are all in general position, there is only a one-dimensional space of equilibrium stresses, and the associated stress matrix does not have maximal rank. The stresses on the members at the vertex $A$ must all be zero. The dotted lines extending the members coming from the vertices of the outside triangle meet at a point and are not part of the framework, as shown. As described in this paper, we will use multiple levels of stresses. In this figure and later ones, the first-level stresses and the corresponding members are colored in dark blue, the next level in red, and the third level in green

5 Dimensional Rigidity

In [2] a notion called dimensional rigidity is introduced. This is closely related to, but distinct from, universal rigidity. Our main result can be best understood in terms of dimensional rigidity, first. Then we can derive the appropriate statements about universal rigidity.

Definition 5.1

We say that a framework $(G,\mathbf{p})$ in $\mathbb {R}^d$, with affine span of dimension $d$, is dimensionally rigid in $\mathbb {R}^d$ if every framework $(G,\mathbf{q})$ equivalent to $(G,\mathbf{p})$ has an affine span of dimension no greater than $d$.

(One might better call this concept dimensionally maximal, since a dimensionally rigid framework may not even be locally rigid, but we refrain from that indulgence.)

In many applications, one often wants to find the minimum dimension for a graph $(G, \mathbf{e})$ with given edge lengths $\mathbf{e}= \{\ldots , e_{ij}, \ldots \}$, so the concept of the maximal dimension seems backward from what is normally desired. For example, finding the minimal dimension of $(G, \mathbf{e})$ is the point of [6, 29]. Nevertheless, dimensional rigidity is quite relevant for universal rigidity.

It is clear that if a framework $(G,\mathbf{p})$ is universally rigid in $\mathbb {R}^d$, then it is dimensionally rigid in $\mathbb {R}^d$, but we shall see several examples of non-rigid dimensionally rigid frameworks. Such cases always occur due to a conic at infinity (in which case, the framework is not even locally rigid). For example, two bars, with a single vertex in common, is dimensionally rigid in the plane, but it is flexible, i.e., not rigid, in the plane.

An important connection between dimensional rigidity and universal rigidity is the following. (This is proved in [2], but we provide a more direct proof here.)

Theorem 5.1

If a framework $(G,\mathbf{p})$ with $n$ vertices in $\mathbb {R}^d$ is dimensionally rigid in $\mathbb {R}^d$, and $(G,\mathbf{q})$ is equivalent to $(G,\mathbf{p})$, then $\mathbf{q}$ is an affine image of $\mathbf{p}$.

Proof

Suppose that $h: \mathbf{p}\rightarrow \mathbf{q}$ is the correspondence between the configurations. Consider the graph of this correspondence $\Gamma (h) = \{ (\mathbf{p}_i, \mathbf{q}_i)\}_{i=1,\ldots , n} \subset \mathbb {R}^d \times \mathbb {R}^D$, where $D$ is sufficiently large to contain $\mathbf{q}$. It is easy to check (see [7] or the proof of Lemma 7.1) that $\frac{1}{\sqrt{2}}\Gamma (h)$ is equivalent to $\mathbf{p}$ and $\mathbf{q}$. Thus there is a $d$-dimensional affine hyperplane that contains $\frac{1}{\sqrt{2}}\Gamma (h)$. This implies that $\mathbf{q}$ is an affine image of $\mathbf{p}$. $\square$

A key consequence of Theorem 5.1 shows that universal rigidity can be determined from dimensional rigidity and Property 3 of Theorem 4.1.

Corollary 5.1

A framework $(G,\mathbf{p})$ with $n$ vertices in $\mathbb {R}^d$ is universally rigid if and only if it is dimensionally rigid and the edge directions do not lie on a conic at infinity.

One result that follows from the proof of Theorem 4.1 from [10] is the following.

Theorem 5.2

If a framework $(G,\mathbf{p})$ with $n$ vertices in $\mathbb {R}^d$ has an equilibrium stress with a PSD stress matrix of rank $n-d-1$, then $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$.

See [2] for similar conditions for dimensional rigidity. This just says that the configuration $\mathbf{p}$ is universal with respect to the given stress. The only other possible equivalent configurations of $(G,\mathbf{p})$, in this case, are affine linear images, which do not raise dimension.

Since universal rigidity implies dimensional rigidity, the examples of Figs. 5 (on the right) and 3 also show that the PSD stress matrix of rank $n-d-1$ is not necessary for dimensional rigidity.

In order to start to understand what is necessary for dimensional (and universal) rigidity we begin with the following, Theorem 6 in [3]. We also provide a simple proof as a special case of the results in Sect. 7.

Theorem 5.3

If $(G,\mathbf{p})$ is a dimensionally rigid framework with $n$ vertices whose affine span is of dimension, $d \le n-2$, then it has a non-zero equilibrium stress with a PSD stress matrix $\Omega$.

Note that the rank of $\Omega$ in Theorem 5.3 could be as low as one. As such, it is weaker than the sufficient conditions above. Later, we will describe a new condition, which is stronger than having a non-zero PSD stress matrix, but weaker than having a non-zero PSD stress matrix of rank $n-d-1$. Our condition instead will be of the form of a sequence of PSD matrices, where the combined rank is $n-d-1$. Briefly, we will apply Theorem 5.3 repeatedly to a smaller and smaller space of possible configurations.

6 The Measurement Set

Fix a finite graph $G$ with $n$ vertices, $m$ edges and fix a Euclidean space $\mathbb {R}^D$, where the dimension $D$ is at least as large as $n$. Let

$$\begin{aligned} {\mathcal {C}}:=\{\mathbf{p}\mid \mathbf{p =(p_1,\ldots , p_n) }\text { is a configuration in } \mathbb {R}^D \} \end{aligned}$$

be the set of configurations in $\mathbb {R}^D$. Each configuration can be regarded as a vector in $\mathbb {R}^{Dn}$.

Definition 6.1

We define the rigidity map as

$$\begin{aligned} f: {\mathcal {C}}=\mathbb {R}^{nD} \rightarrow \mathcal {M}\subset \mathbb {R}^m \end{aligned}$$

by $f(\mathbf{p}) = (\ldots , (\mathbf{p}_i -\mathbf{p}_j)^2, \ldots )$, where the $\{i,j\}$ are the corresponding edges in $G$, and $\mathcal {M}= \mathcal {M}(G)$ is the image of $f$ in $\mathbb {R}^m$ for the graph $G$, which we call the measurement set.

In other words, $\mathcal {M}$ is the set of squared lengths of edges of a framework that are actually achievable in some Euclidean space. The following are some basic properties of ${\mathcal {C}}$ and any affine set $\mathcal {A}$:

• 1. $\mathcal {M}$ is a closed convex cone in $\mathbb {R}^m$.

• 2. For any $\mathbf{e}\in \mathcal {M}$, $f^{-1}(\mathbf{e})$ consists of an equivalence class of frameworks $\mathbf{p}\in {\mathcal {C}}$.

The convexity of Condition 1 is well known and even has an explicit formula for the convexity in [7] and follows from Lemma 7.1 in Sect. 7. Condition 2 follows directly from the definition.

Definition 6.2

The rigidity matrix is defined as $R(\mathbf{p})=\frac{1}{2}df_{\mathbf{p}}$, with respect to the standard basis in Euclidean space, and $f(\mathbf{p})=R(\mathbf{p})\mathbf{p}$, where $df$ is the differential of $f$. Then the energy function associated to a stress $\omega$ can also be written as

$$\begin{aligned} E_{\omega }(\mathbf{p}) = \omega R(\mathbf{p})\mathbf{p}, \end{aligned}$$

where $\omega$ is regarded as a row vector.

7 Affine Sets

Definition 7.1

A subset $\mathcal {A}\subset {\mathcal {C}}$ that is the finite intersection of sets of the form

$$\begin{aligned} \Big \{\mathbf{p}\in {\mathcal {C}}\mid \sum _{ij}\lambda _{ij}( \mathbf{p}_i -\mathbf{p}_j)=0 \Big \}, \end{aligned}$$

(7.1)

for some set $\{ \ldots , \lambda _{ij}, \ldots \}$ of constants, is called an affine set.

Clearly an affine set is a linear subspace of the configuration space ${\mathcal {C}}$ and it is closed under arbitrary affine transformations acting on $\mathbb {R}^D$. Moreover, any such set can be defined by equations of the form (7.1).

For example, if there are three collinear points $\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3$, and $\mathbf{p}_2$ is the midpoint of $\mathbf{p}_1$ and $\mathbf{p}_3$, then $\{\mathbf{p}\in {\mathcal {C}}\mid (\mathbf{p}_1-\mathbf{p}_2)-(\mathbf{p}_3-\mathbf{p}_2)=0\}$ is an affine set. Or $\{\mathbf{p}\in {\mathcal {C}}\mid \mathbf{p}_1-\mathbf{p}_2+ \mathbf{p}_3-\mathbf{p}_4=0\}$, which is a configuration of four points of a parallelogram (possibly degenerate), is another example.

A special case of such an affine set is determined by a stress $\omega$, where the equilibrium condition (2.2) at each vertex supplies the condition (7.1).

In Definition 2.4 we defined what it means for a configuration $\mathbf{p}$ to be universal with respect to a single stress $\omega$. This just means that any other configuration $\mathbf{q}$ that is in equilibrium with respect to $\omega$ is an affine image of $\mathbf{p}$. We generalize this case to that of any affine set as follows.

Definition 7.2

We say that a configuration $\mathbf{p}$ in an affine set $\mathcal {A}$ is universal with respect to $\mathcal {A}$ if any other configuration $\mathbf{q}$ in $\mathcal {A}$ is an affine image of $\mathbf{p}$. We denote by $\mathring{\mathcal {A}} \subset \mathcal {A}$, the set of configurations that are universal with respect to $\mathcal {A}$.

For any set $X$ in a linear space, $\langle X \rangle$ denotes the affine linear span of $X$.

Lemma 7.1

A configuration $\mathbf{p}\in {\mathcal {C}}$ is universal with respect to an affine set $\mathcal {A}$ if and only if it has maximal dimensional affine span for configurations in $\mathcal {A}$. Let $f:\mathcal {A}\rightarrow \mathbb {R}^m$ be the restriction of the rigidity map to the measurement space for some graph $G$. Then $f(\mathcal {A})$ is convex and $f(\mathring{\mathcal {A}})$ is the relative interior of $f(\mathcal {A}) \subset \langle f(\mathcal {A}) \rangle$.

Proof

Clearly any possible universal configuration must have maximal affine span in order for it to map affine linearly onto any other configuration in $\mathcal {A}$. Conversely, let $\mathbf{p}$ be any configuration with maximal dimensional affine span, say $d$, in $\mathcal {A}$, and let $\mathbf{q}$ be any other configuration in $\mathcal {A}$. Define $\tilde{\mathbf{p}}$ to be another configuration where $\tilde{\mathbf{p}}_i=(\mathbf{p}_i,\mathbf{q}_i) \in \mathbb {R}^D \times \mathbb {R}^D$ for $i=1, \ldots , n$. The configuration $\tilde{\mathbf{p}}$ is also in $\mathcal {A}$ since all its coordinates satisfy Eq. (7.1). Since projection is an affine linear map and the affine span of $\mathbf{p}$ is maximal, namely $d$, the dimension of the affine span of $\tilde{\mathbf{p}}$ must also be $d$, and the projection between their spans must be an isomorphism. So the map $\mathbf{p}\rightarrow \tilde{\mathbf{p}} \rightarrow \mathbf{q}$ provides the required affine map since projection onto the other coordinates is an affine map as well.

If $\mathbf{p},\mathbf{q}\in \mathcal {A}$, then, regarding $\mathbf{p}$ and $\mathbf{q}$ as being in complementary spaces,

$$\begin{aligned} f((\cos \theta ) \mathbf{p}, (\sin \theta ) \mathbf{q})=(\cos \theta )^2 f(\mathbf{p})+(\sin \theta )^2 f(\mathbf{q}), \end{aligned}$$

(7.2)

for $0 \le \theta \le \pi /2$ is the segment connecting $f(\mathbf{p})$ to $f(\mathbf{q})$ is in $f(\mathcal {A})$, showing that $f(\mathcal {A})$ and $f(\mathring{\mathcal {A}})$ are convex.

The rank of $df_{\mathbf{p}}$ is constant for non-singular affine images of $\mathbf{p}$ (see [16], for example), which are in $\mathring{\mathcal {A}}$, the universal configurations. This implies that $f$ is locally a projection into $f(\mathcal {A})$ at $\mathbf{p}$, which implies that $f(\mathring{\mathcal {A}})$ is open in $\langle f(\mathcal {A}) \rangle$. This, combined with its being dense in $f(\mathcal {A})$, and its convexity make $f(\mathring{\mathcal {A}})$ equal to the relative interior of $f(\mathcal {A})$. $\square$

The dimension of an affine set $\mathcal {A}$ is $\dim (\mathcal {A})=D(d+1)$, where $D$ is the dimension of the ambient space and $d$ is the dimension of the affine span of a universal configuration $\mathbf{p}$ for $\mathcal {A}$.

For any (symmetric) bilinear form $B$ for a vector space $V$, the radical of B is the set $\{\mathbf{v}\mid B(\mathbf{v}, \mathbf{w}) = 0\,\, \text {for all}\,\, \mathbf{w}\in V\}$. If $V$ is a finite-dimensional vector space and $B$ is given by a symmetric matrix, then the radical of $B$ is the kernel (or co-kernel) of that matrix. We can interpret the stress energy $E_{\omega }$ as such a bilinear form. If $B$ acting on $V$ is PSD, then its zero set must be equal to its radical.

Lemma 7.2

Let $\mathbf{q}\in \mathcal {A}\subset \mathbb {R}^{nD}$. Then $f(\mathbf{q})$ is in the boundary of the relative interior of $f(\mathcal {A}) \subset \langle f(\mathcal {A}) \rangle$ if and only if there is a non-zero stress $\omega$ for $(G, \mathbf{q})$ such that when $E_{\omega }$ is restricted to $\mathcal {A}$, the resulting form is PSD and has $f(\mathbf{q})$ in its radical.

Note that this does NOT mean that the $E_{\omega }$ is necessarily PSD over all of ${\mathcal {C}}$ or that the configuration $\mathbf{q}$ is in the radical of the form $E_{\omega }$ defined over all of ${\mathcal {C}}$.

Proof

Suppose that a stress $\omega \ne 0$ exists for the framework $(G,\mathbf{q})$. The condition that $E_{\omega }$ is PSD on $\mathcal {A}$ is equivalent to $E_{\omega }(\mathbf{q}) \ge 0$ for all $\mathbf{q}$ in $\mathcal {A}$, which is equivalent to the linear inequality $\omega f(\mathbf{q}) \ge 0$ for any $f(\mathbf{q}) \in f(\mathcal {A}$), and any configuration $\mathbf{q}$ in $\mathcal {A}$. When $E_{\omega }(\mathbf{q})=0$, $f(\mathbf{q})$ is in the closure of the complement of that inequality in $\langle f(\mathcal {A}) \rangle$ and thus in the boundary of $f(\mathcal {A}) \subset \langle f(\mathcal {A}) \rangle$.

Conversely, suppose that $f(\mathbf{q})$ is in the boundary of $f(\mathcal {A}) \subset \langle f(\mathcal {A}) \rangle$. Since the set $f(\mathcal {A})$ is convex, $f(\mathbf{q})$ is in a supporting hyperplane

$$\begin{aligned} \mathcal {H}= \{ \mathbf{e}\in \langle f(\mathcal {A}) \rangle \mid \omega \mathbf{e}=0\}, \end{aligned}$$

which is defined by a non-zero stress $\omega$. Then

$$\begin{aligned} 0 \le \frac{1}{2}\omega f(\mathbf{q}) = \omega R(\mathbf{q})\mathbf{q}=\sum _{i<j}\omega _{ij}(\mathbf{q}_i-\mathbf{q}_j)^2=\mathbf{q}^t\Omega \otimes I^D \mathbf{q}= E_{\omega }(\mathbf{q}). \end{aligned}$$

Thus the quadratic form defined by $E_{\omega }$ restricted to the affine set $\mathcal {A}$ is PSD and has $f(\mathbf{q})$ in its radical.

Lemma 7.3

Let $\mathcal {A}$ be an affine set and $E_\omega$ be a stress energy which we restrict to $\mathcal {A}$. Then its radical must be an affine set.

Proof

Let $\mathbf{q}$ be universal for $\mathcal {A}$. Then a configuration $\mathbf{p}\in \mathcal {A}$ is in the radical when

$$\begin{aligned} \sum _{i<j} \omega _{ij} (\mathbf{p}_i-\mathbf{p}_j)\cdot (\tilde{\mathbf{q}}_i-\tilde{\mathbf{q}}_j) =0 \end{aligned}$$

for any $\tilde{\mathbf{q}}$ that is an affine image of $\mathbf{q}$.

Suppose some $\mathbf{p}$ is in the radical. Then clearly so is any translation of $\mathbf{p}$. Any linear transform applied to the coordinates of $\mathbf{p}$ can be defined using the above equation by applying its inverse transpose to $\mathbf{q}$. Thus the radical is invariant for affine transforms, making it an affine set. $\square$

8 Iterated Affine Sets and the Main Theorem

Definition 8.1

If ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is a sequence of affine sets, we call it an iterated affine set.

Definition 8.2

Suppose an iterated affine set has a corresponding sequence of stress-energy functions $E_1, \ldots , E_k$ as defined of the form (2.1) such that each $E_i$ is restricted to act only on $\mathcal {A}_{i-1}$. Suppose that each restricted $E_i$ is PSD (over $\mathcal {A}_{i-1}$), that $E_i(\mathbf{q})=0$ for all $\mathbf{q}\in \mathcal {A}_i$, and that $E_i(\mathbf{q}) > 0$ for all $\mathbf{q}\in \mathcal {A}_{i-1} - \mathcal {A}_i$. Then we call $E_1, \ldots , E_k$ an (associated) iterated PSD stress for this iterated affine set.

Our main result is the following characterization of dimensional rigidity.

Theorem 8.1

Let $(G,\mathbf{p})$ be a framework in $\mathbb {R}^d$, where $\mathbf{p}$ has an affine span of dimension $d$. Suppose ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$ and with an associated iterated PSD stress. If the dimension of $\mathcal {A}_k$ is $(d+1)D$, then $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$.

Conversely, if $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$, then there must be an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$, ${{\mathrm{Dim}}}(\mathcal {A}_k) = (d+1)D$, with an associated iterated PSD stress.

Proof

First we prove the easy direction. Since $E_i$ operates on the squared edge lengths, the energy function forces any equivalent framework $(G,\mathbf{q})$ to be in $\mathcal {A}_{i}$ and ultimately in $\mathcal {A}_k$. Since the dimension of $\mathcal {A}_k$ is $(d+1)D$, $\mathbf{p}$ must be universal for $\mathcal {A}_k$, and so $\mathbf{q}$ must be an affine image of $\mathbf{p}$ and thus has, at most, a $d$-dimensional affine span.

For the converse, suppose that $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$. The configuration $\mathbf{p}$ is such that $\mathbf{p}\in {\mathcal {C}}=\mathcal {A}_0$. If $f(\mathbf{p})$ is in the boundary of $f(\mathcal {A}_0)$, we apply Lemma 7.2 to find a stress $\omega _1$ and a corresponding stress-energy function $E_{1}$ whose radical includes $\mathbf{p}$ and, by Lemma 7.3, is an affine set $\mathcal {A}_1$. In order to iterate the process, we define

$$\begin{aligned} \mathcal {A}_i= \{\mathbf{q}\in \mathcal {A}_{i-1} \mid \omega _iR(\mathbf{q})\mathbf{q}=0\}, \end{aligned}$$

(8.1)

where $\omega _i \ne 0$ is chosen such that $\omega _i R(\mathbf{q})\mathbf{q}= \omega _i f(\mathbf{q}) \ge 0$ for all $\mathbf{q}\in \mathcal {A}_{i-1}$, $\omega _i R(\mathbf{q})\mathbf{q}= \omega _i f(\mathbf{q}) > 0$ for some $\mathbf{q}\in \mathcal {A}_{i-1}$, and $\omega _i R(\mathbf{p})\mathbf{p}= \omega _i f(\mathbf{p}) = 0$. The quadratic form $\mathbf{q}^t \Omega _i \otimes I^D \mathbf{q}$ is PSD when restricted to $\mathcal {A}_{i-1}$, and from Lemma 7.3, the resulting $\mathcal {A}_i$ must also be an affine set. When such an $\omega _i \ne 0$ cannot be found, we stop and that is the end of the sequence of affine sets. This sequence must terminate as each of our subsequent affine sets is of strictly lower dimension.

From Lemma 7.2, we see that we can continue creating stresses $\omega _1, \ldots , \omega _k$ and affine sets until $f(\mathbf{p})$ is in the relative interior of $f(\mathcal {A}_k)$, and is universal with respect to $\mathcal {A}_k$ by Lemma 7.1. If the dimension of $\mathcal {A}_k$ is not $D(d+1)$, then the dimension of $\mathcal {A}_k$ is strictly greater than $D(d+1)$ and the dimension of the affine span of $\mathbf{p}$ would have been greater than $D(d+1)$, a contradiction. $\square$

Figure 4, similar to Fig. 2 of [20], shows a symbolic version of this process in the measurement set, where the indicated point represents the image of the configuration and its relation to the measurement cone. The arrows represent the stress vectors.

Fig. 4

The sets $f(\mathcal {A}_1)$ and $f(\mathcal {A}_2)$ shown as the point and line segment

8.1 The Basis Matrix

An affine set $\mathcal {A}$ can always be represented by a universal configuration $\mathbf{b}= (\mathbf{b}_1 \ldots \mathbf{b}_n)$ of $n$ points in $\mathbb {R}^D$, with an affine span of some dimension, say $d$. Without loss of generality, we can assume (using a translation if needed) that the linear span of the $\mathbf{b}_i$ (thought of as vectors) is of dimension $d+1$.

Definition 8.3

We define a basis matrix $B$, for an affine set as a rank $d+1$ matrix with $n$ columns and $D$ rows given by the coordinates of $\mathbf{b}$.

Since this matrix has rank $d+1$, we can apply row reduction operations so that $B$ has only $d+1$ rows. Additionally (if we want) since the affine span of $\mathbf{b}$ is only $d$-dimensional, we can perform these operations so that the final row is the all-ones vector.

Definition 8.4

Given an iterated affine set, ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$. We define $d_i$ to be the dimension of the affine span of a universal configuration for $\mathcal {A}_i$.

Definition 8.5

Given an iterated PSD equilibrium stress for an iterated affine set, a basis matrix $B_{i-1}$ for each $\mathcal {A}_{i-1}$, and the $n$-by-$n$ stress matrix $\Omega _i$ corresponding to each $E_i$, we define a restricted stress matrix $\Omega ^*_i := B_{i-1} \Omega _i B^t_{i-1}$. Each $\Omega ^*_i$ is a $(d_{i-1}+1)$-by-$(d_{i-1}+1)$ PSD matrix.

The following is a corollary of Theorem 8.1.

Corollary 8.1

Let $(G,\mathbf{p})$ be a framework in $\mathbb {R}^d$ with an affine span of dimension $d$. Suppose ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$, and that this iterated affine set has an associated iterated PSD stress, described by restricted stress matrices $\Omega ^*_i$. Let $r_i$ be the rank of $\Omega _i^*$. If

$$\begin{aligned} \sum _{i=1}^{k} r_i = n-d-1, \end{aligned}$$

(8.2)

then $(G,\mathbf{p})$ is dimensionally rigid. Conversely, if $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$, then there must be an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$, with an associated iterated PSD stress such that (8.2) holds.

The two versions of this theorem are related as follows: the zero set of configurations for the energy function $E_i$ corresponds via the change of basis $B_{i-1}$, to the kernel of the matrix $\Omega ^*_i$. Since the rank of $\Omega ^*_i$ is $r_i$, its kernel has dimension $d_{i-1} +1-r_i=d_i+1$. Thus $d_k+1 = n -\sum _{i=1}^i r_i =(d+1)$. So $\mathcal {A}_k$, which has dimension $(d_k+1)D$, is the set of all affine images of $\mathbf{p}$ in $\mathbb {R}^D$.

Figure 9 is an example of an application of Theorem 8.1. The set of configurations of all the points, where for a pole, one is at the midpoint between the other two, is an affine set. The stress is indicated. Each of the restricted stress matrices has rank one. The horizontal members also have a stress that is in equilibrium when restricted to the intersection of the first two affine sets. This matrix also has rank one. Thus all the stress matrices can be assumed to be (and are) PSD. But $n=6, d=2$, so $d+1 +\sum _{i=1}^i r_i=3+ 3 = 6 = n$, and this $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^2$. This framework has a flex in the plane that is an affine motion, but the point is that it cannot be twisted into a $3$-dimensional shape. The calculations are done in Sect. 15.1.

One application of Theorem 8.1 is to universal rigidity.

Corollary 8.2

Suppose ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is an iterated affine set for a framework $(G,\mathbf{p})$ with $n$ vertices in $\mathbb {R}^d$. Suppose that the iterated affine set has an associated iterated PSD stress. If $\dim (\mathcal {A}_k)=D(d+1)$ and the member directions do not lie on a conic at infinity, then $(G,\mathbf{p})$ is universally rigid.

Conversely if $(G,\mathbf{p})$ is universally rigid in $\mathbb {R}^d$, then there is such an iterated affine set with an iterated PSD stress, and the member directions do not lie on a conic at infinity.

For example, if another bar is inserted between any of two of the vertices that do not already have a bar in Fig. 9, the resulting framework will be universally rigid.

9 Convexity Interpretation

We now point out the connection of the results here from the point of view of basic convexity considerations.

Definition 9.1

For any finite-dimensional convex set $X$ and any point $x$ in $X$, let $F(x)$, called the face of $x$, be the largest convex subset of $X$ containing $x$ in its relative interior. Equivalently [23], $F(x)$ is the set of points $z \in X$ so that there is a $z' \in X$ with $x$ in the relative interior of the segment $[z',z]$.

Definition 9.2

A subset $X_0 \subset X$ is called a face of $X$ if $X_0 = F(x)$ for some $x \in X$.

Definition 9.3

Let $X= X_0 \supset X_1 \supset X_2 \supset \cdots X_k$ be a sequence of faces of $X$, which we call a face flag. If each $X_i = \mathcal {H}_i \cap X_{i-1}$, where $\mathcal {H}_i \subset \langle X_{i-1}\rangle$ is a support hyperplane for $X_{i-1}\subset \langle X_{i-1}\rangle$ for $i=1,\ldots , k$, then we call the face flag supported.

The following is an easy consequence of these definitions.

Lemma 9.1

A subset $Y$ of $X$ is a face of $X$ if and only if $Y = X_k$ for some supported flag face.

We next specialize to the case when the space $X=\mathcal {M}$, the measurement space for the graph $G$ defined in Sect. 6. The function $f$ is the rigidity map as before.

Lemma 9.2

A supporting hyperplane $\mathcal {H}\subset \mathbb {R}^m$ for $\mathcal {M}$ corresponds to a non-zero PSD stress $\omega$ for the graph $G$. A hyperplane $\mathcal {H}$ supports a convex subcone of $X_i \subset \mathcal {M}$ if and only if there is a quadratic energy form $E_{\omega }$ which is PSD on $f^{-1}(X_i)$ and $E_{\omega }(\mathbf{p})=0$ for some $\mathbf{p}\in f^{-1}(X_i)$.

Definition 9.4

If $\mathbf{p}\in {\mathcal {C}}$ is a configuration, define $\mathcal {A}(\mathbf{p})$ to be the set of all affine images of $\mathbf{p}$. As before, we call any $\mathbf{q}$ of maximal dimensional affine span in $\mathcal {A}(\mathbf{p})$ a universal configuration for $\mathcal {A}(\mathbf{p})$. Define $\mathring{\mathcal {A}}(\mathbf{p})$ to be the set of universal configurations of $\mathcal {A}(\mathbf{p})$.

Lemma 9.3

Suppose $(G,\mathbf{p})$ is dimensionally rigid. Then

$$\begin{aligned} f^{-1}(F(f(\mathbf{p}))) \subset \mathcal {A}(\mathbf{p}). \end{aligned}$$

Thus additionally, we have

$$\begin{aligned} F(f(\mathbf{p})) \subset f(\mathcal {A}(\mathbf{p})). \end{aligned}$$

Proof

Suppose not. Then there is a configuration $\mathbf{q}\not \in \mathcal {A}(\mathbf{p}))$ such that $f(\mathbf{q}) \in F(f(\mathbf{p}))$. Since $f(\mathbf{p})$ is in the interior of the face, and f(q) is in the face, then, from the definition of a face, there must be some third configuration $\mathbf{r}$, such that $f(\mathbf{p})$ is in the relative interior of the segment [f(q), f(r)]. As in the proof of Lemma 7.1, we can use two complementary spaces, and find appropriate scalars $\alpha$ and $\beta$ such that $\tilde{\mathbf{p}} := (\alpha \mathbf{q}, \beta \mathbf{r})$ is equivalent to $\mathbf{p}$. Since $\mathbf{q}$ is not an affine image of $\mathbf{p}$, neither is $\tilde{\mathbf{p}}$. This, together with Theorem 5.1, contradicts our assumption that $\mathbf{p}$ was dimensionally rigid. $\square$

Lemma 9.4

Suppose $(G,\mathbf{p})$ is dimensionally rigid. Then

$$\begin{aligned} F(f(\mathbf{p})) \supset f(\mathcal {A}(\mathbf{p})). \end{aligned}$$

Thus additionally, we have

$$\begin{aligned} f^{-1}(F(f(\mathbf{p}))) \supset \mathcal {A}(\mathbf{p}). \end{aligned}$$

Proof

From Lemma 7.1, we know that $f(\mathcal {A}(\mathbf{p}))$ is convex with $f(\mathbf{p})$ in its relative interior. Thus from the definition of a face, we have $F(f(\mathbf{p}))) \supset f(\mathcal {A}(\mathbf{p}))$. $\square$

Corollary 9.1

If $(G,\mathbf{p})$ is dimensionally rigid and the configuration $\mathbf{q}$ is a non-singular affine image of $\mathbf{p}$, then $(G,\mathbf{q})$ is dimensionally rigid as well.

Proof

Since $\mathbf{q}\in \mathcal {A}(\mathbf{p})$, from the above lemmas, we have $f^{-1}(f(\mathbf{q})) \in \mathcal {A}(\mathbf{p})$. But $\mathbf{q}$ is universal for $\mathcal {A}(\mathbf{p})$ and so $\mathcal {A}(\mathbf{p})=\mathcal {A}(\mathbf{q})$, thus making $\mathbf{q}$ dimensionally rigid.

With the above two lemmas in mind, we make the following definition:

Definition 9.5

We say that the affine set $\mathcal {A}$ is a $G$-affine set if $\mathcal {A}$ is equal to the pre-image of some face of the measurement set.

Proposition 9.1

A framework $(G,\mathbf{p})$ is dimensionally rigid if and only if $\mathcal {A}(\mathbf{p})$ is a $G$-affine set.

Proof

Suppose that $(G,\mathbf{p})$ is dimensionally rigid. Then from Lemmas 9.3 and 9.4, we know $f^{-1}(F(f(\mathbf{p})))=\mathcal {A}(\mathbf{p})$, which is thus a $G$-affine set.

For the other direction, let $F'$ be any face of $\mathcal {M}$ containing $f(\mathbf{p})$. Then $F(f(\mathbf{p})) \subset F'$. If $(G,\mathbf{p})$ is not dimensionally rigid, then there is configuration $\mathbf{q}\not \in \mathcal {A}(\mathbf{p})$ such that $f(\mathbf{q})=f(\mathbf{p})$. Thus $f^{-1}(F(\mathbf{p}))$ is not a subset of $\mathcal {A}(\mathbf{p})$, and $f^{-1}(F')$ is not a subset of $\mathcal {A}(\mathbf{p})$. So $\mathcal {A}(\mathbf{p})$ is not a $G$-affine set. $\square$

In summary, this says that the face lattice of the measurement set $\mathcal {M}$ exactly corresponds the lattice of $G$-affine sets. Theorem 8.1 follows directly. The sequence of faces in a face flag of $\mathcal {M}$ corresponds to an iterated sequence of $G$-affine sets $\mathcal {A}_i$ cut out by an appropriate stress sequence $E_i$.

10 Relation to Facial Reduction

Facial reduction is a general technique used in the study of duality in cone programming [9, 35, 36], and we describe the translation between that and our exposition here. In the general setup, one might have a cone programming problem where the feasible set is expressed as points $\mathbf{x}\in \mathbb {R}^N$ that are both in some convex cone $K \subset \mathbb {R}^N$ and satisfy an equality constraint, expressed as $\mathbf{x}\in L + \mathbf{b}$, where $L$ is a linear subspace of $\mathbb {R}^N$ and $\mathbf{b}\in \mathbb {R}^N$. Let $\mathbf{x}_0$ be in the relative interior of the feasible set and let $F_{\min } := F(\mathbf{x}_0)$ be its face in $K$.

In the process of facial reduction, we start with $F_0:=K$ and find a supporting hyperplane $\Omega _1^\perp$ whose intersection with $F_0$ is some subface $F_1$ of $F_0$ such that $F_1 \supset F_{\min }$. This can be iterated on any $F_{i-1}$ by finding a hyperplane $\Omega _i^\perp$ that supports $F_{i-1}$ and whose intersection with $F_{i-1}$ is some subface $F_{i}$ such that $F_i \supset F_{\min }$. In each step, we guarantee that we are not excluding any part of $F_{\min }$ by ensuring that $\Omega _i \in (L^\perp \cap \mathbf{b}^\perp )$. This process is iterated until $F_i = F_{\min }$.

In the setting of graph embedding, we can think of $K$ as $S^n_+$, the cone of n-by-n symmetric PSD matrices. Any configuration $\mathbf{p}$ can be mapped to its Gram matrix in $K$. Each affine set $\mathcal {A}$ corresponds to some face of $S^n_+$. (Note that not every face $F$ of $S^n_+$ corresponds to an affine set. The face $F$ must include the all-ones matrix so that its corresponding configuration set is closed under translations in $\mathbb {R}^D$.)

The linear constraint $\mathbf{x}\in L+\mathbf{b}$ corresponds to a framework being equivalent to $(G,\mathbf{p})$. (The graph $G$ determines the space $L$ and the edge lengths in $\mathbf{p}$ give us a $\mathbf{b}$.) The constraint $\Omega _i \in L^\perp$ means that $\Omega _i$ is a stress matrix for $G$ (zero on non-edges, and rows summing to zero). The constraint $\Omega _i \in \mathbf{b}^\perp$ means that any $\mathbf{p}$ and any equivalent configuration have zero energy under the quadratic form defined by $\Omega _i$. The constraint that $\Omega _i$ supports $F_{i-1}$ corresponds to $\Omega _i$ being PSD over a corresponding affine set $\mathcal {A}_i$.

Under this correspondence, one can see that our process of finding iterated affine sets $\mathcal {A}_i$ using iterated stress matrices $\Omega _i$ corresponds exactly to an application of facial reduction.

We note that, in our exposition, we do not describe the process using $S^n_+$ at all. On the one hand, we describe the affine sets $\mathcal {A}_i$ as subsets of configuration space (instead of as faces of $S^n_+$). On the other hand, instead of picturing of our stresses $\Omega _i$ as support planes for $S^n_+$, we work over the measurement set of our graph $\mathcal {M}(G) := S^n_+/L$, which is a linear projection of $S^n_+$. In this projected picture, our support planes are orthogonal to the stress vectors $\omega _i$ in $\mathbb {R}^m$.

As described in Sect. 9, facial reduction “upstairs” on the cone $K$ (such as $S^n_+$) for the constraint $x \in L+\mathbf{b}$ is exactly mirrored by the facial reduction “downstairs” on the cone $K/L$ (such as $\mathcal {M}$) for the constraint $x = \mathbf{b}/L$.

11 Tensegrities

It is also possible to use the ideas here to get a similar complete characterization of universal rigidity for tensegrity frameworks, where there are upper and lower bounds (cables and struts) on the member lengths corresponding to the sign of the rigidifying stresses.

Definition 11.1

Each edge of a graph $G$ is designated as either a cable, which is constrained to not get longer in length, or a strut, which is constrained not to get shorter in length, or a bar, which, as before, is constrained to stay the same length. So when we have a framework $(G,\mathbf{p})$, where each edge, which we call a member, is so designated, we call it a tensegrity framework, or simply a tensegrity, and we call $G$ a tensegrity graph.

We can then ask whether $(G,\mathbf{p})$ is locally rigid, globally rigid, or universally rigid. For local rigidity and the corresponding concept of infinitesimal rigidity, there is an extensive theory as one can see in [13, 14, 16, 37, 38, 41, 48], for example. For global rigidity and universal rigidity, there is a natural emphasis on stress matrices and related ideas.

Definition 11.2

We say that a stress $\omega =(\ldots , \omega _{ij}, \ldots )$ for a tensegrity graph is a proper stress if $\omega _{ij} \ge 0$, when the member $\{i,j\}$ is cable, and $\omega _{ij} \le 0$, when the member $\{i,j\}$ is a strut. There is no condition for a bar.

Theorem 4.1 takes on the following form for tensegrities. See [10].

Theorem 11.1

Let $(G,\mathbf{p})$ be a tensegrity framework whose affine span of $\mathbf{p}$ is all of $\mathbb {R}^d$, with a proper equilibrium stress $\omega$ and stress matrix $\Omega$. Suppose further

• 1. $\Omega$ is PSD.

• 2. The configuration $\mathbf{p}$ is universal with respect to the stress $\omega$. (In other words, the rank of $\Omega$ is $n - d - 1$.)

• 3. The member directions of $(G,\mathbf{p})$ with a non-zero stress, and bars, do not lie on a conic at infinity.

Then $(G,\mathbf{p})$ is universally rigid.

When we draw a tensegrity, cables are designated by dashed line segments, struts by solid line segments, and bars by thicker line segments, as in Fig. 5.

Fig. 5

These are three examples of super-stable tensegrities. The one on the left is trivially universally rigid when all the members are bars. But as a tensegrity it is also super stable, which follows from its rank one equilibrium stress matrix. The tensegrity in the middle is an example of a Cauchy polygon, one of the class of convex polygonal tensegrity polygons as defined in [10]. The one on the right has a degree three vertex attached by bars to another super-stable planar tensegrity in $\mathbb {R}^3$. The bars must have zero stress, but in order to insure that there is no affine motion, the bar directions must be included in the directions that are to avoid the conic at infinity

12 Iterated Stresses for Tensegrities

For the case of tensegrities, the iterated case is similar.

Definition 12.1

We say that a tensegrity $(G,\mathbf{p})$ in $\mathbb {R}^d$ is dimensionally rigid, if any other configuration $\mathbf{q}$ in any $\mathbb {R}^D$, satisfying the member constraints of $G$, has an affine span of dimension $d$ or less.

Theorem 12.1

Let $(G,\mathbf{p})$ be a tensegrity in $\mathbb {R}^d$, where $\mathbf{p}$ has an affine span of dimension $d$. Suppose ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$ with an associated iterated proper PSD stress. If the dimension of $\mathcal {A}_k$ is $(d+1)D$, then $\mathbf{p}$ is dimensionally rigid in $\mathbb {R}^d$.

Conversely, if $(G,\mathbf{p})$ is dimensionally rigid in $\mathbb {R}^d$, then there must be an iterated affine set with $\mathbf{p}\in \mathcal {A}_k$, ${{\mathrm{Dim}}}(\mathcal {A}_k) = (d+1)D$, with an associated iterated proper PSD stress.

Proof

The proof of this is essentially the same as in Sect. 8 for Theorem 8.1. For the necessity direction, we just need to be careful to maintain the proper signs for a tensegrity stress. When a tensegrity is dimensionally rigid, this means that not only is $f(\mathbf{p})$ on the boundary of $\mathcal {M}$, but also that $\mathcal {P}$, the polyhedral cone of tensegrity constraints of Definition 11.2 (the squared lengths $e^2_{ij} \le (\mathbf{p}_i-\mathbf{p}_j)^2$ for each cable and $e^2_{ij} \ge (\mathbf{p}_i-\mathbf{p}_j)^2$ for each strut), is disjoint from $\mathcal {M}$ except for $f(\mathcal {A}(\mathbf{p}))$. By a standard separation theorem, we can choose a hyperplane that separates the relative interiors of the two convex sets $\mathcal {P}$ and $\mathcal {M}$. (See Fig. 6 in the next section.) This means that the corresponding stress will be a proper stress for the tensegrity. It may be the case that this hyperplane contains other points of the boundary of $\mathcal {P}$ besides just $f(\mathbf{p})$, which means that some of the edges of $G$ will have zero stress components. This argument can be applied at each level of iteration.

Note that once an edge has a non-zero stress component at some level, this strictness can be maintained at any subsequent level. In particular, the stress $\omega _i$ is orthogonal to the configurations in $f(\mathcal {A}_j)$, and thus we can always replace $\omega _j$, for $j > i$, with $\omega _i + \omega _j$. So once a member gets stressed, it can remain stressed from then on.$\square$

Fig. 6

This shows a section of a cone as in Fig. 4, but with the rectangular cone given by the cable and strut constraints. The stress vectors $\omega _1$ determine the rectangular cone since it is proper

The major application of this result is the following.

Corollary 12.1

Suppose ${\mathcal {C}}= \mathcal {A}_0 \supset \mathcal {A}_1 \supset \mathcal {A}_2 \supset \cdots \mathcal {A}_k$ is an iterated affine set for a tensegrity $(G,\mathbf{p})$ with $n$ vertices in $\mathbb {R}^d$, with an associated iterated proper PSD stress described by PSD-restricted stress matrices $\Omega ^*_i$. Let $r_i$ be the rank of $\Omega ^*_i$. If (8.2) holds, and the member directions with non-zero stress directions and bars do not lie on a conic at infinity, then $(G,\mathbf{p})$ is universally rigid.

Conversely if $(G,\mathbf{p})$ is universally rigid in $\mathbb {R}^d$, then there is an iterated affine set with an associated iterated PSD stress determined by proper stresses; the dimension of $\mathcal {A}_k$ is $(d+1)D$, and the members with non-zero stress directions and bars do not lie on a conic at infinity.

Proof

This proof also follows that of the case of a bar framework. The only thing new that we need to establish in the necessity direction is that we will be able to find non-zero stress values on the cable and strut edges to certify that they do not lie on a conic at infinity. The iterated stresses that are guaranteed from the above theorem need not be non-zero on any particular set of edges (see Fig. 7).

To establish this we can use, if needed, one extra stress beyond that needed to establish dimensional rigidity. Suppose at the last level of iteration, we have a sequence of stresses that restricts us to frameworks in the affine set $\mathcal {A}_k$, such that $\mathbf{p}$ is universal for $\mathcal {A}_k$. In this case, we have that $f(\mathbf{p})$ is in the relative interior of $f(\mathcal {A}_k)$. The assumption of universal rigidity means that the polyhedral cone $\mathcal {P}$ is disjoint from $f(\mathcal {A}_k)$ except for the shared point $f(\mathbf{p})$. Since $f(\mathbf{p})$ is in the relative interior of $f(\mathcal {A}_k)$, this means that we can find a hyperplane that includes $f(\mathcal {A}_k)$ and excludes all of $\mathcal {P}$ except for the single point $f(\mathbf{p})$. The corresponding stress must have zero energy for all of $\mathcal {A}_k$ and will have non-zero values on all of the edges. $\square$

Fig. 7

These are two universally rigid tensegrities in the plane. The signs on the members not on the pole can be reversed, and it still remains universally rigid

Figure 7 is an example where one extra iteration is needed for universal rigidity after the iteration process shows dimensional rigidity. There is just one pole in the plane and just one vertex attached to all three vertices. There are two ways (as shown) to assign cables and struts to the remaining three members so that there will be an equilibrium at that vertex. Both possibilities provide a universally rigid tensegrity. At the first level, we can find a rank $1$ stress on the vertical pole. This is sufficient to serve as a certificate for dimensional rigidity. For a bar framework, universal rigidity follows since the edge directions do not lie at a conic at infinity. But for a tensegrity framework, we are not done, since in that case, the conic test only can use cable and strut edges with non-zero stress coefficients. As shown in Fig. 7, for this we can use a second-level stress that has a constant $0$ energy over $\mathcal {A}_1$.

13 Projective Invariance

It is well known that a bar framework $(G,\mathbf{p})$ is infinitesimally rigid if and only if $(G,\mathbf{q})$ is infinitesimally rigid, where the configuration $\mathbf{q}$ is a non-singular projective image of the configuration $\mathbf{p}$. See [16, 44, 45] for a discussion of this property. Infinitesimal rigidity for tensegrities is also projectively invariant, but a cable that “crosses” the hyperplane at infinity is changed to a strut and vice-versa, because the sign of the stress changes. It is also true that any equilibrium stress is also altered by the projective transformation. Indeed a stress matrix $\Omega$ is replaced by another stress matrix $D\Omega D$, where the matrix $D$ is a non-singular diagonal matrix and comes from the non-singular projective transformation. This transformation preserves the rank and PSD nature of the stress. At any subsequent level, we also can set $\Omega _i := D \Omega _i D$ using the same $D$ matrix. The basis matrix which is derived from the kernel is transformed as $B_i \rightarrow B_i D^{-1}$. Thus, the restricted stress matrix $\Omega ^*_i := B_i D^{-1} (D \Omega _i D) D^{-1} B^t_i$ is not changed at all due to the projective transform, thus maintaining its rank and PSD nature. See [17, Prop. 7], for the same idea applied to a bar framework. Thus we get the following result.

Theorem 13.1

Let $f: \mathbb {R}^d - X \rightarrow \mathbb {R}^d$ be non-singular projective transformation, where $X$ is a $(d-1)$-dimensional affine subspace of $\mathbb {R}^d$, and suppose that for each $i$, $\mathbf{p}_i \notin X$. Then for any tensegrity framework, $(G,\mathbf{p})$ is dimensionally rigid if and only if $(G,f(\mathbf{p}))$ is dimensionally rigid, where the strut/cable designation for $\{i,j\}$ changes only when the line segment $[\mathbf{p}_i, \mathbf{p}_j]$ intersects $X$ and bars go to bars.

It is not always true that the universal rigidity of a bar framework is projectively invariant. For example, the orchard ladder, narrower at the top than at the bottom, as in Fig. 8, is universally rigid, whereas the straight ladder, as shown in Fig. 9—a projective image—is flexible in the plane.

Fig. 8

This is an example of a universally rigid framework, but the framework shown in Fig. 9 is a projective image that is not universally rigid. The two poles on the sides are collinear triangles

Fig. 9

This shows a framework with two collinear triangles, each of which provides an affine relation on the space of configurations of the framework $(G,\mathbf{p})$. The stresses are indicated and the member connecting the external vertices of poles is indicated by a curved arc. This framework is dimensionally rigid in the plane, but it is not universally rigid, since it has an affine flex in the plane, and since there are only two member directions. The vertices are labeled in bold

14 Calculation Methods

We test for dimensional rigidity of $(G,\mathbf{p})$ by finding the maximal dimension of any framework $(G,\mathbf{q})$ that is equivalent to $\mathbf{p}$. This is done by building up a maximal iterated affine set with an associated iterated PSD stress as guaranteed by Corollary 8.1. To do this calculation, we always maintain a basis matrix $B_i$, where at the start, $B_0 = I$.

Given $B_{i-1}$ we perform the following steps:

Find the next stress Look for a matrix $\Omega _i$ such that the restricted stress matrix $\Omega ^*_i := B_{i-1} \Omega _i B_{i-1}^t$ is non-zero, PSD and such that the “energy” linear constraint $\mathbf{p}^t (\Omega _i \otimes I^D) \mathbf{p}=0$ holds. If there is no such solution, we are done with the iteration.

Definition 14.1

Given an affine set $\mathcal {A}_{i-1}$ described by a basis matrix $B_{i-1}$. We say that a restricted stress matrix $\Omega ^*_i = B_{i-1} \Omega _i B_{i-1}^t$ is a restricted equilibrium stress matrix for $\mathbf{p}$ if $P \Omega _i B_{i-1}^t = 0$ holds for $\Omega _i$.

For any stress matrix $\Omega _i$ that satisfies the energy constraint and such that the restricted stress matrix $\Omega ^*_i$ is PSD, we also see that $\Omega ^*_i$ must be a restricted equilibrium matrix for $\mathbf{p}$. Since we want to get the most milage out of our linear constraints, we replace the energy constraint with this constraint, which we call a restricted energy constraint.

The resulting problem can be posed as an SDP feasibility problem. If possible, we would like to avoid using an SDP solver, since that is not only expensive, but, as a numerical algorithm, only approaches, and it never exactly hits, a feasible solution. We discuss this issue in detail in Sect. 16.

Sometimes, we can avoid calling an SDP solver by simply looking at the problem and guessing the correct $\Omega _i$. For example, if we see, within some two-dimensional framework, a degenerate triangle (which we will call a pole), it is self-evident how to stress that subgraph.

Another easy case arises when the space of solutions for $\Omega ^*_i$ is only one-dimensional. In this case, there is no need to search for PSD solutions, and thus one only needs to pick one solution $\Omega ^*_i$ and check its eigenvalues. If it is positive semi-definite, then we have succeeded. If it is negative semi-definite, then we can negate the matrix, and we have succeeded. If it is indefinite, then there is no such solution and we are done with the iteration.

An even easier sub-case of this is when the space of $\Omega ^*_i$ is not only one-dimensional, but also that the maximal rank of these matrices is $1$. Then we know immediately that $\Omega ^*_i$ is semi-definite.

Update the basis Given $B_{i-1}$ and a stress $\Omega _i$ we need to update the basis. We do this by finding a maximal set of linearly independent row vectors of length $n$ that are in the row span of $B_{i-1}$, and such that each of these vectors is in the co-kernel of $\Omega _i B_{i-1}^t$.

These vectors form the rows of our new basis $B_i$. We then continue the iteration.

When the iteration is done We simply count the number of rows of the final $B_k$, which we call $d_k +1$. If $d_k$ equals $d$, the dimension of the affine span of $\mathbf{p}$, then we have produced a certificate that $\mathbf{p}$ is dimensionally rigid. Otherwise, we have found a higher dimensional affine set that includes frameworks equivalent to $\mathbf{p}$ and we have a certificate that $\mathbf{p}$ is not dimensionally rigid.

15 Examples

15.1 The Ladder

We first show the process described in Sects. 8.1 and 14 applied to the example in Fig. 9. The first-level stress matrix, using just the stresses on the vertical members of the ladder, is the following:

$$\begin{aligned} \Omega _1 = \left( \begin{array}{rrrrrr} 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad -2 &{}\quad 0\\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad -2 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad -2\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad -2\\ -2 &{}\quad -2 &{}\quad 0 &{}\quad 0 &{}\quad 4 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad -2 &{}\quad -2 &{}\quad 0 &{}\quad 4 \end{array}\right) . \end{aligned}$$

This matrix has rank $r_1=2$, a $4$-dimensional kernel, and $d=2$. The kernel of this matrix defines the affine set $\mathcal {A}_1$. A basis matrix for $\mathcal {A}_1$ is

$$\begin{aligned} B_1 = \left( \begin{array}{rrrrrr} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1/2 &{}\quad 0\\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1/2 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1/2\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1/2 \end{array}\right) . \end{aligned}$$

At the second level, we enforce the restricted equilibrium constraint and find that the possible candidates for $\Omega ^*_2$ must be up to scale, equal to

$$\begin{aligned} B_1\Omega _2 B_1^t = \Omega ^*_2=\left( \begin{array}{rrrr} 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 \\ -1 &{}\quad 1 &{}\quad -1 &{}\quad 1 \\ 1 &{}\quad -1 &{}\quad 1 &{}\quad -1 \\ -1 &{}\quad 1 &{}\quad -1 &{}\quad 1 \end{array}\right) \end{aligned}$$

These are rank 1 with positive trace and thus positive semi-definite. This $\Omega ^*_2$ has an associated second-level stress $\Omega _2$ where $\omega _{14}=\omega _{23}=1$ and $\omega _{56}=-2$ as in Fig. 9. We have ${{\mathrm{rank}}}\Omega _1 +{{\mathrm{rank}}}\Omega ^*_2 = 3 =n-d-1$, making the ladder dimensionally rigid.

15.2 The $4$-pole Example

Consider the configuration shown in Fig. 10 with four vertical parallel line segments, the poles, where each pole is connected to the other three by horizontal members.

Fig. 10

This is a framework that is dimensionally rigid in the plane. Each set of three (nearly) vertical line segments are considered to be a collinear triangle, while the other horizontal members are connected as shown. This involves at least three levels of iteration as described in Sect. 8, where the levels, in order, are marked in dark blue, red, and green

The poles are labeled $A, B, C, D$, and the vertices are simply labeled by their number, $1,\ldots , 12$. The horizontal spacing between the $AB, BC$, and $CD$ poles is equal. The vertical spacing of the horizontal members is such that the distance between the 2–11 line and the 1–7 line is twice the distance between the 2–11 line and the 3–5 line. The $5$ vertex is the midpoint of the $B$ pole, and the $8$ vertex is the midpoint of the $C$ pole. The stresses on this framework are as indicated. These are simply arranged so that the lever arm moments are all $0$. The question is whether the appropriate stress matrices are PSD of the right rank.

The stress for each pole is rank one and they can all be combined to one rank $4$ stress, which can be considered as a stress at the first level. It is simply the certificate, in any equivalent framework, that each pole remains straight maintaining the ratio of each of the lengths. The stress for each of those members is proportional to the reciprocal of its length in absolute value. The stress for the longest member of each collinear triangle is negative, while the other two are positive.

One can then choose a basis for $\mathcal {A}_1$ and search for the restricted equilibrium matrices as in Sect. 14. It turns out that, as in the ladder example, the space of a possible equilibrium $\Omega ^*_2$ is only one-dimensional, and these have rank $4$. We check and find that these matrices are semi-definite. An associated $\Omega _2$ is shown in red in Fig. 10. We then choose a basis for $\mathcal {A}_2$ and use the methods described in Sect. 14 one final time. Again, we find a one-dimensional space of equilibrium matrices $\Omega ^*_3$, and these have rank $1$. An associated $\Omega _3$ can be constructed with $\omega _{1,3} = \omega _{10,12} = 4$ and $\omega _{4,6} = \omega _{7,9} = -1$.

The sum of the ranks is $4 + 4 +1 = 9 = 12 - (2 + 1) = n - ( d+1)$, so this framework is dimensionally rigid in the plane. It is not universally rigid since the original framework has only two member directions. One interesting feature of this example is that the stress $\Omega _2$ involves all of the vertices of the graph $G$ from the second level, and it still needs another level for the complete analysis of its dimensional rigidity.

The first stage in this example involves only the four collinear triangles, which imply the corresponding affine constraints on the configuration. Suppose one initially starts with those four affine constraints and then proceeds with the analysis, where the distance constraints on the poles is dropped? It turns out that the configuration is not dimensionally rigid in the plane, since at the third level the member constraints in the poles are needed again. The maximal dimensional realization, in that case, is $\mathbb {R}^3$.

15.3 The $4$-pole Extended Example

Definition 15.1

A spider web is a tensegrity, where some subset of the vertices are fixed, and all the members are cables.

For a spider web, it was shown in [10] that it is locally rigid if and only if it is universally rigid and that, when it is universally rigid, the iterated construction simplifies to a sequence of proper subgraphs, where the number of vertices decreases at each stage as in Fig. 1. Another example of the iteration process is shown in Fig. 3, where the vertex $A$ is added at the second stage. In each of those examples, there is a proper subgraph that is universally rigid on its own without using the presence of the other vertices.

Figure 11 shows that, in general, when the framework is universally rigid in more than one step of the iteration, there may be no proper sub-framework that is universally rigid on its own. The stresses at each level are shown.

Fig. 11

This is an example of a universally rigid tensegrity framework in the plane that has only one stress that is PSD of rank $8$, one less than the maximal possible $n -d-1=12 - 2 -1 =9$. There is a stress at the second stage which is PSD of rank one in the affine set defined by the stress at the first stage. The vertices of this configuration are the same as those in Fig. 10, except the interior point of each pole has been moved half the distance (left or right as indicated) between adjacent poles

This is a perturbed version of Fig. 10, and it turns out to be universally rigid by the process described here, but using only two stages instead of three as in Sect. 15.2. Since the stressed members have more than two directions in the plane and it is dimensionally rigid in the plane as with Fig. 10, it is universally rigid.

In both of these cases, we were able to find the certifying sequence of stresses without calling a PSD solver. This was because, at each step, there was only a one-dimensional space of restricted equilibrium matrices $\Omega ^*$ as candidates. Since they were rank $1$, we automatically knew that they were semi-definite, and for the second step, for the $4$ poles, we just checked that it was of rank $4$.

More generally, if we end up with a higher dimensional space of equilibrium $\Omega ^*$ as candidates, we might have a harder time determining if that space includes a positive semi-definite one. We discuss this in detail in Sect. 16.

15.4 A Hidden Stress

One of the problems with SDP is finding even one PSD equilibrium stress (or more generally restricted equilibrium stresses at later stages). The following example is a framework where PSD equilibrium stresses form a low-dimensional subcone of the space of all equilibrium stresses.

The two triangles and the members joining corresponding vertices constitute a super-stable PSD sub-framework as in Fig. 3. Since the whole (bar) framework is infinitesimally rigid in the plane, and that there are $18$ members and $9$ vertices, the dimension of the stress space is $18-2\cdot 9 + 3=3$. Equilibrium at each blue vertex implies that the three stresses at a blue vertex must all have the same sign. But any equilibrium stress, non-zero on any of the members adjacent to the blue vertices, cannot be all have the same sign for all the members adjacent to all the blue vertices. This is because the twisting infinitesimal motion of the inner triangle relative to the outer triangle either decreases all the members adjacent to the blue vertices or increases them. So one of the set of three members adjacent to a blue vertex has to have all negative stresses. This stress cannot be PSD since by moving that single blue vertex the stress energy must decrease.

16 Computational Matters

An important property of universal rigidity is that often it can be calculated efficiently using various SDP algorithms. For example, see [5, 9, 28, 30, 35, 36, 47] for information on this vast subject including facial reduction. In particular, if one is given the edge lengths $\mathbf{e}$ for a graph $G$, one can use SDP to find a configuration $\mathbf{p}$ whose edge lengths approximate $\mathbf{e}$. More precisely, an $\varepsilon$-approximate configuration $\mathbf{p}$ can be found, in some unconstrained dimension $D$ if it exists, in time polynomial in $\log (1/\varepsilon )$, where $n$ is the number of vertices of $G$, and $m$ is the number of members of $G$, as described in [47]. So this can be used to attempt to see if the existence problem is feasible and to attempt to find a satisfying configuration when it is feasible.

But, as mentioned in Sect. 1, one problem is that even though the member lengths of the approximation are close to the given lengths, the configuration may be quite a distance from one implied by the actual constraints. Small errors in the edge lengths can imply large errors in the proposed configuration as in the framework in Fig. 1, but see [26]. In principle, one could use the calculation as evidence that a given configuration is universally rigid in $\mathbb {R}^2$, but as shown in Fig. 2 it may appear that $(G,\mathbf{p})$ has equivalent configurations in $\mathbb {R}^3$ or higher, even with $\varepsilon > 0$ is very small.

In contrast to this “primal approach,” we have shown in this paper that when a framework is dimensionally or universally rigid, there must exist a certificate, in the form of an iterated PSD stress, that conclusively proves the dimensional or universal rigidity of the framework.

Although finding these stresses also involves solving an SDP problem, in many cases, we can hope to exactly solve this “dual” SDP. At any level of the analysis here, there is a linear space of restricted equilibrium stress matrices $\Omega ^*_i$ as described in Sect. 14. If there is such a PSD matrix of maximal rank among all such $\Omega ^*_i$, then the PSD-restricted equilibrium stresses include an open subset of the space of all restricted equilibrium stresses. In this case, it reasonable to expect that we can exactly find such a solution. Thus, even if the numerical solution from an SDP solver is, say, PSD but not quite in restricted equilibrium, a sufficiently close restricted equilibrium stress will still be PSD and of maximum rank.

In fact this “maximal rank case” must always occur in the last step of our iterated process so, for example, if the framework $(G,\mathbf{p})$ is super stable (in other words, there is only one step in the iterated process described here), then the PSD solutions are full dimensional within the linear space of equilibrium stress matrices. This is the situation if $\mathbf{p}$ is generic in $\mathbb {R}^d$, and the framework $(G,\mathbf{p})$ is universally rigid, since this must be super stable by Theorem 4.3. The two examples on the left in Fig. 5 have that property.

In other cases, though we may not be able to exactly solve this “dual” SDP, the example of Fig. 12 shows a case where the PSD equilibrium stresses are all of lower rank than the indefinite equilibrium stresses, and thus do NOT form an open subset of the space of equilibrium stresses. If the dimension of PSD matrices is lower than the dimension of all the equilibrium matrices, then we may have to resort to using the SDP to “suggest” what an actual PSD matrix is (since it will only converge to a PSD matrix in the limit).

Fig. 12

This is an example of a universally rigid bar framework in the plane that has a three-dimensional space of equilibrium stresses but only a one-dimensional space that is PSD

More generally, when the configuration is not generic, you have to ask: how is the configuration even defined? It is possible to create configurations precisely so that they become universally rigid. For example, the symmetric tensegrities of many artists are created in such a way that they become super stable, but not at all generic, not even infinitesimally rigid, even though they are super stable. Indeed, they often have certain symmetries that can be used to simplify the calculations and create tensegrities that are super stable. The representation theory of some small finite groups can be exploited to create these configurations. A brief explanation is in [15]. This is called form finding in the Engineering literature, as in [31, 40].

Stresses and iterated stresses might also be useful during the process of calculating a realization $\mathbf{p}$ from an input graph $G$ and input set of edge lengths $\mathbf{e}$. Note though, when we are just given input lengths and are searching for an appropriate $\Omega$, we do not have enough information to express the (restricted) equilibrium linear constraint and can only use the “energy linear constraint”: $0= \sum _{i<j} e_{ij}^2 \omega _{ij}$. Therefore, we do not expect to be in a “maximal rank” setting. Once we have computed the iterated stresses, then we just need to look for $\mathbf{p}$ within the final affine set. As described in the appendix in [22], when $\mathbf{p}$ is universally rigid, this calculation of $\mathbf{p}$ within its affine set can be done easily by solving a certain small linear system. (In the case that $\mathbf{p}$ is not universally rigid but is only dimensionally rigid, then that linear system will be singular. Still, since we have restricted ourselves to the correct affine set, we only need to solve small SDP problem, which must be applied over the space of $(d+1)$-by-$(d+1)$ matrices.)

In addition to the example in [15], a graph coloring problem can be solved using this idea as in [34].

17 Extensions

In general, we propose the following procedure for determining/creating universally rigid frameworks and tensegrities. First a (tensegrity) graph $G$, and a corresponding configuration $\mathbf{p}$, is defined. A priori, a sequence of affine sets in configuration space can be given as well, as in Sect. 8. These sets may or may not be a consequence of the geometry of the configuration $\mathbf{p}$. Then at each stage, one either calculates a PSD stress for the given configuration or one assumes that there is a corresponding affine constraint. If the constraints are consistent, then one has a proof that the configuration is dimensionally rigid or universally rigid, depending on the stressed member directions. For example, if there appears to be a (proper) PSD stress for a given affine set, one can assume that it exists and proceeds, getting further affine sets. It would depend on the circumstance as to whether the particular affine constraint is reasonable or not. For example, in Fig. 1, one might suspect that the eight subdivided vertical members are straight, but initially not the others. Only then one might suspect that the four smaller horizontal members are straight, etc. After this, one can conclude that the whole framework is universally rigid.

The idea of assigning nested affine constraints is a generalization of the idea of a body-and-bar framework as defined by Tay and Whiteley in [42, 43]. The concept of nested affine sets, introduced here, is closely related to the concepts of hypergraphs of points and affine rigidity introduced in [22]. Also, a recent result in [19] shows that body-and-bar frameworks are generically globally rigid in $\mathbb {R}^d$ if they are generically redundantly rigid in $\mathbb {R}^d$.

Definition 17.1

Redundant rigidity means that the framework is locally rigid, and remains so after the removal of any member.

It is also true [19] that such body-and-bar graphs always have a generic configuration that is universally rigid in $\mathbb {R}^d$ as well.

18 Possible Future Directions and Questions

It is also possible to use stresses to estimate the possible perturbations of a given tensegrity or framework. The sign of a PSD stress associated to each member corresponds to an inequality constraint. If all of those constraints are such that at least one of the constraints is violated, we know that the edge length perturbed configuration cannot be achieved. This imposes somewhat weak, but useful, conditions on which sets of members can increase or decrease in length. If there are more PSD stresses on the members, there will be more of these sign constraints that can be calculated even if the tensegrity framework is not rigid.

One could use universal rigidity properties to understand flexible structures by adding members providing parameters for controlling the motion of a flexible framework. For a fixed length of such additional members, the configuration could be determined. As the length varies, the whole configuration could flex in a controlled way.

For the case of generic global rigidity, the notion of globally linked pairs of vertices is discussed in [24, 25]. This means that although the whole framework may not be globally rigid, some pairs of vertices would be forced to have a fixed length for all equivalent configurations in the same dimension. A similar question in the universally rigid category involving configurations in higher dimensions that satisfy the tensegrity inequality constraints would be interesting to explore.

It is also interesting to determine whether a framework is universally rigid on the line. In [27] it is determined when a rigid one-dimensional complete bipartite bar-and-joint framework in the line is universally rigid, as well as several open questions in this direction. We have a forthcoming paper that extends this result, and determines when any complete bipartite framework in any dimension is universally rigid.

The weavings of [32, 33, 44, 45] concern lines in the plane that may or may not arise from projections of configurations of lines in a higher dimension. Particularly, there is a relation to stresses of dual configurations in [44, 45]. Can there be a connection to the poles in universal rigidity?