Tensegrities and Global Rigidity

Abstract

In 1947 a young artist named Kenneth Snelson invented an intriguing structure: a few sticks suspended rigidly in mid air without touching each other. It seemed like a magic trick. He showed this to the entrepreneur, builder, visionary, and self-styled mathematician, R. Buckminster Fuller, who called it a tensegrity because of its “tensional integrity.” Fuller talked about tensegrities and wrote about them extensively. Snelson went on to build a great variety of fascinating tensegrity sculptures all over the world, including the 60-foot work of art at the Hirschhorn Museum in Washington, DC. shown in Figure.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

In 1947 a young artist named Kenneth Snelson invented an intriguing structure: a few sticks suspended rigidly in mid air without touching each other. It seemed like a magic trick. He showed this to the entrepreneur, builder, visionary, and self-styled mathematician, R. Buckminster Fuller, who called it a tensegrity because of its “tensional integrity.” Fuller talked about tensegrities and wrote about them extensively. Snelson went on to build a great variety of fascinating tensegrity sculptures all over the world, including the 60-foot work of art at the Hirschhorn Museum in Washington, DC. shown in Figure 21.1.

Why did these tensegrities hold up? What were the geometric principles? They were often under-braced, and they seemed to need a lot of tension for their stability. So Fuller’s name, tensegrity, is quite appropriate.

Figure 21.1

Kenneth Snelson, Needle Tower, 1968, aluminum and stainless steel, 60 ×20 ×20 ft. — 18. 2 × 6 ×6 m.

In this chapter I will show how to describe the stability of most of the tensegrities that Snelson and others have built, and how to predict their stability. I begin with a set of principles that can be used to understand many of the Snelson-like tensegrities. This relies on the properties of the stress matrix, a symmetric matrix that defines a kind of potential energy that we would like to minimize at a given configuration. This leads to a lot of interesting examples one can build, assured that the structure will not fall down.

Then I will show how the rank of a stress matrix can predict how generic configurations of bar tensegrities (usually called bar frameworks) predict a strong sort of rigidity that I call global rigidity, and mention some exciting new results where the stress matrix plays a central role. There are several quite interesting applications of the theory of tensegrities. Of course, there is a natural application to structural engineering, where the pin-jointed bar-and-joint model is appropriate for an endless collection of structures. In computational geometry, there was the carpenter’s rule conjecture, inspired by a problem in robot arm manipulation. This proposes that a non-intersecting polygonal chain in the plane can be straightened, keeping the edge lengths fixed, without creating any self-intersections. The key idea in that problem uses basic tools in the theory of tensegrity structures and stresses. Granular materials of hard spherical disks can be reasonably modeled as tensegrities, where all the members are struts. Again the theory of tensegrities can be applied to predict behavior and provide the mathematical basis for computer simulations as well as to predict the distribution of internal stresses.

Terminology and Notation

To define a tensegrity we first define a tensegrity graph G with vertices $1,2,\ldots,n$ in d-dimensional space E ^d. Edges are denoted as unordered pairs of different vertices {i, j}, where i≠j. Each edge of G is declared a cable, strut, bar or not connected. The cables, struts, and bars are members of the tensegrity, and are denoted by dashed line segments, bold line segments, or thin line segments respectively.

The next ingredient is a configuration p = (p ₁, …, p _n ) of n points or nodes in the Euclidean plane or space, where each p _i corresponds to a vertex i of G. Nodes connected by cables are allowed to get closer together (or stay the same distance apart), the nodes connected by struts are allowed to get farther apart (or stay the same distance apart), but bars must always stay the same distance apart.

The graph together with the corresponding configuration is a tensegrity G(p). This notation is useful since we sometimes want to consider the abstract graph G without referring to a particular configuration, or the configuration p without referring to any particular graph. The notation is meant to suggest, for example, that there are physical cables connecting pairs of nodes that have cables connecting the corresponding vertices of G.

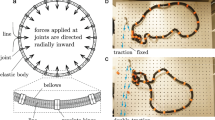
A continuous motion of the nodes, starting at the given configuration of a tensegrity, is called a flex of the tensegrity. A trivial flex is one that moves the configuration as a whole without changing any distances between nodes, for example rotations and translations, in space. If the tensegrity has only trivial flexes, then it is said to be rigid in E ^d. Otherwise it is flexible. Note that, theoretically, members can cross one another (i.e., intersect). For the purposes of our mathematical model, the tensegrity is a purely geometric object, but many of the rigid tensegrities shown here can be built with rubber (or plastic) bands for cables, and dowel rods with a slot at their ends for struts or bars. Figure 21.2 shows some examples of rigid and flexible tensegrities in the plane and space.

Figure 21.2

Nodes are denoted by small round points, cables by dashed line segments, struts by solid line segments, and bars by thin line segments.

The rigid tensegrity in space in Figure 21.2 is one of Snelson’s original objects. It is quite simple but suspends three sticks, the struts, rigidly without any pair of them touching. Indeed, Snelson does not like to call an object made of cables and struts a tensegrity unless all the struts are completely disjoint, even at their nodes. A tensegrity with all its struts disjoint and with no bars (i.e., all the other members are cables) will be called a pure tensegrity.

Now let’s discuss techniques for computing the rigidity of tensegrities. As a by-product, the definition and analysis of global rigidity will emerge naturally. The stress associated to a tensegrity is the vector $\omega = (\ldots,\omega _{ij},\ldots \,)$, where ω _ij  = ω _ji is a scalar associated to the member {i, j} of G. A stress $\omega = (\ldots,\omega _{ij},\ldots \,)$ is proper if ω _ij  ≥ 0 for a cable {i, j} and ω _ij  ≤ 0 for a strut {i, j}. There is no condition when {i, j} is a bar. We set ω _ij  = 0 if the nodes {i, j} are not connected. We say a proper stress ω is strict if ω _ij ≠0 when {i, j} is a cable or strut.

Let $\omega = (\ldots,\omega _{ij},\ldots \,)$ be a proper stress for a tensegrity graph G. For any configuration p of nodes in E ^d, define the stress-energy associated to ω as

$$E_{\omega }(p) =\displaystyle\sum _{i<j}\omega _{ij}{(p_{i} - p_{j})}^{2},$$

(21.1)

where the product of vectors is the ordinary dot product, and the square of a vector is the square of its Euclidean length.

Now think of the configuration p as fixed. We want to compare other configurations q to p. Let us say the tensegrity G(p) dominates the tensegrity G(q), and write G(q) ≤ G(p) for two configurations q and p if

$$\displaystyle\begin{array}{rcl} \vert p_{i} - p_{j}\vert & \geq & \vert q_{i} - q_{j}\vert \qquad \mbox{ for \{i,j\} a cable}, \\ \vert p_{i} - p_{j}\vert & \leq & \vert q_{i} - q_{j}\vert \qquad \mbox{ for \{i,j\} a strut and} \\ \vert p_{i} - p_{j}\vert & =& \vert q_{i} - q_{j}\vert \qquad \mbox{ for \{i,j\} a bar}. \end{array}$$

(21.2)

These are the tensegrity constraints for the configuration p with respect to the tensegrity graph G. So if G(p) dominates G(q) and ω is a proper stress for G, then E _ω(p) ≥ E _ω(q), because the terms of (21.2) that correspond to cables have a positive stress and can only decrease since the cable lengths can only decrease, while the terms corresponding to struts have a negative coefficient and the strut lengths can only increase.

Local and Global Rigidity

A tensegrity G(p) is locally rigid if the only continuous flexes of G(p) that satisfy the tensegrity constraints of Equation (21.2) are congruences. There is a good body of work devoted to the detection and understanding of local rigidity.

However, most of the structures made by Snelson and other artists are globally rigid. This means that for any other configuration q of the same labeled nodes in E ^d, G(q) ≤ G(p) implies that q is congruent to p. Even more strongly, regard E ^d ⊂ E ^D, for d ≤ D. If, even though G(p) is in E ^d, it is true that G(p) is globally rigid in E ^D, for all D ≥ d, then we say G(p) is universally globally rigid. For example, both rigid tensegrities in Figure 21.2, are universally globally rigid. The example in Figure 21.3a is rigid in the plane, but not globally rigid in the plane, since it can reflect the upper left node around a diagonal. Figure 21.3b is globally rigid in the plane but not universally globally rigid, since it is flexible in three-space. Figure 21.3c is universally globally rigid. These are all bar frameworks.

Figure 21.3

Three examples of planar rigid bar frameworks; see the text for details.

What can we say about more complicated tensegrities? The energy function E _ω described above helps. The idea is to look for situations in which the configuration p is a minimum for the functional E _ω. The first step is to determine when p is a critical point for E _ω, i.e., when all directional derivatives given by $p prime = (p prime_{1},\ldots,p prime_{n})$ starting at p are 0. This means that the following equilibrium vector equation must hold for each node i:

$$\displaystyle\sum _{j}\omega _{ij}(p_{j} - p_{i}) = 0.$$

(21.3)

In this case, ω is an equilibrium stress for p, called just a stress when the equilibrium is clear from the context. To get an understanding of how this works, consider the example of a square in the plane as in Figure 21.4. It is easy to see that the vector equilibrium equation (21.3) holds for the three vectors at each node.

Figure 21.4

A square tensegrity with its diagonals, where a proper equilibrium stress is indicated.

If a configuration p were the unique minimum, up to rigid congruences, for E _ω, we would have a global rigidity result immediately, but unfortunately this is almost never the case. We must deal with affine transformations.

Affine Transformations

An affine transformation or affine map of E ^d is determined by a d x d matrix A and a vector b ∈ E ^d. If $p = (p_{1},\ldots,p_{n})$ is any configuration in E ^d, an affine image is given by $q = (q_{1},\ldots,q_{n})$, where $q_{i} = Ap_{i} + b$. If the configuration p is in equilibrium with respect to the stress ω, then so is any affine transformation q of p.

This brings us to the question: for a tensegrity G(p) in E ^d, when is there an affine transformation that preserves the member constraints (21.2)? It is clear that the matrix A is the only relevant part, and it turns out that we also only need to consider the members that are bars. A preserves the length of bar {i, j} if and only if the following holds:

$$\displaystyle\begin{array}{rcl}{ (p_{i} - p_{j})}^{2}& =& {(q_{ i} - q_{j})}^{2} \\ & =& {(Ap_{i} - Ap_{j})}^{2} \\ & =& {[A(p_{i} - p_{j})]}^{T}A(p_{ i} - p_{j}) \\ & =& {(p_{i} - p_{j})}^{T}{A}^{T}A(p_{ i} - p_{j}), \\ \end{array}$$

or equivalently,

$${(p_{i} - p_{j})}^{T}({A}^{T}A - {I}^{d})(p_{ i} - p_{j}) = 0$$

(21.4)

where ()^T is the transpose operation, I ^d is the d x d identity matrix, and vectors are regarded as column vectors in this calculation. If Equation (21.4) holds for all bars in G, we say that it has a bar preserving affine image, which is non-trivial if A is not orthogonal. Similarly, G has a non-trivial affine flex if there is a continuous family of d-by-d matrices A _t , where A ₀ = I ^d, for t in some interval containing 0 such that each A _t satisfies Equation (21.4) for t in the interval.

This suggests the following definition. If $v =\{ v_{1},\ldots,v_{k}\}$ is a collection of vectors in E ^d, we say that they lie on a quadric at infinity if there is a non-zero symmetric d-by-d matrix Q such that for all v _i  ∈ v

$$v_{i}^{T}Qv_{ i} = 0.$$

(21.5)

Notice that since the definition of an orthogonal matrix A is that ${A}^{T}A - {I}^{d} = \mathbf{0}$, the affine transformation defines a quadric at infinity if and only if the affine transformation is not a congruence.

Call the bar directions of a bar tensegrity the set {p _i  − p _j }, for {i, j} a bar of G. With this terminology, Equation (21.5) says that if A preserves bar length, then the member directions of a bar tensegrity lie on a quadric at infinity. We can prove:

Proposition 21.1.

If G(p) is a bar framework in E ^d , such that the nodes do not lie in a (d − 1)-dimensional hyperplane, then it has a non-trivial bar preserving affine image if and only if it has a non-trivial bar-preserving affine flex if and only if the bar directions lie on a quadric at infinity.

Proof.

The “only if” direction is shown above. Conversely suppose that the member directions of a bar tensegrity G(p) lie on a quadric at infinity in e^d given by a non-zero symmetric matrix Q. By the spectral theorem for symmetric matrices, we know that there is an orthogonal d-by-d matrix $X = {({X}^{T})}^{-1}$ such that:

$${ X}^{T}QX = \left (\begin{array}{*{10}c} \lambda _{1} & 0 & 0 &\cdots & 0 \\ 0 &\lambda _{2} & 0 &\cdots & 0 \\ 0 & 0 &\lambda _{3} & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 &\cdots &\lambda _{d} \end{array} \right ).$$

Let λ₋ be the smallest λ _i , and let λ₊ be the largest λ _i . Note $\infty \leq 1/\lambda _{-} < 1/\lambda _{+} \leq \infty$, λ₋ is non-positive, and λ₊ is non-negative when Q defines a non-empty quadric and when $1/\lambda _{-}\leq t \leq 1/\lambda _{+}$, 1 − tλ _i  ≥ 0 for all $i = 1,\ldots,d$. Working Equation (21.4) backwards for $1/\lambda _{-}\leq t \leq 1/\lambda _{+}$ we define:

$$\displaystyle\begin{array}{rcl} A_{t} = {X}^{T}\left (\begin{array}{*{10}c} \sqrt{1 - t\lambda _{1}} & 0 & 0 & \cdots & 0 \\ 0 & \sqrt{1 - t\lambda _{2}} & 0 & \cdots & 0 \\ 0 & 0 & \sqrt{1 - t\lambda _{3}} & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \sqrt{1 - t\lambda _{d}} \end{array} \right )X.& &\end{array}$$

(21.6)

Substituting A _t from Equation (21.6) into Equation (21.4), we see that it provides a non-trivial affine flex of G(p). If the configuration is contained in a lower dimensional hyperplane, we should really restrict to that hyperplane since there are non-orthogonal affine transformations that are rigid when restricted to the configuration itself.

When do bar tensegrities have bar directions that lie on a quadric at infinity? In E ², the quadric at infinity consists of two distinct directions. So a parallelogram or a grid of parallelograms has a non-trivial affine flex. In E ³ it is more interesting. The quadric at infinity is a conic in the projective plane, and such a conic is determined by 5 points. An interesting example is the bar tensegrity in Figure 21.5. The surface is obtained by taking the line (x, 1, x) and rotating it about the z-axis. This creates a ruling of the surface by disjoint lines. Similarly (x, 1, − x) creates another ruling. Each line in one ruling intersects each line in the other ruling or they are parallel. A bar tensegrity is obtained by placing nodes where a line on one ruling intersects a line on the other ruling, and bars such that they join every pair of nodes that lie on same line on either ruling.

Figure 21.5

Figure (a) is the ruled hyperboloid given by ${x}^{2} + {y}^{2} - {z}^{2} = 1$. Figure (b) is the flattened version after an affine flex.

Alexander Barvinok asked when a framework in a space of D dimensions can also be realized in a subspace of d dimensions, d < D. He proved

Theorem 21.2.

If G(p) is a bar framework in E ^D with less than $d(d + 1)/2$ bars, then it has a realization in E ^d with the same bar lengths.

Proof.

The space of d-by-d symmetric matrices is of dimension $d + ({d}^{2} - d)/2 = d(d + 1)/2$. So if the vector directions of the members of a tensegrity are less than $d(d + 1)/2$, then it is possible to find a non-zero d-by-d symmetric matrix that satisfies Equation (21.5), and then flex it into a lower dimensional subspace by using Equation (22.4) until one of the diagonal entries becomes 0.

If every realization G(p) of a bar graph G, where the p’s are configurations in E ^D, can be realized in E ^d with the same bar lengths, then we say that G is d-realizable. Note that this is a property of the graph G: in order to qualify for being d-realizable, one has to be able to push a realization in E ^D down to a realization E ^d for ALL realizations in E ^D. For example, the 1-realizable graphs are forests, graphs with no cycles. In particular, a triangle is not 1-realizable.

This is inspired by a problem in nuclear magnetic resonance (NMR) spectroscopy. The atoms of a protein are tagged and some of the pairwise distances are known. The problem is to identify a configuration in E ³ that satisfies those distance constraints. Finding such a configuration in E ^D, for some large D, is computationally feasible, and if G is 3-realizable, one can expect to find another configuration in E ³ that satisfies the distance constraints.

A graph H is a minor of a graph G if it can be obtained from G by edge contractions or deletions. If a minor of a graph G is not d-realizable, then G itself is not d-realizable. It is easy to show that a graph is 1-realizable if and only if it does not have a triangle as a minor. In other words, the triangle is the one and only forbidden minor for 1-realizability. It is not too hard to show that the graph K ₄, the tetrahedron, is the only forbidden minor for 2-realizability. Maria Belk and I showed:

Theorem 21.3.

A complete list of forbidden minors for 3-realizability is the set of two graphs, K ₅ and edge graph of the regular octahedron.

There is a reasonable algorithm to detect 3-realizablity for an abstract graph and, when the edge lengths are given, to find a realization in E ³. Tensegrity techniques are used in a significant way.

The Stress Matrix and the Fundamental Theorem

The stress-energy function E _ω defined by (21.1) is a quadratic form, and it is an easy matter to compute the matrix associated to it

$$\Omega =\displaystyle\sum _{i<j}\omega _{ij}\Omega (i,j)$$

where the (i, j) entry is − ω _ij for i≠j, and the diagonal entries are such that the row and column sums are 0. (Recall that any stress ω _ij not designated in the vector form ω = (⋯ , ω _ij , ⋯ ) is assumed to be 0.) With this terminology we can regard a configuration $p = (p_{1},\ldots,p_{n})$ in E ^d as a column vector. Then

$$\displaystyle\begin{array}{rcl} E_{\omega }(p)& =& \displaystyle\sum _{i<j}\omega _{ij}{(p_{i} - p_{j})}^{2} \\ & =& \displaystyle\sum _{i<j}\omega _{ij}{(x_{i} - x_{j})}^{2} \\ & & +\displaystyle\sum _{i<j}\omega _{ij}{(y_{i} - y_{j})}^{2} + \ldots \\ & =& \left (\begin{array}{*{10}c} x_{1} & x_{2} & \cdots &x_{n} \end{array} \right )\Omega \left (\begin{array}{*{10}c} x_{1} \\ x_{2}\\ \vdots \\ x_{n} \end{array} \right ) \\ & & +\left (\begin{array}{*{10}c} y_{1} & y_{2} & \cdots &y_{n} \end{array} \right )\Omega \left (\begin{array}{*{10}c} y_{1} \\ y_{2}\\ \vdots \\ y_{n} \end{array} \right ) + \ldots,\\ \end{array}$$

where each $p_{i} = (x_{i},y_{i},\ldots \,)$, for $i = 1,\ldots,n$. So we see that E _ω is essentially given by the matrix Ω repeated d times. The tensor product of matrices (or sometimes the Kronecker product) gives the matrix of E _ω as Ω ⊗ I ^d, and

$$E_{\omega }(p) = {(p)}^{T}\Omega \otimes {I}^{d}p.$$

To rewrite the equilibrium condition (21.3) in terms of matrices, define the configuration matrixP for the configuration p as

$$P = \left (\begin{array}{*{10}c} p_{1} & p_{2} & \cdots &p_{n} \\ 1 & 1 &\cdots & 1 \end{array} \right ).$$

P is a (d + 1)-by-n matrix, and the equilibrium condition (21.3) is equivalent to

$$P\,\Omega = \boldsymbol{0}.$$

Each coordinate of P as a row vector multiplied on the right by Ω represents the equilibrium condition in that coordinate. The last row of ones of P represent the condition that the column sums (and therefore the row sums) of Ω are. It is also easy to see that the linear rank of P is the same as the dimension of the affine span of $p_{1},\ldots,p_{n}$ in E ^d.

Suppose that we add rows to P until all the rows span the co-kernel of Ω. The corresponding configuration p will be called a universal configuration for ω (or equivalently Ω).

Proposition 21.4.

If p is a universal configuration for ω, any other configuration q which is in equilibrium with respect to ω is an affine image of p.

Proof.

Let Q be the configuration matrix for q. Since the rows of P are a basis for the co-kernel of Ω, and the rows of Q are, by definition, in the co-kernel of Ω, there is a (d + 1)-by-(d + 1) matrix A such that AP = Q. Since P and Q share the last row of ones, we know that A takes the form

$$A = \left (\begin{array}{*{10}c} A_{0} & b\\ 0 &1 \end{array} \right ),$$

where A ₀ is a d-by-d matrix, b is a 1-by-d matrix (a vector in E ^d), and the last row is all 0’s except for the 1 in the lower right hand entry. Then we see that for each $i = 1,\ldots,n$, $q_{i} = A_{0}p_{i} + b$, as desired.

The stress matrix plays a central role in this theory. Note that when the configuration $p = (p_{1},\ldots,p_{n})$ in E ^d is universal (i.e., its affine span is all of E ^d), for the stress ω, the dimension of the co-kernel (which is the dimension of the kernel) of Ω is d, and the rank of Ω is $n - d - 1$. But even when the configuration p is not universal for ω, it is the projection of a universal configuration, and so the rank $\Omega \leq n - d - 1$.

Now we come to one of the basic tools for showing that specific tensegrities are globally rigid and more. If ω is a proper equilibrium stress for the tensegrity G(p), then the difference p _i  − p _j , where ω _ij ≠0, is called a stressed direction and the member {i, j} is called a stressed member. Note that if G(q) ≤ G(p), ω _ij ≠0, and $\vert p_{i} - p_{j}\vert \neq \vert q_{i} - q_{j}\vert$, then E _ω(q) < E _ω(p). So if p is a configuration for the minimum of E _ω, the stressed members are effectively bars.

Theorem 21.5.

Let G(p) be a tensegrity, where the affine span of $p = (p_{1},\ldots,p_{n})$ is all of E ^d , with a proper equilibrium stress ω and stress matrix Ω. Suppose further that

• 1. Ω is positive semi-definite.

• 2. The configuration p is universal with respect to the stress ω. (In other words, the rank of Ω is $n - d - 1$ .)

• 3. The stressed directions of G(p) do not lie on a quadric at infinity.

Then G(p) is universally globally rigid in all dimensions.

Proof.

Suppose that q is a configuration such that G(q) ≤ G(p). Then E _ω(q) ≤ E _ω(p). By Condition 21.5, $E_{\omega }(q) = E_{\omega }(p) = 0$, and ω is an equilibrium stress for the configuration q as well as p. By Condition 21.5 and Proposition 21.4, q is an affine image of p. By Condition 21.5 and Proposition 21.1, q is congruent to p.

Notice that in view of Proposition 21.1, Condition 21.5 can be replaced by the condition that G(p) has no affine flexes in E ^d. For example, if it is rigid in E ^d, that would be enough.

With this in mind, we say that a tensegrity is super stable if it has a proper equilibrium stress ω such that Conditions (21.5), (21.5) and (21.5) hold. If just Conditions 21.5 and 21.5 hold and ω is strict (all members stressed), then we say G(p) is unyielding. An unyielding tensegrity, essentially, has all its members replaced by bars.

Examples

The Square Tensegrity

The stress matrix for the square of Figure 21.4 is

$$\Omega = \left (\begin{array}{*{10}c} +1&-1&+1&-1\\ -1 &+1 &-1 &+1 \\ +1&-1&+1&-1\\ -1 &+1 &-1 &+1 \end{array} \right ).$$

(21.7)

So Ω has rank $1 = 4 - 2 - 1 = n - d - 1$, and since its trace is 4, its single eigenvalue is 4, and it is positive semi-definite. This makes it unyielding, and since the underlying graph is the complete graph, it is universally globally rigid. It is also super stable. There are several ways to generalize this example.

Polygon Tensegrities

I showed that a tensegrity, obtained from a planar convex polygon by putting a node at each vertex, a cable along each edge, and struts connecting other nodes such that the resulting tensegrity has some proper equilibrium stress, is always super stable. Figure 21.6 shows some examples.

Figure 21.6

Some planar superstable polygons.

Radon Tensegrities

Radon’s Theorem says that if $p = (p_{1},\ldots,p_{d+2})$ are d + 2 points in E ^d, no d + 1 in a hyperplane, then they can be separated into two simplices σⁱ and σ^d − i of dimension i and d − i such that their intersection is a common point, which is a relative interior point of each simplex. They can also be used to define a super stable tensegrity as well. Write $\sum _{k=1}^{d+2}\lambda _{k}p_{k} = \mathbf{0}$, where $\sum _{k=1}^{d+2}\lambda _{k} = 0$, while λ _k  > 0 for $k = 1,\ldots,i + 1$, and λ _k  < 0 for $k = i + 2,\ldots,d + 2$. Then the stress matrix is

$$\Omega = \left (\begin{array}{*{10}c} \lambda _{1} \\ \lambda _{2}\\ \vdots \\ \lambda _{d+2} \end{array} \right )\left (\begin{array}{*{10}c} \lambda _{1} & \lambda _{2} & \cdots &\lambda _{d+2} \end{array} \right ),$$

(21.8)

since for the configuration matrix P,

$$P\left (\begin{array}{*{10}c} \lambda _{1} \\ \lambda _{2}\\ \vdots \\ \lambda _{d+2} \end{array} \right ) = \mathbf{0}.$$

(21.9)

So the stress $\omega _{ij} = -\lambda _{i}\lambda _{j}$. The edges of σⁱ and σ^d − i are struts, while all the other members are cables. Since the rank is $d + 2 - d - 1 = 1$, and Ω is positive semi-definite, the tensegrity is super stable. Figure 21.7 shows the two examples in the plane and in three-space.

Figure 21.7

Some superstable Radon tensegrities.

Centrally Symmetric Polyhedra

L. Lovasz showed that if one places nodes at the vertices of a centrally symmetric convex polytope, cables along its edges, and struts between its antipodal points, the resulting tensegrity has a strict proper equilibrium stress, and any such stress will have a stress matrix such that Conditions 21.5 and 21.5 hold, while condition 21.5 is easy to check. Thus such a tensegrity is super stable and universally globally rigid. Figure 21.8 shows such an example for the cube, which is easy to check independently.

Figure 21.8

A cube with cables along its edges and struts connecting antipodal nodes, which is super stable.

Prismatic Tensegrities

Consider a tensegrity in E ³ formed by two regular polygons $(p_{1},\ldots,p_{n})$ and $(p_{n+1},\ldots,p_{2n})$ in distinct parallel planes, each symmetric about the same axis. Cables are placed along the edges of each polygon. Each node of each polygon is connected by a cable to a corresponding node in the other polygon, maintaining the rotational symmetry. Similarly, each node of each polygon in connected to a corresponding node in the other polygon by a strut, maintaining the rotational symmetry. The ends of the cable and strut are k steps apart where 1 ≤ k ≤ n − 1. This describes a prismatic tensegrityP(k, n). Each P(n, k) is super stable when the angle of the twist from a node in the top polygon to the projection of the node at the other end of the strut is $\pi (1/2 + i/n)$. Figure 21.9 shows P(6, 1).

Figure 21.9

The prismic tensegrity P(6, 1).

The Snelson tensegrity in the introduction is P(3, 1).

Highly Symmetric Tensegrities

Many of the tensegrities created by artists such as Snelson have the super stable property discussed here. They need the stress for their stability. Their tensional integrity is part of their stability. Symmetry seems to a natural part of art, so I thought it would be interesting to see what symmetric tensegrities were super stable. It turns out that the symmetry simplifies the calculation of the rank and definiteness of the stress matrix. In addition, the theory of the representations of finite groups is a natural tool that can be used to decompose the stress matrix. With Allen Back and later Robert Terrell, we created a website where one can view and rotate the pictures of these tensegrities.

The tensegrity graph G is chosen so that there is an underlying finite group Γ acting on the tensegrity such that the action of Γ takes cables to cables and struts to struts, and the following conditions hold:

• 1. The group Γ acts transitively and freely on the nodes. In other words, for each pair p _i , p _j of nodes, there is a unique element g ∈ Γ such that gp _i  = p _j .

• 2. There is one transitivity class of struts. In other words, if {p _i , p _j } and {p _k , p _l } are struts, then there is g ∈ Γ such that {gp _i , gp _j } = { p _k , p _l } as sets.

• 3. There are exactly two transitivity classes of cables. In other words, all the cables are partitioned into two sets, where Γ permutes the elements of each set transitively, but no group element takes a cable from one partition to the other.

The user must choose the abstract group, the group elements that correspond to the cables, the group element that corresponds to the struts, and the ratio of the stresses on the two classes of cables. Then the tensegrity is rendered. Figure 21.10 shows a typical picture from the catalog at http://www.math.cornell.edu.

Figure 21.10

A super stable tensegrity from the catalog at http://www.math.cornell.edu. In the catalog, the struts are colored green, one cable transitivity class is colored red, and the other blue. In this example, the cables lie on the convex hull of the nodes, and struts are inside.

Compound Tensegrities

The sum of positive semi-definite matrices is positive semi-definite. So we can glue two super stable tensegrities along some common nodes, and maintain Condition 21.5. Condition 21.5 is no problem. The rank Condition 21.5 may be violated, but each of the individual tensegrities will remain globally rigid, even if some of the stresses vanish on overlapping members.

One example of this process is the delta-Y transformation. If one super stable tensegrity has a triangle of cables in it, one can add a tensegrity of the form in the upper right of Figure 21.7 so the stresses on the overlap of the three struts exactly cancel with the three cable stresses in the other tensegrity. So the three triangle cables replace the three other cables joined to a new node inside the triangle. In this case the resulting tensegrity is still super stable since the radon tensegrity is planar and using Condition 21.5. Figure 21.11 shows how this might work for the top triangle of the Snelson tensegrity of Figure 21.2. Figure 21.12 shows this replacement on both triangles.

Figure 21.11

Two superstable tensegrities are added to get a third.

Figure 21.12

The Δ − Y transformation applied to a Snelson Tensegrity.

If the replacement as in Figure 21.12 is done for a polygon of with four or more vertices, the resulting tensegrity may not be super stable or even rigid, but if the polygons have an odd number of vertices and the struts are placed as far away from the vertical cables as possible, then the resulting tensegrity is super stable. In other words, if the star construction is done on P(2k + 1, k) as in Figure 21.13 the resulting tensegrity is super stable.

Figure 21.13

A flexible tensegrity.

It is also possible to put two (or more) super stable tensegrities together on a common polygon to create a tensegrity with a stress matrix that satisfies Condition 21.5 while the universal configuration is 4-dimensional instead of 3-dimensional. But each of the original pieces is universally globally rigid. The 4-dimensional realization has an affine flex around the 2-dimensional polygon used to glue the two pieces together. So the tensegrity has two non-congruent configurations in E ³ as one piece rotates about the other in E ⁴. Meanwhile struts and cable stresses can be arranged to cancel, and thus those members are not needed in the compound tensegrity. Figure 21.14 shows this with two Snelson tensegrities combined along a planar hexagonal tensegrity.

Figure 21.14

A compound rigid but not superstable tensegrity.

This is something like the start of the Snelson tower of Figure 21.1, but the hexagonal polygon in the middle is planar, which seems a bit surprising. This tensegrity is unyielding and rigid, but not super stable. But possibly to create more stability Snelson includes more cables from one unit to the other, and this destroys the planarity of the hexagon.

There are many different ways to combine super stable units, possibly erasing some of the members in the basic units to get similar rigid tensegrities.

Pure and Flexible Examples

Recall that a pure tensegrity is one that has only cables and struts and the struts are all disjoint. We have seen several examples in E ³ of pure tensegrities, the simplest being Snelson’s original as in Figure 21.11 on the left. But what about the plane? One might be tempted to think that the tensegrity of Figure 21.15 is rigid, but it isn’t.

Figure 21.15

A flexible tensegrity in the plane occurs when the struts don’t intersect.

Indeed, there are no pure rigid tensegrities in the plane. This follows from the proof of the carpenter’s rule property. This theorem says that any chain of non-overlaping edges in the plane can be continuously expanded (flexed) until it is straight. This result also allows for disjoint edges and, at least for a short time, the expansion can be run backwards to be a contraction, keeping the struts at a fixed length.

There’s more — much more — to say about this rapidly-evolving subject; see the notes at the end of the book.