Universal Rigidity of Bar Frameworks in General Position: A Euclidean Distance Matrix Approach

Abstract

A configuration p in r-dimensional Euclidean space is a finite collection of labeled points ${p}^{1},\ldots ,{p}^{n}$ in ${\mathbb{R}}^{r}$ that affinely span ${\mathbb{R}}^{r}$. Each configuration p defines a Euclidean distance matrix ${D}_{p} = ({d}_{ij})$ = $(\vert \vert {p}^{i} - {p}^{j}\vert {\vert }^{2})$, where $\vert \vert \cdot \vert \vert$ denotes the Euclidean norm. A fundamental problem in distance geometry is to find out whether or not a given proper subset of the entries of D _p suffices to uniquely determine the entire matrix D _p . This problem is known as the universal rigidity problem of bar frameworks. In this chapter, we present a unified approach for the universal rigidity of bar frameworks, based on Euclidean distance matrices (EDMs), or equivalently, on projected Gram matrices. This approach makes the universal rigidity problem amenable to semidefinite programming methodology. Using this approach, we survey some recently obtained results and their proofs, emphasizing the case where the points ${p}^{1},\ldots ,{p}^{n}$ are in general position.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A configurationp in r-dimensional Euclidean space is a finite collection of labeled points ${p}^{1},\ldots ,{p}^{n}$ in ${\mathbb{R}}^{r}$ that affinely span ${\mathbb{R}}^{r}$. Each configuration p defines the $n \times n$ matrix ${D}_{p} = ({d}_{ij})$ = $(\vert \vert {p}^{i} - {p}^{j}\vert {\vert }^{2})$, where | | . | | denotes the Euclidean norm. D _p is called the Euclidean distance matrix (EDM) generated by configuration p. Obviously, D _p is a real symmetric matrix whose diagonal entries are all zeros. A fundamental problem in distance geometry is to find out whether or not, a given proper subset of the entries of D _p , the EDM generated by configuration p, suffices to uniquely determine the entire matrix D _p , i.e., to uniquely recover p, up to a rigid motion. This problem is known as the universal rigidity problem of bar frameworks.

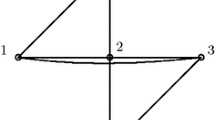
A bar framework, or framework for short, denoted by G(p), in ${\mathbb{R}}^{r}$ is a configuration p in ${\mathbb{R}}^{r}$ together with a simple graph G on the vertices $1,2,\ldots ,n$. To avoid trivialities, we assume throughout this chapter that the graph G is connected and not complete. It is useful to think of each node i of G in a framework G(p) as a universal joint located at p ⁱ and of each edge (i, j) of G as a stiff bar of length $\vert \vert {p}^{i} - {p}^{j}\vert \vert$. Hence, a bar framework is often defined as a collection of stiff bars joined at their ends by universal joints. Figure 1.1 depicts a framework G(p) on 4 vertices in ${\mathbb{R}}^{2}$, where G is the complete graph K ₄ minus an edge and the points ${p}^{1},\ldots ,{p}^{4}$ are the vertices of the unit square.

Fig. 1.1

A bar framework G(p) on 4 vertices in ${\mathbb{R}}^{2}$, where V (G) = { 1, 2, 3, 4}, E(G) =  {(1, 2), (2, 3), (3, 4), (4, 1), (1, 3)} and ${p}^{1},{p}^{2},{p}^{3},{p}^{4}$ are the vertices of the unit square

We say that two frameworks G(p) and G(q) in ${\mathbb{R}}^{r}$ are congruent if ${D}_{p} = {D}_{q}$. Furthermore, let H denote the adjacency matrix of graph G, then two frameworks G(p) in ${\mathbb{R}}^{r}$ and G(q) in ${\mathbb{R}}^{s}$ are said to be equivalent if $H \circ {D}_{p} = H \circ {D}_{q}$, where $\circ$ denotes the Hadamard product, i.e., the element-wise product. We say that framework G(q) in ${\mathbb{R}}^{r}$ is affinely equivalent to framework G(p) in ${\mathbb{R}}^{r}$ if G(q) is equivalent to G(p) and configuration q is obtained from configuration p by an affine motion, i.e., ${q}^{i} = A{p}^{i} + b$, for all $i = 1,\ldots ,n$, for some $r \times r$ matrix A and an r-vector b.

A framework G(p) in ${\mathbb{R}}^{r}$ is said to be universally rigid if every framework G(q) in any dimension that is equivalent to G(p) is in fact congruent to G(p), i.e., if for every framework G(q) in any dimension such that $H \circ {D}_{q} = H \circ {D}_{p}$, it follows that ${D}_{q} = {D}_{p}$.

Thus, given ${D}_{p} = ({d}_{ij})$, the EDM generated by configuration p, let $K \subset \{ (i,j) : i < j;\ for\ i,j = 1,2,\ldots ,n\}$. Then the proper subset of entries of D _p given by $\{{d}_{ij} : (i,j) \in K\}$ suffices to uniquely determine the entire matrix D _p if and only if framework G(p) is universally rigid, where G = (V, E) is the graph with vertex set $V =\{ 1,2,\ldots ,n\}$ and edge set E = K. For example, consider the framework G(p) given in Fig. 1.1 and its corresponding EDM

$${D}_{p} = \left [\begin{array}{cccc} 0&\quad 1&\quad 2&\quad 1\\ 1 &\quad 0 &\quad 1 &\quad 2 \\ 2&\quad 1&\quad 0&\quad 1\\ 1 &\quad 2 &\quad 1 &\quad 0 \end{array} \right ].$$

In the process of folding G(p) along the edge (1, 3), the distance $\vert \vert {p}^{2} - {p}^{4}\vert \vert$ varies between $\sqrt{2}$ and 0. Thus, the subset of entries of D _p given by $\{{d}_{ij} : (i,j) \in E(G)\}$ does not uniquely determine the entire matrix D _p since the entry d ₂₄ can assume any value between 2 and 0. Accordingly, G(p) is not universally rigid.

The notion of dimensional rigidity is closely related to that of universal rigidity. A framework G(p) in ${\mathbb{R}}^{r}$ is said to be dimensionally rigid if there does not exist a framework G(q) that is equivalent to G(p) in any Euclidean space of dimension $\geq r + 1$. For example, the framework G(p) given in Fig. 1.1 is obviously not dimensionally rigid since there is an infinite number of frameworks G(q) in ${\mathbb{R}}^{3}$ that are equivalent to G(p). This can be seen by rotating the triangle 123 of the framework G(p) about the edge (1, 3).

In this chapter, we survey some recently obtained results concerning framework universal as well as dimensional rigidity. These results are given in Sect. 1.2 and their proofs are given in Sect. 1.4. Section 1.3 is dedicated to the mathematical preliminaries needed for our proofs. Our EDM approach of universal rigidity of bar frameworks extends to the closely related notion of “local” rigidity. However, due to space limitation, “local” rigidity [3] will not be considered here. Also, we will not consider the other closely related notion of global rigidity [10, 14].

Throughout this chapter, | C | denotes the cardinality of a finite set C. We denote the node set and the edge set of a simple graph G by V (G) and E(G), respectively. ${\mathcal{S}}_{n}$ denotes the space of $n \times n$ real symmetric matrices. Positive semi-definiteness (positive definiteness) of a symmetric matrix A is denoted by $A \succcurlyeq \mathbf{0}$ ($A \succ \mathbf{0}$). For a matrix A in ${\mathcal{S}}_{n}$, $diag(A)$ denotes the n-vector formed from the diagonal entries of A. e denotes the vector of all ones in ${\mathbb{R}}^{n}$. Finally, the $n \times n$ identity matrix is denoted by I _n ; and 0 denotes the zero matrix or the zero vector of the appropriate dimension.

2 Main Results

The following theorem characterizes universal rigidity in terms of dimensional rigidity and affine-equivalence.

Theorem 1.1 (Alfakih [2]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ , $r \leq n - 2$ . Then G(p) is universally rigid if and only if the following two conditions hold:

• 1. G(p) is dimensionally rigid.

• 2. There does not exist a bar framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

The proof of Theorem 1.1 is given in Sect. 1.4. The notion of a stress matrix S of a framework G(p) plays an important role in the characterization of universal rigidity of G(p). Let G(p) be a framework on n vertices in ${\mathbb{R}}^{r}$, $r \leq n - 2$. An equilibrium stress of G(p) is a real valued function $\omega$ on E(G), the set of edges of G, such that

$${\sum \nolimits }_{j:(i,j)\in E(G)}{\omega }_{ij}({p}^{i} - {p}^{j}) = \mathbf{0}\quad \ for all\ i = 1,\ldots ,n.$$

(1.1)

Let $\omega$ be an equilibrium stress of G(p). Then the $n \times n$ symmetric matrix S = (s _ij ) where

$${ s}_{ij} = \left \{\begin{array}{@{}l@{\quad }l@{}} -{\omega }_{ij} \quad &if\ (i,j) \in E(G), \\ 0 \quad &if\ i\neq j\ and\ (i,j)\not\in E(G), \\ {\sum \nolimits }_{k:(i,k)\in E(G)}{\omega }_{ik}\quad &if\ i = j, \end{array} \right.$$

(1.2)

is called the stress matrix associated with $\omega$, or a stress matrix of G(p).

Given framework G(p) on n vertices in ${\mathbb{R}}^{r}$, we define the following $n \times r$ matrix

$$P := \left [\begin{array}{c} {{p}^{1}}^{T} \\ {{p}^{2}}^{T}\\ \vdots \\ {{p}^{n}}^{T} \end{array} \right ].$$

(1.3)

P is called the configuration matrix of G(p). Note that P has full column rank since ${p}^{1},\ldots ,{p}^{n}$ affinely span ${\mathbb{R}}^{r}$. The following lemma provides an upper bound on the rank of a stress matrix S.

Lemma 1.1.

Let G(p) be a bar framework on n nodes in ${\mathbb{R}}^{r}$ , $r \leq n - 2$ , and let S and P be a stress matrix and the configuration matrix of G(p), respectively. Then $SP = \mathbf{0}$ and $Se = \mathbf{0}$ , where e is the vector of all 1’s. Consequently, rank $S \leq n - r - 1$ .

Proof.

It follows from Eqs. (1.1) and (1.2) that the ith row of SP is given by

$${s}_{ii}{({p}^{i})}^{T} +{ \sum \nolimits }_{k=1,k\neq i}^{n}{s}_{ ik}{({p}^{k})}^{T} ={ \sum \nolimits }_{k:(i,k)\in E(G)}{\omega }_{ik}{({p}^{i} - {p}^{k})}^{T} = \mathbf{0}.$$

Also, e is obviously in the null space of S. Hence, the result follows.

2.1 Dimensional and Universal Rigidity in Terms of Stress Matrices

The following theorem provides a sufficient condition for the dimensional rigidity of frameworks.

Theorem 1.2 (Alfakih [2]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ for some $r \leq n - 2$ . If G(p) admits a positive semidefinite stress matrix S of rank n − r − 1, then G(p) is dimensionally rigid.

The proof of Theorem 1.2 is given in Sect. 1.4. It is worth pointing out that the converse of Theorem 1.2 is not true. Consider the following framework [2] G(p) on 5 vertices in ${\mathbb{R}}^{2}$ (see Fig 1.2), where the configuration matrix P is given by

$$P = \left [\begin{array}{rr} - 3& - 5\\ 1 & 2 \\ 0& - 1\\ 2 & 0 \\ 0& 4 \end{array} \right ],$$

and where the missing edges of G are (1, 2) and (3, 4). It is clear that G(p) is dimensionally rigid (in fact G(p) is also universally rigid) while G(p) has no positive semidefinite stress matrix of rank 2.

Fig. 1.2

A dimensionally rigid framework G(p) in ${\mathbb{R}}^{2}$ (in fact G(p) is also universally rigid) that does not admit a positive semidefinite stress matrix of rank 2. Note that the points ${p}^{2},{p}^{4}$, and p ⁵ are collinear, i.e., G(p) is not in general position

The following result, which provides a sufficient condition for the universal rigidity of a given framework, is a direct consequence of Theorems 1.1 and 1.2.

Theorem 1.3 (Connelly [8, 9], Alfakih [2]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . If the following two conditions hold:

• 1. G(p) admits a positive semidefinite stress matrix S of rank n − r − 1.

• 2. There does not exist a bar framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

Then G(p) is universally rigid.

A configuration p (or a framework G(p)) is said to be generic if all the coordinates of ${p}^{1},\ldots ,{p}^{n}$ are algebraically independent over the integers. That is, if there does not exist a nonzero polynomial f with integer coefficients such that $f({p}^{1},\ldots ,{p}^{n}) = 0$. Thus, for a generic framework, Theorem 1.3 reduces to the following theorem.

Theorem 1.4 (Connelly [9], Alfakih [4]). 

Let G(p) be a generic bar framework on n nodes in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . If G(p) admits a positive semidefinite stress matrix S of rank n − r − 1, then G(p) is universally rigid.

The proof of Theorem 1.4 is given in Sect. 1.4. The converse of Theorem 1.4 is also true.

Theorem 1.5 (Gortler and Thurston [15]). 

Let G(p) be a generic bar framework on n nodes in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . If G(p) is universally rigid, then there exists a positive semidefinite stress matrix S of G(p) of rank n − r − 1.

The proof of Theorem 1.5 given in [15] goes beyond the scope of this chapter and will not be presented here.

At this point, one is tempted to ask whether a result similar to Theorem 1.4 holds if the genericity assumption of G(p) is replaced by the weaker assumption of general position. A configuration p (or a framework G(p)) in ${\mathbb{R}}^{r}$ is said to be in general position if no r + 1 points in ${p}^{1},\ldots ,{p}^{n}$ are affinely dependent. For example, a set of points in the plane are in general position if no 3 of them are collinear. The following theorem answers this question in the affirmative.

Theorem 1.6 (Alfakih and Ye [7]). 

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . If G(p) admits a positive semidefinite stress matrix S of rank n − r − 1, then G(p) is universally rigid.

The proof of Theorem 1.6 is given in Sect. 1.4. The following result shows that the converse of Theorem 1.6 holds for frameworks G(p) where graph G is an (r + 1)-lateration graph. Such frameworks were shown to be universally rigid in [22]. However, it is still an open question whether the converse of Theorem 1.6 holds for frameworks of general graphs.

A graph G on n vertices is called an (r + 1)-lateration graph [12, 18] if there is a permutation $\pi$ of the vertices of G, $\pi (1),\pi (2),\ldots ,\pi (n)$, such that

• 1. The first (r + 1) vertices, $\pi (1),\ldots ,\pi (r + 1)$, induce a clique in G.

• 2. Each remaining vertex $\pi (j)$, for $j = (r + 2),(r + 3),\ldots ,n$, is adjacent to (r + 1) vertices in the set $\{\pi (1),\pi (2),\ldots ,\pi (j - 1)\}$.

Theorem 1.7 (Alfakih et al [6]). 

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ , for some $n \geq r + 2$ , where G is an (r + 1)-lateration graph. Then there exists a positive semidefinite stress matrix S of G(p) of rank n − r − 1.

The proof of Theorem 1.7 is given in Sect. 1.4. The preceding theorems have been stated in terms of stress matrices. The same theorems can be equivalently stated in terms of Gale matrices, as will be shown in the next section.

2.2 Dimensional and Universal Rigidity in Terms of Gale Matrices

Let G(p) be a framework on n vertices in ${\mathbb{R}}^{r}$, $r \leq n - 2$, and let P be the configuration matrix of G(p). Then the following $(r + 1) \times n$ matrix

$$\mathcal{P} := \left [\begin{array}{c} {P}^{T} \\ {e}^{T} \end{array} \right ] = \left [\begin{array}{ccc} {p}^{1} & \ldots &{p}^{n} \\ 1 &\ldots & 1 \end{array} \right ]$$

(1.4)

has full row rank since ${p}^{1},\ldots ,{p}^{n}$ affinely span ${\mathbb{R}}^{r}$. Note that $r \leq n - 1$. Let

$$\bar{r} = the dimension of the null space of\ \mathcal{P},\ i.e.,\ \bar{r} = n - 1 - r.$$

(1.5)

Definition 1.1.

Suppose that the null space of $\mathcal{P}$ is nontrivial, i.e., $\bar{r} \geq 1$. Any $n \times \bar{ r}$ matrix Z whose columns form a basis of the null space of $\mathcal{P}$ is called a Gale matrix of configuration p (or framework G(p)). Furthermore, the ith row of Z, considered as a vector in ${\mathbb{R}}^{\bar{r}}$, is called a Gale transform of p ⁱ [13].

The Gale transform plays an important role in the theory of polytopes [17]. It follows from Lemma 1.1 and Eq. (1.2) that S is a stress matrix of G(p) if and only if

$$\mathcal{P}S = \mathbf{0},\ and\ {s}_{ij} = 0\ for all\ ij : i\neq j,(i,j)\not\in E(G).$$

(1.6)

Equivalently, S is a stress matrix of G(p) if and only if there exists an $\bar{r} \times \bar{ r}$ symmetric matrix $\Psi$ such that

$$S = Z\Psi {Z}^{T},\ and\ {s}_{ ij} ={ ({z}^{i})}^{T}\Psi {z}^{j} = 0\ for all\ ij : i\neq j,(i,j)\not\in E(G),$$

(1.7)

where ${({z}^{i})}^{T}$ is the ith row of Z. Therefore, the stress matrix $S = Z\Psi {Z}^{T}$ attains its maximum rank of $\bar{r} = n - 1 - r$ if and only if $\Psi$ is nonsingular, i.e., rank $\Psi =\bar{ r}$, since rank S = rank $\Psi$.

Then Theorems 1.2, 1.4, 1.5, and 1.6 can be stated in terms of Gale matrices as follows.

Theorem 1.8 (Alfakih [2]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ for some $r \leq n - 2$ , and let Z be a Gale matrix of G(p). If there exists a positive definite symmetric matrix $\Psi$ such that

$${({z}^{i})}^{T}\Psi {z}^{j} = 0\ for each\ ij : i\neq j,(i,j)\not\in E(G),$$

where ${({z}^{i})}^{T}$ is the ith row of Z, then G(p) is dimensionally rigid.

Theorem 1.9 (Connelly [9], Alfakih [4], Gortler and Thurston [15]). 

Let G(p) be a generic bar framework on n nodes in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . Let Z be a Gale matrix of G(p). Then G(p) is universally rigid if and only if there exists a positive definite symmetric matrix $\Psi$ such that

$${({z}^{i})}^{T}\Psi {z}^{j} = 0\ for each\ ij : i\neq j,(i,j)\not\in E(G),$$

where ${({z}^{i})}^{T}$ is the ith row of Z.

Theorem 1.10 (Alfakih and Ye [7]). 

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ , for some $r \leq n - 2$ . Let Z be a Gale matrix of G(p). Then G(p) is universally rigid if there exists a positive definite symmetric matrix $\Psi$ such that

$${({z}^{i})}^{T}\Psi {z}^{j} = 0\ for each\ ij : i\neq j,(i,j)\not\in E(G),$$

where ${({z}^{i})}^{T}$ is the ith row of Z.

3 Preliminaries

In this section we give the mathematical preliminaries needed for our proofs. In particular, we review some basic terminology and results concerning Euclidean distance matrices (EDMs) and affine motions.

3.1 Euclidean Distance Matrices

It is well known [11, 16, 20, 21] that a symmetric $n \times n$ matrix D whose diagonal entries are all zeros is EDM if and only if D is negative semidefinite on the subspace

$$M :=\{ x \in {\mathbb{R}}^{n} : {e}^{T}x = 0\},$$

where e is the vector of all 1’s.

Let V be the $n \times (n - 1)$ matrix whose columns form an orthonormal basis of M, i.e., V satisfies

$${V }^{T}e = \mathbf{0}\;,\;\;\;\;{V }^{T}V = {I}_{ n-1}\;.$$

(1.8)

Then the orthogonal projection on M, denoted by J, is given by $J := V {V }^{T} = {I}_{n} - e{e}^{T}/n$.

Recall that ${\mathcal{S}}_{n-1}$ denotes the subspace of symmetric matrices of order n − 1 and let ${\mathcal{S}}_{H} =\{ A \in {\mathcal{S}}_{n} : diag(A) = \mathbf{0}\}$. Consider the linear operator ${\mathcal{T}}_{V } : {\mathcal{S}}_{H} \rightarrow {\mathcal{S}}_{n-1}$ such that

$${\mathcal{T}}_{V }(D) := -\frac{1} {2}{V }^{T}DV,$$

(1.9)

Then we have the following lemma.

Lemma 1.2 ([5]). 

Let $D \in {\mathcal{S}}_{H}$ . Then D is a Euclidean distance matrix of embedding dimension r if and only if ${\mathcal{T}}_{V }(D) \succcurlyeq \mathbf{0}$ and rank ${\mathcal{T}}_{V }(D) = r$ .

Let ${\mathcal{K}}_{V } : {\mathcal{S}}_{n-1} \rightarrow {\mathcal{S}}_{H}$ defined by

$${\mathcal{K}}_{V }(X) := diag(V X{V }^{T})\,{e}^{T} + e\,{(diag(V X{V }^{T}))}^{T} - 2\,V X{V }^{T}.$$

(1.10)

Then it is not difficult to show that the operators ${\mathcal{T}}_{V }$ and ${\mathcal{K}}_{V }$ are mutually inverse [5]. Thus, Lemma 1.2 implies that D in ${\mathcal{S}}_{H}$ is an EDM of embedding dimension r if and only if $D = {\mathcal{K}}_{V }(X)$ for some positive semidefinite matrix X of rank r.

Lemma 1.2 is used in the following section to characterize the set of equivalent frameworks.

3.2 Characterizing Equivalent Bar Frameworks

Since all congruent frameworks have the same EDM (or equivalently, the same projected Gram matrix), in the rest of this chapter, we will identify congruent frameworks. Accordingly, for a given framework G(p), we assume without loss of generality that the centroid of the points ${p}^{1},\ldots ,{p}^{n}$ coincides with the origin, i.e., ${P}^{T}e = \mathbf{0}$, where P is the configuration matrix of G(p).

Let D = (d _ij ) be the EDM generated by framework G(p) in ${\mathbb{R}}^{r}$ and let P be the configuration matrix of G(p) defined in Eq. (1.3). Let $X = {\mathcal{T}}_{V }(D)$, or equivalently, $D = {\mathcal{K}}_{V }(X)$; and let B = PP ^T be the Gram matrix generated by the points ${p}^{1},\ldots ,{p}^{n}$. Clearly, B is positive semidefinite of rank r. Observe that

$$\begin{array}{rcl}{ d}_{ij} =& & \vert \vert {p}^{i} - {p}^{j}\vert {\vert }^{2} \\ =& &{ ({p}^{i})}^{T}{p}^{i} +{ ({p}^{j})}^{T}{p}^{j} - 2\;{({p}^{i})}^{T}{p}^{j} \\ =& & {(P{P}^{T})}_{ ii} + {(P{P}^{T})}_{ jj} - 2\;{(P{P}^{T})}_{ ij}\end{array}$$

Therefore,

$$D = diag(B){e}^{T} + e{(diag(B))}^{T} - 2B = {\mathcal{K}}_{ V }(X).$$

Hence,

$$B = V X{V }^{T},\ and\ X = {V }^{T}BV = {V }^{T}P{P}^{T}V.$$

(1.11)

Furthermore, matrix X is $(n - 1) \times (n - 1)$ positive semidefinite of rank r. Accordingly, X is called the projected Gram matrix of G(p).

Now let G(q) in ${\mathbb{R}}^{s}$ be a framework equivalent to G(p). Let D _q and D _p be the EDMs generated by G(q) and G(p), respectively. Then $H \circ {D}_{q} = H \circ {D}_{p}$ where H is the adjacency matrix of graph G. Thus,

$$H \circ ({D}_{q} - {D}_{p}) = H \circ {\mathcal{K}}_{V }({X}_{q} - {X}_{p}) = \mathbf{0},$$

(1.12)

where X _q and X _p are the projected Gram matrices of G(q) and G(p), respectively.

Let E ^ij be the $n \times n$ symmetric matrix with 1’s in the ijth and jith entries and zeros elsewhere. Further, let

$${M}^{ij} := {\mathcal{T}}_{ V }({E}^{ij}) = -\frac{1} {2}{V }^{T}{E}^{ij}V.$$

(1.13)

Then one can easily show that the set $\{{M}^{ij} : i\neq j,\;(i,j)\not\in E(G)\}$ forms a basis for the null space of $H \circ {\mathcal{K}}_{V }$. Hence, it follows from Eq. (1.12) that

$${X}_{q} - {X}_{p} ={ \sum \nolimits }_{ij:i\neq j,(i,j)\not\in E(G)}{y}_{ij}{M}^{ij},$$

(1.14)

for some scalars y _ij . Therefore, given a framework G(p) in ${\mathbb{R}}^{r}$, the set of projected Gram matrices of all frameworks G(q) that are equivalent to G(p) is given by

$$\{X : X = {X}_{p} +{ \sum \nolimits }_{ij:i\neq j,(i,j)\not\in E(G)}{y}_{ij}{M}^{ij} \succcurlyeq \mathbf{0}\}.$$

(1.15)

The following lemma establishes the connection between Gale matrices and projected Gram matrices.

Lemma 1.3 (Alfakih [1]). 

Let G(p) be a bar framework in ${\mathbb{R}}^{r}$ and let P and X be the configuration matrix and the projected Gram matrix of G(p), respectively. Further, let U and W be the matrices whose columns form orthonormal bases for the null space and the column space of X. Then

• 1. V U is a Gale matrix of G(p).

• 2. V W = PQ for some $r \times r$ nonsingular matrix Q.

Proof.

It follows from Eq. (1.11) that $XU = {V }^{T}P{P}^{T}V U = \mathbf{0}$. Thus ${P}^{T}V U = \mathbf{0}$. Hence, VU is a Gale matrix of G(p) since obviously ${e}^{T}V U = \mathbf{0}$.

Now, ${(V W)}^{T}V U = \mathbf{0}$. Thus VW = PQ for some matrix Q since ${P}^{T}e = \mathbf{0}$. Moreover, Q is nonsingular since rank PQ = r.

3.3 Affine Motions

Affine motions play an important role in the problem of universal rigidity of bar frameworks. An affine motion in ${\mathbb{R}}^{r}$ is a map $f : {\mathbb{R}}^{r} \rightarrow {\mathbb{R}}^{r}$ of the form

$$f({p}^{i}) = A{p}^{i} + b,$$

for all p ⁱ in ${\mathbb{R}}^{r}$, where A is an $r \times r$ matrix and b is an r-vector. A rigid motion is an affine motion where matrix A is orthogonal.

Vectors ${v}^{1},\ldots ,{v}^{m}$ in ${\mathbb{R}}^{r}$ are said to lie on a quadratic at infinity if there exists a nonzero symmetric $r \times r$ matrix $\Phi$ such that

$${({v}^{i})}^{T}\Phi {v}^{i} = 0,\ for all\ i = 1,\ldots ,m.$$

The following lemma establishes the connection between the notion of a quadratic at infinity and affine motions.

Lemma 1.4 (Connelly [10]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ . Then the following two conditions are equivalent:

• 1. There exists a bar framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

• 2. The vectors ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ lie on a quadratic at infinity.

Proof.

Suppose that there exists a framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p); and let ${q}^{i} = A{p}^{i} + b$ for all $i = 1,\ldots ,n$. Then ${({q}^{i} - {q}^{j})}^{T}({q}^{i} - {q}^{j})$ = ${({p}^{i} - {p}^{j})}^{T}{A}^{T}A({p}^{i} - {p}^{j})$ = ${({p}^{i} - {p}^{j})}^{T}({p}^{i} - {p}^{j})$ for all $(i,j) \in E(G)$. Note that matrix A is not orthogonal since G(q) and G(p) are not congruent. Therefore, ${({p}^{i} - {p}^{j})}^{T}\Phi ({p}^{i} - {p}^{j}) =$ 0 for all $(i,j) \in E(G)$, where $\Phi = {I}_{r} - {A}^{T}A$ is a nonzero symmetric matrix.

On the other hand, suppose that there exists a nonzero symmetric matrix $\Phi$ such that ${({p}^{i} - {p}^{j})}^{T}\Phi ({p}^{i} - {p}^{j}) = 0$, for all $(i,j) \in E(G)$. Then ${I}_{r} - \delta \Phi \succ \mathbf{0}$ for sufficiently small $\delta$. Hence, there exists a matrix A such that ${I}_{r} - \delta \Phi = {A}^{T}A$. Note that matrix A is not orthogonal since $\Phi$ is nonzero. Thus, ${({p}^{i} - {p}^{j})}^{T}({I}_{r} - {A}^{T}A)({p}^{i} - {p}^{j}) = 0$ for all $(i,j) \in E(G)$. Therefore, there exists a framework G(q) in ${\mathbb{R}}^{r}$ that is equivalent to G(q), where ${q}^{i} = A{p}^{i}$ for all $i = 1,\ldots ,n$. Furthermore, G(q) is not congruent to G(p) since A is not orthogonal.

Note that Condition 2 in Lemma 1.4 is expressed in terms of the edges of G. An equivalent condition in terms of the missing edges of G can also be obtained using Gale matrices. To this end, let $\bar{m}$ be the number of missing edges of graph G and let y = (y _ij ) be a vector in ${\mathbb{R}}^{\bar{m}}$. Let $\mathcal{E}(y)$ be the $n \times n$ symmetric matrix whose ijth entry is given by

$$\mathcal{E}{(y)}_{ij} = \left \{\begin{array}{cl} {y}_{ij}&\ if\ i\neq j\ and\ (i,j)\not\in E(G),\\ 0 &\ Otherwise. \end{array} \right.$$

(1.16)

Then we have the following result.

Lemma 1.5 (Alfakih [4]). 

Let G(p) be a bar framework on n vertices in ${\mathbb{R}}^{r}$ and let Z be any Gale matrix of G(p). Then the following two conditions are equivalent:

• 1. The vectors ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ lie on a quadratic at infinity.

• 2. There exists a nonzero $y = ({y}_{ij}) \in {\mathbb{R}}^{\bar{m}}$ such that:

  $${V }^{T}\mathcal{E}(y)Z = \mathbf{0},$$

  (1.17)

  where V is defined in Eq. (1.8).

Proof.

Let P be the configuration matrix of G(p), and let U and W be the matrices whose columns form orthonormal bases for the null space and the column space of X, the projected Gram matrix of G(p). Then by Lemma 1.3 we have

$$\begin{array}{rcl}{ ({p}^{i} - {p}^{j})}^{T}\Phi ({p}^{i} - {p}^{j})& & ={ ({p}^{i})}^{T}\Phi {p}^{i} +{ ({p}^{j})}^{T}\Phi {p}^{j} - 2{({p}^{i})}^{T}\Phi {p}^{j} \\ & & = {(P\Phi {P}^{T})}_{ ii} + {(P\Phi {P}^{T})}_{ jj} - 2{(P\Phi {P}^{T})}_{ ij} \\ & & = {(V W\Phi {^\prime}{W}^{T}{V }^{T})}_{ ii} + {(V W\Phi {^\prime}{W}^{T}{V }^{T})}_{ jj} - 2{(V W\Phi {^\prime}{W}^{T}{V }^{T})}_{ ij} \\ & & = {\mathcal{K}}_{V }{(W\Phi {^\prime}{W}^{T})}_{ ij}, \\ \end{array}$$

where $\Phi {^\prime} = Q\Phi {Q}^{T}$ for some nonsingular matrix Q, and where ${\mathcal{K}}_{V }$ is defined in Eq. (1.10).

Therefore, ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ lie on a quadratic at infinity if and only if there exists a nonzero matrix $\Phi {^\prime}$ such that $H \circ {\mathcal{K}}_{V }(W\Phi {^\prime}{W}^{T}) = \mathbf{0}$. But since the set $\{{M}^{ij} : i\neq j,(i,j)\not\in E(G)\}$ forms a basis for the null space of $H \circ {\mathcal{K}}_{V }$, it follows that vectors ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ lie on a quadratic at infinity if and only if there exists a nonzero $r \times r$ matrix $\Phi {^\prime}$ and a nonzero y = (y _ij ) in ${\mathbb{R}}^{\bar{m}}$ such that

$$W\Phi {^\prime}{W}^{T} ={ \sum \nolimits }_{ij:i\neq j,(i,j)\not\in E(G)}{y}_{ij}{M}^{ij} = -\frac{1} {2}{\sum \nolimits }_{ij:i\neq j,(i,j)\not\in E(G)}{y}_{ij}{V }^{T}{E}^{ij}V = -\frac{1} {2}{V }^{T}\mathcal{E}(y)V.$$

(1.18)

Next we show that Eq. (1.18) is equivalent to Eq. (1.17). Suppose there exists a nonzero y that satisfies Eq. (1.18). Then by multiplying Eq. (1.18) from the right by U we have that y also satisfies Eq. (1.17). Now suppose that there exists a nonzero y that satisfies Eq. (1.17). Then

$$\begin{array}{rcl}{ V }^{T}\mathcal{E}(y)V & =& [W\,U]\left [\begin{array}{c} {W}^{T} \\ {U}^{T} \end{array} \right ]{V }^{T}\mathcal{E}(y)V \;[W\,U]\left [\begin{array}{c} {W}^{T} \\ {U}^{T} \end{array} \right ], \\ & =& [W\,U]\left [\begin{array}{cc} - 2\Phi {^\prime}&0\\ 0 &0 \end{array} \right ]\left [\begin{array}{c} {W}^{T} \\ {U}^{T} \end{array} \right ], \\ & =& -2W\Phi {^\prime}{W}^{T}\end{array}$$

Thus y also satisfies Eq. (1.18) and the result follows.

3.4 Miscellaneous Lemmas

We conclude this section with the following lemmas that will be needed in our proofs. We begin with the following well-known Farkas lemma on the cone of positive semidefinite matrices.

Lemma 1.6.

Let ${A}^{1},\ldots ,{A}^{k}$ be given $n \times n$ symmetric matrices. Then exactly one of the following two statements hold:

• 1. There exists $Y \succ \mathbf{0}$ such that trace (A ⁱ Y ) = 0 for all $i = 1,\ldots ,k$ .

• 2. There exists $x = ({x}_{i}) \in {\mathbb{R}}^{k}$ such that ${x}_{1}{A}^{1} + \cdots + {x}_{k}{A}^{k} \succcurlyeq \mathbf{0},\neq \mathbf{0}$ .

Proof.

Assume that statement 1 does not hold, and let

$$\mathcal{L} =\{ Y \in {\mathcal{S}}_{n} :\mathrm{ trace}({A}^{i}Y ) = 0,\ for all\ i = 1,\ldots ,k\}.$$

Then the subspace $\mathcal{L}$ is disjoint from the interior of the cone of $n \times n$ positive semidefinite matrices. By the separation theorem [19, page 96], there exists a nonzero symmetric matrix $\Theta$ such that $\mathrm{trace}(\Theta Y ) = 0$ for all $Y \in \mathcal{L}$ and $\mathrm{trace}(\Theta C) \geq 0$ for all $C \succ \mathbf{0}$. Therefore, $\Theta \succcurlyeq \mathbf{0}$ and $\Theta ={ \sum \nolimits }_{i=1}^{k}\,{x}_{i}{A}^{i}$ for some nonzero $x = ({x}_{i}) \in {\mathbb{R}}^{k}$. Hence, statement 2 holds.

Now assume that statements 1 and 2 hold and let $\Theta = {x}_{1}{A}^{1} + \cdots + {x}_{k}{A}^{k}$. Then on one hand, trace $(\Theta Y ) > 0$; and on the other hand trace ($\Theta Y ) =$ ${\sum \nolimits }_{i=1}^{k}{x}_{i}\mathrm{trace}({A}^{i}Y ) = 0$, a contradiction. Hence, the result follows.

The following lemma shows that Gale matrices have a useful property under the general position assumption.

Lemma 1.7.

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ and let Z be any Gale matrix of G(p). Then any $\bar{r} \times \bar{ r}$ sub-matrix of Z is nonsingular.

Proof.

Assume $\bar{r} \leq r$. The proof of the case where $\bar{r} \geq r + 1$ is similar. Let Z′ be any $\bar{r} \times \bar{ r}$ sub-matrix of Z, and without loss of generality, assume that it is the sub-matrix defined by the rows $\bar{r} + 1,\bar{r} + 2,\ldots ,2\bar{r}$. Then, Z′ is singular if and only if there exists a nonzero $\xi \in {\mathfrak{R}}^{\bar{r}}$ such that $Z{^\prime}\xi = \mathbf{0}$. Clearly, $Z\xi$ is in the null space of $\mathcal{P}$. Furthermore, $Z{^\prime}\xi = \mathbf{0}$ if and only if the components ${(Z\xi )}_{\bar{r}+1}$ = ${(Z\xi )}_{\bar{r}+2}$ = $\ldots$ = ${(Z\xi )}_{2\bar{r}} = \mathbf{0}$. Now since $Z\xi \neq \mathbf{0}$, this last statement holds if and only if the following r + 1 points ${p}^{1},{p}^{2},\ldots ,{p}^{\bar{r}},{p}^{2\bar{r}+1},\ldots ,{p}^{n}$ are affinely dependent, i.e., G(p) is not in general position.

4 Proofs

In this section we present the proofs of the theorems stated in Sect. 1.2.

4.1 Proof of Theorem 1.1

Let G(p) be a given framework on n vertices in ${\mathbb{R}}^{r}$ for some $r \leq n - 2$. Clearly, if G(p) is universally rigid, then G(p) is dimensionally rigid, and there does not exist a framework G(p) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

To prove the other direction, let X _p be the projected Gram matrix of G(p). Let Q = [W U] be the orthogonal matrix whose columns are the eigenvectors of X _p , where the columns of U form an orthonormal basis for the null space of X _p .

Now suppose that G(p) is not universally rigid. Then there exists a framework G(q) in ${\mathbb{R}}^{s}$, which is equivalent, but not congruent, to G(p), for some s: $1 \leq s \leq n - 1$. Therefore, there exists a nonzero $\hat{y}$ in ${\mathbb{R}}^{\bar{m}}$ such that $X(\hat{y}) = {X}_{p} + \mathcal{M}(\hat{y}) \succcurlyeq \mathbf{0}$ where $\mathcal{M}(\hat{y}) ={ \sum \nolimits }_{(i,j)\not\in E}\hat{{y}}_{ij}{M}^{ij}$. Now for a sufficiently small positive scalar $\delta$ we have¹

$$X(t\hat{y}) = {X}_{p} + \mathcal{M}(t\hat{y}) \succcurlyeq \mathbf{0},\ and\ rank(X(t\hat{y})) = rank({X}_{p} + \mathcal{M}(t\hat{y})) \geq r,$$

for all $t : 0 \leq t \leq \delta$. But

$${Q}^{T}({X}_{ p}+\mathcal{M}(t\hat{y}))Q = \left [\begin{array}{rcc} \Lambda + t{W}^{T}\mathcal{M}(\hat{y})W &&t{W}^{T}\mathcal{M}(\hat{y})U \\ t{U}^{T}\mathcal{M}(\hat{y})W && t{U}^{T}\mathcal{M}(\hat{y})U \end{array} \right ] \succcurlyeq \mathbf{0},$$

where $\Lambda$ is the $r \times r$ diagonal matrix consisting of the positive eigenvalues of X _p . Thus ${U}^{T}\mathcal{M}(\hat{y})\,U \succcurlyeq \mathbf{0}$ and the null space of ${U}^{T}\mathcal{M}(\hat{y})\,U \subseteq$ the null space of ${W}^{T}\mathcal{M}(\hat{y})\,U$.

Therefore, if rank ($X({t}_{0}\hat{y})) \geq r + 1$ for some $0 < {t}_{0} \leq \delta$ we have a contradiction since G(p) is dimensionally rigid. Hence, rank ($X(t\hat{y})) = r$ for all $t : 0 \leq t \leq \delta$. Thus, both matrices ${U}^{T}\mathcal{M}(\hat{y})U$ and ${W}^{T}\mathcal{M}(\hat{y})U$ must be zero. This implies that $\mathcal{M}(\hat{y})U = \mathbf{0}$, i.e., ${V }^{T}\mathcal{E}(\hat{y})Z = \mathbf{0}$ which is also a contradiction by Lemma 1.5. Therefore, G(p) is universally rigid. □ 

4.2 Proof of Theorem 1.2

Let G(p) be a given framework on n vertices in ${\mathbb{R}}^{r}$ for some $r \leq n - 2$ and let Z be a Gale matrix of G(p). Let X _p be the projected Gram matrix of G(p), and let Q = [W U] be the orthogonal matrix whose columns are the eigenvectors of X _p , where the columns of U form an orthonormal basis for the null space of X _p .

Assume that G(p) admits a positive semidefinite stress matrix S of rank n − r − 1. Therefore, there exists a positive definite symmetric matrix $\Psi$ such that ${({z}^{i})}^{T}\Psi {z}^{j} = 0$ for all $ij : i\neq j,(i,j)\not\in E(G)$. Hence, by lemma 1.6, there does not exist $y = ({y}_{ij}) \in {\mathbb{R}}^{\bar{m}}$ such that ${\sum \nolimits }_{ij:i\neq j,(i,j)\not\in E(G)}{y}_{ij}({z}^{i}{({z}^{j})}^{T} + {z}^{j}{({z}^{i})}^{T})$ is a non zero positive semidefinite matrix. But ${z}^{i}{({z}^{j})}^{T} + {z}^{j}{({z}^{i})}^{T}$ = ${Z}^{T}{E}^{ij}Z$. Thus, there does not exist $y = ({y}_{ij}) \in {\mathbb{R}}^{\bar{m}}$ such that ${Z}^{T}\mathcal{E}(y)Z$ is a nonzero positive semidefinite matrix. Hence, there does not exist $y = ({y}_{ij}) \in {\mathbb{R}}^{\bar{m}}$ such that ${U}^{T}\mathcal{M}(y)U$ is a nonzero positive semidefinite matrix.

Now assume that G(p) is not dimensionally rigid, then there exists a nonzero y such that $X = {X}_{p} + \mathcal{M}(y) \succcurlyeq \mathbf{0}$ and rank $X \geq r + 1$. But

$${Q}^{T}({X}_{ p}+\mathcal{M}(y))Q = \left [\begin{array}{rcc} \Lambda + {W}^{T}\mathcal{M}(y)W &&{W}^{T}\mathcal{M}(y)U \\ {U}^{T}\mathcal{M}(y)W && {U}^{T}\mathcal{M}(y)U \end{array} \right ] \succcurlyeq \mathbf{0}.$$

Since $\Lambda + {W}^{T}\mathcal{M}(y)W$ is $r \times r$, it follows that ${U}^{T}\mathcal{M}(y)U$ is a nonzero positive semidefinite, a contradiction. □ 

4.3 Proof of Theorem 1.4

We begin with the following lemma.

Lemma 1.8 (Connelly [10]). 

Let G(p) be a generic bar framework on n vertices in ${\mathbb{R}}^{r}$ . Assume that each node of G has degree at least r. Then the vectors ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ do not lie on a quadratic at infinity.

Now let G(p) be a generic bar framework on n vertices in ${\mathbb{R}}^{r}$. If G(p) admits a positive semidefinite stress matrix of rank n − r − 1, then each vertex of G has degree at least r + 1 [2, Theorem 3.2]. Thus Theorem 1.4 follows from Lemmas 1.4 and 1.8 and Theorem 1.3.

4.4 Proof of Theorem 1.6

The main idea of the proof is to show that Condition 2 of Lemma 1.5 does not hold under the assumptions of the theorem. The choice of the particular Gale matrix to be used in Eq. (1.17) is critical in this regard. The proof presented here is that given in [7].

Let $\bar{N}(i)$ denote the set of nodes of graph G that are nonadjacent to node i, i.e.,

$$\bar{N}(i) =\{ j \in V (G) : j\neq i\ and\ (i,j)\not\in E(G)\}.$$

(1.19)

Lemma 1.9.

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ , $r \leq n - 2$ . Assume that G(p) has a stress matrix S of rank n − 1 − r. Then there exists a Gale matrix $\hat{Z}$ of G(p) such that $\hat{{z}}_{ij} = 0$ for all $j = 1,\ldots ,\bar{r}$ and $i \in \bar{ N}(j + r + 1)$ .

Proof.

Let G(p) be in general position in ${\mathbb{R}}^{r}$ and assume that it has a stress matrix S of rank $\bar{r} = (n - 1 - r)$. Let Z be any Gale matrix of G(p), then it follows from Eq. (1.7) that $S = Z\Psi {Z}^{T}$ for some nonsingular symmetric $\bar{r} \times \bar{ r}$ matrix $\Psi$. Let us write Z as:

$$Z = \left [\begin{array}{c} {Z}_{1} \\ {Z}_{2} \end{array} \right ],$$

where Z ₂ is $\bar{r} \times \bar{ r}$. Then it follows from Lemma  1.7 that Z ₂ is nonsingular. Now let

$$\hat{Z} = (\hat{{z}}_{ij}) = Z\Psi {{Z}_{2}}^{T}.$$

(1.20)

Then $\hat{Z}$ is a Gale matrix of G(p) since both $\Psi$ and Z ₂ are nonsingular. Furthermore,

$$S = Z\Psi {Z}^{T} = Z\Psi \,[{Z}_{ 1}^{T}\;\;{Z}_{ 2}^{T}] = [Z\Psi {Z}_{ 1}^{T}\;\;\hat{Z}].$$

In other words, $\hat{Z}$ consists of the last $\bar{r}$ columns of S. Thus $\hat{{z}}_{ij} = {s}_{i,j+r+1}$. It follows by the definition of S that s _{i, j + r + 1} = 0 for all i, j such that $i\neq (j + r + 1)$ and $(i,j + r + 1)\not\in E(G)$. Therefore, $\hat{{z}}_{ij} = 0$ for all $j = 1,\ldots ,\bar{r}$ and $i \in \bar{ N}(j + r + 1)$.

Lemma 1.10.

Let the Gale matrix in Eq. (1.17) be $\hat{Z}$ as defined in Eq. (1.20). Then the system of Eq. (1.17) is equivalent to the system of equations

$$\mathcal{E}(y)\hat{Z} = \mathbf{0}.$$

(1.21)

Proof.

System of Eq. (1.17) is equivalent to the following system of equations in the unknowns, y _ij ($i\neq j$ and $(i,j)\not\in E(G)$) and $\xi = ({\xi }_{j}) \in {\mathbb{R}}^{\bar{r}}$:

$$\mathcal{E}(y)\hat{Z} = e\,{\xi }^{T}.$$

(1.22)

Now for $j = 1,\ldots ,\bar{r}$, we have that the (j + r + 1, j)th entry of $\mathcal{E}(y)\hat{Z}$ is equal to ${\xi }_{j}$. But using Eq. (1.16) and Lemma 1.9 we have

$${(\mathcal{E}(y)\hat{Z})}_{j+r+1,j} ={ \sum \nolimits }_{i=1}^{n}\mathcal{E}{(y)}_{ j+r+1,i}\;\hat{{z}}_{ij} ={ \sum \nolimits }_{i:i\in \bar{N}(j+r+1)}{y}_{j+r+1,i}\;\hat{{z}}_{ij} = 0.$$

Thus, $\xi = 0$ and the result follows.

Lemma 1.11.

Let G(p) be a bar framework on n nodes in general position in ${\mathbb{R}}^{r}$ , $r \leq n - 2$ . Assume that G(p) has a positive semidefinite stress matrix S of rank $\bar{r} = n - 1 - r$ . Then there does not exist a framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

Proof.

Under the assumption of the lemma, we have that deg$(i) \geq r + 1$ for all $i \in V (G)$, i.e., every node of G is adjacent to at least r + 1 nodes (for a proof see [2, Theorem 3.2]). Thus

$$\vert \bar{N}(i)\vert \leq n - r - 2 =\bar{ r} - 1\ for all\ i \in V (G).$$

(1.23)

Furthermore, it follows from Lemmas 1.9, 1.10, and 1.5 that the vectors ${p}^{i} - {p}^{j}$ for all $(i,j) \in E(G)$ lie on a quadratic at infinity if and only if system of Eq. (1.21) has a nonzero solution y. But Eq. (1.21) can be written as

$${\sum \nolimits }_{j:\in \bar{N}(i)}{y}_{ij}\hat{{z}}^{j} = 0,\ for\ i = 1,\ldots ,n,$$

where ${(\hat{{z}}^{i})}^{T}$ is the ith row of $\hat{Z}$. Now it follows from Eq. (1.23) that y _ij  = 0 for all $(i,j)\not\in E(G)$ since by Lemma 1.7 any subset of $\{\hat{{z}}^{1},\ldots ,\hat{{z}}^{n}\}$ of cardinality $\leq \bar{ r} - 1$ is linearly independent.

Thus system (1.21) does not have a nonzero solution y. Hence the vectors ${p}^{i} - {p}^{j}$, for all $(i,j) \in E(G)$, do not lie on a quadratic at infinity. Therefore, by Lemma 1.4, there does not exist a framework G(q) in ${\mathbb{R}}^{r}$ that is affinely equivalent, but not congruent, to G(p).

Thus, Theorem 1.6 follows from Lemma 1.11 and Theorem 1.3.

4.5 Proof of Theorem 1.7

The proof of Theorem 1.7 is constructive, i.e., an algorithm is presented to construct the desired stress matrix. The proof presented here is a slight modification of that given in [6].

Let G(p) be a framework on n vertices in general position in ${\mathbb{R}}^{r}$, $n \geq r + 2$, and let Z be a Gale matrix of G(p). An $n \times n$ symmetric matrix S that satisfies

$$\mathcal{P}S = 0,\ or equivalently\ S = Z\Psi {Z}^{T}\ for some symmetric matrix\ \Psi ,$$

is called a prestress matrix, where $\mathcal{P}$ is defined in Eq. (1.4). Thus, it follows from Eqs. (1.6) and (1.7) that S is a stress matrix of G(p) if and only if S is a prestress matrix and s _ij  = 0 for all $ij : i\neq j$, $(i,j)\not\in E(G)$.

Clearly, ${S}^{n} = Z{Z}^{T}$ is a positive semidefinite prestress matrix of rank $\bar{r} = n - r - 1$. If S ⁿ satisfies ${s}_{ij}^{n} = 0$ for all $ij : i\neq j$, $(i,j)\not\in E(G)$, then we are done since S ⁿ is the desired stress matrix. Otherwise, if S ⁿ is not a stress matrix, we need to zero out the entries which should be zero but are not, i.e., the entries ${s}_{ij}^{n}\neq 0$, $i\neq j$ and $(i,j)\not\in E(G)$. We do this in reverse order by column (row); first, we zero out the entries ${s}_{in}^{n}\neq 0$, for i < n and $(i,n)\not\in E(G)$, and then do the same for columns (rows) $(n - 1),(n - 2),\ldots ,(r + 3)$. This “purification” process will keep the pre-stress matrix positive semidefinite and maintain rank n − r − 1.

Let G be an (r + 1)-lateration graph with lateration order $1,2,\ldots ,n$, i.e., the vertices, $1,2,\ldots ,r + 2$, induce a clique in G, and each remaining vertex k, for $k = r + 3,\ldots ,n$, is adjacent to (r + 1) vertices in the set $\{1,2,\ldots ,k - 1\}$. Let

$$\bar{N}{^\prime}(k) =\{ i \in V (G) : i < k\ and\ (i,k)\not\in E(G)\}.$$

(1.24)

Then for $k = r + 3,\ldots ,n$,

$$\vert \bar{N}{^\prime}(k)\vert = k - r - 2.$$

(1.25)

We first show how to purify the last column (or row) of ${S}^{n} = Z{Z}^{T}$. Let Z ⁿ denote the sub-matrix of Z obtained by keeping only rows with indices in $\bar{N}{^\prime}(n) \cup \{ n\}$. Then Z ⁿ is a square matrix of order $\bar{r} = n - r - 1$. Furthermore, by Lemma 1.7, it follows that Z ⁿ is nonsingular. Let b ⁿ denote the vector in ${\mathbb{R}}^{\bar{r}}$ such that

$${b}_{i}^{n} = \left \{\begin{array}{cl} - {s}_{in}^{n}&\quad if\ i \in \bar{ N}{^\prime}(n), \\ 1 &\quad if\ i = n. \end{array} \right.$$

Now let ${\xi }_{n} \in {\mathbb{R}}^{\bar{r}}$ be the unique solution of the system of equations

$${Z}^{n}{\xi }_{ n} = {b}^{n}.$$

Lemma 1.12.

Let ${S}^{n-1} = {S}^{n} + Z\,{\xi }_{n}{{\xi }_{n}}^{T}{Z}^{T} = Z(I + {\xi }_{n}{{\xi }_{n}}^{T}){Z}^{T}$ . Then

• 1. S ⁿ⁻¹ is a prestress matrix of G(p), i.e., $\mathcal{P}{S}^{n-1} = 0$ .

• 2. ${S}^{n-1} \succcurlyeq \mathbf{0}$ and the rank of S ⁿ⁻¹ remains n − r − 1.

• 3. ${s}_{in}^{n-1} = 0$ for all $i : i < n,\ (i,n)\not\in E(G)$ .

Proof.

The first statement is obvious. The second statement follows since $I + {\xi }_{n}{\xi }_{n}^{T} \succ \mathbf{0}$. The third statement is also true by construction. For all $i < n,\ (i,n)\not\in E(G)$, i.e., for all $i \in \bar{ N}{^\prime}(n)$, we have ${s}_{in}^{n-1} = {s}_{in}^{n} + {b}_{i}^{n}{b}_{n}^{n} = {s}_{in}^{n} - {s}_{in}^{n} = 0$.

We continue this purification process for columns $(n - 1),\ldots ,k,\ldots ,(r + 3)$. Before the kth purification step, we have ${S}^{k} \succcurlyeq \mathbf{0}$, $\mathcal{P}{S}^{k} = 0$, rank S ^k = n − r − 1, and

$${s}_{ij}^{k} = 0,\ for all\ ij : i\neq j,\;(i,j)\not\in E(G),\ and for all\ j = k + 1,\ldots ,n.$$

Let Z ^k denote the sub-matrix of Z obtained by keeping only rows with indices in $\bar{N}{^\prime}(k) \cup \{ k,k + 1,\ldots ,n\}$. Then Z ^k is a square matrix of order $\bar{r} = n - r - 1$. Furthermore, by Lemma 1.7, it follows that Z ^k is nonsingular. Let b ^k denote the vector in ${\mathbb{R}}^{\bar{r}}$ such that

$${b}_{i}^{k} = \left \{\begin{array}{cl} - {s}_{ik}^{k}&\quad if\ i \in \bar{ N}{^\prime}(k), \\ 1 &\quad if\ i = k, \\ 0 &\quad if\ i = k + 1,\ldots ,n. \end{array} \right.$$

Now let ${\xi }_{k} \in {\mathbb{R}}^{\bar{r}}$ be the unique solution of the system of equations

$${Z}^{k}{\xi }_{ k} = {b}^{k}.$$

The following lemma shows results analogous to those in Lemma 1.12, for the remaining columns.

Lemma 1.13.

Let ${S}^{k-1} = {S}^{k} + Z\,{\xi }_{k}{\xi }_{k}^{T}{Z}^{T}$ . Then

• 1. S ^k−1 is a prestress matrix of G(p), i.e., $\mathcal{P}{S}^{k-1} = 0$ .

• 2. ${S}^{k-1} \succcurlyeq \mathbf{0}$ and the rank of S ^k−1 remains n − r − 1.

• 3. ${s}_{ij}^{k-1} = 0$ for all $i : i < j,\;(i,j)\not\in E(G)$ and for all $j = k,\ldots ,n$ .

Proof.

The proof of the first two statements is identical to that in Lemma 1.12. The third statement is again true by construction. For each $i < k,\ (i,k)\not\in E(G)$, i.e., for all $i \in \bar{ N}{^\prime}(k)$, we have

$${s}_{ik}^{k-1} = {s}_{ ik}^{k} + {b}_{ i}^{k}{b}_{ k}^{k} = {s}_{ ik}^{k} - {s}_{ ik}^{k} = 0.$$

Furthermore, for $j = k + 1,\ldots ,n$, the jth column (or row) of $Z\,{\xi }_{k}{\xi }_{k}^{T}{Z}^{T}$ has all zero entries, which means that the entries in the jth column (or row) of S ^k − 1 remain unchanged from S ^k.

4.6 Now we are ready to prove Theorem 1.7

The matrix

$${S}^{r+2} = {S}^{r+3} + Z\,{\xi }_{ r+3}{\xi }_{r+3}^{T}{Z}^{T} = Z(I + {\xi }_{ n}{\xi }_{n}^{T} + \cdots + {\xi }_{ r+3}{\xi }_{r+3}^{T}){Z}^{T},$$

obtained at the “(r + 3)th” step of the above process, is by Lemmas 1.12 and 1.13 a positive semidefinite prestress matrix of rank n − r − 1. Furthermore, ${s}_{ij}^{r+2} = 0$ for all $ij : i\neq j,\;(i,j)\not\in E(G)$ and for all $j = r + 3,r + 4,\ldots ,n$. But since the vertices $1,2,\ldots ,r + 2$ induce a clique in G, it follows that

$${s}_{ij}^{r+2} = 0\ for all\ ij : i\neq j,\;(i,j)\not\in E(G).$$

Hence, S = S ^r + 2 is a positive semidefinite stress matrix of G(p) of rank n − r − 1, i.e., S ^r + 2 is the desired stress matrix.