1 Introduction

Passive isolation techniques using linear vibration isolators are widely and effectively used in the industry for solving various vibration-related problems, a very common one of which is the protection of sensitive measurement devices from vibratory environment. There is, however, a particular limitation of the performance of the passive linear isolation systems, which is static deflection caused by the weight of the payload. Decreasing the natural frequency of the vibration isolation system, which can be achieved by means of softer isolators, extends the isolation frequency range. However, due to the limitation of the maximum static deflection in the design of vibration isolation systems, it is not possible to decrease the stiffness of the isolators below a certain value, which adversely affects isolation performance. As a remedy for this trade-off in the isolation performance, passive nonlinear isolators containing high-static-low-dynamic stiffness are utilized [1,2,3,4,5,6,7,8]. These nonlinear isolators provide ultra-low frequency isolation with the smaller static deflections compared to similar linear isolators. If parameters are chosen carefully, one can obtain even quasi-zero stiffness around the equilibrium of the system [9].

There are a variety of studies to obtain the quasi-zero stiffness (QZS) character by utilizing elastic and magnetic elements. These methods are reviewed by Ibrahim [3] in his review of passive vibration isolation methods. The most common method is integrating pre-compressed linear springs to the system horizontally. Liu et al. [10] obtained this horizontal stiffness by means of buckled Euler beams; whereas, Wu et al. [4] obtained similar nonlinear stiffness characteristic by means of magnetic springs. Recently, a similar nonlinear magnetic isolator possessing high-static-low-dynamic behavior is studied experimentally by Yan et al. [11]. Zhou et al. [12] conducted experimental and theoretical research on QZS vibration isolator and obtained QZS characteristics using cam-roller mechanisms. Sun and Jing [13] proposed a scissor-like structure to obtain high-static-low-dynamic stiffness. Although the aforementioned nonlinear QZS elements widen the isolation region (frequency range), their response is highly nonlinear and input dependent which presents challenges in design, modeling, and analysis of the isolation system performance. Carrella et al. [9] analyzed a negative stiffness mechanism and obtained an approximate expression of the nonlinear stiffness force around the equilibrium position utilizing Taylor Series. This analysis reveals that the nonlinear equation of motion contains cubic nonlinearity. Therefore, equivalent stiffness is highly dependent on excitation levels and unless excitation levels are well defined, even worse performance than the linear vibration isolator systems can be obtained by using QZS isolation systems. Another issue is the bifurcation of the system to chaotic motions where non-periodic solutions may occur depending on excitation amplitude and frequency, which may be a disadvantage for an isolation system [12].

Another important design parameter which affects the isolation performance is damping in the QZS element, since resonance response depends on the damping characteristic of the mechanical system. Although the highly nonlinear response of QZS isolator systems can be limited by increasing linear damping in the QZS element, it adversely affects the performance of the isolation system away from the resonance frequency [14,15,16]. Therefore, it can be concluded that a more favorable damping characteristic is the one that should be effective only in the resonance regions. Jing and Lang [17] and Xiao et al. [18] state that this type of damping characteristic can be obtained through a geometrically nonlinear damping mechanism. A combination of the QZS isolators and geometrically nonlinear damping is studied by Cheng et al. [19] and Dong et al. [7]. It is observed in these studies that highly nonlinear dynamics of the QZS isolator can be limited by introducing nonlinear damping.

Dry friction damping is a potential candidate for enhancing the damping characteristic of QZS isolator systems. It is a nonlinear damping mechanism used for vibration control in mechanical systems [20] such as gas turbine engines [21,22,23], large space structures [24] and railway bogies [25, 26]. In this paper, a QZS mechanism coupled with a dry friction damper is proposed in order to overcome these shortcomings of the nonlinear QZS isolators. Such a combination provides low frequency isolation, at a relatively high loading capacity and effective isolation in a larger excitation range due to the nonlinear stick–slip behavior of the dry friction damper. Furthermore, since dry friction damping is only effective at large relative displacements, i.e., around the resonance region, the negative effect of damping in the isolation region is eliminated. In the following parts of the paper, the nonlinear stiffness and damping models of the proposed isolator are introduced. Performance of the QZS vibration isolator coupled with a dry friction damper is investigated under base excitation by utilizing a single term harmonic balance method (HBM). Stability of the steady-state solutions is studied by utilizing Hill’s Method. Isolation performance of isolation system having a QZS dry friction element is compared with the one having QZS element, i.e., no friction damping, and the effect of slip force on the isolation performance is investigated.

2 Mathematical development

2.1 Quasi-zero stiffness model

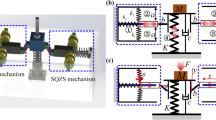
The stiffness properties of the QZS mechanism shown in Fig. 1a are studied in detail by Carrella et al. [9]. Pre-compressed spring which is hinged at both ends is placed horizontally. This spring is called as the “negative stiffness”, since it provides force in the direction of the motion. Although all the components are linear, the isolator is nonlinear because of the isolator geometry.

Fig. 1
figure 1

a Schematic diagram of QZS vibration isolation system, b free-body diagram of the mass suspended on QZS vibration isolation system

Full size image

In the equilibrium position, the vertical component of the compressed spring is zero. kh, \( k_{v} \) are the horizontal and vertical spring stiffnesses, respectively, and \( c_{v} \) is the viscous damping coefficient. The distance between the two ends of the horizontal spring is designated by \( y\left( t \right) \); whereas, the free length of the horizontal spring is \( L_{o} \). The length of the horizontal spring at the equilibrium point is \( a \), the vertical displacement of the mass is \( x\left( t \right) \), and \( g \) is the gravitational acceleration. The free body diagram of the mass for the static loadings can be seen in Fig. 1b.

When loading, i.e., \( f_{k} \) is applied to the mass, it will deflect from its equilibrium point which is defined as \( x \). The vertical force component of the horizontal spring can be found as follows [14]

$$ f_{v} = f\sin \theta = k_{h} \left( {L_{o} - y} \right)\frac{x}{{\sqrt {x^{2} + a^{2} } }}, $$
(1)

where \( f_{v} \) is the vertical component of the force exerted by the horizontal spring, \( \theta \) is the angle between the horizontal spring force vector and horizontal axis. The relationship between the vertical displacement of the mass and the distance between two ends of the horizontal spring can be defined as

$$ y\left( t \right) = \sqrt {x^{2} + a^{2} } , $$
(2)

which is the source of nonlinear behavior. Considering the vertical spring and the applied load, force balance in the vertical direction can be written as

$$ f_{k} + k_{h} \left( {\frac{{L_{o} }}{{\sqrt {x^{2} + a^{2} } }} - 1} \right)x + k_{v} \left( {x_{o} - x} \right) = mg, $$
(3)

where \( x_{o} \) is defined as the vertical displacement of the mass when the horizontal spring is at its free length such that \( x_{o} = \sqrt {L_{o}^{2} + a^{2} } \). Assuming \( mg = k_{v} x_{o} \), the applied force \( f_{k} \) can be given as

$$ f_{k} = \left( {k_{v} + k_{h} \left( {1 - \frac{{L_{o} }}{{\sqrt {x^{2} + a^{2} } }}} \right)} \right)x. $$
(4)

The non-dimensional form can be obtained as follows

$$ \frac{{f_{k} }}{{k_{v} a}} = \left( {\gamma \left( {1 - \frac{\delta }{{\sqrt {\hat{x}^{2} + 1} }}} \right) + 1} \right)\hat{x}, $$
(5)

where \( \delta = L_{o} /a,\,\,\gamma = k_{h} /k_{v} ,\,\hat{x} = x/a. \)

Differentiating the non-dimensional force with respect to displacement, stiffness of the nonlinear isolator can be obtained as follows

$$ \hat{k}[\hat{x}] = \gamma \left( {1 - \frac{\delta }{{\left( {\hat{x}^{2} + 1} \right)^{3/4} }}} \right) + 1. $$
(6)

The effect of non-dimensional parameters \( \delta \) and \( \gamma \) was investigated in [14]. The authors indicated that an increase of \( L_{o} /a \) ratio may result in even overall negative stiffness around the equilibrium point. Likely, if stiffer horizontal springs relative to vertical ones are placed, the effect of negative stiffness becomes more dominant and overall negative stiffness may be obtained. Furthermore, a proper choice of \( \delta \) and \( \gamma \) values results in quasi-zero stiffness around the equilibrium point. If the QZS condition is satisfied, \( \hat{k}[\hat{x} = 0] = 0 \) which results in \( \gamma \left( {1 - \delta } \right) + 1 = 0 \).

2.2 QZS dry friction element

In modeling of dry friction damping, macroslip model is widely used in the literature due to its mathematical simplicity compared to microslip models. According to macroslip friction model, in which Coulomb friction model with a constant coefficient of friction is used, the entire friction interface is either at slip or stick states. Friction damper is modeled as a spring one end of which slips if the spring force exceeds a certain value, which is referred as the slip force. Therefore, damping is only possible if relative displacement is large enough to overcome the slip force which is usually the case at resonance regions if slip force is chosen properly. However, it should be noted that in the case where friction damper is in complete stuck state, it only acts like an additional stiffness [27]. It will be shown later that, for the isolator problem considered in this study, stick–slip motion of the friction interface occurs at very low frequencies; hence, the dependency of coefficient of friction on sliding velocity can be neglected.

QZS system coupled with a dry friction damper proposed in this study is shown in Fig. 2. As it is detailed in Sect. 2, the overall vertical stiffness is nonlinear and dependent on the position of the mass. Therefore, overall stiffness can be defined as a position-dependent nonlinear stiffness element as shown in Fig. 2. Friction force in the proposed system is different than the macroslip friction models used in the literature due to the presence of nonlinear contact stiffness caused by the geometric nonlinearity of the isolator. Therefore, for this new friction element, friction force can be defined as

$$ F_{f} = \left\{ {\begin{array}{*{20}c} {k\left[ {x\left( t \right) - w\left( t \right)} \right] \cdot \left( {x\left( t \right) - w\left( t \right)} \right)} & \vert{k\left[ {x\left( t \right) - w\left( t \right)} \right] \cdot \left( {x\left( t \right) - w\left( t \right)} \right)\vert \le \mu N} \\ {\mu N\text{sign} \left( {\dot{w}\left( t \right)} \right)} & \vert{k\left[ {x\left( t \right) - w\left( t \right)} \right] \cdot \left( {x\left( t \right) - w\left( t \right)} \right)\vert > \mu N} \\ \end{array} } \right\}, $$
(7)

where \( k\left[ {} \right] \) is the position-dependent stiffness, \( w\left( t \right) \) is the slip motion, \( \mu N \) is the slip force, \( x\left( t \right) \) is the input relative displacement.

Fig. 2
figure 2

QZS dry friction element model proposed in this study

Full size image

2.2.1 Stick–slip case

For single harmonic input, i.e., \( x\left( t \right) = X\sin \left( {\omega t + \phi } \right) = X\sin \left( \psi \right) \), slip to stick transitions occur when the relative motion reverses its direction, i.e., \( \psi = \frac{\pi }{2},\frac{3\pi }{2} \). During the stick state, it is known that slip velocity is zero, i.e., \( \dot{w} = 0 \), and \( w = w_{o} \). Therefore, the friction force during stick state can be given by

$$ F_{f} = k\left[ {x\left( t \right) - w_{0} } \right] \cdot \left( {x\left( t \right) - w_{0} } \right). $$
(8)

The position-dependent stiffness of the QZS dry friction element given in Eq. (8) is obtained by the analysis of the QZS isolator as described in Sect. 2.1, which results in the following relation

$$ k\left[ {x\left( t \right) - w_{0} } \right] = k_{v} + k_{h} \left( {1 - \frac{{L_{o} }}{{\sqrt {\left( {x\left( t \right) - w_{0} } \right)^{2} + a^{2} } }}} \right). $$
(9)

At the time of transition from positive slip to stick state transition angle \( \psi \) equals to \( {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} \); hence, initial values of the displacement and the friction force at the beginning of stick state can be obtained as follows

$$ x\left( {\psi = \pi /2} \right)_{\,} = X\sin \left( {\frac{\pi }{2}} \right) = X, $$
(10)
$$ F_{f} = \mu N , $$
(11)

where \( X \) is the amplitude of harmonic input relative motion. Substituting Eqs. (9)–(11) into Eq. (8) results in

$$ \mu N = \left( {k_{v} + k_{h} \left( {1 - \frac{{L_{0} }}{{\sqrt {\left( {X - w_{0} } \right)^{2} + a^{2} } }}} \right)} \right)\left( {X - w_{0} } \right). $$
(12)

Squaring both sides of Eq. (12) and rewriting it, yields the following fourth-order polynomial

$$ \begin{aligned} & \left( {k_{h} + k_{v} } \right)^{2} \left( {X - w_{0} } \right)^{4} - 2\mu N\left( {k_{h} + k_{v} } \right)\left( {X - w_{0} } \right)^{3} \\ & \quad + \left( {a^{2} \left( {k_{h} + k_{v} } \right)^{2} - Lo^{2} k_{h}^{2} + \left( {\mu N} \right)^{2} } \right)\left( {X - w_{0} } \right)^{2} \\ & \quad - 2a^{2} \mu N\left( {k_{h} + k_{v} } \right)\left( {X - w_{0} } \right) + \left( {\mu Na} \right)^{2} = 0, \\ \end{aligned} $$
(13)

largest real root of which gives \( w_{o} \). When the magnitude of the force across the nonlinear stiffness element reaches to \( - \mu N \), the transition from stick to negative slip occurs

$$ - \mu N = k\left[ {X\sin \psi_{1} - w_{o} } \right] \cdot \left( {X\sin \psi_{1} - w_{o} } \right) . $$
(14)

Substitution of Eq. (12) into Eq. (14) and utilizing the symmetry of the stiffness with respect to x-axis, transition angle from stick to negative slip, \( \psi_{1} \), can be obtained as follows

$$ \psi_{1} = \arcsin \left( {\frac{{2w_{o} }}{X} - 1} \right){\text{ and }}\frac{\pi }{2} < \psi_{1} < \frac{3\pi }{2} . $$
(15)

Due to the single harmonic input motion, hysteresis curve is symmetric with respect to the origin; hence, the transition from stick to positive slip occurs at \( \psi_{2} = \psi_{1} + \pi \).

For single harmonic input motion, hysteresis curve can be obtained by using Eqs. (8) and (15) as shown in Fig. 3. As can be seen from in Fig. 3, the resulting hysteresis curve is symmetric and consists of a positive slip, a negative slip, and two stick regions.

Fig. 3
figure 3

Hysteresis loop of the proposed QZS dry friction element

Full size image

After determining transition angles, nonlinear friction force can be written as follows by using a single harmonic Fourier series representation

$$ \begin{aligned} F_{f} & = f_{\text{ns}} \sin \left( {\omega t + \phi } \right) + f_{\text{nc}} \cos \left( {\omega t + \phi } \right) \\ & = \left( {f_{\text{ns}} \cos \phi + f_{\text{nc}} \sin \phi } \right)\sin \omega t + \left( {f_{\text{nc}} \cos \phi + f_{\text{ns}} \sin \phi } \right)\cos \omega t, \\ \end{aligned} $$
(16)

where \( f_{\text{ns}} \) and \( f_{\text{nc}} \) are the sine and cosine Fourier coefficients, considering the symmetry of the hysteresis loop, which can be obtained as follows

$$ f_{\text{ns}} = \frac{2}{\pi }\left( {\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}}^{{\psi_{1} }} {k\left[ {X\sin \psi - w_{o} } \right]\left( {X\sin \psi - w_{o} } \right)} \sin \psi {\text{d}}\psi - \int\limits_{{\psi_{1} }}^{{{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0pt} 2}}} {\mu N\sin \psi {\text{d}}\psi } } \right) , $$
(17)
$$ f_{\text{nc}} = \frac{2}{\pi }\left( {\int\limits_{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}}^{{\psi_{1} }} {k\left[ {X\sin \psi - w_{0} } \right]\left( {X\sin \psi - w_{0} } \right)} \cos \psi {\text{d}}\psi - \int\limits_{{\psi_{1} }}^{{{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0pt} 2}}} {\mu N\cos \psi {\text{d}}\psi } } \right) . $$
(18)

Analytical results for Fourier coefficients \( f_{\text{ns}} \) and \( f_{\text{nc}} \) are provided in “Appendix”.

2.2.2 Fully stuck case

For the fully stuck case, only the QZS element is effective; hence, the friction force can be written as

$$ F_{f} = k\left[ {x\left( t \right)} \right] \cdot x\left( t \right) . $$
(19)

Therefore, the coefficients of single harmonic Fourier series friction force representation can be written as

$$ f_{\text{ns}} = \frac{2}{\pi }\int\limits_{0}^{\pi } {\left( {k\left[ {X\sin \psi } \right] \cdot X\sin \psi } \right)} \sin \psi {\text{d}}\psi , $$
(20)
$$ f_{\text{nc}} = \frac{2}{\pi }\int\limits_{0}^{\pi } {\left( {k\left[ {X\sin \psi } \right] \cdot X\sin \psi } \right)} \cos \psi {\text{d}}\psi . $$
(21)

Evaluation of the integrals yields

$$ f_{\text{ns}} = \left( {k_{v} + k_{h} } \right)X + \frac{{4L_{o} k_{h} }}{X\pi }\left[ {\frac{{a^{2} }}{{\sqrt {X^{2} + a^{2} } }} \cdot K\left[ {\frac{X}{{\sqrt {X^{2} + a^{2} } }}} \right] - \sqrt {X^{2} + a^{2} } \cdot E\left[ {1,\frac{X}{{\sqrt {X^{2} + a^{2} } }}} \right]} \right] , $$
(22)
$$ f_{\text{nc}} = 0 . $$
(23)

where \( K\left[ x \right] \) and \( E\left[ x \right] \) are Elliptic integrals which are defined in “Appendix”.

2.3 Vibration isolation system with QZS dry friction element

The mathematical development of the QZS dry friction element is given in Sect. 2.2 in detail. In this section, this nonlinear element is integrated into a single degree of freedom base excitation problem as shown in Fig. 4, which is referred as QZS dry friction isolator. As can be seen from Fig. 4, the friction interface is placed between the mass and massless platform on which the vertical and pre-stressed horizontal springs are attached. The base excitation is defined as \( z\left( t \right) \) and the absolute displacement of the mass is \( x\left( t \right) \). Equation of motion of the mass suspended by the proposed nonlinear QZS dry friction element can be given as

$$ m\ddot{x} + c_{v} \dot{x} + F_{f} \left[ {x - z} \right] = c_{v} \dot{z} , $$
(24)

where \( F_{f} \left[ {x - z} \right] \) is the friction force due to the QZS dry friction element which is defined in Eq. (7).

Fig. 4
figure 4

Base excitation model of the isolation system with QZS dry friction element

Full size image

For a single harmonic base input, i.e., \( z\left( t \right) = Z\sin \omega t \), the response of the mass can as well be assumed harmonic in the following form \( x\left( t \right) = X_{s} \sin \omega t + X_{c} \cos \omega t \) utilizing a single harmonic representation. Then, the nonlinear differential equation of motion given in Eq. (24) can be converted into a set of nonlinear algebraic equations [14, 23] by using harmonic balance method (HBM). The resulting set of nonlinear algebraic equations of motion becomes as

$$ {\mathbf{R}}\left( {{\mathbf{x}},\omega } \right) = \left[ {\begin{array}{*{20}c} { - \omega^{2} m} & { - c_{v} \omega } \\ {c_{v} \omega } & { - \omega^{2} m} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {X_{s} } \\ {X_{c} } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {f_{\text{ns}} } \\ {f_{\text{nc}} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} Z \\ {c_{v} \omega Z} \\ \end{array} } \right\} = {\mathbf{0}} , $$
(25)

where \( {\mathbf{R}}\left( {{\mathbf{x}},\omega } \right) \) is the nonlinear vector function, \( {\mathbf{x}} = \left( {\begin{array}{*{20}c} {X_{s} } & {X_{c} } \\ \end{array} } \right)^{T} \) and, \( X_{s} \) and \( X_{c} \) are the sine and cosine coefficients of the absolute displacement. \( f_{\text{ns}} \) and \( f_{\text{nc}} \) are the sine and cosine coefficients of the friction force to be determined by Eqs. (17)–(18) or Eqs. (22)–(23). \( \omega \) and \( Z \) are the frequency and the amplitude of the base excitation, respectively.

The solution of the resulting set of nonlinear algebraic equations is obtained by Newton’s method, and arc-length continuation is used in order to follow the solution path even it reverses its direction. A single step of Newton’s method with arc-length continuation is given as

$$ {\mathbf{q}}_{k}^{i + 1} = {\mathbf{q}}_{k}^{i} - \left[ {\begin{array}{*{20}c} {\frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{x}}}}_{{{\mathbf{q}} = {\mathbf{q}}_{k}^{i} }} } & {\frac{{\partial {\mathbf{R}}}}{\partial \omega }_{{{\mathbf{q}} = {\mathbf{q}}_{k}^{i} }} } \\ {\frac{\partial h}{{\partial {\mathbf{x}}}}_{{{\mathbf{q}} = {\mathbf{q}}_{k}^{i} }} } & {\frac{\partial h}{\partial \omega }_{{{\mathbf{q}} = {\mathbf{q}}_{k}^{i} }} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\mathbf{R}}\left( {{\mathbf{q}}_{k}^{i} } \right)} \\ {h\left( {{\mathbf{q}}_{k}^{i} } \right)} \\ \end{array} } \right\} , $$
(26)

where \( i \) is the iteration number. Details of the solution method can be found in [23, 28]. The additional arc-length equation can be defined as follows which represents an n-dimensional sphere in which the solution is sought

$$ h\left( {{\mathbf{q}}_{k}^{i} } \right) = \Delta {\mathbf{q}}_{k}^{T} \Delta {\mathbf{q}}_{k} - s^{2} . $$
(27)

Here \( {\mathbf{q}}_{k}^{i} = \left( {\begin{array}{*{20}c} {{\mathbf{x}}_{k} } & \omega \\ \end{array} } \right), \, \Delta {\mathbf{q}}_{k} = {\mathbf{q}}_{k}^{i} - {\mathbf{q}}_{k - 1} \), \( k \) corresponds to the \( k^{th} \) solution point, \( i \) is the iteration number and \( s \) is the radius of the hypothetical sphere.

2.4 Absolute and relative transmissibility

Isolation performance of the proposed QZS dry friction isolator is evaluated by comparing the absolute and relative transmissibility for different case studies in Sect. 4. The relative displacement of mass \( m \) given in Fig. 4 with respect to the input platform motion can be defined as

$$ u\left( t \right) = x\left( t \right) - z\left( t \right) = \left( {X_{s} - Z} \right)\sin \omega t + X_{c} \cos \omega t. $$
(28)

Then, the magnitude of the relative transmissibility is given by

$$ \frac{U}{Z} = \frac{{\sqrt {\left( {X_{s} - Z} \right)^{2} + X_{c}^{2} } }}{Z}, $$
(29)

where \( U \) is the amplitude of the relative motion \( u\left( t \right) \). Similarly, the absolute transmissibility can be obtained as

$$ \frac{X}{Z} = \frac{{\sqrt {X_{s}^{2} + X_{c}^{2} } }}{Z}, $$
(30)

where \( X \) is the amplitude of motion of mass \( m \).

2.5 Stability of steady-state solutions

Periodic solutions can be found by HBM as described in Sect. 2.3. However, HBM does not give any information on the stability of the solutions. Hill’s Method, which is based on the Floquet Theory, is used to determine the stability of the solutions obtained from HBM. In this method, the perturbation around the periodic solution is defined as the combination of harmonic functions and exponential functions, the substitution of which into equation of motion yields below quadratic eigenvalue problem [28].

$$ \left( {\frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{x}}}} + \lambda {\varvec{\Delta}}_{{\mathbf{1}}} + \lambda^{2} {\varvec{\Delta}}_{2} } \right){\mathbf{\varphi }} = {\mathbf{0}} , $$
(31)

where \( {\mathbf{\varphi }} \) is the complex eigenvector, \( {{\partial {\mathbf{R}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{R}}} {\partial {\mathbf{x}}}}} \right. \kern-0pt} {\partial {\mathbf{x}}}} \) is the Jacobian Matrix, \( {\varvec{\Delta}}_{{\mathbf{1}}} \) and \( {\varvec{\Delta}}_{{\mathbf{2}}} \) are defined as follows

$$ {\varvec{\Delta}}_{{\mathbf{1}}} = \left[ {\begin{array}{*{20}c} {c_{v} } & { - 2\omega m} \\ {2\omega m} & {c_{v} } \\ \end{array} } \right] , $$
(32)
$$ {\varvec{\Delta}}_{{\mathbf{2}}} = \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right] . $$
(33)

The solution of this eigenvalue problem can be used to obtain Floquet exponentials which contains information about the stability of the solution [29, 30]. Since the Jacobian matrix, \( {{\partial {\mathbf{R}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{R}}} {\partial {\mathbf{x}}}}} \right. \kern-0pt} {\partial {\mathbf{x}}}} \), is already calculated during the solution process, one can easily obtain complex eigenvalues \( \lambda_{i} \). For single harmonic motion, Jacobian matrix given in Eq. (34) can be represented as follows

$$ \frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{x}}}} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } \\ {a_{21} } & {a_{22} } \\ \end{array} } \right] $$
(34)

In order to have a non-trivial solution, determinant of the coefficient matrix given in Eq. (31) must be equal to zero. Substituting Eqs. (32) to (34) into Eq. (31) and equating determinant to zero yields the following fourth-order polynomial

$$ \begin{aligned} & m^{2} \lambda^{4} + 2c_{v} m\lambda^{3} + \left( {4m^{2} \omega^{2} + m\left( {a_{11} + a_{22} } \right) + c_{v}^{2} } \right)\lambda^{2} \\ & \quad + \left( {2\omega m\left( {a_{21} - a_{12} } \right) + c_{v} \left( {a_{11} + a_{22} } \right)} \right)\lambda + a_{11} a_{22} - a_{12} a_{21} = 0. \\ \end{aligned} $$
(35)

As stated in [29, 30], only two complex eigenvalues \( \lambda \) which have the smallest imaginary parts correspond to Floquent exponents. The stability of the solution can be determined by checking whether the real part of any \( \lambda_{i} \) is negative or not. Therefore, condition for the stability follows that

$$ \text{Re} \left( {\lambda_{i} } \right) < 0,\, \, i = 1,2 . $$
(36)

3 Validation of the solution method

In this section, results obtained by HBM for the isolation system with a QZS dry friction element are validated by time integration. MATLAB ode45 is used for the time integration. To determine the slip-stick states, zero-crossing detection (ZCD) method explained in [31] is used. ZCD algorithms seek the events defined in Eq. (37). The friction force for stick and slip case is defined in Eq. (7). The transition from stick to slip and slip to stick are defined as zero-crossing events following as

$$ \begin{array}{*{20}c} {\left| {F_{f} } \right| - \mu N = 0} & {{\text{stick}}\;{\text{to}}\;{\text{slip}}\;{\text{transition}}\;{\text{event}}} \\ {\left| {\dot{x}\left( t \right) - \dot{w}\left( t \right)} \right| = 0} & {{\text{slip}}\;{\text{to}}\;{\text{stick}}\;{\text{transition}}\;{\text{event}} .} \\ \end{array} $$
(37)

Whenever one of the below events is detected by the solver, the integrator stops and the zero-crossing point is solved numerically. Numerical integration is restarted by using the following equations until the next zero-crossing event is detected

$$ \begin{array}{*{20}c} {\dot{w}\left( t \right) = \dot{z}\left( t \right)} & {{\text{stick}}\;{\text{to}}\;{\text{slip}}\;{\text{transition}}} \\ {\dot{w}\left( t \right) = \dot{x}\left( t \right)} & {{\text{slip}}\;{\text{to}}\;{\text{stick}}\;{\text{transition,}}} \\ \end{array} $$
(38)

where \( w\left( t \right) \) is the slip motion, \( x\left( t \right) \) is the absolute motion of the mass, and \( z\left( t \right) \) is the motion of the base as defined in Fig. 4. The following non-dimensional parameters are defined to be used in the simulations

$$ \xi_{v} = \frac{c}{{2\sqrt {k_{v} m} }}, \, \omega_{n} = \sqrt {\frac{{k_{v} }}{m}} , \, \varOmega = \frac{\omega }{{\omega_{n} }}, \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = \frac{Z}{a} , $$
(39)

where \( \omega \) is the frequency of base excitation. Parameters given in Table 1 are used in the simulations. The excitation frequency \( \omega \) is first increased and then decreased stepwise at a 0.1 rad/s increment. At each frequency, after the solution reaches to steady-state, the maximum of the absolute displacement time history at that frequency step is recorded, since the nonlinearity is odd symmetric, i.e., bias component of the response is zero. The response at the end of each frequency step is used as the initial condition for the next frequency step.

Table 1 Parameters used in the simulations
Full size table

Comparison of the results obtained by HBM and time integration is given in Fig. 5 for low-level \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.035 \) and high-level excitations \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.055 \). As can be seen from the results, both solutions agree well with each other having only some minor deviations around the resonance region where the relative displacement has its peak value. Therefore, it can be concluded that utilizing a single harmonic term in the solution is sufficient. This agreement is observed in fully stuck case as well as the stick–slip case for both low-level and high-level excitations. Stick–slip occurs within \( \varOmega \subset [0.161,0.164] \) at upper branch of Fig. 5a while it has a larger frequency range \( \varOmega \subset [0.145,0.183] \) for high-level excitations as shown in Fig. 5b. For both cases, absolute transmissibility decreases after the transition from fully stuck to stick–slip. This trend and the effect of additional damping introduced by the friction interface will be subjected to further examination in Sect. 4. A sample time history of the friction force, i.e., \( F_{f} \left( t \right) \), is shown in Fig. 6 which clearly shows when the damper is fully stuck or goes under stick–slip behavior. Moreover, the jump-down phenomena can also be observed. For this plot, the frequency is varied by a 0.1 rad/s increments within \( \omega \subset [3,50] \) for \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.055 \). Other parameters are given in Table 1. At each step, time integration is performed for 15 forcing cycles for which the frequency is kept constant. It can be seen that friction force increases as the excitation frequency increases for \( t < 1800\,\,\text{s} \) and the friction interface is at stuck state, since \( F_{f} \left( t \right) \) is less than \( \mu N = 10\,\text{N} \). Around \( t = 1800\,\text{s} \), friction force reaches the slip force (10 N) and the friction interface transforms from fully stuck to stick–slip behavior. A closer examination of the time history around \( t = 2000\,\text{s} \) demonstrates the transition between the positive slip–stick-negative slip where the friction force is limited by ± μN. Further increase of the frequency causes the jump down of the solution to the lower branch of the frequency response as shown in Fig. 5b. Figure 7 shows the relative displacement \( u(t) \) versus friction force \( F_{f} \left( t \right) \), i.e., the hysteresis curve, for a selected normalized frequency of \( \varOmega = 0.155 \) as shown in Fig. 6.

Fig. 5
figure 5

Comparison of time simulation results and HBM solution a low level \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.035 \), b high-level base excitations \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.055 \), ‘dashed line’ single harmonic balance method, ‘double dashed’: unstable solutions, ‘green circle’ increasing frequency-ODE45, ‘red cross’ decreasing frequency-ODE45

Full size image
Fig. 6
figure 6

Time history of friction force \( F_{f} (t) \) obtained by varying frequency \( \omega \subset [3,50] \) for \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.055 \)

Full size image
Fig. 7
figure 7

Hysteresis loop for \( \varOmega = 0.155 \)

Full size image

4 Case studies

In this section, performance of the proposed isolator is investigated under harmonic base excitation by using the parameter set given in Table 1. In these case studies, different features of QZS dry friction isolator are studied. In Case Study-1 and Case Study-2, displacement transmissibility of the proposed isolator is compared with that of QZS isolator for various base excitation amplitudes and damping ratios. In Case Study-3, the influence of the damping ratio on the transmissibility of the proposed isolator is discussed. Case Study-4 is the assessment of the effect of slip force amplitude on the transmissibility, which is one of the critical design parameters of QZS dry friction isolator.

4.1 Case study-1: Comparison of QZS dry friction isolator and QZS isolator for various base excitation amplitudes

To observe the isolation performance of the QZS dry friction isolator with respect to the classical QZS isolator, three different isolation systems with: (a) QZS dry friction isolator (b) QZS isolator, i.e., \( \mu N = \infty \) and (c) linear spring-damper isolator, schematics of which are given in Fig. 8, are studied under different base excitation amplitudes. Based on the QZS condition given in Sect. 2, the non-dimensional parameters \( \delta \) and \( \gamma \) are taken as \( \delta = 2 \), \( \gamma = 1 \) which results in zero stiffness at the equilibrium point. The other parameters are given in Table 1.

Fig. 8
figure 8

Isolation system with a QZS dry friction isolator, b QZS isolator, c linear isolator

Full size image

The displacement transmissibility plots for low and high-level excitations are given in Fig. 9a, b, respectively. The low excitation levels can be considered as the input range for which the QZS isolator is designed to work. For this excitation range, the addition of the pre-stressed horizontal springs reduces the resonance frequency and dry friction has little influence on the frequency response only around the resonance region of the case where \( \hat{Z} = 0.035 \). As reported by many researchers [3, 6, 10], FRF bends towards higher frequencies due to the cubic stiffness of the QZS mechanism with the increase of the base excitation amplitude. If one keeps increasing the base excitation, resonance amplitude increases and even worse performance than the simple linear isolator can be observed as shown in Fig. 9b. This undesired behavior can be reduced in the QZS dry friction isolator, thanks to the dry friction damping introduced by the slip motion at the friction interface. The decrease in absolute transmissibility after the transition from fully stuck to stick–slip can be seen in Fig. 9b within \( \varOmega \subset [0.148,0.176] \) for \( \hat{Z} = 0.045 \) and within \( \varOmega \subset [0.146,0.191] \) for \( \hat{Z} = 0.065 \) where the results for QZS Dry Friction isolator and the QZS isolator are splitted from each other. These normalized frequency bands represent the range of stick–slip motion and depending on the slip force and excitation level it shifts. This trend will be examined further in Case Study-4. Although increasing linear damping has an effect around the resonance region; however, it adversely affects the transmissibility in the isolation region [16]. Unlike linear viscous damping, the friction interface introduces damping only around the resonance region where the absolute and relative displacements are large. As can be seen from Fig. 9, the friction interface is in fully stuck at the off-resonance regions. The low damping QZS isolator and the QZS dry friction isolator both behave completely the same. In other words, there is no adverse effect of the additional damping introduced by dry friction on the isolation performance at the off-resonance frequency range.

Fig. 9
figure 9

Comparison of QZS dry friction isolator and QZS isolator for various base excitation amplitudes. a Low level, b high-level base excitations (\( \mu N = 10\;\text{N} \)\( \delta = 2 \), \( \gamma = 1 \), \( \xi_{v} = 0.015 \), ‘circle’ indicates the range of unstable solutions)

Full size image

4.2 Case study-2: Comparison of QZS dry friction isolator and QZS isolator for various damping ratios

In order to observe the adverse effect of increasing damping in the isolation frequency range, displacement transmissibility of the QZS isolator and QZS dry friction isolator are compared for various damping ratios. These two isolation systems are shown in Fig. 8a, b. The damping ratio of the QZS mechanism is varied from 0.01 to 0.05. Slip force of the dry friction element, i.e., μN is set to be 10 N and the damping coefficient \( c_{v} \) is zero; hence, the only source of damping is due to dry friction. Absolute transmissibility results for the normalized base excitation of \( \hat{Z} = 0.045 \) are given in Fig. 10. It can be observed that resonance amplitude can be reduced without affecting the off-resonance regions by means of dry friction. Since dry friction element is in fully stuck state in the isolation frequency range, the isolator acts as a QZS element with no damping in this frequency range. Therefore, QZS dry friction isolator provides a significantly improved isolation performance with respect to the QZS isolator for while maintaining a similar or lower absolute transmissibility at the resonance frequency which can be observed from Fig. 10.

Fig. 10
figure 10

Comparison of QZS Dry friction isolator and QZS isolator for various damping ratios, \( \delta = 2 \), \( \gamma = 1 \), \( \hat{Z} = 0.045 \), ‘circle’: indicates the range of unstable solutions

Full size image

4.3 Case study-3: Effect of viscous damping

In this case study, the effect of viscous damping on the transmissibility of the QZS dry friction isolator is studied. Absolute and relative transmissibility plots for different damping ratios are given in Figs. 11 and 12, respectively, while keeping the normalized base excitation and slip force constant. It is clearly observed that the best isolation performance is obtained for the case with no viscous damper without increasing the resonance amplitude. It should be noted that since the dry friction provides damping as the amplitude of the relative motion increases, response of the system is bounded at the resonance even without using a viscous damper. An increase in the viscous damping ratio has an adverse effect on the isolation performance while having a slight decrease in the resonance amplitude. However, it should be noted that transient solutions are not damped out for the case when the friction damper is fully stuck and there is no viscous damping. For that case, total system response is composed of the summation of both steady-state and transient responses. In order for the system to reach steady-state, the isolation system should have some amount of viscous damping. Hence, the best isolation performance, while damping out the transient solutions, can be obtained by considering a very small amount of viscous damping.

Fig. 11
figure 11

Absolute transmissibility for various damping ratio, \( \mu N = 10\,\text{N} \), \( \hat{Z} = 0.045 \), ‘circle’: indicates the range of unstable solutions

Full size image
Fig. 12
figure 12

Relative transmissibility for various damping ratios, \( \mu N = 10\,\text{N} \), \( \hat{Z} = 0.045 \), ‘circle’: indicates the range of unstable solutions

Full size image

4.4 Case study-4: Effect of slip force

In this case study, the effect of slip force on the displacement transmissibility is studied for normalized base excitation amplitude of \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Z} = 0.045 \). Based on the observations of Case Study-3, the damping ratio \( \xi_{v} \) is set to be 0.001. Absolute transmissibility results are shown in Fig. 13. It can be clearly seen that as the slip force decreases, the friction interface starts to slip at lower frequencies, which yields attenuation of the resonance transmissibility amplitudes. It should be noted that since dry friction element only affects the resonance region, the isolation performances of all cases are identical; hence, the smallest possible slip force should be used. However, it should be noted that the slip force must be greater than the deadweight of the system. Even if the case where \( \mu N = 5\text{N} \) provides the best isolation performance among other options, since the deadweight for this example, i.e., \( mg \), is equal to \( 9.81\,\text{N} \) a slip force larger than this value should be used. It should be noted that performance of the QZS dry friction isolator is independent of the slip force in the isolation frequency range and it only affects the amplitude at the resonance frequency.

Fig. 13
figure 13

Effect of slip force \( \delta = 2 \), \( \gamma = 1 \), \( \xi_{v} = 0.001 \), \( \hat{Z} = 0.045 \), ‘circle’: indicates the range of unstable solutions

Full size image

5 Performance of QZS dry friction isolator under broadband random excitation

Harmonic excitation employed in Sect. 4 allows the analytical treatment of the problem for parametric studies and for the determination of the optimum parameters of the QZS dry friction isolator in a computationally efficient way. However, in many applications, a vibration isolator is as well subjected to broadband random excitations. In this section, the performance of the proposed isolator under stochastic excitations is investigated through the comparisons of time-domain analyses. The response to a random base acceleration is obtained by employing the integration scheme provided in Sect. 3. Here, the base acceleration is assumed to be a Gaussian white noise covering the frequency range of 1–500 Hz with a constant power spectral density of \( S_{0} = 0.1\,\text{g}^{2} /Hz \). The parameters used in the analyses are provided in Table 1. The base acceleration used in the time domain analyses and the corresponding power spectral density (PSD) of it are shown in Fig. 14. It is seen that the input PSD covers a wide frequency range including the natural frequency of the system, i.e., \( f_{n} = 22.51\;\text{Hz} \).

Fig. 14
figure 14

Random base acceleration \( \ddot{z}(t) \)a the time signal and b PSD

Full size image

Figure 15 shows a comparison of PSD of the acceleration response \( \ddot{x}(t) \) for the linear isolator, QZS isolator, and QZS dry friction isolator. It is seen that the addition of the QZS mechanism reduces the resonance frequency as well as the resonance amplitude under the given excitation level, i.e., \( S_{0} = 0.1\,\text{g}^{2} /Hz \). It can be seen that response PSD of the QZS dry friction isolator converges to the response PSD of the QZS isolator for \( \mu N = 50N \), whereas, slip force of \( \mu N = 10N \) results in the smallest resonance amplitude and the largest isolation region. These results are in agreement with the observations of Sect. 4 that are obtained by the use HBM analytical Fourier coefficients, which is significantly more efficient compared to time integration.

Fig. 15
figure 15

Acceleration response PSD to the random base excitation given in Fig. 14

Full size image

6 Conclusion

In this study, a new QZS isolator is proposed by adding dry friction damping between the isolated mass and the stiffness of the isolator. Steady-state response of this nonlinear system is obtained by utilizing HBM which transforms the nonlinear differential equations of motion into a set of nonlinear algebraic equations. Analytical Fourier sine and cosine coefficients of the nonlinear element are derived to be used in HBM. The resulting set of nonlinear algebraic equations is solved numerically by using Newton’s method with arc-length continuation, and stability of the obtained solutions is identified by using Hill’s method. The proposed QZS dry friction isolator is compared with the existing QZS isolator under different excitation levels and different system parameters.

Based on the frequency and time domain analyses the following conclusions can be made:

  • First, from time simulation analyses, it can be concluded that a single solution is sufficient to represent the dynamics of the proposed QZS dry friction isolator.

  • The input dependency of QZS dry friction isolator is reduced due to the use of dry friction element

  • Proposed isolator does not affect the transmissibility in the isolation region, since the dry friction introduces damping only around the resonance region. Thus, the adverse effect of increasing linear viscous damping on the isolation performance is eliminated.

  • It is observed that decreasing slip force of the dry friction element reduces the resonance amplitudes. However, since the friction interface shall carry deadweight of the system, the minimum slip force is limited by the deadweight of the isolated mass.

  • It is observed that the isolation performance of the proposed QZS dry friction isolator is maximized by considering the smallest possible viscous damping that provides sufficient time to reduce the transient response of the system.

  • Overall, it is observed that QZS dry friction isolator improved the isolation performance significantly compared to the QZS isolator without sacrificing from the transmissibility around the resonance region.