Asymptotic analysis of an anti-plane shear dispersion of an elastic five-layered structure amidst contrasting properties

Abstract

The present paper studies the anti-plane shear motion of an inhomogeneous elastic five-layered plate amidst the four contrasting material setups. The asymptotic analysis method in regard to the various material parameters is adopted for the study. The respective displacements, stresses and the Rayleigh-Lamb dispersion relation corresponding to the antisymmetric anti-plane motion with perfect interlayer and traction-free (on the outer faces) boundary conditions are determined. Furthermore, in order to analyze the said dispersion relation in the presence of these contrasts, a unification of parameters was proposed. The overall cutoff frequencies and the low-frequency estimates are determined for both the generalized and unified settings. A comparative analysis between the unified Rayleigh-Lamb dispersion relation and the optimal shortened polynomial dispersion relation is carried for each contrast. We also established some asymptotic formulae for the related unified displacements and stresses.

1 Introduction

Elastic wave propagation through various kinds of composite and multilayered structures has been an area of great interest in solid mechanics [1,2,3,4,5] and plays a pivotal role in many engineering professions including civil, mechanical, automotive and aeronautics among others [6,7,8,9,10, 12,13,14,15]. Some of these structures appearing in multiply-bond layers include elastic beams, plates, laminates, panels, cylindrical shells and rods to mention a few, see [16,17,18,19,20,21,22,23,24]. Besides, in multilayered composite structures, layers involving different constituents are put together to make a single structure depending on the industrial or application needs. This need is basically geared to exploit the advantages of different layers involved of weightlessness, strength, resistance, toughness and stiffness in the high-density materials. Mathematically, various considerations have been carried out in the past literature to study a variety of wave propagation phenomena arising in multilayered media. For instance, a very good review on the buckling and bending analyses of vibrating sandwich beams and laminated composites are demonstrated by Sayyad and Ghugal [25]. The layer-wise theory for sandwich plates and laminated composite is developed using finite element formulation by Belarbi et al. [26], while that of the photovoltaic panels and laminated glass are presented by Naumenko and Eremeyev [27]. On the three-layered plates that arise in modern technology, a three-layered plate characterized by a thin soft core layer is analyzed using the shear deformation theory (first-order) by Altenbach et al. [28], while its dispersion is investigated using the asymptotic approach by Kaplunov et al. [29]. In [29], the plate is considered to be a strongly inhomogeneous layered plate with varying stiffnesses and densities under the four contrast configurations. Additionally, inhomogeneous infinite three-layered plates described by anti-plane shear motion are analyzed in regard to the low-frequency vibration modes and in the presence of material contrasts by Prikazchikov et al. [30] and Baris [31], respectively. More explicitly, the material contrasts that appear in [29,30,31] are characterized by mix stiff-soft materials that arise in the design of modern structures including the photovoltaic panels, laminated glasses, electrostatic precipitators and the typical sandwich plates, see also [32,33,34]. Furthermore, there has been a growing interest among many researchers in the dynamicity of five-layered structures. For examples, the five-layered glass plates recently appear in modern roofing, flooring and other glazing applications [35, 36], while the five-layered timber laminates in wooden buildings, surfaces and partitioning purposes with aim to controlling sounds and less density [37]. In [35], the authors dealt with the free vibration analysis of a five-layered plate using Navier’s method. More precisely, a three-layered plate with elastic core with viscoelastic skin layers was sandwiched between elastic layers and analyzed in regard to varying material properties for the loss factor and frequency, while in [36], a derivation of static deflection behavior of a five-layered plate composed of three laminated glass and two polymeric interlayers was presented via the corresponding principle. In addition, a simply supported five-layer sandwich plate in the presence of uniformly distributed transverse excitation was investigated by Raissi et al. [38], while Khalil and Hadi [39] assessed a five-layer laminate of alternating fiber glass-polyester composite layers for damage detection using lamb waves simulation [39], see also [40,41,42,43,44,45,46,47,48] and the references therein for more related study on waves propagation and dispersion in various structures.

However, in this paper, we study the anti-plane shear motion of an isotropic inhomogeneous elastic five-layered plate using the asymptotic analysis method in regard to the various material parameters (also known as the multi-parametric analysis, [46]). The respective displacements and stresses in addition to the Rayleigh-Lamb dispersion relation corresponding to the antisymmetric motion will be determined. Beside, it is vital to note here that the antisymmetric motion associated with the five-layered plate with prescribed free-face conditions possesses a global low-frequency regime, whereas its symmetric version does not, see Kaplunov et al. [19] and Prikazchikova et al. [30] for similar considerations in the case of three-layered circular rods and laminate, respectively. Further, we investigate the possibilities to obtaining an optimal estimate or rather the range for the low-dimensionless parameters leading to the exact and approximate fundamental mode with a zero cutoff frequency in relation to the Rayleigh-Lamb dispersion relation under the four contrasting material setups recently examined in [29] and [30, 31] for a plane and anti-plate wave propagation problems, respectively. Also, the asymptotic behavior of the displacements and stresses in the respective layers will be examined. Further, the paper is organized as follows: In Sect. 3, we give the general formulation of the problem together with the four types of material contrasts to be examined. The Rayleigh-Lamb dispersion relation and the cutoff frequency are determined in Sect. 4 for the generalized case and in Sect. 5 for the unified case of the problem. The shortened polynomial dispersion analysis for the unified case in relation to the four contrasts is given in Sect. 6, while Sect. 7 presented the asymptotic behaviors of the displacements and stresses in the plate, and finally, Section 7 gives some concluding remarks.

2 Problem fomulation

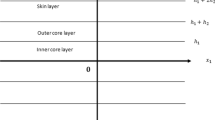
An anti-plane shear motion of an inhomogeneous elastic five-layered symmetric plate is considered. The plate comprises of the inner core layer of thickness $2h_1$, the outer core layers of thickness $h_2$ and the skin layers of thickness $h_3$. Further, as the plate is symmetric, the three layers of the plate are assumed to be different isotropic materials of which the overall plate is placed symmetrically about the mid-layer at (0, 0) as shown in Fig. 1.

Fig. 1

A symmetric inhomogeneous five-layered plate

The two-dimensional equation of motion in $(x_1, x_2)$ takes the form

$$\begin{aligned} \frac{\partial \sigma ^i_{13}}{\partial x_1}+ \frac{\partial \sigma ^i_{23}}{\partial x_2}= \rho _i \frac{\partial ^2 U_i}{\partial t^2}, \ \ i=ic, oc, s, \end{aligned}$$

(1)

where $x_n (n=1,2)$ are the spatial variables, t is the temporal variable, $U_i=U_i(x_1,x_2,t)$ are the out-of-plane displacements for $i=ic$ (inner core layer), $i=oc$ (outer core layer) and $i=s$ (skin layer). Further, the shear stresses $\sigma ^i_{j3},(j=1,2,)$ defined, respectively, as

$$\begin{aligned} \sigma ^i_{j3}=\mu _i \frac{\partial U_i}{\partial x_j}, \ j=1,2, \end{aligned}$$

(2)

where $\mu _i$ are the stiffnesses, also known as the Lame’s elastic constants of motion. We also prescribe the continuity conditions comprising of the continuity of displacements and stresses along the interfaces of the layers as follows:

$$\begin{aligned} \begin{aligned} \text {(a)} \ U_{ic}\left( x_1,x_2,t\right)&=U_{oc}\left( x_1,x_2,t\right) , \ \text {at} \ x_2=\pm h_1,\\ \text {(b)} \ \sigma ^{ic}_{23}(x_1,x_2,t)&=\sigma ^{oc}_{23}(x_1,x_2,t),\ \text {at} \ x_2=\pm h_1,\\ \text {(c)} \ U_{oc}\left( x_1,x_2,t\right)&=U_s\left( x_1,x_2,t\right) , \ \text {at} \ x_2=\pm (h_1+h_2), \\ \text {(d)} \ \sigma ^{oc}_{23}(x_1,x_2,t)&=\sigma ^{s}_{23}(x_1,x_2,t),\ \text {at} \ x_2=\pm (h_1+h_2), \end{aligned} \end{aligned}$$

(3)

and the traction-free conditions on the outer faces as follows:

$$\begin{aligned} \text { (e)} \ \sigma ^{s}_{23}(x_1,x_2,t)=0,\ \text {at} \ x_2 =\pm (h_1+h_2+h_3). \end{aligned}$$

(4)

Furthermore, we investigate the anti-plane shear motion to the inhomogeneous five-layered plate under the four contrasting material setups lately studied and given by ratios of the material constants via the following asymptotic relations [29,30,31]:

$$\begin{aligned} \begin{aligned} \text {(i)} \,&\mu \ll 1, \ h\thicksim 1, \ \rho \thicksim \mu , \ \ \\ \text {(ii)} \,&\mu \ll 1, \ h\thicksim \mu , \ \rho \thicksim \mu ^2, \\ \text {(iii)}\,&\mu \ll 1, \ h\thicksim \mu ^{-1/2}, \ \rho \thicksim \mu ^{1/2}, \\ \text {(iv)}\,&\mu \gg 1, \ h\thicksim \mu ^{-2}, \ \rho \thicksim \mu ^{-3}, \end{aligned} \end{aligned}$$

(5)

corresponding to a three-layered plate with stiff skin layers and light core, stiff thin skin layers and light core, stiff skin layers and thin light core and light thin skin layers and light core layers, respectively. Also in Eq. (5), $\mu , \ h \ \text {and} \ \rho$ are the Lame’s elastic constant (stiffness), thickness and density ratios, respectively. Additionally, we will devise a means to use the relations given in Eq. (5) to analyze the dispersion relation of a five-layered plate asymptotically. Note also that in a multi-layered or composite structure; it is pertinent to note that consecutive layers are never exactly the same.

3 Asymptotic approach to Rayleigh-Lamb dispersion relation and cutoff frequency

We determine the Rayleigh-Lamb dispersion relation and cutoff frequency of the formulated problem given in Eqs. (1)–(4). Also from Eqs. (1)–(2), we get the classical wave equation of the form

$$\begin{aligned} \frac{\partial ^2 U_i}{\partial x^2_1}+ \frac{\partial ^2 U_i}{\partial x^2_2}= \frac{1}{c^2_i} \frac{\partial ^2 U_i}{\partial t^2}, \ \ i=ic, oc, s, \end{aligned}$$

(6)

where $c_i=\sqrt{\frac{\mu _i}{\rho _i}},$ is the transverse speed. Now, if the harmonic solution of the form

$$\begin{aligned} U_i(x_1,x_2,t)=u_i(x_2)e^{i(kx_1-\omega t)}, \end{aligned}$$

is assumed, where $i=\sqrt{-1},$k is the dimensional wavenumber and $\omega$ is the dimensional frequency; then the solution of Eq. (6) becomes

$$\begin{aligned} u_i(x_2)=A_i \cosh \left( \sqrt{k^2-\frac{\omega ^2}{c_i^2}}x_2\right) +B_i \sinh \left( \sqrt{k^2-\frac{\omega ^2}{c_i^2}}x_2\right) , \ i=s,oc,ic, \end{aligned}$$

(7)

where $A_i, B_i,$ for $i=s,oc,ic$ are constants to be determined from the prescribed continuity and boundary conditions. Also, it is worth noting here that the solution determined in Eq. (7) was based on the assumption that the five-layered plate under consideration is symmetric.

Furthermore, the formulated problem via the solutions obtained in Eq. (7) coupled to the boundary conditions in Eqs. (3)–(4) posed a $5 \times 5$ dispersion matrix given in “Appendix A”. Also from the dispersion matrix, we obtain the Rayleigh-Lamb dispersion relation for the antisymmetric case given by

$$\begin{aligned} \begin{aligned}&\alpha _2 \mu ^* \cosh \left( \alpha _2 h\right) \left( \alpha _1 h h_* \mu \sinh \left( \alpha _1\right) \sinh \left( \alpha _3 h^*\right) +\alpha _3 h^* \mu _* \cosh \left( \alpha _1\right) \cosh \left( \alpha _3 h^*\right) \right) \\&\quad + \alpha _3 h^* \mu \mu _* \sinh \left( \alpha _2 h\right) \left( \alpha _1 \mu ^* \sinh \left( \alpha _1\right) \cosh \left( \alpha _3 h^*\right) +\alpha _3 \cosh \left( \alpha _1\right) \sinh \left( \alpha _3 h^*\right) \right) =0, \end{aligned} \end{aligned}$$

(8)

with

$$\begin{aligned} \alpha _1=\sqrt{K^2-\Omega ^2}, \ \alpha _2=\sqrt{K^2-\frac{\mu }{\rho }\Omega ^2}, \ \alpha _3=\sqrt{K^2-\frac{\mu ^* }{\rho ^*}\Omega ^2}, \end{aligned}$$

(9)

and the dimensionless frequency $\Omega$ and wavenumber K given by

$$\begin{aligned} \Omega =\frac{\omega h_3}{c_s}, \ \ \ \ \ K=kh_3, \ \end{aligned}$$

(10)

together with the following dimensionless parameters

$$\begin{aligned} \begin{aligned} \mu =&\frac{\mu _s}{\mu _{ic}}, \ \ \mu _* = \frac{\mu _{oc}}{\mu _{ic}}, \ \ \mu ^*= \frac{\mu _s}{\mu _{oc}}, \\ h=&\frac{h_1}{h_3}, \ \ h_*=\frac{h_2}{h_1}, \ \ \ h^*=\frac{h_2}{h_3}, \\ \rho =&\frac{\rho _s}{\rho _{ic}}, \ \ \rho ^*=\frac{\rho _s}{\rho _{oc}}, \\ \end{aligned} \end{aligned}$$

(11)

where $\{\mu , \mu _*, \mu ^*\}$, $\{h, h_*, h^*\}$ and $\{\rho , \rho ^*\}$ are the dimensionless stiffnesses, thicknesses and densities ratios, respectively. We thus obtain the cutoff frequency from the Rayleigh-Lamb dispersion relation given in Eq. (8) by setting $K=0$ as follows

$$\begin{aligned} \begin{aligned}&\sqrt{\rho ^*} \cos \left( h\sqrt{\frac{\mu }{\rho }}\Omega \right) \left( h h_* \mu \sqrt{\rho ^*} \sin (\Omega ) \sin \left( h^*\sqrt{\frac{\mu ^*}{\rho ^*}}\Omega \right) -h^* \mu _* \sqrt{\mu ^*} \cos (\Omega ) \cos \left( h^*\sqrt{\frac{\mu ^*}{\rho ^*}}\Omega \right) \right) \\&\quad + h^* \mu _*\sqrt{\mu \rho } \sin \left( h\sqrt{\frac{\mu }{\rho }}\Omega \right) \left( \sqrt{\mu ^*\rho ^*} \sin (\Omega ) \cos \left( h^*\sqrt{\frac{\mu ^*}{\rho ^*}}\Omega \right) +\cos (\Omega ) \sin \left( h^*\sqrt{\frac{\mu ^*}{\rho ^*}}\Omega \right) \right) =0. \end{aligned} \end{aligned}$$

(12)

From Eq. (12), we get the predicted single cutoff frequency as

$$\begin{aligned} \Omega \approx \sqrt{\frac{\mu _* \rho ^*}{h \mu r_1}} \ll 1, \end{aligned}$$

(13)

over the low-frequency range

$$\begin{aligned} \left( \frac{\mu _* \rho ^*}{\mu r_1}\ll h\ll \frac{\rho r_1}{\mu _* \rho ^*} \right) \ {\cap }\ \left( \frac{\mu _*(h*)^2 \mu ^*}{\mu r_1}\ll h\ll \frac{\rho r_1}{\mu _* \rho ^*}\right) , \end{aligned}$$

(14)

where

$$\begin{aligned} r_1= \mu _* \left( h^*+\rho ^*\right) +h_* \rho ^*. \end{aligned}$$

It is worth mentioning here that the low frequency is attained when $\Omega \ll 1$, while long-wave motion is achieved when $K\ll 1$, [2].

Further, the polynomial dispersion relation is determined by the application of Taylor’s series expansion method from Eq. (8) as:

$$\begin{aligned} \mu ^*\mu _*+\gamma _1 K^2+\gamma _2 K^4+ \gamma _3 K^2 \Omega ^2+\gamma _4 \Omega ^2+\gamma _5 \Omega ^4+\gamma _6 K^2 \Omega ^4+\gamma _7 K^4 \Omega ^2+...=0, \end{aligned}$$

(15)

see, “Appendix B” for $\gamma _l, (l=1,2,...,7)$. Dispersion curves from the exact dispersion relation Eq. (8) are plotted in Fig. 2 for the non-estimated range and Fig. 3 for the estimated range of zero cutoff frequencies, respectively. As anticipated, the cutoff frequency is not observed in Fig. 2 since the choice of parameters is outside the estimated range given in Eq. (14); while lowest low frequency is achieved in Fig. 3 over the stated range.

Fig. 2

Dispersion curves from Eq. (8) for the non-estimated range case with the following parameter: $\rho = 0.77, \rho ^* = 0.9, h_*= 7.7, h^* =8.7, \mu ^* = 0.83, \mu _* = 0.012, \mu = 0.2, h= 1.0$

Fig. 3

Dispersion curves from Eq. (8) for the estimated range case with the following parameter: $\rho = 0.22, \rho ^* = 0.012, h_*= 1.1, h^* =0.64, \mu ^* = 0.3, \mu _* = 169, \mu = 0.183, h= 1.0$

The displacements and stresses in the respective layers are found to be

$$\begin{aligned}&\begin{aligned} U_{ic}=&h_3\frac{\sinh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) }{\alpha _2},\\ \sigma _{13}^{ic}=&i \mu _{ic} K\frac{\sinh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) }{\alpha _2},\\ \sigma _{23}^{ic}=&\mu _{ic} \cosh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) , \end{aligned} \end{aligned}$$

(16)

$$\begin{aligned}&\begin{aligned} U_{oc}=&\frac{h_3}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \sinh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) \right) , \\ \sigma _{13}^{oc}=&i \mu _{oc} \frac{K}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \sinh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) \right) , \\ \sigma _{23}^{oc}=&\mu _{oc} \frac{\alpha _3}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \sinh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \cosh \left( \alpha _3 h^* \xi _{2_{\text {oc}}}\right) \right) , \end{aligned} \end{aligned}$$

(17)

and

$$\begin{aligned} \begin{aligned} U_s=&h_3\lambda \left( \cosh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) -\tanh \left( \alpha _1 \left( h^*+h+1\right) \right) \sinh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) \right) ,\\ \sigma _{13}^s=&i \mu _{s} K \lambda \left( \cosh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) -\tanh \left( \alpha _1 \left( h^*+h+1\right) \right) \sinh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) \right) ,\\ \sigma _{23}^s=&\mu _s\alpha _1\lambda \left( \sinh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) -\tanh \left( \alpha _1 \left( h^*+h+1\right) \right) \cosh \left( \alpha _1 \left( \xi _{2_s}+h^*+h\right) \right) \right) , \end{aligned} \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{aligned} \beta =\frac{\alpha _2 h h_*}{\alpha _3 h^* \mu _*},\ \ \lambda =\frac{\sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 h^*\right) +\beta \sinh \left( \alpha _3 h^*\right) \cosh \left( \alpha _2 h\right) }{\alpha _2 [\cosh \left( \alpha _1 \left( h^*+h\right) \right) -\sinh \left( \alpha _1 \left( h^*+h\right) \right) \tanh \left( \alpha _1 \left( h^*+h+1\right) \right) ]}, \end{aligned} \end{aligned}$$

(19)

coupled to the corresponding scaled variables

$$\begin{aligned} \begin{aligned} \xi _{2_{\text {ic}}}=&\frac{x_2}{h_1},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \le x_2 \le h_1,\\ \xi _{2_{\text {oc}}} =&\frac{x_2-h_1}{h_2},\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h_1 \le x_2 \le h_1+h_2,\\ \xi _{2_{\text {s}}} =&\frac{x_2-(h_1+h_2)}{h_3},\ \ \ \ \ \ \ \ \ \ h_1+h_2 \le x_2 \le h_1+h_2+h_3. \end{aligned} \end{aligned}$$

(20)

Note that we omitted the exponential factor $e^{i(kx_1-\omega t)}$ in Eqs. (16)–(18).

4 Unified Rayleigh-Lamb dispersion relation and cut-off frequency

Due to the varying parameters posed by the problem as can be seen in from Eq. (11), we therefore aim in this section to unify these parameters in order to be able to carry out further analysis in the next section for the four contrasting material setups mentioned. Thus, we unify the posed parameters as a case of interest under the following realistic assumptions that:

(1):

the length of the outer core layer is a multiple of the length of the inner core layer, i.e., $h_2=\eta h_1$, with $\eta \in \mathbb {R^{+}} \backslash \{0,1\}$,

(2):

the Lame’s elastic constant of the outer core layer is a multiple of the Lame’s elastic constant of the inner core layer, i.e., $\mu _{oc}=\delta \mu _{ic},$ for $\delta \in \mathbb {R^{+}} \backslash \{0,1\},$ and

(3):

the density of the outer core layer is a multiple of the density of the inner core layer, i.e., $\rho _{oc}= \gamma \rho _{ic}$, where $\gamma \in \mathbb {R^{+}} \backslash \{0,1\}$.

Thus with the above assumptions, Eq. (11) now reduces to

$$\begin{aligned} \begin{aligned} h=&\frac{h_1}{h_3}, \ h_*=\eta , \ h^*=\eta h, \\ \mu =&\frac{\mu _s}{\mu _{\text {ic}}}, \ \mu _* = \delta , \ \mu ^*= \frac{1}{\delta } \mu , \\ \rho =&\frac{\rho _s}{\rho _{\text {ic}}}, \ \rho ^*=\frac{1}{\gamma }\rho , \end{aligned} \end{aligned}$$

(21)

where $\eta , \ \delta$ and $\gamma$ are the unification (controlling/scaling) parameters.

Therefore, with the present development outlined in the above equation, the Rayleigh-Lamb dispersion relation given in Eq. (8) reduces to the new unified Rayleigh-Lamb dispersion as follows

$$\begin{aligned} \begin{aligned}&\alpha _1 \mu \sinh \left( \alpha _1\right) \left( \alpha _3 \delta \sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h\right) +\alpha _2 \cosh \left( \alpha _2 h\right) \sinh \left( \alpha _3 \eta h\right) \right) \\&\quad + \alpha _3 \delta \cosh \left( \alpha _1\right) \left( \alpha _3 \delta \sinh \left( \alpha _2 h\right) \sinh \left( \alpha _3 \eta h\right) +\alpha _2 \cosh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h\right) \right) =0, \end{aligned} \end{aligned}$$

(22)

where

$$\begin{aligned} \alpha _1=\sqrt{K^2-\Omega ^2}, \ \ \ \ \alpha _2=\sqrt{K^2-\frac{\mu }{\rho } \Omega ^2}, \ \ \ \ \alpha _3=\sqrt{K^2-\frac{\gamma \mu }{\delta \rho } \Omega ^2}. \end{aligned}$$

(23)

From Eq.(22), the resultant cutoff frequency and the predicted single cutoff frequency are, respectively, found as proceeded to be

$$\begin{aligned} \begin{aligned}&\sqrt{\gamma \delta } \cos \left( \eta h \sqrt{\frac{\gamma \mu }{\delta \rho }}\Omega \right) \left( \sqrt{\rho \mu } \sin (\Omega ) \sin \left( h \sqrt{\frac{ \mu }{ \rho }}\Omega \right) -\cos (\Omega ) \cos \left( h \sqrt{\frac{ \mu }{ \rho }}\Omega \right) \right) \\&\quad +\sin \left( \eta h \sqrt{\frac{\gamma \mu }{\delta \rho }}\Omega \right) \left( \gamma \delta \cos (\Omega ) \sin \left( h \sqrt{\frac{ \mu }{ \rho }}\Omega \right) +\sqrt{\rho \mu } \sin (\Omega ) \cos \left( h \sqrt{\frac{ \mu }{ \rho }}\Omega \right) \right) =0, \end{aligned} \end{aligned}$$

(24)

and

$$\begin{aligned} \Omega \approx \sqrt{\frac{\delta \rho }{h \mu r_2}} \ll 1, \end{aligned}$$

(25)

over the range

$$\begin{aligned} \frac{\delta \rho }{\mu r_2}\ll h\ll \frac{r_2}{\delta }, \end{aligned}$$

(26)

where

$$\begin{aligned} r_2=\delta \rho +\eta \rho +\gamma \delta \eta h. \end{aligned}$$

Similarly, expanding all the hyperbolic functions of the unified Rayleigh-Lamb dispersion given in Eq. (22) by virtue of the Taylor’s series expansion, we get the unified polynomial dispersion relation as follows

$$\begin{aligned} \delta + G_1K^2+G_2 K^4+G_3K^2 \Omega ^2 +G_4 \Omega ^2 +G_5 \Omega ^4+G_6 K^2 \Omega ^4 +G_7 K^4 \Omega ^2+...=0, \end{aligned}$$

(27)

where

$$\begin{aligned} \begin{aligned} G_1=&\frac{\delta }{2}+h (\delta +\eta )\mu +h^2 \left( \delta \eta +\frac{ \eta ^2}{2}+\frac{1 }{2}\right) \delta ,\\ G_2=&\frac{\delta }{24}+h \left( \frac{\delta }{6}+\frac{\eta }{6}\right) \mu +h^2 \left( \frac{\delta \eta }{2}+\frac{ \eta ^2}{4}+\frac{1}{4}\right) \delta +h^3 \left( \frac{1}{2} \delta \eta ^2 +\frac{\delta }{6}+\frac{\eta ^3 }{6}+\frac{\eta }{2}\right) \mu , \\ G_3=&-\frac{\delta }{12}-h \left( \frac{\delta }{3}+\frac{\eta }{3}\right) \mu -h^2 \left( \ \left( \frac{\gamma \delta \eta }{2 \rho }+\frac{\gamma \eta ^2}{4 \rho }+\frac{\delta }{4 \rho }\right) \mu +\frac{\delta ^2 \eta }{2}+\frac{\delta \eta ^2}{4}+\frac{\delta }{4}\right) \\&- h^3 \left( \left( \frac{\gamma \eta ^3}{6 \delta \rho }+\frac{\gamma \eta ^2}{2 \rho }+\frac{\delta }{6 \rho }+\frac{\eta }{2 \rho }\right) \mu ^2+ \left( \frac{\delta \eta ^2}{2}+\frac{\delta }{6}+\frac{\eta ^3}{6}+\frac{\eta }{2}\right) \mu \right) ,\\ G_4=&-\frac{\delta }{2}-h (\delta +\eta )\mu -h^2 \left( \frac{\gamma \delta \eta }{\rho }+\frac{\gamma \eta ^2}{2 \rho }+\frac{\delta }{2 \rho }\right) \mu ,\\ G_5=&\frac{\delta }{24}+h \left( \frac{\delta }{6}+\frac{\eta }{6}\right) \mu +h^2 \left( \frac{\gamma \delta \eta }{2 \rho }+\frac{\gamma \eta ^2}{4 \rho }+\frac{\delta }{4 \rho }\right) \mu +h^3 \left( \frac{\gamma \eta ^3}{6 \delta \rho }+\frac{\gamma \eta ^2}{2 \rho }+\frac{\delta }{6 \rho }+\frac{\eta }{2 \rho }\right) \mu ^2,\\ G_6=&h^2 \left( \frac{\gamma \delta \eta }{12 \rho }+\frac{\gamma \eta ^2}{24 \rho }+\frac{\delta }{24 \rho }\right) \mu +h^2 \left( \frac{\delta ^2 \eta }{24}+\frac{\delta \eta ^2}{48}+\frac{\delta }{48}\right) ,\\ G_7=&-h^2 \left( \frac{\gamma \delta \eta }{24 \rho }+\frac{\gamma \eta ^2}{48 \rho }+\frac{\delta }{48 \rho }\right) \mu -h^2 \left( \frac{\delta ^2 \eta }{12}+\frac{\delta \eta ^2}{24}+\frac{\delta }{24}\right) ,\\ \vdots&\end{aligned} \end{aligned}$$

(28)

Therefore we are now at the liberty to consider the aforementioned contrasting setups in Sect. 2, Eq. (5) having unified the dimensionless parameters. It is worth noting here that based on the unification assumptions that led to the new relations given Eq. (21); that the outer core layers are strongly depend on the material properties of the inner core layer. Also, Eq. (5) remains the same for both the five-layered plate under consideration and the three-layered plates analyzed in [29,30,31].

We thus present the dispersion curves from the unified exact dispersion relation Eq. (22) in Figs. 4 and 5 for the non-estimated and estimated (Eq. (26) of zero cutoff frequencies) ranges, respectively.

Fig. 4

Dispersion curves from Eq. (22) for the non-estimated range case with the following parameter: $\eta =0.45, \delta =20, \gamma =14, \rho =0.8, \mu =0.07, h=1$

Fig. 5

Dispersion curves from Eq. (22) for the estimated range case with the following parameter: $\eta =0.45, \delta =20, \gamma =14, \rho =0.03, \mu =0.05, h=1.0$

5 Shortened polynomial dispersion relations

In this section, we approximate the obtained unified polynomial dispersion relation in Eq. (27) in connection to the four contrasting material setups to obtain the corresponding optimal shortened polynomial dispersion in each setup. It is worth mentioning here that we consider $\eta$ to be $\in (0,1)$ and $\delta ,\gamma > 1$ for the ordering analysis.

5.1 Stiff skin layers, inner core dependant outer core layers and light inner core layer ($\mu \ll 1, \ h\thicksim 1, \ \rho \thicksim \mu$)

Here, the outer skin layers are made up of stiff material while both the inner core layer and the outer core layers are made up of different soft materials, that is, they are not identically the same, (also, similar assumption is made in the subsequent cases).

So, on using the present setup, it can be seen from Eq. (28) that the following behavior

$$\begin{aligned} G_1\thicksim G_2\thicksim \delta , \ G_3\thicksim G_4\thicksim G_5\thicksim G_6\thicksim G_7\thicksim \gamma \delta \eta , \end{aligned}$$

(29)

is obtained at the leading orders, where

$$\begin{aligned} G_1= & {} \frac{\delta }{2}+\left( \delta \eta +\frac{ \eta ^2}{2}+\frac{1 }{2}\right) \delta , \nonumber \\ G_2= & {} \frac{\delta }{24}+ \left( \frac{\delta \eta }{2}+\frac{ \eta ^2}{4}+\frac{1}{4}\right) \delta , \nonumber \\ G_3= & {} -\left( \ \frac{\delta ^2 \eta }{2}+\frac{\delta \eta ^2}{4}+\frac{\delta }{3}\right) - \left( \frac{\gamma \delta \eta }{2 }+\frac{\gamma \eta ^2}{4 }+\frac{\delta }{4 }\right) \nu ,\nonumber \\ G_4= & {} -\frac{\delta }{2}- \left( \gamma \delta \eta +\frac{\gamma \eta ^2}{2 }+\frac{\delta }{2 }\right) \nu , \nonumber \\ G_5= & {} \frac{\delta }{24}+ \left( \frac{\gamma \delta \eta }{2 }+\frac{\gamma \eta ^2}{4 }+\frac{\delta }{4 }\right) \nu ,\nonumber \\ G_6= & {} \left( \frac{\delta ^2 \eta }{24}+\frac{\delta \eta ^2}{48}+\frac{\delta }{48}\right) +\left( \frac{\gamma \delta \eta }{12 }+\frac{\gamma \eta ^2}{24 }+\frac{\delta }{24 }\right) \nu ,\nonumber \\ G_7= & {} - \left( \frac{\delta ^2 \eta }{12}+\frac{\delta \eta ^2}{24}+\frac{\delta }{24}\right) - \left( \frac{\gamma \delta \eta }{24 }+\frac{\gamma \eta ^2}{48 }+\frac{\delta }{48 }\right) \nu ,\nonumber \\&\vdots&\end{aligned}$$

(30)

where $\nu =\frac{\mu }{\rho } \thicksim 1.$ Thus, we obtain the shortened polynomial dispersion relation as follows

$$\begin{aligned} \delta + G_1K^2+G_2 K^4+G_3K^2 \Omega ^2 +G_4 \Omega ^2 +G_5 \Omega ^4=0. \end{aligned}$$

(31)

We, therefore, normalize the dimensionless frequency and wave number in Eq. (31) using

$$\begin{aligned} \Omega ^2=\mu \Psi ^2, \ \ \ \ K^2=\mu K_*^2, \end{aligned}$$

(32)

to obtain

$$\begin{aligned} \frac{\delta }{\mu }+G_1K_*^2 +\mu G_2 K_{*}^4+\mu G_3K_*^2 \Psi ^2+G_4 \Psi ^2+ \mu G_5 \Psi ^4=0, \end{aligned}$$

(33)

and thereafter make use of a near cutoff asymptotic expansion of the form

$$\begin{aligned} \Psi ^2=\Psi ^2_0+\mu \Psi ^2_1+\mu ^2 \Psi ^2_2+... \end{aligned}$$

(34)

Substituting Eq. (34) into (33), we get

$$\begin{aligned} \begin{aligned} \Psi ^2_0 =\delta , \ \ \Psi ^2_1 =-\frac{\delta ^2}{2}+\delta \left( \delta \eta +\frac{1}{2} \eta ^2+1 \right) K_*^2, \end{aligned} \end{aligned}$$

(35)

and yielding the optimal shortened dispersion relation below

$$\begin{aligned} \delta \left( \delta \eta +\frac{ \eta ^2}{2}+1 \right) K^2-\frac{1}{\mu }\Omega ^2 +\delta \left( 1-\frac{\delta }{2}\mu \right) =0. \end{aligned}$$

(36)

Thus, we give in Fig. 6 the lowest dispersion branch for the exact (black solid line) and the shortened polynomial (dashed red line) unified dispersion relations (22) and (36) for the set of parameters $\eta =0.45, \ \delta =20, \ \gamma =14, \ \rho =0.0076, \ \mu =0.0072, \ h=1.1$.

Fig. 6

Lowest dispersion branch for the exact (black solid line) and shortened polynomial (dashed red line) dispersion relations Eqs. (22) and (36)

5.2 Stiff thin skin layers, inner core dependant outer core layers and light inner core layer ($\mu \ll 1, \ h\thicksim \mu , \ \rho \thicksim \mu ^2$)

Using the present setup, the following behavior can be obtained from Eq. (28)

$$\begin{aligned} G_1\thicksim G_2\thicksim G_3\thicksim G_4 \thicksim G_5 \thicksim \delta , \ G_6\thicksim G_7\thicksim \mu , \end{aligned}$$

(37)

where

$$\begin{aligned} \begin{aligned} G_1=&\frac{\delta }{2}+h^2 \left( \delta ^2 \eta +\frac{\delta \eta ^2}{2}+\frac{\delta }{2}\right) ,\\ G_2=&\frac{\delta }{24}+h^2 \left( \frac{\delta ^2 \eta }{2}+\frac{\delta \eta ^2}{4}+\frac{\delta }{4}\right) , \\ G_3=&-\frac{\delta }{12}-h \left( \frac{\gamma \delta \eta }{2}+\frac{\gamma \eta ^2}{4}+\frac{\delta }{4}\right) \nu ,\\ G_4=&-\frac{\delta }{2}-h\left( \gamma \delta \eta +\frac{\gamma \eta ^2}{2}+\frac{\delta }{2}\right) \nu ,\\ G_5=&\frac{\delta }{24}+h \left( \frac{\gamma \delta \eta }{2}+\frac{\gamma \eta ^2}{4}+\frac{\delta }{4}\right) \nu ,\\ G_6=&\nu \left( \frac{\gamma \delta \eta }{12 }+\frac{\gamma \eta ^2}{24 }+\frac{\delta }{24 }\right) \mu ,\\ G_7=&-\nu \left( \frac{\gamma \delta \eta }{24 }+\frac{\gamma \eta ^2}{48 }+\frac{\delta }{48 }\right) \mu ,\\&\vdots \end{aligned} \end{aligned}$$

(38)

where $h \thicksim \mu , \ \nu =\frac{\mu ^2}{\rho } \thicksim 1$. Therefore, we obtain the shortened polynomial dispersion relation as follows

$$\begin{aligned} \delta + G_1K^2+G_2 K^4+G_3K^2 \Omega ^2 +G_4 \Omega ^2 +G_5 \Omega ^4=0. \end{aligned}$$

(39)

So, we give in Fig. 7 the lowest dispersion branch for the exact (black solid line) and the shortened polynomial (dashed red line) dispersion relations (22) and (39) using the parameters $\eta =0.45, \ \delta =20, \ \gamma =14, \ \rho =0.007, \ \mu =0.59, \ h=0.968$.

Fig. 7

Lowest dispersion branch for the exact (black solid line) and shortened polynomial (dashed red line) dispersion relations Eqs. (22) and (39)

5.3 Stiff skin layers, inner core dependant outer core layers and thin light inner core layer $( \mu \ll 1, \ h\thicksim \mu ^{-1/2}, \ \rho \thicksim \mu ^{1/2})$

Using the current setup, it can be deduced from Eq. (28) that the following asymptotic relation at the leading powers is obtained to be

$$\begin{aligned} G_1\thicksim G_2\thicksim G_3\thicksim G_6\thicksim G_7\thicksim \mu ^{-1}, \ G_4\thicksim G_5 \thicksim \mu ^{-1/2}, \end{aligned}$$

(40)

with

$$\begin{aligned} \begin{aligned} G_1=&\frac{\delta }{2}+\frac{1}{\mu } \left( \delta \eta +\frac{ \eta ^2}{2}+\frac{1 }{2}\right) \delta ,\\ G_2=&\frac{\delta }{24}+\frac{1}{\mu } \left( \frac{\delta \eta }{2}+\frac{ \eta ^2}{4}+\frac{1}{4}\right) \delta , \\ G_3=&-\left( \frac{\gamma \eta ^3}{6 \delta }+\frac{\gamma \eta ^2}{2 }+\frac{\delta }{4 }+\frac{\eta }{2 }\right) - \frac{1}{\mu }\left( \ \frac{\delta ^2 \eta }{2}+\frac{\delta \eta ^2}{4}+\frac{\delta }{4}\right) ,\\ G_4=&-\frac{\delta }{2}- \frac{1}{\sqrt{\mu }}\left( \gamma \delta \eta +\frac{\gamma \eta ^2}{2}+\frac{\delta }{2 }\right) ,\\ G_5=&\left( \frac{\gamma \eta ^3}{6 \delta }+\frac{\gamma \eta ^2}{2 }+\frac{5\delta }{24 }+\frac{\eta }{2 }\right) +\frac{1}{\sqrt{\mu }} \left( \frac{\gamma \delta \eta }{2 }+\frac{\gamma \eta ^2}{4 }+\frac{\delta }{4 }\right) ,\\ G_6=&\frac{1}{\mu } \left( \frac{\delta ^2 \eta }{24}+\frac{\delta \eta ^2}{48}+\frac{\delta }{48}\right) ,\\ G_7=&- \frac{1}{\mu } \left( \frac{\delta ^2 \eta }{12}+\frac{\delta \eta ^2}{24}+\frac{\delta }{24}\right) ,\\&\vdots \end{aligned} \end{aligned}$$

(41)

Thus, we obtain the following shortened polynomial dispersion relation

$$\begin{aligned} \begin{aligned} \delta + G_1K^2+G_2 K^4+G_3K^2 \Omega ^2 +G_4 \Omega ^2 +G_5 \Omega ^4=0. \end{aligned} \end{aligned}$$

(42)

We equivalently set $\mu = 1/\beta ^2$ in Eq. (42) and further normalize the resultant equation using the following dimensionless frequency and wave number

$$\begin{aligned} \Omega ^2=\beta \Psi ^2, \ \ \ \ K^2=\beta K_*^2. \end{aligned}$$

(43)

Furthermore, the near cutoff asymptotic expansion is needed by the problem which takes the form

$$\begin{aligned} \Psi ^2=\Psi ^2_0+\beta \Psi ^2_1+\beta ^2 \Psi ^2_2+... \end{aligned}$$

(44)

Substituting Eq. (44) into the resultant equation of (42) coupled to the normalization in (43), we get

$$\begin{aligned} \begin{aligned} \Psi ^2_0 =\delta , \ \ \Psi ^2_1 =\frac{\delta }{2}(K_*^2-\delta ), \end{aligned} \end{aligned}$$

(45)

and yielding the optimal shortened dispersion relation below

$$\begin{aligned} \frac{\delta }{2} K^2-\frac{1}{\beta }\Omega ^2+\delta \left( 1 -\beta \frac{ \delta }{2}\right) =0. \end{aligned}$$

(46)

Also, we give in Fig. 8 the lowest dispersion branch for the exact (black solid line) and the shortened polynomial (dashed red line) dispersion relations (22) and (46) using the parameters $\eta =0.45, \ \delta =20, \ \gamma =14, \ \rho =0.0628, \ \ \beta =0.095, \ h=1$.

Fig. 8

Lowest dispersion branch for the exact (black solid line) and shortened polynomial (dashed red line) dispersion relations Eqs. (22) and (46)

5.4 Light thin skin layers, inner core dependant outer core layers and light inner core layer $(\mu \gg 1, \ h\thicksim \mu ^{-2}, \ \rho \thicksim \mu ^{-3})$

Using the present setup, it can be deduced from Eq. (28) that the following asymptotic relation

$$\begin{aligned} G_1\thicksim G_2\thicksim G_3\thicksim G_4\thicksim G_5 \thicksim \mu ^{-1}, \ G_6\thicksim G_7 \thicksim \gamma \delta \eta , \end{aligned}$$

(47)

with

$$\begin{aligned} \begin{aligned} G_1=&\frac{\delta }{2}+ \frac{1}{\mu }(\delta +\eta ),\\ G_2=&\frac{\delta }{24}+\frac{1}{\mu } \left( \frac{\delta }{6}+\frac{\eta }{6}\right) ,\\ G_3=&-\left( \frac{\gamma \delta \eta }{2}+\frac{\gamma \eta ^2}{4}+\frac{\delta }{3}\right) -\frac{1}{\mu } \left( \frac{\gamma \eta ^3}{6 \delta }+\frac{\gamma \eta ^2}{2}+\frac{\delta }{2}+\frac{5 \eta }{6}\right) ,\\ G_4=&-\left( \gamma \delta \eta +\frac{\gamma \eta ^2}{2}\right) -\frac{1 }{\mu }(\delta +\eta ),\\ G_5=&\left( \frac{\gamma \delta \eta }{2}+\frac{\gamma \eta ^2}{4}+\frac{7 \delta }{24}\right) +\frac{1}{\mu } \left( \frac{\gamma \eta ^3}{6 \delta }+\frac{\gamma \eta ^2}{2}+\frac{\delta }{3}+\frac{2 \eta }{3}\right) ,\\ G_6=&\left( \frac{\gamma \delta \eta }{12}+\frac{\gamma \eta ^2}{24}+\frac{\delta }{24}\right) ,\\ G_7=&-\left( \frac{\gamma \delta \eta }{24}+\frac{\gamma \eta ^2}{48}+\frac{\delta }{48}\right) ,\\&\vdots \end{aligned} \end{aligned}$$

(48)

In the same manner as in above, we obtain the following shortened polynomial dispersion as follows

$$\begin{aligned} \delta + G_1K^2+G_2 K^4+G_3K^2 \Omega ^2 +G_4 \Omega ^2 +G_5 \Omega ^4=0. \end{aligned}$$

(49)

Figure 9 gives the lowest dispersion branch for the exact (black solid line) and the shortened polynomial (dashed red line) dispersion relations (22) and (49) using the parameters $\eta =0.88,\ \delta =20,\ \gamma =18,\ \rho =0.000306,\ \mu =14.6,\ h=0.0045$.

Fig. 9

Lowest dispersion branch for the exact (black solid line) and shortened polynomial (dashed red line) dispersion relations Eqs. (22) and (49)

6 Asymptotic behavior for the displacements and stresses

In this section, we study the asymptotic behaviors of the obtained displacements and stresses in the respective layers given in Sect. 4, Eqs. (16)–(18). It is also vital to note that these asymptotic behaviors are studied for the unified displacements and stresses at the leading order by employing the assumptions made in Sect. 5, Eq. (21) on the exact displacements and stresses. We thus obtain the following unified formulae from Eqs. (16)–(18):

$$\begin{aligned}&\begin{aligned} U_{ic}=&h_3\frac{\sinh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) }{\alpha _2},\\ \sigma _{13}^{ic}=&i \mu _{ic} K\frac{\sinh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) }{\alpha _2},\\ \sigma _{23}^{ic}=&\mu _{ic} \cosh \left( \alpha _2 h \xi _{2_{\text {ic}}}\right) , \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned}&\begin{aligned} U_{oc}=&\frac{h_3}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \sinh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) \right) , \\ \sigma _{13}^{oc}=&i \delta \mu _{ic} \frac{K}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \sinh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) \right) , \\ \sigma _{23}^{oc}=&\delta \mu _{ic} \frac{\alpha _3}{\alpha _2}\left( \sinh \left( \alpha _2 h\right) \sinh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) +\beta \cosh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h \xi _{2_{\text {oc}}}\right) \right) , \end{aligned} \end{aligned}$$

(51)

and

$$\begin{aligned} \begin{aligned} U_s=&h_3\lambda \left( \cosh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) -\tanh \left( \alpha _1 \left( \eta h+h+1\right) \right) \sinh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) \right) ,\\ \sigma _{13}^s=&i \mu _{s} K \lambda \left( \cosh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) -\tanh \left( \alpha _1 \left( \eta h+h+1\right) \right) \sinh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) \right) ,\\ \sigma _{23}^s=&\mu _s\alpha _1\lambda \left( \sinh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) -\tanh \left( \alpha _1 \left( \eta h+h+1\right) \right) \cosh \left( \alpha _1 \left( \xi _{2_s}+\eta h+h\right) \right) \right) , \end{aligned} \end{aligned}$$

(52)

where

$$\begin{aligned} \begin{aligned} \beta =&\frac{\alpha _2 }{\alpha _3 \delta },\ \ \lambda =\frac{\sinh \left( \alpha _2 h\right) \cosh \left( \alpha _3 \eta h\right) +\beta \sinh \left( \alpha _3 \eta h\right) \cosh \left( \alpha _2 h\right) }{\alpha _2 [\cosh \left( \alpha _1 h\left( \eta +1\right) \right) -\sinh \left( \alpha _1 h \left( \eta +1\right) \right) \tanh \left( \alpha _1 \left( \eta h+h+1\right) \right) ]}, \end{aligned} \end{aligned}$$

(53)

also valid for the scaled intervals in Eq. (20) with $h_2=\eta h_1$; where $\alpha _j (j=1,2,3)$ are given in Eq. (23). Thus, we present the asymptotic formulae in Table 1 for setups (i) and (ii) and Table 2 for setups (iii) and (iv) by using the following dimensionless normalized qualities: $\Omega ^2=\mu \Psi ^2,$$K^2=\mu K_*^2.$

Table 1 Asymptotic formulae for setups (i) and (ii)

Table 2 Asymptotic formulae for setups (iii) and (iv)

7 Conclusion

In conclusion, the antisymmetric anti-plane shear dispersion of an elastic five-layered plate is analyzed via the asymptotic analysis. The five-layered plate considered is made up of three different layers of varying material properties arranged in a symmetrical form as shown in Fig. 1. The obtained exact Rayleigh-Lamb dispersion relation was further analyzed for the best fundamental mode approximations (estimates) and its corresponding polynomial dispersion relation. Furthermore, due to the number of dimensionless problem parameters posed by the system comprising of 3 thicknesses, 3 stiffnesses (Lame’s elastic constants) and 2 mass densities; a unification of parameters was necessary to further analyze the problem for the determination of optimal shortened polynomial dispersion relations in connection to the four contrasting material setups as examined in [29,30,31] for a three-layered laminate. It is remarkable to mention that within the estimated range, more modes are observed in the present study in comparison with the three-layered case [30, 31]. Finally, since the unification of parameters has been proposed in this paper to further analyze the Rayleigh-Lamb dispersion relation and to be able to carry out all the analysis involved, it is highly recommended that a procedure leading to the said analysis should be devised without the unification.

Appendices

Appendix A

The dispersion matrix posed by the problem in Sect. 4 is as follows:

$$\begin{aligned} \left( \begin{array}{ccccc} \sinh \left( p_1\right) &{} -\cosh \left( p_2\right) &{} -\sinh \left( p_2\right) &{} 0 &{} 0 \\ 0 &{} \cosh \left( p_3\right) &{} \sinh \left( p_3\right) &{} -\cosh \left( p_4\right) &{} -\sinh \left( p_4\right) \\ \cosh \left( p_1\right) R_{\text {ic}} \mu _{\text {ic}} &{} -\sinh \left( p_2\right) R_{\text {oc}} \mu _{\text {oc}} &{} -\cosh \left( p_2\right) R_{\text {oc}} \mu _{\text {oc}} &{} 0 &{} 0 \\ 0 &{} \sinh \left( p_3\right) R_{\text {oc}} \mu _{\text {oc}} &{} \cosh \left( p_3\right) R_{\text {oc}} \mu _{\text {oc}} &{} -\sinh \left( p_4\right) R_s \mu _s &{} -\cosh \left( p_4\right) R_s \mu _s \\ 0 &{} 0 &{} 0 &{} \sinh \left( p_5\right) &{} \cosh \left( p_5\right) \\ \end{array} \right) , \end{aligned}$$

with the following shortend terms in the matrix above

$$\begin{aligned} p_1=h_1 R_{\text {ic}}, \ \ p_2=h_1 R_{\text {oc}}, \ \ p_3=\left( h_1+h_2\right) R_{\text {oc}}, \ \ p_4=\left( h_1+h_2\right) R_s, \ \ p_5=\left( h_1+h_2+h_3\right) R_s, \end{aligned}$$

where

$$\begin{aligned} R_s=\sqrt{k^2-\frac{\omega ^2}{c_s^2}}, \ \ \ \ R_{\text {ic}}=\sqrt{k^2-\frac{\omega ^2}{c_{\text {ic}}^2}}, \ \ \ \ R_{\text {oc}}=\sqrt{k^2-\frac{\omega ^2}{c_{\text {oc}}^2}}. \end{aligned}$$

Note that the dimensionless form of the above formulae is used in the main text via Eqs. (9)–(11).

Appendix B

Some of the polynomial coefficients of Eq. (15) of Sect. 4 are as follows:

$$\begin{aligned} \gamma _1= & {} \frac{1}{2} \left( h^*\right) ^2 \mu _* \mu ^*+h h^* \mu \mu _*+h h_* \mu \mu ^*+h \mu \mu _* \mu ^*+\frac{\mu _* \mu ^*}{2}, \nonumber \\ \gamma _2= & {} \frac{1}{6} h^3 \mu \mu _* \mu ^*+\frac{1}{6} h_* \left( h^*\right) ^2 h \mu \mu ^*+\frac{1}{2} \left( h^*\right) ^2 h \mu \mu _* \mu ^*+\frac{1}{4} \left( h^*\right) ^2 \mu _* \mu ^* +\frac{1}{6} \left( h^*\right) ^3 h \mu \mu _* \nonumber \\&+ \frac{1}{2} h^* h \mu \mu _* + \frac{1}{6} h^* h^3 \mu \mu _* + \frac{1}{6} h_* h \mu \mu ^* +\frac{1}{6} h \mu \mu _* \mu ^*, \nonumber \\ \gamma _3= & {} -\frac{1}{6} h^3 \mu \mu _* \mu ^*-\frac{h_* h^3 \mu ^2 \mu ^*}{2 \rho }-\frac{h^3 \mu ^2 \mu _* \mu ^*}{6 \rho }-\frac{h^2 \mu \mu _* \mu ^*}{4 \rho }-\frac{\left( h^*\right) ^2 h \mu \mu _* \left( \mu ^*\right) ^2}{2 \rho ^*} \nonumber \\&-\frac{h^* h \mu \mu _* \mu ^*}{2 \rho ^*}-\frac{\left( h^*\right) ^3 h \mu \mu _* \mu ^*}{3 \rho ^*} -\frac{h_* \left( h^*\right) ^2 h \mu \left( \mu ^*\right) ^2}{6 \rho ^*}-\frac{\left( h^*\right) ^2 \mu _* \left( \mu ^*\right) ^2}{4 \rho ^*} \nonumber \\&-\frac{1}{6} h_* \left( h^*\right) ^2 h \mu \mu ^*-\frac{1}{2} \left( h^*\right) ^2 h \mu \mu _* \mu ^*-\frac{1}{4} \left( h^*\right) ^2 \mu _* \mu ^*-\frac{1}{2} h^* h \mu \mu _*, \nonumber \\ \gamma _4= & {} -\frac{h^2 \mu \mu _* \mu ^*}{2 \rho }-\frac{h^* h \mu \mu _* \mu ^*}{\rho ^*}-\frac{\left( h^*\right) ^2 \mu _* \left( \mu ^*\right) ^2}{2 \rho ^*}-h \mu \mu _* \mu ^*-h h_* \mu \mu ^*-\frac{\mu _* \mu ^*}{2},\nonumber \\ \gamma _5= & {} \frac{h_* h^3 \mu ^2 \mu ^*}{2 \rho }+\frac{h^3 \mu ^2 \mu _* \mu ^*}{6 \rho }+\frac{h^2 \mu \mu _* \mu ^*}{4 \rho }+\frac{\left( h^*\right) ^2 h \mu \mu _* \left( \mu ^*\right) ^2}{2 \rho ^*}+\frac{h^* h \mu \mu _* \mu ^*}{2 \rho ^*} \nonumber \\&+\frac{h_* \left( h^*\right) ^2 h \mu \left( \mu ^*\right) ^2}{6 \rho ^*} + \frac{\left( h^*\right) ^3 h \mu \mu _* \left( \mu ^*\right) ^2}{6 \left( \rho ^*\right) ^2}+\frac{\left( h^*\right) ^2 \mu _* \left( \mu ^*\right) ^2}{4 \rho ^*} \nonumber \\&+\frac{h^* h^3 \mu ^2 \mu _* \mu ^*}{6 \rho \rho ^*}+\frac{\left( h^*\right) ^2 h^2 \mu \mu _* \left( \mu ^*\right) ^2}{4 \rho \rho ^*}+\frac{1}{6} h_* h \mu \mu ^*+\frac{1}{6} h \mu \mu _* \mu ^*, \nonumber \\ \gamma _6= & {} \frac{1}{36} h^3 \mu \mu _* \mu ^*+\frac{h_* h^3 \mu ^2 \mu ^*}{6 \rho }+\frac{h^3 \mu ^2 \mu _* \mu ^*}{18 \rho }+\frac{\left( h^*\right) ^3 h \mu \mu _* \mu ^*}{6 \rho ^*}+\frac{h_* \left( h^*\right) ^2 h \mu \left( \mu ^*\right) ^2}{18 \rho ^*} \nonumber \\&+\frac{\left( h^*\right) ^3 h \mu \mu _* \left( \mu ^*\right) ^2}{12 \left( \rho ^*\right) ^2} +\frac{1}{36} h_* \left( h^*\right) ^2 h \mu \mu ^*+\frac{1}{12} \left( h^*\right) ^2 h \mu \mu _* \mu ^* +\frac{h^* h^3 \mu ^2 \mu _*}{12 \rho } \nonumber \\&+\frac{h^* h^3 \mu \mu _* \mu ^*}{12 \rho ^*}+\frac{\left( h^*\right) ^3 h^3 \mu \mu _* \left( \mu ^*\right) ^2}{36 \left( \rho ^*\right) ^2}+\frac{h_* \left( h^*\right) ^2 h^3 \mu ^2 \left( \mu ^*\right) ^2}{12 \rho \rho ^*} +\frac{h^* h^3 \mu ^2 \mu _* \mu ^*}{12 \rho \rho ^*} \nonumber \\&+\frac{\left( h^*\right) ^3 h^3 \mu ^2 \mu _* \mu ^*}{18 \rho \rho ^*}+\frac{h_* \left( h^*\right) ^2 h^3 \mu ^2 \mu ^*}{12 \rho }+\frac{\left( h^*\right) ^2 h^3 \mu ^2 \mu _* \mu ^*}{12 \rho }+\frac{\left( h^*\right) ^2 h^2 \mu \mu _* \mu ^*}{8 \rho }, \nonumber \\ \gamma _7= & {} -\frac{1}{18} h^3 \mu \mu _* \mu ^*-\frac{h_* h^3 \mu ^2 \mu ^*}{12 \rho }-\frac{h^3 \mu ^2 \mu _* \mu ^*}{36 \rho }-\frac{\left( h^*\right) ^3 h \mu \mu _* \mu ^*}{6 \rho ^*}-\frac{\left( h^*\right) ^2 h \mu \mu _* \left( \mu ^*\right) ^2}{12 \rho ^*} \nonumber \\&-\frac{h_* \left( h^*\right) ^2 h \mu \left( \mu ^*\right) ^2}{36 \rho ^*} -\frac{1}{18} h_* \left( h^*\right) ^2 h \mu \mu ^*-\frac{1}{6} \left( h^*\right) ^2 h \mu \mu _* \mu ^*-\frac{1}{12} \left( h^*\right) ^3 h \mu \mu _* \nonumber \\&-\frac{h^* h^3 \mu ^2 \mu _*}{12 \rho } -\frac{\left( h^*\right) ^3 h^3 \mu ^2 \mu _*}{36 \rho }-\frac{\left( h^*\right) ^2 h^3 \mu \mu _* \left( \mu ^*\right) ^2}{12 \rho ^*} -\frac{h^* h^3 \mu \mu _* \mu ^*}{12 \rho ^*} \nonumber \\&-\frac{\left( h^*\right) ^3 h^3 \mu \mu _* \mu ^*}{18 \rho ^*}-\frac{1}{12} \left( h^*\right) ^2 h^3 \mu \mu _* \mu ^* -\frac{h_* \left( h^*\right) ^2 h^3 \mu ^2 \mu ^*}{12 \rho }-\frac{\left( h^*\right) ^2 h^3 \mu ^2 \mu _* \mu ^*}{12 \rho }, \nonumber \\&\vdots \end{aligned}$$