Long-Wave Motion in Pre-stressed Layered Media

Abstract

Motion in pre-stressed compressible elastic layers is considered, focusing on anti-plane shear-type waves propagating in two-layered and three-layered laminates. Guided by a numerical analysis of the dispersion relation asymptotic approximations are derived for the long-wave regime. Two types of boundary conditions are considered and the framework is established to consider more complicated geometric layered structures. In both cases, the values of the cut-off frequencies corresponding to the harmonics mode are obtained. A comparison of numerical and asymptotic approximations has been shown.

1 Introduction

Theoretical study of wave propagation in layered media has been an area of sustained research activity for many years. Elucidation of the mechanical and dynamic properties of such structures has become increasingly necessary by their widespread use in mechanical design. This has not only been in the aerospace industries and military domain, but also numerous other applications, for example, bio-mechanics, geo-mechanics and marine construction. Inhomogeneous layered structures are also one element within the development of modern smart materials. In the context of a single layer plates and plane strain, the effects of pre-stress have previously been investigated for free faces, see, for example, Ogden and Roxburgh [1], Rogerson and Fu [2]. We can also cite, Rogerson and Sandiford [3], who examined the effects of pre-stress on small amplitude waves in multi-layered media and obtained a general asymptotic analysis for both the high and low wave number in plane strain.

Fig. 1

2-layered structure

Within this paper we will investigate the propagation of waves in 2- and 3-layered structures, each layer is composed of compressible pre-stressed elastic material and subject to either free or fixed faces. The pre-stress is envisaged to be either some inherent material property or the result of external forces. Our aim is to investigate small amplitude long motion in the form of anti-plane shear waves. The governing equations , along with the dispersion relation, are presented in Sect. 2. A numerical investigation is carried out in Sect. 3, with long-wave low-frequency approximations carried out in Sect. 4. In the case of fixed faces it has previously been established that no so-called low-frequency motion is possible. In Sect. 5, long-wave high-frequency approximations are established and shown to provide excellent approximations to the numerical solution. The work is carried out within the framework of the propagator matrix and thus the basis is provided for future studies of associated multi-layered media problems. The work also provides the basis for development of asymptotically consistent lower dimensional models.

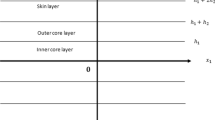
Our concern in this paper is 2-layered and 3-layered structures of thickness 2h and 3h, respectively. We begin with 2 layers of thickness h, composed of compressible pre-stressed material. The structure is finite in $x_2$ direction and of infinite in both the $x_1$ and $x_3$ directions, see Fig. 1. We consider a state of anti-plane shear. Therefore, the displacement is independent of $Ox_3$ and of the form $(u_1,u_2,u_3)=(0,0,u_3)$ and the equations of motion

$$\begin{aligned} C_{1313}^{(n)} u_{3,11} + C_{2323}^{(n)} u_{3,22}=\rho \ddot{u}_3, \end{aligned}$$

(1)

with $n=1,2$. The solution of (1) is sought in the form

$$\begin{aligned} u_3^{(n)}(x_1,x_2,t)=U e^{k q_n x_2} e^{ik(x_1-\upsilon t)}, \end{aligned}$$

(2)

with k the wave number, U an arbitrary constant, t time, $C_{2323}^{(n)}, \;\;C_{1313}^{(n)}$ material parameters, $\rho$ the density of layers, $\upsilon$ the phase wave speed, prescript (n) the layer number and $q_n$ to be determined. After substituting the above solution into (1), we obtain a linearised equation, with a non-trivial solution provided

$$\begin{aligned} q_{n}^{2}=\dfrac{C_{1313}^{(n)}-\bar{\upsilon }^2}{C_{2323}^{(n)}}, \quad \bar{\upsilon }^2=\rho \upsilon ^2. \end{aligned}$$

(3)

The displacement can be written after suppressing the $e^{ik(x_1-\upsilon t)}$ factor as linear combinations, associated with the two solutions indicated in (3), thus

$$\begin{aligned} u_{3}^{(n)}=U_n e^{k q_n x_2}+V_n e^{-k q_n x_2}. \end{aligned}$$

(4)

The incremental traction may be defined in the component form

$$\begin{aligned} \hat{\tau }^{(n)}=\dfrac{\tau _{3}^{(n)}}{ k}=C_{2323}^{(n)}\left( U_n q_n e^{k q_n x_2}- V_n q_n e^{-k q_n x_2}\right) . \end{aligned}$$

(5)

A matrix form of the solution (4) and (5) may be introduced as

$$\begin{aligned} \left( \begin{array}{cccccc} u_{3}^{(n)}\\ \hat{\tau }^{(n)} \end{array}\right) =\left( \begin{array}{cccccc} e^{k q_n h}&{}e^{-k q_n h}\\ q_n C_{2323}^{(n)} e^{k q_n h}&{}-q_n C_{2323}^{(n)} e^{-k q_n h} \end{array}\right) \left( \begin{array}{cccccc} U_n\\ V_n \end{array}\right) . \end{aligned}$$

(6)

The solution can be rewritten in the following form:

$$\begin{aligned} \mathbf{Y} = \mathbf{Q} ^{(n)}\; \mathbf{U} , \end{aligned}$$

(7)

where $\mathbf{U} =(U_n, V_n )^T$, $\mathbf{Y} =(u_{3}^{(n)},\hat{\tau }^{(n)} )^T$ and $\mathbf{Q} ^{(n)}$ is the $2\times 2$ matrix

$$\begin{aligned} Q^{(n)}=\left( \begin{array}{cccccc} e^{k q_n h}&{}e^{-k q_n h}\\ q_n C_{2323}^{(n)} e^{k q_n h}&{}-q_n C_{2323}^{(n)} e^{-k q_n h} \end{array}\right) . \end{aligned}$$

(8)

The vector $\mathbf{U}$ may be eliminated from (7) to yield

$$\begin{aligned} \mathbf {Y}^{(h)}=\mathbf {P}^{(1)}\;\mathbf {Y}^{(0)}. \end{aligned}$$

(9)

Similarly, relation (9) may be expressed as

$$\begin{aligned} \mathbf {Y}^{(2h)}=\mathbf {P}^{(2)}\;\mathbf {Y}^{(h)}, \end{aligned}$$

(10)

where

$$\begin{aligned} \mathbf {P}^{(n)}=\left( \begin{array}{cccccc} \cosh {k q_n h}&{}\dfrac{1}{C_{2323}^{(n)} q_n} \sinh {k q_n h }\\ C_{2323}^{(n)} q_n \sinh {k q_n h }&{}\cosh {k q_n h} \end{array}\right) ,\; n=1,2. \end{aligned}$$

(11)

The solutions of $x_2=2h$ may be represented in the form

$$\begin{aligned} \mathbf {Y}^{u}=\mathbf {P}\;\mathbf {Y}^{l}, \end{aligned}$$

(12)

with a matrix form

$$\begin{aligned} \left( \begin{array}{cccccc} u_{3}^{(2h)}\\ \hat{\tau }^{(2h)} \end{array}\right) =\left( \begin{array}{cccccc} P_{11}&{} P_{12}\\ P_{21}&{}P_{22} \end{array}\right) \left( \begin{array}{cccccc} u_{3}^{(0)}\\ \hat{\tau }^{(0)} \end{array}\right) , \end{aligned}$$

(13)

with

$$\begin{aligned} P_{11}=C_{2323}^{(1)} q_1 C_2 C_1+C_{2323}^{(2)} q_2 S_1 S_2, \;P_{12}=C_{2323}^{(1)}q_1 S_2 C_1+ C_{2323}^{(2)} q_2 C_2 S_1,\end{aligned}$$

(14)

$$\begin{aligned} P_{21}= C_{2323}^{(1)} q_1 C_2 S_1+ C_{2323}^{(2)} q_2 S_2 C_1, \;P_{22}=C_{2323}^{(2)} q_2 C_1 C_2 +C_{2323}^{(1)} q_1 S_1 S_2, \end{aligned}$$

(15)

where $S_n=\sinh {k q_n h}, \;C_n=\cosh {k q_n h}.$ We can also generate the propagator matrix for a 3-layered structure of 3h thickness. To begin we note that this structure has been built by adding another layer of the same thickness h to the structure in Fig. 1, i.e. the third layer occupying $2h\le x_2 \le 3h$, and thus

$$\begin{aligned} \mathbf {Y}^{(3h)}=\mathbf {P}^{(3)}\;\mathbf {Y}^{(2h)}. \end{aligned}$$

(16)

$\mathbf {P}^{(3)}$ can be obtained by substituting $n=3$ in (11). Now, (12) for (3 layers) is of the same form but the propagator $\mathbf{P} =\mathbf{P} ^{(1)}{} \mathbf{P} ^{(2)}{} \mathbf{P} ^{(3)}$ and

$$\begin{aligned} \left( \begin{array}{cccccc} u_{3}^{(3h)}\\ \hat{\tau }^{(3h)} \end{array}\right) =\left( \begin{array}{cccccc} P_{11}&{}P_{12}\\ P_{21}&{}P_{22} \end{array}\right) \left( \begin{array}{cccccc} u_{3}^{(0)}\\ \hat{\tau }^{(0)} \end{array}\right) . \end{aligned}$$

(17)

The components of $\mathbf{P}$ for the (3 layers) laminate can be expressed as

$$\begin{aligned} P_{11}=\left( C_{2323}^{(3)} q_3 C_{2323}^{(1)} q_1 C_1 C_2+C_{2323}^{(2)} q_2 S_1 S_2 \right) C_3+ C_{2323}^{(1)} q_1S_3 \nonumber \\ \left( C_{2323}^{(1)} q_1 S_1 C_2+C_{2323}^{(2)} q_2 S_2 C_1 \right) ,\end{aligned}$$

(18)

$$\begin{aligned} \nonumber \ P_{12}=C_{2323}^{(3)} q_3\left( C_{2323}^{(2)} q_2S_1 C_2 +C_{2323}^{(1)} q_1 C_1 S_2 \right) C_3 + C_{2323}^{(2)} q_2 \nonumber \\ \left( C_{2323}^{(1)} q_1 C_1 C_2+C_{2323}^{(2)} q_2 S_1 S_2 \right) S_3,\end{aligned}$$

(19)

$$\begin{aligned} \nonumber \ P_{21}=C_{2323}^{(2)} q_2\left( C_{2323}^{(1)} q_1S_1 C_2+ C_{2323}^{(2)} q_2 C_1 S_2\right) C_3+ C_{2323}^{(3)} q_3 \nonumber \\ \left( C_{2323}^{(1)} q_1S_1 S_2+ C_{2323}^{(2)} q_2C_1 C_2 \right) S_3,\end{aligned}$$

(20)

$$\begin{aligned} \nonumber \ P_{22}= C_{2323}^{(3)} q_3\left( C_{2323}^{(2)} q_2 C_1 C_2+C_{2323}^{(1)} q_1 S_1 S_2\right) C_3+ C_{2323}^{(2)} q_2 \nonumber \\ \left( C_{2323}^{(1)} q_1 S_1 C_2+C_{2323}^{(2)} q_2 S_2 C_1 \right) S_3. \end{aligned}$$

(21)

Applying the boundary conditions of zero traction and the condition of continuity across the perfectly bonded interface within (7) to provide the dispersion relation for the free-faces 2-layered structure as

$$\begin{aligned} C_{2323}^{(1)} q_1 S_1 C_2+ C_{2323}^{(2)} q_2 S_2 C_1=0, \end{aligned}$$

(22)

with the associated dispersion relation for the 3-layer relation given by

$$\begin{aligned} C_{2323}^{(2)} q_2\left( C_{2323}^{(1)} q_1 S_1 C_2+ C_{2323}^{(2)} q_2 C_1 S_2\right) C_3+ C_{2323}^{(3)} q_3 \nonumber \\ \left( C_{2323}^{(1)} q_1S_1 S_2+ C_{2323}^{(2)} q_2 C_1 C_2 \right) S_3=0. \end{aligned}$$

(23)

We now impose zero displacement on the faces of the 2-layered structure, resulting in a dispersion relation given by

$$\begin{aligned} C_{2323}^{(1)} q_1 S_2 C_1 + C_{2323}^{(2)} q_2 S_1 C_2=0. \end{aligned}$$

(24)

The analogous dispersion 3-layer is given by

$$\begin{aligned} C_{2323}^{(3)} q_3\left( C_{2323}^{(2)} q_2 S_1 C_2+ C_{2323}^{(1)} q_1 C_1 S_2 \right) C_3+ C_{2323}^{(2)} q_2 \nonumber \ \\ \left( C_{2323}^{(1)} q_1 C_1 C_2+C_{2323}^{(2)} q_2 S_1 S_2 \right) S_3=0. \end{aligned}$$

(25)

2 Numerical Results

The material parameters have been chosen in this section to demonstrate the possible range of material response and $K=kh$ in all numerical results. The dispersion curves computed from equation (22) are plotted in Fig. 2a for the material parameters $C_{1313}^{(1)}=0.524, C_{2323}^{(1)}=0.513$, and $C_{1313}^{(2)}=1.55, C_{2323}^{(2)}=1.53$ and this shows a zero frequency limit as $K\rightarrow 0$.

Fig. 2

Scaled frequency against scaled wave number for the free-faces dispersion relation (22) (a), and for the fixed-faces dispersion relation (24) (b)

Figure 2b shows the dispersion relation form the equation (24) with the same material parameters. We note that, no cut-off frequency observed in the low-frequency range in the fixed-faces case, see Fig. 2b. Similar 3-layer results are presented in Fig. 3 with $C_{1313}^{(1)}=0.524, C_{2323}^{(1)}=0.513$, $C_{1313}^{(3)}=1.2$ and $C_{1313}^{(2)}=1.55, C_{2323}^{(2)}=1.53$, $C_{1313}^{(3)}=1.6$.

Fig. 3

Scaled frequency against scaled wave number for the free-faces dispersion relation (23) (a), and for the fixed-faces dispersion relation (25) (b)

3 Long-Wave Low-Frequency Approximation

In the long-wave low-frequency region $K\rightarrow 0$ and $\bar{\upsilon }$ is not large. Thus, by expanding all trigonometric functions in (22) and (23) as Taylor series, we derive the approximation

$$\begin{aligned} \bar{\varOmega }^2=\left( \dfrac{C_{1313}^{(1)}+C_{1313}^{(2)}}{2} \right) K^2+O(K^4). \end{aligned}$$

(26)

For 3-layer we have

$$\begin{aligned} \bar{\varOmega }^2=\left( \dfrac{C_{1313}^{(1)}+C_{1313}^{(2)}+C_{1313}^{(3)}}{3} \right) K^2+O(K^4). \end{aligned}$$

(27)

Fig. (4) shows appropriate comparison of numerical solutions (22) and (23) with asymptotic expansion (30) and (30) for the free-faces cases.

Fig. 4

Fundamental mode branch corresponding to (22) (solid line) and (26) (dashed line) in 2a, corresponding to (23) (solid line) and (27) (dashed line) in 4b. The same material parameters from Fig. (3a) are used

4 Long-Wave High-Frequency Approximation

In this section, we consider the long-wave high-frequency regime of the dispersion curves. In this type of motion $\bar{\upsilon }^2\gg 1$. We remark that, $q_n^{2}$ are negative as $K\rightarrow 0$, i.e. $q_n=i \hat{q}_n$, $n=1,2,3$, thus

$$\begin{aligned} \hat{q}_n^{2}=\dfrac{\bar{\upsilon }^2-C_{1313}^{(n)}}{C_{2323}^{(n)}}. \end{aligned}$$

(28)

We assume $\bar{\varOmega }^2=\bar{\upsilon }^2 K^2$ has the following expansion:

$$\begin{aligned} \bar{\varOmega }^2=\varOmega _0+\varOmega _2 K^2+O(K^4). \end{aligned}$$

(29)

The dispersion (22) may be expressed in the form

$$\begin{aligned} C_{2323}^{(1)} \hat{q_1}\tan {K \hat{q_1} }+C_{2323}^{(2)} \hat{q_2} \tan {K \hat{q_2}}=0. \end{aligned}$$

(30)

By considering the following expansions:

$$\begin{aligned} K \hat{q}_n=\dfrac{\bar{\varOmega }}{\sqrt{C_{2323}^{(n)}}}\left( 1-\dfrac{C_{1313}^{(n)} K^2}{2\bar{\varOmega }^{2}}+\ldots \right) , \end{aligned}$$

(31)

together with the approximation (29), the dispersion relation (22) may be used to show that frequency is a solution of

$$\begin{aligned} \sqrt{C_{2323}^{(1)}}\tan \sqrt{\dfrac{\varOmega _0}{C_{2323}^{(1)}}} +\sqrt{C_{2323}^{(2)}} \tan \sqrt{\dfrac{\varOmega _0}{C_{2323}^{(2)}}}=0, \end{aligned}$$

(32)

where $\varOmega _0$ a solution of equation (32), defines the cut-off frequencies. The next order term $\varOmega _2$ in the following formula:

$$\begin{aligned} \varOmega _2=\tilde{F}_2(\varOmega _0)/\tilde{F}_1(\varOmega _0), \end{aligned}$$

(33)

where $\tilde{F}_1(\varOmega _0)$ and $\tilde{F}_2(\varOmega _0)$ are given by

$$\begin{aligned} \begin{aligned} \tilde{F}_1(\varOmega _0)&= \sqrt{C_{2323}^{(1)}}F_1(\varOmega _0)+\sqrt{C_{2323}^{(2)}}F_2(\varOmega _0)+\sqrt{\varOmega _0 }\left( F_1^{2}(\varOmega _0) +1\right) \\&+\sqrt{\varOmega _0 }\left( F_2^{2}(\varOmega _0)+1 \right) ,\\ \tilde{F}_2(\varOmega _0)&= -\dfrac{1}{2}\left( C_{1313}^{(1)}\left( 1+F_{1}^{2}(\varOmega _0)\right) \sqrt{\varOmega _0}+\right. C_{1313}^{(2)}\left( 1+F_{2}^{2}(\varOmega _0) \right) \sqrt{\varOmega _0}\\&+ \sqrt{C_{2323}^{(1)}}F_1(\varOmega _0)C_{1313}^{(1)}+\sqrt{C_{2323}^{(2)}}F_2(\varOmega _0)\left. C_{1313}^{(2)}\right) . \end{aligned} \end{aligned}$$

(34)

The scaled frequency (29) may therefore be written in the form

$$\begin{aligned} \bar{\varOmega }^2=\varOmega _0+\dfrac{\tilde{F}_2(\varOmega _0)}{\tilde{F}_1(\varOmega _0)}K^2+O(K^4). \end{aligned}$$

(35)

Asymptotic approximation for long-wave high-frequency motion for (3 layers) will now be considered. Accordingly the previous knowledge for high-frequency limits may be used to establish that

$$\begin{aligned}&\sqrt{C_{2323}^{(1)}\;C_{2323}^{(3)}}F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\nonumber \\ & -C_{2323}^{(2)}F_2(\varOmega _0)- \sqrt{C_{2323}^{(1)} C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;C_{2323}^{(3)}}F_3(\varOmega _0)=0, \end{aligned}$$

(36)

where $\varOmega _0$ may be shown to be a solution of (36). The next order frequency approximation $\varOmega _2$ is given by

$$\begin{aligned} \varOmega _2=\varLambda _2(\varOmega _0)/ \varLambda _1(\varOmega _0), \end{aligned}$$

(37)

where $\varLambda _1(\varOmega _0)$ and $\varLambda _2(\varOmega _0)$ are given by

$$\begin{aligned} \begin{aligned} \varLambda _1(\varOmega _0)&=C_{1313}^{(2)}\;\,C_{2323}^{(2)}\sqrt{\varOmega _0} \left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) C_{1313}^{(2)}\;\,-C_{2323}^{(2)}\sqrt{\varOmega _0}\\ {}&\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) \sqrt{C_{2323}^{(1)}\;\,C_{2323}^{(3)}} F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\\ {}&- C_{2323}^{(2)}F_2(\varOmega _0)-\sqrt{C_{2323}^{(1)}\;\;C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;C_{2323}^{(3)}}F_3(\varOmega _0),\\ \varLambda _2(\varOmega _0)&=C_{1313}^{(2)}\;C_{2323}^{(2)}\sqrt{\varOmega _0}\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) C_{1313}^{(2)}\;-C_{2323}^{(2)}\sqrt{\varOmega _0}\\ {}&\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) \sqrt{C_{2323}^{(1)}C_{2323}^{(3)}} F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\\ {}&- C_{2323}^{(2)}F_2(\varOmega _0)-\sqrt{C_{2323}^{(1)}\;\;C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;C_{2323}^{(3)}}F_3(\varOmega _0). \end{aligned} \end{aligned}$$

(38)

The scaled frequency (29) for (3 layers) may therefore be written in the form

$$\begin{aligned} \bar{\varOmega }^2=\varOmega _0+\dfrac{\varLambda _2(\varOmega _0)}{\varLambda _1(\varOmega _0)}K^2+O(K^4). \end{aligned}$$

(39)

Fig. 5

Long-wave high-frequency approximations corresponding to numerical solutions of the dispersion relations for 2 layers with free-faces (a) and for 3 layers (b). The same material parameters from figures (2) and (3) are used

In Fig. (5) comparison of asymptotic solutions (35) and (39) with numerical solutions (22) and (23) are made in (5a) and (5b), respectively, for the first three harmonic within the vicinity of cut-off frequencies. These clearly reveal excellent agreement over the long-wave regime.

The dispersion (24) can be expressed in the form

$$\begin{aligned} C_{2323}^{(2)}\hat{q_2} \tan {K \hat{q_1}}+ C_{2323}^{(1)}\hat{q_1}\tan {K \hat{q_2}}=0. \end{aligned}$$

(40)

A similar analysis to that just carried out in respect of the free-faces case can be performed for the fixed faces, leading to the leading order term of (40) in the following form:

$$\begin{aligned} \sqrt{C_{2323}^{(2)}}\tan \sqrt{\dfrac{\varOmega _0}{C_{2323}^{(1)}}} +\sqrt{C_{2323}^{(1)}} \tan \sqrt{\dfrac{\varOmega _0}{C_{2323}^{(2)}}}=0. \end{aligned}$$

(41)

The next order term of (40) provides

$$\begin{aligned} \varOmega _2=\tilde{F}_4(\varOmega _0) / \tilde{F}_3(\varOmega _0), \end{aligned}$$

(42)

where

$$\begin{aligned} \tilde{F}_3(\varOmega _0)&=\sqrt{\varOmega _0}\left[ C_{2323}^{(2)}F_1^{2}(\varOmega _0) \sqrt{ C_{1313}^{(1)}}+C_{2323}^{(1)}F_2^{2}(\varOmega _0) \sqrt{ C_{1313}^{(2)}}\right. \\ {}&\quad +C_{2323}^{(1)} \sqrt{ C_{1313}^{(2)}}+ C_{2323}^{(2)}\left. \sqrt{ C_{1313}^{(1)}}\right] -\sqrt{C_{2323}^{(2)}}\; \sqrt{C_{2323}^{(1)}}\\ {}&\quad \left( \sqrt{ C_{1313}^{(2)}} F_2(\varOmega _0)+ \sqrt{ C_{1313}^{(1)}} F_1(\varOmega _0)\right) ,\nonumber \\ \tilde{F}_4(\varOmega _0)&=\sqrt{\varOmega _0}\left[ C_{2323}^{(1)} C_{2323}^{(2)}F_2^{2}(\varOmega _0) F_1(\varOmega _0)+ C_{2323}^{(1)} C_{2323}^{(2)}\right] \nonumber \\ {}&\quad -\left( C_{2323}^{(2)}\sqrt{C_{2323}^{(1)}}\;F_1(\varOmega _0)+C_{2323}^{(1)}\sqrt{C_{2323}^{(2)}}\;F_2(\varOmega _0)\right) . \end{aligned}$$

For 3-layer, (25) may be rewritten as

$$\begin{aligned}&\left( C_{2323}^{(1)}\hat{q}_1 \tan (K\hat{q}_1)+C_{2323}^{(2)}\hat{q}_2\tan (K\hat{q}_2)\right) C_{2323}^{(2)}\hat{q}_2\nonumber \\ {}&\quad +C_{2323}^{(3)} \hat{q}_3\tan (K\hat{q}_3) \left( C_{2323}^{(1)}\hat{q}_1\tan (K\hat{q}_1)\tan (K\hat{q}_2)-C_{2323}^{(2)}\hat{q}_2\right) =0.&\end{aligned}$$

(43)

The scaled frequency is in the form

$$\begin{aligned} \bar{\varOmega }^2=\varOmega _0+\dfrac{\bar{\varLambda }_1(\varOmega _0)}{\bar{\varLambda }_2(\varOmega _0)}K^2+O(K^4), \end{aligned}$$

(44)

with $\varOmega _0$ is a solution of

$$\begin{aligned}&\sqrt{C_{2323}^{(1)}\;C_{2323}^{(3)}}F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\nonumber \\ {}&\quad -C_{2323}^{(2)}F_2(\varOmega _0)-\sqrt{C_{2323}^{(1)}\;\;C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;C_{2323}^{(3)}}F_3(\varOmega _0)=0,&\end{aligned}$$

(45)

and

$$\begin{aligned} \begin{aligned} \bar{\varLambda }_1(\varOmega _0)&=C_{1313}^{(2)}\;\,C_{2323}^{(2)}\sqrt{\varOmega _0}\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) C_{1313}^{(2)} -C_{2323}^{(2)}\sqrt{\varOmega _0}\\&\;\;\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) \sqrt{C_{2323}^{(1)}\;\,C_{2323}^{(3)}} F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\\&-C_{2323}^{(2)}F_2(\varOmega _0)-\sqrt{C_{2323}^{(1)}\;\,C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;\,C_{2323}^{(3)}}F_3(\varOmega _0),\\ \bar{\varLambda }_2(\varOmega _0)&=C_{1313}^{(2)}\;C_{2323}^{(2)}\sqrt{\varOmega _0}\left( 2 F_2(\varOmega _0)+F_2^{2}(\varOmega _0) \right) C_{1313}^{(2)}-C_{2323}^{(2)} \sqrt{\varOmega _0}\\ {}&\left( 2 F_2(\varOmega _0) +F_2^{2}(\varOmega _0) \right) \sqrt{C_{2323}^{(1)}\;\,C_{2323}^{(3)}} F_1(\varOmega _0) F_2(\varOmega _0)F_3(\varOmega _0)\\&- C_{2323}^{(2)}F_2(\varOmega _0)-\sqrt{C_{2323}^{(1)}\;\,C_{2323}^{(2)}}F_1(\varOmega _0)-\sqrt{C_{2323}^{(2)}\;C_{2323}^{(3)}}F_3(\varOmega _0). \end{aligned} \end{aligned}$$

(46)

Fig. 6 displays dispersion curves obtained using the expansions (24) and (25) and the dispersion relations (24) and (25). Again good agreement over long-wave region is observed.

Fig. 6

A comparison of numerical solutions (solid line) and asymptotic expansion (dashed line) for scaled frequency against scaled wave number for the fixed-faces dispersion relation (24) in (a) and for (3 layers) in (b). The same material parameters from figure (2) and (3) are used

5 Some Concluding Remarks

The dispersions of small amplitude waves, in anti-plane shear for multi-layered structures have been derived. Those relations are algebraically complicated and solved numerically and asymptotically. Asymptotic equations of motion are established for two cases of boundaries of non-contrast parameters. The former is applicable over the whole long-wave low- and high-frequency range. However, the second is only valid over a narrow vicinity of the cut-off frequency.