The lowest vibration modes of an elastic beam composed of alternating stiff and soft components

Abstract

Harmonic vibrations of a strongly inhomogeneous elastic beam with piecewise uniform stiffnesses and densities are considered. The focus is on the lowest eigenmodes, which are often most harmful and unwanted. They are evaluated by perturbing the limiting rigid body translations and rotations of stiff beam components. The developed methodology is adapted for two particular configurations of a three-span beam. The derived approximate formulae are tested by comparison with the exact solution of a symmetric beam with two stiff outer components and free ends.

1 Introduction

Dynamics of inhomogeneous elastic solids is an important research area due to its numerical applications in modern industries, e.g., see [1, 2]. In particular, multilayered structures, also known as sandwich ones, are widely used in aerospace, aircraft and automotive engineering, see [3] and references therein. High contrast in material and geometrical characteristics of the components of elastic laminates is a major focus of a number of recent developments [4], including laminated glass beams and plates [5, 6], photovoltaic panels [7], energy scavenging devices [8] and functionally graded materials [9]. The related theoretical considerations include both traditional engineering approaches starting from various physical assumptions, see [10,11,12] along with multi-parametric asymptotic approach, see [13, 14]. We also mention strongly inhomogeneous multilayered shells finding interesting implementations in metamaterial design, see [15]. Soft robotics is another advanced domain concerned with high-contrast structures [16, 17]. Finally, we cite the paper [27] investigating bioinspired soft composite.

Longitudinal vibrations of piecewise homogeneous rods composed of alternating stiff and soft components were studied in [19, 20], see also [21]. The main emphasis of these papers is the lowest vibration modes arising as a perturbation of the rigid body motions of stiff parts. In addition, we cite publications [22,23,24], dealing with high-contrast periodic problems. Similarity of periodic and vertically inhomogeneous thin structures was addressed in [25]. We also mention [26] which investigates the effect of a small misplacement on the deflection response of the two-span column subjected to transverse loading.

This paper is concerned with time-harmonic vibrations of strongly piecewise inhomogeneous beams consisting of altering stiff and soft components. Specific low-frequency modes, characteristic only of high-contrast structure, are studied, see [19]. An asymptotic approach relying on the concept of “almost rigid body motion” developed earlier in [19] for elastic rods is adapted. Unlike rod demonstrating a single rigid body translation, a multicomponent beam generally possesses not only vertical translation, but also rigid body translation. As an example, we consider a three-span beam with one or two stiff elements. Explicit asymptotic formulae are derived for the lowest eigenfrequencies and eigenforms. The accuracy of the asymptotic results is verified by comparison with the exact solution of the original problem in case of symmetry.

The paper consists of five sections. In Sect. 1, the governing relations are presented and then rewritten in nondimensional form. In Sect. 2, for further reference, the exact solution of a three-component beam with free ends is given for symmetric vibration modes. In Sect. 3, a perturbation scheme is established. The scaling motivated by the contrast of material parameters and an appropriate small parameter is introduced. The chosen setups of a beam with two stiff components with free ends and a beam with one stiff component with clamped ends are treated separately. The explicit formulae for the lowest eigenfrequencies and eigenforms are derived for a beam of arbitrary geometry. In the next section, the aforementioned formulae are specialized for a geometrical symmetric beam. In the last section, numerical comparisons of the exact and asymptotic results, see Sects. 2 and 3, respectively, are presented along with computations for an asymmetric beam.

2 Formulation of the problem

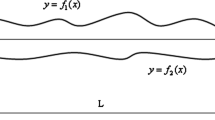
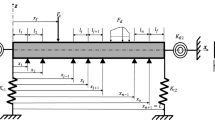
Consider two types of three-span elastic beams composed of stiff and soft components as shown in Figs. 1 and 2 by black and white colors, respectively. In the first case, a beam with free ends contains two stiffer outer parts whereas in the second case, it has two soft outer parts clamped at both ends.

Fig. 1

A composite beam with two stiff outer components

Fig. 2

A composite beam with two soft outer components

In what follows, we adapt the Euler–Bernoulli beam theory assuming that the lengths of all homogeneous beam components are much greater than a typical size of its transverse cross section. Then, each of them is governed by the equation

$$\begin{aligned} \frac{d^4y_\beta }{dx_\beta ^4}- \frac{\omega ^2 }{a_{\alpha }^2}y_\beta =0,\qquad \beta =l,c,r, \end{aligned}$$

(1)

with

$$\begin{aligned} a_{\alpha }=\sqrt{D_{\alpha }/m_{\alpha }} \end{aligned}$$

(2)

where $y_\beta$ are displacements, $x_\beta$ are local longitudinal coordinates, $\omega$ is vibration frequency, $D_{\alpha }=E_{\alpha } I$ is stiffness and $m_{\alpha }=\rho _{\alpha }A$ is linear mass density with $E_\beta$, I, $\rho _\beta$ and A denoting Young’s moduli, moment of inertia, material density and the cross-sectional area, respectively. Throughout the paper, the suffixes l, c and r correspond to the left, central and right components of the beam, whereas the parameter $\alpha$ stands for the outer $(\alpha =o)$ or inner $(\alpha =i)$ components of the beam.

The continuity of the displacements, stresses, bending moments and shear forces at the interfaces is given, respectively, by

$$\begin{aligned}&y_\mathrm{l}\left( x_\mathrm{l}\right) =y_\mathrm{c}\left( -\,x_\mathrm{c}\right) ,&\quad y_\mathrm{r}\left( -\,x_\mathrm{r}\right) =y_\mathrm{c}\left( x_\mathrm{c}\right) ,\nonumber \\&y_\mathrm{l}'\left( x_\mathrm{l}\right) =y_\mathrm{c}'\left( -\,x_\mathrm{c}\right) ,&\quad y_\mathrm{r}'\left( -\,x_\mathrm{r}\right) =y_\mathrm{c}'\left( x_\mathrm{c}\right) ,\nonumber \\&D_o y_\mathrm{l}''\left( x_\mathrm{l}\right) =D_i y_\mathrm{c}''\left( -\,x_\mathrm{c}\right) ,&\quad D_o y_\mathrm{r}''\left( -\,x_\mathrm{r}\right) =D_i y_\mathrm{c}''\left( x_\mathrm{c}\right) ,\nonumber \\&D_o y_\mathrm{l}'''\left( x_\mathrm{l}\right) =D_i y_\mathrm{c}'''\left( -\,x_\mathrm{c}\right) ,&\quad D_o y_\mathrm{r}'''\left( -\,x_\mathrm{r}\right) =D_i y_\mathrm{c}'''\left( x_\mathrm{c}\right) . \end{aligned}$$

(3)

It is well known that a homogeneous beam with free ends has a double zero eigenfrequency $\omega =0$, corresponding to rigid body translation, ($y=A=\text {const}$), and rotation, ($y=B x, B=\text {const}$), see Fig. 3.

Fig. 3

Rigid body motions of a beam with free ends

Therefore, for a stiff component contacted with the soft one, we should expect two lowest eigenfrequencies arising from perturbation of zero eigenfrequencies of the aforementioned. Below, we concentrate on the analysis of such frequencies for the geometrical setups in Figs. 1 and 2.

Let us now introduce local nondimensional longitudinal coordinates and frequency parameters by

$$\begin{aligned} \xi _\beta =\frac{x_\beta }{L_\beta } \qquad \text {and}\qquad \varOmega _\beta =\ L_\beta \sqrt{\frac{\omega }{a_{\alpha }}},\quad \beta =l,c,r. \end{aligned}$$

(4)

We, then, have from Eqs. (1) and (3),

$$\begin{aligned} \frac{d^4y_\beta }{d\xi _\beta ^4}-\varOmega _\beta ^4 y_\beta =0,\; -\,1\leqslant \xi _\beta \leqslant 1 \end{aligned}$$

(5)

with

$$\begin{aligned} y_\mathrm{l}\left( 1\right) =y_\mathrm{c}\left( -\,1\right) ,\qquad&y_\mathrm{c}\left( 1\right) =y_\mathrm{r}\left( -\,1\right) , \end{aligned}$$

(6)

$$\begin{aligned} \frac{L_\mathrm{c}}{L_\mathrm{l}}y_\mathrm{l}'\left( 1\right) =y_\mathrm{c}'\left( -\,1\right) ,\qquad&\frac{L_\mathrm{c}}{L_\mathrm{r}}y_\mathrm{r}'\left( -\,1\right) =y_\mathrm{c}'\left( 1\right) , \end{aligned}$$

(7)

$$\begin{aligned} \left( \frac{L_\mathrm{c}}{L_\mathrm{l}}\right) ^2D_o y_\mathrm{l}''\left( 1\right) =D_i y_\mathrm{c}''\left( -\,1\right) ,\qquad&\left( \frac{L_\mathrm{c}}{L_\mathrm{r}}\right) ^2D_o y_\mathrm{r}''\left( -\,1\right) =D_i y_\mathrm{c}''\left( 1\right) , \end{aligned}$$

(8)

and

$$\begin{aligned} \left( \frac{L_\mathrm{c}}{L_\mathrm{l}}\right) ^3D_o y_\mathrm{l}'''\left( 1\right) =D_i y_\mathrm{c}'''\left( -\,1\right) ,\quad \left( \frac{L_\mathrm{c}}{L_\mathrm{r}}\right) ^3D_o y_\mathrm{r}'''\left( -\,1\right) =D_i y_\mathrm{c}'''\left( 1\right) , \end{aligned}$$

(9)

, respectively. In what follows, we restrict ourselves to a beam with free (Fig. 1) or clamped (Fig. 2) ends, for which

$$\begin{aligned} \begin{aligned} y_\mathrm{l}''\left( -\,1\right) =y_\mathrm{r}''\left( 1\right) =0,\\ y_\mathrm{l}'''\left( -\,1\right) =y_\mathrm{r}'''\left( 1\right) =0, \end{aligned} \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned} y_\mathrm{l}\left( -\,1\right) =y_\mathrm{r}\left( 1\right) =0,\\ y_\mathrm{l}'\left( -\,1\right) =y_\mathrm{r}'\left( 1\right) =0. \end{aligned} \end{aligned}$$

(11)

Finally, we define a small parameter as the ratio of soft and stiff components, i.e.,

$$\begin{aligned} \varepsilon =\left( \frac{D_i}{D_o}\right) ^j\quad j=1 \quad \text {or}\quad j=-\,1 \end{aligned}$$

(12)

for the configurations in Fig. 1 ($j=1$) or Fig. 2 ($j=-\,1$), respectively.

3 The exact solution of a three-span beam with two stiff outer components and free ends

In this section, we present the benchmark solution for the symmetric vibration modes of a beam with

$$\begin{aligned} L_\mathrm{l}=L_\mathrm{r},\quad \varOmega _\mathrm{l}=\varOmega _\mathrm{r}. \end{aligned}$$

(13)

In this case, we introduce the dimensionless quantities:

$$\begin{aligned} D=\frac{D_i}{D_o},\, m=\frac{m_i}{m_o},\, a=\frac{a_i}{a_o}, \, l=\frac{L_i}{L_o}. \end{aligned}$$

(14)

Then, the symmetric solutions of Eq. (5) are given by

$$\begin{aligned} y_\mathrm{c}\left( \xi _\mathrm{c}\right) =A_\mathrm{c} \cos \left( \varOmega _\mathrm{c}\xi _\mathrm{c}\right) +C_\mathrm{c} \cosh \left( \varOmega _\mathrm{c}\xi _\mathrm{c}\right) ,\quad |\xi _\mathrm{c}|\le 1, \end{aligned}$$

(15)

and

$$\begin{aligned} \begin{aligned} y_\mathrm{r}\left( \xi _\mathrm{r}\right) =&A_\mathrm{r} \cos \left( \varOmega _\mathrm{r} \xi _\mathrm{r}\right) +B_\mathrm{r} \sin \left( \varOmega _\mathrm{r} \xi _\mathrm{r}\right) +\\&+\,C_\mathrm{r} \cosh \left( \varOmega _\mathrm{r} \xi _\mathrm{r}\right) +D_\mathrm{r} \sinh \left( \varOmega _\mathrm{r} \xi _\mathrm{r}\right) ,\quad |\xi _\mathrm{r}|\le 1. \end{aligned} \end{aligned}$$

(16)

Next, applying the continuity conditions along with boundary conditions (6)–(9), we arrive at a set of linear equations in $A_\mathrm{c}, C_\mathrm{c}, A_\mathrm{r}, B_\mathrm{r}, C_\mathrm{r}$ and $D_\mathrm{r}$ having a nontrivial solution provided that the determinant of the matrix of coefficients vanishes resulting in

$$\begin{aligned}&\cosh (\varOmega _\mathrm{c})\left( \cosh (\varOmega _\mathrm{r})^2\left( D^2\cos (\varOmega _\mathrm{r})^2\sin (\varOmega _\mathrm{c})-a^2\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})^2\right. \right. \nonumber \\&\left. \left. \quad +a^{3/2}D\cos (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\!\right) -aD\sin (\varOmega _\mathrm{r})\sinh (2\varOmega _\mathrm{r})\left( 2\cos (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})\right. \right. \nonumber \\&\left. \left. \quad +\sqrt{a}\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) +\left( a^2\cos (\varOmega _\mathrm{r})^2\sin (\varOmega _\mathrm{c})-D^2\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})^2\right. \right. \nonumber \\&\left. \left. \quad +a^{3/2}D\cos (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\!\right) \sinh (\varOmega _\mathrm{r})^2+a^{3/2}D\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})^2\sin (2\varOmega _\mathrm{r})\right) \nonumber \\&\quad +\sinh (\varOmega _\mathrm{c})\left( \cosh (\varOmega _\mathrm{r})^2\left( -\,\sqrt{a}D\sin (2\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})+\cos (\varOmega _\mathrm{c})\left( D^2\cos (\varOmega _\mathrm{r})^2\right. \right. \right. \nonumber \\&\left. \left. \left. \quad -a^2\sin (\varOmega _\mathrm{r})^2\right) \right) -\sqrt{a}D\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})^2\sinh (2\varOmega _\mathrm{r})+\sinh (\varOmega _\mathrm{r})^2\right. \\&\left. \quad \left( a^2\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})^2-\sqrt{a}D\sin (2\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})-D^2\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})^2\right) \right. \nonumber \\&\left. \quad +\sqrt{a}D\sinh (2\varOmega _\mathrm{r})\left( \cos (\varOmega _\mathrm{r})^2\sin (\varOmega _\mathrm{c})+\sqrt{a}\cos (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\right) \right) \!=\!0.\nonumber \end{aligned}$$

(17)

This is the sought for exact frequency equation which will be used for testing the asymptotic results in what follows.

4 Perturbation analysis

In this section, we study the lowest eigenmodes of the beams as shown in Figs. 1 and 2 using perturbation techniques earlier developed for longitudinal vibrations of strongly inhomogeneous elastic rods, see [19, 20]. Below, we do not impose any conditions on the sizes of beam components.

4.1 Two stiff outer components

First, consider the beam in Fig. 1, for which the small physical parameter is given by (12) with $j=1$. We also assume

$$\begin{aligned} \varepsilon \frac{m_o}{m_i}= m_*,\quad m_*\sim 1, \end{aligned}$$

(18)

and

$$\begin{aligned} \delta _\mathrm{l}=\frac{L_\mathrm{l}}{L_\mathrm{c}} \sim 1,\,\ \delta _\mathrm{r}=\frac{L_\mathrm{r}}{L_\mathrm{c}}\sim 1 \end{aligned}$$

(19)

keeping in mind that $\varOmega _\mathrm{c}^4\sim \varOmega _\mathrm{l}^4\sim \varOmega _\mathrm{r}^4\sim \varepsilon$ over the low-frequency range of interest.

Let us now expand the frequency parameters and displacements into the asymptotic series

$$\begin{aligned} \begin{aligned}&\varOmega _{\beta }^{4}=\varepsilon \left( \varOmega _{\beta ,0}^{4}+\varepsilon \varOmega _{\beta ,1}^{4}+\varepsilon ^2\varOmega _{\beta ,2}^{4}+\cdots \right) ,\\&y_{\beta }=y_{\beta ,0}+\varepsilon y_{\beta ,1}+\varepsilon ^2y_{\beta ,2}+\cdots ,\quad \beta =l,c,r \end{aligned} \end{aligned}$$

(20)

where

$$\begin{aligned} \varOmega _\mathrm{l}^4=\varOmega _\mathrm{c}^4 \ \delta _\mathrm{l}^4 \ m_*,\qquad \varOmega _\mathrm{r}^4=\varOmega _\mathrm{c}^4 \ \delta _\mathrm{r}^4 \ m_*. \end{aligned}$$

(21)

Thus, the continuity and boundary conditions take the form

$$\begin{aligned} \begin{aligned}&y_\mathrm{l}\left( 1\right) =y_\mathrm{c}\left( -\,1\right) ,\!&y_\mathrm{r}\left( -\,1\right) =y_\mathrm{c}\left( 1\right) , \\&y'_\mathrm{l}\left( 1\right) =\delta _\mathrm{l} y'_\mathrm{c}\left( -\,1\right) ,&y'_\mathrm{r}\left( -\,1\right) =\delta _\mathrm{r} y'_\mathrm{c}\left( 1\right) , \\&y''_\mathrm{l}\left( 1\right) =\varepsilon \delta _\mathrm{l}^2 y''_\mathrm{c}\left( -\,1\right) ,&y''_\mathrm{r}\left( -\,1\right) =\varepsilon \delta _\mathrm{r}^2 y''_\mathrm{c}\left( 1\right) , \\&y'''_\mathrm{l}\left( 1\right) =\varepsilon \delta _\mathrm{l}^3 y'''_\mathrm{c}\left( -\,1\right) ,&y'''_\mathrm{r}\left( -\,1\right) =\varepsilon \delta _\mathrm{r}^3 y'''_\mathrm{c}\left( 1\right) , \end{aligned} \end{aligned}$$

(22)

and

$$\begin{aligned} \begin{aligned}&y''_\mathrm{l}\left( -\,1\right) = y'''_\mathrm{l}\left( -\,1\right) =0,\\&y'''_\mathrm{r}\left( 1\right) =y'''_\mathrm{r}\left( 1\right) =0. \end{aligned} \end{aligned}$$

(23)

On substituting the asymptotic expansions (20) into the equations of motion (5), we arrive at the leading-order static approximation given by

$$\begin{aligned} \frac{d^4 y_{\beta ,0}}{d \xi _\beta ^4}=0, \quad \beta =l,c,r. \end{aligned}$$

(24)

In this case, for stiff components, we have the leading-order boundary conditions

$$\begin{aligned} y''_{\beta ,0}\left( \pm \,1\right) = y'''_{\beta ,0}\left( \pm \,1\right) =0,\qquad \beta =l, r \end{aligned}$$

(25)

following from the substitution of the second expansion in (20) into the formulae (22) and (23). The solutions of the boundary value problems (24) and (25) take the form of rigid body motions, i.e.,

$$\begin{aligned} y_{\beta ,0}=A_\beta \xi _\beta +B_\beta ,\qquad \beta =l,r \end{aligned}$$

(26)

involving both the rigid body translations and rotations, see Fig. 3.

For soft component ($\beta =c$), Eq. (24) has to be subjected to the boundary conditions

$$\begin{aligned} \begin{aligned}&y_{c,0}\left( -\,1\right) =y_{l,0}\left( 1\right) ,\quad&y_{c,0}\left( 1\right) =y_{r,0}\left( -\,1\right) , \\&\delta _\mathrm{l} y'_{c,0}\left( -\,1\right) =y'_{l,0}\left( 1\right) ,\quad&\delta _\mathrm{r} y'_{c,0}\left( 1\right) =y'_{r,0}\left( -\,1\right) . \end{aligned} \end{aligned}$$

(27)

As a result, we have from (24) and (27) taking into account (26)

$$\begin{aligned} y_{c,0}=A_\mathrm{c} \xi _\mathrm{c}^3+B_\mathrm{c} \xi _\mathrm{c}^2+C_\mathrm{c}\xi _\mathrm{c}+D_\mathrm{c} \end{aligned}$$

(28)

with the coefficients $A_\mathrm{c}$, $B_\mathrm{c}$, $C_\mathrm{c}$ and $D_\mathrm{c}$ satisfying the equations

$$\begin{aligned} \begin{aligned}&A_\mathrm{l}=(3A_\mathrm{c}-2B_\mathrm{c}+C_\mathrm{c})\delta _\mathrm{l},\\&B_\mathrm{l}=-\,(1+3\delta _\mathrm{l})A_\mathrm{c}+(1+2\delta _\mathrm{l})B_\mathrm{c}-(1+\delta _\mathrm{l})C_\mathrm{c}+D_\mathrm{c},\\&A_\mathrm{r}=(3A_\mathrm{c}+2B_\mathrm{c}+C_\mathrm{c})\delta _\mathrm{r},\\&B_\mathrm{r}=(1+3\delta _\mathrm{r})A_\mathrm{c}+(1+2\delta _\mathrm{r})B_\mathrm{c}+(1+\delta _\mathrm{r})C_\mathrm{c}+D_\mathrm{c}. \end{aligned} \end{aligned}$$

(29)

Now, we proceed to the next-order problems for stiff components having for the left component the “dynamic” equation of motion

$$\begin{aligned} \frac{d ^4 y_{l,1}}{d \xi _\mathrm{l}^4}-\varOmega _{l,0}^4\ y_{l,0}=0, \end{aligned}$$

(30)

with the boundary conditions

$$\begin{aligned} \left. \frac{d ^2 y_{l,1}}{d \xi _\mathrm{l}^2}\right| _{\xi _\mathrm{l}=1}=\left. \delta _\mathrm{l}^2 \frac{d ^2 y_{c,0}}{d \xi _\mathrm{c}^2}\right| _{\xi _\mathrm{c}=-\,1}, \quad \left. \frac{d ^3 y_{l,1}}{d \xi _\mathrm{l}^3}\right| _{\xi _\mathrm{l}=1}=\left. \delta _\mathrm{l}^3 \frac{d ^3 y_{c,0}}{d \xi _\mathrm{c}^3}\right| _{\xi _\mathrm{c}=-\,1}, \end{aligned}$$

(31)

and

$$\begin{aligned} \left. \frac{d^2 y_{l,1}}{d \xi _\mathrm{l}^2}\right| _{\xi _\mathrm{l}=-\,1}=\left. \frac{d^3 y_{l,1}}{d \xi _\mathrm{l}^3}\right| _{\xi _\mathrm{l}=-\,1}=0. \end{aligned}$$

(32)

Inserting $y_{l,0}$ from (26) into Eq. (30) and then integrating over $\xi _\mathrm{l}\,(-\,1\leqslant \xi _\mathrm{l}\leqslant 1)$, we obtain

$$\begin{aligned} 3\delta _\mathrm{l}^3 A_\mathrm{c}= B_\mathrm{l} \varOmega _{l,0}^4. \end{aligned}$$

(33)

Next, multiplying (30) by $\xi _\mathrm{l}$ and integrating, again, over $\xi _\mathrm{l}$, we have

$$\begin{aligned} 6\delta _\mathrm{l}^3 A_\mathrm{c}+\left( 6 A_\mathrm{c}-2B_\mathrm{c}\right) \delta _\mathrm{l}^2=\frac{2 A_\mathrm{l} \varOmega _{l,0}^4}{3}. \end{aligned}$$

(34)

Similarly, we derive for the right component

$$\begin{aligned} -\,3\delta _\mathrm{r}^3 A_\mathrm{c}= B_\mathrm{r} \varOmega _{r,0}^4, \end{aligned}$$

(35)

and

$$\begin{aligned} 6\delta _\mathrm{r}^3 A_\mathrm{c}+\left( 6 A_\mathrm{c}+2B_\mathrm{c}\right) \delta _\mathrm{r}^2=\frac{2 A_\mathrm{r} \varOmega _{l,0}^4}{3}. \end{aligned}$$

(36)

The coefficients $A_\beta$ and $B_\beta$$(\beta =l,r)$ in the right-hand side of Eqs. (33)–(36) can be expressed through the coefficients in (29), leading to the linear set of equations

$$\begin{aligned}&3\delta _\mathrm{l}^3 A_\mathrm{c}+\left( \left( 1+3\delta _\mathrm{l}\right) A_\mathrm{c}-\left( 1+2\delta _\mathrm{l}\right) B_\mathrm{c}+\left( 1+\delta _\mathrm{l}\right) C_\mathrm{c}-D_\mathrm{c}\right) \varOmega _{l,0}^4=0,\nonumber \\&9\left( \delta _\mathrm{l}^3 + \delta _\mathrm{l}^2\right) A_\mathrm{c}-3\delta _\mathrm{l}^2 B_\mathrm{c}-\delta _\mathrm{l}\left( 3 A_\mathrm{c}-2 B_\mathrm{c}+C_\mathrm{c}\right) \varOmega _{l,0}^4=0,\\&3\delta _\mathrm{r}^3 A_\mathrm{c}+\left( \left( 1+3\delta _\mathrm{r}\right) A_\mathrm{c}+\left( 1+2\delta _\mathrm{r}\right) B_\mathrm{c}+\left( 1+\delta _\mathrm{r}\right) C_\mathrm{c}+D_\mathrm{c}\right) \varOmega _{r,0}^4=0,\nonumber \\&9\left( \delta _\mathrm{r}^3 + \delta _\mathrm{r}^2\right) A_\mathrm{c}+3\delta _\mathrm{r}^2 B_\mathrm{c}-\delta _\mathrm{r}\left( 3 A_\mathrm{c}+2 B_\mathrm{c}+C_\mathrm{c}\right) \varOmega _{r,0}^4=0.\nonumber \end{aligned}$$

(37)

The latter has a nontrivial solution provided that

$$\begin{aligned}&9 \delta _\mathrm{r}^4 \varOmega _{l,0}^8 + 6 \delta _\mathrm{r} \varOmega _{l,0}^4 \left( 6 \delta _\mathrm{l}^3+ 9 \delta _\mathrm{l}^2 \left( 2 + \delta _\mathrm{r}\right) \right. \nonumber \\&\left. \quad +6 \delta _\mathrm{l} \left( 3 + \delta _\mathrm{r} \left( 3 + \delta _\mathrm{r}\right) \right) -4 \left( 2 + \delta _\mathrm{r} \left( 3+ 2 \delta _\mathrm{r}\right) \right) \varOmega _{l,0}^4\right) \varOmega _{r,0}^4\\&\quad + \left( 9 \delta _\mathrm{l}^4-24 \delta _\mathrm{l} \left( 2 + \delta _\mathrm{l} \left( 3 + 2 \delta _\mathrm{l}\right) \right) \varOmega _{l,0}^4+16 \varOmega _{l,0}^8\right) \varOmega _{r,0}^8=0.\nonumber \end{aligned}$$

(38)

in which $\varOmega _{r,0} \delta _\mathrm{l}=\varOmega _{l,0}\delta _\mathrm{r}$. The obtained frequency equation has two nonzero solutions given by

$$\begin{aligned} \varOmega _{l,0}^4&=\frac{3\delta _\mathrm{l}}{4\delta _\mathrm{r}^3}\left\{ \delta _\mathrm{r}^3\left( 2\delta _\mathrm{l}^2+3\delta _\mathrm{l}+2\right) \!-\!2\left[ \delta _\mathrm{l}^6+3\delta _\mathrm{l}^6\delta _\mathrm{r}+4 \delta _\mathrm{l}^6\delta _\mathrm{r}^2+\delta _\mathrm{l}^3\delta _\mathrm{r}^3\left( 3\delta _\mathrm{l}^3+\delta _\mathrm{l}^2-1\right) \right. \right. \nonumber \\&\left. \left. \quad +\,\delta _\mathrm{l}^4\delta _\mathrm{r}^4\left( \delta _\mathrm{l}^2+3\delta _\mathrm{l}+3\right) +\delta _\mathrm{l}^3\delta _\mathrm{r}^5\left( 2\delta _\mathrm{l}^2+3\delta _\mathrm{l}+1\right) +\left( \delta _\mathrm{l}+1\right) ^2\delta _\mathrm{r}^6\left( \delta _\mathrm{l}^2+\delta _\mathrm{l}+1\right) \right. \right. \\&\left. \left. \quad +\,\delta _\mathrm{l}^3\left( 2\delta _\mathrm{r}^2+3\delta _\mathrm{l}+2\right) \right] ^{1/2}\right\} \nonumber , \end{aligned}$$

(39)

and

$$\begin{aligned} \varOmega _{l,0}^4&=\frac{3\delta _\mathrm{l}}{4\delta _\mathrm{r}^3}\left\{ \delta _\mathrm{r}^3\left( 2\delta _\mathrm{l}^2+3\delta _\mathrm{l}+2\right) +2\left[ \delta _\mathrm{l}^6+3\delta _\mathrm{l}^6\delta _\mathrm{r}+4 \delta _\mathrm{l}^6\delta _\mathrm{r}^2+\delta _\mathrm{l}^3\delta _\mathrm{r}^3\left( 3\delta _\mathrm{l}^3+\delta _\mathrm{l}^2-1\right) \right. \right. \nonumber \\&\left. \left. \quad +\,\delta _\mathrm{l}^4\delta _\mathrm{r}^4\left( \delta _\mathrm{l}^2+3\delta _\mathrm{l}+3\right) +\delta _\mathrm{l}^3\delta _\mathrm{r}^5\left( 2\delta _\mathrm{l}^2+3\delta _\mathrm{l}+1\right) +\left( \delta _\mathrm{l}+1\right) ^2\delta _\mathrm{r}^6\left( \delta _\mathrm{l}^2+\delta _\mathrm{l}+1\right) \right. \right. \\&\left. \left. \quad +\,\delta _\mathrm{l}^3\left( 2\delta _\mathrm{r}^2+3\delta _\mathrm{l}+2\right) \right] ^{1/2}\right\} \nonumber . \end{aligned}$$

(40)

As might be expected, Eq. (38) has also a double zero eigenvalue corresponding to “pure” rigid body motions for which the displacement profile of the whole beam is a superposition of translation and rotation as given in Fig. 3. The eigenform corresponding to the almost rigid body motion of the stiff components can be found from the linear set of Eq. (37) in which the eigenfrequencies are given by formulae (39) and (40).

4.2 Two soft outer components

Similar to the previous subsection, we start here from the same asymptotic expansions (20) in the small parameter $\varepsilon$ at $j=-\,1$ in (12) having Eq. (5) with

$$\begin{aligned} \begin{aligned}&y_\mathrm{l}\left( 1\right) =y_\mathrm{c}\left( -\,1\right) ,\!&y_\mathrm{r}\left( -\,1\right) =y_\mathrm{c}\left( 1\right) , \\&y'_\mathrm{l}\left( 1\right) =\delta _\mathrm{l} y'_\mathrm{c}\left( -\,1\right) ,&y'_\mathrm{r}\left( -\,1\right) =\delta _\mathrm{r} y'_\mathrm{c}\left( 1\right) , \\&\varepsilon y''_\mathrm{l}\left( 1\right) =\delta _\mathrm{l}^2 y''_\mathrm{c}\left( -\,1\right) ,&\varepsilon y''_\mathrm{r}\left( -\,1\right) = \delta _\mathrm{r}^2 y''_\mathrm{c}\left( 1\right) , \\&\varepsilon y'''_\mathrm{l}\left( 1\right) = \delta _\mathrm{l}^3 y'''_\mathrm{c}\left( -\,1\right) ,&\varepsilon y'''_\mathrm{r}\left( -\,1\right) = \delta _\mathrm{r}^3 y'''_\mathrm{c}\left( 1\right) , \end{aligned} \end{aligned}$$

(41)

and

$$\begin{aligned} \begin{aligned}&y_\mathrm{l}\left( -\,1\right) = y'_\mathrm{l}\left( -\,1\right) =0,\\&y_\mathrm{r}\left( 1\right) = y'_\mathrm{r}\left( 1\right) =0, \end{aligned} \end{aligned}$$

(42)

The last formula corresponds to a beam with clamped ends.

The leading-order displacements of the beam are written as, see (24),

$$\begin{aligned} \begin{aligned}&y_{c,0}=A_\mathrm{c} \xi _\mathrm{c}+B_\mathrm{c},\\&y_{l,0}=A_\mathrm{l} \xi _\mathrm{l}^3+B_\mathrm{l} \xi _\mathrm{l}^2+C_\mathrm{l}\xi _\mathrm{l}+D_\mathrm{l},\\&y_{r,0}=A_\mathrm{r} \xi _\mathrm{r}^3+B_\mathrm{r} \xi _\mathrm{r}^2+C_\mathrm{r}\xi _\mathrm{r}+D_\mathrm{r}. \end{aligned} \end{aligned}$$

(43)

They satisfy the conditions

$$\begin{aligned} \begin{aligned}&y_{l,0}\left( 1\right) =y_{c,0}\left( -\,1\right) ,\quad&y'_{l,0}\left( 1\right) =\delta _\mathrm{l} y'_{c,0}\left( -\,1\right) , \\&y_{r,0}\left( -\,1\right) =y_{c,0}\left( 1\right) ,\quad&y'_{r,0}\left( -\,1\right) =\delta _\mathrm{r} y'_{c,0}\left( 1\right) . \end{aligned} \end{aligned}$$

(44)

and

$$\begin{aligned} \begin{aligned}&y_{l,0}\left( -\,1\right) = y'_{l,0}\left( -\,1\right) =0,\\&y_{r,0}\left( 1\right) =y'_{r,0}\left( 1\right) =0, \end{aligned} \end{aligned}$$

(45)

following at the leading order from substituting the second equation in (20) into (44) and (45). Then, we have

$$\begin{aligned} \begin{aligned}&A_\mathrm{l}=\frac{A_\mathrm{c}}{4}\left( 1+\delta _\mathrm{l}\right) -\frac{B_\mathrm{c}}{4},\! B_\mathrm{l}=\frac{A_\mathrm{c}}{4}\delta _\mathrm{l},\\&C_\mathrm{l}=-\,\frac{A_\mathrm{c}}{4}\left( 3+\delta _\mathrm{l}\right) +\frac{3 B_\mathrm{c}}{4}, \! D_\mathrm{l}=-\,\frac{A_\mathrm{c}}{4}\left( 2+\delta _\mathrm{l}\right) +\frac{2 B_\mathrm{c}}{4}, \end{aligned} \end{aligned}$$

(46)

and

$$\begin{aligned} \begin{aligned}&A_\mathrm{r}=\frac{A_\mathrm{c}}{4}\left( 1+\delta _\mathrm{r}\right) +\frac{B_\mathrm{c}}{4}, \! B_\mathrm{r}=-\,\frac{A_\mathrm{c}}{4}\delta _\mathrm{r},\\&C_\mathrm{r}=-\,\frac{A_\mathrm{c}}{4}\left( 3+\delta _\mathrm{r}\right) -\frac{3 B_\mathrm{c}}{4}, \! D_\mathrm{r}=\frac{A_\mathrm{c}}{4}\left( 2+\delta _\mathrm{r}\right) +\frac{2 B_\mathrm{c}}{4}. \end{aligned} \end{aligned}$$

(47)

It readily follows from (43), (46) and (47) that

$$\begin{aligned} \begin{aligned} y_{l,0}\left( \xi _\mathrm{l}\right) =&\left( \frac{A_\mathrm{c}}{4}\left( 1+\delta _\mathrm{l}\right) -\frac{B_\mathrm{c}}{4}\right) \xi _\mathrm{l}^3+\frac{A_\mathrm{c}}{4}\delta _\mathrm{l} \xi _\mathrm{l}^2+\left( -\,\frac{A_\mathrm{c}}{4}\left( 3+\delta _\mathrm{l}\right) +\frac{3 B_\mathrm{c}}{4}\right) \xi _\mathrm{l}\\&-\,\frac{A_\mathrm{c}}{4}\left( 2+\delta _\mathrm{l}\right) +\frac{2 B_\mathrm{c}}{4}, \end{aligned} \end{aligned}$$

(48)

and

$$\begin{aligned} \begin{aligned} y_{r,0}\left( \xi _\mathrm{l}\right) =&\left( \frac{A_\mathrm{c}}{4}\left( 1+\delta _\mathrm{r}\right) +\frac{B_\mathrm{c}}{4}\right) \xi _\mathrm{r}^3-\frac{A_\mathrm{c}}{4}\delta _\mathrm{r} \xi _\mathrm{r}^2-\left( \frac{A_\mathrm{c}}{4}\left( 3+\delta _\mathrm{r}\right) +\frac{3 B_\mathrm{c}}{4}\right) \xi _\mathrm{r}\\&+\,\frac{A_\mathrm{c}}{4}\left( 2+\delta _\mathrm{r}\right) +\frac{2 B_\mathrm{c}}{4}. \end{aligned} \end{aligned}$$

(49)

At the next order, we obtain from (5) and (41) the boundary value problem

$$\begin{aligned} \frac{d ^4 y_{c,1}}{d \xi _\mathrm{c}^4}-\varOmega _{c,0}^4\ y_{c,0}=0, \end{aligned}$$

(50)

with

$$\begin{aligned} \left. \frac{d ^2 y_{c,1}}{d \xi _\mathrm{c}^2}\right| _{\xi _\mathrm{c}=-\,1}\!=\left. \frac{1}{\delta _\mathrm{l}^2 }\frac{d ^2 y_{l,0}}{d \xi _\mathrm{l}^2}\right| _{\xi _\mathrm{l}=1},\quad \left. \frac{d ^3 y_{c,1}}{d \xi _\mathrm{c}^3}\right| _{\xi _\mathrm{c}=-\,1}\!=\left. \frac{1}{\delta _\mathrm{l}^3 }\frac{d ^3 y_{l,0}}{d \xi _\mathrm{l}^3}\right| _{\xi _\mathrm{l}=1}, \end{aligned}$$

(51)

$$\begin{aligned} \left. \frac{d ^2 y_{c,1}}{d \xi _\mathrm{c}^2}\right| _{\xi _\mathrm{c}=1}\!=\left. \frac{1}{\delta _\mathrm{r}^2 }\frac{d ^2 y_{r,0}}{d \xi _\mathrm{r}^2}\right| _{\xi _\mathrm{r}=-\,1},\quad \left. \frac{d ^3 y_{c,1}}{d \xi _\mathrm{c}^3}\right| _{\xi _\mathrm{c}=1}\!=\left. \frac{1}{\delta _\mathrm{r}^3 }\frac{d ^3 y_{r,0}}{d \xi _\mathrm{r}^3}\right| _{\xi _\mathrm{r}=-\,1}, \end{aligned}$$

(52)

First, integrating Eq. (50) over the interval $-1\leqslant \xi _\mathrm{c}\leqslant 1$ and applying the conditions (51) and (52), we find

$$\begin{aligned} \frac{3}{2\delta _\mathrm{r}^3}\left( A_\mathrm{c}\left( 1+\delta _\mathrm{r}\right) +B_\mathrm{c}\right) -\frac{3}{2\delta _\mathrm{l}^3}\left( A_\mathrm{c}\left( 1+\delta _\mathrm{l}\right) -B_\mathrm{c}\right) =2B_\mathrm{c}\varOmega _{c,0}^4. \end{aligned}$$

(53)

Next, multiplying (50) by $\xi _\mathrm{c}$ and integrating over the same interval, we obtain, taking into account (51) and (52),

$$\begin{aligned} \begin{aligned}&\frac{3}{2\delta _\mathrm{r}^3}\left( A_\mathrm{c}\left( 1+\delta _\mathrm{r}\right) +B_\mathrm{c}\right) +\frac{3}{2\delta _\mathrm{l}^3}\left( A_\mathrm{c}\left( 1+\delta _\mathrm{l}\right) -B_\mathrm{c}\right) \\&\quad +\frac{3}{2\delta _\mathrm{r}^2}\left( A_\mathrm{c}\left( 1+\frac{4}{3}\delta _\mathrm{r}\right) +B_\mathrm{c}\right) +\frac{3}{2\delta _\mathrm{l}^2}\left( A_\mathrm{c}\left( 1+\frac{4}{3}\delta _\mathrm{l}\right) -B_\mathrm{c}\right) =\frac{2 A_\mathrm{c} \varOmega _{c,0}^4}{3} \end{aligned} \end{aligned}$$

(54)

Computability of the last two equations leads to the asymptotic formulae for the lowest eigenfrequencies given by

$$\begin{aligned} \varOmega _{c,0}^4=&\frac{3}{4\delta _\mathrm{l}^3\delta _\mathrm{r}^3}\left\{ 2\delta _\mathrm{r}^3+3\delta _\mathrm{l}\delta _\mathrm{r}^3+2\delta _\mathrm{l}^2\delta _\mathrm{r}^3+\delta _\mathrm{l}^3\left( 2\delta _\mathrm{r}^2+3 \delta _\mathrm{r}+2\right) -2\left[ \delta _\mathrm{r}^6+3\delta _\mathrm{l}\delta _\mathrm{r}^6\right. \right. \nonumber \\&\left. \left. +\,4\delta _\mathrm{l}^2\delta _\mathrm{r}^6+\delta _\mathrm{l}^6\left( \delta _\mathrm{r}+1\right) ^2\left( \delta _\mathrm{r}^2+\delta _\mathrm{r}+1\right) +\delta _\mathrm{l}^5\delta _\mathrm{r}^3\left( 2\delta _\mathrm{r}^2+3\delta _\mathrm{r}+1\right) \right. \right. \\&\left. \left. +\,\delta _\mathrm{l}^3\delta _\mathrm{r}^3\left( 3\delta _\mathrm{r}^3+\delta _\mathrm{r}^2-1\right) +\delta _\mathrm{l}^4\delta _\mathrm{r}^4\left( \delta _\mathrm{r}^2+3\delta _\mathrm{r}+3\right) \right] ^{1/2}\right\} \nonumber , \end{aligned}$$

(55)

and

$$\begin{aligned} \varOmega _{c,0}^4=&\frac{3}{4\delta _\mathrm{l}^3\delta _\mathrm{r}^3}\left\{ 2\delta _\mathrm{r}^3+3\delta _\mathrm{l}\delta _\mathrm{r}^3+2\delta _\mathrm{l}^2\delta _\mathrm{r}^3+\delta _\mathrm{l}^3\left( 2\delta _\mathrm{r}^2+3 \delta _\mathrm{r}+2\right) +2\left[ \delta _\mathrm{r}^6+3\delta _\mathrm{l}\delta _\mathrm{r}^6\right. \right. \nonumber \\&\left. \left. +\,4\delta _\mathrm{l}^2\delta _\mathrm{r}^6+\delta _\mathrm{l}^6\left( \delta _\mathrm{r}+1\right) ^2\left( \delta _\mathrm{r}^2+\delta _\mathrm{r}+1\right) +\delta _\mathrm{l}^5\delta _\mathrm{r}^3\left( 2\delta _\mathrm{r}^2+3\delta _\mathrm{r}+1\right) \right. \right. \\&\left. \left. +\,\delta _\mathrm{l}^3\delta _\mathrm{r}^3\left( 3\delta _\mathrm{r}^3+\delta _\mathrm{r}^2-1\right) +\delta _\mathrm{l}^4\delta _\mathrm{r}^4\left( \delta _\mathrm{r}^2+3\delta _\mathrm{r}+3\right) \right] ^{1/2}\right\} \nonumber , \end{aligned}$$

(56)

In contrast to the setup analyzed in the previous section, the boundary conditions corresponding to the clamped ends do not support “pure” rigid body motions with zero eigenfrequencies.

5 Symmetric structure

Here, we consider an important particular case, in which $\delta _\mathrm{l}=\delta _\mathrm{r}=\delta$. This assumption will drastically simplify the pretty lengthy formulae (39), (40), (55) and (56) for the lowest eigenfrequencies and also the expressions of the associated eigenforms. In this case, due to symmetry of the problem, the derivation may be reduced to analysis of simpler problems for only one, say left, half of the structure.

First, analyze the symmetric vibration modes of the beam shown in Fig. 1, for which, we have from (26) and (28)

$$\begin{aligned} \begin{aligned}&y_{l,0}=A_\mathrm{l} \xi _\mathrm{l}+B_\mathrm{l},\\&y_{c,0}=A_\mathrm{c} \xi _\mathrm{c}^2+B_\mathrm{c}, \end{aligned} \end{aligned}$$

(57)

On substituting these eigenforms into the continuity conditions given by the first and the third equations in (27), we get

$$\begin{aligned} y_{c,0}\left( \xi _\mathrm{c}\right) =-\,\frac{A_\mathrm{l}}{2 \delta }\xi _\mathrm{c}^2+A_\mathrm{l}\left( 1+\frac{1}{2 \delta }\right) +B_\mathrm{l}. \end{aligned}$$

(58)

At the next order, we arrive at the boundary value problem for Eq. (30) subjected to the conditions (32) and (51) with $\delta _\mathrm{l}=\delta$.

Similar to the consideration above, the solvability of the aforementioned boundary value problem gives the expression for the sought for lowest nonzero eigenfrequency. It is

$$\begin{aligned} \varOmega _{l,0}^4=\frac{3 \delta }{2}, \end{aligned}$$

(59)

corresponding to the eigenform with $B_\mathrm{l}=0$.

For the antisymmetric modes, we have

$$\begin{aligned} \begin{aligned} y_{l,0}\left( \xi _\mathrm{l}\right)&=A_\mathrm{l} \xi _\mathrm{l}+B_\mathrm{l},\\ y_{c,0}\left( \xi _\mathrm{c}\right)&=\left( \frac{A_\mathrm{l}}{2 }\left( 1+\frac{1}{\delta }\right) +\frac{B_\mathrm{l}}{2 }\right) \xi _\mathrm{c}^3-\left( \frac{A_\mathrm{l}}{2 }\left( 3+\frac{1}{\delta }\right) +\frac{3 B_\mathrm{l}}{2 }\right) \xi _\mathrm{c} \end{aligned} \end{aligned}$$

(60)

satisfying the continuity conditions at the interface between stiff and soft components. Finally, we arrive at the asymptotic formula for nonzero eigenfrequency given by

$$\begin{aligned} \varOmega _{l,0}^4=\frac{3\delta }{2}\left( 3\left( 1+\delta \right) ^2+\delta ^2\right) . \end{aligned}$$

(61)

In this case, the coefficients of the left displacement are related by

$$\begin{aligned} A_\mathrm{l}=\displaystyle \frac{3(\delta +1)}{\delta }B_\mathrm{l}. \end{aligned}$$

(62)

Comparison of formulae (59) and (61) with their general counterparts (39) and (40) at $\delta _\mathrm{l}=\delta$ shows that they are identical.

For symmetric $(y_{c,0}=A_\mathrm{c})$ and antisymmetric $(y_{c,0}=B_\mathrm{c} \xi _\mathrm{c})$ vibration modes of the beam in Fig. 2, we have, by substituting $\delta _\mathrm{l}=\delta _\mathrm{r}=\delta$ into formulae (55) and (56), respectively,

$$\begin{aligned} \varOmega _{c,0}^4=\frac{3}{2 \delta ^3}, \end{aligned}$$

(63)

and

$$\begin{aligned} \varOmega _{c,0}^4=\frac{3\left( 4\delta ^2+6\delta +3\right) }{2 \delta ^3}. \end{aligned}$$

(64)

6 Numerical results

Below, we compute the lowest eigenfrequencies and eigenforms for the beams in Figs. 1 and 2.

Figures 4 and 5 show the eigenforms of the beam with two stiff parts given by the asymptotic formulae in the previous section, see (57), (58) at $B_\mathrm{l}=0$ and (60), (62), respectively. The associated eigenfrequency is estimated by (59) and (61). In these figures, $\varepsilon =0.1$, $\delta =4$ and $\delta =1.01$.

Figures 6 and 7 illustrate the effect of beam’s asymmetry at $\varepsilon =0.1$$\delta _\mathrm{r}=0.2$, $\delta _\mathrm{l}=0.4$ or $\delta _\mathrm{l}=0.8$, for a beam with two stiff and two soft components, respectively. The eigenforms are calculated using the linear Eqs. (37) and (53), (54) leading to the asymptotic formulae (39) and (55).

Fig. 4

The asymptotic eigenform of a symmetric beam with two stiff outer components for the eigenfrequency (39), $\varepsilon =0.1$

Fig. 5

The asymptotic eigenform of an antisymmetric beam with two stiff outer components for the eigenfrequency (55), $\varepsilon =0.1$

Fig. 6

The asymptotic eigenform of a beam with two stiff outer components for the eigenfrequency (39), $\varepsilon =0.1$ and $\delta _\mathrm{r}=0.2$

Fig. 7

The asymptotic eigenform of a beam with two soft outer components for the eigenfrequency (55), $\varepsilon =0.1$ and $\delta _\mathrm{r}=0.2$

Figure 8 illustrates the comparison of the exact and approximate values of the lowest eigenfrequency evaluated from transcendental Eq. (17) and the approximate formula (39) plotted by dotted and solid lines, respectively, at $\delta =1.01$.

Fig. 8

The asymptotic formula (39) versus the numerical solution of the transcendental Eq. (17) at $\delta =1.01$

The comparison of the associated eigenforms is presented in Fig. 9, where $\varepsilon =0.1$. The exact eigenform is given by (15) and (16) while the asymptotic one is expressed by (57).

Fig. 9

The asymptotic eigenform (57) versus the exact one (15) and (16) at $\varepsilon =0.1$ and $\delta =1.01$

7 Concluding remarks

An asymptotic procedure for evaluating the lowest eigenfrequency of strongly inhomogeneous beams with piecewise uniform material parameters is developed. The procedure starts from perturbations around rigid body translations and rotations of stiff components in small parameter arising from the contrast in stiffnesses. At the leading order, the displacements of stiff components are given by linear functions of the longitudinal coordinate, while the displacements of soft component are generally expressed in the form of third-order polynomials. Comparison with the exact sinusoidal solution of a symmetric beam with two stiff outer components and free ends demonstrated the efficiency of the asymptotic formulae for the lowest eigenvalue and eigenform.

Although the results are obtained for two types of three-span beams, see Figs. 1 and 2, the methodology is not seemingly restricted to the considered layouts and it may be implemented for multilayered structures resting on elastic foundation, see, for example [27]. The proposed approach is not strict to the extra restriction on the contrast in densities presented by formula (18) as well as assumption (19) excluding very short or long components. It also has a potential to be extended two multi-span high-contrast plates. Finally, the so-called local low-frequency regimes with a sinusoidal (not polynomial) behavior along soft components, similar to those in rods, [19], might be also studied.

Appendix

The coefficients in the expression (15) and (16) for the eigenform of a symmetric beam with two outer stiff components and free ends can be written as

$$\begin{aligned} A_\mathrm{c}=&\frac{2}{a^{3/2}}\left\{ \sqrt{a}\cosh (\varOmega _\mathrm{c})\left( (a-D)\cos (2 \varOmega _\mathrm{r})-(a+D)\cos (2 \varOmega _\mathrm{r})\right) \right. \\&\left. +\,\sinh (\varOmega _\mathrm{c})\left( (a-D)\sin (2 \varOmega _\mathrm{r})-(a+D)\sin (2 \varOmega _\mathrm{r})\right) \right\} , \\ C_\mathrm{c}=&\frac{2}{a^{3/2}}\left\{ \sqrt{a}\cos (\varOmega _\mathrm{c})\left( (a-D)\cosh (2 \varOmega _\mathrm{r})-(a+D)\cos (2 \varOmega _\mathrm{r})\right) \right. \\&\left. -\,\sin (\varOmega _\mathrm{c})\left( (a-D)\sinh (2 \varOmega _\mathrm{r})-(a+D)\sin (2 \varOmega _\mathrm{r})\right) \right\} , \\ A_\mathrm{r}=&-\frac{2 }{a^{5/2}}\left\{ \cosh (\varOmega _\mathrm{c})\left( a\cosh (\varOmega _\mathrm{r})^2\left( 2\sqrt{a}D\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})\right. \right. \right. \\&\left. \left. \left. -\,(a+M)\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) +(a-D)^2\sin (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})\cosh (\varOmega _\mathrm{r})\right. \right. \\&\left. \left. +\,D\sinh (\varOmega _\mathrm{r})^2\left( 2a^{3/2}\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})-(a+D)\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\!\right) \!\right) \right. \\&\left. \sinh (\varOmega _\mathrm{c})\left( -\,a(a-D)\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\cosh (\varOmega _\mathrm{r})^2+\cosh (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})\right. \right. \\&\left. \left. \left( (a^2+D^2)\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})-4\sqrt{a}D\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) +D \cos (\varOmega _\mathrm{c})\left( (a-D)\right. \right. \right. \\&\left. \left. \left. \sin (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})^2+a\cos (\varOmega _\mathrm{r})\sinh (2\varOmega _\mathrm{r})\right) \right) \!\right\} , \end{aligned}$$

$$\begin{aligned} B_\mathrm{r}=&\frac{2}{a^{5/2}}\left\{ \cosh (\varOmega _\mathrm{c})\left( D\cosh (\varOmega _\mathrm{r})^2\left( (a+D)\cos (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})\right. \right. \right. \\&\left. \left. \left. +\,2a^{3/2}\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) +(a-D)^2\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})\cosh (\varOmega _\mathrm{r})\right. \right. \\&\left. \left. +\,a\sinh (\varOmega _\mathrm{r})^2\left( (a+D)\cos (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})+2\sqrt{a}D\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) \right) \right. \\&\left. +\sinh (\varOmega _\mathrm{c})\left( -\,D(a-D)\cos (\varOmega _\mathrm{c})\cos (\varOmega _\mathrm{r})\cosh (\varOmega _\mathrm{r})^2+\cosh (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})\right. \right. \\&\left. \left. \left( 4\sqrt{a}D\cos (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})+(a^2+D^2)\cos (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) +a\cos (\varOmega _\mathrm{c})\left( (a-D)\right. \right. \right. \\&\left. \left. \left. \cos (\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})^2+D\sin (\varOmega _\mathrm{r})\sinh (2\varOmega _\mathrm{r})\right) \right) \!\right\} , \\ C_\mathrm{r}=&\frac{ 1}{a^{5/2}}\!\left\{ \!\cosh (\varOmega _\mathrm{r})\!\left( \!\cosh (\varOmega _\mathrm{c})\!\left( \!-4 a^{3/2}D \cos (\varOmega _\mathrm{c})\!\cos (2\varOmega _\mathrm{r})\!+\!(a\!+\!D)^2\!\sin (\varOmega _\mathrm{c})\!\sin (2\varOmega _\mathrm{r})\right. \right. \right. \\&\left. \left. \left. +\,(a-D)^2\cos (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{c})\right) \right) -\sinh (\varOmega _\mathrm{r})\left( (a-D)\left( a+D \right. \right. \right. \\&\left. \left. \left. +\,(a-D)\cos (2\varOmega _\mathrm{r})\right) \cosh (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{c})+\sinh (\varOmega _\mathrm{c})\left( (a+D)\cos (\varOmega _\mathrm{c})\right. \right. \right. \\&\left. \left. \left. \left( a-D+(a+D)\cos (2\varOmega _\mathrm{r})\right) -8\sqrt{a}D\cos (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})\sin (\varOmega _\mathrm{r})\right) \right) \right\} , \\ D_\mathrm{r}=&\frac{1}{a^{5/2}}\left\{ \sinh (\varOmega _\mathrm{c})\left( \cosh (\varOmega _\mathrm{r})\left( -\,(a+D)\cos (\varOmega _\mathrm{c})\left( -\,a\!+\!D\!+\!(a\!+\!D)\cos (2\varOmega _\mathrm{r})\right) \!\right. \right. \right. \\&\left. \left. \left. +\,\!4\sqrt{a}D\sin (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\right) +(a-D)^2\cos (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\sinh (\varOmega _\mathrm{r})\right) +\cosh (\varOmega _\mathrm{c})\right. \\&\left. \left( \!-(a\!-\!D)\left( \!-a\!-\!D\!+\!(a\!-\!D)\cos (2\varOmega _\mathrm{r})\right) \cosh (\varOmega _\mathrm{r})\sin (\varOmega _\mathrm{c})+\sin (2\varOmega _\mathrm{r})\right. \right. \\&\left. \left. \left( -\,4a^{3/2}D\cos (\varOmega _\mathrm{c})\cos (2\varOmega _\mathrm{r})+(a+D)^2\sin (\varOmega _\mathrm{c})\sin (2\varOmega _\mathrm{r})\right) \right) \right\} . \end{aligned}$$