Performance analysis of parametrically and directly excited nonlinear piezoelectric energy harvester

Abstract

The performance of bimorph cantilever energy harvester subjected to horizontal and vertical excitations is investigated. The energy harvester is simulated as an inextensible piezoelectric beam with the Euler–Bernoulli assumptions. A horizontal base excitation along the axis of the beam is converted into the parametric excitation. The governing equations include geometric, inertia and electromechanical coupling nonlinearities. Using the Galerkin method, the electromechanical coupling Mathieu–Duffing equation is developed. Analytical solutions of the frequency response curves are presented by using the method of multiple scales. Some analytical results are obtained, which reveal the influence of different parameters such as the damping, load resistance and excitation amplitude on the output power of the energy harvester. In the case of parametric excitation, the effect of mechanical damping and load resistance on the initiation excitation threshold is studied. In the case of combination of parametric and direct excitations, the dynamic characteristics and performance of the nonlinear piezoelectric energy harvesters are studied. Our studies revealed that the bending deformation generated by direct excitation pushes the system out of axial deformation and overcomes the limitation of initial threshold of parametric excitation system. The combination of parametric and direct excitations, which compensates and complements each other, can be served as a better solution which enhances performance of energy harvesters.

1 Introduction

Vibration energy harvesting provides a promising approach for a self-power source of portable devices or wireless sensor network system. The electromechanical coupling theory of piezoelectric composite beam has been developed [1, 2]. Some reviews of piezoelectric energy harvesting system have recently been published [3,4,5,6,7,8,9]. Most of the researchers have focused on using a linear model of vibration energy harvesters [10,11,12,13,14,15,16,17,18,19,20]. In the case of the resonance frequency, the linear model of the harvester will maximize the output power for a given excitation frequency spectrum. Once the excitation frequency drifts away from the harvester’s resonance frequency, the harvesting energy drops significantly and results in the energy harvesting process inefficient. Meanwhile, the linear model is not suitable for vibration sources which are with time-varying frequency or distributed over a wide frequency range because of the narrow frequency bandwidth of the linear resonators. To overcome this shortcoming, various nonlinear energy harvesters have recently been proposed to achieve harvesting energy over a broad frequency band.

Some researchers have investigated the nonlinear hysteretic behaviors such as the hardening or softening hysteresis. The nonlinear hysteretic behaviors can be deliberately invoked to broaden the frequency range of the harvesters. Mahmoodi and Jalili [21] analytically studied and experimentally verified the vibration response of the piezoelectric cantilevered beam which considered the inextensible condition, geometrical nonlinearities and the electromechanical coupling. Triplett and Quinn [22] studied the effects of the electromechanical coupling nonlinearities on the performance of vibration-based energy harvester by using the lumped-parameter nonlinear model and the perturbation analysis. The performance of the corresponding energy harvesting system was compared with the linear energy harvesting systems. Cottone et al. [23], Ferrari et al. [24] and Stanton et al. [25] derived an analytical model of cantilevered piezoelectric beam coupled to permanent magnets to create a bistable system and studied the spectral response of the bistable harvesting system under stochastic excitation. The study showed that the bistable energy harvesting system can provide better performances compared to the linear one in terms of the energy extracted from a generic wide spectrum vibration. Stanton et al. [26], Abdelkefi et al. [27] and Leadenham and Erturk [28] proposed and experimentally validated a nonlinear distributed parameters model of cantilevered piezoelectric beam which included piezoelectric nonlinearities. Panyam et al. [29] used the method of multiple scales to construct analytical solutions of bistable vibration energy harvesters and investigated the amplitude and stability of the intrawell and interwell dynamics of the harvester under harmonic excitations. Vijayan et al. [30] developed a vibration impacting system for converting low frequency response to high frequencies to explore the effect of frequency up-conversion on the output power of the harvester. Daqaq et al. [31] highlighted the role of nonlinearities in the transduction of energy harvesters under different types of excitations, which focused on the use of nonlinearity to improve the performance of vibratory harvesters. Pasharavesh et al. [32, 33] proposed a nonlinear mathematical model of cantilever and doubly clamped piezoelectric energy harvesters by variational approach. Firoozy et al. [34] studied the nonlinear dynamic behavior of a unimorph piezoelectric cantilever energy harvester with and without a tip mass subjected to a harmonic excitation. Gafforelli et al. [35, 36] reported a comprehensive modeling and experimental verification of a bridge-shaped nonlinear energy harvester. Yang and Towfighian [37] presented a hybrid nonlinear energy harvester which combined bistability and internal resonance effects to broaden the frequency bandwidth of energy harvesters. Wang et al. [38] investigated the response of nonlinear piezoelectric energy harvester by harmonic balance and the method of multiple scales and compared the relative accuracy of the two methods. Zhu et al. [39] developed a novel tristable energy harvester with two external magnets to improve the efficiency of harvesting vibration energy.

The parametric resonance can significantly enhance the performance of the energy harvester and raise the interest of many researchers. Daqaq et al. [40] investigated a cantilever piezoelectric energy harvester under parametric excitation. In their study, a nonlinear lumped-parameter model was proposed to describe the first-mode dynamics of the harvester. Jia et al. [41,42,43,44] proposed a novel design and working mechanism in order to reduce the initiation threshold and overcome the shortcomings of the parametric resonance. The results showed the parametric resonance could serve to widen the operational frequency bandwidth and enhance the energy harvesting. Abdelkefi et al. [45] derived a global nonlinear distributed-parameter model of parametrically excited piezoelectric cantilevered harvester. The proposed model accounted for geometric, inertia, piezoelectric and fluid drag nonlinearities. Bitar et al. [46] presented a discrete model for the collective dynamics of periodic nonlinear oscillators under simultaneous parametric and direct excitations, which was suitable for several physical applications. Chiba et al. [47] investigated the dynamic stability of a vertically standing cantilever beam under simultaneous horizontal and vertical excitations. Mam et al. [48] presented a nonlinear distributed-parameter model of the piezoelectric energy harvester under direct and parametric excitation, in which geometric and piezoelectric nonlinearities were considered. Based on the proposed model, some critical issues related to the energy harvester are investigated. But they did not study the performance of the energy harvester under combination of parametric and direct excitations. Considering geometrical nonlinearity, Fang et al. [49] investigated the performance of cantilever piezoelectric energy harvester under parametric and direct excitations. In their study, the harmonic balance method was used to find analytical expressions of the frequency response curves. But the stability of the solutions and the effect of the load resistance on the initiation threshold were not investigated.

Le and Yi [50,51,52,53] demonstrated that the rigorous first-order approximate 2-D theory of thin smart sandwich shells can be derived from the exact 3-D piezoelectricity theory by the variational asymptotic method. An error estimation of the approximate 2-D and 1-D equations has been obtained [52, 53]. When the length of the beam is much larger than the thickness, the Euler–Bernoulli assumptions can be applied to sandwich piezoelectric beam. In this paper, the nonlinear dynamic performance of parametrically and directly excited cantilevered piezoelectric energy harvester is investigated. Based on that the authors proposed the governing partial differential equations [49], analytical expressions of the vertical displacement and output voltage are obtained by the method of multiple scales. Some critical issues related to energy harvesting are investigated, such as the influences of the damping, load resistance and excitation amplitude on the performance of the energy harvester. Meanwhile, improving the performance of the energy harvester is studied by the combination of parametric and direct excitations.

2 Mathematical model of energy harvesting system

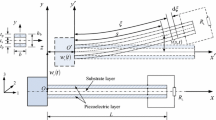
A uniform bimorph piezoelectric cantilever beam under its base horizontal and vertical excitations is shown in Fig. 1.

Fig. 1

Model of cantilevered piezoelectric beam for energy harvesting

The beam consists of one substrate and two piezoelectric layers, in which L is the length, b is the width, $h_\mathrm{b} =t_\mathrm{s} +2t_\mathrm{p}$ is the thickness of the beam, $t_\mathrm{s}$ is the thickness of the substrate layer and $t_\mathrm{p}$ is the thickness of each piezoelectric layer. $R_\mathrm{L}$ is the load resistance. The piezoelectric layers and substrate layer are perfectly bonded to each other by two in-plane electrode layers of negligible thickness connected to the load resistance. The continuous electrode pairs covering the top and the bottom faces of the piezoelectric layers are assumed to be perfectly conductive so that a single electric potential difference can be defined across them. Therefore, the instantaneous electric fields induced in the piezoelectric layers are assumed to be uniform throughout the length of the beam [12]. The beam is treated as the Euler–Bernoulli model, in which shear deformation and rotatory motion are neglected. Setting the oxy coordinate as the inertia coordinate, the fixed-end displacements of the beam are $w_x (t)$ and $w_y (t)$ in the horizontal direction and vertical direction, respectively. The ${o}'{x}'{y}'$coordinate is set at the fixed end of the beam. s is the coordinate along the middle plane of the beam. u(s, t) and v(s, t) are the displacements of the beam relative to the ${o}'{x}'{y}'$coordinate system. u(s, t) is in the ${x}'$ direction and v(s, t) in the ${y}'$ direction. The beam is assumed to be inextensible.

Based on the Euler–Bernoulli beam theory and the generalized Hamilton principle, and taking up to the cubic order of v, the governing differential equations of motion can be obtained as follows [49]:

$$\begin{aligned}&m_t [{ v}+w_y ]_{,tt} +c{v}_{,t} +YI\left( {{{{ v}}''''}+{{v}}'^{2}{{{ v}}''''}+4{{ v}}'{{ v}}''{{ v}}'''+{{ v}}''^{3}} \right) \nonumber \\&\quad +\left[ {{{ v}}''(L-s)-{{ v}}'} \right] m_t w_{x,tt} +\frac{1}{2}m_t \left[ {{{ v}}'\int _{0}^{s} {\left( {{{ v}}'^{2}} \right) _{,tt} \mathrm{d}s} -{{ v}}''\int _{s}^{L} {\int _{0}^{\xi } {\left( {{{ v}}'^{2}} \right) _{,tt} \mathrm{d}s \mathrm{d}\xi } } } \right] \nonumber \\&\quad -\alpha V\left\{ {(1+\frac{1}{2}{{ v}}'^{2})\left[ {\frac{\mathrm{d}\delta (s)}{\mathrm{d}s}-\frac{\mathrm{d}\delta (s-L)}{\mathrm{d}s}} \right] +{{ v}}''{v}'\left[ {\delta \left( s \right) -\delta \left( {s-L} \right) } \right] } \right\} =0 \end{aligned}$$

(1)

$$\begin{aligned}&\alpha \int _{0}^{L} {\left[ {{v}''\left( {1+\frac{1}{2}{v}'^{2}} \right) } \right] } _{,t} \mathrm{d}s+C_\mathrm{p} V_{,t} +\frac{V}{R_\mathrm{L} }=0 \end{aligned}$$

(2)

where $\delta {(}s{)}$ is the Dirac delta function prime $(')$ indicates the derivative with respect to the arc length, $s.~m_t =2\rho _\mathrm{p} t_\mathrm{p} b+\rho _\mathrm{s} t_\mathrm{s} b$, $\rho _\mathrm{p}$ and $\rho _\mathrm{s}$ are the density of the piezoelectric and substrate layers, respectively. $YI=Y_\mathrm{s} I_\mathrm{s} +\frac{2}{3}Y_\mathrm{p} b\left( {3h^{2}t_\mathrm{p} +3ht_\mathrm{p} ^{2}+t_\mathrm{p} ^{3}} \right)$, $Y_\mathrm{s} I_\mathrm{s}$ is the bending stiffness of the substrate layer, $h=t_\mathrm{s} /2$. $\alpha =Y_\mathrm{p} bd_{31} \left( {h+\frac{t_\mathrm{p} }{2}} \right)$, $\bar{{C}}_\mathrm{p} =\frac{b\varepsilon _{33}^S }{2t_\mathrm{p} },C_\mathrm{p} =\bar{{C}}_\mathrm{p} L$. $\alpha$ is related to the electromechanical coupling coefficient. $C_\mathrm{p}$ is the capacitance of the piezoelectric layers. The above equations are a nonlinear distributed-parameter model of the cantilever piezoelectric harvester under parametric and direct excitations. The horizontal excitation has been converted into the parametric excitation.

Introducing the dimensionless parameters shown in Eq. (3), the governing equations (1) and (2) can be rewritten as Eqs. (4) and (5) in the dimensionless form.

$$\begin{aligned} \bar{{s}}= & {} s/L,\bar{{\xi }}=\xi /L,\bar{{v}}=v/L,\bar{{w}}_x =w_x /L,\bar{{w}}_y =w_y /L \nonumber \\ \omega _0= & {} \sqrt{YI/m_t L^{4}},\tau =\omega _0 t,\bar{{c}}=c/(m_t \omega _0 ),\omega _y =\Omega _y /\omega _0 ,\omega _x =\Omega _x /\omega _0 \nonumber \\ V= & {} \omega _0 L\sqrt{m_t /\bar{{C}}_\mathrm{p} }\bar{{V}},\alpha =\omega _0 L^{2}\sqrt{m_t \bar{{C}}_\mathrm{p} }\bar{{\alpha }} \end{aligned}$$

(3)

$$\begin{aligned}&\ddot{\bar{{{v}}}}+\bar{{c}}\dot{\bar{{{v}}}}+{{\bar{{{v}}}}''''}+{\bar{{{v}}}}'^{2}{{\bar{{{v}}}}''''}+4{\bar{{{v}}}}' {\bar{{{v}}}''}{\bar{{{v}}}'''}+{\bar{{{v}}}}''^{3} \nonumber \\&\quad +\left[ {{\bar{{{v}}}}''\left( {1-\bar{{s}}} \right) -{\bar{{{v}}}}'} \right] \ddot{\bar{{w}}}_x +{\bar{{{v}}}}'\int _0^{\bar{{s}}} {\left( \dot{{\bar{{{v}}}}}'{\dot{\bar{{{v}}}}'}+{\bar{{{v}}}}'{\ddot{{\bar{{{v}}}}}'}\right) \mathrm{d}\bar{{s}}-} {\bar{{{v}}}}''\int _{\bar{{s}}}^1 {\left( \int _0^{\bar{{\xi }}} {({\dot{{\bar{{{v}}}}}'}{\dot{\bar{{{v}}}}}'+{\bar{{{v}}}}'{\ddot{{\bar{{{v}}}}}'})\mathrm{d}\bar{{s}}} \right) } \mathrm{d}\bar{{\xi }} \nonumber \\&\quad -\bar{{\alpha }}\bar{{V}}\left\{ {\left( {1+\frac{1}{2}{\bar{{{v}}}}'^{2}} \right) \left[ {\frac{\mathrm{d}\delta (\bar{{s}})}{\mathrm{d}\bar{{s}}}-\frac{\mathrm{d}\delta (\bar{{s}}-1)}{\mathrm{d}\bar{{s}}}} \right] +{\bar{{{v}}}}''{\bar{{{v}}}}'\left[ {\delta (\bar{{s}})-\delta (\bar{{s}}-1)} \right] } \right\} =-\ddot{\bar{{w}}}_y \end{aligned}$$

(4)

$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\int _0^1 \left[ {{\dot{{\bar{{{v}}}}}''}+\frac{1}{2}{\bar{{{v}}}}'^{2}{\dot{{\bar{{{v}}}}}''}+{\bar{{{v}}}}''{\bar{{{v}}}}'{\dot{\bar{{{v}}}}}'} \right] \mathrm{d}\bar{{s}}=0 \end{aligned}$$

(5)

where $\Omega _x$ and $\Omega _y$ are the parametric and direct excited frequencies, respectively. $\bar{{v}}$ is dimensionless vertical displacement and $\bar{{V}}$ dimensionless voltage. $\mu =\frac{1}{R_\mathrm{L} \omega _0 C_\mathrm{p} }$, ($\cdot$) indicates the derivative with respect to the time variable, $\tau$.

3 Approximate analytical solutions

To obtain analytical solutions of the nonlinear governing equations (4) and (5), the Galerkin method and the method of multiple scales are used.

3.1 Reduced-order model

Using the Galerkin method and assuming the excitation frequency is very close to the nth modal frequency, we focused on the n-th vibration mode of the beam and neglected the interactions with other modes. The transverse displacement $\bar{{v}}(\bar{{s}},\tau )$ is decomposed into the products of generalized time-dependent displacement amplitude $\bar{{w}}_n (\tau )$ and orthogonal mode shape function $\phi _n (\bar{{s}})$ as

$$\begin{aligned} \bar{{v}}(\bar{{s}},\tau )=\bar{{w}}_n \left( \tau \right) \phi _n \left( {\bar{{s}}} \right) \end{aligned}$$

(6)

where $\phi _n (\bar{{s}})$ is the linear normalized mode shape functions of the Euler–Bernoulli beam with fixed-free boundary conditions, which can be expressed as:

$$\begin{aligned} \phi _n \left( {\bar{{s}}} \right) =\cosh \bar{{\beta }}_n \bar{{s}}-\cos \bar{{\beta }}_n \bar{{s}}+\frac{\cos \bar{{\beta }}_n +\cosh \bar{{\beta }}_n }{\sin \bar{{\beta }}_n +\sinh \bar{{\beta }}_n }\left( {\sin \bar{{\beta }}_n \bar{{s}}-\sinh \bar{{\beta }}_n \bar{{s}}} \right) \end{aligned}$$

(7)

where $\bar{{\beta }}_n^2 =\bar{{\omega }}_n$, $\bar{{\omega }}_n =\omega _n /\omega _0$, $\omega _n$ is the n-th eigenfrequency of free bending vibration of the cantilever beam, $\bar{{\beta }}_n$ are the roots of the following frequency equation.

$$\begin{aligned} \cosh \bar{\beta }_n\cos \bar{\beta }_n+1=0 \end{aligned}$$

(8)

Substituting Eq. (6) into Eqs. (4) and (5), multiplying Eq. (4) by $\phi _n (\bar{{s}})$, and subsequently integrating over the length of the beam, we yield a set of nonlinear ordinary differential equations of motion.

$$\begin{aligned}&\ddot{\bar{{w}}}_n +2{\tilde{c}}\dot{\bar{{w}}}_n +\left( {\bar{{\omega }}_n^2 +2\bar{{\sigma }}_n \ddot{\bar{{w}}}_x } \right) \bar{{w}}_n +\beta _n \bar{{w}}_n^3 +\kappa _n \left( {\dot{\bar{{w}}}_n^2 +\bar{{w}}_n \ddot{\bar{{w}}}_n } \right) \bar{{w}}_n -\bar{{\alpha }}\left( {\zeta _n +\gamma _n \bar{{w}}_n^2 } \right) \bar{{V}}=-\bar{{\lambda }}_n \ddot{\bar{{w}}}_y \end{aligned}$$

(9)

$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\left( {\eta _n +\chi _n \bar{{w}}_n^2 } \right) \dot{\bar{{w}}}_n =0 \end{aligned}$$

(10)

where the coefficients are defined in Eq. (A1) (see “Appendix A”). We can prove $\eta _n =\zeta _n ,\chi _n =\gamma _n$ (see Eq. (A2) in “Appendix A”). The term $\beta _n \bar{{w}}_n^3$ describes cubic geometric nonlinearity, $\kappa _n (\dot{\bar{{w}}}_n^2 +\bar{{w}}_n \ddot{\bar{{w}}}_n )\bar{{w}}_n$ is inertia nonlinearity. $2\bar{{\sigma }}_n \ddot{\bar{{w}}}_x$ and $\bar{{\lambda }}_n \ddot{\bar{{w}}}_y$ are the parametric and direct excitations, respectively. Equation (9) is the electromechanical coupling Mathieu–Duffing equations with geometric and inertia nonlinearities as well as the external force and voltage terms, which describes the nonlinear dynamical equation of cantilever piezoelectric beam of a single mode approximation under parametric and direct excitations. The electromechanical terms of Eq. (9) are proportional to voltage and the square of the displacement amplitude. The electromechanical terms of Eq. (10) are proportional to the velocity and the square of the displacement amplitude. Equations (9) and (10) are similar to the equations of the lumped-parameter nonlinear model presented by Daqaq et al. [40], but different from them. The electromechanical coupling terms of Eqs. (9) and (10) include nonlinearity.

3.2 The method of multiple scales

The method of multiple scales [54, 55] will be used to obtain the frequency response curves of the nonlinear piezoelectric energy harvester. For an analytical solution of the present problem, harmonic excitations are assumed as the following form:

$$\begin{aligned} \ddot{\bar{{w}}}_x \left( t \right) =\delta _x \cos \omega _x \tau \quad \quad \ddot{\bar{{w}}}_y \left( t \right) =\delta _y \cos \left( {\omega _y \tau +\psi } \right) \end{aligned}$$

(11)

where $\delta _x$ and $\delta _y$ are the non-dimensional amplitudes, respectively. $\psi$ is the phase angle.

Using Eq. (11) and introducing a small perturbation parameter $\varepsilon$, Eqs. (9) and (10) are rewritten in the following form:

$$\begin{aligned}&\ddot{\bar{{w}}}_n +2\hat{{c}}\varepsilon \dot{\bar{{w}}}_n +\left( {\bar{{\omega }}_n^2 +2\hat{{\delta }}_{xn} \varepsilon \cos \omega _x \tau } \right) \bar{{w}}_n +\hat{{\beta }}_n \varepsilon \bar{{w}}_n^3 +\hat{{\kappa }}_n \varepsilon \left( {\dot{\bar{{w}}}_n^2 +\bar{{w}}_n \ddot{\bar{{w}}}_n } \right) \bar{{w}}_n \nonumber \\&\quad -\bar{{\alpha }}\varepsilon \left( {\hat{{\zeta }}_n +\hat{{\gamma }}_n \bar{{w}}_n^2 } \right) \bar{{V}}+\hat{{\delta }}_{yn} \varepsilon \cos (\omega _y \tau +\psi )=0 \end{aligned}$$

(12)

$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\left( {\eta _n +\chi _n \bar{{w}}_n^2 } \right) \dot{\bar{{w}}}_n =0 \end{aligned}$$

(13)

where ${\tilde{c}}=\varepsilon \hat{{c}},\bar{{\sigma }}_n \delta _x =\varepsilon \hat{{\delta }}_{xn} ,\beta _n =\varepsilon \hat{{\beta }}_n ,\kappa _n =\varepsilon \hat{{\kappa }}_n ,\zeta _n =\varepsilon \hat{{\zeta }}_n ,\gamma _n =\varepsilon \hat{{\gamma }}_n ,\bar{{\lambda }}_n \delta _y =\varepsilon \hat{{\delta }}_{yn}$.

In the present analysis, assuming that the first bending modal of the beam should be the dominant mode of the system, only one modal ($n=1$) is retained and others are neglected. In what follows, the subscript n of Eqs. (12) and (13) will be omitted. In order to achieve parametric resonance, it has been shown that the horizontal excitation frequency $\omega _x$ needs to be approximately twice the vertical excitation frequency $\omega _y$. Introducing the non-dimensional excitation frequency, $\bar{{\omega }}$, $\omega _x$ and $\omega _y$ should be expressed as $\omega _x =2\bar{{\omega }}$ and $\omega _y =\bar{{\omega }}$ [40, 41].

Using the method of multiple scales, approximate analytical solutions of Eqs. (12) and (13) can be obtained. The time dependence is expanded into multiple time scales in the form [54, 55]

$$\begin{aligned} T_n =\varepsilon ^{n}\tau \quad \hbox {for } \ n=0,1,2,\ldots \end{aligned}$$

(14)

where $\varepsilon$ is a perturbation parameter. $T_0$ and $T_1$ are the time scales. $T_0 =\tau$ and $T_1 =\varepsilon \tau$.

The time derivative can be expressed as the following form [54, 55]:

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\tau }=D_0 +\varepsilon D_1 +\cdots ,\frac{\mathrm{d}^{2}}{\mathrm{d}\tau ^{2}}=D_0^2 +2\varepsilon D_0 D_1 +\cdots \end{aligned}$$

(15)

where $D_n =\partial /\partial T_n$. $\bar{{w}}(\tau )$ and $\bar{{V}}(\tau )$ can be expanded by order of $\varepsilon$ as follows:

$$\begin{aligned} \bar{{w}}(\tau ,\varepsilon )= & {} \bar{{w}}_0 (T_0 ,T_1 )+\varepsilon \bar{{w}}_1 (T_0 ,T_1 )+\cdots \nonumber \\ \bar{{V}}(\tau ,\varepsilon )= & {} \bar{{V}}_0 (T_0 ,T_1 )+\varepsilon \bar{{V}}_1 (T_0 ,T_1 )+\cdots \end{aligned}$$

(16)

To express the nearness of the excitation frequency to the first modal frequency of the harvester, we introduce a detuning parameter $\sigma$.

$$\begin{aligned} \omega _y= & {} \bar{{\omega }}+\varepsilon \sigma \nonumber \\ \omega _x= & {} 2\bar{{\omega }}+2\varepsilon \sigma \end{aligned}$$

(17)

where $\sigma$ quantitatively describes the nearness of the resonance frequency $\bar{{\omega }}$ [54, 55]. Substituting Eqs. (14)–(17) into Eqs. (12) and (13), and truncating at order $\varepsilon$ and separating the terms of different orders of $\varepsilon$, the following equations are obtained.

$$\begin{aligned}&\varepsilon ^{0}:\nonumber \\&D_0^2 \bar{{w}}_0 +\bar{{\omega }}^{2}\bar{{w}}_0 =0 \end{aligned}$$

(18)

$$\begin{aligned}&D_0 \bar{{V}}_0 +\mu \bar{{V}}_0 =-\bar{{\alpha }}(\eta +\chi \bar{{w}}_0^2 )D_0 \bar{{w}}_0 \end{aligned}$$

(19)

$$\begin{aligned}&\varepsilon ^{1}:\nonumber \\&D_0^2 \bar{{w}}_1 +\bar{{\omega }}^{2}\bar{{w}}_1 =-2D_0 D_1 \bar{{w}}_0 -2\hat{{c}}D_0 \bar{{w}}_0 -2\hat{{\delta }}_x \bar{{w}}_0 \cos (2\bar{{\omega }}\tau +2\varepsilon \sigma \tau )-\hat{{\beta }}\bar{{w}}_0^3 \nonumber \\&\quad -\hat{{\kappa }}(\bar{{w}}_0 (D_0 \bar{{w}}_0 )^{2}+\bar{{w}}_0^2 D_0^2 \bar{{w}}_0 )+\bar{{\alpha }}(\hat{{\zeta }}+\hat{{\gamma }}\bar{{w}}_0^2 )\bar{{V}}_0 -\hat{{\delta }}_y \cos (\bar{{\omega }}\tau +\varepsilon \sigma \tau +\psi ) \end{aligned}$$

(20)

$$\begin{aligned}&D_0 \bar{{V}}_1 +\mu \bar{{V}}_1 =-\bar{{\alpha }}(\eta +\chi \bar{{w}}_0^2 )(D_0 \bar{{w}}_1 +D_1 \bar{{w}}_0 )-D_1 \bar{{V}}_0 -2\bar{{\alpha }}\chi \bar{{w}}_1 \bar{{w}}_0 D_0 \bar{{w}}_0 \end{aligned}$$

(21)

The solutions of Eqs. (18) and (19) can be obtained as follows.

$$\begin{aligned} \bar{{w}}_0= & {} A(T_1 )\exp (i\bar{\omega }T_0 )+ \hbox {cc} \end{aligned}$$

(22)

$$\begin{aligned} \bar{{V}}_0= & {} -\frac{\bar{{\alpha }}(\eta +\chi A\bar{{A}})i\bar{{\omega }}A}{i\bar{{\omega }}+\mu }\exp (i\bar{{\omega }}T_0 )-\frac{\bar{{\alpha }}\chi i\bar{{\omega }}A^{3}}{3i\bar{{\omega }}+\mu }\exp (3i\bar{{\omega }}T_0 )+\hbox {cc} \end{aligned}$$

(23)

where cc is the complex conjugate of the preceding term and $A(T_1 )$ is a complex-valued function that will be determined by imposing the solvability condition at the next level of approximation. Substituting Eqs. (22) and (23) into Eqs. (20) and (21), the solvability condition is derived by disregarding higher harmonics and setting secular terms, which have the coefficient $\exp (i\bar{{\omega }}_n T_0 )$, to zero [54, 55]. Assuming $\psi =0$, the following equation is obtained.

$$\begin{aligned}&-2i\bar{{\omega }}D_1 A-2\hat{{c}}i\bar{{\omega }}A-3\hat{{\beta }}A^{2}\bar{{A}}+2A^{2}\bar{{A}}\bar{{\omega }}^{2}\hat{{\kappa }} \nonumber \\&\quad -\bar{{\alpha }}^{2}\hat{{\zeta }}\frac{(\eta +\chi A\bar{{A}})i\bar{{\omega }}A}{i\bar{{\omega }}+\mu }-\bar{{\alpha }}^{2}\hat{{\gamma }}\frac{(\eta +\chi A\bar{{A}})i\bar{{\omega }}2A^{2}\bar{{A}}}{i\bar{{\omega }}+\mu }-\bar{{\alpha }}^{2}\hat{{\gamma }}\frac{\chi i\bar{{\omega }}A^{3}\bar{{A}}^{2}}{3i\bar{{\omega }}+\mu } \nonumber \\&\quad -\hat{{\delta }}_x \bar{{A}}\exp (i2\sigma T_1 )-\hat{{\delta }}_y \frac{1}{2}\exp (i\sigma T_1 )=0 \end{aligned}$$

(24)

To find the solution of Eq. (24), the complex-valued function A is expressed in the polar form [54, 55]:

$$\begin{aligned} A=\frac{1}{2}a\exp (i\theta ) \end{aligned}$$

(25)

where a and $\theta$ are the function with respect to $T_1$. Substituting Eq. (25) into Eq. (24), and separating the real and imaginary parts, the following equations can be obtained.

$$\begin{aligned} {\dot{a}}= & {} -c_1 a-c_2 a^{3}-c_3 a^{5}-c_4 \sin (\sigma T_1 -\theta )-c_8 a\sin [2(\sigma T_1 -\theta )] \end{aligned}$$

(26)

$$\begin{aligned} -a{\dot{\theta }}= & {} -c_5 a-c_6 a^{3}-c_7 a^{5}-c_4 \cos (\sigma T_1 -\theta )-c_8 a\cos [2(\sigma T_1 -\theta )] \end{aligned}$$

(27)

Introducing $\varphi =\sigma T_1 -\theta$, we obtain.

$$\begin{aligned} {\dot{a}}= & {} -c_1 a-c_2 a^{3}-c_3 a^{5}-c_4 \sin \varphi -c_8 a\sin 2\varphi \end{aligned}$$

(28)

$$\begin{aligned} a{\dot{\varphi }}= & {} \sigma a-c_5 a-c_6 a^{3}-c_7 a^{5}-c_4 \cos \varphi -c_8 a\cos 2\varphi \end{aligned}$$

(29)

where the coefficients, $c_i (i=1,2,\ldots ,8)$, are defined in “Appendix B”.

The steady-state solution of Eqs. (28) and (29) can be found by setting ${\dot{a}}=0$ and ${\dot{\varphi }}=0$. The equations of the steady-state solution can be rewritten as

$$\begin{aligned}&c_1 a+c_2 a^{3}+c_3 a^{5}+c_4 \sin \varphi +c_8 a\sin 2\varphi =0 \end{aligned}$$

(30)

$$\begin{aligned}&\sigma =c_5 +c_6 a^{2}+c_7 a^{4}+\frac{c_4 \cos \varphi }{a}+c_8 \cos 2\varphi \end{aligned}$$

(31)

For Eqs. (30) and (31), there are multi-valued solutions, and not all solutions approximate a realizable response of the actual physical system [54]. Those solutions, which are unstable, do not describe a possible response. The results are obtained by first specifying a value for $\varphi$, solving for a from Eq. (30) and then $\sigma$ is obtained from Eq. (31). The values of $\varphi$ are specified systematically in rather small increments from $-\pi$ to $\pi$ [54]. Depending on the excitation amplitude and frequency, there exist positive real-valued solutions. The stability of the solution can be determined by assessing the eigenvalues of the associated Jacobian matrix. Upon consideration of the zeroth-order perturbation to the displacement and voltage, the higher harmonics of Eq. (23) is neglected. The steady-state solutions of the displacement and voltage can be expressed as the following form.

$$\begin{aligned} \bar{{w}}= & {} a\cos (\omega _y \tau -\phi ) \end{aligned}$$

(32)

$$\begin{aligned} \bar{{V}}= & {} \frac{\bar{{\omega }}\bar{{\alpha }}\left[ {4\eta +\chi a^{2}} \right] }{4\sqrt{\bar{{\omega }}^{2}+\mu ^{2}}}a\cos (\omega _y \tau -\phi +\theta _1 ) \end{aligned}$$

(33)

$$\begin{aligned} \theta _1= & {} \tan ^{-1}\left( {\frac{\mu }{\bar{{\omega }}}} \right) \end{aligned}$$

(34)

The steady-state solutions of output power can be expressed as the following form.

$$\begin{aligned} P=\frac{m\omega _0^2 L^{3}}{C_\mathrm{p} R_\mathrm{L} }\bar{{V}}^{2} \end{aligned}$$

(35)

3.3 Stability of the non-trivial solutions

The stability of the non-trivial solutions at a given fixed point $(a_0 ,\varphi _0 )$ can be found by introducing a time-dependent disturbance $(\delta a\hbox {(}t),\delta \varphi (t))$ on the fixed point, that is,

$$\begin{aligned} a=a_0 +\delta a(t),\varphi =\varphi _0 +\delta \varphi (t) \end{aligned}$$

(36)

Substituting Eq. (36) into Eqs. (28) and (29), linearizing in the disturbance, and determining the eigenvalues of the Jacobian matrix of the linearized equations, the Jacobian matrix can be expressed as:

$$\begin{aligned} \mathbf{J}=\left[ {{\begin{array}{ll} {k_{11} }&{} \quad {k_{12} } \\ {k_{21} }&{} \quad {k_{22} } \\ \end{array} }} \right] \end{aligned}$$

(37)

where

$$\begin{aligned} k_{11}= & {} -c_1 -3c_2 a_0^2 -5c_3 a_0^4 -c_8 \sin 2\varphi _0 \nonumber \\ k_{12}= & {} -c_4 \cos \varphi _0 -2c_8 a_0 \cos 2\varphi _0 \nonumber \\ k_{21}= & {} -2c_6 a_0 -4c_7 a_0^3 +c_4 \frac{1}{a_0^2 }\cos \varphi _0 \nonumber \\ k_{22}= & {} c_4 \frac{1}{a_0 }\sin \varphi _0 +2c_8 \sin 2\varphi _0 \end{aligned}$$

(38)

Using Eq. (37), the characteristic equation of the Jacobian matrix can be written as

$$\begin{aligned} \lambda ^{2}-(k_{11} +k_{22} )\lambda +k_{11} k_{22} -k_{12} k_{21} =0 \end{aligned}$$

(39)

Using the Routh–Hurwitz criterion, the steady-state solutions are locally asymptotically stable if and only if

$$\begin{aligned} (k_{11} +k_{22} )<\hbox {0}, \quad k_{11} k_{22} -k_{12} k_{21} >0 \end{aligned}$$

(40)

Fig. 2

The amplitude–frequency response curves for different excited amplitudes (short-circuit): a deflection; b output voltage

Fig. 3

The amplitude–frequency response curves for different excited amplitudes (open-circuit): a deflection; b output voltage

4 Results and discussion

In the previous section, analytical solutions of the cantilever piezoelectric energy harvester have been presented under parametric and direct excitations. In this section, the frequency response curves of the energy harvesting system will be given and discussed in detail. The geometric and material properties are as follows:

$$\begin{aligned} m_t= & {} 96\,{\hbox {g/m}}, \quad b=20\,\hbox {mm}, \quad L=50\,{\hbox {mm}},\quad t_\mathrm{p} =0.2\,\hbox {mm}, \quad t_\mathrm{s} =0.2\,\hbox {mm}, \quad Y_\mathrm{p} =61\,\hbox {GPa} \nonumber \\ Y_\mathrm{s}= & {} 20\hbox {GPa}, \quad d_{31} =-320\times 10^{-12}\,\hbox {C}/{\hbox {N}, \quad \varepsilon _{33}^T }=3.98\times 10^{-8}\,\hbox {F}/\hbox {m}, \quad \varepsilon _{33}^S =\varepsilon _{33}^T -d_{31}^2 Y_\mathrm{p} \end{aligned}$$

(41)

Using $n=1$, the influences of several different parameters on the performance of the harvester are investigated. These parameters are excitation amplitudes $\delta _x$ and $\delta _y$, mechanical damping coefficient $\bar{{c}}$, and load resistance parameter $R_\mathrm{L}$. The base excitation is considered as harmonic excitation. Small perturbation parameter is taken as $\varepsilon =0.01$. Using the geometric and material coefficients defined in Eq. (41), all parameters of Eqs. (9) and (10) are as follows:

$$\begin{aligned} \bar{{\sigma }}= & {} -0.7854, \quad \beta =40.4407,\quad \kappa =4.5968,\quad \zeta =2.7530,\quad \gamma =10.4326,\quad \bar{{\lambda }}=0.7830 \nonumber \\ \bar{{\alpha }}= & {} -0.4119,\quad \bar{{\omega }}=3.5160,\quad \omega _0 =188.9150,\quad C_\mathrm{p} =8.3884\times 10^{-8} \end{aligned}$$

(42)

where $\eta =\zeta , \chi =\gamma$ which have been proved in “Appendix A”. In all analytical results, solid lines represent stable solutions and dashed lines represent unstable solutions.

4.1 Parametric Excitation

We investigate the characteristics of the amplitude frequency response curves under parametric excitation. Figures 2, 3, 4 and 5 show the amplitude frequency response curves of the steady-state displacement and output voltage for different load resistances and different excited amplitudes. For parametric excitation ($\delta _y =0$), Figs. 2, 3, 4 and 5 show that electrical energy can only be harvested within a certain range of excitation frequencies where the non-trivial solutions exist. Outside of this range, only the trivial solution ($\bar{{w}}=0$) exists and no electrical energy can be harvested. Meanwhile, our studies show that the frequency response curves have both the open-circuit and the short-circuit resonant region. Figure 2 (the short circuit) and Fig. 3 (the open circuit) show that the ranges of excited frequencies, where the non-trivial solutions exist, are distinct for different excited amplitudes, $\delta _x$. Figure 4 (the short circuit) and Fig. 5 (the open circuit) show that the ranges of excited frequencies, where the non-trivial solutions exist, are distinct for different load resistances. Figures 2, 3, 4 and 5 also show that the frequency response curves have the hardening characteristics. It has a merit of increasing operating frequency range. In the case of the short circuit, Fig. 4 shows that as the load resistance increases, the output voltage decreases. In the case of the open circuit, Fig. 5 shows that as the load resistance increases, the output voltage increases and the frequency of peak voltage shifts toward larger values of the excited frequency. Our results are consistent with the conclusion of the theoretical analysis and the experimental verification presented by Daqaq et al. [40].

Fig. 4

The amplitude–frequency response curves for different load resistances (short-circuit): a deflection; b output voltage

Fig. 5

The amplitude–frequency response curves for different load resistances (open-circuit): a deflection; b output voltage

Figures 6, 7 and 8 show the amplitude response curves of the displacement and output voltage with the variation of the frequency detuning parameter $\sigma$ and the excitation amplitude $\delta _x$. Figure 6 shows that parametric resonances exist only when the excitation amplitude exceeds a certain threshold value. When the excited amplitude $\delta _x$ exceeds the initiation threshold for $\sigma =0.0$, a rapid amplitude growth is obtained. Figure 7 shows the amplitude response curves of $\sigma =1.2$. When $\delta _x <\delta _{xA}$, only the trivial solution exists. Increasing $\delta _x$ beyond point A, two stable solutions and one unstable solution coexist. The amplitude response curves have multi-value solutions, resulting in a subcritical instability. Because the nonlinearity is the hardening type, the subcritical instability exists only when the frequency detuning parameter $\sigma$ is positive. Figure 8 shows that when the frequency detuning parameter $\sigma$ is negative, the initiation threshold highly increases and multi-value solution does not exist.

Fig. 6

The amplitude response curves with excited amplitude when $\sigma =0.0$: a deflection; b output voltage

Fig. 7

The amplitude response curves with excited amplitude when $\sigma =1.2$: a deflection; b output voltage

Fig. 8

The amplitude response curves with excited amplitude when $\sigma =0.0,-1.2$: a deflection; b output voltage

In the follows, we will study the effect of the load resistance and damping on the initiation threshold under parametric excitation. Figures 9 and 10 show the effect of different damping on the initial threshold in the case of the fixed load resistance. With the damping increasing, the initiation threshold highly increases. Figures 11 and 12 show the effect of different load resistances on the initial threshold for the fixed damping coefficient $\bar{{c}}=0.01$. Figure 11 (the short circuit) shows that the initiation threshold increases with the increase in load resistance. Figure 12 (the open circuit) shows that the initiation threshold decreases with the increase in load resistance.

Parametric resonance converges to a zero steady-state response below the initiation threshold. With excitation amplitudes increasing beyond this threshold barrier, it is able to ultimately obtain higher response amplitude. Figures 9, 10, 11 and 12 show that this initiation threshold is relatively larger values, whereas the ambient vibration available for energy harvester is usually very small. Accordingly, this initiation threshold must be minimized in order to use the advantages of parametric resonance in practical application.

Fig. 9

Variation of deflection and voltage with excited amplitude for different damping (short-circuit): a deflection; b voltage

Fig. 10

Variation of deflection and voltage with excited amplitude for different damping (open-circuit): a deflection; b voltage

Fig. 11

Variation of deflection and voltage with excited amplitude for different load resistances (short-circuit): a deflection; b voltage

Fig. 12

Variation of deflection and voltage with excited amplitude for different load resistances (open-circuit): a deflection; b voltage

In the case of parametric excitation, why is there an initial threshold for parametric resonance? A reasonable explanation of this behavior can be obtained from the state of the beam deformation. In this paper, the horizontal base excitation along the axis of the beam is converted into the parametric excitation. For parametric excitation, the vertical base excitation is equal to zero. The beam is only subjected to horizontal base excitation. When parametric excited amplitude $\delta _x$ is very small, the beam is subjected to axial inertia force, the bending deformation of the beam is equal to zero, and hence no electrical energy is harvested. When parametric excited amplitude $\delta _x$ exceeds a critical value, the beam occurs the elastic buckling and the bending deformation in the axial inertia force. The beam bending deformation increases rapidly with parametric excited amplitude increasing and the harvesting power can be raised dramatically.

Buckling is a phenomenon that is generally avoided through special design modifications, but some new applications consider such behavior to be favorable. Recent studies of buckling and postbuckling have tried to transform this effect from a negative into a positive. Hu and Burgueño [56] indicated that the buckling can be applied to energy harvesting system and explained why the buckling responses have certain advantages in the design of energy harvesters. In practical application, the bending deformation of the beam, which is caused by the buckling, should be constrained in a certain range to prevent the damage of the beam.

To further study the characteristics of parametric excitation, we plot variation of the output voltage and power with the load resistance for a given excited frequency in two cases of short circuit and open circuit. In the case of the short circuit, Fig. 13 clearly shows that as the load resistance increases, the output voltage and output power increase initially and reach a maximum at an optimal load resistance, then decreases again as the load resistance increases beyond the optimal value. In the case of the open circuit, Fig. 14 shows that the output voltage continues to increase and trends to stable as load resistance increases, and variation of the output power has the same trend of the short-circuit condition. In the open-circuit condition, our conclusion is consistent with Daqaq et al. [40]. For the short-circuit condition, Daqaq et al. [40] have not given the related results.

Fig. 13

Variation of voltage and power with the load resistance in short-circuit condition: a voltage; b power

Fig. 14

Variation of voltage and power with the load resistance in open-circuit condition: a voltage; b power

4.2 Combination of parametric and direct excitations

In this section, we will demonstrate that the frequency response curves of combination of parametric and direct excitations have the special dynamic characteristics compared with parametric excitation. Figures 15, 16, 17 and 18 show the frequency response curves under combination of parametric and direct excitations for different $\delta _x$, $\delta _y$ and $R_\mathrm{L}$. Figures 15 and 16 show the frequency response curves of the displacement and output power for different parameters $\delta _x$ when $\delta _y =0.0055$, 0.00275, $R_\mathrm{L} =500\hbox {k}\Omega$ and $\bar{{c}}=0.01$. Figures 17 and 18 show the frequency response curves of the displacement and output power for different parameters $\delta _x$ when $\delta _y =0.0055$, 0.00275, $R_\mathrm{L} =500\Omega$ and $\bar{{c}}=0.01$. Figures 15, 16, 17 and 18 show that although parameter $\delta _x$ is below the initiation threshold, the displacement and output power increase with the parameter $\delta _x$ increasing. This is because the direct excitation ($\delta _y \ne 0)$ pushes the system out of axial stable equilibrium and results in an initial nonzero bending deformation. Figures 15 and 17 also show that when the excited amplitude is small, there do not exist the hardening behavior, multi-value solutions and unstable solution. Figures 16 and 18 show that when the excited amplitude is larger, there exit the hardening behavior, multi-value solutions and unstable solution. The operating bandwidths of the energy harvester are widened.

Fig. 15

The amplitude–frequency response curves for different $\delta _x$ (open-circuit, $\delta _y =0.00275$): a deflection; b voltage

Fig. 16

The amplitude–frequency response curves for different $\delta _x$: (open-circuit, $\delta _y = 0.0055)$: a deflection; b voltage

Fig. 17

The amplitude–frequency response curves for different $\delta _x$ (short-circuit, $\delta _y = 0.00275$): a deflection; b voltage

Fig. 18

The amplitude–frequency response curves for different $\delta _x$ (short-circuit, $\delta _y = 0.0055$): a deflection; b voltage

Figures 15, 16, 17 and 18 demonstrate that a nonzero initial displacement to push the system out of axial deformation can overcome the limitation of initiation threshold for parametric excited system. The advantages of parametric resonance can be fully played. Therefore, the combination of direct and parametric excitations, which compensates and complements each other, can be used as an ideal solution for improving the performance of the vibration energy harvester.

Fig. 19

Variation of voltage and power with the load resistance in short-circuit case: a voltage; b power

Fig. 20

Variation of voltage and power with the load resistance in open-circuit case: a voltage; b power

Fig. 21

Variation of voltage and power with the load resistance for different $\delta _x$ in short-circuit case: a voltage; b power

Fig. 22

Variation of voltage and power with the load resistance for different $\delta _x$ in open-circuit case: a voltage; b power

In order to further investigate the characteristics of combination of parametric and direct excitations, we plot variation of the output voltage and power with the load resistance for a given excited frequency. Figures 19 and 20 show that in the two cases of the short circuit and the open circuit, the output voltage continues to increase and trends to stable as the load resistance increasing, and the output power increases initially, exhibits a maximum at an optimal load resistance and drops again beyond the optimal value. Figures 21 and 22 show the varying curves of output voltage and power with the load resistance increasing in the two cases of short-circuit and open-circuit conditions. We observe that for the different parametric excited amplitudes, the amplitudes of output voltage and power increase significantly with the increase in the amplitude of parametric excitation and there is an optimal load resistance for output power.

5 Conclusions

The nonlinear performance of parametrically and directly excited energy harvesters, which includes geometric, inertia and electromechanical coupling nonlinearities, is studied. Using the Galerkin method, the electromechanical coupling Mathieu–Duffing equations are developed. Based on the method of multiple scales, analytical expressions of the frequency response curves are presented when the first bending mode of the beam plays a dominant role. Some analytical results are obtained, which reveal the influence of different parameters, such as the damping, load resistance and excited amplitude, on the performance of the energy harvesters.

For parametric excitation, the mechanical damping and the load resistance affect the initiation threshold of parametric excited energy harvesting system. With the damping increasing, the initiation threshold increases. In the case of the short circuit, the initiation threshold increases with the increase in load resistance. In the case of the open circuit, the initiation threshold decreases with the increase in load resistance.

We discover that for parametric excitation and combination of parametric and direct excitations, with the increase in load resistance, output power increases initially, exhibits a maximum at an optimal load resistance and drops again beyond the optimal value.

Our studies also demonstrate that the bending deformation generated by direct excitation pushes the system out of axial deformation and overcomes the limitation of initial threshold of parametric excitation system. In the case of combination of parametric and direct excitations, the amplitudes of output voltage and power increase significantly with the increase in the parametric excited amplitude. Therefore, the combination of parametric and direct excitations to compensate and complement each other can be served as a better solution that enhances performance of energy harvesters.

Appendices

Appendix A

The coefficients defined in Eqs. (9) and (10) are given as:

$$\begin{aligned} a_{1n} \left( {\bar{{s}}} \right)= & {} \int _{\bar{{s}}}^1 {\int _0^{{\bar{{\xi }}}}{{\phi '}_{n}^{2} \left( {\bar{{\eta }}} \right) \mathrm{d}\bar{{\eta }}\mathrm{d}\bar{{\xi }}}} ,\, a_{2n} \left( {\bar{{s}}} \right) =\int _0^{\bar{{s}}}{{\phi '}_{n}^{2} \left( {\bar{{\eta }}} \right) \mathrm{d}\bar{{\eta }}} \nonumber \\ b{ }_{1nn}= & {} \int _0^1 {\phi _n \phi _n \mathrm{d}\bar{{s}}} ,\,b{ }_{2nn}=\int _0^{1} {\left( {\bar{{\beta }}_{n}^{4} {\phi '}_{n}^{2} X_{n} +4{\phi '}_{n} {\phi ''}_{n} {\phi '''}_{n} +{\phi ''}_n ^{3}} \right) \phi _n \mathrm{d}\bar{{s}}} ,b{ }_{3nn}=\int _0^1 {{\phi ''}_{n} \phi _n \mathrm{d}\bar{{s}}}\nonumber \\ b{ }_{4nn}= & {} \int _0^1 {\bar{{s}}{\phi }''_n \phi _n \mathrm{d}\bar{{s}}} , b{ }_{5nn}=\int _0^1 {a_{1n} \left( {\bar{{s}}} \right) {\phi }''_n \phi _n \mathrm{d}\bar{{s}}} ,~b{ }_{6nn}=\int _0^1 {{\phi }'_n \phi _n \mathrm{d}\bar{{s}}} ,\,b{ }_{7nn}=\int _0^1 {a_{2n} \left( {\bar{{s}}} \right) {\phi }'_n \phi _n \mathrm{d}\bar{{s}}}\nonumber \\ b{ }_{8nn}= & {} \int _0^1 {\phi _n \mathrm{d}\bar{{s}}} , \quad b{ }_{9nn}=\left. {\frac{\mathrm{d}\phi _n \left( {\bar{{s}}} \right) }{\mathrm{d}\bar{{s}}}} \right| _{\bar{{s}}=1} ,\, b{ }_{10nn}=\left. {\frac{\mathrm{d}\left[ {\phi _n \left( {\bar{{s}}} \right) {\phi '}_{{n}}^{2} \left( {\bar{{s}}} \right) } \right] }{\mathrm{d}\bar{{s}}}} \right| _{\bar{{s}}=1} ,\,b{ }_{11nn}=\phi _{n} \left( 1 \right) {\phi '}_{n} \left( 1 \right) {\phi ''}_{n} \left( 1 \right) \nonumber \\ b_{12nn}= & {} \int _0^1 {{\phi }''_n } \mathrm{d}\bar{{s}},\,b_{13nn} =\int _0^1 {{\phi '}_{{n}}^{2} {\phi ''}_n \mathrm{d}\bar{{s}}}\nonumber \\ {\tilde{c}}= & {} \frac{1}{2}\bar{{c}},\bar{{\sigma }}_n =\frac{b{ }_{3nn}-b{ }_{4nn}-b{ }_{6nn}}{2b{ }_{1nn}},\beta _n =\frac{b{ }_{2nn}}{b{ }_{1nn}},\kappa _n =\frac{b{ }_{7nn}-b{ }_{5nn}}{b{ }_{1nn}} \nonumber \\ \zeta _n= & {} \frac{b{ }_{9nn}}{b{ }_{1nn}},\gamma _n =\frac{b{ }_{10nn}-2b{ }_{11nn}}{2b{ }_{1nn}},\bar{{\lambda }}_n =\frac{b_{8nn} }{b_{1nn} },\eta _n =b{ }_{12nn},\chi _n =\frac{3}{2}b_{13nn} \nonumber \\ \end{aligned}$$

(A1)

$$\begin{aligned} b_{1nn}= & {} \int _0^1 {\phi _n } \phi _n \mathrm{d}\bar{{s}}=1,b_{12nn} =\int _0^1 {{\phi }''_n \mathrm{d}\bar{{s}}=\left. {\frac{\mathrm{d}\phi _n (\bar{{s}})}{\mathrm{d}\bar{{s}}}} \right| } _{\bar{{s}}=1} =b_{9nn} \nonumber \\ b_{10nn}= & {} \frac{\mathrm{d}\left[ {{\phi '}_{n} (\bar{{s}}){\phi '}_{n} (\bar{{s}})\phi _n (\bar{{s}})} \right] }{\mathrm{d}\bar{{s}}} \big |_{\bar{{s}}=1} =2\phi _n (1){\phi '}_n (1){\phi ''}_{n} (1)+{\phi '}_{n}^{3} (1) \nonumber \\ b_{13nn}= & {} \int _0^1 {{\phi '}_n {\phi '}_n {\phi ''}_{n}} \mathrm{d}\bar{{s}}=\frac{1}{3}{\phi '}_n^3 (1),\eta _n =\zeta _n ,\chi _n =\gamma _n \end{aligned}$$

(A2)

Appendix B

The coefficients defined in Eqs. (26)–(31) are as following:

$$\begin{aligned} c_1= & {} \hat{{c}}+\bar{{\alpha }}^{2}\frac{\hat{{\zeta }}\eta \mu }{2(\mu ^{2}+\bar{{\omega }}^{2})},\,c_2 =\bar{{\alpha }}^{2}\frac{\chi \hat{{\zeta }}\mu }{8(\bar{{\omega }}^{2}+\mu ^{2})}+\bar{{\alpha }}^{2}\frac{\eta \mu \hat{{\gamma }}}{4(\bar{{\omega }}^{2}+\mu ^{2})} \\ c_3= & {} \bar{{\alpha }}^{2}\frac{\mu \hat{{\gamma }}\chi }{16(\bar{{\omega }}^{2}+\mu ^{2})}+\bar{{\alpha }}^{2}\frac{\mu \hat{{\gamma }}\chi }{32(9\bar{{\omega }}^{2}+\mu ^{2})},\,c_4 =\frac{\hat{{\delta }}_y }{2\bar{{\omega }}},c_5 =\bar{{\alpha }}^{2}\frac{\bar{{\omega }}\eta \hat{{\zeta }}}{2(\bar{{\omega }}^{2}+\mu ^{2})} \\ c_6= & {} \frac{3\hat{{\beta }}}{8\bar{{\omega }}}+\bar{{\alpha }}^{2}\frac{\hat{{\zeta }}\bar{{\omega }}\chi }{8(\bar{{\omega }}^{2}+\mu ^{2})}-\frac{1}{4}\bar{{\omega }}\hat{{\kappa }}+\bar{{\alpha }}^{2}\frac{\mu \bar{{\omega }}\eta }{4(\bar{{\omega }}^{2}+\mu ^{2})} \\ c_7= & {} \bar{{\alpha }}^{2}\frac{\mu \bar{{\omega }}\chi }{16(\bar{{\omega }}^{2}+\mu ^{2})}+\alpha _0 ^{2}\frac{3\mu \bar{{\omega }}\chi }{32(9\bar{{\omega }}^{2}+\mu ^{2})},\,c_8 =\frac{\hat{{\delta }}_x }{2\bar{{\omega }}} \end{aligned}$$