1 Introduction

Recent progresses in two tightly interconnected fields of engineering including microelectronics and microelectromechanical systems (MEMS) technologies have provided the possibility of fabricating various sensors and actuators along with a widespread variety of integrated circuitry such as processors and signal conditioning circuits with vastly reduced size and very low amounts of power consumption. These advances have led to the ability of design and fabrication of new low power consuming devices with applications to industrial, medical and civil engineering and have proposed the idea of environmental energy harvesting to provide their required energy. Energy harvesting micro power generators can be employed as an efficient alternative for conventional heavy batteries with limited service lives and will be very beneficial in powering inaccessible remote electronics including a medical apparatus implanted in a human body for diagnostic or therapeutic purposes (Miao et al. 2006; He et al. 2009), a remote sensor node of a wireless sensor network where large number of the nodes makes battery replacement or delivering energy through cables impossible (Elfrink et al. 2010; Yu et al. 2014), or a mobile device such as an active radio frequency identification system (Hande et al. 2009; Kaya and Koser 2007).

Considering two factors of availability and efficiency, the kinetic energy stored in mechanical vibrations has shown to be a promising candidate for energy harvesting through different potential sources of environmental energy such as solar, thermal and electromagnetic radiation energies (Roundy et al. 2004). Three transduction mechanisms can be exploited to convert vibration energy to electrical energy including piezoelectric (Liu et al. 2008; Chung and Lee 2015), electromagnetic (Wang et al. 2009; Williams et al. 2001) and electrostatic (Mitcheson et al. 2004; Sheu et al. 2011) techniques among which piezoelectric transducers have shown to have the most practical energy storage density (Roundy et al. 2005). In addition to energy density, some deficiencies of the latter two methods such as complicated micro-fabrication processes and low levels of generated output voltages of electromagnetic mechanism as well as separate voltage sources requirement and low quality factors of electrostatic technique, have caused the increasing application of piezoelectric materials especially in MEMS-based harvesters (Sue and Tsai 2012).

Piezoelectric harvesters generally consist of a cantilevered laminated beam in a bimorph configuration with two layers of piezoelectric material which are poled along the thickness and electroded at both sides. A proof (tip) mass is attached to the free end of the beam for the sake of resonance frequency reduction to push the natural frequency of the system to the range of environmental vibrations frequencies. This design has main advantages such as low resonance frequency, uncomplicated fabrication process and high sensitivity which is the ability to create large strains in the piezoelectric material through low acceleration excitations. This cantilever type generator made from a piezoelectric bimorph with two PZT layers attached to the upper and bottom surfaces of a supporting beam, has been well-developed in both micro and macro scale devices (Roundy and Wright 2004; Benasciutti et al. 2010; Lee et al. 2010).

Exploiting nonlinearities as a tool which has the ability to extend the coupling between the response of the harvester and the excitations to a wider range of frequencies and slightly suppress the main challenge of linear harvesters namely narrow operational bandwidths, have shown to be beneficent and is in the center of focus of many researchers in the field of energy harvesting. Mono and bi-stable nonlinear harvesters under various types of excitations including single fixed-frequency harmonic or random vibrations have been investigated by the researchers (Masana and Daqaq 2011; Daqaq 2010; Panyam and Daqaq 2016; Ferrari et al. 2010). In most of these investigations the nonlinearity is induced through added mechanisms such as placement of magnets (Cottone et al. 2009), pendulum (Jia et al. 2014) and etc.

There are several publications investigating the behavior of cantilevered piezoelectric harvesters which implement coupled or uncoupled electromechanical models where many of them contain linear equations. Vibrations of a linear MEMS-based harvester using a single mode assumption for the beam vibrations was studied by Lu et al., and expressions for output power, voltage, current and conversion efficiency of the harvester were derived (Lu et al. 2004). To increase the accuracy of the model, Jiang et al. (2005) derived a set of mode shapes for a piezoelectric bimorph with an attached tip mass and utilized them to analyze the vibratory behavior of the harvester. Erturk and Inman performed a detailed study on the cantilevered piezoelectric harvesters using the Euler–Bernoulli beam theory (Erturk and Inman 2008). Assuming resistive external load, they extracted the coupled governing electrical and mechanical equations and solved them implementing the mode summation method. At the next effort Erturk employed two other prevalent theories namely Rayleigh and Timoshenko in addition to Euler–Bernoulli theory (Erturk 2012). The axial displacements of the beam elements were considered in the model and employing assumed-mode method, the governing equations were first order-reduced and then analytically solved. Andosca et al. brought into account the effect of other layers in the laminated microbeam including conducting electrodes, using a multimorph beam model (Andosca et al. 2012). Employing a linear damping coefficient representing both dissipated mechanical and harvested electrical energies, governing equations were derived and then solved using a single-mode assumption. Nonlinear vibrations of a micro-scale piezoelectric-driven unimorph beam in sensor applications was studied by Mahmoodi et al. (2008a). Assuming a specified voltage to be applied to the piezoelectric layer, they derived a single nonlinear equation governing the lateral deflection of the beam and presented a numerical solution. Inextensibility condition was considered in large amplitude bending of the beam which has limitations in unimorph piezoelectric beams exhibiting axial deformation due to induced forces in the piezoelectric layer. Daqaq et al. (2009) presented a lumped parameter nonlinear model describing the first mode dynamics of a cantilever-type harvester. They employed their model to study parametrically excited vibrations of cantilevered harvesters.

Some researchers have made efforts on enhancement of output power through optimization of geometric parameters of the bimorph beam. Paquin and St-Amant (2010) improved the performance of a piezoelectric energy harvester using a variable thickness beam. The main idea of their work was to employ a tapered beam in order to have a more uniform stress distribution across the piezoelectric material and consequently increase the stored energy and harvesting performance. Shindo and Narita (2014) proposed a new harvester made of an S-shaped wavy beam. They showed that both numerical calculations implementing 3D finite element method and experimental observations prove that coupled bending/torsion of this proposed harvester yields to smaller maximum stress at the clamped end of the beam for the same output voltage and therefore can enhance the value of extractable power.

Piezoelectric ceramics as a specific type of electroelastic materials exhibit nonlinear behavior at relatively large stress and electric fields and their linear response which is represented by standard piezoelectric constitutive equations, is generally confined to small electromechanical fields. This nonlinear phenomena is more evident in ferroelectric materials due to their intrinsically nonlinear polarization mechanisms namely domain wall motion and domain switching (Damjanovic 1998; Hall 2001; Yang 2005). Nonlinear behavior of piezoelectric laminated beams due to material nonlinearities of the piezoelectric layer is investigated in actuator (Guyomar et al. 1997) and sensor (Mahmoodi et al. 2008b) applications. Experimental studies by Stanton et al. (2010) showed that a geometrically linear bimorph harvester can exhibit nonlinearity as a result of nonlinear piezoelectricity. They assumed the vibration amplitude to be small and neglecting geometrical nonlinearities presented a single mode model of the system and comparing to experimental results found an optimal set of values for the nonlinear coefficients of the piezoelectric material.

In this paper, nonlinear behavior of a piezoelectric harvester composed of a cantilevered bimorph beam is investigated. A Fully-coupled electromechanical nonlinear model of the harvester is extracted through a comprehensive variational approach taking into account nonlinearities due to both piezoelectric material and beam geometry. For excitations in the neighborhood of first mode resonance frequency the governing equations are order-reduced and solved implementing the perturbation method of multiple scales. The system response and harvested power are analyzed in the primary resonance of the system and extracted results are validated using a numerical solution.

2 Mathematical modelling

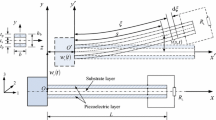
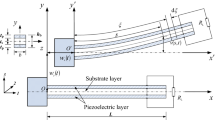
Figure 1 shows schematic of a typical micro harvester consisting of a cantilevered beam of length L, width b and thickness h B covered with two surface bounded layers of piezoelectric material of thickness h P . l 1 and l 2 represent the starting and ending edges of the deposited piezoelectric layers. The proof mass M is attached to the free end of the beam in order to decrease the natural frequency of the system. ρ B , ρ P and E B are mass densities of the base and piezoelectric materials and effective Young’s modulus of the base material, respectively. Base vibration is represented by d(t) which denotes the displacement of the clamped end in y direction. According to the displacement of the clamped end of the beam, the xyz coordinates system connected to the support base is a non-inertial reference frame and therefore the effect of displacement can be taken into account by a fictitious force proportional to the acceleration \(\ddot{d}\left( t \right)\).

Fig. 1
figure 1

Schematic view of a piezoelectric bimorph harvester

Full size image

As shown in Fig. 2 energy extraction is performed by placement of two electrodes which are very thin layers of conductive material on the both sides of each piezoelectric layer. The effect of these electrodes stiffness is negligible on the mechanical properties of the system. The electrodes are connected to an external load which is supposed to be a pure resistance R substituted for input impedance of the harvesting circuit, in this study.

Fig. 2
figure 2

Electrodes connections

Full size image

Figure 3 depicts an arbitrary element of the beam neutral axis before and after deflection. According to this figure, angle θ which shows the slope of the beam with respect to undeformed position is derived as:

$$\tan \theta = \frac{{v^{{\prime }} }}{{1 + u^{{\prime }} }}$$
(1)
Fig. 3
figure 3

An element of the neutral axis before and after deflection

Full size image

Also the neutral axis elongation can be expressed by the following relation:

$$e = \sqrt {\left( {1 + u^{{\prime }} } \right)^{2} +\, v^{{{\prime }2}} } - 1$$
(2)

According to Euler–Bernoulli beam theory which supposes that all planes which are initially perpendicular to neutral axis remain plane and perpendicular to neutral axis after deformation, the only nonzero component of the strain is:

$$S_{1} = e - y\theta^{{\prime }}$$
(3)

The inextensibility condition as a result of no external longitudinal force application to the beam, demands no relative elongation of the neutral axis. Therefore, equating neutral axis stretching to zero in Eq. (2) and using a Taylor series expansion, yields in:

$$u^{{\prime }} = - \frac{1}{2}v^{{{\prime }2}} + O\left( {\varepsilon^{4} } \right)$$
(4)

where lateral displacement v is assumed to be O(ɛ). Integrating the above relation considering the boundary condition for axial displacement results in:

$$u = - \frac{1}{2}\int\limits_{0}^{x} {v^{{{\prime }2}} dx}$$
(5)

Upon expanding Eq. (1) in a Taylor series and keeping terms up to third order of epsilon while using Eq. (4), one obtains:

$$\theta = v^{{\prime }} + \frac{1}{6}v^{{{\prime }3}} + O\left( {\varepsilon^{5} } \right)$$
(6)

The kinetic energy of the beam and attached mass can be written as:

$$T = \frac{1}{2}\int\limits_{0}^{L} {\left( {m + M\delta \left( {x - L} \right)} \right)\left( {\left( { - \frac{1}{2}\left( {\int\limits_{0}^{x} {v^{{{\prime }2}} dx}}\right)^{ \cdot}}\right)^{2} + \dot{v}^{2} } \right)dx}$$
(7)

The mass per unit length of the beam is:

$$m = b\left( {\rho_{B} h_{B} + 2\rho_{P} h_{P} \varPi \left( x \right)} \right)$$
(8)

where Π(x) is the rectangular function:

$$\varPi \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {x < l_{1} } \hfill \\ 1 \hfill & {l_{1} < x < l_{2} } \hfill \\ 0 \hfill & {x > l_{2} } \hfill \\ \end{array} } \right.$$
(9)

Total free energy of a nonlinear electroelastic material which is the summation of mechanical and electrical energies stored per unit mass of the electroelastic body, for the case of axial strains can be written as (Yang 2005):

$$\psi \left( {S_{i} ,E_{j} } \right) = \frac{1}{2}\mathop c\limits_{{2_{ij} }} S_{i} S_{j} - e_{ij} E_{i} S_{j} - \frac{1}{2}\varepsilon_{ij} E_{i} E_{j} + \frac{1}{24}\mathop c\limits_{{4_{ijkl} }} S_{i} S_{j} S_{k} S_{l} + \frac{1}{6}\mathop k\limits_{{2_{ijkl} }} E_{i} S_{j} S_{k} S_{l}$$
(10)

where the material constants c 2ij , e ij , ɛ ij , \(c_{{4_{ijkl} }}\) and \(k_{{2_{ijkl} }}\) are second-order elastic, piezoelectric, electric permittivity, fourth order elastic and second odd electroelastic coefficients, respectively. The first three terms yield to linear theory of piezoelectricity and the last two terms are due to nonlinear effects. Since the electromechanical coupling factor is usually small for piezoelectric materials such as PZT, in an energy harvester the generated electrical fields are generally small. Therefore the weak nature of the electric field motivates the exclusion of nonlinear terms due to electric field-dependent behavior of dielectric or piezoelectric constants. Also terms proportional to third-order elastic and first electroelastic coefficients which lead to even nonlinearities are not considered, since they vanish due to symmetry of the bimorph configuration.

Introducing an electrical potential function ϕ inside the piezoelectric media, one has:

$$E_{i} = - \phi_{,i}$$
(11)

Assuming that the piezoelectric material is polarized in y direction, one obtains by substituting Eq. (11) into Eq. (10) and neglecting the x-component of electrical field due to slenderness of the piezoelectric layer:

$$\begin{aligned} \psi \left( {\theta ,\phi } \right) & = \frac{1}{2}\mathop c\limits_{{2_{11} }} \left( {\left( {y - y_{N} } \right)\theta^{{\prime }} } \right)^{2} - e_{21} \phi_{,2} \left( {\left( {y - y_{N} } \right)\theta^{{\prime }} } \right) - \frac{1}{2}\varepsilon_{22} \phi_{,2}^{2} \\ \quad + \frac{1}{24}\mathop c\limits_{{4_{1111} }} \left( {\left( {y - y_{N} } \right)\theta^{{\prime }} } \right)^{4} + \frac{1}{6}\mathop k\limits_{{2_{2111} }} \phi_{,2} \left( {\left( {y - y_{N} } \right)\theta^{{\prime }} } \right)^{3} \\ \end{aligned}$$
(12)

The above energy function yields to following nonlinear constitutive equations:

$$\begin{aligned} T_{1} & = & \frac{\partial \psi }{{\partial S_{1} }} = \left( {\mathop c\limits_{{2_{11} }} + \frac{1}{6}\mathop c\limits_{{4_{1111} }} S_{1}^{2} } \right)S_{1} - \left( {e_{21} - \frac{1}{2}\mathop k\limits_{{2_{2111} }} S_{1}^{2} } \right)E_{2} \\ D_{2} & = & - \frac{\partial \psi }{{\partial E_{2} }} = \left( {e_{21} - \frac{1}{6}\mathop k\limits_{{2_{2111} }} S_{1}^{2} } \right)S_{1} + \varepsilon_{22} E_{2} \\ \end{aligned}$$
(13)

As can be seen in the above equations both piezoelectric and elastic coefficients are functions of applied mechanical strain in the nonlinear model.

The potential energy stored in beam and piezoelectric layers will be:

$$U = U_{M} + U_{E}$$
(14)

in which U M is pure mechanical part of potential energy and U E is sum of electromechanical and electrical parts as follows:

$$\begin{aligned} U_{M} & = \frac{1}{2}\int\limits_{0}^{L} {\left( {D_{2} \theta^{{{\prime }2}} + D_{4} \theta^{{{\prime }4}} } \right)dx} \\ U_{E} & = \int\limits_{0}^{L} {\left( {\int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {b\left( { - 2e_{21} \phi_{,2} y\theta^{{\prime }} - \varepsilon_{22} \phi_{,2}^{2} + \frac{1}{3}\mathop k\limits_{{2_{2111} }} \phi_{,2} \left( {y\theta^{{\prime }} } \right)^{3} } \right)dy} } \right)\varPi \left( x \right)dx} \\ \end{aligned}$$
(15)

where D 2 and D 4 are second and fourth order bending stiffness, respectively:

$$\begin{aligned} D_{2} & = \frac{2}{3}b\left( {E_{B} \left( {\frac{{h_{B} }}{2}} \right)^{3} + \mathop c\limits_{{2_{11} }} \left( {\left( {\frac{{h_{B} }}{2} + h_{P} } \right)^{3} - \left( {\frac{{h_{B} }}{2}} \right)^{3} } \right)\varPi \left( x \right)} \right) \\ D_{4} & = \frac{1}{30}b\mathop c\limits_{{4_{1111} }} \left( {\left( {\frac{{h_{B} }}{2} + h_{P} } \right)^{5} - \left( {\frac{{h_{B} }}{2}} \right)^{5} } \right)\varPi \left( x \right) \\ \end{aligned}$$
(16)

The virtual work which is the summation of the work done by nonconservative forces including inertial and damping forces and the work done by the electrical charges stored on the electrodes, is:

$$\delta W_{nc} = \int_{0}^{L} {\left[ { - \left( {m + M\delta \left( {x - L} \right)} \right)\ddot{d}\left( t \right) - c\dot{v}} \right]\delta vdx} - \left. {q\delta \phi } \right|_{{y = \frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }}$$
(17)

where c represents the mechanical or parasitic damping, which arises from material or air damping.

Extended Hamilton’s principle indicates:

$$\int_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U + \delta W_{nc} } \right)dt} = 0$$
(18)

After performing some mathematical operations in accordance with the variational calculus including some integrations by parts, the variations of the kinetic and potential energies are obtained as:

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\delta Tdt} = - \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left( {\frac{1}{2}\left( {\left( {\int\limits_{L}^{x} {\left( {m + M\delta \left( {x - L} \right)} \right)\left( {\int\limits_{0}^{x} {v^{{{\prime }2}} dx} } \right)^{ \cdot \cdot } } dx} \right)v^{{\prime }} } \right)^{{\prime }} + \left( {m + M\delta \left( {x - L} \right)} \right)\ddot{v}} \right)\delta vdx} dt}$$
(19)
$$\int\limits_{{t_{1} }}^{{t_{2} }} {\delta U_{M} dt} = \int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left( {\left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{\prime}}}} \right)^{{\prime }} \delta vdx} dt} + \int\limits_{{t_{1} }}^{{t_{2} }} {\left. {\left( {\left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)\frac{\partial \theta }{{\partial v^{{\prime }} }}\delta v^{{\prime }} - \left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{{\prime }} }}\delta v} \right)} \right|_{x = 0}^{L} dt}$$
(20)
$$\begin{aligned} \int\limits_{{t_{1} }}^{{t_{2} }} {\delta U_{E} dt} & = \\ 2\int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left( \begin{aligned} \left( {\left( {\left( {\int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {b\left( {\left( { - e_{21} \phi_{,2} y + \frac{1}{2}\mathop k\limits_{{2_{2111} }} \phi_{,2} \left( {y\theta^{{\prime }} } \right)^{2} y} \right)} \right)dy} } \right)\varPi \left( x \right)} \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{{\prime }} }}} \right)^{{\prime }} \delta v \hfill \\ - \left( {\int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {b\left( {\left( { - e_{21} \theta^{{\prime }} - \varepsilon_{22} \phi_{,22} + \frac{1}{2}\mathop k\limits_{{2_{2111} }} \left( {y\theta^{{\prime }} } \right)^{2} \theta^{{\prime }} } \right)\delta \phi } \right)dy} } \right)\varPi \left( x \right) \hfill \\ \end{aligned} \right)dx} dt} \\ + 2\int\limits_{{t_{1} }}^{{t_{2} }} {\int\limits_{0}^{L} {\left. {\left( {b\left( {\left( { - e_{21} y\theta^{{\prime }} - \varepsilon_{22} \phi_{,2} + \frac{1}{6}\mathop k\limits_{{2_{2111} }} \left( {y\theta^{{\prime }} } \right)^{3} } \right)\delta \phi } \right)\varPi \left( x \right)} \right)} \right|_{{y = \frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} dx} dt} \\ \end{aligned}$$
(21)

Substituting Eqs. (17) and (19)–(21) into Eq. (18), the governing equations of motion are obtained as:

$$\left( {m + M\delta \left( {x - L} \right)} \right)\ddot{v} + c\dot{v} + \left( {\left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{{\prime }} }}} \right)^{{\prime }} + \frac{1}{2}\left( {\left( {\int\limits_{L}^{x} {\left( {m + M\delta \left( {x - L} \right)} \right)\left( {\int\limits_{0}^{x} {v^{{{\prime }2}} dx} } \right)^{ \cdot \cdot } } dx} \right)v^{{\prime }} } \right)^{{\prime }}+\, 2\left( {\left( {\left( {\int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {b\left( {\left( { - e_{21} \phi_{,2} y + \frac{1}{2}\mathop k\limits_{{2_{2111} }} \phi_{,2} \left( {y\theta^{{\prime }} } \right)^{2} y} \right)} \right)dy} } \right)\varPi \left( x \right)} \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{{\prime }} }}} \right)^{{\prime }} = - \left( {m + M\delta \left( {x - L} \right)} \right)\ddot{d}\left( t \right)$$
(22a)
$$\varepsilon_{22} \phi_{,22} = \left( { - e_{21} + \frac{1}{2}\mathop k\limits_{{2_{2111} }} \left( {y\theta^{{\prime }} } \right)^{2} } \right)\theta^{{\prime }}$$
(22b)

where associated boundary conditions are:

$$\left. {\left( {\left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)\frac{\partial \theta }{{\partial v^{{\prime }} }}\delta v^{{\prime }} - \left( {D_{2} \theta^{{\prime }} + 2D_{4} \theta^{{{\prime }3}} } \right)^{{\prime }} \frac{\partial \theta }{{\partial v^{{\prime }} }}\delta v} \right)} \right|_{x = 0}^{L} = 0$$
(23a)
$$\left. {\left( {\left( {2\int\limits_{0}^{L} {\left( {b\left( { - e_{21} y\theta^{{\prime }} - \varepsilon_{22} \phi_{,2} + \frac{1}{6}\mathop k\limits_{{2_{2111} }} \left( {y\theta^{{\prime }} } \right)^{3} } \right)\varPi \left( x \right)dx} \right)} + q} \right)\delta \phi } \right)} \right|_{{y = \frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} = 0$$
(23b)

Twice integration of Eq. (22b) assuming that the lower electrode is grounded and showing the voltage of the upper one by V, yileds in following electrical potential distribution function:

$$\phi = \frac{{2y - h_{B} }}{{2h_{P} }}V + \frac{{h_{P}^{2} }}{{2\varepsilon_{22} }}\left( {e_{21} c_{1} \left( y \right) + \mathop k\limits_{{2_{2111} }} c_{2} \left( y \right)h_{P}^{2} \theta^{{{\prime }2}} } \right)\theta^{{\prime }}$$
(24)

where:

$$\begin{aligned} c_{1} \left( y \right) & = \frac{1}{{h_{P}^{2} }}\left( {\left( {\left( {\frac{{h_{B} }}{2}} \right)^{2} - y^{2} } \right) + \left( {\frac{{2y - h_{B} }}{{2h_{P} }}} \right)\left( {\left( {\frac{{h_{B} }}{2} + h_{P} } \right)^{2} - \left( {\frac{{h_{B} }}{2}} \right)^{2} } \right)} \right) \\ c_{2} \left( y \right) & = - \frac{1}{{12h_{P}^{4} }}\left( {\left( {\left( {\frac{{h_{B} }}{2}} \right)^{4} - y^{4} } \right) + \left( {\frac{{2y - h_{B} }}{{2h_{P} }}} \right)\left( {\left( {\frac{{h_{B} }}{2} + h_{P} } \right)^{4} - \left( {\frac{{h_{B} }}{2}} \right)^{4} } \right)} \right) \\ \end{aligned}$$
(25)

Based on Kirchhoff’s voltage law:

$$V + R\dot{q} = 0$$
(26)

Using second boundary condition (23b) and the above equation one obtains:

$$V + 2Rb\int\limits_{0}^{L} {\left. {\left( {e_{21} \left( {y - y_{N} } \right)\theta^{{\prime }} + \varepsilon_{22} \phi_{,2} - \frac{1}{6}\mathop k\limits_{{2_{2111} }} \left( {\left( {y - y_{N} } \right)\theta^{{\prime }} } \right)^{3} } \right)^{ \cdot } } \right|_{{y = \frac{{h_{B} }}{2} + h_{P} }} \varPi \left( x \right)dx} = 0$$
(27)

Substituting Eqs. (6) and (25) into Eqs. (22a) and (27) and keeping nonlinear terms up to third order, coupled electromechanical equations of the harvester assuming the beam is completely covered by the piezoelectric layers, governing lateral deflection and output voltage are obtained:

$$\left\{ \begin{aligned} \left( {m + M\delta \left( {x - L} \right)} \right)\ddot{v} + c\dot{v} + D_{2} \left( {v^{{{\prime \prime \prime }}} + v^{{{\prime }2}} v^{{{\prime \prime \prime }}} + v^{{\prime }} v^{{{\prime \prime }2}} } \right)^{{\prime }} + 6D_{4} \left( {v^{{{\prime \prime }2}} v^{{{\prime \prime \prime }}} } \right)^{{\prime }} + \frac{1}{2}\left( {\left( {\int\limits_{L}^{x} {\left( {m + M\delta \left( {x - L} \right)} \right)\left( {\int\limits_{0}^{x} {v^{{{\prime }2}} dx} } \right)^{\cdot\cdot } } dx} \right)v^{{\prime }} } \right)^{{\prime }} \hfill \\ + \left( {2b\mathop k\limits_{{2_{2111} }} \int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {\left( {\frac{1}{{h_{P} }}V + \frac{1}{{2\varepsilon_{22} }}e_{211} h_{P}^{2} c_{1}^{{\prime }} \left( y \right)v^{{\prime \prime }} } \right)y^{3} dy} } \right)\left( {v^{{\prime \prime }} v^{{{\prime \prime \prime }}} } \right)^{{\prime }} + \left( {\frac{{2be_{211} }}{{h_{P} }}\int\limits_{{\frac{{h_{B} }}{2}}}^{{\frac{{h_{B} }}{2} + h_{P} }} {ydy} } \right)V\delta^{{\prime }} \left( {x - L} \right) = - \left( {m + M\delta \left( {x - L} \right)} \right)\ddot{d}\left( t \right) \hfill \\ V + 2Rb\int\limits_{0}^{L} {\left( \begin{aligned} \frac{{\varepsilon_{22} }}{{h_{P} }}V + e_{211} \left( {\frac{{h_{B} }}{2} + h_{P} } \right)\left( {1 + \frac{1}{2}v^{{{\prime }2}} } \right)v^{{\prime \prime }} \hfill \\ + \frac{1}{2}\left( {e_{211} h_{P}^{2} c_{1}^{{\prime }} \left( {\frac{{h_{B} }}{2} + h_{P} } \right)\left( {1 + \frac{1}{2}v^{{{\prime }2}} } \right) + \mathop k\limits_{{2_{2111} }} h_{P}^{4} c_{2}^{{\prime }} \left( {\frac{{h_{B} }}{2} + h_{P} } \right)v^{{{\prime \prime }2}} } \right)v^{{\prime \prime }} \hfill \\ - \frac{1}{6}\mathop k\limits_{{2_{2111} }} \left( {\frac{{h_{B} }}{2} + h_{P} } \right)^{3} v^{{{\prime \prime }3}} \hfill \\ \end{aligned} \right)^{ \cdot } dx} = 0 \hfill \\ \end{aligned} \right.$$
(28)

where terms with ϕ ,1 are neglected due to slenderness of the beam and piezoelectric layers. The boundary conditions are:

$$\left\{ \begin{aligned} v = v^{{\prime }} = 0\quad x = 0 \hfill \\ v^{{\prime \prime }} = v^{{{\prime \prime \prime }}} = 0\quad x = L \hfill \\ \end{aligned} \right.$$
(29)

Introducing the following dimensionless parameters:

$$\hat{x} = \frac{x}{L},\hat{y} = \frac{y}{h},\hat{v} = \frac{v}{L},\hat{t} = \frac{t}{\tau },\hat{M} = \frac{M}{mL},\hat{d} = \frac{d}{L},\hat{c} = \frac{c\tau }{m},\hat{V} = \frac{V}{{V^{*} }},\hat{y}_{N} = \frac{{y_{N} }}{h},\hat{R} = \frac{R}{{R^{*} }},\tau = L^{2} \sqrt {\frac{m}{{D_{2} }}} ,V^{*} = \frac{1}{L}\sqrt {\frac{{D_{2} h_{P} }}{{b\varepsilon_{22} }}} ,R^{*} = \frac{{h_{P} \tau }}{{2\varepsilon_{22} bL}},h = h_{B} + h_{P}$$
(30)

Equation (28) may be non-dimensionalized as following equations where hat superscripts are omitted for the sake of notational simplicity:

$$\left( {1 + M\delta \left( {x - 1} \right)} \right)\ddot{v} + c\dot{v} + \left( {v^{{{\prime \prime \prime }}} + v^{{{\prime }2}} v^{{{\prime \prime \prime }}} + v^{{\prime }} v^{{{\prime \prime }2}} } \right)^{{\prime }} + 6\beta_{1} \left( {v^{{{\prime \prime }2}} v^{{{\prime \prime \prime }}} } \right)^{{\prime }} + \frac{1}{2}\left( {\left( {\int\limits_{1}^{x} {\left( {1 + M\delta \left( {x - 1} \right)} \right)\left( {\int\limits_{0}^{x} {v^{{{\prime }2}} dx} } \right)^{ \cdot \cdot } } dx} \right)v^{{\prime }} } \right)^{{\prime }} + 2\beta_{3} \beta_{4} \beta_{6} V\left( {v^{{\prime \prime }} v^{{{\prime \prime \prime }}} } \right)^{{\prime }} + \beta_{2}^{2} \beta_{3} \beta_{4}^{2} \beta_{7} \left( {v^{{\prime \prime }} v^{{{\prime \prime \prime }}} } \right)^{{\prime }} v^{{\prime \prime }} + 2\beta_{4} \beta_{5} V\delta^{{\prime }} \left( {x - 1} \right) = - \left( {1 + M\delta \left( {x - 1} \right)} \right)\ddot{d}\left( t \right)$$
(31)
$$V + R\int\limits_{0}^{1} {\left( \begin{aligned} V + \beta_{4} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)\left( {1 + \frac{1}{2}v^{{{\prime }2}} } \right)v^{{\prime \prime }} - \frac{1}{6}\beta_{4} \beta_{3} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)^{3} v^{{{\prime \prime }3}} \hfill \\ + \frac{1}{2}\beta_{4} \beta_{2}^{2} \left( {c_{1}^{{\prime }} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)\left( {1 + \frac{1}{2}v^{{{\prime }2}} } \right) + \beta_{2}^{2} \beta_{3} c_{2}^{{\prime }} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)v^{{{\prime \prime }2}} } \right)v^{{\prime \prime }} \hfill \\ \end{aligned} \right)^{ \cdot } dx}$$
(32)

where:

$$\begin{aligned} \beta_{1} & = \frac{{D_{4} }}{{L^{2} D_{2} }}\beta_{2} = \frac{{h_{P} }}{h}\beta_{3} = \frac{{\mathop k\limits_{{2_{2111} }} }}{{e_{21} }}\frac{{h^{2} }}{{L^{2} }}\beta_{4} = he_{21} \sqrt {\frac{{bh_{P} }}{{D_{2} \varepsilon_{22} }}} \\ \beta_{5} & = \frac{h}{{h_{P} }}\left( {\int\limits_{{\frac{{h_{B} }}{2h}}}^{{\frac{{h_{B} + 2h_{P} }}{2h}}} {ydy} } \right)\beta_{6} = \frac{h}{{h_{P} }}\left( {\int\limits_{{\frac{{h_{B} }}{2h}}}^{{\frac{{h_{B} + 2h_{P} }}{2h}}} {y^{3} dy} } \right)\beta_{7} = \frac{h}{{h_{P} }}\left( {\int\limits_{{\frac{{h_{B} }}{2h}}}^{{\frac{{h_{B} + 2h_{P} }}{2h}}} {c_{1}^{{\prime }} \left( y \right)y^{3} dy} } \right) \\ \end{aligned}$$
(33)

The Galerkin method can be employed to reduce the order of the equations and derive the governing ordinary differential equations. To this end v(x, t) is assumed to be:

$$v\left( {x,t} \right) = \sum\limits_{i = 1}^{n} {\psi_{i} \left( x \right)\eta_{i} \left( t \right)}$$
(34)

where ψ i (x) are the mode shapes. Substituting the above equation in Eqs. (31) and (32), multiplying the first equation by ψ i (x) and integrating over the beam length, the ordinary differential equations are derived.

Generally in vibrational harvesters the resonance frequencies are high in comparison to environmental vibration frequencies and the excitation frequency rarely falls into the neighborhood of higher mode frequencies, therefore a single mode response suffices for the analysis. Assuming:

$$v\left( {x,t} \right) = \psi \left( x \right)\eta \left( t \right)$$
(35)

where ψ(x) is the first mode shape of the cantilever beam (Rao 2007):

$$\psi \left( x \right) = \left( {\cos \beta x - \cosh \beta x} \right) - \frac{\cos \beta + \cosh \beta }{\sin \beta + \sinh \beta }\left( {\sin \beta x - \sinh \beta x} \right)\quad \beta = 1.8751$$
(36)

The ordinary differential equations may be written as:

$$\left\{ \begin{aligned} \ddot{\eta } + \mu \dot{\eta } + \omega_{E}^{2} \eta + \alpha_{1} \eta^{3} + \alpha_{2} \left( {\eta \ddot{\eta } + \dot{\eta }^{2} } \right)\eta - \alpha_{3} V + \alpha_{4} \eta^{2} V = K\cos \left( {\varOmega t} \right) \hfill \\ V + R\left( {\dot{V} + \alpha_{5} \dot{\eta } + \alpha_{6} \eta^{2} \dot{\eta }} \right) = 0 \hfill \\ \end{aligned} \right.$$
(37)

where:

$$\begin{aligned} m_{eq} & = \int\limits_{0}^{1} {\left( {1 + M\delta \left( {x - 1} \right)} \right)\psi^{2} dx} \quad k_{eq} = \int\limits_{0}^{1} {\psi^{iv} \psi dx} \quad \omega_{E} = \sqrt {\frac{{k_{eq} }}{{m_{eq} }}} \quad \mu = \frac{{\int\limits_{0}^{1} {c\psi^{2} dx} }}{{m_{eq} }} \\ \alpha_{1} & = \frac{{\int\limits_{0}^{1} {\left( {\left( {\psi^{{{\prime }2}} \psi^{{{\prime \prime \prime }}} + \psi^{{\prime }} \psi^{{{\prime \prime }2}} + 6\beta_{1} \psi^{{{\prime \prime }2}} \psi^{{{\prime \prime \prime }}} } \right)^{{\prime }} + \beta_{2}^{2} \beta_{3} \beta_{4}^{2} \beta_{7} \left( {\psi^{{\prime \prime }} \psi^{{{\prime \prime \prime }}} } \right)^{{\prime }} \psi^{{\prime \prime }} } \right)\psi dx} }}{{m_{eq} }} \\ \alpha_{2} & = \frac{{\int\limits_{0}^{1} {\left( {\left( {\int\limits_{1}^{x} {\left( {1 + M\delta \left( {x - 1} \right)} \right)\left( {\int\limits_{0}^{x} {\psi^{{{\prime }2}} dx} } \right)dx} } \right)\psi^{{\prime }} } \right)^{{\prime }} \psi dx} }}{{m_{eq} }}\quad \alpha_{3} = \frac{{2\beta_{4} \beta_{5} \left. {\left( {\psi^{{\prime }} } \right)} \right|_{x = 1} }}{{m_{eq} }}\quad \alpha_{4} = \frac{{2\beta_{3} \beta_{4} \beta_{6} \int\limits_{0}^{1} {\left( {\psi^{{\prime \prime }} \psi^{{{\prime \prime \prime }}} } \right)^{{\prime }} \psi dx} }}{{m_{eq} }} \\ \alpha_{5} & = \beta_{4} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right) + \frac{1}{2}\beta_{2}^{2} c_{1}^{{\prime }} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)} \right)\left. {\left( {\psi^{{\prime }} } \right)} \right|_{x = 1} \\ \alpha_{6} & = \frac{1}{2}\beta_{4} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right) + \frac{1}{2}\beta_{2}^{2} c_{1}^{{\prime }} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)} \right)\left. {\left( {\psi^{{{\prime }3}} } \right)} \right|_{x = 1} \\ \quad + \frac{1}{2}\beta_{4} \beta_{3} \left( {3\beta_{2}^{4} c_{2}^{{\prime }} \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right) - \left( {\frac{1}{2}\left( {1 + \beta_{2} } \right)} \right)^{3} } \right)\int\limits_{0}^{1} {\psi^{{{\prime \prime }3}} dx} \\ K & = - \frac{{\int\limits_{0}^{1} {\left( {1 + M\delta \left( {x - 1} \right)} \right)\psi dx} }}{{m_{eq} }}A_{Base} \\ \end{aligned}$$
(38)

Here ω E is the linear short circuit resonance frequency of the bimorph. The damping coefficient can be derived from mechanical quality factor of the system in the case of no energy harvesting:

$$\mu = \frac{{\omega_{E} }}{Q}$$
(39)

The base motion is supposed to be a single harmonic with excitation frequency Ω as:

$$\ddot{d}\left( t \right) = A_{Base} \cos \left( {\varOmega t} \right)$$
(40)

3 Analytical solution

To analytically solve the governing nonlinear equations of the system and investigate the vibratory behavior of the nonlinear harvester, the method of multiple scales as a perturbation technique which can represent the solution of a nonlinear problem by an asymptotic expansion is implemented in this section (Nayfeh 2008). To use the method of multiple scales the following assumptions are made (Nayfeh and Mook 2008):

$$\mu = \varepsilon^{2} \hat{\mu },\quad K = \varepsilon^{2} k$$
(41)

This guarantees the terms to be ordered so that excitation and damping terms appear simultaneously with the highest order of nonlinearity. By introducing new independent variables accordingly as:

$$T_{n} = \varepsilon^{n} t\quad for\quad n = 0,1,2, \ldots$$
(42)

Then derivatives with respect to t may be written as an expansion of partial derivatives with respect to T n :

$$\begin{aligned} \frac{d}{dt} & = \frac{{dT_{0} }}{dt}\frac{\partial }{{\partial T_{0} }} + \frac{{dT_{1} }}{dt}\frac{\partial }{{\partial T_{1} }} + \ldots = D_{0} + \varepsilon D_{1} + \ldots \\ \frac{{d^{2} }}{{dt^{2} }} & = D_{0}^{2} + 2\varepsilon D_{0} D_{1} + \varepsilon^{2} \left( {D_{1}^{2} + 2D_{0} D_{2} } \right) + \ldots \\ \end{aligned}$$
(43)

The coefficients α 1 to α 6 are ordered as follows:

$$\alpha_{1} = \varepsilon^{2} \hat{\alpha }_{1} \quad \alpha_{2} = \varepsilon^{2} \hat{\alpha }_{2} \quad \alpha_{3} = \varepsilon \hat{\alpha }_{3} \quad \alpha_{4} = \varepsilon \hat{\alpha }_{4} \quad \alpha_{5} = \varepsilon \hat{\alpha }_{5} \quad \alpha_{6} = \varepsilon \hat{\alpha }_{6}$$
(44)

The solution can be represented by expanding η and V as follows:

$$\begin{aligned} \eta & = \eta_{0} \left( {T_{0} ,T_{1} , \ldots } \right) + \varepsilon \eta_{1} \left( {T_{0} ,T_{1} , \ldots } \right) + \ldots \\ V & = V_{0} \left( {T_{0} ,T_{1} , \ldots } \right) + \varepsilon V_{1} \left( {T_{0} ,T_{1} , \ldots } \right) + \ldots \\ \end{aligned}$$
(45)

Since the excitation is O(ɛ 2), Ω − ω E should be O(ɛ 2) for consistency. Therefore introducing the detuning parameter σ as:

$$\varOmega = \omega_{E} + \varepsilon^{2} \sigma$$
(46)

then substituting Eqs. (41) and (43) to (45) into Eq. (37) and equating the coefficients of the same powers of ɛ, one obtains the following sets of equations:

$$\varepsilon^{0} :\left\{ {D_{0}^{2} \eta_{0} + \omega_{E}^{2} \eta_{0} = 0} \right.$$
(47a)
$$\varepsilon^{0} :\left\{ {V_{0} + RD_{0} V_{0} = 0} \right.$$
(47b)
$$\varepsilon^{1} :\left\{ {D_{0}^{2} \eta_{1} + \omega_{E}^{2} \eta_{1} = - 2D_{0} D_{1} \eta_{0} + \hat{\alpha }_{3} V_{0} - \hat{\alpha }_{4} \eta_{0}^{2} V_{0} } \right.$$
(48a)
$$\varepsilon^{1} :\left\{ {V_{1} + RD_{0} V_{1} = - R\left( {D_{1} V_{0} + \left( {\hat{\alpha }_{5} + \hat{\alpha }_{6} \eta_{0}^{2} } \right)D_{0} \eta_{0} } \right)} \right.$$
(48b)
$$\varepsilon^{2} :\left\{ {D_{0}^{2} \eta_{2} + \omega_{E}^{2} \eta_{2} = - 2D_{0} D_{1} \eta_{1} - \left( {D_{1}^{2} + 2D_{0} D_{2} } \right)\eta_{0} - \hat{\mu }D_{0} \eta_{0} - \hat{\alpha }_{1} \eta_{0}^{3} - \hat{\alpha }_{2} \left( {\eta_{0} D_{0}^{2} \eta_{0} + \left( {D_{0} \eta_{0} } \right)^{2} } \right)\eta_{0} + \hat{\alpha }_{3} V_{1} (a - \hat{\alpha }_{4} \left( {\eta_{0}^{2} V_{1} + 2\eta_{0} \eta_{1} V_{0} } \right) + k\cos \left( {\varOmega t} \right)} \right.$$
(49a)
$$\varepsilon^{2} :\left\{ {V_{2} + RD_{0} V_{2} = - R\left( {D_{1} V_{1} + D_{2} V_{0} + \hat{\alpha }_{5} \left( {D_{0} \eta_{1} + D_{1} \eta_{0} } \right) + \hat{\alpha }_{6} \left( {\eta_{0}^{2} D_{0} \eta_{1} + \eta_{0}^{2} D_{1} \eta_{0} + 2\eta_{0} \eta_{1} D_{0} \eta_{0} } \right)} \right)} \right.$$
(49b)

The solution of Eqs. (47a) and (47b) can be written as:

$$\begin{aligned} \eta_{0} & = A\left( {T_{1} ,T_{2} , \ldots } \right)\exp \left( {i\omega_{E} T_{0} } \right) + \bar{A}\left( {T_{1} ,T_{2} , \ldots } \right)\exp \left( { - i\omega_{E} T_{0} } \right) \\ V_{0} & = 0 \\ \end{aligned}$$
(50)

Substituting the above solution into Eq. (48a) and eliminating the secular terms one obtains:

$$D_{1} A = 0,\quad \eta_{1} = 0$$
(51)

Substituting in Eq. (48b) results in:

$$V_{1} = - \frac{{Ri\omega_{E} }}{{1 + Ri\omega_{E} }}\left( {\hat{\alpha }_{5} A + \hat{\alpha }_{6} A^{2} \bar{A}} \right)\exp \left( {i\omega_{E} T_{0} } \right) - \frac{{R\hat{\alpha }_{6} i\omega_{E} A^{3} }}{{1 + 3Ri\omega_{E} }}\exp \left( {3i\omega_{E} T_{0} } \right) + cc$$
(52)

The following equation is obtained by substituting Eqs. (50)–(52) into Eq. (49a):

$$D_{0}^{2} \eta_{2} + \omega_{E}^{2} \eta_{2} = \left[ \begin{aligned} - 2i\omega_{E} D_{2} A - \left( {\hat{\mu } + \frac{{R\hat{\alpha }_{3} \hat{\alpha }_{5} }}{{1 + Ri\omega_{E} }}} \right)i\omega_{E} A \hfill \\ + \left( \begin{aligned} 2\hat{\alpha }_{2} \omega_{E}^{2} - 3\hat{\alpha }_{1} + \frac{{\left( {\hat{\alpha }_{4} \hat{\alpha }_{5} - \hat{\alpha }_{3} \hat{\alpha }_{6} } \right)Ri\omega_{E} }}{{1 + R^{2} \omega_{E}^{2} }} \hfill \\ - \frac{{\left( {\hat{\alpha }_{3} \hat{\alpha }_{6} - 3\hat{\alpha }_{4} \hat{\alpha }_{5} } \right)R^{2} \omega_{E}^{2} }}{{1 + R^{2} \omega_{E}^{2} }} \hfill \\ \end{aligned} \right)A^{2} \bar{A} \hfill \\ + \left( {\frac{{R\hat{\alpha }_{6} i\omega_{E} \hat{\alpha }_{4} \left( {2 + 10R^{2} \omega_{E}^{2} } \right)\left( {1 - 3Ri\omega_{E} } \right)}}{{\left( {1 + R^{2} \omega_{E}^{2} } \right)\left( {1 + 9R^{2} \omega_{E}^{2} } \right)}}} \right)A^{3} \bar{A}^{2} \hfill \\ \end{aligned} \right]\exp \left( {i\omega_{E} T_{0} } \right) + \frac{1}{2}k\exp \left( {i\varOmega t} \right) + cc + NST$$
(53)

where NST stands for non-secular terms with frequencies 3ω E and 5ω E . Therefore eliminating the secular terms results in:

$$- 2i\omega_{E} D_{2} A - \left( {\hat{\mu } + \frac{{R\hat{\alpha }_{3} \hat{\alpha }_{5} }}{{1 + Ri\omega_{E} }}} \right)i\omega_{E} A + \left( \begin{aligned} 2\hat{\alpha }_{2} \omega_{E}^{2} - 3\hat{\alpha }_{1} \hfill \\ + \frac{{\left( {\hat{\alpha }_{4} \hat{\alpha }_{5} - \hat{\alpha }_{3} \hat{\alpha }_{6} } \right)Ri\omega_{E} }}{{1 + R^{2} \omega_{E}^{2} }} - \frac{{\left( {\hat{\alpha }_{3} \hat{\alpha }_{6} - 3\hat{\alpha }_{4} \hat{\alpha }_{5} } \right)R^{2} \omega_{E}^{2} }}{{1 + R^{2} \omega_{E}^{2} }} \hfill \\ \end{aligned} \right)A^{2} \bar{A} + \left( {\frac{{R\hat{\alpha }_{6} i\omega_{E} \hat{\alpha }_{4} \left( {2 + 10R^{2} \omega_{E}^{2} } \right)\left( {1 - 3Ri\omega_{E} } \right)}}{{\left( {1 + R^{2} \omega_{E}^{2} } \right)\left( {1 + 9R^{2} \omega_{E}^{2} } \right)}}} \right)A^{3} \bar{A}^{2} +\, \frac{1}{2}k\exp \left( {i\sigma T_{2} } \right) = 0$$
(54)

Representing A in polar form:

$$A = \frac{1}{2}a\exp \left( {i\beta } \right)$$
(55)

And substituting into Eq. (54), then separating real and imaginary parts one obtains:

$$\begin{aligned} \left\{ \begin{array}{llll} a^{{\prime }} = - \frac{1}{2}\left( {\hat{\mu } + \frac{{R\hat{\alpha }_{3} \hat{\alpha }_{5} }}{{1 + R^{2} \omega_{E}^{2} }}} \right)a + \left( {\frac{{R\left( {\hat{\alpha }_{4} \hat{\alpha }_{5} - \hat{\alpha }_{3} \hat{\alpha }_{6} } \right)}}{{8\left( {1 + R^{2} \omega_{E}^{2} } \right)}}} \right)a^{3} + \left( {\frac{{R\hat{\alpha }_{4} \hat{\alpha }_{6} \left( {1 + 5R^{2} \omega_{E}^{2} } \right)}}{{16\left( {1 + R^{2} \omega_{E}^{2} } \right)\left( {1 + 9R^{2} \omega_{E}^{2} } \right)}}} \right)a^{5} + \frac{1}{{2\omega_{E} }}k\sin \left( \gamma \right) \hfill \\ a\gamma^{{\prime }} = \left( {\sigma - \frac{{R^{2} \hat{\alpha }_{3} \hat{\alpha }_{5} \omega_{E} }}{{2\left( {1 + R^{2} \omega_{E}^{2} } \right)}}} \right)a + \left( {\frac{{2\hat{\alpha }_{2} \omega_{E}^{2} - 3\hat{\alpha }_{1} }}{{8\omega_{E} }} - \frac{{R^{2} \omega_{E} \left( {\hat{\alpha }_{3} \hat{\alpha }_{6} - 3\hat{\alpha }_{4} \hat{\alpha }_{5} } \right)}}{{8\left( {1 + R^{2} \omega_{E}^{2} } \right)}}} \right)a^{3} + \left( {\frac{{3R^{2} \hat{\alpha }_{4} \hat{\alpha }_{6} \omega_{E} \left( {1 + 5R^{2} \omega_{E}^{2} } \right)}}{{16\left( {1 + R^{2} \omega_{E}^{2} } \right)\left( {1 + 9R^{2} \omega_{E}^{2} } \right)}}} \right)a^{5} + \frac{1}{{2\omega_{E} }}k\cos \left( \gamma \right) \end{array}\right.\end{aligned}$$
(56)

where the following change of variable is made to transform the equations to an autonomous system:

$$\gamma = \sigma T_{2} - \beta$$
(57)

The steady state solution of the dynamical system described by equations set (56) can be found by setting \(a^{{\prime }} = \gamma^{{\prime }} = 0\). The linear stability of equilibrium points (a E, γ E) and location of bifurcation points can be found through eigenvalues of the Jacobian matrix.

Substituting Eq. (55) into Eq. (51), an expression for the output voltage is obtained:

$$V = \frac{{R\omega_{E} }}{{\sqrt {1 + R^{2} \omega_{E}^{2} } }}\left( {\alpha_{5} a^{E} + \frac{{\alpha_{6} }}{4}\left( {a^{E} } \right)^{3} } \right)\cos \left( {\varOmega t + \phi_{1} - \gamma^{E} } \right) + \, \frac{{R\omega_{E} \alpha_{6} }}{{4\sqrt {1 + 9R^{2} \omega_{E}^{2} } }}\left( {a^{E} } \right)^{3} \cos \left( {3\varOmega t + \phi_{2} - 3\gamma^{E} } \right)$$
(58)

where:

$$\begin{aligned} \phi_{1} = \pi + \arctan \left( {\frac{1}{{R\omega_{E} }}} \right) \hfill \\ \phi_{2} = \pi + \arctan \left( {\frac{1}{{3R\omega_{E} }}} \right) \hfill \\ \end{aligned}$$
(59)

The average output power is:

$$P = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_{0}^{T} {\frac{{V^{2} }}{R}dt}$$
(60)

Substituting V from Eq. (58) into the above equation one obtains:

$$P = \frac{{R\omega_{E}^{2} \left( {a^{E} } \right)^{2} }}{32}\left( {\frac{{\left( {4\alpha_{5} + \alpha_{6} \left( {a^{E} } \right)^{2} } \right)^{2} }}{{1 + R^{2} \omega_{E}^{2} }} + \frac{{\alpha_{6}^{2} \left( {a^{E} } \right)^{4} }}{{1 + 9R^{2} \omega_{E}^{2} }}} \right)$$
(61)

4 Results and discussion

As a case study to explore the effect of nonlinearities on the system response and particularly the amount of extractable power, we consider here a micro-scale harvester composed of a cantilever beam with width b = 5 mm, length L = 5 mm and a tip mass M = 10 mg. The beam is constructed of a base silicon layer of thickness h B  = 33 μm and two PZT deposited layers of thickness h P  = 1 μm. The mechanical quality factor of the system is Q = 200 which has been derived in the case of no energy harvesting. Material properties of silicon and PZT-5H (poled along the thickness) are given in Table 1.

Table 1 Material properties of the harvester
Full size table

The short circuit resonance frequency for this assumed configuration is calculated to be f E  = 410 Hz. The value of the external load R is chosen so that the output power flowing from the piezo layers to the harvesting circuit is maximized. Calculations show that this optimum point is achieved at R = 0.6 kΩ which can approximately be calculated by matching the external load with the capacitive impedance of the piezoelectric layers at the resonance frequency (Ottman et al. 2002).

Figure 4 shows the system frequency response at various excitation levels defined by different base acceleration amplitudes. As can be seen in this figure the response curves are simple left-bended ones which traditionally appear in the response of Duffing-type oscillators with nonlinearities of the softening type. At sufficiently high amplitudes of excitation, the response includes two stable high and low energy branches connected through a curve with saddle stability which is the locus of system saddle points. There are two saddle-node bifurcation points in the response of the system in which the saddle point collides with a stable node.

Fig. 4
figure 4

Frequency response curves at primary resonance for various input accelerations

Full size image

Although geometric nonlinearities result in hardening response of cantilever beams in the first mode (Nayfeh and Pai 2008), the softening behavior of the response curves indicates that the material nonlinearities of the piezoelectric ceramic has the dominant effect on the nonlinear behavior of the harvester, leading to left bended response curves. It illustrates that in the nonlinear analysis of piezoelectric harvesting beams especially when ferroelectric ceramics are employed as piezoelectric material, the material nonlinearities must be taken into account together with geometric ones.

Figure 5 depicts the variation of tip deflection amplitude with respect to the excitation amplitude at different frequencies which again is a multivalued response for excitation frequencies lower than the resonance one.

Fig. 5
figure 5

Amplitude of the response as a function of input acceleration for different excitation frequencies

Full size image

As can be seen in Eq. (58), up to this order of approximation the output voltage of the harvester is a multi-frequency waveform consisted of two harmonic components, one with a frequency equal to that of excitation and the other with a frequency three times the excitation frequency. This generation of higher order electric signals from a pure sinusoidal single-frequency excitation which shows the nonlinear nature of piezoelectric and dielectric properties of piezoelectric materials is known as harmonic generation (Hall 2001). While in the case of resonant piezoelectric actuators it is usually an unwanted effect since it causes a significant portion of the input energy to be wasted in the generation of unwanted vibrational modes, in the field of energy harvesting due to collection of the energy of all harmonics by the harvesting circuit it doesn’t create the same problem. Figure 6 presents the temporal response of the output voltage where the existence of these harmonics is evident. To examine the validity of our analytical solution, the equations are also solved numerically by employing Runge–Kutta method. As can be seen in this figure the comparison of this two solution results, shows a good agreement between them.

Fig. 6
figure 6

Output voltage of the harvester (A Base  = 0.5 g, Ω − ω E  = −20 rad/s)

Full size image

The output power of the harvester is calculated from Eq. (61) and presented in Fig. 7. As can be seen in this figure at low levels of excitation the frequency response slightly bends toward the low frequencies. As excitation grows saddle-node bifurcation points are observed. Increasing the excitation beyond this point leads to output power decrease which is due to decrease of the amplitude of the first harmonic as a result of nonlinearity. Further increasing of the excitation causes the amplitude of the third harmonic to grow and consequently yields in power enhancement again.

Fig. 7
figure 7

Output power versus excitation frequency for various acceleration levels

Full size image

The frequency responses of Fig. 7 are presented separately in Figs. 8, 9, 10, and 11 together with a numerical solution for the sake of validation. Similar to frequency response curves for vibration amplitude, the output power is multivalued too, so that the correct value of output power depends on the trajectory of the excitation. Ramping down the frequency from high excitation frequencies pushes the harvester along the high energy stable branch of the response curve while ramping it up causes the harvester power to lie on the low energy branch. The numerical solution is conducted employing the Runge–Kutta method and first in a forward sweep the excitation frequency ramps up smoothly, then through a backward one ramps down again. The solution of each step is used as initial condition for the next one as frequency increases or decreases. The comparison is presented for all cases and as can be seen in these figures, a very good agreement is observed between the results of both analytical and numerical methods.

Fig. 8
figure 8

Output power versus excitation frequency (A Base  = 0.2 g)

Full size image
Fig. 9
figure 9

Output power versus excitation frequency (A Base  = 0.3 g)

Full size image
Fig. 10
figure 10

Output power versus excitation frequency (A Base  = 0.4 g)

Full size image
Fig. 11
figure 11

Output power versus excitation frequency (A Base  = 0.5 g)

Full size image

Figure 12 illustrates the variation of extracted power with respect to the excitation amplitude at different frequencies. As can be seen in this figure while similar to Fig. 5 the response curves are constructed of two stable and saddle branches at frequencies lower than that of the resonance, unlike deflection response different behaviors can be distinguished at different excitation frequencies.

Fig. 12
figure 12

Output power as a function of input acceleration for different excitation frequencies

Full size image

The peak-to-peak output voltage of the harvester for different values of excitation amplitude is presented in Fig. 13. Similar to the output power, by increasing the excitation the output voltage is enhanced while the response curves are bended toward lower frequencies. Continuation of increasing the excitation leads to reduction of the output voltage due to decrease of first harmonic amplitude as a consequence of nonlinearity. In this case although the third harmonic amplitude is increasing, the total voltage amplitude decreases due to higher rate of the first harmonic amplitude reduction together with the existence of a phase difference between the harmonics. Further increasing of the excitation amplitude leads the first harmonic to grow again in the opposite phase and this simultaneous enhancement of both harmonics amplitude leads the peak-to-peak amplitude of the output voltage to increase again.

Fig. 13
figure 13

Peak-to-peak output voltage of the harvester for the input acceleration A Base equal to a 0.2 g, b 0.3 g, c 0.4 g, d 0.5 g

Full size image

5 Conclusion

Nonlinear dynamics of piezoelectric bimorph beams employed as vibrational energy harvesters during large amplitude motions is investigated. To that end first of all a comprehensive procedure implementing a variational approach is followed to extract a fully-coupled electromechanical nonlinear model of the system. In the proposed model both sources of nonlinear behavior including geometric and material nonlinearities are considered through exploiting nonlinear constitutive relations of piezoelectricity together with nonlinear strain relations which bring into account large curvature and shortening effects. To investigate the harvester behavior in the neighborhood of first resonance frequency, derived nonlinear coupled partial differential equations of the proposed model are order-reduced by means of Galerkin method and governing nonlinear ordinary differential equations are extracted. An analytical solution employing the perturbation method of multiple scales is presented for the equations at the primary resonance. To explore the effect of nonlinearities on dynamic characteristics and output power of piezoelectric harvesters, results are presented for a PZT/Silicon/PZT laminated beam as a case study. Findings indicate that although the nonlinear curvature effect in large amplitude vibrations of a cantilever beam leads to a hardening behavior in the first vibration mode, material nonlinearities of the PZT layer which lead to softening behavior of the frequency response have the dominant effect in comparison to geometric ones. The output voltage of the harvester is a multi-frequency waveform consisted of harmonics of the excitation frequency due to harmonic generation effect as a consequence of nonlinearity. At the primary resonance, different frequency responses of the extracted power can be distinguished at different excitation amplitudes arising from the accumulation of powers of voltage harmonics at the output harvesting circuit. A numerical solution implementing the Runge–Kutta method is conducted and the results are employed to validate the analytical solution where a very good agreement is observed.