1 Introduction

Nowadays, brittle or quasi-brittle materials are significantly more employed in various industries such as automotive and aerospace for their particular properties. Hence, researching on the fracture behavior of these materials is an important issue for designers, engineers, and manufacturers. The occurrence of mechanical rupture in the brittle materials happens unexpectedly and without any caution. Empirical study of fracture behavior is usually time-consuming, expensive, and needs numerous tests. Therefore, realizing the material behavior and using the validated numerical simulations leads to time and costs reduction of experimental tests.

Unlike cracks which are not desired, U-shape and V-shape notches are often utilized in engineering components for particular aims. A notch in a part increases the amount of stress concentration, causes cracks and failures or decreases the structural life.

Different failure criteria have been proposed to estimate the brittle rupture in engineering parts with U, V, and key-hole notches under in-plane loading. For instance, Seweryn [1], Gomez et al. [2], Gomez and Elices [3], Ayatollahi and Torabi [4], and Torabi [5] focused on the mode I of fracture in U-shaped and V-shaped notches. Recently, important researches on the mixed mode I/II brittle rupture of notched components were performed by Yosibash et al. [6], Ayatollahi and Torabi [7, 8], Torabi and Pirhadi [9], Gomez et al. [10, 11], and Berto et al. [12, 13]. Additionally, to probe the brittle fracture in the pure mode II, Ayatollahi and Torabi [14] examined the Brazilian disk (BD) with a central U-notch. As already mentioned, most of these scholars took into account the in-plane loading and few works such as Zheng et al. [15] and Berto et al. [16] carried out on the pure mode III, mixed mode I/III, and II/III.

In the above investigations, the approach is founded on determining the critical value for the notch stress intensity factors (NSIF), so-called notch fracture toughness and the equations are established based on the linear elastic fracture mechanics (LEFM) that ignores non-linear effects and energy balance considerations. Meanwhile, it is assumed that crack growth step consumes a few proportion of the total energy required for final rupture and all energy consumption is almost spent for the crack initiation step. Since rupture quickly happens in fully brittle materials and parts with sharp notches, it is reasonable to neglect the energy consumption in the crack growth step. But, in quasi-brittle and ductile materials, and also for components with curved notches, ignoring the energy consumption in the crack growth step generates further discrepancies.

In brittle materials, crack initiation is not detected by the conventional finite element method (CFEM) which only deals with the growth of pre-existing cracks. To face this challenge, a new approach of the finite fracture mechanics (FFM) has been suggested. Founded on the FFM approach, a fracture criterion assumes that crack grows by finite steps. The length of this finite extension is achieved by a consistency condition of both energy and stress requirements. Thus, the crack advancement is not a material constant and taken into account as a structural parameter [17].

Moreover, in numerical simulations of the CFEM, other limitations in the calculation of the NSIF are the sensitivity of results to mesh and singularity in stress field at crack front, which imposes the use of tiny elements in this zone. Although employing the singular elements allow applying of larger elements, number of the needed elements will be added and the computational costs increase. Constructed on the concept of partition of unity, Belytschko and Black firstly offered the extended finite element method (XFEM) and modeled the discontinuities by the special enriched functions in conjunction with additional degrees of freedom [18]. The XFEM reduces the shortcomings of the CFEM, especially in the step of crack growth by engaging local enrichment functions. Besides, it is able to specify crack initiation length with consideration of both crack initiation and crack growth formulas.

In the previous researches, prediction of fracture in notched specimens under mixed mode loading is established based on theoretical formulas. In most of them, toughness and crack initiation angle in notched specimens are two topics which have been studied. The main contribution and objective of the current paper is to utilize several fracture criteria constructed on the CFEM and XFEM methods, in order to numerically predict the load carrying capacity and crack initiation angle for the polymethylmethacrylate (PMMA) U-notch coupons under mixed mode loading. Furthermore, the novelty is to reveal accuracy of the CFEM- and XFEM-based method criteria in predicting the load carrying capacity and crack initiation angle of U-notch specimens subjected to the mixed mode loading. It should be noted that the present study focuses on the prediction of load carrying capacity as well as crack initiation angle, and the crack initiation length is not determined. Due to predicting the load carrying capacity of the material, the results of the current investigation can be certainly used by sheet polymer industries and assist engineers to manufacture safer products.

2 XFEM theory

In 1999, the XFEM theory and modeling the discontinuities via the special enriched functions, combined with extra degrees of freedom and regarding the concept of partition of unity, was initially proposed by Belytschko and Black [18], and then completed by Moes et al. [19]:

The considered domain \(\Omega \) is surrounded by boundary \(\varGamma \) which is composed of the sets \(\varGamma _\mathrm{u} \), \(\varGamma _\mathrm{t} \), and \(\varGamma _\mathrm{c} \) such that \(\varGamma =\varGamma _\mathrm{u} \cup \varGamma _\mathrm{t} \cup \varGamma _\mathrm{c} \). Prescribed displacements and tractions are imposed on \(\varGamma _\mathrm{u} \), \( \varGamma _\mathrm{t} \), respectively, while the crack surface \(\varGamma _\mathrm{c} \) is assumed to be free of traction. The equilibrium equations and boundary conditions are represented as follows:

$$\begin{aligned} \begin{array}{ll} \nabla .\;{\varvec{\sigma }} +{\varvec{b}}=0 &{}\quad \hbox {in}\;\Omega \\ {\varvec{\sigma }} .\; {\varvec{n}}=\bar{{{\varvec{t}}}} &{}\quad \hbox {on}\;\varGamma _\mathrm{t} \\ {\varvec{\sigma }} .\; {\varvec{n}}=0 &{}\quad \hbox {on}\;\varGamma _\mathrm{c} \\ \end{array} \end{aligned}$$
(1)

where \({\varvec{n}}\) , \({\varvec{\sigma }}\) , \({\varvec{b}}\) in sequence are the unit outward normal, the Cauchy stress, and the body force per unit volume. The strain–displacement equation is written as:

$$\begin{aligned} {\varvec{\varepsilon }} =\nabla _\mathrm{S} {\varvec{u}} \end{aligned}$$
(2)

\(\nabla _\mathrm{S}\) is the symmetric part of the gradient operator and the boundary conditions are:

$$\begin{aligned} {\varvec{u}}=\bar{{{\varvec{u}}}} \quad \hbox {on}\;\varGamma _\mathrm{u} \end{aligned}$$
(3)

Additionally, the constitutive equation is specified by Hooke’s law:

$$\begin{aligned} {\varvec{\sigma }} ={\varvec{C}}:{\varvec{\varepsilon }} \end{aligned}$$
(4)

In which, \({\varvec{C}}\) is the Hooke’s tensor.

On the other hand, the enriched functions consist of discontinuous functions, illustrating the displacement jump across the crack surfaces and the near-tip asymptotic functions to overcome the crack-tip singularity. The displacement vector defined within the unity enrichment is given through the next equation:

$$\begin{aligned} {\varvec{u}}=\sum _{i\in N} {{\varvec{u}}_i } \varphi _i +\sum _{j\in M} {{\varvec{b}}_j } \varphi _j H(x)+\sum _{k\in L} \varphi _k \left( {\sum _{\alpha =1}^4 {c_k^\alpha F_\alpha (x)} } \right) \end{aligned}$$
(5)
Fig. 1
figure 1

Normal and tangential coordinates for a smooth crack [18]

Full size image

In which, \({\varvec{u}}_i \), \(\varphi _i \), \({\varvec{b}}_j \), H(x), \(c_k^\alpha \), and \(F_\alpha (x)\), respectively, are the vector of usual nodal displacements associated with the continuous part of the finite element method (FEM) solution, the usual nodal shape functions, the vector of the nodal enriched degree of freedom, the associated function of discontinuous jump across the crack surfaces, extra degrees of freedom associated with the asymptotic crack-tip functions, and the elastic asymptotic crack-tip functions. Furthermore, it is emphasized that the first term in the right-hand side of Eq. (5) is used for all nodes of the FE model, while the middle and the last terms are, respectively, engaged for nodes whose shape function support is cut by the crack interior and the crack tip. Respecting Fig. 1 [18] which displays the normal and tangential coordinates for a smooth crack, the discontinuous jump function, H(x) , is defined by:

$$\begin{aligned} H(x)=\left\{ {\begin{array}{ll} 1 &{}\quad \;\;\;({\varvec{X}}-{\varvec{X}}^{*}) \cdot {\varvec{n}}\ge 0 \\ -1 &{}\quad ({\varvec{X}}-{\varvec{X}}^{*})\cdot \;{\varvec{n}}< 0 \\ \end{array}} \right. \end{aligned}$$
(6)

\({\varvec{X}}, {\varvec{X}}^{*},\) and \({\varvec{n}}\) in sequence are a desired Gauss point, the nearest point to \({\varvec{X}}\) on the crack, and the unit outward normal to the crack at \({\varvec{X}}^{*}\). Meanwhile, the asymptotic crack-tip functions for an isotropic elastic material are specified by:

$$\begin{aligned} F_\alpha (r,\theta )=\left\{ {\sqrt{r}\sin \left( {\frac{\theta }{2}} \right) ,\sqrt{r}\cos \left( {\frac{\theta }{2}} \right) ,\sqrt{r}\sin \left( {\frac{\theta }{2}} \right) \sin (\theta ),\sqrt{r}\cos \left( {\frac{\theta }{2}} \right) \sin (\theta )} \right\} \end{aligned}$$
(7)

where \((r,\theta )\) represents the polar frame which origin is located at the crack tip, while \(\theta =0\) is tangent to the crack tip.

3 Prediction of crack initiation and propagation by CFEM and XFEM

In this section, two different approaches based on the CFEM and XFEM are employed to numerically predict load carrying capacity and crack initiation angle in U-notch coupons under mixed mode loading.

  • CFEM:

Numerous criteria constructed on the CFEM have been developed and implemented by many scholars to numerically estimate the load carrying capacity and crack initiation angle. In this research, two of the most common criteria including maximum tangential stress (MTS) and minimum strain energy density (MSED) are applied to be compared with results of the XFEM criteria and experimental observations.

The MTS criterion assumes that crack propagates along a direction perpendicular to the maximum tangential stress, \(\sigma _{\theta \theta } (\theta _\mathrm{c} )\) in radial direction from the notch tip. Along this direction, fracture onsets when this maximum stress reaches its critical value, \(\sigma _\mathrm{c}\) which is determined by tensile strength. The conditions for crack growth can be presented by following mathematical equations:

$$\begin{aligned} \frac{\partial \sigma _{\theta \theta } (r,\theta )}{\partial \theta }= & {} 0\;;\quad \frac{\partial ^{2}\sigma _{\theta \theta } (r,\theta )}{\partial \theta ^{2}}\le 0 \end{aligned}$$
(8)
$$\begin{aligned} \sigma _{\theta \theta } (\theta _\mathrm{c} )= & {} \sigma _\mathrm{c} \end{aligned}$$
(9)

Regarding Torabi et al. investigation [20], a U-notch can be geometrically considered as a rounded-tip V-notch with zero notch angle, but the stress field must be rewritten for around the notch. It means that the formulations of U-notches can be fundamentally obtained from those of blunt V-notches. In this paper, the stress field for U-notched specimens proposed by reference [20] is used.

According to the MSED criterion, brittle fracture occurs when the strain energy density averaged over a given control volume \({\overline{W}}\) meets a critical magnitude \(W_\mathrm{c} \) that depends on material property, not notch geometry or sharpness. For the brittle materials subjected to static loading, the control volume is related to the ultimate tensile strength, \(\sigma _\mathrm{u} \), the fracture toughness, \(K_{\mathrm{IC}} \) and for the U-shaped notch, it is crescent in shape. The critical volume under mixed mode loading condition is centered on the point where the principal stress reaches its maximum values along the notch edge with the radius of:

$$\begin{aligned} R_0= & {} \frac{(5-3\nu )}{4\pi }\left( {\frac{K_{\mathrm{IC}} }{\sigma _\mathrm{u} }} \right) ^{2};\;\;(\hbox {Plane}\;\hbox {stress})\nonumber \\ R_0= & {} \frac{(1+\nu )(5-8\nu )}{4\pi }\left( {\frac{K_{\mathrm{IC}} }{\sigma _\mathrm{u} }} \right) ^{2};\;\;(\hbox {Plane}\;\hbox {strain}) \end{aligned}$$
(10)

The critical value for strain energy density is achieved by [13]:

$$\begin{aligned} W_\mathrm{c} =\frac{\sigma _\mathrm{u}^2 }{2E} \end{aligned}$$
(11)

  • XFEM:

In this theory, the failure mechanism is different from the two previous criteria, including the two steps of crack initiation and crack growth. The crack initiation happens when degradation of the traction–separation response at the enriched elements begins. In other words, when the stress or strain meets a crack initiation criterion, the initiation process starts and the initiated crack propagates until final failure. As illustrated in the following, several proposed fracture criteria [18, 21,22,23] are utilized to numerically investigate the crack initiation in U-notch samples under planar mixed mode loading:

1. :

Maximum principal stress (MPS):

The MPS criterion is defined by the next equation:

$$\begin{aligned} f=\left\{ {\frac{\langle \sigma _{\max } \rangle }{\sigma _{\max }^0 }} \right\} \end{aligned}$$
(12)

\(\sigma _{\max }\) and \(\sigma _{\max }^0\) in sequence denote the maximum principal stress and maximum allowable principal stress. The Macaulay bracket symbol \(\langle \; \rangle \) is applied to omit effect of a purely compressive stress on crack initiation via the relation:

$$\begin{aligned} \langle \sigma _{\max } \rangle =\left\{ {\begin{array}{ll} \sigma _{\max }&{} \quad \sigma _{\max } >0 \\ 0 &{} \quad \sigma _{\max } \le 0 \\ \end{array}} \right. \end{aligned}$$
(13)
2. :

Maximum principal strain (MPE):

Similar to the MPS criterion, the MPE criterion is expressed as:

$$\begin{aligned} f=\left\{ {\frac{\langle \varepsilon _{\max } \rangle }{\varepsilon _{\max }^0 }} \right\} \end{aligned}$$
(14)

In which, \(\varepsilon _{\max }\) and \(\varepsilon _{\max }^0\) represent the maximum principal strain and maximum allowable principal strain, respectively.

3. :

Maximum nominal stress (MNS):

The MNS criterion is written by:

$$\begin{aligned} f=\max \left\{ {\frac{\langle t_n \rangle }{t_n^0 },\frac{t_s }{t_s^0 },\frac{t_\mathrm{t} }{t_\mathrm{t}^0 }} \right\} \end{aligned}$$
(15)

where \(t_n \) is the normal component of nominal stress and \(t_s \), \(t_\mathrm{t} \) are shear components of nominal stress in the crack plane. Moreover, \(t_n^0 \), \(t_s^0 \), \(t_\mathrm{t}^0 \) signify peak values of nominal stress in the probable crack surface, related to the material properties and determined by practical tests.

4. :

Maximum nominal strain (MNE):

This criterion is similarly illustrated by the next equation:

$$\begin{aligned} f=\max \left\{ {\frac{\langle \varepsilon _n \rangle }{\varepsilon _n^0 },\frac{\varepsilon _s }{\varepsilon _s^0 },\frac{\varepsilon _\mathrm{t} }{\varepsilon _\mathrm{t}^0 }} \right\} \end{aligned}$$
(16)

In which, \(\varepsilon _n \) is the normal component of nominal strain and \(\varepsilon _s \), \(\varepsilon _\mathrm{t}\) are shear components of nominal strain in the crack plane. Also, \(\varepsilon _n^0 \), \(\varepsilon _s^0 \), \(\varepsilon _\mathrm{t}^0 \) denote peak values of nominal strain in the probable crack surface, depending on the material properties and estimated through empirical tests.

5. :

Quadratic nominal stress (QNS):

The QNS criterion is stated as:

$$\begin{aligned} f=\left\{ {\frac{\langle t_n \rangle }{t_n^0 }} \right\} ^{2}+\left\{ {\frac{t_s }{t_s^0 }} \right\} ^{2}+\left\{ {\frac{t_\mathrm{t} }{t_\mathrm{t}^0 }} \right\} ^{2} \end{aligned}$$
(17)
6. :

Quadratic nominal strain (QNE):

Alike the previous one, this criterion is expressed as following:

$$\begin{aligned} f=\left\{ {\frac{\langle \varepsilon _n \rangle }{\varepsilon _n^0 }} \right\} ^{2}+\left\{ {\frac{\varepsilon _s }{\varepsilon _s^0 }} \right\} ^{2}+\left\{ {\frac{\varepsilon _\mathrm{t} }{\varepsilon _\mathrm{t}^0 }} \right\} ^{2} \end{aligned}$$
(18)

According to each of the above-discussed criteria, crack is expected to initiate when f reaches a value of one. Additionally, among the mentioned criteria, only the first and second (MPS and MPE) are able to predict the direction of crack initiation in a manner that when the fracture criterion is satisfied, crack onsets along a direction orthogonal to the maximum principal stress/strain directions. In other cases (MNS, MNE, QNS, and QNE), crack initiation direction cannot be specified because the related parameters should be given in the expected crack surface. Hence, these criteria are not capable to predict the angle of crack initiation.

  • Crack propagation:

Regarding the LEFM theory, when the strain energy release rate (SERR) founded on the virtual crack closure technique (VCCT) at the crack tip, meets its critical magnitude then crack propagates. The Benzeggagh and Kenane (BK) law firstly proposed in 1996 [24], works on estimating the equivalent fracture energy release rate in mixed mode loading as the next formula:

$$\begin{aligned} G_{\mathrm{eq,C}} =G_{\mathrm{IC}} +(G_{\mathrm{IIC}} -G_{\mathrm{IC}} ) \left( {\frac{G_{\mathrm{II}} +G_{\mathrm{III}} }{G_\mathrm{I} +G_{\mathrm{II}} +G_{\mathrm{III}} }} \right) ^{\eta } \end{aligned}$$
(19)

\(G_{\mathrm{IC}} , G_{\mathrm{IIC}} \), respectively, indicate the critical SERR of mode I and II, obtained by standard rupture tests. Meanwhile, \(G_\mathrm{I} \), \(G_{\mathrm{II}} \), \(G_{\mathrm{III}} \) in sequence represent the SERR for mode I, II, and III, calculated by VCCT. Exponent \(\eta \) is a power law coefficient, concerning mode mixity in mixed mode loading and is assumed to be 2 for brittle materials [24]. Through this method, assigning a fracture criterion to the enriched elements, the XFEM-based LEFM approach can be engaged to numerically simulate the propagation of a crack along an arbitrary, solution-dependent path in the bulk material with or without an initial crack. For this purpose, damage parameter (d) is defined. This parameter is zero for magnitudes of SERR less than the critical value, while it is equal to one when the SERR reaches the critical value. Taking into account the damage parameter, the elasticity matrix (\({\varvec{C}})\) at the surface of the crack is written as following [25]:

$$\begin{aligned} {\varvec{C}}=\left\{ {\begin{array}{ll} K{\varvec{I}}&{}\quad d=0 \\ K{\varvec{I}}_\mathrm{c} &{} \quad d=1 \\ \end{array}} \right. \end{aligned}$$
(20)

where K, \({\varvec{I}}\), respectively, are the penalty stiffness and identity matrix, and \({\varvec{I}}_\mathrm{c}\) is a compression identifier matrix as:

$$\begin{aligned} {\varvec{I}}_\mathrm{c} =\left[ {{\begin{array}{ccc} 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad {\frac{\left\langle {-\varepsilon _n } \right\rangle }{-\varepsilon _n }} \\ \end{array} }} \right] \end{aligned}$$
(21)

The constitutive equation is also specified by:

$$\begin{aligned} {\varvec{\sigma }} ={\varvec{C}}{\varvec{\varepsilon }} \end{aligned}$$
(22)

4 Experimental tests

The commercial glassy polymer, polymethylmethacrylate (PMMA), which is relatively homogenous, isotropic, and often fails in a brittle manner even at room temperature, is selected for preparing the specimens. In order to identify the material properties, ASTM D638-03 standard [26] was employed and a high-precision 2D laser cutting machine was used to provide the samples from a PMMA 2.2-mm-thick sheet. Then, the cut surfaces of the instances were polished by a fine abrasive paper to remove the effects of local defects. For the reliability, five coupons were prepared and tested at the velocity of 0.5 mm/min by an electromechanical SANTAM tensile test machine, equipped with a 50 KN load cell and strain gauge extensometer with 100 mm gauge length, + 50%/− 50% maximum strain.

Fig. 2
figure 2

The PMMA standard specimen, fixed in the tensile test machine

Full size image
Fig. 3
figure 3

The fractured coupons after the tensile tests

Full size image

Figure 2 depicts the PMMA standard specimen, fixed in the tensile test machine. The tensile tests were continued until rupture of the samples. As Fig. 3 exhibits the fractured coupons, except the fourth specimen (A4) which broke near the filleted section (probably due to existing a defect or stress concentration), all of the instances ruptured at the expected and reasonable zones. Figure 4 displays load–displacement curves, while Table 1 demonstrates the extracted results of material properties at room temperature. The results are averaged, but the A4 coupon does not take into account because of its breakage at the unsuitable place.

Fig. 4
figure 4

Load–displacement curves for different acceptable fractured coupons

Full size image
Table 1 Material properties of PMMA at room temperature
Full size table

4.1 Central U-notch specimens under mixed mode loading

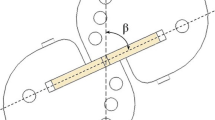
To study brittle fracture of the U-notch specimens under mixed mode loading, the test coupons were fabricated by 2D laser cutting machine from the chosen material, as revealed in Fig. 5. Four various loading angles of \(\beta \) (the angle between horizontal axis of the specimen and slit bisector line) equal 0, 30, 45, and 60 were opted to make different in-plane modes of loading around the U-notch ends. Zero angle represents the pure mode I of loading, while nonzero values indicate the mixed mode I/II and pure mode II loading. As the angle \(\beta \) grows from zero (horizontal notch), in-plane shear deformation slowly appears around the notch and it simultaneously endures both of the tension and shear deformations which exactly implies the mixed mode I/II loading.

Fig. 5
figure 5

Geometry of central U-notch specimens under mixed mode loading (all dimensions are in mm)

Full size image

As Fig. 6 illustrates, samples were tested until fracture at the velocity of 0.5 mm/min by the tensile test machine and load–displacement curves were attained for the instances. Each experiment was repeated three times for the reliability of the experimental setups, and the results were averaged. Figure 7 shows the U-notch specimens after the rupture. To specify the crack initiation angle, images of the cracked surfaces were accurately processed by digitizer software in accordance with Fig. 8. The values of crack initiation angle and load carrying capacity are shown in Table 2. The mean values are considered to be compared with numerical simulation results.

Fig. 6
figure 6

A U-notch sample, fixed in the tensile test machine

Full size image
Fig. 7
figure 7

Different U-notch specimens after the rupture

Full size image
Fig. 8
figure 8

Specification of crack initiation angle by the digitizer software for a \(\beta =0\), b \(\beta =30\), c \(\beta =45\), and d \(\beta =60\)

Full size image

5 Numerical simulations and validation

The central U-notch samples are numerically simulated and compared with both theoretical formulas and practical tests. Due to the symmetry, only one half of the geometry was modeled for the case of pure mode I loading (\(\beta =0)\), the symmetry conditions were applied to the model, while, for nonzero magnitudes of angle (\(\beta \ne 0)\), the whole model was constructed. The Young’s modulus and Poisson’s ratio extracted from the experimental tests as \(E=3316.07\,\hbox {MPa},\;\nu =0.38\) were assigned to the model. In-plane and static loading conditions were utilized, and geometry was discretized by continuous three-dimensional 8-node linear brick elements with reduced integration points and hourglass control. Due to the stress concentration, fine elements were applied around the notch and coarse elements were engaged for the rest of areas. Mesh convergence tests were performed for the number of mesh sizes to validate the mesh density. After converging of the results, the final optimum selected mesh was achieved as exhibited in Fig. 9. The FE models were solved by a finite element code for all of the cases. Figure 10 depicts normalized tangential stress results for the nodes located along the bisector line of the notch vs. normalized distance from the notch tip. Because of using normalized stresses and also normalized distances for different magnitudes of \(\beta \), the results are nearly identical.

Table 2 Rupture load and crack initiation angle for different U-notch specimens
Full size table

To validate the FE model and numerical results, first, magnitudes of normalized tangential stress vs. the normalized distance are compared with the corresponding values calculated from the theoretical equations, proposed by Zappalorto and Lazzarin [27]. The next equation is used to theoretically evaluate the computed normalized tangential stress:

$$\begin{aligned} \sigma _{\theta \theta } (r,\theta )=\frac{K_\mathrm{I}^{V,\rho } }{\sqrt{2\pi }r^{1-\lambda _1 }}\left[ {m_{\theta \theta } ^{(\mathrm{I})}+\left( {\frac{r}{r_0 }} \right) ^{\mu _1 -\lambda _1 }n_{\theta \theta } ^{(\mathrm{I})}} \right] +\frac{K_{\mathrm{II}}^{V,\rho } }{\sqrt{2\pi }r^{1-\lambda _2 }}\left[ {m_{\theta \theta } ^{(\mathrm{II})}+\left( {\frac{r}{r_0 }} \right) ^{\mu _2 -\lambda _2 }n_{\theta \theta } ^{(\mathrm{II})}} \right] \end{aligned}$$
(23)

where \(K_\mathrm{I}^{V,\rho }\) and \(K_{\mathrm{II}}^{V,\rho }\) in sequence are the mode I and mode II NSIF. According to Fig. 11, the parameters \(\rho , r_0\) are the notch radius and distance of the notch tip from origin of the polar coordinates system, respectively. The functions \(m_{\theta \theta }\) , \(n_{\theta \theta }\) and the eigenvalues \(\mu _i\) and \(\lambda _i\) which depend upon the notch angle are reported in Appendix 1, in terms of notch opening angle (\(2\alpha )\). It should be emphasized that Eq. (23) is a general equation for computing the tangential stress around the V-shaped notches. Thus, the notch opening angle is assumed to be zero for the U-notched specimens [28]. Employing the above theoretical procedure, the normalized tangential stresses are theoretically attained and compared with the numerical results of Fig. 10. The comparison shows good conformity, and hence the versatility of the FE model is validated.

Fig. 9
figure 9

FE models: a mode I loading and b mixed mode loading

Full size image
Fig. 10
figure 10

Numerical prediction of normalized tangential stress vs. normalized distance from the notch tip for different magnitudes of \(\beta \)

Full size image
Fig. 11
figure 11

V-notch polar coordinate system with the origin [27]

Full size image

5.1 Numerical and experimental results

After validation of the FE model, results of the CFEM and XFEM in predicting the mixed mode load carrying capacity and the fracture initiation angle of U-notch coupons are extracted and compared with the empirical data. To compute the load carrying capacity and crack initiation angle via the MTS criterion, first, tangential and shear stresses are determined for a test load of 1000N through FE model. Then, the NSIF \(K_\mathrm{I} \) and \(K_{\mathrm{II}} \) for the test load are estimated, utilizing the revealed stresses and following relations [29]:

$$\begin{aligned} \begin{array}{l} K_\mathrm{I} =\frac{\sqrt{\pi \rho }}{2}\sigma _{\theta \theta } \left( {\frac{\rho }{2},0} \right) \\ K_{\mathrm{II}} =\lim _{r\rightarrow \frac{\rho }{2}} \sqrt{2\pi r}\frac{(\sigma _{r\theta } )_{\theta =0} }{\left( {1-\frac{\rho }{2r}} \right) } \\ \end{array} \end{aligned}$$
(24)

In the above equations, \(\sigma _{\theta \theta }\) is the tangential stress at the U-notch tip and \(\sigma _{r\theta }\) is the in-plane shear stress along the notch bisector line, specified for the test load by the FE model.

Using values of \(K_\mathrm{I}\) , \(K_{\mathrm{II}}\), employing the NSIF fracture curves and fracture initiation angle curves presented by Torabi [29], the material toughness and initiation angle are achieved. To evaluate the values of fracture initiation angle from fracture initiation angle curves, a useful parameter called the mode mixity (\(M_e^U )\) is defined:

$$\begin{aligned} M_e^U =\frac{2}{\pi }\tan ^{-1}\left( {\frac{K_\mathrm{I} }{K_{\mathrm{II}} }} \right) \end{aligned}$$
(25)

In order to obtain load carrying capacity under mixed mode loading conditions, a parameter, named the effective NSIF, is expressed as:

$$\begin{aligned} K_{\mathrm{eff}} =\sqrt{K_\mathrm{I}^2 +K_{\mathrm{II}}^2 } \end{aligned}$$
(26)

Finally, substituting the values in the next equation, the load carrying capacity is stated by:

$$\begin{aligned} \frac{K_{\mathrm{eff}} }{K_{\mathrm{eff},c} }=\left( {\frac{F_{\mathrm{appl}} }{F_{\mathrm{cr}} }} \right) \end{aligned}$$
(27)

In which, \(K_{\mathrm{eff}}\), \(K_{\mathrm{eff},c}\), \(F_{\mathrm{appl}}\), and \(F_{\mathrm{cr}}\), respectively, are effective NSIF in mixed mode condition for the test load, effective toughness in mixed mode loading attained from fracture curves [29], the test load and load carrying capacity.

To estimate the load carrying capacity and crack initiation angle by MSED criterion, first, radius of control volume is calculated. Then, amount of strain energy density is determined in specific volume for the test load of 1000N in the FE model. Finally, critical failure load for different mixed modes is given by:

$$\begin{aligned} \frac{\overline{{W}}}{W_{\mathrm{cr}} }= \left( {\frac{F_{\mathrm{appl}} }{F_{\mathrm{cr}} }} \right) ^{2} \end{aligned}$$
(28)

where \(\overline{{W}}\) and \(W_{\mathrm{cr}}\) in sequence are strain energy density for the test load and critical strain energy density, dependent on material properties and computed by Eq. (11). Besides, in this criterion, crack initiation angle is orthogonal to the direction of maximum principal stress.

To obtain the crack initiation angle and load carrying capacity by the XFEM criteria, experimental test conditions are applied to the validated FE model. Also, material properties required for the XFEM criteria are extracted from the empirical tests and assigned in accordance with Table 3. Moreover, elements are enriched by appropriate degrees of freedom in the whole model. After the simulations, the numerical results are achieved and compared with the practical tests.

Table 3 Material properties required for the XFEM criteria
Full size table
Table 4 Comparison of the experimental and predicted rupture load by different criteria for various notch directions
Full size table
Table 5 Comparison of the experimental and predicted crack initiation angle by different criteria for various notch directions
Full size table

Tables 4 and 5, respectively, display the practical and predicted results of the load carrying capacity and crack initiation angle for notch directions of 0, 30, 45, and 60. As Table 4 denotes, comparing the numerical and empirical magnitudes of the load carrying capacity shows that between the CFEM criteria (MTS, MSED), averaged percentage of errors (APE) for MSED is less than for MTS; therefore, MSED is more exact than MTS. Furthermore, among the XFEM criteria (MPS, MPE, MNS, MNE, QNS, and QNE), the stress-based criteria (MPS, MNS, QNS) are evidently more precise than the strain-based (MPE, MNE, MQE) ones. Meanwhile, the results demonstrate that the MNS and QNS criteria have the highest accuracy, while the MNE and QNE criteria have the least precision in prediction of the load carrying capacity among all criteria of CFEM and XFEM.

To evaluate the accuracy of different criteria in crack initiation prediction, as mentioned before, among the six XFEM-based criteria, only MPS and MPE can predict the crack initiation angle. According to Table 5, the APE for MSED and MPS is less than for MTS and MPE and the results approve that the best predictions belong to MPS and MSED, while the worst is related to MTS.

6 Conclusions

In this paper, the main contribution and objective was to numerically predict the load carrying capacity and crack initiation angle in components weakened by a U-notch under mixed mode tensile loading, employing CFEM and XFEM. The numerical results were compared with the experimental results of PMMA U-notched specimens and acceptable correlation was found between them for various loading angles. Besides, the novelty was to evaluate and reveal the precision of the mentioned criteria in predicting the load carrying capacity and crack initiation angle of U-notch samples subjected to the mixed mode loading. The results indicated that the XFEM criteria were more accurate than the CFEM ones, in addition to decrease the mesh sensitivity and computational costs. Moreover, it was concluded that among all criteria of CFEM and XFEM, the MNS and QNS criteria have the best accuracy in predicting the load carrying capacity, while the MPS and MSED are the most suitable criteria for estimating the crack initiation angle among those criteria which are able to do it.