Keywords

1 Introduction

Structures or machine components often contain sharp V-notches. The singular stress field exists in the vicinity of the notch tip of sharp V-notches. In linear elastic fracture mechanics, Williams [1] suggested that the singular stress field can be stated in the form of \(Kr^{ \lambda - 1 } f_{ij} \left( \theta \right)\), here \(K\) is the notch stress intensity factor (NSIF), \(r\) is the radial distance from the notch tip, \(\lambda - 1\) is the order of stress singularity, and \(f_{ij} \left( \theta \right)\) are the angular functions of stress components. Among the various brittle fracture criteria developed, the more popular and widely employed criteria are based on the critical values of NSIF [2,3,4,5].

In past decades, many techniques have been developed by researchers to compute the NSIFs. Gross and Mendelson [6] proposed the boundary collocation method (BCM) to determine the NSIFs of sharp V-notches. Chen [7] developed a body force method (BFM) to evaluate the NSIFs for specimens under mixed mode (I/II) tensile and in-plane bending loading conditions. Moreover, Ju and Chung [8] and Liu et al. [9] used finite element (FE) stresses, and utilizing the least-squares method determined the NSIFs. These least-squares methods [8, 9] require higher order Williams coefficients and/or very fine meshes for attaining the accurate values of NSIFs. In another research, Ayatollahi and Nejati [10] proposed an over deterministic method using the FE displacements to calculate the NSIFs along with the higher order terms of Williams coefficients. Recently, a collocation technique and a point substitution technique were proposed by authors [11, 12] to obtain the mixed mode (I/II) NSIFs using the FE displacements along the notch flanks.

It is worth mentioning here that, unlike the availability of popular quarter-point elements (QPEs) in the crack problems, no such singular elements are currently available for the sharp V-notched problems. Moreover, even though the displacement components are more accurate than the stress components in the FE method and the notch flank displacements are the most accurate in the entire domain, there are not many popular methods available for the determination of NSIFs using notch flank FE displacements. One of the reasons for neglecting the advantages of the notch flank displacement may be the presence of rigid body displacements in the displacement components which are absent in stress components. Therefore, the method proposed by authors [11], the rotational components in the displacements are not neglected; rather, nicely negotiated using a simple formula. Thus, the main thrust of the present work is to demonstrate the efficacy and capabilities of the collocation technique proposed by authors [11] in terms of accurate estimation of the NSIFs of a four-point bend (FPB) specimens with sharp V-notches. The FPB specimens with sharp V-notches are one of the widely used specimens to study the fracture of brittle materials.

In this research, the mode I and mode II NSIFs of the FPB are determined under various loading and geometry conditions using the collocation technique. The dimensionless notch shape factors and the mixing ratios are also presented for all the examples. The results obtained in the present investigation are then compared with the available solutions [13].

2 Theoretical Background

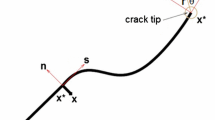
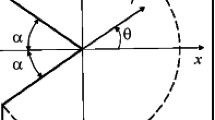
Consider a homogeneous elastic 2D geometry containing a sharp V-notch having notch angle \(\gamma ( = 180 - 2\alpha )\) as shown in Fig. 1. Considering the singular terms and the constant displacement terms, the displacement field at any pint point \(P\left( {r,\theta } \right)\) near to the notch tip \(O\) under any arbitrary in-plane loading can be given as [8]

Fig. 1
figure 1

Notch geometry

Full size image
$$\begin{aligned} u & = \frac{\kappa + 1}{{2G}}A_{0} + \frac{{A_{1} }}{2G}r^{{\lambda_{1}^{I} }} \left\{ {\left( {\kappa + \lambda_{1}^{I} \cos 2\alpha + \cos 2\alpha \lambda_{1}^{I} } \right)\cos \lambda_{1}^{I} \theta - \lambda_{1}^{I} \cos \left( {\lambda_{1}^{I} - 2} \right)\theta } \right\} \\ & \quad + \frac{{B_{1} }}{2G}r^{{\lambda_{1}^{II} }} \left\{ {\left( { - \kappa - \lambda_{1}^{II} \cos 2\alpha + \cos 2\alpha \lambda_{1}^{II} } \right)\sin \lambda_{1}^{II} \theta + \lambda_{1}^{II} \sin \left( {\lambda_{1}^{II} - 2} \right)\theta } \right\} - \frac{\kappa + 1}{{2G}}B_{2} r\sin \theta \\ v & = \frac{{A_{1} }}{2G}r^{{\lambda_{1}^{I} }} \left\{ {\left( {\kappa - \lambda_{1}^{I} \cos 2\alpha - \cos 2\alpha \lambda_{1}^{I} } \right)\sin \lambda_{1}^{I} \theta + \lambda_{n}^{I} \sin \left( {\lambda_{1}^{I} - 2} \right)\theta } \right\} + \frac{\kappa + 1}{{2G}}B_{0} \\ & \quad + \frac{{B_{1} }}{2G}r^{{\lambda_{1}^{II} }} \left\{ {\left( {\kappa - \lambda_{1}^{II} \cos 2\alpha + \cos 2\alpha \lambda_{1}^{II} } \right)\cos \lambda_{1}^{II} \theta + \lambda_{1}^{II} \cos \left( {\lambda_{1}^{II} - 2} \right)\theta } \right\} + \frac{\kappa + 1}{{2G}}B_{2} r\cos \theta \, \\ \end{aligned}$$
(1)

where \(A_{0}\), \(A_{1}\), \(B_{0}\), \(B_{1}\), and \(B_{2}\) are Williams’ coefficients, \(A_{0}\) and \(B_{0}\) are coefficients corresponding to the rigid body translation and \(B_{2}\) is coefficient corresponding to the rigid body rotations, Kolosov constant \(\kappa\) is equal to \({{\left( {3 - \nu } \right)} \mathord{\left/ {\vphantom {{\left( {3 - \nu } \right)} {\left( {1 + \nu } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + \nu } \right)}}\) for plane stress and \(3 - 4\nu\) for plane strain conditions, \(G = {E \mathord{\left/ {\vphantom {E {2\left( {1 + \nu } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {1 + \nu } \right)}}\) is the shear modulus, \(\nu\) and \(E\) are the Poisson’s ratio and Young’s modulus, respectively, and \(\lambda_{1}^{I}\) and \(\lambda_{1}^{II}\) are the modes I and II eigenvalues, respectively.

Similar to the crack problems, mode I and mode II NSIFs can be defined as [6]

$$\begin{gathered} K_{I} = \sqrt {2\pi } \lambda_{1}^{I} \left( {1 + \lambda_{1}^{I} - \lambda_{1}^{I} \cos 2\alpha - \cos 2\alpha \lambda_{1}^{I} } \right)A_{1} \hfill \\ K_{II} = \sqrt {2\pi } \lambda_{1}^{II} \left( { - 1 + \lambda_{1}^{II} - \lambda_{1}^{II} \cos 2\alpha + \cos 2\alpha \lambda_{1}^{II} } \right)B_{1} \hfill \\ \end{gathered}$$
(2)

It can be shown that [11], the notch opening displacement (NOD) can be written as

$$\begin{aligned} \Delta v & = v_{\theta = + \alpha }^{I} - v_{\theta = - \alpha }^{I} = 2v_{\theta = + \alpha }^{I} = 2\frac{{A_{1} }}{2G}r^{{\lambda_{1}^{I} }} \left[ \begin{gathered} \left( {\kappa - \lambda_{1}^{I} \cos 2\alpha - \cos 2\alpha \lambda_{1}^{I} } \right)\sin \lambda_{1}^{I} \alpha \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \lambda_{1}^{I} \sin \left( {\lambda_{1}^{I} - 2} \right)\alpha \hfill \\ \end{gathered} \right] \\ & = 2A_{1} C_{1} r^{{\lambda_{1}^{I} }} \\ \end{aligned}$$
(3)

Similarly, the notch sliding displacement (NSD) can be obtained as [11]

$$\begin{gathered} \Delta u = u_{\theta = + \alpha }^{II} - u_{\theta = - \alpha }^{II} = 2u_{\theta = + \alpha }^{II} = 2\frac{{B_{1} }}{2G}r^{{\lambda_{1}^{II} }} \left[ \begin{gathered} \left( { - \kappa - \lambda_{1}^{II} \cos 2\alpha + \cos 2\alpha \lambda_{1}^{II} } \right)\sin \lambda_{1}^{II} \alpha \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \lambda_{1}^{II} \sin \left( {\lambda_{1}^{II} - 2} \right)\alpha \hfill \\ \end{gathered} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 2\frac{\kappa + 1}{{2G}}B_{2} r\sin \alpha \,\,\,\, = 2B_{1} C_{2} r^{{\lambda_{1}^{II} }} + 2B_{2} C_{3} r \hfill \\ \end{gathered}$$
(4)

where \(C_{1}\), \(C_{2}\), and \(C_{3}\) are constants which depend upon the geometry of the notch and material property.

Considering \(N\) number of nodes are considered along the notch flanks (as shown in Fig. 2a), and the residual \(R_{I}\) between the analytical and the FE NOD can be obtained as

Fig. 2
figure 2

a Selection of the collocation nodes and b typical mesh arrangement around the notch tip

Full size image
$$R_{I} = \sum\limits_{j = 1}^{N} {\left[ {\ln \left( {\Delta v_{j}^{FE} } \right) - \ln \left( {A_{1} } \right) - \ln \left( {2C_{1} } \right) - \lambda_{1}^{I} \ln \left( {r_{j} } \right)} \right]^{2} }$$
(5)

For the minimum value of \(R_{I}\), the partial differentiation of \(R_{I}\) with respect to \(\ln \left( {A_{1} } \right)\) should be equals to zero

$$\frac{{\partial R_{I} }}{{\partial \ln \left( {A_{1} } \right)}} = 0$$
(6)

From (6), the Williams’ constant \(A_{1}\) can be obtained as [11]

$$A_{1} = \frac{{\exp \left[ {\frac{1}{N}\sum\nolimits_{j = 1}^{N} {\ln \left( {\Delta v_{j}^{FE} r_{j}^{{ - \lambda_{1}^{I} }} } \right)} } \right]}}{{2C_{1} }}$$
(7)

The NSD (Eq. (4)) contains two unknown Williams constants (\(B_{1}\) and \(B_{2}\)) and therefore, computation of \(B_{1}\) is not straight forward. Hence, two additional radial lines (radial line 1 and radial line 2 as shown in Fig. 2b) along \(\theta = + \alpha^{\prime}\) and \(\theta = - \alpha^{\prime}\) apart from the notch flanks (\(\theta = + \alpha\) and \(\theta = - \alpha\)) are considered. Similar to mode I, using effective NSD (\(\Delta u_{eff,j}^{FE}\)) at \(N\) number of nodes along the notch flanks and the radial lines 1 and 2, \(B_{1}\) can be obtained as [11]

$$B_{1} = \frac{{\exp \left[ {\frac{1}{N}\sum\nolimits_{j = 1}^{N} {\ln \left( {\Delta u_{eff,j}^{FE} r_{j}^{{ - \lambda_{1}^{II} }} } \right)} } \right]}}{{2C_{4} }}$$
(8)

Using the Williams constants the mode I and mode II NSIFs can be obtained from Eq. (2). The NSIFs can be normalized using the following equation [13]

$$F_{I} = \left( {2\pi a} \right)^{{\lambda_{1}^{I} - 1}} \frac{2L}{{P_{1} }}K_{I} \,\,\,\,\,{\text{and}}\,\,\,\,\,F_{II} = \left( {2\pi a} \right)^{{\lambda_{1}^{II} - 1}} \frac{2L}{{P_{1} }}K_{II} \,$$
(9)

Moreover, the state of mixity can be defined by an auxiliary parameter notch mode mixity ratio parameter \(\left( {M^{e} } \right)\), which can be defined as [13]

$$M^{e} = \frac{2}{\pi }\tan^{ - 1} \left( {\frac{{F_{I} }}{{F_{II} }}} \right)$$
(10)

3 Numerical Results and Discussions

A four-point bend (FPB) specimen is considered for the present analysis, as shown in Fig. 3a. The geometry and loading conditions for the FPB are shown in Fig. 3a. The length and width of the specimen are \(L\) = 80 and \(w\) = 10, respectively. The point load \(P =\) 10 is applied as shown in Fig. 3. The notch length to width ratio \({a \mathord{\left/ {\vphantom {a w}} \right. \kern-\nulldelimiterspace} w}\) = 0.4 is considered.

Fig. 3
figure 3

a FPB specimen, b typical FE mesh used for the FPB specimen, and c typical mesh arrangement around the notch tip

Full size image

The finite element solution is completed in ANSYS. Eight-noded quadratic elements are used in the entire domain, and the notch tip elements are collapsed to form a spider web pattern at the notch tip. The typical FE mesh used for the FPB specimen is shown in Fig. 3b. The enlarged notch tip elements are shown in Fig. 3c.

At first, the results for the FPB for the notch angle \(\gamma =\) 30º obtained using the collocation method [11] are validated with the results of Ref. [13]. In Ref [13], the shape factors were determined using an overdeterministic technique [10]. For the validation the following configurations were considered: \({{L_{1} } \mathord{\left/ {\vphantom {{L_{1} } L}} \right. \kern-\nulldelimiterspace} L} = {{L_{2} } \mathord{\left/ {\vphantom {{L_{2} } L}} \right. \kern-\nulldelimiterspace} L} = 0.45\), \({{L_{4} } \mathord{\left/ {\vphantom {{L_{4} } L}} \right. \kern-\nulldelimiterspace} L} = 0.3\), and \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} =\) 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9. The present and published results are shown in Fig. 4. From Fig. 4, it can be seen that both mode I and mode II shape factors using the present approach are in good agreement with the published results [13]. After that, some new results for the shape factors with the new configurations, \({{L_{1} } \mathord{\left/ {\vphantom {{L_{1} } L}} \right. \kern-\nulldelimiterspace} L} = {{L_{2} } \mathord{\left/ {\vphantom {{L_{2} } L}} \right. \kern-\nulldelimiterspace} L} = 0.6,\) \({{L_{4} } \mathord{\left/ {\vphantom {{L_{4} } L}} \right. \kern-\nulldelimiterspace} L} = 0.45\), and \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} =\) 0.45, 0.5, 0.6, 0.7, 0.8, and 0.9 are plotted in Figs. 5 and 6 for \(\gamma =\) 60º and 90º, respectively. Moreover, the mixity ratio parameters \(\left( {M^{e} } \right)\) are also plotted in Figs. 5c and 6c. It can be seen that when \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} = {{L_{4} } \mathord{\left/ {\vphantom {{L_{4} } L}} \right. \kern-\nulldelimiterspace} L}\), the specimen will be under pure mode I condition and as \(L_{4}\) increases the specimen will be under mixed-mode loading conditions. It has been also observed that when \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} = 0.9\) the specimen will be under pure mode II loading conditions. Therefore, the mixity ratio \(\left( {M^{e} } \right)\) is 1 for \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} = {{L_{4} } \mathord{\left/ {\vphantom {{L_{4} } L}} \right. \kern-\nulldelimiterspace} L} = 0.45\), and the ratio of \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L}\) changes, the value of \(M^{e}\) decreases and becomes equal to zero at \({{L_{3} } \mathord{\left/ {\vphantom {{L_{3} } L}} \right. \kern-\nulldelimiterspace} L} = 0.9\).

Fig. 4
figure 4

Validation of shape factors for a \(F_{I}\) and b \(F_{II}\) for \(\gamma = 30^\circ\)

Full size image
Fig. 5
figure 5

Results for a \(F_{I}\), b \(F_{II}\) and c \(M^{e}\) for \(\gamma = 60^\circ\)

Full size image
Fig. 6
figure 6

Results for a \(F_{I}\), b \(F_{II}\) and c \(M^{e}\) for \(\gamma = 90^\circ\)

Full size image

4 Conclusions

In this paper, the efficacy of an FE based NSIF extraction technique has been demonstrated by determining the NSIFs of four-point bending specimens. The notch flank opening and sliding finite element (FE) displacements are considered for determining the NSIFs. The rigid body displacements are nicely bypassed to evaluate the mixed mode (I/II) NSIFs. The NSIFs obtained using the present technique are found to be in good agreement with the available solutions. The mixed mode mixity ratio parameters are also determined for various loading positions from pure mode I to pure mode II. The results verify that the present collocation technique is simple, straightforward, and easy to be implemented in the available FE code.