Linear viscoelastic analysis using frequency-domain algorithm on oscillating circular shear flows for bubble suspensions

Abstract

To achieve a stable evaluation of the linear viscoelasticity of bubble suspensions, which have difficulties for conventional rheometers from spatial distributions of rheological properties with bubble deformations, we proposed a novel rheometry based on spatio-temporal velocity data obtained by ultrasonic velocity profiling (UVP). A frequency-domain algorithm was adopted to overcome a critical influence of measurement noise on the rheological assessment, which is inferred from error propagation characteristics through the equations of motion in discretized form. Applicability and advantage of the present rheometry with the frequency-domain algorithm were verified by two kinds of fluids: high viscous oil as a Newtonian fluid and polyacrylamide aqueous solution as a shear thinning, viscoelastic fluid. The rheometry was finally adopted for bubble suspensions subject to high oscillatory shear, and it could validly extract elasticity-originated momentum transfer as a function of space.

Introduction

Regarding aspects such as quality control of products, safety issues, and more efficient processing in any industrial field, details of rheological properties of fluid media are required. The development of highly precise torque meters has made it possible to provide good estimations of such details. Along with rheological models that are constitutive equations describing the stress response in materials, rotational rheometry has provided details of properties using only a small number of characteristic constants. Nevertheless, rotational rheometry assumes simple Couette flows produced in a narrow gap between the stator and rotor connected to torque meters. However, dispersed multiphase media, which are not seen as a continuum even at the macroscopic scale, are difficult to measure. Non-ideal conditions run counter to the assumption of Couette flows required to solve the “Couette inverse problem” to obtain the original rheological properties (e.g., Yeow et al. 2000; Ancey 2005; Heirman et al. 2008). Furthermore, in measurements of multiphase media, additional complexities arise for example from the presence of interfaces in gap size (e.g., Doi and Ohta 1991; Stickel and Powell 2005).

A focus of our studies on the rheology of multiphase media is bubble suspensions for understanding the mechanisms underpinning drag reduction from injected bubbles (e.g., Ceccio 2010; Murai 2014). Bubbles accumulated in flow elements, strong shear layers, and vortices create locally different rheological properties in conditions of unsteady shear flow in turbulence. Beginning with the appearance of the classical theory on dilute spherical suspensions (assuming that surface tension is strong enough to sustain the spherical shape) in Einstein (1906) and Taylor (1932), the study of suspension rheology has a century-long history. By considering capillary number, the theory was extended to deformable bubbles in simple steady shear flows (Frankel and Acrivos 1970), and its applicability was validated by experiments (Rust and Manga 2002). Choi and Schowalter (1975) provided a more sophisticated equation that considered higher orders in the volume fraction to extend the theory to larger volume fractions. Despite the progress made over the century, there remain aspects to be explained about the elastic response attributed to surface tension effect in unsteady shear flows (Llewellin et al. 2002; Llewellin and Manga 2005; Tasaka et al. 2015).

For a rheological evaluation of multiphase media, there are two issues to be solved: (1) the narrow-gap problem and (2) the inverse Couette problem. The Stokes-type rheometry, for instance, the falling sphere rheometry (bubble suspensions; e.g., see Murai and Oiwa (2008)) and commercial turning sphere rheometry (BMS, Anton Paar GmbH), can avoid the issues arising from Couette-type rheometry. However, the rheological properties evaluated using these methods correspond to aggregated rheological properties because of the multidimensional, multicomponent flows dealt with. Thus, the rheological properties obtained are difficult to interpret along standard approaches in rheology.

In solving the issues in regard to Couette-type rheometry, a combination of a wide-gap cylinder system and velocimetry has been tried; spatial profiling of velocity measured in a wider gap using different kinds of velocimetry can reveal deviations to ideal Couette flow that arises from complex rheological properties, for example, shear banding (e.g., Dimitriou et al. 2012). Supplementing the data by torque measurements to give an integrated boundary condition on a rotor in the system has supported evaluation of complex rheological properties. The kinds of velocimetry adopted include particle image velocimetry (PIV), specially named “Rheo-PIV” (Rodríguez-González et al. 2010; Dimitriou et al. 2012; Pérez-González et al. 2012; Serrano-Aguilera et al. 2016), magnetic resonance imaging velocimetry (Jarny et al. 2005; Ovarlez et al. 2005), laser Doppler velocimetry (Quinzani et al. 1995; Rothstein and Mckinley 2002), and ultrasonic imaging velocimetry (Gurung et al. 2016).

In contrast to these types of velocimetry, ultrasonic Doppler velocimetry or ultrasonic velocity profiling (UVP) (Takeda 2012) offers ease of handling and access to opaque fluids. Also, UVP is being further developed in both hardware and software (Fischer et al. 2008; Meacci et al. 2016; Muramatsu et al. 2015), and we can expect in the near future greater sophistication in its methodology. Moreover, recent progress in combining it with Doppler optical coherent tomography has overcome several disadvantages of UVP in near-wall measurements of the velocity field (Salmela et al. 2013). UVP was applied to a circular Couette system (Murai 2012; Derakhshandeh and Vlassopoulos 2012) and also to pipe flow with measurements of the pressure drop along the pipe (Ouriev and Windhab 2002; Wiklund and Stading 2008). The latter technique has been termed the in-line UVP-PD method and has been recognized as a semi-standard evaluation tool in food rheology (Rao et al. 2014) as ultrasonic velocimetry has been applied avidly in the food processing industry.

Because of its spatio-temporal velocity profiling, UVP has also been explored in visualizing rheological behaviors (Shiratori et al. 2013). Our group has been developing ultrasonic spinning rheometry (USR) that uses such data to evaluate rheological properties modeled by equations of motion of fluid media and has extended its applicability to viscoelastic analyses of multiphase media including bubble suspensions.

This study evaluates the applicability of USR in linear viscoelastic analysis in general and bubble suspensions in particular. We investigate the influence of measurement noise on spatio-temporal velocity data measured by UVP that is required for a viscoelastic analysis. We propose a novel algorithm for USR applying the Fourier transform theory to the velocity data to achieve more stable analysis. The structure of this paper is as follows: USR including theory and fundamental measurement configuration is briefly summarized in “Ultrasonic spinning rheometry”. The applicability of the USR and the numerical experiments in investigating the influence of the measurement noise on USR are presented in “Influence of measurement error on USR”. The theory of “frequency-domain analysis” is described. Its applicability to viscosity analysis is evaluated in numerical experiments and on actual velocity data obtained from viscous oil treated as a Newtonian fluid. Then, linear viscoelasticity analysis using the algorithm on bubble suspension is performed in “Frequency-domain analysis”. Finally, concluding remarks are presented in “Conclusion”.

Ultrasonic spinning rheometry

Measurement configuration

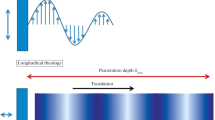
The USR process involves two main steps: the measurements of the velocity profile of test fluids placed in a cylindrical vessel and the post-processing of the velocity data to evaluate rheological properties. In preparation for explaining the post-processing, a brief explanation of the measuring of velocity profiles is given here. The basic configuration of the measurement (Fig. 1a) comprises an open-type cylindrical vessel of radius R filled with a test fluid rotating under set conditions. Measurements of the velocity are performed using an ultrasonic transducer (TDX) mounted on the outside of the cylinder. The measurement line for UVP (e.g., Takeda 2012) is set parallel to the centerline of the cylinder with a certain displacement of ${\Delta } y$ to measure the azimuthal component of velocity u; UVP measures the on-axis velocity component $u_{\xi }$ along the measurement line $\xi$, and thus, the azimuthal velocity component is given as u = u _ξ r/Δy when the radial velocity component is negligibly small. Test fluids are required to be seeded where there are no ingredients that can scatter ultrasonic waves. Further details of individual measurements are described elsewhere (Tasaka et al. 2015; Yoshida et al. 2017).

Fig. 1

Schematics of a the experimental setup showing the rotating cylinder and the measurement line for ultrasonic velocity profiling (UVP) and b the measurement volume of UVP

In measurements by UVP, representative velocities in the disk-shaped volume of the test sample are captured as on-axis velocity components at each radial position along the measurement line (Fig. 1b). The diameter and width of the measurement volume are determined from the size of the piezo-element in the transducers and the wavelength of the ultrasonic wave in the test fluids; typically, these are around 5 and 1 mm, respectively. Velocities $u(r, t)$ calculated from the on-axis velocity component measured in UVP at each volume are processed. They reflect flow behaviors determined by the local characteristics of the test fluids responding to cylinder motions. These characteristics include rheological characteristics, for example, shear-rate-dependent viscosity, viscoelasticity, and non-uniformity of ingredients and local structures. USR extracts from $u(r, t)$ the local characteristics with post-processing, which shall be summarized below.

USR concept and procedure

USR is concerned with deriving rheological characteristics from spatio-temporal velocity distributions measured by UVP.

Here we summarize the post-processing procedure used in USR. The rheological characteristics of fluids are reflected in the spatio-temporal velocity distributions which are governed by the equation of motions and the constitutive equations (in rheological modeling) describing the relationships between stress $\tau$, strain $\gamma$, and strain rate $\dot {{\gamma }}$. To simplify the model, we assume just two-dimensional one-directional flows in the azimuthal direction that can be realized in the setup mentioned in the last section. The corresponding equation of motion, Cauchy’s equation, is

$$ \rho\frac{\partial u}{\partial t} = \frac{\partial \tau}{\partial r} + \frac{2\tau}{r}, $$

(1)

where $\rho$ is the density of the fluid. To determine the rheological properties, Murai (2012) proposed minimizing a cost function expressed by the least-squares approximation,

$$ F(A, B, C, \cdots) = \left( \rho\frac{\partial u}{\partial t} - \frac{\partial \tau}{\partial r} - \frac{2\tau}{r} \right)^{2}, $$

(2)

where the parameters, $A, B, C, \cdots$, denote constants in rheological models representing rheological properties. In the equation above, $u(r, t)$ is given as measurement data in circular shear flows measured by UVP, and $\tau$ is also calculated from $u(r, t)$ through a rheological model adopted.

Influence of measurement error on USR

Viscoelastic analysis of bubble suspensions

We performed an analysis using the above equations of motion to evaluate viscoelasticity of bubble suspensions, having examined their effective Newtonian viscosity in a previous paper (Tasaka et al. 2015). Experiments measuring velocity profiles were performed with a cylinder of inner diameter $2R = 145$ mm filled with 1000 mm²/s silicone oil to a depth of 330 mm. Small bubbles of around 1 mm diameter were dispersed in the fluid layer to a volume fraction of about 2%. The cylinder underwent sinusoidal oscillations of frequency $f_{0} = 1$ Hz and angular amplitude = 90^∘. The spatio-temporal velocity profiles were captured in ultrasonic velocimetry at a spatial resolution of 0.99 mm along the measurement axis and a time resolution of 30 ms.

We recall Cauchy’s equation of motion, Eq. 1, and adopt Maxwell’s spring-dashpot model in describing viscoelastic fluids,

$$ \tau + \frac{\mu}{E}\frac{\partial \tau}{\partial t} = \mu \left( \frac{\partial u}{\partial r} -\frac{u}{r} \right), $$

(3)

in establishing the simplest model to describe linear viscoelasticity, which is evaluated by first determining viscosity $\mu$ and elasticity E from measurement data of $u(r, t)$. A suitable set of $\mu$ and E that satisfy these equations is derived as a constraint condition on $\tau$. Mathematically, the calculation is

$$\begin{array}{@{}rcl@{}} &&\min_{\tau, \mu, E} {\int}_{r} {\int}_{t} \left[\tau + \frac{\mu}{E}\frac{\partial \tau}{\partial t} - \mu \left( \frac{\partial u}{\partial r} -\frac{u}{r} \right) \right]^{2}dtdr, \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} &&\mathrm{s.t.:}\ \rho\frac{\partial u}{\partial t} - \frac{\partial \tau}{\partial r} - \frac{2\tau}{r} = 0. \end{array} $$

(5)

In terms of difference expressions for $u(r, t)$ and $\tau (r, t)$, these become

$$\begin{array}{@{}rcl@{}} &&\min_{\tau, \mu, E} \sum\limits_{i} \sum\limits_{j} \left[\tau_{i,j} + \frac{\mu}{E}\frac{\tau_{i + 1,j} - \tau_{i,j}}{{\Delta} t}\right.\\ &&\qquad\qquad\qquad- \left. \mu \left( \frac{u_{i, j + 1} - u_{i,j}}{{\Delta} r} - \frac{u_{i,j}}{r_{j}} \right) \right]^{2}, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} &&\mathrm{s.t.:}\ \rho \frac{u_{i + 1, j} - u_{i,j}}{{\Delta} t} - \frac{\tau_{i,j + 1} - \tau_{i,j}}{{\Delta} r} - \frac{2\tau_{i,j}}{r_{j}} = 0, \end{array} $$

(7)

where ${\Delta } t$ and ${\Delta } r$ correspond to the spatial and radial resolutions, respectively, of the velocity profile measurements. More precisely, the radial positions are calculated from the positions on the measurement line with $\xi$ and ${\Delta } r$ varying depending on radial positions.

The calculations described above are performed after applying a filter to $u(r, t)$ to suppress the influence of measurement noise. Here we adopt a Savitzky–Golay FIR smoothing filter (Savizky and Golay 1964) with various filter sizes in time and space to examine the influence of the filter. As radial variations of the viscoelasticity are expected, a narrow radial range of velocity profiles in $r/R$ = 0.86–0.96 are analyzed over a period of 4 s. The evaluation results for viscosity $\mu$ and elasticity E under different filter sizes are summarized in Table 1. The phase difference in linear viscoelasticity $\delta$ is defined as the fraction of storage modulus to loss modulus and has the following relation with elasticity and viscosity in the Maxwell model:

$$ \tan \delta = \frac{G^{\prime\prime}}{G^{\prime}} = \frac{E}{2\pi f_{0} \mu}. $$

(8)

Table 1 Evaluation results of viscosity $\mu$ and elasticity E, with phase difference in linear viscoelasticity δ for the differently filtered data of u(r,t) for measurements ranging from r/R = 0.86 to r/R = 0.96 over a period of 4 s; N _t and N _s correspond to the number of time and space points used in filtering, respectively

Phase values of around 90^∘ mean that a fluid is close to a pure viscous body and smaller values indicate larger elastic contributions to stress in the fluids.

From the various analyses with different filter sizes, designated by the serial number in Table 1, the evaluation results of $\mu$ and E are widely scattered. Taking similar values for different analyses, the phase difference $\delta$, however, is stable against the variation in filter size. This trend may arise from two factors: one is that $\mu$ and E appear as a fraction (or product) in the equation to be analyzed, and the other is that the influence of measurement error and noise on $u(r, t)$ including the influence of filtering buries local minima on the surface of the cost function, Eq. 6, in parameter space. We therefore evaluated the influence of noise in determining the local minima of the cost function.

Numerical evaluation of influence of noise

For this purpose, we reduce the problem to a Newtonian viscosity analysis. For Newtonian fluids, the equation of motion in Eq. 1 becomes

$$ \frac{\partial u}{\partial t} = \nu \left( \frac{\partial^{2} u}{\partial r^{2}} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{r^{2}} \right) = \nu D_{r}u, $$

(9)

where $\nu$ is the kinematic viscosity and $D_{r}$ is a differential operator with respect to r defined as

$$D_{r} = \frac{\partial^{2}}{\partial r^{2}} + \frac{1}{r}\frac{\partial}{\partial r} - \frac{1}{r^{2}}. $$

This can be reduced into the cylindrical Bessel differential equation by separation of variables about t and r. Then, it can be solved by inserting the infinite series

$$\begin{array}{@{}rcl@{}} u(r, t) &=& \frac{U}{{{\Phi}_{R}^{2}} + {{\Psi}_{R}^{2}}} \left[({\Phi} {\Phi}_{R} + {\Psi} {\Psi}_{R})\sin \omega t \right. \\ &&\left. +\, ({\Phi}_{R} {\Psi} - {\Phi} {\Psi}_{R}) \cos \omega t \right] , \end{array} $$

(10)

where U is the angular velocity of the side wall, and

$$\begin{array}{@{}rcl@{}} {\Phi} (r) = \sum\limits_{m = 0}^{\infty} \phi_{m}(r),\ \ {\Phi}_{R} = \sum\limits_{m = 0}^{\infty} \phi_{m}(r=R), \\ {\Psi} (r) = \sum\limits_{m = 0}^{\infty} \psi_{m}(r),\ \ {\Psi}_{R} = \sum\limits_{m = 0}^{\infty} \psi_{m}(r=R), \end{array} $$

and

$$\begin{array}{@{}rcl@{}} \phi_{m}(r) &=& \frac{2^{m}}{m!(m + 1)!} \left( \frac{kr}{2} \right)^{2m + 1}f_{m} , \ \ k = \sqrt{\frac{\omega}{2\nu}}, \\ f_{m} &=& \left\{\begin{array}{ll} (-1)^{(m + 2)/2}&: m = \text{even number}\\ (-1)^{(m + 1)/2}&: m = \text{odd number}\\ \end{array}\right. \\ \psi_{m}(r) &=& \frac{ 2^{m}}{m!(m + 1)!} \left( \frac{kr}{2} \right)^{2m + 1}g_{m}, \\ g_{m} &=& \left\{\begin{array}{ll} (-1)^{m/2}&: m = \text{even number}\\ (-1)^{(m + 1)/2}&: m = \text{odd number}\\ \end{array}\right.. \end{array} $$

Details of the derivation are described in Tasaka et al. (2015). We performed numerical experiments to evaluate the influence of measurement noise using this exact solution, Eq. 10, with a sufficiently large number of terms and $f_{0} = \omega /(2\pi ) = 1$ Hz.

To represent measurement noise, and in particular the typical spikey noise seen in UVP measurements, the Mersenne twister method (Saito and Matsumoto 2008) was used to artificially generate the random noise by modifying the standard deviation $\sigma _{\mathrm {N}}$ in regard to the noise level. The cost function to be minimized is derived from Eq. 9 in differential form,

$$\begin{array}{@{}rcl@{}} F(\nu) &=& \sum\limits_{r,t}\left[\!\frac{u_{i + 1,j}\,-\,u_{i,j}}{{\Delta} t} \,-\, \nu \left( \!\frac{u_{i,j + 1} \,-\, 2u_{i,j} \,+\, u_{i,j-1}}{{{\Delta} r^{2}}} \right. \right. \\ &&\quad\quad\,+ \left.\left. \frac{u_{i,j + 1} - u_{i,j}}{2r_{j}{\Delta} r} - \frac{u_{i,j}}{{r_{j}^{2}}} \right) \right]^{2}. \end{array} $$

(11)

The correct value for the kinematic viscosity is set at $\nu _{0} = 1000$ mm²/s, and the cost function is calculated over the range $\nu =$ 800–1200 mm²/s in increments of ${\Delta } \nu = 4$ mm²/s over the radial range $r/R =$ 0.95–0.98. The dependence of the cost function on $\nu$ (Fig. 2) is calculated from the exact solution without noise using Eq. 11; note that $F(\nu )$ has been normalized by the number of velocity data, $N_{\text {total}}$, used for the calculation. In the range explored for $\nu$, the cost function has a unique minimum corresponding to $\nu _{0}$, signifying that the methodology to evaluate $\nu$ from spatio-temporal velocity distributions works well in instances without noise.

Fig. 2

Variation of the cost function with ν around minimum setting value of ν₀ = 1000 mm²/s

In assessing the influence of noise on the evaluation of $\nu$, the variation of the cost function is investigated near where it takes a minimum value. Here, Gaussian noise of zero-mean is generated at every data point of $u(r, t)$ and is added to the velocity data. Noise level σ_N is given as the fraction normalized by the local maximum velocity $U_{\max }(r)$. The actual noise level on $u(r, t)$ measured by UVP is at least larger than 0.1% (σ_N/U_max(r) > 10^− 3). The results obtained from the velocity data calculated from the exact solution in Eq. 10 with different time resolutions, ${\Delta } t$, $f_{0}{\Delta } t = 0.03$ and 0.005, are plotted in Fig. 3. Here, fitted parabolic curves, obtained using the least-squares method, have been superimposed on the plots. The viscosities evaluated decrease monotonically with respect to $-\sigma _{\mathrm {N}}^{2}$ for both time resolutions and have large deviations even at relatively small noise levels of around 0.01% in $\sigma _{\mathrm {N}}/U_{\max }(r)$. For larger ${\Delta } t$, there is less influence from the added noise because enhancements of noise contributed by the numerical differentials are smaller.

Fig. 3

Estimated values of ν for different noise levels σ_N obtained using two different sampling times, without POD filtering and frequency-domain analysis; the solid and dashed lines represent fitted parabolic curves of the plots obtained using the least-squares approximation

The monotonic decrease of $\nu$ may be explained as larger noise amplification in the radial derivatives in Eq. 9, especially the second-order derivative (the other two terms produce no strong impact on noise transfer). The radial derivative term in Eq. 11 always has a larger deviation from the correct values without noise than the time derivative term, because of the second-order derivative in the radial term. To satisfy the balance of equation, the estimated $\nu$ must be smaller. By simplifying the equation for the cost function, Eq. 11, this is modeled simply as

$$ F({\Delta} \nu, \epsilon) = \sum \left[ A - (\nu_{0} + {\Delta} \nu)B\epsilon \right]^{2} $$

(12)

where A and B are values of the differential calculations in condition without noise, so that $A \approx \nu _{0} B$, and ${\Delta } \nu$ and $\epsilon$ are the deviations from $\nu$ and the noise amplification rate, $\epsilon > 1$. The local minimum of the cost function is found to be $\nu _{0} + {\Delta } \nu$ satisfying the relation

$$\frac{\partial F}{\partial {\Delta} \nu}= -2\sum AB\epsilon + 2(\nu_{0} + {\Delta} \nu)\sum B^{2}\epsilon^{2} = 0. $$

Assuming $A = \nu _{0} B$, the estimated value from the preceding condition is a fraction of the correct value of $\nu$, $\nu _{0}$, specifically

$$ \frac{\nu_{0}+{\Delta} \nu}{\nu_{0}} = \frac{\sum B^{2} \epsilon}{\sum B^{2} \epsilon^{2}}. $$

(13)

This fraction is always smaller than unity. That is, the monotonic decreasing trend in $\nu$ stems from the enhancement in noise from the second-order derivative in the radial direction.

From Fig. 3, the influence of measurement noise on the evaluation of $\nu$ is significant and non-negligible, and therefore, eliminating noise from the velocity data is required. From the standard treatment of measured UVP data, filtering based on the (snapshot) proper orthogonal decomposition (POD) (Sirovich 1987) provides an effective solution in achieving this purpose (Takeda 1999; Furuichi et al. 2003; Tasaka et al. 2016). POD is good and objective at extracting organized flow structures. In the present configuration, the flows are well-organized structures and unorganized components are filtered out as noise. From Fig. 3, the present POD filtering can suppress the influence of noise, but there is still a certain influence of noise remaining in the evaluation. Here we remark that, after the filtering, data with a fine time resolution provides much better results than rougher ones. This is because the enhancement of noise by taking numerical differentials is reduced by POD filtering, and the fine time resolution now can provide better estimation of the differentials.

Frequency-domain analysis

As examined above, the influence of noise and its enhancement using numerical differentials cannot be avoided completely by filtering the velocity data. Instead, here we propose a novel algorithm to evaluate rheological properties from the velocity data employing the equation of motion as the method of analysis in the frequency domain free of difference calculation.

Theory

Taking the Fourier transform with respect to t, Eq. 3 becomes

$$ \hat{\tau} + i\omega \frac{\mu}{E} \hat{\tau} = \mu\left( \frac{\partial \hat{u}}{\partial r} - \frac{\hat{u}}{r}\right), $$

(14)

where the Fourier transform is denoted

$$ \hat{\tau}(r, \omega) = \mathcal{F}[\tau(r, t)], \ \hat{u}(r, \omega) = \mathcal{F}[u(r, t)]. $$

(15)

The Fourier transform changes the differential equation into an algebraic equation that can be solved for $\hat {\tau }$,

$$ \hat{\tau}(r, \omega) = \frac{\mu\left( \frac{\partial \hat{u}}{\partial r} - \frac{\hat{u}}{r}\right) \left( 1-i\omega \frac{\mu}{E}\right)}{1+ \left( \omega \frac{\mu}{E} \right)^{2}}. $$

(16)

Cauchy’s equation of motion, Eq. 1, is also converted into

$$ i\omega \rho \hat{u} = \left( \frac{\partial}{\partial r} + \frac{2}{r} \right) \hat{\tau}. $$

(17)

Using Eqs. 16 and 17, finding $\mu$ and E become an optimization problem for the cost function,

$$ F(E, \mu; r) = {\int}_{0}^{{\Omega}} \left[i\omega \rho \hat{u} - \left( \frac{\partial }{\partial r} + \frac{2}{r} \right)\hat{\tau} \right]^{2} d\omega. $$

(18)

That is, $\mu$ and E are determined by $\min _{\mu , E} F(E,\mu ; r)$. Inside the square bracket of Eq. 18 is a complex function that needs to be decomposed into its real and imaginary parts for the numerical calculation. We define

$$ \hat{\tau}(r, \omega) = \frac{\mu}{1+ \left( \omega \frac{\mu}{E} \right)^{2}}\left[R_{e}(r, \omega) + iI_{m}(r, \omega) \right], $$

(19)

where

$$\begin{array}{@{}rcl@{}} R_{e}(r, \omega) = \partial_{r} \Re[\hat{u}] - \frac{1}{r}\Re[\hat{u}] + \omega \frac{\mu}{E} \left( \partial_{r} \Im [\hat{u}] - \frac{1}{r} \Im[\hat{u}] \right), \\ I_{m}(r, \omega) = \partial_{r} \Im[\hat{u}] - \frac{1}{r}\Im[\hat{u}] - \omega \frac{\mu}{E} \left( \partial_{r} \Re [\hat{u}] - \frac{1}{r} \Re[\hat{u}] \right). \end{array} $$

Substituting these into Eq. 18, the integrand becomes

$$\begin{array}{@{}rcl@{}} \!\left[\!i\omega \rho \hat{u} \,-\, \left( \!\frac{\partial }{\partial r} \,+\, \frac{2}{r} \right)\!\hat{\tau} \!\right]^{2} &\,=\,& \left[\!\omega \rho \Im[\hat{u}] + {\Gamma} \!\left( \!\frac{\partial }{\partial r} \,+\, \frac{2}{r} \right)\!R_{e} \right]^{2} \\ &&+ \!\left[\!\omega \rho \Re[\hat{u}] \,-\, {\Gamma} \!\left( \!\frac{\partial }{\partial r} \,+\, \frac{2}{r} \!\right)\!I_{m} \!\right]^{2}\!, \end{array} $$

(20)

where

$${\Gamma} = \frac{\mu}{1+ \left( \omega \frac{\mu}{E} \right)^{2}} . $$

Viscometry

To evaluate the applicability of the frequency-domain analysis proposed in this study, we perform a viscosity analysis on both velocity data created from the exact solution in Eq. 10 with artificial noise and UVP measurement data.

Taking the Fourier transform of the equation for Newtonian fluids yields

$$ i\omega \hat{u} = \nu D_{r} \hat{u}, \ \ \hat{u} = R_{u}(r, \omega) + iI_{u}(r, \omega). $$

(21)

The cost function defined in Eq. 18 becomes

$$\begin{array}{@{}rcl@{}} F\!(\nu; r)\! &=& {\int}_{{\Omega}} \left[i\omega \hat{u} - \nu D_{r} \hat{u} \right]^{2} d\omega \\ &=& {\int}_{{\Omega}} \left[\!\left( \nu D_{r} R_{u} \,+\, \omega I_{u} \right)^{2} \,+\, \left( \omega R_{u} \,-\, \nu D_{r} I_{u} \right)^{2} \right]\!d\omega. \end{array} $$

(22)

The actual flows in the USR system are time periodic and discrete Fourier transform (DFT) is applicable for the analysis. From the definition of the Fourier series expansion,

$$ u(r, t) = \frac{a_{0}(r)}{2} + \sum\limits_{k = 1}^{N}\left[a_{k}(r)\cos {\Delta} \omega kt+b_{k}(r)\sin {\Delta} \omega kt \right], $$

(23)

where

$$ {\Delta} \omega = 2\pi {\Delta} f. $$

(24)

The cost function is expressed as

$$ F(\nu; r) = \sum\limits_{k = 1}^{N}\left( {A_{k}^{2}} + {B_{k}^{2}} \right), $$

(25)

where

$$ A_{k}(r) = {\Delta} \omega kb_{k} - \nu D_{r} a_{k}, \ B_{k} = {\Delta} \omega k a_{k} + \nu D_{r} b_{k}. $$

(26)

The range of frequencies (or range of k) for the summation above is determined from the sampling frequency on $u(r, t)$, ${\Delta } f$, and the number of data, $N,$ from ${\Delta } f$ (k = 1) to $N{\Delta } f$ (k = N). Taking a wide range of frequencies, however, would induce noise caused by measurement error that is not related to the cylinder oscillation. A narrow range, $k_{1}{\Delta } f < f_{0} < k_{2}{\Delta } f$, is set around the driving frequency of the cylinder oscillation $f_{0}$. The cost function is little modified as

$$ F_{f_{0}}(\nu; r) = \sum\limits_{k=k_{1}}^{k_{2}}\left( {A_{k}^{2}} + {B_{k}^{2}} \right). $$

(27)

To avoid the propagation of measurement noise caused by the numerical differentials of r included in the differential operator $D_{r}$, an M th power series approximation on $a_{k}(r)$ and $b_{k}(r)$ is introduced,

$$ a_{k}(r) = \sum\limits_{m = 0}^{M} \alpha_{m} r^{m}, \ \ b_{k}(r) = \sum\limits_{m = 0}^{M} \beta_{m} r^{m}. $$

(28)

Substituting this into definitions of $A_{k}$ and $B_{k}$, Eq. 26, provides

$$\begin{array}{@{}rcl@{}} A_{k}(r) &=& {\Delta} \omega k \sum\limits_{m = 0}^{M} \beta_{m} r^{m} - \nu \sum\limits_{m = 0}^{M} (m^{2}-1)\alpha_{m} r^{m-2}, \end{array} $$

(29)

$$\begin{array}{@{}rcl@{}} B_{k}(r) &=& {\Delta} \omega k \sum\limits_{m = 0}^{M} \alpha_{m} r^{m} + \nu \sum\limits_{m = 0}^{M} (m^{2}-1)\beta_{m} r^{m-2}. \end{array} $$

(30)

We perform numerical experiment as in “Numerical evaluation of influence of noise” to check the applicability of the present theory and procedure. The velocity data is processed by DFT, and $a_{k}$ and $b_{k}$ in the Fourier series are approximated by fifth-order polynomials (i.e., $M = 5$ in Eq. 28). In the power spectrum of $\sqrt {{a_{k}^{2}}+{b_{k}^{2}}}$, there is a sharp peak corresponding to the oscillation frequency $f_{0}$. Because the frequency resolution, ${\Delta } f$, is determined by the number of data and the time resolution, the peak frequency $f_{\mathrm {c}}$ does not always coincide with $f_{0}$ and spreads over several frequencies. In the present case, $f_{\mathrm {c}} = 1.0101$ Hz and three frequencies nearby contribute more than 97% of the total fluctuation in kinetic energy. Within the frequency band, $k_{1}$–k₂ in Eq. 27, two conditions, f = f_c ∼ f₀ and $f = f_{\mathrm {c}} \pm {\Delta } f$, are examined. Nevertheless, there is no quantitative difference in values of ν associated with the conditions. Hence, we adopt the condition $f = f_{\mathrm {c}}$ from here on. The results of evaluation of kinematic viscosity at different noise levels are summarized in Fig. 3 with the original results (without noise treatment) and the POD-filtered velocity data. The value of $\nu$ evaluated in the present frequency-domain analysis stays the same regardless of the noise level, whereas the others decrease with increasing the noise level. The frequency-domain analysis provides slightly smaller values than the others and the correct value, ν₀ = 1000 mm²/s, in relatively low noise conditions. This is mainly caused by small disagreement between $f_{\mathrm {c}}$ and $f_{0}$ due to the sampling frequency and sampling data number of $u(r, t)$. Nevertheless, it produces the small deviation even at relatively large noise levels than expected in actual situations with UVP measurements.

Application of viscometry

The frequency-domain analysis is applied on spatio-temporal velocity measurement data obtained from silicone oil (ν = 300 mm²/s at 25 ^∘C) and presented in Yoshida et al. (2017) with an evaluation of its kinematic viscosity using phase information. A 145-mm-diameter acrylic cylinder filled with oil was periodically oscillated with $f_{0} =$ 1 Hz frequency and through an 80^∘ angular amplitude. The measurement line of the velocity profiles was set at ${\Delta } y$ = 15 mm; the UVP was performed with a 30-ms time resolution and a 0.62-mm spatial resolution (measurement direction). Figure 4 shows the spatio-temporal velocity distribution over three oscillation cycles. The velocity variation appears smooth compared with typical velocity profile measurements; considerable roughness is apparent in comparison with ideal velocity profiles.

Fig. 4

Spatio-temporal velocity distribution measured for 300 mm²/s silicone oil in a cylinder oscillating at f₀ = 1 Hz frequency through an 80^∘ angular amplitude

We processed the velocity distribution using the DFT method and obtained Fourier coefficients $a_{k}$ and $b_{k}$ as radial profiles. Then, a fifth-order polynomial fitting was performed on the profiles with $f = f_{\mathrm {c}} \approx f_{0}$ to ensure a smooth radial dependence (Fig. 5). An unavoidable characteristic of the UVP measurement is relatively large deviations near the boundaries around $r/R = 1$. The deviations appear mainly in $b_{k}(r)$, and therefore, we have omitted these points in the fitting. The fitted curves approximate the plotted data well apart from data points for $b_{k}$ near the cylinder wall. Following the process established in the last section, the cost function, Eq. 27, was calculated at each radial position in the range, 100 ≤ ν ≤ 500, and is displayed as a distribution over the $\nu$–r plane (Fig. 6). The local viscosity is taken to be the local minimum of the cost function at each radial position. The radial profiles of the cost function form a “valley” with $\nu$ uniquely determined. This valley is shallower in the inner region of the cylinder because the amplitude of the velocity fluctuations is smaller and information is not sufficient for the evaluation.

Fig. 5

Fifth-order polynomial fittings (white curve) of the radial profiles for a _k and b _k , where red and blue plots represent the original discrete values of a _k and b _k , respectively

Fig. 6

Gray-scale distribution of the cost function F(r;ν)

From the frequency-domain analysis, the radial profile of $\nu$ was estimated (Fig. 7) using the polynomial approximation and compared with $\nu$ estimated from a phase-slope analysis on the same data given in Yoshida et al. (2017). The local slope of the phase delay of the velocity fluctuation with respect to the cylinder oscillation reflects the local viscosity, and comparing the phase slopes obtained from the analytical solution, Eq. 10, and experimental data yields the local kinematic viscosity. Similar values were obtained although with deviations; $\nu$ given by the phase analysis exhibit large deviations in the interior of the cylinder, whereas those obtained from the frequency-domain analysis yield similar values. The phase analysis also employs the Fourier transform and suppresses the influence of measurement error on the velocity fluctuations. Nevertheless, the phase information extracted from very small velocity fluctuations is not representative of the flow, and hence, calculations using numerical differentials propagate errors. In contrast, profiles of the Fourier coefficients at the main frequency retain almost all information in representing the flow, and thus, this method provides an advantage when analyzing viscometric data. Further, returning to the original purpose of the study, the frequency-domain analysis is applicable to linear viscoelastic analysis using the rheological model. We remark that the evaluation of the kinematic viscosity from the experimental data of 300 mm²/s oil using the cost function in Eq. 11 is unable to determine the local minimum of $\nu$ over the range $100 \le \nu \le 500$ even with POD filtering.

Fig. 7

Radial profiles of the estimated kinematic viscosity from a frequency-domain analysis (solid line) and for comparison a phase profile analysis (circles) from Yoshida et al. (2017)

Linear viscoelastic analysis of bubble suspension

According to the same idea on the viscometry adopting Fourier series expansion of $u(r, t)$ (Eq. 23) and power series approximation on the Fourier coefficients (Eq. 28), the cost function for the linear viscoelastic analysis in Eq. 18 is modified into

$$ F_{f_{0}}(E, \mu; r) = \sum\limits_{k=k_{1}}^{k_{2}}\left( {A_{k}^{2}} + {B_{k}^{2}} \right), $$

(31)

where

$$\begin{array}{@{}rcl@{}} A_{k}(r) &=& \sum\limits_{m = 0}^{M}\left[-\rho {\Delta} \omega k \beta_{m} r^{m} \right. \\ &&\left. +\, {\Gamma} (m^{2}-1)(\alpha_{m} -{\Delta} \omega k \mu \beta_{m}/E)r^{m-2} \right], \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} B_{k}(r) &=& \sum\limits_{m = 0}^{M}\left[\rho {\Delta} \omega k \alpha_{m} r^{m} \right. \\ &&\left. +\, {\Gamma} (m^{2}-1)(\beta_{m} + {\Delta} \omega k \mu \alpha_{m}/E)r^{m-2} \right] . \end{array} $$

(33)

Fig. 8

Variations of viscosity μ and phase difference in linear viscoelasticity δ with respect to shear rate $\dot {\gamma }$ for 1 wt% polyacrylamide aqueous solution, where μ calculated by the phase profile analysis (Yoshida et al. 2017) from the same velocity data is also plotted

Fig. 9

Fifth-order polynomial fittings (white curve) of the radial profiles for a _k and b _k obtained in the bubble suspension, where red and blue plots represent the original discrete values of a _k and b _k , respectively

The algorithm is examined on an analysis of a polyacrylamide aqueous solution (1 wt%), which has shear-rate-dependent viscosity and elasticity, to check its applicability for more complex fluids before performing linear viscoelastic analysis of bubble suspensions. Spatio-temporal velocity information was captured in the same system of oscillating cylinder (see Fig. 1) that was also used in our previous studies (Tasaka et al. 2015; Yoshida et al. 2017). The setting parameters for the oscillation are $f_{0} = 1$ Hz (in frequency) and ${\Theta } = 90^{\circ }$ (in amplitude). For the analysis, the velocity data was processed by the DFT method to derive Fourier coefficients $a_{k}(r)$ and $b_{k}(r)$ in Eqs. 32 and 33 corresponding to the Fourier component of $f = f_{0}$. Fifth-order power series approximation is then adopted to approximate their radial profiles. In the evaluation of the cost function in Eq. 31 for the linear viscoelastic analysis, the phase difference in linear viscoelastic analysis $\delta$ is used as a parameter instead of E. Viscosity $\mu$ and $\delta$ are obtained at each radial position by the analysis as shown in Fig. 8; the values are plotted against the amplitude of shear-rate variations $\dot {\gamma }_{0}$, which is given from the Fourier coefficients and calculated using power series approximation in Eq. 28 as

$$ \dot{\gamma}_{0} \,=\, \sqrt{\!\left[\sum\limits_{m = 0}^{M}(m\,-\,1)\alpha_{m}r^{m-1}\!\right]^{2} \,+\, \left[\sum\limits_{m = 0}^{M}(m-1)\beta_{m}r^{m-1}\right]^{2} } . $$

(34)

In the figure, the viscosity calculated by phase profile analysis (Yoshida et al. 2017) from the same velocity data is also plotted for comparison. The viscosity evaluated by the linear viscoelastic analysis gradually decreases with $\dot {\gamma }_{0}$ and expresses shear thinning characteristics of the solution. Along the decrease of viscosity, $\delta$ approaches to 90^∘, meaning that the solution loses elastic property toward a pure viscous body.

We now come back to the linear viscoelastic analysis of a bubble suspension by the frequency-domain analysis established above. Fourier coefficients a _k (r) and $b_{k}(r)$ in Eqs. 32 and 33 are given by the DFT method performed on the velocity data of the bubble suspension used in “Viscoelastic analysis of bubble suspensions”. Then, fifth-order power series approximation is performed on radial profiles of the coefficients corresponding to f = f_c ≈ f₀ (1 Hz). The profiles are approximated well as shown in Fig. 9. In the calculation of the cost function, phase delay of the linear viscoelasticity described in Eq. 8 is changed as a parameter instead of E in the range from $50^{\circ }$ to $90^{\circ }$ with an increment of 0.1^∘. Exploring the range of $\mu$ was set around the original viscosity of the base liquid of the suspension, 1000 mm²/s silicone oil, $\mu _{0} = 0.97$ Pas, from 0.5 to 1.5 Pas with an increment of 0.005 Pas.

An example of the calculated cost function is shown in Fig. 10 as the distribution of F on the $\delta$–μ plane for $r = 0.9R$. The distribution is expressed in logarithmic gray scale, and there is a single local minimum point; values of $\delta$ and $\mu$ are given as values on this point. At least in the range of $\delta$ and $\mu$ we examined, the cost function increases monotonically from the local minimum point, and the values are uniquely given. For $r/R < 0.9$, the local minimum point attaches to the boundary of $\delta = 90^{\circ }$, but uniqueness of the solution is unchanged.

Fig. 10

Gray-scale distribution of the cost function, F(δ,μ;r = 0.9R), for the bubble suspension

Results of estimations of $\delta$ and $\mu$ according to the cost function calculated at each radial position from $r/R = 0.6$ to $r/R = 0.95$ are summarized in Table 2. Elasticity E is calculated through Eq. 8 with $\mu$ and $f_{0}$ in cases that δ < 90°. $|\mu ^{*}|$ denotes effective complex viscosity defined as

$$ |\mu^{*}| = \frac{\mu}{\sqrt{1+(\omega\mu/E)^{2}}}. $$

(35)

The linear viscoelastic analysis separated influences of unsteady bubble deformations in the oscillating shear flows on the momentum propagation into viscous and elastic contributions. In the table, $\delta$ takes 90^∘ without a region $r/R \ge 0.9$, and the elastic contribution appears in the region. This is reasonable because the capillary number exceeds effectively the critical capillary number to allow bubble deformations in this range, and the deformation bubbles existing nearby the wall show considerable deformations (Tasaka et al. 2015). In the oscillating shear flows, the bubbles experience periodically strong shear and relaxation. The elastic effect may be provided by restoring the original spherical shape in the relaxation. Effective viscosity normalized by original viscosity of the oil, $|\mu ^{*}|/\mu _{0}$, distributes around unity within the deviation order of the volume fraction of bubbles, 2% for $r/R \le 0.8$. This is in good agreement with knowledge of effective viscosity for spherical bubbles.

Table 2 Evaluation results of viscosity $\mu$, phase difference in linear viscoelasticity δ, and elasticity E calculated from μ and δ through Eq. 8 at different radial position r/R, where the amplitude of local shear-rate variation $\dot {\gamma }_{0}$ is calculated from the velocity data through Eq. 34, and |μ^∗| indicates effective viscosity normalized by the original viscosity value of the oil, μ₀ = 0.97 Pas

Conclusion

To achieve a stable evaluation of the linear viscoelasticity in bubble suspensions as complex multiphase fluids using USR, we assessed the influence of measurement noise enhancement in the evaluation of rheological properties using the equation of motion with measurement data of spatio-temporal velocity fluctuations. By avoiding calculations of numerical differential using velocity data, a frequency-domain analysis was proposed for applications in linear viscoelastic analysis. By taking the Fourier transform of the equation of motion and the constitutive equations (the rheological models), time derivatives are converted to algebraic calculations, and further, approximating the radial profiles of Fourier coefficients by finite power series enables an evaluation of the rheological properties without requiring calculation of numerical differentials. In rheology, this novel combination of techniques was scrutinized using numerical experiments by considering noise artificially generated in viscometric data. The present method provided better estimates of viscosity in comparison with dealing with raw velocity data and POD filtering. The technique was also applied to actual velocity data measured in 300 mm²/s silicone oil as a Newtonian fluid, and the estimations were in reasonable agreement with previous results. The frequency-domain analysis was then extended to the linear viscoelastic analysis, and its applicability was examined on a polyacrylamide aqueous solution, which is a shear thinning, viscoelastic fluid. The analysis finally achieved separation of influences of unsteady bubble deformation into viscous and elastic contributions on the momentum propagation.

The algorithm proposed here is aptly applicable in a wider range of velocity-profiling rheometry. And, it may be able to support to evaluate, e.g., fluids taking shear banding effects and solutions with distributions of concentration.