1 Introduction

1.1 Effective viscosity

Fluid flows of multi-phase media and their physical properties in bulk have been investigated in engineering fields, to improve transport efficiency in pipe lines, elucidate circulation mechanisms in dams, and in other applications. Our group has focused on modification of the effective viscosity of bubbly flows (gas bubbles dispersed in continuous liquid media) which may decrease the frictional drag acting in large vessels with modifications of the vortex structures in turbulent boundary layers. There are many studies on modifications of vortex structures adding bubbles to investigate drag reduction of ship hulls (Lu and Tryggvason 2007; Ceccio 2010). Investigations of the ideas of bulk rheology of bubble suspensions to understand the mechanisms of the modification are, however, still few in spite of the importance of a better understanding. This study aims to elucidate the modifications of rheological properties, effective viscosity especially, of bubble suspensions in bulk volumes arising from non-equilibrium bubble deformations in oscillatory shear flows.

An early study dealing with the effective viscosity of dilute suspensions was performed by Einstein (1906) around a century ago. Here, the effective viscosity of dilute particle suspensions, \(\mu ^*\), was derived theoretically to be

$$\begin{aligned} \eta = \frac{\mu ^*}{\mu } = 1 + \frac{5}{2}\alpha , \end{aligned}$$
(1)

The effective viscosity takes the form of the relative viscosity normalized by the viscosity of the continuous phase medium, \(\mu \) and is represented as a function of the volume fraction of the dispersed phase, \(\alpha \). Taylor (1932) generalized the equation to be applicable to bubble suspensions as

$$\begin{aligned} \eta = \frac{\mu ^*}{\mu } = 1 + \frac{\mu + 5\mu _{\rm D}/2}{\mu + \mu _{\rm D}}\alpha = 1 + \alpha \quad (\mu _{\rm D} \ll \mu ), \end{aligned}$$
(2)

where \(\mu _{\rm D}\) represents the viscosity of the dispersion phase. The effective viscosity of bubble suspensions can be obtained by assuming that \(\mu _{\rm D}\) is much smaller than the viscosity of the continuous phase. Applications of Eq. (2) have provided approximations of the effective viscosity, also in three-dimensional numerical simulations (Kuwagi and Ozoe 1999). Such estimates, however, assume specific conditions of the bubble suspensions, like (1) a very low void (volume) fraction (dilute conditions), (2) a small slip velocity of bubbles against the ambient fluid (fluid surrounding the bubbles), and (3) spherical bubbles. In actual cases of turbulent flows, these conditions are rarely satisfied however. As a result, better estimates of the effective viscosity are necessary for cases to better describe the situation where the conditions are not satisfied. For condition (1), the effective viscosity deviates from linearity for \(\alpha \) exceeding 30 %, where it increases exponentially (Mooney 1951; Vand 1948). For (2), the diffusion coefficient of the momentum is assumed as fluctuating in space and time for larger slip velocities, and so, no unique effective viscosity can be proposed (Murai and Oiwa 2008; Tokuhiro et al. 1998). For (3), the surface tension of bubbles and their deformation are very important: Shear stresses acting on bubble suspensions in bulk are modified by applying a sufficiently high rate of strain. The bubble deformation in a simple steady shear stress field has a unique relation with the shear rate around the bubble and is expressed as a function of the capillary number,

$$\hbox{Ca} = \frac{\mu d\dot{\gamma }}{\sigma }$$
(3)

where \(\sigma \) is the surface tension on the bubble interface, \(\mu \) is the viscosity of the liquid media, \(d\) is bubble diameter, and \(\dot{\gamma }\) is strain rate, respectively. For small \(\hbox{Ca}\) conditions, bubbles are nearly spherical, because the surface tension is dominant. When \(\hbox{Ca}\) becomes larger, bubbles are deformed in the direction of the principal strain because the surface tension cannot sustain the spherical shape against the acting shear stress (Rust and Manga 2002a). Frankel and Acrivos (1970) proposed the following equation to account for small bubble deformations on the effective viscosity using \(\hbox{Ca}\):

$$\begin{aligned} \eta = \frac{\mu ^*}{\mu } = 1 + \frac{1- 12\hbox{Ca}^2/5}{1 + (6\hbox{Ca}/5)^2}\alpha . \end{aligned}$$
(4)

Rust and Manga (2002b) validated the above equation experimentally: The effective viscosity of bubble suspensions with bubble deformations measured by rotational cylindrical rheometer agrees well with the corresponding values estimated by both Eq. (4) and the advanced equation derived by Choi and Schowalter (1975) when adding a high-order term to the void fraction:

$$\begin{aligned} \eta&= \frac{\mu ^*}{\mu }\nonumber \\&= 1 + \frac{1 + (6\hbox{Ca}/5)^2(1+20\alpha /3)(1+4\alpha )}{1 + (6\hbox{Ca}/5)^2(1+20\hbox{Ca}/3)^2}\left( 1+\alpha +\frac{5}{2}\alpha ^2 \right) . \end{aligned}$$
(5)

In Eq. (4), the relative viscosity depends on \(\hbox{Ca}\), but the variation is not monotonic against \(\hbox{Ca}\). The \(\eta \) takes larger values than unity for smaller \(\hbox{Ca} < 0.65\), and decreases with increasing \(\hbox{Ca}\), falling below unity at \(\hbox{Ca} = 0.65\) (termed the critical \(\hbox{Ca}\) number, \(\hbox{Ca}_{\rm c}\)). The theoretical estimates agree with the experimental results over wide range of \(\hbox{Ca}\), at least to \(\hbox{Ca} \le 3\) at which bubbles display considerable deformation, even though the equations assume only “small deformations” of bubbles. It must be borne in mind that these equations considering bubble deformations apply only to simple shear flows in equilibrium states between the bubble deformation and the acting shear stress, and cannot be applied to the complicated multi-dimensional, unsteady shear flows that occur in almost all actual flows.

For more general, but still simple shear flows, many researchers have provided empirical and semi-empirical models based on measured data to represent the behavior of the effective viscosity with increasing bubble volume fractions. Llewellin and Manga (2005) summarized these and proposed flow chart to determine the effective viscosity of bubble suspensions considering unsteady conditions using three parameters, \(\alpha \), \(\hbox{Ca}\) and the dynamic capillary number, \(\hbox{Cd}\) defined as

$$\hbox{Cd} = \frac{\mu d}{\sigma }\frac{\ddot{\gamma }}{\dot{\gamma }}.$$
(6)

Here, \(\hbox{Cd}\) represents the degree of unsteadiness of the flow. When \(\hbox{Cd} > 1\), the shear environment around the bubbles changes very rapidly for the response of the bubbles to reach equilibrium deformation, and the condition will be non-equilibrium. According to the flow chart, the conditions with \(\hbox{Ca} \ll 1\) and \(\hbox{Cd} < 1\), for very small deformations in steady conditions are classified as Regime 1. In this regime, the chart provides the minimum and maximum influences of bubbles on the effective viscosity based on empirical and semi-empirical models as

$$\begin{aligned} \begin{array}{ll} {\rm min.} &{} \eta = (1-\alpha )^{-1}\\ {\rm max.} &{} \eta = 1+9\alpha \\ \end{array}, \end{aligned}$$
(7)

where the Taylor expansion of the first equation around \(\alpha = 0\), very dilute conditions, becomes \(\eta = 1 + \alpha + O(\alpha ^2) +\cdots \) and the limiting value of Eq. (4) with \(\hbox{Ca} \rightarrow 0\) corresponds to the first-order approximation. For \(\hbox{Ca} \gg 1\) or \(\hbox{Cd} > 1\), large deformations or unsteady, non-equilibrium, conditions, are classified as Regime 2, where the maximum and minimum influences of bubbles (not the minimum and maximum values) on the effective viscosity are given as

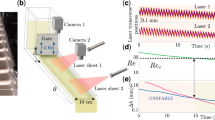
$$\begin{aligned} \begin{array}{ll} {\rm min.} &{} \eta = (1-\alpha )^{5/3}\\ {\rm max.} &{} \eta = (1+22.4\alpha )^{-1}\\ \end{array}, \end{aligned}$$
(8)

with the Taylor expansion of the first equation around \(\alpha = 0\) as \(\eta = 1 - 5\alpha /3 + O(\alpha ^2) +\cdots \) and the limiting value of Eq. (4) with \(\hbox{Ca} \rightarrow \infty \) corresponding to the first-order approximation. As suggested by these equations, the effective viscosity does not depend on \(\hbox{Ca}\) or \(\hbox{Cd}\) and is determined only by \(\alpha \). The applicability of the equations has been confirmed for dilute conditions, \(\alpha < 0.07\) (Llewellin and Manga 2005), assuming that the effect of bubbles on the effective viscosity will be somewhere between that predicted values using the minimum and maximum models. Details of the effective viscosity for unsteady flows have been summarized in Llewellin et al. (2002). Figure 1 shows the classification of regimes in estimates of the effective viscosity of bubble suspensions, where F.-A. is for Eq. (4), the Frankel and Acrivos equation.

To obtain a universal formula for the effective viscosity that is widely applicable to engineering fields, the discussion so far suggests that a detailed understanding of the modifications of the effective viscosity of bubble suspensions in non-equilibrium conditions of general flow situations is necessary. There is, however, little research dealing with non-equilibrium bubble deformations. One example is Murai and Oiwa (2008) which investigated the effective viscosity of bubbly liquids accompanied by transient bubble deformations utilizing the falling ball method. They reported that the critical \(\hbox{Ca}\), where the relative viscosity becomes smaller than unity, is 3.3 (0.65 in the simple, steady shear flows mentioned above), and the effect of modification of the effective viscosity in non-equilibrium conditions is clearly different from that in equilibrium conditions (Rust and Manga 2002a, b). However, it is difficult to evaluate the relationship between flows and bubble deformations here, because the phenomena are also accompanied by multi-dimensional shear flows.

Fig. 1
figure 1

Classification of regimes in estimating the effective viscosity of bubble suspensions

Full size image

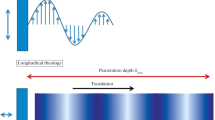
In this study, we will provide a more general evaluation of modifications of the effective viscosity arising from non-equilibrium bubble deformations in periodic shear flows. In rheology, Newtonian viscosity, shear-dependent viscosity (non-Newtonian viscosity) which depends on shear stress, and complex viscosity derived from elasticity have mainly been considered. The viscosity and elasticity respond to the shear rate and strain, respectively, and there is a phase lag between the shear stresses originating due to the viscosity and elasticity. Bubble deformations are elastic, and bubble suspensions in non-equilibrium states have to be treated as viscoelastic fluids. As a first step in the study, we evaluated the influence of non-equilibrium deformation of bubbles in investigations of the effective Newtonian viscosity (effective viscosity) in bulk reflecting all the factors induced by the dispersed bubbles in unsteady flows (see Fig. 2). To evaluate the effective viscosity, we developed an ultrasonic spinning rheometry that can measure the local viscosity in a rotating cylinder utilizing the spatio-temporal velocity information measured by ultrasonic velocity profiling (UVP) (Takeda 1995, 2012). The applicability of the spinning rheometry was evaluated by measurements of the effective viscosity of particle suspensions. Oscillating rotation of the cylinder provides results in continuous non-equilibrium bubble deformations in unsteady simple shear flows. Modifications of the effective viscosity of bubble suspensions were estimated by comparing the Newtonian viscosities obtained in both single-phase liquid and bubble suspension. The results are evaluated by comparing with the effective viscosity determined according to the procedures summarized by Llewellin and Manga (2005).

Fig. 2
figure 2

Conceptual diagram of ultrasonic spinning rheometry

Full size image

1.2 Rheometry

Rheology dealing with the deformation properties of materials is discussed in the fields of polymer, biology, dispersed media and food processing, and others. Here, we deal with rheology of dispersed media containing gas bubbles or solid particles. In the previous study of bubble suspension with equilibrium bubble deformation, the effective viscosity was measured by a conventional viscometer with the assumption of a constant shear stress profile (Rust and Manga 2002b). In unsteady flow fields accompanied by non-equilibrium bubble deformation, however, it is necessary to take account of the spatial distribution on the effective viscosity and shear stress depending on the magnitude of bubble deformation. So for the present purposes, it is not satisfactory to conduct integrated measurements of stresses assuming steady, uniform shear flows determined by ordinal viscometers or torque meters.

For cases with non-uniform strain rates including the present case, rheometry based on velocity profile measurements is effective however. Examples of rheometry include non-uniform strain rate measurements (Wang et al. 2011), rheological property measurements of fluids with slip velocities (Gonzalez et al. 2010, 2012), physical property measurements of flows accompanied by shear banding (Derakhshandeh and Vlassopoulos 2012), and in-line rheometry using velocity profiles and pressure gradient information (Wiklund and Standing 2008). We have also developed a visualization technique providing an intuitive representation of the rheological characteristics, the spatial distribution of strain rates, utilizing UVP (Shiratori et al. 2013). This study will also discuss the spatio-temporal distribution of rheological properties by velocity profile measurements. Modifications of the viscosity are reflected in the characteristics of momentum propagation. For example, in the flows on a two-dimensional vibration plate that commonly appear in text books as a problem-solving exercise of viscous fluid dynamics, vibrations of the plate propagate as a traveling wave with damping into the fluid, and the phase delay of the waves increases in proportion to the distance from the plate with the square root of the kinematic viscosity as the proportionality constant. The present study calculated the phase information of momentum propagation from the spatio-temporal velocity information measured by UVP in a cylinder with oscillating rotation. We have also estimated the effective viscosity in multi-phase fluids modified from that of the single-phase fluids based on the phase information.

2 Concept of ultrasonic spinning rheometry and experimental setup

2.1 Ultrasonic spinning rheometry

As mentioned in the last section, the effective viscosity of the bubble suspensions in the oscillating cylinder adopted in this study displays a spatial distribution due to non-equilibrium bubble deformation. Measurements of a unique viscosity from integrating the measurements of the stress assuming steady, uniform shear flows by a conventional viscometer and torque meter do not satisfy the present purpose. Therefore, it is necessary to estimate the local effective viscosity from the spatio-temporal velocity distributions. This is achieved by a unique technique hereafter termed “ultrasonic spinning rheometry”. Figure 2 is a conceptual diagram of the phenomena involved in spinning rheometry. When the cylinder is subject to oscillations, the information of the oscillation (or azimuthal momentum) propagates in the form of a wave from the cylinder wall to the inner part of the fluid. When the assumption of an axisymmetric flow field and one-directional flow in the azimuthal direction is satisfied, the propagation of the momentum in the radial direction can be described as the diffusion equation of a two-phase flow,

$$\begin{aligned} \frac{\partial }{\partial t}\left[ \rho (1-\alpha )u_{\theta } \right] = \frac{\partial }{\partial r}\left[ \mu \left( \frac{\partial u_{\theta }}{\partial r} + \frac{u_{\theta }}{r} \right) \right] . \end{aligned}$$
(9)

This equation, however, does not account for surface tension effects of the bubbles involved in the momentum propagation. Bubbles dispersed in the fluid layer are deformed differently at different radial positions, because the strain rate of the fluid has a radial distribution in the rotating cylinder. The different bubble deformations cause different degrees of modifications on the viscosity as expressed by Eqs. (4) and (5), and thus, the momentum propagation would show differences at each test volume. From viscous fluid dynamics considerations, the phase information of the momentum propagation at a radial position expresses the influence of the local effective viscosity. In other words, the effective viscosity of a bubble suspension can be estimated from the phase information. As typical effects of dispersed bubbles in unsteady shear flows, there is the shear-dependent viscosity, non-uniformity of the bubble distribution in the rotating cylinder, and the complex viscosity introduced by the elasticity of the bubbles. The present study evaluates the influence of non-equilibrium bubble deformations on the viscosity with the effective, representative Newtonian viscosity of bubble suspensions in bulk, incorporating the all of these factors. The viscosity is determined from the local velocity distribution measured in each test volume, and here, the effective viscosity is defined as the bulk viscosity including the effects of non-Newtonian viscosity and the elastic stress derived from the surface tension of bubbles in the test volume.

The phase differences in the momentum propagation from the cylinder wall to the center of the fluid are calculated to estimate the modification of effective viscosity from the spatio-temporal velocity distribution. To calculate the phase differences, frequency analyses of spatio-temporal velocity distributions are utilized. Ordinal UVP measurements consider deviations due to lack of tracer particles in the measurement volume as well as other reasons (see Fig. 6b). Utilizing the phase information rather than the velocity distribution itself can reduce the influence of noise in the data. To compare with experimental results of the characteristics of momentum propagation, we derived the analytical solution to the spatio-temporal velocity distribution in the single-phase condition from the diffusion equation,

$$\begin{aligned} \frac{\partial u_{\theta }}{\partial t} = \nu \left( \frac{\partial ^2 u_{\theta }}{\partial r^2} + \frac{1}{r}\frac{\partial u_{\theta }}{\partial r} - \frac{u_{\theta }}{r^2} \right) . \end{aligned}$$
(10)

Given the initial condition, \(u_{\theta }(r, t=0) = 0\), and the boundary conditions, \(u_{\theta }(r=R, t) = U\sin \omega t ={\rm Im}[U\exp (i\omega t)]\) and \(u_{\theta }(r=0, t) = 0\), it is possible to derive the analytical solution to Eq. (10). The details of the derivation are summarized in the “Appendix”. The phase differences between the cylinder wall and the measurement points are shown in Fig. 3 plotting both the experimental results and the analytical solution, Eq. (24). The horizontal axis represents the non-dimensional radius normalized by the cylinder radius. The analytical solution presented here is for \(1{,}000\,{\rm mm}^2/\hbox {s}\) in kinematic viscosity. In the single-phase condition, the experimental results show good agreement with the analytical solution, making it possible to assume that the analytical solution represents the correct phase difference corresponding to the local viscosity. In the present procedure, the modifications of the effective viscosity are estimated by comparing the phase differences between the analytical solution and the experimental results obtained in the multi-phase conditions. In Fig. 3, the phase differences obtained in the bubble suspension are also shown and it is clearly different from the single-phase condition. The local effective viscosity is determined by matching the local slope of the phase difference between the analytical solution and the experimental result by adjusting the viscosity given by the analytical solution. Figure 4 shows the flowchart for estimating the effective viscosity from the spatio-temporal velocity profiles measured in the multi-phase condition. The kinematic viscosity is varied at \(1\, {\rm mm}^2/\hbox {s}\) in the range from \(500\,\text{to}\,1{,}500\ {\rm mm}^2/\hbox {s}\) in the analytical solution, and the phase difference is calculated for each kinematic viscosity. After that the slope of the phase difference between each of two points in the spatial direction is compared with the analytical solution and the experimental results. The effective kinematic viscosity in each experimental condition is determined as the least mean square error in the comparison range.

Fig. 3
figure 3

Phase lag of momentum propagation at non-dimensional radial positions \( r^{*} (=r/R)\), where the \(r\) is the distance from center of the cylinder and \(R\) is the radius of the cylinder, the black line represents the case of the single-phase condition, the gray line is for the multi-phase condition, and the gray dashed line is the analytical solution with \(1{,}000\ {\rm mm}^2/\hbox {s}\) in kinematic viscosity, the experimental data have error bars

Full size image
Fig. 4
figure 4

Procedure of the analysis to estimate the effective viscosity of multi-phase flows from velocity distributions

Full size image

2.2 Experimental setup

The experiments were conducted in a rotating cylinder as illustrated in Fig. 5a with inner diameter 145 mm, height 330 mm, and thickness of the lateral wall 2.5 mm. The cylinder is made of acrylic resin and filled with silicone oil with \(\nu = 1{,}000\ {\rm mm}^2/\hbox {s}\) in kinematic viscosity at 25 °C, \(\rho = 970\ \hbox {kg/m}^3\), and \(\sigma = 21.0\ \hbox {mN/m}\) in surface tension. The cylinder has no lid leaving the top surface of the fluid layer unconstrained. The cylinder was mounted at the center of a water chamber to maintain uniform temperatures and to allow transmission of ultrasonic waves from the outside of the cylinder. The oscillation of the cylinder is controlled by a stepping motor, where the angle of oscillation is fixed at 90°, and the frequency is changed as 0.5, 1.0, 2.0, and 2.5 Hz. The resonance frequency of 1-mm-diameter bubbles in the elliptic mode according to

$$f_n = \frac{1}{2\pi }\sqrt{(n+1)(n-1)(n+2)\frac{\sigma }{a^3\rho }}$$
(11)

with \(n = 2\) is \(f_2 = 229\) Hz, where \(a\) is the radius of the bubbles (Lamb 1932; Feng and Leal 1997). The setting frequency of the cylinder oscillation is much smaller than the resonance frequency. During the cylinder oscillation, the velocity distribution was measured by UVP in both single-phase and bubble suspension conditions. An ultrasonic transducer with 2 MHz resonance frequency was fixed in the chamber with a horizontal displacement \(\varDelta y\) from the center line of the cylinder to obtain the azimuthal velocity component (see Fig. 5b). The obtained ultrasonic echo signals were processed by a UVP monitor model Duo (Met-Flow, S.A.) into spatio-temporal velocity information. In the UVP measurements, the velocity component \(u_{\xi }\), parallel to the measurement line, is measured at each measurement point on the measurement line \(\xi \). Assuming that the axisymmetric flow field and the velocity component in the radial direction is negligibly small compared with the azimuthal velocity component, the azimuthal velocity component \(u_{\theta }\) is obtained as \(u_{\theta }= u_{\xi }r/\varDelta y\) at a radial position \(r\). If \(\varDelta y\) is assumed as too large, the velocity distribution on the measurement line cannot be measured due to the effect of the curvature of the cylindrical wall. If \(\varDelta y\) is too small, measurement errors become large because of the considerable measurement volume involved in the UVP measurements, as will be mentioned later in this section. Empirically, \(\varDelta y = 15\ \hbox {mm}\) was selected based on the results of previous studies (for example, Shiratori et al. 2013). The transducer was set 230 mm from the bottom of the cylinder to avoid effects of shear stress due to oscillation of the cylinder bottom plate. In the UVP measurements, instantaneous velocity profiles are obtained along the ultrasonic propagation line with the signal processing of the ultrasonic echo from the ultrasonic reflectors dispersed in the test fluid resulting from the repeated irradiation of the ultrasonic pulse to the test fluid (Shiratori et al. 2013; Takeda 2012). The measurement volume is disk-shaped at each measurement point, and the diameter is around 10 and 0.99 mm thick determined by the speed of sound in the silicone oil (990 m/s) and the number of waves in a single emission (four waves). In dilute conditions of bubble mixtures, almost all ultrasonic waves propagate into the fluid layer even though some of the irradiated ultrasonic waves are scattered by the dispersed bubbles because of the relatively large measurement volume and dilute condition of the bubble suspension. Measurement conditions of the UVP are 1.892 mm/s in velocity resolution, 0.99 mm in spatial resolution, and 30 ms in time resolution.

Fig. 5
figure 5

a Schematic diagram of experimental setup, b top view of the rotating cylinder

Full size image

Bubble shapes were captured by a high-speed video camera (HSV) simultaneously with the UVP measurements by triggering with a function generator. The HSV was mounted above the cylinder and recorded the bubble shapes through the free surface of the fluid layer with 1,000 frames/s (fps). Deformations of the free surface are negligibly small, so distortions due to deformation here can be neglected. A metal halide lamp was used as the light source for the visualization. Bubbles around the lower part of the fluid layer were illuminated, and the scattered light there worked to highlight the interfaces of bubbles in the upper part of the fluid layer, like backlighting with a diffusion filter. Bubbles dispersed in the test fluid were injected by a compressor through a generator mounted at the bottom of the cylinder. The diameter of the bubbles is up to 1 mm, and the void fraction is around 2 %, allowing the assumption of dilute conditions. Since the bubble size is small, the ascending motion of bubbles due to buoyancy in the highly viscous fluid is negligibly small during the typical measurement time, 30 s, when making 1,024 profiles at the instantaneous velocity with 0.030-s time resolution. In the flow field, therefore, the azimuthal fluid motion induced by the cylinder oscillation is dominant. Assuming a uniform distribution of bubbles in the fluid layer, each measurement volume would include two or three bubbles on average. As the reflectors of ultrasonic waves, polyethylene resin particles of \(919\, \hbox {kg/m }^3\) density and \(180\,\upmu {\rm m}\) in diameter were seeded in the fluid layer. The volume fraction of the dispersed particles is around 0.05 %, and thus, their influence on the effective viscosity would be around 0.1 % according to the Eq. (1).

Figure 6 shows a comparison of the spatio-temporal distribution of the non-dimensional azimuthal velocity \(u_{\theta }^* = u_{\theta }/U\) for 1.0 Hz in the oscillation frequency, where the analytical solution (Fig. 6a) is calculated from Eqs. (19) to (23) in the “Appendix”. The experimental result determined from the spatio-temporal map obtained by UVP with the assumption of axisymmetric, one-directional flow in the azimuthal direction (Fig. 6b) shows quite similar variations in time and space when compared with the analytical solution shown in Fig. 6a. The distribution has deviations due to measurement errors, but these cause no significant influence on the apparent fluid motion: Oscillation of the azimuthal velocity propagates from the wall to the center of the cylinder as a damping wave. In the experiments, the cylinder starts oscillation at \(t = 0\), while the analytical solution assumes equilibrium conditions from \(t = 0\). The distributions are different at the initial stage because of this, but the influence of the initial condition disappears after a single cycle. This agreement between the analytical solution and the experimental result indicates that the assumptions in the experiment, the axisymmetric one-directional flow, are satisfied.

Fig. 6
figure 6

Spatio-temporal velocity distribution of non-dimensional azimuthal velocity \(u_{\theta }^*\) of the flow induced by cylinder oscillations with 1.0 Hz in oscillation frequency; a analytical solution given by Eqs. (19)–(23), and b experimental result

Full size image

3 Validation of spinning rheometry measurements

3.1 Viscosity measurements of solid particle suspensions

To validate the measurement technique to establish effective viscosity values utilizing ultrasonic spinning rheometry described in Sect. 2.1, we applied it to solid particle suspensions. This was selected because there it is not needed to consider particle deformations and investigations have established that the effective viscosity increases exponentially with increasing volume fractions of solid particles (Mooney 1951). We used two kinds of particles of polyethylene, \(180\,\upmu {\rm m}\) mean diameter CL-2507 and \(600\,\upmu {\rm m}\) mean diameter CL-8007. Because of the differences in the diameter, the solutions have different number densities of particles with the same volume fractions. The relative viscosity, \(\eta = \mu ^*/\mu = [\rho (1-\alpha ) + \rho _{\rm p} \alpha ]\nu _{\rm s}/(\rho \nu )\) (\(\nu _{\rm s}\): kinematic viscosity of particle suspensions, \(\nu \): kinematic viscosity of single-phase condition, \(\rho _{\rm p}\): density of particles), with respect to the volume fraction is shown in Fig. 7a for CL-2507 and in Fig. 7b for CL-8007. The symbols in the figure indicate the rotation frequency, \(f\), of the cylinder in Fig. 7a. UVP is applicable for CL-2507 up to \(\alpha \sim ~3\) % volume fractions, because large number densities of solid particles greatly modify the ultrasonic propagation. With CL-8007 (Fig. 7b), the UVP measurements allow larger values of \(\alpha \), up to \(\alpha \sim 10\) %. An evaluation of the superficial area shows that both limits on the volume fraction have similar values. The black lines in the figures represent the theoretically estimated curves for mono-dispersed suspensions (Mooney 1951; Vand 1948),

$$\eta = \exp \left( \frac{2.5\alpha }{1-1.43\alpha } \right).$$
(12)

The obtained results show good agreement with the theory especially at volume fractions smaller than \(\alpha = 3\) %. These results indicate the applicability of the present approach to estimate the effective viscosity for suspensions at dilute conditions.

We expected that these would be an influence of the oscillation frequency on the viscosity estimation induced by the differences in the number of particles passing across the test volume per unit time or in the non-uniformity of the particle distribution due to the weak, but considerable centrifugal force. However, these were no systematic differences in the viscosity in these results. The differences between the experimental results and the empirical equation become gradually larger with increasing volume fraction of solid particles. This may be caused by the distribution of the diameters of the solid particles. The particle size has a distribution around the mean diameter (\(180\,\upmu {\rm m}\) in CL-2507, \(600\,\upmu {\rm m}\) in CL-8007). According to the production data for the particles, there is a size distribution from 75 to \(285\,\upmu {\rm m}\) with CL-2507 and from 350 to 800 \(\upmu {\rm m}\) with CL-8007. We confirmed that the particle size distribution obeys a normal distribution in these ranges by microscopic image analyses. The volume fraction of solid particles is determined from particle density and total mass of particles under the assumption that the diameter of all particles corresponds to the mean diameter, without deviations. This would mean that deviations in the particle size induce errors in the estimates of the volume fraction, and the effects of the volume fraction due to the particle size and non-uniform number distribution of the particles are discussed in the next section.

Fig. 7
figure 7

Relative viscosity plotted against the volume fraction of solid particles a (\(180\,\upmu {\rm m}\) mean diameter) b (\(600\,\upmu {\rm m}\) mean diameter)

Full size image

3.2 Error factor analysis

To evaluate the errors in the effective viscosity obtained by the proposed technique, the dispersion of particle diameters and the number of particles included in the test volumes are discussed in this section. In actual situations, the particle distribution displays small non-uniformities even with large efforts to achieve homogenized products, and the number of particles included in a test volume has a spatial distribution. Errors due to the dispersion of the particle diameters also appear even for uniform particle distributions, because the volume fraction of particles is determined by particle density and measured mass of the particles. To evaluate the influence of these factors, we performed numerical investigations for the smaller particle polyethylene (CL-2507) with 1.0 % in the volume fraction, a value that corresponds to the volume fraction of the bubble suspension case. Figure 8 shows the spatial distributions of the volume fraction with the various dispersions, where the dispersions of either or both the particle diameter and the number of particles are given by a function generated by random numbers available in the programming language. The added dispersions obey normal distributions with a set center value \(E\) and standard deviation \(D_{\rm s}\). For the particle diameter distribution, the mean diameter, \(180\,\upmu {\rm m}\), is used as \(E\), and \(D_{\rm s}\) is determined by assuming that the range of the distribution, 75 to 285 \(\upmu {\rm m}\), is the range of \(-3D_{\rm s}\) to \(3D_{\rm s}\), the corresponding \(D_{\rm s}\) is \(35\,\upmu {\rm m}\). For the particle number distribution, the center value estimated from the volume fraction and the size of the test volume is around \(E = 255\,\upmu {\rm m}\). Assuming the zero particle condition in the test volume as \(-3D_{\rm s}\) gives \(D_{\rm s} = 85\upmu {\rm m}\). This condition represents the maximum possible non-uniformity of the particle number distribution. Solid gray, black, and dashed black lines represent the dispersion due to the particle diameter, the number of solid particles included in each test volume, and both factors combined. The vertical and horizontal axes represent the volume fraction of the solid particles in each test volume and the dimensionless radial position in the cylinder reduced by the radius of the cylinder.

This graph indicates that the volume fraction varies from 0.2 to 2.0 %. Also that the number of solid particles included in each test volume more strongly influences the dispersion of the volume fraction than the dispersion of the particle diameters. The center values of the variations influenced by the particle size distribution take somewhat larger values than the 1.0 %. The volume of the particles used to estimate the volume fraction is proportional to the cube of the particle diameter. Therefore, the distribution of particle diameters increases the center value. In this case, the increase in the center value estimated from the standard deviation is around 10 %, roughly corresponding to the increase of the center value indicated in Fig. 7. Deviations of the estimated effective viscosity at smaller volume fractions than \(\alpha = 3.0\) % can be explained by the influence of the non-uniform particle distributions. But it cannot explain the large systematic deviation for larger volume fractions above \(\alpha = 3.0\) %. In such conditions of relatively high volume fractions, collisions of the particles would occur and these would enhance the transportation of the momentum. Then, the effective viscosity may be greatly increased in the larger volume fractions. We may conclude that the applicable range where this technique may be applied is restricted to volume fractions below \(\alpha = 3.0\) %, and the technique provides reliable results in this range with relatively small errors.

Fig. 8
figure 8

Spatial fluctuations of the volume fraction due to size and number distribution of the suspended particles with \(\alpha = 1.0\) %, the gray line represents the case considering particle size distribution, the dashed line represents the case considering particle number distribution in the test volume, and the black line represents the case considering these two together

Full size image

4 Application for bubble suspensions

4.1 Relative viscosity of bubble suspensions

The previous sections indicated that the present technique to estimate the effective viscosity works well up until a volume fraction of \(\alpha \sim 3.0,\) % and next, we will apply the technique to bubble suspensions. Figure 9 shows the relative effective viscosity \(\eta = \mu ^*/\mu = (1-\alpha ) \nu _{\rm s}/\nu \) obtained from bubble suspensions with 2.0 % bubble volume fraction (void fraction) at different dimensionless radial positions \(r^{*} \) and different oscillation frequencies \(f\) from 0.5 to 2.5 Hz. The values were obtained from the slope of the phases in the momentum transfer at different ranges corresponding to \(r^{*} =\) 1.0–0.9, 0.9–0.8, 0.8–0.7, 0.7–0.6, and 0.6–0.5, respectively. In these results, the effective viscosity varies around unity: It has values smaller than unity near the wall (\(r^{*} = 0.95\)) and larger than unity inside the cylinder (\(r^{*} =\) 0.85–0.55). The \(\eta \) also depends on the oscillation frequency, and faster oscillations result in relatively smaller values. For the procedure to estimate the effective viscosity proposed by Llewellin and Manga (2005), the flow is assumed to be steady flow, because of the small value of the dynamic capillary number \(\hbox{Cd}\), \(\hbox{Cd} \sim 0.16\) at \(f =\) 2.5 Hz [\(\ddot{\gamma }/\dot{\gamma }\) in Eq. (6) \(\sim 2\pi f\)]. This makes it necessary for the procedure to evaluate the capillary number, \(\hbox{Ca}\). Figure 10 shows the radial profiles of \(\hbox{Ca}\) at each \(f\) calculated from the exact solution of the flow field, Eqs. (19) and (3), where the gray lines are the maximum values of the time series of \(\hbox{Ca}\) (\(\hbox{Ca}_{\rm max}\)), and the black lines are the effective value of the time series (\(\hbox{Ca}_{\rm rms}\)), the lines correspond to \(f\) values. As shown, \(\hbox{Ca}\) remains below 4 and cannot be assumed as \(\hbox{Ca} \gg 1\).

Fig. 9
figure 9

Radial distribution of the relative viscosity of bubble suspensions with 2.0 % in the volume fraction obtained at different oscillation frequencies, 0.5, 1.0, 2.0, and 2.5 Hz. The vertical bars indicate the maximum and minimum values corresponding to each regime of the estimates of the effective viscosity (Llewellin and Manga 2005), the solid curve represents the effective viscosity estimated from Eq. (4) with \(\hbox{Ca}_{\rm max}\) for \(f = 2.0\,\hbox {Hz}\)

Full size image
Fig. 10
figure 10

Radial profiles of the capillary number at different oscillation frequencies; \(\hbox{Ca}_{\rm max}\), maximum \(\hbox{Ca}\) in the time series; \(\hbox{Ca}_{\rm rms}\), effective value of the time series

Full size image

According to Eqs. (4) and (5), the effective viscosity of bubble suspensions with equilibrium bubble deformations increases for small deformations (the deformation evaluated by \(\hbox{Ca}\)). As the result, the trend of the variation of the effective viscosity with \(\hbox{Ca}\) changes to negative and the effective viscosity assumes smaller values than unity for the larger values of \(\hbox{Ca}\) than at the critical capillary number \(\hbox{Ca}_{\rm c} = 0.65\). In the present configuration, both of the faster oscillations and regions near the cylinder wall provide larger shear stresses to the bubble suspension. So, the results detailed above are consistent with the suggested modifications of the effective viscosity in the bubble suspension at equilibrium bubble deformations. The rate of the modification of the effective viscosity decreases around 10 %, while the modification rate is the order of the volume fraction in the bubble suspensions with equilibrium bubble deformations (Rust and Manga 2002b) as shown in Fig. 9 with the solid curve that is estimated from Eq. (4) with \(\hbox{Ca}_{\rm max}\) for \(f = 2.0\) Hz. Further, the tendency of the radial variation of \(\eta \) is quite different for the estimated and experimental results: The estimated value is below unity for \(r^{*} > 0.7,\) while the experimental results are below unity only at \(r^{*} = 0.95\). The \(\hbox{Ca}_{\rm rms}\) shown in Fig. 10 has tendency similar to the experimental results, while the value of \(\hbox{Ca}_{\rm rms}\) does not provide a good estimate of the effective viscosity. A study dealing with non-equilibrium bubble deformations in steady flows also reported that the modification rate is the same order as the volume fraction (Murai and Oiwa 2008). These results suggest that the present flow conditions cannot be considered steady, equilibrium conditions in spite of the small \(\hbox{Cd}\). In the definition of \(\hbox{Cd}\) in Eq. (6), the unsteadiness is evaluated as the fraction of the temporal derivative of the strain rate, \(\ddot{\gamma }\), to the strain rate \(\dot{\gamma }\). In the present cases, the applied strain rate is large, and thus, the relative influence of the unsteadiness is evaluated as smaller values. If we assume unsteady conditions near the wall, Regime 2, for \(\hbox{Cd} > 1\) shown in Fig. 1 provide \(\eta = 0.97\) as the largest value and \(\eta = 0.69\) as the smallest value [calculated from Eq. (8)] indicated in Fig. 9 as the vertical bar labeled Regime 2. The results obtained here are within this range. For conditions \(\hbox{Ca} \ll 1\), especially the results for \(r^{*} < 0.7\), we may assume as Regime 1. Equation (7) corresponding to Regime 1 provides \(\eta = 1.18\) and \(\eta = 1.02\) as the maximum and minimum values. These values are larger than the maximum value, but the linear constant of the equation for obtaining the maximum value in Eq. (7), here 9, must be obtained empirically to be meaningful (Llewellin et al. 2002). This suggests the need for adjustments to the linear constant to obtain the better estimate in this measurement system.

4.2 Considerations related to bubble deformation on the effective viscosity

The relationship between bubble deformation and the modification of effective viscosity will now be discussed applying the present method estimating the effective viscosity to the bubble suspensions. In particular, we focus on the bubble deformation pattern near the cylinder wall (at \(r^{*} = 0.95\) in Fig. 9) in which there is an apparent difference depending on the rotation frequency of the cylinder, \(f\), in the modification of effective viscosity. Figure 12 shows the bubble deformations corresponding to the variations in the speed of rotation of the cylinder, where the gray ellipsoids represent schematic outlines of the instantaneous bubble shape obtained from the image in Fig. 11. The bubble deformations are quantitatively evaluated by the ratio of the major dimension \(l\) (see Fig. 12) determined from the outlines to the original diameter \(d\) of the bubbles. The figures also display the corresponding time variations of \(\hbox{Ca}\) calculated from the exact solution of the flow field Eqs. (19) and (3).

For \(f = 0.5\,\hbox {Hz}\) (Fig. 12a), the bubbles return to the spherical shape after reaching the maximum deformation around \(l/d = 1.6\). Here, the maximum capillary number is around 0.3 making the surface tension is everywhere dominant during the cylinder oscillation. Also, in the oscillation, the surrounding fluid reacts to frequent deformation of the bubbles from spherical shape to semi-ellipsoid shapes. In such a deformation process, the bubbles provide the maximum resistance against the shear flows and it may introduce the dramatic increase of the effective viscosity at low oscillation frequency conditions and in inner radial positions as shown in Fig. 9.

Fig. 11
figure 11

Images of bubbles in the rotating cylinder in cases of a stationary, b oscillation with \(f = 0.5\) Hz, c 2.0 Hz, left and right ends of the images correspond to the center of the cylinder and the cylinder wall

Full size image
Fig. 12
figure 12

Time variations of capillary numbers and bubble shapes around \(r^{*} = 0.95\) against the cylinder oscillation with a \(f = 0.5\,\hbox {Hz}\) and b 2.0 Hz, where \(l/d\) indicates the deformation rate

Full size image

At \(f = 2.0\ \hbox {Hz}\) at which the effective viscosity decreases near the cylinder wall, the bubbles deform strongly with \(l/d \sim 3.0\) as the maximum (Fig. 12b), and the bubbles do not return to the spherical shape during the oscillation, with \(l/d \sim 1.2\) as the minimum value. According to Rust and Manga (2002a), the relaxation of bubble deformations in stationary fluids can be described as

$$\frac{l-d}{l_{\rm i}-d} = \hbox{e}^{-0.67t/\tau },$$
(13)

where \(l_{\rm i}\) is the initial major dimension before the relaxation, \(t\) is time and \(\tau ,\) is the relaxation time defined as \(\mu (d/2)/\sigma. \) The estimated time of the relaxation from \(l_{\rm i} = 3\) to \(l = 1.1\) in the present conditions is 0.12 s. Periodic oscillation of the cylinder allows conditions where \(\hbox{Ca} \ll 1\) are momentary but the duration, for example, where \(\hbox{Ca}\) is below the critical capillary number \(\hbox{Ca}_{\rm c} = 0.65\), is shorter than the estimated time for the relaxation. In the steady simple shear flows, the bubble shape can be determined by only \(\hbox{Ca}\). Using slender body theory and the assumption of circular cross sections on the bubbles (Hinch and Acrivos 1980), the deformation can be predicted as

$$\frac{l}{d} \simeq 3.45\hbox{Ca}^{1/2}.$$
(14)

Using the maximum \(\hbox{Ca}\) in this oscillation, \(\hbox{Ca} \sim 2.45\), in the equation gives an \(l/d = 4.55\). This is much larger than the maximum value of \(l/d\) in the experimental observations suggesting that the bubble deformation has not reached the equilibrium state for applying shear flows. As these the instantaneous value of the \(\hbox{Ca}\) is not physically meaningful in this unsteady condition in spite of the small \(\hbox{Cd}\). Here, we suggest using the effective value of the capillary number as indication of the bubble deformation and modification of the relative viscosity. In this case, the value is \(\hbox{Ca}_{\rm rms} = 0.75\) and larger than \(\hbox{Ca}_{\rm c}\). Namely, the bubbles effectively yield against the applying periodic shear flows. In such a case, the effective viscosity may be categorized as Regime 2 shown in Fig. 1 even though flows do not satisfy the conditions of \(\hbox{Ca} \gg 1\) or \(\hbox{Cd} > 1\).

This study assumed modifications of the effective viscosity as in a Newtonian fluid, and the contributions of viscoelastic effects related to the non-equilibrium bubble deformations with the surface tension are included. If the fluid has the characteristic of viscoelasticity, the elasticity influences the viscosity. Then, it is necessary to consider two types of viscosity, the original viscosity and different viscosity derived from the elasticity. The viscosity incorporating these two features is categorized as complex viscosity, and it includes the elasticity as the imaginary part. The modification of the effective viscosity due to non-equilibrium bubble deformation, therefore, becomes expressed by the complex viscosity derived from the surface tension of the bubbles in the viscous liquid (Llewellin et al. 2002).

5 Conclusions

We have investigated the modification of effective viscosity of bubble suspensions accompanied by non-equilibrium bubble deformations in periodic shear flows to understand the drag reduction mechanism working when injecting bubbles into boundary layers. A novel method to estimate the effective viscosity of multi-phase flows is proposed using an oscillating cylinder with ultrasonic velocity profile measurements. By assuming Newtonian viscosity, the modification of the effective viscosity is reflected in changes in the phase lag in the momentum propagation from the cylinder wall to the inner fluid. To evaluate the validity of the present method, we estimated the effective viscosity of a suspension containing solid particles. The results correspond to the empirical equation for volume fraction of particles smaller than 3.0 % and indicate the validity of the method in this range of volume fraction. Applying this to bubble suspensions with non-equilibrium bubble deformations suggests;

  1. 1.

    In oscillating shear flow environments, the radial profiles of the effective viscosity display a spatial distribution in the cylinder due to bubble deformation.

  2. 2.

    In large amplitude oscillation environments introducing large deformations of bubbles, the effective viscosity cannot be estimated as for the steady bubble deformations in spite of the small dynamic capillary numbers less than unity.

  3. 3.

    In oscillating shear flows, the effective value of the temporal fluctuations in the capillary number provides a good estimate of the increases and decreases in the effective viscosity.

  4. 4.

    The effective value of the time fluctuations of the capillary number is above the critical capillary number, \(\hbox{Ca}_{\rm c} = 0.65\) in simple shear flows, may be categorized into the Regime 2 proposed by Llewellin and Manga (2005) for estimating effective viscosity.