Rheology in Longitudinal (Ultrasound) Mode. Review

Abstract

This review is dedicated to the topic of longitudinal rheology, a branch of rheology that is complementary to traditional shear rheology, and yet not as widely explored. Longitudinal rheology differs from typical shear rheology by the type of stress applied. Longitudinal stress is a wave, which causes liquid expansion and compression that occurs when ultrasound propagates through such liquid. The penetration depth of a longitudinal stress is much longer than for a shear stress, which allows this method to be used for studying liquid bulk properties at the MHz range. The concept of longitudinal rheology has been known for centuries, but only became available in commercial instruments as recently as the 1990s. We describe here the main principles of this technique, as well as present an overview of existing published applications, which include:

—Bulk viscosity

—Microviscosity

—Hookean coefficient of inter-particle bonds

—Newtonian liquid test at MHz range

—Compressibility

—Sol-gel transition

—Micellar systems

—Dissolution of polymers

—Liquid mixtures

1 INTRODUCTION

The first study on the field of longitudinal rheology was conducted 330 years ago by Sir Isaac Newton [1]. He discovered a relationship between a fluid’s elastic property compressibility, β, and the speed, V, of a sound wave traveling through it. This wave is a wave of longitudinal stress:

$${{V}^{2}} = \frac{{\text{1}}}{{\beta \rho }},$$

(1)

where ρ is fluid density.

The relationship between the fluid’s viscosity, η, and sound attenuation, α_long, was established 170 years ago by another famous scientist: Sir George Stokes [2, 3]:

$${{\alpha }_{{{\text{long}}}}} = \frac{{{\text{2}}{{\omega }^{2}}\eta }}{{3\rho {{V}^{3}}}},$$

(2)

where ω is frequency of the sound wave.

Many other famous scientists —including Laplace, Maxwell, Rayleigh, and Kirkwood—contributed to this field producing hundreds of published papers. A detailed historical review of their work can be found in the book by Dukhin and Goetz [4].

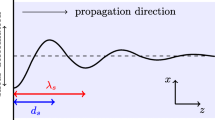
Longitudinal rheology differs from shear rheology by the type of stress that we impose on the fluid. In the case of shear rheology the stress is a shear stress, and the applied force is tangential to the direction of propagation. For longitudinal rheology and its related longitudinal stress, the direction of the force and the direction of propagation coincide. Figure 1 illustrates this difference. Additionally, a longitudinal stress expands and collapses the fluid which, consequently, is related to the fluid’s compressibility. In the case where the fluid is liquid, this phenomenon becomes increasingly important and pronounced at high frequencies, due to liquids typically behaving as incompressible at both steady state and at low frequencies.

Fig. 1.

Illustration of the difference between shear stress and longitudinal stress.

A liquid’s response to longitudinal stress can be characterized with a complex visco-elastic modulus, G_long. This parameter is similar to the shear visco-elastic modulus, G_shear, which is employed in shear rheology. Looking at the equations for these moduli, one can see that there is a universal functional relationship between these moduli and what is referred to as “penetration length”, δ, which depends on the type of the stress:

$$G_{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{{'}}} = \rho {{\omega }^{2}}{{V}^{2}}\delta _{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{\text{2}}}\frac{{{{\omega }^{2}}\delta _{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{\text{2}}} - {{V}^{2}}}}{{{{{[{{\omega }^{2}}\delta _{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{\text{2}}} + {{V}^{2}}]}}^{2}}}},$$

(3)

$$G_{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{{{''}}}} = 2\rho {{\omega }^{3}}{{V}^{2}}\delta _{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{\text{3}}}\frac{V}{{{{{[{{\omega }^{2}}\delta _{{\begin{subarray}{l} {\text{shear}} \\ {\text{long}} \end{subarray}} }^{{\text{2}}} + {{V}^{2}}]}}^{2}}}}.$$

(4)

Where the index “shear” corresponds to shear rheology and the index “long” corresponds to longitudinal rheology.

The derivation of Eqs. (3) and (4) for the case of shear rheology case come from the papers by Williams and Williams [5–7], who in turn make reference to a much earlier book by Whorlow [8]. The derivations of the identical equations for the longitudinal rheology case are taken from a review by Litovitz and Davis [9]. They, in turn, make reference to much earlier works by Miexner [10, 11], who apparently derived general thermodynamic theory of stress-strain relationship in liquids.

A critical distinction between shear rheology and longitudinal rheology, aside from the direction of force in relation to propagation descried earlier, is the specific differences in penetration depth. As was described in a recent review of shear rheology by Schroyen et al. [12]: “The penetration depth is of particular importance at very high frequencies since it defines the maximal distance over which the sample can be probed”.

As is the case, it is possible to make some estimates of the each penetration depth using well known theories.

The penetration depth of the shear stress, δ_shear, can be estimated using following equation for viscous boundary layer, as is described in the recent review by Schroyen et al. [12]:

$${{\delta }_{{{\text{shear}}}}} \approx \sqrt {\frac{\eta }{{\rho \omega }}} {\kern 1pt} .$$

(5)

Unfortunately, most liquids do not support shear waves very well, resulting in a shear penetration depth that is rather short and quickly decreases with frequency. In the case of ultrasound, for a frequency of 1 MHz the penetration depth is only 10 microns, and diminishes to just 1 micron at 100 MHz.

As stated in the review by Schroyen et al. [12]: “At large ultrasonic frequencies (>1 MHz), the penetration depth becomes so small that surface properties rather than bulk properties are probed”.

However, this problem with regards to the testing of bulk rheological properties of a liquid at high frequencies can be resolved by exploring the liquid’s longitudinal rheology. Where shear waves have very small penetration depths, longitudinal waves are able to penetrate much further into the liquid. We can use Stokes’s law, Eq. (2), for estimating the longitudinal penetration depth, δ_long, which is simply the reciprocal of the attenuation coefficient. It yields the following simple expression for estimating δ_long:

$${{\delta }_{{{\text{long}}}}} = \frac{1}{\alpha } \approx \frac{{\rho {{V}^{3}}}}{{{{\omega }^{2}}\eta }}.$$

(6)

Using Eq. (6), penetration depth can be determined from a liquid ultrasound attenuation coefficient: In the case where the liquid is water, the longitudinal penetration depth is roughly 1000 meters at 1 MHz. Even at 100 MHz the longitudinal penetration depth is approximately 10 cm, which is by orders of magnitude larger than the shear penetration depth at this frequency range. The reason for such a discrepancy in penetration depth is that longitudinal waves propagate longer distances in liquids.

It is easy to both generate and measure longitudinal waves in the MHz range, even for very highly attenuating liquid materials such as curing cement, battery slurries, inks, and paints, without the need for dilution. Examples of such experiments can be found in the book by Dukhin and Goetz [4].

The ability to measure rheological properties at high frequency using longitudinal rheology approaches described above begs the following question:

“Why are longitudinal rheology methods not widely used, if it is as well established as presented above?”

We can offer two reasons here as to why there is a dearth scientific research utilizing longitudinal rheology techniques.

The first reason pertains to the history of the measurement technique development for longitudinal rheology measurements. The main principles of longitudinal rheology measurement were formulated between the 1940s and the 1960s. A main requirement formulated at that time for such measurements is that they be conducted in pulse mode, meaning that waves would be propagated through the liquid media in pulses rather than continuously. Such an approach requires many data points to be collected for statistical purposes. Dealing with such a large number of pulses, and corresponding data points, requires a significant amount computation. This in turn limited the viability of developing a commercially available instrument which could utilize such an approach; the computing power required to conduct data analysis is significant. It wasn’t until the mid-1990s that computers were capable of handling the workload, at which times commercially available ultrasound spectrometers (for particle size and rheological analysis) began appearing. However, by that time shear rheology was solidly established as a dominant measuring technique in the field.

The second reason we suspect for limited use of longitudinal rheology methods is a lack of publication on these methods in rheological journals. There are dozens publications in the scientific journals of other fields about longitudinal rheology, as shown in the book [4], but not in rheological science journals, as far as we know. With this review we hope to begin solving this problem.

First we present here a short overview of an existing commercial Acoustic Spectrometers capable of longitudinal rheology measurements, which functions in the frequency range of 1–100 MHz and are capable of measuring both attenuation frequency spectra and sound speed. There are roughly 1000 such instruments in use worldwide produced by different manufacturers, currently. Most of these spectrometers are used for particle sizing of concentrated dispersions and emulsions. However, some of them have software for converting acoustic properties of complex liquids into longitudinal visco-elastic properties.

Then, we present the rheological applications that have been developed with these instruments. These applications can be separated into two distinctively different groups depending on parameterization of the sample:

The first group employs only macroscopic modeling, considering the sample as a homogeneous liquid, either Newtonian or non-Newtonian, with certain visco-elastic properties. The list of such applications includes:

(1) Newtonian/non-Newtonian liquid test at MHz range;

(2) Determination of bulk viscosity, which is the second fundamental viscosity coefficient of Newtonian liquids;

(3) Calculation of compressibility and its relationship to molecular solvating layer;

(4) Presence of micelles and sol-gel transition;

(5) Dissolution of polymers.

The second group encompasses applications that require modeling of the sample as heterogeneous: a collection of particles in the liquid. These particles could be solid, liquid, or more complex macromolecules. The liquid (i.e. the continuous phase) can be Newtonian or non-Newtonian, homogeneous or gel like.

To date there have been 3 different models used for describing the micro-structure of such systems, according to the book by Dukhin and Goetz [4]. Illustration of these different models can be found in Fig. 2. Only models 2 and 3 will be discussed here. Model 1, the flocculation model, is related more to the particle sizing, and therefore less relevant for rheology.

Fig. 2.

Block diagram of Acoustic Spectrometer that yields raw data for longitudinal rheology.

Consequently, the list of these model-dependent applications includes:

(1) Model 2: Hookean coefficient of inter-particles bonds;

(2) Model 3: Micro-viscosity measurement at the MHz range and particle sizing in non-Newtonian liquids.

We would like to emphasize here one peculiar feature pertaining to the characterization of complex liquids using ultrasound. The raw data collected with an acoustic spectrometer (i.e. attenuation frequency spectra and sound speed) can be used for two purposes, depending on the model selected for the raw data interpretation.

Use of the homogeneous model leads to rheological outputs, and as is such the instrument can be considered a Rheometer.

Selection of the heterogeneous model makes the instrument function as Particle Size Analyzer, because the typical output result is a particle size distribution. Of the 1,000 instruments of this type installed currently, most function as Particle Sizers Analyzers.

However, these instruments make it possible to combine both models in the software. In such case the instrument can perform both functions: Rheometer and Particle Size Analyzer.

An apt analogy for understanding the differences between the homogeneous and heterogeneous models is milk: from a macroscopic standpoint, milk can be considered a single homogenous liquid, which we refer to simply as “milk.” However, if we take a more microscopic viewpoint, milk can also be classified as milk fat and proteins suspended in water. In both cases the liquid is the same, but the viewpoint from which we explore the liquid is different. And as is such, the properties of the liquid that we explore change, depending on the viewpoint used.

Lastly, we do not claim for this review to be an overview of all existing experiments conducted and published in the field of longitudinal rheology. We did our best to include as much relevant work as we could find, however it is possible that some important studies might remain unmentioned here because we are not aware of them, and we present an apology to the authors if such is the case.

2 INSTRUMENTS AND PRINCIPLES OF MEASUREMENT

There are several commercial Acoustic Spectrometers that claim the capability of measuring attenuation and sound speed in the MHz range. They are produced by following companies, among others: Sympatec, Inc.; Matec; Colloidal Dynamics; Thermo Fisher Scientific; and Dispersion Technology Inc.

Despite all being Acoustic Spectrometers making measurements in the MHz range, there are large differences between all of these instruments. Rather than discuss those differences here, we refer interested readers to International Standards ISO-20 998, Parts 1, 2, and 3 [13–15]; and the Elsevier published book, 3d Edition, on this subject by Dukhin and Goetz [4].

The general principles of acoustic spectrometry were initially formulated in the early 1940s by Pellam and Galt [16], and independently by Pinkerton [17], with further developments continuing through the mid-1960s. These early investigators were perhaps the first to apply and justify two basic principles:

(1) The use of a pulse technique;

(2) The use of a sensor with a variable acoustic path length (i.e. variable gap measurements).

Figure 3 presents a block-diagram for a generic acoustic spectrometer. For such an instrument, the electronic block generates electric pulses of a certain length and repetition. The frequency of these pulses should be variable within range of 1–100 MHz. A transmitting piezoelectric transducer converts these electric pulses to ultrasound pulses of the same frequency and with intensity I₀. These ultrasound pulses then propagate through the liquid sample and are attenuated. The receiving piezo-electric transducer measures these attenuated ultrasound pulses and converts them back into electric pulses, which are then sent back to the electronic block for comparison.

Fig. 3.

Various models used for describing structured complex liquid studied using longitudinal rheology.

The intensity of a received ultrasound pulse, I_x, depends on the distance between transmitter and receiver, x, and attenuation coefficient, α, which is a characteristic of the liquid sample. There is a law known as the “Beer–Lambert law” [18, 19] which predicts the exponential decay of an energy beam as it propagates through media:

$${{I}_{x}} = {{I}_{0}}{\text{exp}}( - \alpha x).$$

(7)

This law allows for calculation of the attenuation coefficient if the initial intensity, I₀, is known. This initial intensity can be determined via calibration with a known material. However, such an approach complicates these measurements, making them less reproducible.

Another approach which utilizes the Beer–Lambert law employs multiple gaps between the transmitter and receiver. Doing so eliminates the need for calibration. This is achieved because instead of using an absolute intensity, this approach focuses on the ratio of input to output ultrasound intensities. The Beer–Lambert law states that, the ratio of ultrasound intensities is linked to the particular gap X_i and attenuation coefficient α as follows:

$$\alpha {{X}_{i}} = \ln \frac{{{{I}_{0}}}}{{{{I}_{{{{x}_{i}}}}}}}.$$

(8)

This means that the ratio of ultrasound intensities, measured at different gaps between the transmitter and receiver (expressed in decibels), should be a linear function of the gap. This conclusion is easily verifiable experimentally. Figure 4 shows the intensity ratios (in decibels) versus gap for various frequencies measured for distilled water at room temperature. The linearity of this data confirms the Beer–Lambert law.

Fig. 4.

Loss of acoustic energy in the sample (logarithm of the ratio initial pulse energy to transmitted pulse energy) versus distance between transmitter and receiver at different frequencies for distilled water at 25°C [4].

Accordingly, the slope of each linear regression is the attenuation coefficient at that frequency.

There are multiple benefits of using this “multiple gaps” approach in combination with the Beer–Lambert law:

(1) This method eliminates the need for calibration, because instead of absolute intensity the acoustic sensor measures rate of energy loss.

(2) This approach has a low sensitivity to contamination of the transducer surfaces. Concentrated samples could potentially build up deposits on the faces of the two transducers. These deposits of particles would affect absolute acoustic energy, but not the rate of its decay during pulse propagation through the sample. As is such, the ratio of input to output intensities would not be affected.

(3) Verification that sample remains unchanged during the measurement, which is necessary condition for Beer−Lambert law. This verification is confirmed via a high coefficient of determination, r ², for the linear regression data.

(4) This approach is non-destructive to the sample. This sets longitudinal rheology measurements apart from classic shear rheology measurements.

In addition to reliable attenuation measurements, the multiple gap method offers a simple way to measure sound speed: the instrument measures “time of the pulse flight” for the each gap. The slope of the time of flight versus gap dependence yields sound speed.

Upon completion of an ultrasound attenuation measurement, the instrument uses the measured raw data (attenuation frequency spectra and sound speed) for calculation of parameters that are more useful for the end user. As was stated earlier, most of existing instruments of this function as particle sizers, and so typically this raw data is converted into a particle size distribution, using known theory and input parameters, as described in the book by Dukhin and Goetz [4].

However, some of such instruments operate as longitudinal rheometers. Their software uses the raw data to calculate the following visco-elastic high frequency properties:

(1) Elastic modulus G ' and viscous modulus G '', according to Eqs. (3) and (4).

(2) Longitudinal viscosity, η_long, according to the following equation:

$$G^{*} = G{\kern 1pt} '\, + jG{\kern 1pt} '' = G{\kern 1pt} '\, + i\omega {{\eta }_{{{\text{long}}}}}(\omega ).$$

(9)

(3) Bulk viscosity, η_b, using following expression:

$${{\eta }_{{\text{b}}}} = \eta _{{{\text{long}}}}^{{}} - \frac{{\text{4}}}{{\text{3}}}\eta {\kern 1pt} {\text{.}}$$

(10)

(4) Compressibility of the liquid, β, using Eq. (1).

(5) Micro-viscosity if particle size and sample composition are known.

(6) Hookean coefficient of inter-particle bonds, as described in the US patent 6 910 367 [20].

(7) The instrument can also conduct a “Newtonian/non-Newtonian liquid test”.

Below we present some critical specifications of such an acoustic spectrometer instrument, which would ensure its capability of characterizing practically any complex liquid, from pure water to curing cement slurries and bitumen emulsions:

Shear rate: for a longitudinal rheometer this can be estimated as the frequency of ultrasound, which must be in the range from 10⁶ up to 10⁸ (1/s).

Viscosity of the sample: up to 20 000 cP.

Attenuation coefficient range: up to 20 dB/cm for 1 MHz, and up to 2000 dB/cm at 100 MHz.

Attenuation coefficient precision: 0.01 dB/cm/MHz.

Sound speed precision: 0.1 m/s.

3 APPLICATIONS: HOMOGENOUS MODEL FRAMEWORK

We discuss here only those applications of longitudinal rheology that employ macroscopic characteristics of the liquid samples, such as visco-elastic modulus, viscosity, and compressibility. The relationship of these properties to the microscopic structure is discussed, but only on qualitative level. However, microscopic structures, such as colloidal particles in suspension, are a part of the heterogeneous model, and will be discussed in the section pertaining to this model specifically.

3.1 Newtonian/non-Newtonian Liquid Test in the MHz Range

A “Newtonian liquid” is a fluid in which the relationship between applied stress and resulting strain is linear. Consequently, in the case of an oscillating stress, the visco-elastic modulus for such a fluid is independent of both shear rate and frequency. Deviation from Newtonian behavior is usually associated with the existence of some sort of structure in the liquid. High frequency longitudinal rheology, with a wavelength pulses on the micron scale, is capable of determining micro-structure with a characteristic length on the same micron size scale. Such a test was developed and described in detail in the paper by Dukhin and Goetz [21].

The first step in this Newtonian/Non-Newtonian test is to measure the attenuation spectra of the liquid. Figure 5 presents experimental attenuation spectra for 12 simple liquids. Most of them are typically considered Newtonian, except of pyridine, which is obviously non-Newtonian due to high viscosity. The precision of these attenuation measurements is 0.7% at 35°C and 0.3% at 28°C. This is a significant improvement upon past experiments in this field, such as those conducted by Malbrunot et al. [22].

Fig. 5.

Attenuation spectra of 12 presumably Newtonian liquids [4].

The next step is to convert the attenuation spectra into longitudinal viscosity, η_long, using Eqs. (2) and (9). Figures 6 and 7 present the results of this conversion for 11 presumably Newtonian liquids, except pyridine. In order for a liquid to be Newtonian the longitudinal viscosity must be frequency independent. Figure 6 shows this to be true for 9 of the liquids measured. On the other hand, cyclohexane and butyl acetate, which are shown in Fig. 7, exhibit regular frequency dependence indicating that they are non-Newtonian in the MHz range.

Fig. 6.

Longitudinal viscosity versus frequency for 9 Newtonian liquids [4].

Fig. 7.

Longitudinal viscosity versus frequency for non-Newtonian liquids—butyl acetate and cyclohexane [4].

However, this trend for cyclohexane and butyl acetate is just a qualitative observation. It would be useful to have a way to qualitatively measure how much the longitudinal viscosity deviates from what would be expected for a Newtonian fluid. Fortunately, there are multiple ways to measure this deviation, and it turns out that the linear variation coefficient is best at serving this purpose. This parameter, the linear variation coefficient, is the standard deviation between the linear frequency fit to the experimental data and average attenuation, normalized with the average attenuation. Table 1 presents value of this parameter for the liquids being discussed.

Table 1.   Dynamic and bulk viscosity, compressibility for 12 liquids at 25°C [4]

Table 1 shows that the linear variation coefficient is much larger for the two non-Newtonian liquids than it is for the 8 Newtonian ones. It has been suggested to use a linear variation coefficient values equal to 0.05 as the threshold that separates Newtonian and non-Newtonian liquids.

The data for cyclohexane and butyl acetate demonstrate the value of employing longitudinal rheology measurements. Both liquids behave as Newtonian liquids when measured with shear rheometers, yet their longitudinal viscosities are non-Newtonian. Depending on the application, use of only shear viscosity data could be misleading. Furthermore, these results reveal the value in comprehensive rheological assessment of liquids.

In their 2019 paper, Dukhin, Parlia, and Somasundaran applied this test to binary mixtures of a non-polar Newtonian liquid (toluene) with various non-Newtonian liquid surfactants [23]. The longitudinal viscosities of these mixtures are shown in Figs. 8 and 9, with Fig. 8 presenting the data for mixtures with short-chain Span surfactants, and Fig. 9 for long-chain Xiameter surfactants.

Fig. 8.

Longitudinal viscosity calculated from ultrasound attenuation at frequencies from 10 MHz to 100 MHz for (a) Span 20 and (b) Span 80 mixtures with toluene. Legend contains results of Newtonian liquid test conducted according to statistical verification test presented in the paper [21].

Fig. 9.

Longitudinal viscosity calculated from ultrasound attenuation at frequencies from 10 MHz to 100 MHz for (a) OFX-5098 and (b) OFX-0400 mixtures with toluene. Legend contains results of Newtonian liquid test conducted according to statistical verification test presented in the paper [23].

For all cases explored in the 2019 paper, mixtures with significantly high surfactant content were non-Newtonian on the MHz scale, because their longitudinal viscosity is frequency dependent. However, dilution with toluene caused them to eventually become Newtonian at certain critical surfactant concentrations. The legends of Figs. 8 and 9 indicate this transition. Here we present the concentration threshold in numbers for each mixture with toluene (in weight %):

• Span 20                                      —below 1.5%

• Span 80                                      —below 1.5%

• Xiameter OFX-5098                —above 12.8%

• Xiameter OFX-0400                —above 25%

The data above makes clear that there is a significant difference in critical concentration between the short-and long-chain surfactants.

The short-chain Span surfactants behave as non-Newtonian liquid mixtures even at very low concentrations. It is only around 1% that we begin to see them transition to being Newtonian. This non-Newtonian behavior, even at moderately low concentrations (e.g. 5%) is possibly the result of micelle formation.

By contrast, the longitudinal viscosity curves for mixtures with long-chain surfactants become nearly identical to that of pure toluene at rather high concentrations, on scale of tens of percent. We can assume that their contribution to the longitudinal viscosity at higher concentrations is related to macroscopic structure. However as macroscopic structure disappears due to dilution, the contribution from individual molecules becomes indistinguishable from pure toluene.

The fact that oscillation of the long-chain molecules in an ultrasound wave does not contribute to the overall longitudinal viscosity of the system indicates that these long-chain molecules are practically purely elastic. Their oscillation is thermodynamically reversible and does not lead to energy dissipation.

3.2 Bulk Viscosity: the Second Fundamental Viscosity Coefficient

The Newtonian liquid dynamics described by the Navier−Stokes equation can be found in most books on hydrodynamics, for example by Happel and Brenner [24], Landau and Lifshitz [25] and the fundamental work on Theoretical Acoustics by Morse and Ingard [26, 27]. For a compressible Newtonian liquid, the Navier–Stokes equation can be written as:

$$\begin{gathered} \rho \left[ {\frac{{\partial {v}}}{{\partial t}} + ({v}\nabla ){v}} \right] \\ = - {\text{grad}}P + \eta \Delta {v} + \left( {{{{{\eta }}}_{{\text{b}}}} + \frac{4}{3}\eta } \right){\text{grad}}{\kern 1pt} {\text{div}}{\kern 1pt} {v}{\text{,}} \\ \end{gathered} $$

(11)

where v is velocity, P is pressure, t is time, and ρ is density. The last term on the right hand side of this equation takes into account the compressibility of the liquid and becomes important only for such scenarios where liquid compressibility cannot be neglected. It contains two viscosity coefficients. One is familiar dynamic viscosity, η, which is typically measured with shear rheometers. The other one, η_b, is much less known. We use term “bulk viscosity” for this parameter throughout this study, but this same property has been referred to by many different names in various scientific disciplines, as discussed in detail in the book by Dukhin and Goetz [4].

We present here two reasons which justify the importance of bulk viscosity and being able to determine it for liquid media.

The first reason was given by Temkin [28]. He presented a very clear physical interpretation of both dynamic and bulk viscosity in terms of molecular motion. He points out that molecules have translational, rotational, and vibrational degrees of freedom in liquids and gases. The classical dynamic viscosity, η, is only associated with translational motion. Bulk viscosity, η_b, in contrast, reflects the relaxation of both rotational and vibrational degrees of freedom. This leads to the conclusion that if one wants to study rotational and vibrational molecular effects in complex liquids, they must learn how to measure bulk viscosity.

The second reason is that bulk viscosity appears in many commonly used theories of liquids. The well-known classical theories of liquids by Enskog [29], as well as Kirkwood et al. [30, 31] present expressions for both dynamic and bulk viscosity. Additionally there are several recent theories for calculating bulk viscosity for Lennard−Jones liquids using the Green−Kubo model. They are described in theoretical papers by Hoheisel et al. [32], Okumura and Yonezawa [33, 34], Maier et al. [35], Dyer et al. [36], and Bertolini and Tani [37]. However, all of these theories have problems with bulk viscosity calculations. As was stated by Kirkwood at the end of his paper, the numerical calculation of the integrals is possible only for dynamic viscosity, stating that a numerical procedure for calculating bulk viscosity is not possible due to “extraordinary sensitivity to the equilibrium radial distribution function” [31].

Verification of these theories requires experimental data for the bulk viscosity of Newtonian liquids. Unfortunately, to the best of our knowledge, there was only one study that reported experimental bulk viscosities for Newtonian liquids as recently as 2009 (after which time we began publishing papers on the subject). It was a 1964 review by Litovitz and Davis [9] that reported a bulk viscosity for water of 3.09 cP at 15°C, and 2.1 cP for methanol at 2°C. These values were confirmed recently by Holmes et al [38]. These reported values for the bulk viscosity for water and methanol can serve as reference points for new studies on this subject, as well as validate applied experimental procedure.

Dukhin and Goetz published a new study on bulk viscosity in 2009 [21]. They presented data for the 12 liquids that were discussed in the previous section, and which are listed in Table 1. Table 1 also reports data for these liquids’ bulk viscosities. The measurements were conducted with a modern longitudinal rheometer like the ones described earlier.

Bulk viscosity was calculated as a difference between longitudinal viscosity and dynamic viscosity, as specified with Eq. (10), which we repeat here:

$${{\eta }_{{\text{b}}}} = \eta _{{{\text{long}}}}^{{}} - \frac{4}{3}\eta {\kern 1pt} .$$

Interestingly, the bulk viscosity for these twelve liquids varies over a much wider range than the dynamic viscosity, by almost an order of magnitude. This seems to confirm that the bulk viscosity is more sensitive to the molecular structure of the liquid.

There is no established correlation between bulk viscosity and other intensive properties of these liquids, which confirms that bulk viscosity is an independent characteristic of the liquid.

While the concept of “bulk viscosity” can be scientifically justified only for Newtonian liquids, it is often introduced for non-Newtonian liquids as well [39]. Examples of such exist for inks and ionic liquids. Even Dukhin and Goetz in the 2009 paper [21] had assigned bulk viscosity values to three liquids, pyridine, cyclohexane and butyl acetate, which are non-Newtonian at MHz range. Nevertheless, usage of bulk viscosity can be justified to some degree in such cases as at least a qualitative measure of rotational and oscillational molecular motion. This might be considered as the third reason for studying this characteristic of liquids.

3.3 Compressibility and its Relationship to Molecular Solvating Layers and Micelles

Compressibility is another parameter that can be easy measurable with a longitudinal rheometer. These devices measure sound speed in liquids using the “time-of-flight method”, as was described in Section 2. Sound speed is link to the compressibility according to the Eq. (1) reprinted below:

$${{V}^{2}} = \frac{{\text{1}}}{{\beta \rho }}.$$

Table 1 presents compressibility data attained via sound speed measurement, for the 12 liquids discussed in the previous sections. These data is taken from the book by Dukhin and Goetz [4], whereas the table in their initial 2009 paper [21] contains an error in reporting the compressibility of these liquids.

Compressibility is useful by itself as a measure of a liquid’s elastic properties. However, there is a unique application in which compressibility data is especially valuable. Compressibility can be used for estimating the solvating number of ions, as well as to study solvating layers in general. This method is associated with name of Passynski [40] and sometimes is referred to as the “Passynski method” [41, 42].

This Passynski method is based on the observation that the polar molecules of a solvent experience a strong compression in the vicinity of ions, due to strong electric field present there, making the solvent molecules less flexible (i.e. elastic). This effect is comparable to a very high static pressure in that area, which would similarly make solvent molecules more rigid. In both cases the visco-elastic properties of the solvent in these layers are quite different compared to the bulk. In particular, this would lead to a decline in compressibility (i.e. increased rigidity) of the polar solvent with increased ionic strength and, consequently, increased sound speed.

Figure 10 shows the dependence of sound speed on ion concentration for 7 aqueous electrolytes. The data shows that sound speed does in fact increase with electrolyte concentration. This effect can be measured even at concentrations below 0.1 M, taking into account that the precision of the sound speed measurements is about 0.1 m/s.

Fig. 10.

Sound speed dependence of the aqueous electrolyte solution on the concentration of various electrolytes [4].

Compressibility values for these electrolyte solutions at 1 M concentration are shown in Table 2. It appears as if, at this concentration, the ions enforce some structure within the liquid. This effect is stronger for the more highly charged ions, which agrees with the underlying observation that rigidness of the solvating layers is responsible for this effect.

Table 2.   Compressibility of various aqueous electrolytes at 1 M concentration [4]

Compressibility of electrolyte solutions is linked to solvating numbers via the “Passynski equation,” which is part of the described Passynski method [40]. It links the solvating number, n_sol, with compressibility of water, β_wat, and compressibility of the electrolyte solution, β_el, as follows:

$${{n}_{{{\text{sol}}}}} = \frac{{{{n}_{1}}}}{{{{n}_{2}}}}\left( {1 - \frac{{\beta _{{{\text{el}}}}^{{}}}}{{\beta _{{{\text{wat}}}}^{{}}}}\frac{{{{{v}}_{{{\text{el}}}}}}}{{{{n}_{1}}{{{v}}_{{{\text{wat}}}}}}}} \right),$$

(12)

where n₁ and n₂ are the numbers of moles of solvent and solute in the solution, respectively, v_el is the partial volume of electrolyte solution, and v_wat is the partial molar volume of pure solvent.

Papers by Glinski and Burakowski [41], and Bockris and Saluja [42] present solvating numbers calculated with this method for various solutions.

The fact that electrostatic interaction causes a measurable effect on compressibility and sound speed must have some implications for low-polar solutions that contain micelles. The electrostatic interactions between polar heads of the surfactants molecules that form micelles should affect the compressibility of these objects, making them stiffer (i.e. more rigid). Consequently, compressibility must decline with increasing concentration of surfactant and other amphiphilic substances in such liquid mixtures.

The recently published paper by Dukhin, Parlia, and Somasundaran [23] confirms this conclusion. Figure 11 presents compressibility data for 4 different surfactant solutions in toluene. Compressibility indeed declines with increasing surfactant concentration for 3 of these surfactants. It remains constant for the fourth one due to that surfactant’s own compressibility equaling that of the continuous phase toluene.

Fig. 11.

Compressibility calculated from the sound speed measured at 10 MHz for toluene mixtures with Span and OFX surfactants [4].

Longitudinal measurements of compressibility can also be applied for characterizing the compressibility of soft colloidal particles. This method was applied for determining the compressibility of erythrocytes by Toubal et al. [43] and Dukhin et al. [44]; and for polymeric latex particles by Stieler et al. [45] and Barrett-Gultepe et al. [46].

It is important to mention here that attenuation, and consequently viscosity, is much less sensitive to presence of ions. The data in Table 2 indicates that mono-valent ions do not cause any measurable effect on attenuation data. Multi-valent ions do affect attenuation, but only at very high ionic strength.

Additionally, longitudinal rheology overlaps with another scientific discipline known as “relaxation spectroscopy”, popularized in the 20th century. In 1967 Manfred Eigen, Ronald Norrish, and George Porter received a Nobel Prize for their relaxation spectroscopy research into high-speed chemical reactions. Relaxation spectroscopy includes any experimental technique based on the variation of a thermodynamic parameter with time. Therefore, by definition, acoustic spectroscopy is a form of relaxation spectroscopy. Dielectric spectroscopy, another technique perhaps more familiar in Colloid Science, is another. Both acoustic and dielectric spectroscopies were used in the middle of the 20th century for investigating the properties of electrolyte solutions [47–49]. These studies are associated usually with the scientist Dr. Manfred Eigen.

3.4 Micelles and Sol-Gel Transition

The application of acoustic spectroscopy for studying solutions of soft particles, and critical phenomena within them, was discussed 60 years ago by Mason [50]. Since then there have been number of related studies on this subject. For instance, a group from Guelph University applied longitudinal rheology methods for study of milk gelation [51]. A 2009 paper by Ting et al. [52] is dedicated to study of tofu gelation. This method has also been used for determining critical micelle concentration [53, 54].

We reproduce here results presented in the paper published by Prof. Palmieri’s lab group [55], because they specifically used longitudinal rheology for describing both micellar solution and sol-gel transition. They used poloxamers, which are triblock copo-lymers of polyethylene oxide (PEO) and polypropylene oxide (PPO), available in different molecular weights and PPO/PEO ratios. These amphiphilic substances form micelles and strong gels at certain temperatures.

The authors of this paper measured the attenuation frequency spectra and sound speed of these solutions at different temperatures. This data was explored from a longitudinal rheology standpoint to determine elastic $G_{{{\text{long}}}}^{{{'}}}$ and viscous $G_{{{\text{long}}}}^{{{{''}}}}$ modulus. They used just a single frequency for measurements (50 MHz), which turned out to be sufficient for observing both micellization and sol-gel transition as function of temperature.

Elastic modulus $G_{{{\text{long}}}}^{{{'}}}$ (Fig. 12) decreases during micellization until reaching a plateau value, a trend that more evident in the concentrated systems For the 17.5 and 20% samples it is also possible to identify a slight inflexion after the plateau, which may be identified as the sol/gel transition since the corresponding values of temperature are in agreement with those determined via shear rheology and thermal analysis.

Fig. 12.

G ' and G '' values of Poloxamer 407 samples at different concentration (6–20% w/v) at different temperature calculated at the frequency of 50 MHz [55].

The decrease in the $G_{{{\text{long}}}}^{{{'}}}$ values with micellization and sol/gel transition is related to the water molecules’ interactions with both micelles and the sol structure. This effect was mentioned previously in the section dedicated to compressibility. Water that is trapped in the solvating layers has a higher rigidity due to the effects of surface forces. Consequently, increasing the amount of such water (in the solvating layers) via micellization causes a reduction of the total system compressibility. This decrease in compressibility yields an increase in sound speed, connected with increased micelle rigidity.

Viscous modulus $G_{{{\text{long}}}}^{{{{''}}}}$ exhibits similar two transition points, but they are more pronounced, as shown in Fig. 12. In this case the increase in modulus values corresponds to the monomer/micelle transition, which is accompanied by an initial increase of $G_{{{\text{long}}}}^{{{{''}}}}$, followed by a plateau at the end of the transition. For the samples with concentrations of 20 and 17.5%, gelation is also visible. This gelation can be identified by an increase in the $G_{{{\text{long}}}}^{{{{''}}}}$ modulus, in tandem with the reduction of the $G_{{{\text{long}}}}^{{{'}}}$ modulus previously described.

3.5 Dissolution of Polymers

Water-soluble polymers and hydrocolloids are important materials used for wide variety of applications. Accordingly, it is necessary to understand the mechanisms by which they interact with water. Solvent penetration and swelling of the particle surface are two phenomena known to occur during polymer dissolution. The transition from a glassy to a rubbery state is followed by swelling, after which the polymeric chains disentangle from the surface of the swollen layer, allowing the free polymeric chains to move into the bulk solution through the boundary layer [56–58].

A paper by Prof. Palmieri [59] describes the feasibility of using acoustic spectroscopy as a method for studying the dissolution kinetics of hydrophilic polymers. The variation of the longitudinal rheological parameters $G_{{{\text{long}}}}^{{{'}}}$ and $G_{{{\text{long}}}}^{{{{''}}}}$ with time is used for the step-by-step monitoring of hydrophilic polymer dissolution. In order to compare acoustic spectroscopy results, classical shear viscosity measurements were also performed to follow the variation of viscosity over time, as this physical parameter is directly proportional to the concentration of the dissolved polymer.

In the work by Prof. Palmieri well-known polysaccharides λ-carrageenan, xanthan gum and gellan gum were chosen as model polymers because they are among the most widely used of their kind, not only in the pharmaceutical field, but in foods and cosmetics as well.

Figure 13 reports $G_{{{\text{long}}}}^{{{'}}}$ and $G_{{{\text{long}}}}^{{{{''}}}}$ versus time for solutions with unsieved gellan gum powder, as an example to demonstrate their behavior as a function of time. The data shows complete dissolution occurs after 100 minutes. The moduli themselves showed opposing trends: $G_{{{\text{long}}}}^{{{'}}}$ increased with time while $G_{{{\text{long}}}}^{{{{''}}}}$ decreased. These results denote progressive polymer solvation, which corresponds to an increase of the elastic contribution ($G_{{{\text{long}}}}^{{{'}}}$) and a decrease of the viscous contribution ($G_{{{\text{long}}}}^{{{{''}}}}$). Calculation of the slope from the initial part of the $G_{{{\text{long}}}}^{{{'}}}$ curve (t < 4000 s) yielded a solvation rate of 2.55 × 10⁵ min^–1.

Fig. 13.

Evolution of (1) $G_{{{\text{long}}}}^{{{'}}}$ and (2) $G_{{{\text{long}}}}^{{{{''}}}}$ moduli for the unsieved gellan gum powder at 1% (w/w) concentration calculated at the frequency 50 MHz and at the temperature 25°C [55].

Further exploration of these samples revealed that $G_{{{\text{long}}}}^{{{'}}}$ evolution depends on the particle size, as is shown in Fig. 14. The smaller fraction (<0.053 mm) reached the plateau value for both moduli, showing complete polymer dissolution after 50 minutes. This particle size-dependent impact on dissolution rate is not unusual, as smaller particles have a greater specific surface than larger ones. The other fractions showed complete dissolution, but at a slower rate, with values of $G_{{{\text{long}}}}^{{{'}}}$ only reaching the plateau at the end of the analysis (which lasted 10 000 seconds in total).

Fig. 14.

Evolution of $G_{{{\text{long}}}}^{{{'}}}$ and $G_{{{\text{long}}}}^{{{{''}}}}$ moduli for the different fractions of gellan gum powder at 1% (w/w) concentration calculated at the frequency 50 MHz and at the temperature (a) 25 and (b) 45°C [58].

The analysis performed at 45°C, presented in Fig. 14b, depicts a higher dissolution rate, as expected. The fraction of larger sized particles (0.143 mm), as an example, showed an initial solvation rate of 6.37 × 10⁵ min^–1. However, at this temperature the slope for all $G_{{{\text{long}}}}^{{{'}}}$ curves were quite similar, implying that a temperature increase tends to reduce the differences in the dissolution rate.

The paper by Brochards and De Gennes from which this data derives is significant because, in addition to acoustical longitudinal rheology analysis, the authors conducted traditional rheological measurements of the shear viscosity for comparison [58].

Figure 15 demonstrates the evolution of measured shear viscosity over time for the same samples that were measured with longitudinal rheology, see Fig. 14. It turns out that shear viscosity reaches a plateau similarly to $G_{{{\text{long}}}}^{{{'}}}$ and $G_{{{\text{long}}}}^{{{{''}}}}$, corresponding to the full dissolution of the polymer.

Fig. 15.

Evolution of the shear viscosity for the unsieved powder and for the different fractions of gellan gum powder at 1% (w/w) concentration calculated at the frequency 50 MHz and at the temperature (a) 25 and (b) 45°C [58].

The authors of this study concluded that the kinetics of polymers dissolution observed by both methods are of the same rank order. However, the absolute value of the dissolution rates differs between methods. There are several factors which might be responsible for these differences.

First, longitudinal viscoelastic parameters are measured at very high frequencies, whereas shear viscosity is measured with a classical rheometer at low frequency.

Secondly, the mixing conditions in an acoustic spectrometer differ significantly from that of a classical rheological instrument with moving coaxial cylinders. The shear rheometer applies much more vigorous stirring, which might contribute to more rapid kinetics of dissolution observed with that technique.

The authors concluded that, from a scientific point of view, these two techniques can be considered complementary. Classical shear rheological analyses essentially describe the “in bulk” properties of a system, even if some considerations pertaining to the microstructure of the system can be obtained from the modelling of frequency sweep tests. Acoustic longitudinal elastic moduli, because they depend strictly on the energy and phase variation of the ultrasound wave, reflect the microstructural changes of the system, such as those concerning the interface between colloid and medium, and the amount of water bound to the colloid itself.

4 APPLICATIONS WITHIN THE HETEROGENEOUS MODEL FRAMEWORK

In this section we discuss only applications of longitudinal rheology which model the liquid sample as heterogeneous system, i.e. as a collection of particles in liquid. In Section 1 three models for describing micro-structure in heterogeneous systems were introduced. In this section we provide more detail for Model 2 and Model 3.

4.1 Micro-Viscosity Measurement at MHz Range

The concept of “micro-viscosity” has been known for several decades, although it is not clear who invented it initially. There are two recent reviews on this subject [60, 61] that outline this idea and the related research. The concept of micro-viscosity is relevant for complex systems with particles imbedded into Newtonian or non-Newtonian liquids. Model 3 in Fig. 2 illustrates two extreme cases of such systems.

Case (A) corresponds to small particles in gel formed by large macromolecules, with mesh exceeding particle size. In the case, the macro-structure gel is too large to impact the small particles, and therefore the viscosity experienced by the particles is that of the pure background liquid.

Case (B) is the opposite scenario, where large particles are present in a gel with a small mesh. In this case particles will sense “macro-viscosity” of the gel.

There exists an intermediate case where particle size is comparable with gel mesh size, and moving particles would experience a so-called “micro-viscosity” that lies in between the viscosity of the pure background liquid and the macro-viscosity of the gel. Determination of micro-viscosity is critical for proper particle sizing in such systems. The only known way of finding this value is by using particles of known size as testers of such viscosity. In the case where the measurement conducted utilizes dynamic light scattering (DLS), the equation for diffusion coefficient is solved with regard to viscosity by using the known particle size.

This method can be applied for ultrasound-based measurements as well. Commercial acoustic particle sizers have been offering this option for the last 2 decades. Here we present the results of such tests conducted by Prof. Berg’s lab group from Washington State University, and published in Langmuir in 2010 [62].

The authors of this paper used three different silica particle types of different sizes: Ludox SM-30, Ludox HS-30, and Ludox TM-40, all from Grace Davison (Columbia, MD). The particle hydrodynamic dimensions were first determined by DLS. Samples for acoustic testing were prepared by mixing the desired quantity of Ludox particles with a 0.5 wt % solution of hydroxypropyl cellulose (HPC). The HPC solutions were cross linked to varying degrees using divinyl sulfone (DVS). The HPC polymer gel mesh was characterized in each case by bulk oscillatory rheological measurements, within the frequency sweep of 1–100 Hz for angular frequency.

The first measurements were made with silica Ludox particles of increasing size (15.9 nm, 20.8 nm, and 29.6 nm) at 6 wt % of dispersed silica in a 0.5 wt % HPC gel, prepared using 100 mM of the DVS cross-linker.

In the second set of measurements, the particle size was kept constant at 29.6 nm using Ludox TM-40. The cross-link density of the gel varied due to increasing concentrations of DVS from 75 to 400 mM.

Table 3 summarizes the results of particle sizing by two methods, acoustic spectroscopy and DLS, when gel mesh is much larger than particle size (Case (A)). It is seen that both methods yield very close sizes, statistically identical, when particle size is much smaller than mesh size.

Table 3.   Mean particle diameters obtained with DLS and acoustics for 6 wt % Ludox nanoparticles in a 0.5 wt % HPC gel prepared with 100 mM cross-linker; mesh size 56.8 nm [62]

Table 4 presents particle size data for increasing concentration of the cross-linker (and, accordingly, decreasing mesh size) assuming the viscosity of the continuous phase is equal to that of pure water. This data confirms that the particle size determined via acoustic spectroscopy begins to deviate from the known correct value when the mesh size becomes less than particle diameter. This occurs for 400 mM cross-linker concentration when mesh size is 19 nm, which is less than the particle size of 30 nm. For lower cross-linker concentrations and higher mesh-sizes, the particle size in gel is identical to the calculated particle size in water.

Table 4.   Mean particle diameter obtained with acoustics for 6 wt % Ludox TM-40 with expected size 30 nm nanoparticles at 0.5 wt % HPC and different cross-linker concentration [62]

These results emphasize the importance that viscosity plays in particle size calculations and begs the question: What viscosity value should be used for the proper particle size characterization if the mesh-size becomes comparable to particle size?

This question is a general one and exists for all techniques that depend on viscosity for calculating particle size: DLS, acoustic spectroscopy, sedimentation, etc. Particle sizing in non-Newtonian liquids using these methods becomes significantly truncated due to the uncertainty of the viscosity value.

Here we present an answer to this question for one example given in the book by Dukhin and Goetz [4]. Dispersion was formed with rutile at 50 wt % in a polymeric liquid. This liquid was non-Newtonian, which was confirmed by a well pronounced frequency dependence of the longitudinal viscosity, as shown in Fig. 16.

Fig. 16.

Longitudinal viscosity of polymeric liquid discussed in the section 4.1.

There are 3 approaches that can be used for selecting a value for micro-viscosity to be used in particle size calculations for particles in a non-Newtonian liquid.

Approach 1: One can assume that this dynamic micro-viscosity is equal to the macroscopic shear viscosity measured at low frequency with traditional shear rheometer. In the case of this sample the polymeric liquid has a viscosity of 1000 cP.

Approach 2: One can assume a certain relationship between the bulk viscosity and dynamic micro-viscosity as components of the longitudinal viscosity. The software of the commercial instrument used in this study [62] contains an algorithm for estimating dynamic viscosity from the measured attenuation spectra. In the case, according to this approach, the polymeric liquid has a viscosity of 185 cP.

Approach 3: One can assume that the dynamic micro-viscosity is approximately the same as that of water, 1 cP. High frequency of ultrasound measurement provides some justification for this assumption. The amplitude of particle displacement is very small, on the scale of 1 nm for 1 micron particles [4]. This motion only disturbs part of the large molecules of non-Newtonian liquid, just slightly bending them. The corresponding dissipation is therefore much smaller than in the case of strong sliding motion caused by shear rheometers.

Figure 17 presents particle size distributions calculated from the same experimental attenuation spectrum using all three Approaches. The median particle sizes (d50) corresponding to the different viscosities are as follows:

Fig. 17.

Particle size distribution for 50 wt % in polymeric liquid for different micro-viscosities that correspond to different assumptions discussed in the section 4.1.

—Approach 1, viscosity 1000 cP, d50 = 19.96 microns

—Approach 2, viscosity 185 cP, d50 = 7.722 microns

—Approach 3, viscosity 1 cP, d50 = 0.613 microns.

An independent microscopic study indicated that the median particle size is close to 0.6 micron. This points towards Approach 3 as being valid in this case, and that the viscosity experienced by the particles, under the force of an ultrasound wave, is mostly that of the background liquid.

It is our general experience that Approach 3 (micro-viscosity = 1 cP) is valid in many practical cases of particle sizing in non-Newtonian liquids, and is quite useful in many practical applications, such as battery slurries, pigments, electrophoretic displays, etc.

4.2 Hookean Coefficient of Interparticle Bonds

This section is dedicated to the micro-rheology of concentrated dispersions where particles experience specific colloid-chemical interactions. Polymer bonds between particles and overlapped interacting double layers are just a few examples of such interactions. The motion of particles in an ultrasound field would be affected by these interactions, creating an additional contribution to ultrasound attenuation. As a result, attenuation frequency spectra contain information on these inter-particle bonds. This information can be extracted using an appropriate theory.

This theory of “structural loss” was created and described in the book by Dukhin and Goetz [4], as well as in US Patents 6.910.367, B1 and 6.487.894 [20, 64]. This theory follows the Rouse–Bueche–Zimm model [50], which represents a colloidal suspension as N + 1 beads joined together by N springs, as shown in Fig. 2, Model 2.

The viscous resistance of the beads moving through the liquid is inversely proportional to the Stokes’ drag coefficient, and causes viscous dissipation. The springs between the beads represent the stress-strain relationship. This model is successfully used to describe classical rheological behavior. It was applied to acoustics and longitudinal rheology initially by McCann [63]. He added a Hookean factor to the force balance, but only used the first term, in which force is proportional to displacement. The next logical step was made in the study [64], following Voigt’s model, which states that the stress is proportional not only to displacement, but also to the rate of displacement. Consequently, this additional force F ^hook was presented as superposition of two terms:

$$F_{{}}^{{{\text{hook}}}} = {{H}_{1}}{\kern 1pt} \Delta x + {{H}_{2}}\frac{{\partial x}}{{\partial t}},$$

where Δx is particle displacement in the ultrasound field, and t is time.

Mathematical model is given in the Section 4.3.4 of the book by Dukhin and Goetz [4].

It turns out that the first Hookean coefficient simply shifts the critical frequency, keeping the shape of the curve more or less intact and the peak attenuation constant. This effect is identical to the effect caused by a change in the viscosity of the background liquid.

However, the effect of the second Hookean coefficient H₂ is quite different. It is illustrated in Fig. 18 for a dispersion of 40 vol % alumina having a median particle size of 1 micron. This parameter changes the shape of attenuation frequency spectra and adds additional attenuation at high frequency.

Fig. 18.

Influence of the loss Hookean coefficient, H₂, on the attenuation of sound [4].

This effect was observed experimentally first in research done by Hayashi et al. [65]. These experiments were conducted at the National Institute for Resources and Environment in Tsukuba, Japan [43]. The authors used alumina powders to prepare slurries that were then stabilized using surfactant, a sodium polycarboxylic acid, and ball milled for three days before measurement. They were prepared at various concentrations from 1 to 40 vol % and the acoustic attenuation spectrum was measured.

For concentrations up to 20 vol %, the particle size calculated from these attenuation spectra agreed quite well with independent data on dilute samples. However, the experimentally measured data deviated from the expected results as the volume fraction increased to 40%, as can is shown in Fig. 19.

Fig. 19.

Experimental attenuation for alumina slurry [65] and theoretical fit with (a) no structural loss and (b) with added structural losses.

The addition of structural loss to the theory for ultrasound attenuation fixed this problem, resulting in the theoretical curve fitting the experimental data almost perfectly, as is shown in Fig. 19. To achieve these results, the software in this case conducted a search for particle size distribution and second Hookean coefficient H₂.

5 CONCLUSIONS

Longitudinal rheology is field of study complimentary to traditional shear rheology. It offers a unique opportunity for studying the bulk properties of complex liquids at the MHz frequency range, which is unavailable for shear rheology due to very short penetration depth. This allows for longitudinal rheology to be used to probe structures with characteristic lengths on the scale of microns, and processes with characteristic times on the scale of micro-seconds.

Additionally, this method allows for testing of the Newtonian liquid hypothesis at the MHz range.

Longitudinal rheology is the only method capable of determining a fundamental property of Newtonian liquids, bulk viscosity, which characterizes the rotational and vibrational degrees of freedom.

The application of ultrasound offers a very simple and fast way of measuring sound speed and, consequently, liquid compressibility, which is a characteristic of liquid elasticity.

It can also be applied for monitoring fast processes, such as dissolution.

Longitudinal viscosity offers a way to study the micro-structure of complex liquids, as well as micelle formation.

Lastly, it can be used for measuring the micro-viscosity and Hookean coefficient of slurries with interacting particles.