Diffusiophoretic velocity of a large spherical colloidal particle in a solution of general electrolytes

Abstract

The general expression is derived for the diffusiophoretic velocity of a large spherical colloidal particle of radius a in a concentration gradient of general electrolytes of Debye-Hückel parameter κ. On the basis of this expression, simple approximate analytic expressions for the diffusiophoretic velocity correct to the order of (1/κa)⁰ are derived, which can be applied for large particles with κa ≥ 50 at arbitrary values of the particle zeta potential with negligible errors.

Introduction

Our understanding of diffusiophoresis, that is, the motion of charged colloidal particles in an electrolyte concentration gradient, has been advanced by a lot of theoretical studies [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. In particular, the readers should refer to a review article by Keh [8]. Experimentally observed diffusiophoretic mobility of latex particles was in good agreement theoretical results [25]. In a previous paper [24], we derived a general expression for the diffusiophoretic mobility of a spherical particle of radius a in a solution of symmetrical electrolytes of Debye-Hückel parameter κ. On the basis of this general expression, we obtained an approximate diffusiophoretic velocity expression correct to the order of 1/κa, which is found to be applicable for κa ≥ 20 at arbitrary values of the particle zeta potential. The obtained expression takes a much simpler form than those previously obtained. The leading-order term of the expression is correct to the order of (1/κa)⁰, which is applicable for κa ≥ 50 with negligible errors. In the present paper, we extend the previous theory for the case of symmetrical electrolytes to the diffusiophoresis of large spherical particles in a solution of general electrolytes and obtain approximate diffusiophoretic velocity expressions correct to the order of (1/κa)⁰. Our theory is based on the standard Poisson-Boltzmann theory on the electrical diffuse double layer around a colloidal particle. A comprehensive review of recent advances in the theory of diffuse double layer accounting for the effects of structural details of the ions and the solvent was given by Bohinc et al. [26]. The analytic expressions for the diffusiophoretic velocity of colloidal particles derived in the present paper can thus be applied to the case where the above effects may be neglected.

Theory

Consider a spherical particle of radius a moving with diffusiophoretic velocity U in an aqueous liquid of viscosity η and relative permittivity ε_r containing a general electrolyte under a constant applied gradient of electrolyte concentration. We suppose that the electrolyte consists of N ionic species with valence z_i and drag coefficient λ_i (i = 1, 2, …, N). Let ${n}_{i}^{\infty }$ be the bulk concentration (number density) of the i th ionic species in the absence of the applied electrolyte concentration gradient. The electroneutrality condition is given by $\sum_{i=1}^{N}{z}_{i}{n}_{i}^{\infty }=0$. Let n_i(r) be the concentration (number density) of the i th ionic species at position r. The concentration gradient for the i th ionic species is expressed as ∇n_i in the region beyond the electrical double layer around the particle. We treat the case where all the ionic species have the same relative concentration gradient ∇n_i /${n}_{i}^{\infty }$ and introduce a constant vector a proportional to ∇n_oi:

$$\boldsymbol{\alpha }=\frac{kT}{e{n}_{1}^{\infty }}\nabla {n}_{1}=\frac{kT}{e{n}_{2}^{\infty }}\nabla {n}_{2}=\cdots =\frac{kT}{e{n}_{N}^{\infty }}\nabla {n}_{N}$$

(1)

where e is the elementary electric charge, k is the Boltzmann constant, and T is the absolute temperature. The origin of the spherical polar coordinate system (r, θ, ϕ) is held fixed at the center of the particle and the polar axis (θ = 0) is put parallel to a. For a spherical particle, U is parallel to a. We treat the case where the following conditions are satisfied: (i) The electrolyte concentration gradient field a is weak so that U is linear in a, where a =|a| and U is the magnitude with sign of U (positive (negative) values of U correspond to migration toward higher (lower) electrolyte concentration). (ii) In the absence of a, the particle has a uniform surface potential, which is regarded as the particle zeta potential z at r = a, where r =|r|. (iii) The Reynolds number of the liquid flow is small enough to ignore inertial terms in the Navier–Stokes equation and the liquid can be regarded as incompressible. (iv) Electrolyte ions cannot penetrate the particle surface. (v) The liquid flow velocity relative to the particle is zero at the particle surface.

The Navier-Stoke equation for a steady incompressible liquid flow velocity u(r) = (u_r(r), u_θ(r), 0) at low Reynolds numbers and the continuity equation for u(r) are given by

$$\eta \Delta {\varvec{u}}\left({\varvec{r}}\right)-\nabla p\left({\varvec{r}}\right)-{\rho }_{\mathrm{el}}({\varvec{r}})\nabla \psi ({\varvec{r}})={\varvec{0}}$$

(2)

$$\nabla \cdot {\varvec{u}}({\varvec{r}})=0$$

(3)

where p(r) is the pressure, ψ(r) is the electric potential, and ρ_el(r) is the charge density given by

$${\rho }_{\mathrm{el}}\left({\varvec{r}}\right)=\sum_{i=1}^{N}{z}_{i}e{n}_{i}\left({\varvec{r}}\right)$$

(4)

The velocity v_i(r) = (v_ir(r), v_iθ(r), 0) of the i th ionic species, which is given by

$${{\varvec{v}}}_{i}({\varvec{r}})={\varvec{u}}({\varvec{r}})-\frac{1}{{\lambda }_{i}}\nabla {\mu }_{i}({\varvec{r}})$$

(5)

satisfies the following continuity condition:

$$\nabla \cdot {(n}_{i}{{\varvec{v}}}_{i}({\varvec{r}}))=0$$

(6)

where

$${\mu }_{i}\left({\varvec{r}}\right)={\mu }_{\mathrm{o}}^{i}+{z}_{i}e\psi \left({\varvec{r}}\right)+kT\mathrm{ln}{n}_{i}\left({\varvec{r}}\right)$$

(7)

is the electrochemical potential of the i th ionic species and ${\mu }_{\mathrm{o}}^{i}$ is a constant terms of μ_i(r).

The deviations of n_i(r), ψ(r), μ_i(r), and ρ_el(r) from their equilibrium values are small for a weak field a, so that we may write

$${n}_{i}\left({\varvec{r}}\right)={n}_{i}^{(0)}\left(r\right)+\delta {n}_{i}({\varvec{r}})$$

(8)

$$\psi \left({\varvec{r}}\right)={\psi }^{(0)}\left(r\right)+\delta \psi \left({\varvec{r}}\right)$$

(9)

$${\mu }_{i}\left({\varvec{r}}\right)={\mu }_{i}^{(0)}+\delta {\mu }_{i}\left({\varvec{r}}\right)$$

(10)

$${\rho }_{\mathrm{el}}\left({\varvec{r}}\right)={\rho }_{\mathrm{el}}^{\left(0\right)}\left(r\right)+\delta {\rho }_{\mathrm{el}}\left({\varvec{r}}\right)$$

(11)

where the quantities with superscript (0) refer to those at equilibrium in the absence of a.

We assume that the equilibrium concentration ${n}_{i}^{(0)}\left(r\right)$ obeys the Boltzmann distribution and the equilibrium electric potential y⁽⁰⁾(r) satisfies the Poisson-Boltzmann equation, viz.,

$${n}_{i}^{(0)}\left(r\right)={n}_{i}^{\infty }\left(r\right){e}^{-{z}_{i}y(r)}$$

(12)

$$\Delta y\left(r\right)=-{\kappa }^{2}\frac{\sum_{i=1}^{N}{z}_{{\varvec{i}}}{n}_{i}^{\infty }{e}^{-{z}_{i}y(r)}}{\sum_{i=1}^{N}{z}_{i}^{2}{n}_{i}^{\infty }}$$

(13)

with

$$y(r)=\frac{e{\psi }^{(0)}(r)}{kT}$$

(14)

$$\kappa =\sqrt{\frac{\sum_{i=1}^{N}{z}_{i}^{2}{e}^{2}{n}_{i}^{\infty }}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}}$$

(15)

where y(r) is the scaled equilibrium electric potential, κ is the Debye-Hückel parameter, and ε_o is the permittivity of a vacuum.

The boundary conditions for n_i⁽⁰⁾(r), ψ⁽⁰⁾(r),u(r), and δn_i(r) are given by

$${n}_{i}^{(0)}\left(r\right)\to {n}_{i}^{\infty }\ \mathrm{as} \ r\to \infty$$

(16)

$${\psi }^{(0)}(r)\to 0\ \mathrm{as} \ r\to \infty$$

(17)

$${\psi }^{\left(0\right)}\left(a\right)=\zeta$$

(18)

$${\varvec{u}}\left({\varvec{r}}\right)\to -{\varvec{U}}\boldsymbol{ }\ \mathrm{as} \ r\to \infty$$

(19)

$${\varvec{u}}\left({\varvec{r}}\right)=0\ \mathrm{at}\ r = a$$

(20)

$$\delta {n}_{i}\left({\varvec{r}}\right)\to \left|\nabla {n}_{i}\right|r\mathrm{cos}\theta =\frac{e{n}_{i}^{\infty }}{kT}\alpha r\mathrm{cos}\theta\ \mathrm{as }\ r \to \infty$$

(21)

The ionic flows v_i(r) induce the diffusion potential field, which nullifies the net electric current. The electric current density i(r) is given by

$${\varvec{i}}\left({\varvec{r}}\right)=\sum_{i=1}^{N}{z}_{i}e{n}_{i}\left({\varvec{r}}\right){{\varvec{v}}}_{i}\left({\varvec{r}}\right)$$

(22)

By substituting Eqs. (5), (8), and (10) into Eq. (22) and neglecting the products of the small quantities u, δn_i, and δμ_i, we obtain

$${\varvec{i}}\left({\varvec{r}}\right)={\rho }_{\mathrm{el}}^{\left(0\right)}\left(r\right){\varvec{u}}\left({\varvec{r}}\right)-\sum_{i=1}^{N}\frac{{z}_{i}e}{{\lambda }_{i}}{n}_{i}^{\left(0\right)}\left(r\right)\nabla {\updelta \mu }_{i}\left({\varvec{r}}\right)$$

(23)

which must be zero beyond the particle double layer. We thus find that (see Appendix)

$$\updelta \psi \left({\varvec{r}}\right)\to -\beta \alpha r\mathrm{cos}\theta\ \mathrm{as}\ r\to \infty$$

(24)

with

$$\beta =\frac{\sum_{i=1}^{N}\frac{{z}_{i}{n}_{i}^{\infty }}{{\lambda }_{i}}}{\sum_{i=1}^{N}\frac{{z}_{i}^{2}{n}_{i}^{\infty }}{{\lambda }_{i}}}=\frac{\sum_{i=1}^{N}\frac{{n}_{i}^{\infty }}{{{z}_{i}m}_{{i}}}}{\sum_{i=1}^{N}\frac{{n}_{i}^{\infty }}{{m}_{i}}}$$

(25)

where

$${m}_{i}=\frac{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}{3\eta {z}_{i}^{2}{e}^{2}}{\lambda }_{i}$$

(26)

is the scaled drag coefficient of i th ionic species. It follows from Eqs. (21) and (24) that the boundary condition for δμ_i(r) is given by

$${\delta \mu }_{i}\left({\varvec{r}}\right)={z}_{i}e\delta \psi \left({\varvec{r}}\right)+kT\frac{{\delta n}_{i}\left({\varvec{r}}\right)}{{n}_{i}^{\infty }}\to {z}_{i}e\left(\frac{1}{{z}_{i}}-\beta \right)\alpha r\mathrm{cos}\theta\ \mathrm{as}\ r \to \infty$$

(27)

Finally, the boundary condition for v_i(r) is given by

$${v}_{ir}\left({\varvec{r}}\right)=0\mathrm{ \ at\ }r=a$$

(28)

which follows from the condition (iv). In addition, we have the constraint that the net force acting on the particle must be zero.

By symmetry, we may write

$${\delta \mu }_{i}\left({\varvec{r}}\right)=-{z}_{i}e\alpha {\phi }_{i}\left(r\right)\mathrm{cos}\theta$$

(29)

$${\varvec{u}}\left({\varvec{r}}\right)=\left(-\frac{2}{r}h\left(r\right)\alpha \ \mathrm{cos}\ \theta , \frac{1}{r}\frac{d}{dr}\left[rh(r)\right]\alpha \ \mathrm{sin}\ \theta , 0\right)$$

(30)

where ϕ_i(r) and h(r) are functions of r. By substituting Eqs. (29) and (30) into Eqs. (2)–(6), the following equations for ϕ_i(r) and h(r) are obtained:

$$L{\phi }_{i}\left(r\right)={g}_{i}\left(r\right)$$

(31)

$$L(Lh\left(r\right))=G\left(r\right)$$

(32)

with

$$L=\frac{{d}^{2}}{d{r}^{2}}+\frac{2}{r}\frac{d}{dr}-\frac{2}{{r}^{2}}$$

(33)

$${g}_{i}\left(r\right)=\frac{dy}{dr}\left({z}_{i}\frac{d{\phi }_{i}}{dr}-\frac{2{\lambda }_{i}}{e}\frac{h}{r}\right)$$

(34)

$$G\left(r\right)=-\frac{e}{\eta r}\frac{dy}{dr}\sum_{i=1}^{N}{z}_{i}^{2}{n}_{i}^{\infty }{e}^{-{z}_{i}y}{\phi }_{i}\left(r\right)$$

(35)

The boundary conditions, Eqs. (19), (20), (27), and (28) reduce to

$$\frac{d{\phi }_{i}}{dr}=0\ \mathrm{at}\ r=a$$

(36)

$${\phi }_{i}\left(r\right)\to \left(-\frac{1}{{z}_{i}}+\beta \right)r\ \mathrm{as}\ r \to \infty$$

(37)

$$h=\frac{dh}{dr}=0\ \mathrm{at}\ r=a$$

(38)

$$h\left(r\right)\to \frac{U}{2\alpha }r+O\left(\frac{1}{r}\right) \mathrm{as }\ r \to \infty$$

(39)

Equations (31) and (32) subject to Eqs. (36)–(39) can be solved to give

$${\phi }_{i}\left(r\right)=\left(-\frac{1}{{z}_{i}}+\beta \right)\left(r+\frac{{a}^{3}}{2{r}^{2}}\right)-\frac{1}{3}\left(r+\frac{{a}^{3}}{2{r}^{2}}\right){\int }_{a}^{\infty }{g}_{i}\left(r\right)dr+\frac{1}{3}{\int }_{a}^{r}\left(r-\frac{{x}^{3}}{{r}^{2}}\right){g}_{i}\left(x\right)dx$$

(40)

and

$$h\left(r\right)=-\left(\frac{{r}^{3}}{30}-\frac{{a}^{2}r}{18}+\frac{{a}^{5}}{45{r}^{2}}\right){\int }_{a}^{\infty }G\left(x\right)dx+\left(\frac{r}{9a}-\frac{1}{6}+\frac{{a}^{2}}{18{r}^{2}}\right){\int }_{a}^{\infty }{x}^{3}G\left(x\right)dx-{\int }_{a}^{r}\left(-\frac{{r}^{3}}{30}+\frac{r{x}^{2}}{6}-\frac{{x}^{3}}{6}+\frac{{x}^{5}}{30{r}^{2}}\right)G\left(x\right)dx$$

(41)

By using Eq. (39), the magnitude (with sign) U of the diffusiophoretic velocity U is given by

$$U=2\alpha \underset{r\to \infty }{\mathrm{lim}}\frac{h(r)}{r}$$

(42)

From Eqs. (41) and (42), we find that

$$U=\frac{\alpha {a}^{2}}{9}{\int }_{a}^{\infty }\left(1-\frac{3{r}^{2}}{{a}^{2}}+\frac{2{r}^{3}}{{a}^{3}}\right)G\left(r\right)dr$$

(43)

We note that the fundamental electrokinetic equations for the electrophoresis and diffusiophoresis problems are the same except for the boundary condition for ϕ_i(r) for r → ∞. Indeed, Eq. (43) is obtained from the expression for the electrophoretic velocity of a spherical particle in an applied electric field E [27,28,29] by replacing E with α. Thus, by applying the same approximation method as in Ref. [28], we can derive similar approximate formulas for the diffusiophoretic velocity U correct to order (1/κa)⁰ with the same accuracy as those derived for the electrophoresis problem [28]. We define the scaled diffusiophoretic mobility U* as

$${U}^{*}=\frac{3\eta e}{2{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}\frac{U}{\alpha }$$

(44)

We give the results applicable for large particles with κa ≥ 50 at arbitrary values of ζ as follows.

$${U}^{*}=-\frac{1}{2a}{\sum }_{i=1}^{N}{z}_{i}{n}_{i}^{\infty }{\phi }_{i}(a){\int }_{0}^{\stackrel{\sim }{\zeta }}\{{\int }_{0}^{y}\frac{{e}^{-{z}_{i}{y}^{^{\prime}}}-1}{K\left({y}^{^{\prime}} \right)}d{y}^{^{\prime}} \}\frac{dy}{K(y)}$$

(45)

with

$$\begin {aligned}{\phi }_{i}\left(a\right) & =-\frac{3}{2}\left(\frac{1}{{z}_{i}}-\beta \right)a+sgn(\zeta )\frac{{\phi }_{i}(a)}{\kappa a}W{\int }_{0}^{\stackrel{\sim }{\zeta }}\frac{{e}^{-{z}_{i}y}-1}{K(y)}dy\\ &+sgn(\zeta )\frac{3{z}_{i}{m}_{i}}{4\kappa a}W{\int }_{0}^{\stackrel{\sim }{\zeta }}\left[({e}^{-{z}_{i}y}-1){\sum }_{i=1}^{N}{z}_{i}{n}_{i}^{\infty }{\phi }_{i}(a) {\int }_{\stackrel{\sim }{\zeta }}^{y}\left\{{\int }_{0}^{y{^{\prime}}}\frac{{e}^{-{z}_{j}y{^{\prime}}{^{\prime}}}-1}{K({y}^{{^{\prime}}{^{\prime}}} )}dy{^{\prime}}{^{\prime}} \right\}\frac{dy{^{\prime}}}{K({y}^{^{\prime}} )}\right]\frac{dy}{K(y)} \end {aligned}$$

(46)

$$\stackrel{\sim }{\zeta }=\frac{e\zeta }{kT}$$

(47)

and

$$W=\sqrt{\frac{1}{2}{\sum }_{i=1}^{N}{z}_{i}^{2}{n}_{i}^{\infty }},\ K\left(y\right)=\sqrt{{\sum }_{i=1}^{N}{n}_{i}^{\infty }({e}^{-{z}_{i}y}-1)}$$

(48)

where $\stackrel{\sim }{\zeta }$ is the scale zeta potential and sgn(ζ) is + 1(-1) if ζ > 0 (ζ < 0).

Results and discussion

We have derived the general expression (45) for the scaled diffusiophoretic mobility U*. We give below explicit expressions for U* for the case of binary electrolytes.

(i) z₊:z_- binary electrolytes (z₊ > 0 and z_- < 0)

$${U}^{*}=-\frac{1}{2a}{\int }_{0}^{\stackrel{\sim }{\zeta }}\left\{{\int }_{0}^{y}\frac{{\phi }_{+}(a)\left({e}^{-{z}_{+}y{^{\prime}}}-1\right)-{\phi }_{-}(a)\left({e}^{-{z}_{-}y{^{\prime}}}-1\right)}{M({y}^{^{\prime}})}dy{^{\prime}} \right\}\frac{dy}{M(y)}$$

(49)

with

$$M(y)=\sqrt{{(e}^{-{z}_{+}y}-1)/{z}_{+}-({e}^{-{z}_{-}y}-1)/{z}_{-}}$$

(50)

$$\frac{{\phi }_{+}(a)}{a}=-\frac{3}{2}\left(\frac{1}{{z}_{+}}-\beta \right),\ \frac{{\phi }_{-}\left(a\right)}{a}=-\frac{3}{2}\left(\frac{1}{{z}_{-}}-\beta \right)\frac{1}{\left(1+F\right)}\ \mathrm{for } \stackrel{\sim }{\zeta }>0$$

(51)

$$\frac{{\phi }_{+}(a)}{a}=-\frac{3}{2}\left(\frac{1}{{z}_{+}}-\beta \right)\frac{1}{(1+F)},\ \frac{{\phi }_{-}(a)}{a}=-\frac{3}{2}\left(\frac{1}{{z}_{-}}-\beta \right) \mathrm{for } \stackrel{\sim }{\zeta }<0$$

(52)

$$F=\frac{1}{\kappa a}\sqrt{2\left(1-\frac{{z}_{+}}{{z}_{-}}\right)}\left(1+3{m}_{-}\right)\left({e}^{-{z}_{-}\stackrel{\sim }{\zeta /2}}-1\right) \mathrm{for } \stackrel{\sim }{\zeta }>0$$

(53)

$$F=\frac{1}{\kappa a}\sqrt{2\left(1-\frac{{z}_{-}}{{z}_{+}}\right)}\left(1+3{m}_{+}\right)\left({e}^{{-z}_{+}\stackrel{\sim }{\zeta }/2}-1\right) \mathrm{for } \stackrel{\sim }{\zeta }<0$$

(54)

$$\beta =\frac{{(z}_{+}/{z}_{-}){m}_{+}-{(z}_{-}/{z}_{+}){m}_{-}}{{z}_{+}{m}_{+}-{z}_{-}{m}_{-}},\ { m}_{+}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {z}_{+}^{2}{e}^{2}}{\lambda }_{+},\ {m}_{-}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {z}_{-}^{2}{e}^{2}}{\lambda }_{-}$$

(55)

(ii) z:z symmetrical electrolytes (z₊ = -z_- = z > 0)

$${U}^{*}=\frac{6}{{z}^{2}{(m}_{+}+{m}_{-})}\left\{{m}_{+}\mathrm{ln}\left(\frac{1+{e}^{-z\stackrel{\sim }{\zeta }/2}}{2}\right)+\frac{{m}_{-}}{\left(1+F\right)}\mathrm{ln}\left(\frac{1+{e}^{z\stackrel{\sim }{\zeta }/2}}{2}\right)\right\} \mathrm{ for} \ \zeta >0$$

(56)

$${U}^{*}=\frac{6}{{z}^{2}{(m}_{+}+{m}_{-})}\left\{\frac{{m}_{+}}{\left(1+F\right)}\mathrm{ln}\left(\frac{1+{e}^{-z\stackrel{\sim }{\zeta }/2}}{2}\right)+{m}_{-}\mathrm{ln}\left(\frac{1+{e}^{z\stackrel{\sim }{\zeta }/2}}{2}\right)\right\} \mathrm{ for}\ \zeta >0$$

(57)

with

$$F=\frac{2}{\kappa a}\left(1+3{m}_{-}\right)\left({e}^{z\stackrel{\sim }{\zeta }/2}-1\right) \mathrm{for} \stackrel{\sim }{\zeta }>0$$

(58)

$$F=\frac{2}{\kappa a}\left(1+3{m}_{+}\right)\left({e}^{-z\stackrel{\sim }{\zeta }/2}-1\right) \mathrm{ for} \stackrel{\sim }{\zeta }<0$$

(59)

$${m}_{+}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {z}^{2}{e}^{2}}{\lambda }_{+},\ {m}_{-}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {z}^{2}{e}^{2}}{\lambda }_{-}$$

(60)

Note that Eqs. (56) and (57) differ from Eq. (54) in Ref. [23] by a factor of 1/z², because of the different definitions of U* and a.

In the limit of κa → ∞, Eqs. (56) and (57) reduce to

$${U}^{*}=\frac{3}{2{z}^{2}}\left\{4\mathrm{ln}\left(\mathrm{cosh}\left(\frac{z\stackrel{\sim }{\zeta }}{4}\right)\right)-\left(\frac{{m}_{+}-{m}_{-}}{{m}_{+}+{m}_{-}}\right)z\stackrel{\sim }{\zeta }\right\}$$

(61)

which agrees with previously derived well-known expression [1,2,3]

(iii) 2:1 electrolytes

$${U}^{*}=-\frac{3}{2}\left(\frac{1}{2}-\beta \right)\stackrel{\sim }{\zeta }+\frac{3\left\{3+\left(1-2\beta \right)F\right\}}{2\left(1+F\right)}\mathrm{ln}\left(\frac{1}{2}+\frac{1}{2}\sqrt{\frac{2}{3}{e}^{\stackrel{\sim }{\zeta }}+\frac{1}{3}}\right)\mathrm{ for} \stackrel{\sim }{\zeta }>0$$

(62)

$${U}^{*}=\frac{3}{2}\left(1+\beta \right)\stackrel{\sim }{\zeta }+\frac{3\left\{3+2\left(1+\beta \right)F\right\}}{2\left(1+F\right)}\mathrm{ln}\left(\frac{{e}^{-\stackrel{\sim }{\zeta /2}}}{2}+\frac{1}{2}\sqrt{\frac{1}{3}{e}^{-\stackrel{\sim }{\zeta }}+\frac{2}{3}}\right)\mathrm{ for} \stackrel{\sim }{\zeta }<0$$

(63)

with

$$F=\frac{\sqrt{6}}{\kappa a}\left(1+3{m}_{-}\right)\left({e}^{\stackrel{\sim }{\zeta }/2}-1\right)\mathrm{ for} \stackrel{\sim }{\zeta }>0$$

(64)

$$F=\frac{\sqrt{3}}{\kappa a}\left(1+3{m}_{+}\right)\left({e}^{-\stackrel{\sim }{\zeta }}-1\right)\mathrm{ for} \stackrel{\sim }{\zeta }<0$$

(65)

$$\beta =-\frac{4{m}_{+}-{m}_{-}}{2\left(2{m}_{+}+{m}_{-}\right)},\ { m}_{+}=\frac{{\varepsilon }_{r}{\varepsilon }_{o}kT}{6\eta {e}^{2}}{\lambda }_{+},\ {m}_{-}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {e}^{2}}{\lambda }_{-},$$

(66)

(iv) 1:2 electrolytes

$${U}^{*}=-\frac{3}{2}\left(1-\beta \right)\stackrel{\sim }{\zeta }+\frac{3\left\{3+2\left(1-\beta \right)F\right\}}{2\left(1+F\right)}\mathrm{ln}\left(\frac{{e}^{\stackrel{\sim }{\zeta }/2}}{2}+\frac{1}{2}\sqrt{\frac{1}{3}{e}^{\stackrel{\sim }{\zeta }}+\frac{2}{3}}\right) \mathrm{for} \stackrel{\sim }{\zeta }>0$$

(67)

$${U}^{*}=\frac{3}{2}\left(\frac{1}{2}+\beta \right)\stackrel{\sim }{\zeta }+\frac{3\left\{3+\left(1+2\beta \right)F\right\}}{2\left(1+F\right)}\mathrm{ln}\left(\frac{1}{2}+\frac{1}{2}\sqrt{\frac{2}{3}{e}^{-\stackrel{\sim }{\zeta }}+\frac{1}{3}}\right) \mathrm{for} \stackrel{\sim }{\zeta }<0$$

(68)

with

$$F=\frac{\sqrt{3}}{\kappa a}\left(1+3{m}_{-}\right)\left({e}^{\stackrel{\sim }{\zeta }}-1\right)\mathrm{ for} \stackrel{\sim }{\zeta }>0$$

(69)

$$F=\frac{\sqrt{6}}{\kappa a}\left(1+3{m}_{+}\right)\left({e}^{-\stackrel{\sim }{\zeta }/2}-1\right)\mathrm{ for} \stackrel{\sim }{\zeta }<0$$

(70)

$$\beta =-\frac{{m}_{+}-4{m}_{-}}{2\left({m}_{+}+2{m}_{-}\right)},\ {m}_{+}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{3\eta {e}^{2}}{\lambda }_{+},\ {m}_{-}=\frac{2{\varepsilon }_{r}{\varepsilon }_{o}kT}{6\eta {e}^{2}}{\lambda }_{-}$$

(71)

Note that F corresponds to Dukhin’s number.

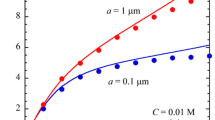
Figure 1 shows examples of the results of the calculation of the reduced diffusiophoretic velocity U* of a charged spherical particle of radius a calculated with Eqs. (56) and (57) as a function of the particle zeta potential ζ for m₊ = 0.176 and m_- = 0.169, which are, respectively, the values of m₊ for K⁺ ions and m_- for Cl⁻ ions in an aqueous KCl solution at 25 °C. Figures 2, 3, respectively, show the results for MgCl₂ with m₊ = 0.122 and m_- = 0.169 at 25 °C and those for LaCl₃ with m₊ = 0.0618 and m_- = 0.169 at 25 °C. It is seen that there are maxima in the mobility curves plotted as a function of the particle zeta potential ζ. This is caused by the relaxation effect, which becomes appreciable for higher zeta potential values as in the electrophoresis problem. We also note that U* reaches a nonzero finite value as the magnitude of the zeta potential tends to infinity. This is a kind of counterion condensation effect, as in the case of electrophoresis [30, 31]. The limiting values for several types of electrolytes can be obtained from the above expressions for U* with the result that.

Fig. 1

Scaled diffusiophoretic mobility U* of a spherical particle of radius a as a function of scaled zeta potential $\stackrel{\sim }{\zeta }$ for various values of $\kappa$a in an aqueous KCl solution at 25 °C. Calculated with Eqs. (56) and (57)

Fig. 2

Same as Fig. 1 but for MgCl₂. Calculated with Eqs. (62) and (63)

Fig. 3

Same as Fig. 1 but LaCl₃. Calculated with Eq. (49)

(i) z:z symmetrical electrolytes

$${U}^{*}\to -\frac{6{m}_{+}}{{z}^{2}\left({m}_{+}+{m}_{-}\right)}\mathrm{ln}2\ \mathrm{as} \stackrel{\sim }{\zeta }\to +\infty$$

(72)

$${U}^{*}\to -\frac{6{m}_{-}}{{z}^{2}\left({m}_{+}+{m}_{-}\right)}\mathrm{ln}2\ \mathrm{ as} \stackrel{\sim }{\zeta }\to -\infty$$

(73)

(ii) 2:1 electrolytes

$${U}^{*}\to -\frac{3}{4}\left(1-2\beta \right)\mathrm{ln}6\ \mathrm{as} \stackrel{\sim }{\zeta }\to +\infty$$

(74)

$${U}^{*}\to -3\left(1+\beta \right)\mathrm{ln}\left(3-\sqrt{3}\right) \mathrm{as} \stackrel{\sim }{\zeta }\to -\infty$$

(75)

(iii) 1:2 electrolytes

$${U}^{*}\to -3\left(1-\beta \right)\mathrm{ln}\left(3-\sqrt{3}\right)\mathrm{ as} \stackrel{\sim }{\zeta }\to +\infty$$

(76)

$${U}^{*}\to -\frac{3}{4}\left(1+2\beta \right)\mathrm{ln}6\ \mathrm{ as} \stackrel{\sim }{\zeta }\to -\infty$$

(77)

Concluding remarks

We have derived the general expression for the diffusiophoretic mobility U* of a spherical colloidal particle of radius a in a concentration gradient of general electrolyte (Eq. (43)). On the basis of this expression, we have derived simple approximate analytic expressions for U correct up to the order of (1/κa)⁰ (Eq. (45)) applicable for large particles with κa ≥ 50 at arbitrary zeta potential with negligible errors. Explicit expressions for U* for particles in z₊:z_-, z:z, 2:1, and 1:2 electrolyte solutions are given (Eqs. (49), (56), (57), (62), (63), (67), and (68)).

Appendix

Equation (24) can be derived from Eq. (23) as follows. Since beyond the particle double layer, ${\rho }_{\mathrm{el}}^{\left(0\right)}\left(r\right)$→0 and ${n}_{i}^{\left(0\right)}\left(r\right)$ → ${n}_{i}^{\infty }$, we obtain from Eq. (23)

$$\sum_{i=1}^{N}\frac{{z}_{i}e{n}_{i}^{\infty }}{{\lambda }_{i}}\nabla {\delta \mu }_{i}\left({\varvec{r}}\right)\to 0\ \mathrm{as}\ r\to \infty$$

(78)

From Eqs. (7) and (10), we have

$$\nabla {\delta \mu }_{i}\left({\varvec{r}}\right)={z}_{i}e\nabla\updelta \psi \left({\varvec{r}}\right)+kT\frac{\nabla {\delta n}_{i}}{{n}_{i}^{\infty }}$$

(79)

By substituting Eq. (79) into Eq. (78) and using Eq. (21), we obtain Eq. (24). Here, it must be noted that unlike the electrophoresis problem, in the diffusiophoresis problem dn_i does not tend to zero but to a nonzero value given by Eq. (21).