Introduction

Diffusiophoresis is a motion of colloidal particles in a concentration gradient of electrolytes. That is, the particle moves toward regions of higher or lower electrolyte concentrations depending on the particle zeta potential and the relative ionic mobilities. It is thus possible to evaluate the particle zeta potential from the relation between the particle diffusiophoretic mobility and the zeta potential as in the case of electrophoresis, which is a motion of colloidal particles in an externally applied electric field. The governing equations for diffusiophoresis are the same as those for electrophoresis with the only difference being the boundary conditions for the ionic electrochemical potentials. There are many theoretical studies on diffusiophoresis of different types of particles such as rigid particles [1,2,3,4,5,6,7,8,9,10,11,12,13,14], liquid drops [15,16,17], and soft particles [18,19,20,21,22,23].

The theory of the diffusiophoresis of colloidal particles in an electrolyte solution is usually based on the Poisson-Boltzmann equation for the electric potential distribution around the particles [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The standard Poisson-Boltzmann equation, however, assumes that electrolyte ions are point charges by neglecting the effects of ionic size. There are many theoretical studies on the modified Poisson-Boltzmann equation, which considers the effect of ionic size by introducing the activity coefficients of electrolyte ions (see, e.g., Refs [24,25,26,27,28,29,30,31]). López-García et al. [24, 25, 27] provided the numerical results of the electrophoretic mobility of a spherical particle in an electrolyte solution considering the ionic size effect. Hoshyargar et al. [26], in particular, demonstrated a significant effect of finite ion size on diffusioosmosis, which is an electrokinetic phenomenon closely related to diffusiophoresis. In a previous paper [29], on the basis of the equation for the ionic activity coefficients given by Carnahan and Starling [32], which is the most accurate among existing theories, we presented a simple algorithm for the calculation of an approximate electrophoretic mobility of a charged spherical colloidal particle in an electrolyte solution.

In the present paper, we derive an algorithm for the calculation of the diffusiophoretic velocity of a large colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann equation [28, 29]. The obtained expression is applicable when the particle size is much larger than the Debye length so that the particle surface can be regarded as planar.

Modified Poisson-Boltzmann equation

Consider a large particle carrying zeta potential ζ in an aqueous liquid of viscosity η and relative permittivity εr containing a symmetrical electrolyte. The electrolyte is of the Z:Z symmetrical type with valence Z but may have different ionic drag coefficients λ+ and λ− for cations and anions, respectively. We treat the case where the particle size is large enough to regard the particle surface as a planar surface. We take an x-axis to be perpendicular to the particle surface with its origin on it and a z-axis to be parallel to the particle surface (Fig. 1).

Fig. 1
figure 1

Diffusiophoresis of a large colloidal particle moving with a diffusiophoretic velocity U in an electrolyte concentration gradient ∇n∞ or the corresponding vector α. U is parallel to ∇n∞ and α

Full size image

Consider first the equilibrium situation where there is no electrolyte concentration gradient. Let n+(x) and n−(x), which depend on only x, be the concentrations (number densities) of electrolyte cations and anions, respectively, and n∞ be their concentration beyond the electrical double layer around the particle, where n+(∞) = n−(∞) = n∞. The equilibrium electric potential ψ(x) and the space charge density ρel(x), which also depend only on x, obey the Poisson equation:

$$\frac{{d}^{2}\psi }{d{x}^{2}}=-\frac{{\rho }_{\mathrm{el}}(x)}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}}$$
(1)

with

$${\rho }_{\mathrm{el}}\left(x\right)=Ze\left\{{n}_{+}\left(x\right)-{n}_{-}\left(x\right)\right\}$$
(2)

where εo is the permittivity of a vacuum and e is the elementary electric charge. We take into account steric interactions among ions of the finite size by introducing an ionic activity coefficient. We assume that the activity coefficients of cations and anions have the same value γ(x). The electrochemical potential μ+(x) of cations and that of anions μ−(x) are thus given by

$${\mu }_{\pm }(x)={\mu }_{\pm }^{o}\pm Ze\psi (x)+kT\ \mathrm{ln}[\gamma (x){n}_{\pm }(x)]$$
(3)

where k is Boltzmann’s constant and T is the absolute temperature. The electrochemical potentials μ±(x) must take the same value as those in the bulk solution phase (where ψ(∞) = 0), viz.,

$${\mu }_{\pm }(\infty )={\mu }_{\pm }^{\mathrm{o}}+kT\ \mathrm{ln}({\gamma }^{\infty }{n}^{\infty })$$
(4)

with \({\gamma }^{\infty }=\gamma (\infty )\). By equating \({\mu }_{\pm }(x)={\mu }_{\pm }(\infty )\), we obtain

$${n}_{\pm }(x)=\frac{{\gamma }^{\infty }{n}^{\infty }}{\gamma (x)}{e}^{\mp y(x)}$$
(5)

where

$$y(x)=\frac{Ze\psi (x)}{kT}$$
(6)

is the scaled electric potential. Thus, Eq. (2) gives

$${\rho }_{\mathrm{el}}(x)=-\frac{2{\gamma }^{\infty }}{\gamma (x)}Ze{n}^{\infty }\ \mathrm{sinh}\ y(x)$$
(7)

so that Eq. (1) becomes the following modified Poisson-Boltzmann equation:

$$\frac{{d}^{2}y}{d{x}^{2}}={\kappa }^{2}\frac{{\gamma }^{\infty }}{\gamma (x)}\mathrm{sinh}\ y(x)$$
(8)

where

$$\kappa =\sqrt{\frac{2{Z}^{2}{e}^{2}{n}^{\infty }}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT}}$$
(9)

is the Debye-Hückel parameter and 1/κ is the Debye length. When γ(x) = 1, Eq. (8) tends back to the standard Poisson-Boltzmann equation without taking into account the ion size effect, viz.,

$$\frac{{d}^{2}y}{d{x}^{2}}={\kappa }^{2}\ \mathrm{sinh}\ y(x)$$
(10)

We now assume that cations and anions have the same radius a. This assumption is particularly valid for diffusiophoresis in a KCl solution, in which the hydrated radii of the anions and cations can be considered equal to 0.33 nm. For details, the readers should refer to the work by Ganjizade et al. [33, 34]. We introduce the volume fraction ϕ+(x) of cations and that of anions ϕ−(x) at position x. Then, we have

$${\phi }_{\pm }(x)=\left(\frac{4}{3}\pi {a}^{3}\right){n}_{\pm }(x)$$
(11)

The total ion volume fraction ϕ(x) at position x is thus given by

$$\phi (x)={\phi }_{+}(x)+{\phi }_{-}(x)=\left(\frac{4}{3}\pi {a}^{3}\right)\{{n}_{+}(x)+{n}_{-}(x)\}$$
(12)

Let the total ion volume fraction in the bulk solution phase be ϕB ≡ ϕ(∞). Then from Eq. (12), we obtain

$${\phi }_{B}=\left(\frac{4}{3}\pi {a}^{3}\right)\cdot 2{n}^{\infty }$$
(13)

so that Eq. (12) becomes

$$\phi (x)=\frac{{\phi }_{B}\left\{{n}_{+}(x)+{n}_{-}(x)\right\}}{2{n}^{\infty }}$$
(14)

By substituting Eq. (5) into Eq. (14), we obtain

$$\phi (x)={\phi }_{B}\frac{{\gamma }^{\infty }}{\gamma \left(x\right)}\mathrm{cosh}y(x)$$
(15)

The modified Poisson-Boltzmann Eq. (8) becomes by using Eq. (15)

$$\frac{{d}^{2}y}{d{x}^{2}}={\kappa }^{2}\frac{\phi (x)}{{\phi }_{B}}\mathrm{tanh}\ y(x)$$
(16)

Now we employ the expressions for γ(x) derived by Carnahan and Starling [32], viz.,

$$\gamma (x)=\mathrm{exp}\left[\frac{\phi (x)\left\{8-9\phi (x)+3{\phi }^{2}(x)\right\}}{\{1-\phi (x){\}}^{3}}\right]$$
(17)

and

$${\gamma }^{\infty }=\mathrm{exp}\left[\frac{{\phi }_{B}(8-9{\phi }_{B}+3{\phi }_{B}^{2})}{(1-{\phi }_{B}{)}^{3}}\right]$$
(18)

Then, Eq. (15) becomes

$$\phi (x)={\phi }_{B}\mathrm{exp}\left[-\left(\frac{\phi (x)\left\{8-9\phi (x)+3\phi (x)\right\}}{\{1-\phi (x){\}}^{3}}-\frac{{\phi }_{B}\left(8-9{\phi }_{B}+3{\phi }_{\mathrm{B}}^{2}\right)}{(1-{\phi }_{B}{)}^{3}}\right)\right]\mathrm{cosh}y(x)$$
(19)

which is a transcendental equation for ϕ(x) for given values of ϕB and y(x). Since ϕ(x) thus obtained is a function of y(x), we rewrite ϕ(x) as ϕ(y).

Equation (16) is subject to the following boundary conditions:

$$y\left(x\right)\to 0\ \mathrm{as}\ x \to \infty$$
(20)
$$y(0)=\stackrel{\sim }{\zeta }$$
(21)

where \(\stackrel{\sim }{\zeta }\) is the scaled zeta potential defined by

$$\stackrel{\sim }{\zeta }=\frac{Ze\zeta }{kT}$$
(22)

Electrokinetic equations

Now consider the case where the electrolyte concentration gradient ∇n∞ (0, 0, dn∞/dz) is applied so that n∞ becomes a function of z and the particle is moving with a diffusiophoretic velocity U. We treat the case where the applied electrolyte concentration gradient ∇n∞(0, 0, dn∞/dz), the diffusiophoretic velocity U(0, 0, U), and thus the liquid flow u(r) are parallel to the z-axis, as shown in Fig. 1. We introduce a constant vector α(0, 0, α) proportional to ∇n, viz.,

$$\boldsymbol{\alpha }=\frac{kT}{Ze}\nabla \mathrm{ln}{(n}^{\infty })$$
(23)

We assume that the liquid velocity u(r) = (0, 0, u(x, z)) at position r satisfies the following Navier–Stokes equation:

$$\eta \Delta {\varvec{u}}\left({\varvec{r}}\right)-\nabla p\left({\varvec{r}}\right)-{\rho }_{\mathrm{el}}\left({\varvec{r}}\right)\nabla \psi \left({\varvec{r}}\right)={\varvec{0}}$$
(24)

where p(r) is the pressure. The boundary conditions for u(r) are

$${\varvec{u}}\left({\varvec{r}}\right)=\boldsymbol{0}\ \mathrm{at}\ x=0$$
(25)
$${\varvec{u}}\left({\varvec{r}}\right)=-\boldsymbol{U}\ \mathrm{as}\ x\to \infty$$
(26)

The boundary condition for the electric potential ψ(r) far from the particle at x → ∞ can be derived as follows. The ionic flows caused by ∇n∞ induce a macroscopic electric field, i.e., the diffusion potential field E(0, 0, E), which nullifies the net electric current and hence ψ(r) tends to − Ez as x → ∞. The electric current density i(r) at position r is given by

$${\varvec{i}}\left({\varvec{r}}\right)=Ze\left\{{n}_{+}\left({\varvec{r}}\right){{\varvec{v}}}_{+}\left({\varvec{r}}\right)-{n}_{-}\left({\varvec{r}}\right){{\varvec{v}}}_{-}\left({\varvec{r}}\right)\right\}$$
(27)

with

$${{\varvec{v}}}_{\pm }({\varvec{r}})={\varvec{u}}({\varvec{r}})-\frac{1}{{\lambda }_{\pm }}\nabla {\mu }_{\pm }({\varvec{r}})$$
(28)

where are the velocities of cations and anions, respectively. From the condition that i(r) must be zero beyond the electrical double layer around the particle (x → ∞), we find that

$$\psi \left({\varvec{r}}\right)\to -\beta \alpha z\ \mathrm{as}\ x\to \infty$$
(29)

and

$$E=\beta \alpha$$
(30)

where β is defined by

$$\beta =\frac{{1/\lambda }_{+}-{1/\lambda }_{-}}{1/{\lambda }_{+}+1/{\lambda }_{-}}=-\frac{{\lambda }_{+}-{\lambda }_{-}}{{\lambda }_{+}+{\lambda }_{-}}$$
(31)

and α is the z-component of α given by (see Eq. (23))

$$\alpha =\frac{kT}{Ze}\frac{d\mathrm{ln}{(n}^{\infty })}{dz}$$
(32)

Following Prieve [2], from the x-component of Eq. (24), we obtain

$$p\left(x,z\right)-p\left(\infty ,z\right)=2{n}^{\infty }(z)kTM(y)$$
(33)

with

$$M(y)={\int }_{0}^{y}\frac{\phi (y\mathrm{^{\prime}})}{{\phi }_{B}}\mathrm{tanh}\ y\mathrm{^{\prime}}dy\mathrm{^{\prime}}$$
(34)

where y′ is an integral variable. Substituting Eq. (34) back into Eq. (24) and solving its z-component, we finally obtain the following expression for the scaled diffusiophoretic mobility U*:

$${U}^{*}=\frac{1}{2}{\int }_{0}^{\stackrel{\sim }{\zeta }}\left\{{\int }_{0}^{y}\sqrt{M(y\mathrm{^{\prime}})}dy\mathrm{^{\prime}}\right\}\frac{dy}{\sqrt{M(y)}}+\beta \stackrel{\sim }{\zeta }$$
(35)

where we have defined U* as

$${U}^{*}=\frac{\eta Ze}{{\varepsilon }_{\mathrm{r}}{\varepsilon }_{\mathrm{o}}kT\alpha }U$$
(36)

Results and discussion

The principal result of the present paper is Eq. (35) for the diffusiophoretic mobility U* of a large colloidal particle in an electrolyte solution based on the modified Poisson-Boltzmann equation (Eq. (16)) by taking into account the ion size effect through the Carnahan-Starling activity coefficient [32]. In the limiting case of ϕB → 0, Eq. (35) tends to the following electrophoretic mobility expression based on the standard Poisson-Boltzmann approach [1,2,3]:

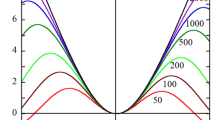
$${U}^{*}=4\mathrm{ln}\left[\mathrm{cosh}\left(\frac{\stackrel{\sim }{\zeta }}{4}\right)\right]+\beta \stackrel{\sim }{\zeta }$$
(37)

Figure 2 shows some examples of the exact results (solid lines) of the calculation of the scaled diffusiophoretic mobility U* in a KCl solution (β =  − 0.02) obtained via Eq. (35) as a function of the scale zeta potential \(\stackrel{\sim }{\zeta }\) for several values of the total ion volume fraction ϕB. It is seen that the ionic size effect gives rise to an increase in the magnitude of U*. This is because the ionic size effect leads to a decrease in the ionic shielding effect so that the magnitude of U* increases. Figure 2 also shows results (dotted lines) obtained via an approximate expression for U* given by

Fig. 2
figure 2

Scaled diffusiophoretic mobility U* in a KCl solution (β =  − 0.02) as a function of the scaled zeta potential \(\stackrel{\sim }{\zeta }\) for several values of the total ion volume fraction ϕB. Solid curves represent exact results calculated with Eq. (35), which is based on the modified Poisson-Boltzmann equation (Eq. 16)). The curve with ϕB = 0 corresponds to the result obtained via the standard Poisson-Boltzmann equation (Eq. 10). Dotted curves represent approximate results calculated with Eq. (38)

Full size image
$${U}^{*}=\frac{1}{2}{\int }_{0}^{\stackrel{\sim }{\zeta }}\left\{{\int }_{0}^{y}\sqrt{\mathrm{ln}H(y\mathrm{^{\prime}})}dy\mathrm{^{\prime}}\right\}\frac{dy}{\sqrt{\mathrm{ln}H(y)}}+\beta \stackrel{\sim }{\zeta }$$
(38)

with

$$H\left(y\right)=1+B{\mathrm{sinh}}^{2}(y/2)$$
(39)
$$B=\frac{16{\phi }_{B}}{1+8{\phi }_{B}}$$
(40)

Equation (38) can be derived from the following approximate form valid at low values of ϕ and low to moderate values of y(x) for the Carnahan-Starling activity coefficient (Eq. 17) [28, 29]:

$$\gamma (x)={\gamma }^{\infty }H(y)$$
(41)

or equivalently (see Eq. (15))

$$\phi (x)=\frac{{\phi }_{B}\mathrm{cosh}y}{H(y)}$$
(42)

which is the first-order approximation for ϕ(x) obtained by expanding Eq. (19) in a power series of ϕ(x) and ϕB.

The approximate results (dotted lines) agree well with the exact results (solid lines). The maximum error in Fig. 2 is found to be about 6%.

Conclusion

We have derived an expression (35) for the diffusiophoretic mobility U* of a large colloidal particle in a symmetrical electrolyte solution based on the modified Poisson-Boltzmann equation (Eq. (8) or Eq. (16)), which takes into account the effects of ionic size on the basis of ionic activity coefficient given by Carnahan and Starling [32]. The obtained expression is applicable when the particle size is much larger than Debye length 1/κ. It has been shown that U* increases with increasing total ionic volume fraction ϕB. We have also derived an approximate expression for U* (Eq. (38)), which is in good agreement with the exact results (Eq. (35)).