Total Domination Versus Domination in Cubic Graphs

Abstract

A dominating set in a graph G is a set S of vertices of G such that every vertex not in S has a neighbor in S. Further, if every vertex of G has a neighbor in S, then S is a total dominating set of G. The domination number, $\gamma (G)$, and total domination number, $\gamma _{t}(G)$, are the minimum cardinalities of a dominating set and total dominating set, respectively, in G. The upper domination number, $\Gamma (G)$, and the upper total domination number, $\Gamma _t(G)$, are the maximum cardinalities of a minimal dominating set and total dominating set, respectively, in G. It is known that $\gamma _{t}(G)/\gamma (G) \le 2$ and $\Gamma _{t}(G)/\Gamma (G) \le 2$ for all graphs G with no isolated vertex. In this paper we characterize the connected cubic graphs G satisfying $\gamma _{t}(G)/\gamma (G) = 2$, and we characterize the connected cubic graphs G satisfying $\Gamma _{t}(G)/\Gamma (G) = 2$.

1 Introduction

In this paper we continue the study of domination and total domination in graphs. Let $G=(V,E)$ be a simple graph. If $u,v\in V(G)$, then u dominates v if u and v are adjacent. A dominating set of a graph G is a set S of vertices of G such that every vertex outside S is dominated by at least one vertex in S. A total dominating set, abbreviated TD-set, of G is a set S of vertices of G such that every vertex in V(G) is adjacent to at least one vertex in S. A neighbor of a vertex v in G is a vertex adjacent to v. A vertex totally dominates its neighbors. The domination number of G, denoted $\gamma (G)$, is the minimum cardinality of a dominating set of G, while the total domination number of G, denoted by $\gamma _{t}(G)$, is the minimum cardinality of a TD-set of G. A TD-set S in G is minimal if for all vertices $v \in S$, the set $S {\setminus } \{v\}$ is not a TD-set of G. The upper total domination number of G, denoted $\Gamma _t(G)$, is the maximum cardinality of a minimal TD-set in G. We refer to a minimum total dominating set of G as a $\gamma _{t}(G)$-set. A minimal TD-set of cardinality $\Gamma _t(G)$ we call a $\Gamma _t(G)$-set.

The literature on this subject of domination and its variations has been surveyed and detailed in the two books by Haynes, Hedetniemi, and Slater [9, 10]. For a recent book on total domination in graphs we refer the reader to [15]. A survey of total domination in graphs can also be found in [14]. For a survey of known results on the upper total domination we refer the reader to [16]. Recent papers on total domination in graphs can be found, for example, in [3, 6, 17, 18] and elsewhere.

Let S be a set of vertices in a graph G, and let $v \in S$. The open neighborhood of v is the set $N_G(v) = \{u \in V(G) \, | \, uv \in E(G)\}$ and the closed neighborhood of v is $N_G[v] = \{v\} \cup N_G(v)$. We denote the degree of v in G by $d_G(v) = |N_G(v)|$, or simply by d(v) if the graph G is clear from context. For a subset S of vertices of G, we let $d_S(v)$ denote the number of vertices in S that are adjacent to v. A graph G is k-regular if every vertex has degree k in G. A regular graph is a graph that is k-regular for some integer $k \ge 0$. We remark that 3-regular graphs are also called cubic graphs in the literature. The open neighborhood of S is the set $N_G(S) = \bigcup _{v \in S} N_G(v)$ and its closed neighborhood is the set $N_G[S] = N_G(S) \cup S$. The subgraph induced by the set S is denoted by G[S].

The private neighborhood $\mathrm{pn}(v,S)$ of $v \in S$ is defined by $\mathrm{pn}(v,S)= N(v) {\setminus } N(S {\setminus } \{v\})$. Equivalently, $\mathrm{pn}(v,S) = \{ u \in V \mid N(u) \cap S = \{v\} \}$. Each vertex in $\mathrm{pn}(v,S)$ is called a private neighbor of v. The external private neighborhood $\mathrm{epn}(v,S)$ of v with respect to S consists of the private neighbors of v in $V {\setminus } S$, while the internal private neighborhood $\mathrm{ipn}(v,S)$ of v with respect to S consists of the private neighbors of v in S. Thus, $\mathrm{epn}(v,S) = \mathrm{pn}(v,S) \cap (V {\setminus } S)$ and $\mathrm{ipn}(v,S) = \mathrm{pn}(v,S) \cap S$, while $\mathrm{pn}(v,S) = \mathrm{epn}(v,S) \cup \mathrm{ipn}(v,S)$. The following property of minimal total dominating sets is established in [5].

Observation 1.1

[5] Let S be a TD-set of a graph G with no isolated vertex. Then, S is a minimal TDS of G if and only if for each $v \in S$, $\mathrm{epn}(v,S) \ne \emptyset$ or $\mathrm{pn}(v,S)= \mathrm{ipn}(v,S) \ne \emptyset$.

A packing in a graph G is a set of vertices whose closed neighborhoods are pairwise disjoint. Thus, if S is a packing in G, then $N_G[u] \cap N_G[v] = \emptyset$ for all pairs $u,v \in S$; equivalently, the vertices in S are pairwise at distance at least 3 apart in G. A perfect packing in G is a packing whose closed neighborhoods partition V(G).

We use the standard notation $[k] = \{1,2,\ldots ,k\}$.

2 Domination Versus Total Domination

We shall need the following well known lower bound on the domination number of a graph (see, for example, [9]). For completeness, we provide the elementary proof of this result.

Lemma 2.1

[9] If G is a graph of order n and $\Delta = \Delta (G)$, then $\gamma (G) \ge n/(\Delta + 1)$, with equality if and only if every minimum dominating set in G is a perfect packing that contains only vertices of degree $\Delta$.

Proof

If D is an arbitrary minimum dominating set of G, then

$$\begin{aligned} n - |D| = \left| V(G) {\setminus } D\right| \le \left| \bigcup _{v \in D} N_G(v)\right| \le \sum _{v \in D} d_G(v) \le |D| \cdot \Delta , \end{aligned}$$

and so $\gamma (G) = |D| \ge n/(\Delta + 1)$. Further, if $\gamma (G) = n/(\Delta + 1)$, then we must have equality throughout the above inequality chain, implying that $d_G(v) = \Delta$ for all $v \in D$ and that the closed neighborhoods, $N_G[v]$, of the vertices $v \in D$ are pairwise disjoint. Thus, D is a perfect packing in G that contains only vertices of degree $\Delta$. Conversely, if D is a perfect packing in G that contains only vertices of degree $\Delta$, then every dominating set D of G contains at least one vertex from every closed neighborhood, $N_G[u]$, for all $u \in D$, and so $\gamma (G) \ge |D|$. However, the set D is a dominating set of G, and so $\gamma (G) \le |D|$. Consequently, $\gamma (G) = |D| = n/(\Delta + 1)$. $\square$

The following relationship between the domination and total domination numbers of a graph with no isolated vertex was first observed by Bollobás and Cockayne [2].

Theorem 2.2

[2] For every graph G with no isolated vertex, $\gamma _{t}(G) \le 2\gamma (G)$.

A constructive characterization of trees T satisfying $\gamma _{t}(T) = 2\gamma (T)$ is given in [12]. However, it remains an open problem to characterize general graphs G satisfying $\gamma _{t}(G) = 2\gamma (G)$. We shall need the following lemma.

Lemma 2.3

For $k \ge 2$, let G be a k-regular graph of order n. If $\gamma _{t}(G) = 2\gamma (G)$, then $\gamma (G) = n/(k+1)$.

Proof

Let G be a k-regular graph of order n satisfying $\gamma _{t}(G) = 2\gamma (G)$. Let D be a minimum dominating set of G, and so $|D| = \gamma (G)$. For each vertex $v \in D$, let $v'$ be an arbitrary neighbor of v, and let

$$\begin{aligned} X = \bigcup _{v \in D} \{v,v'\}. \end{aligned}$$

Then, X is a TD-set of G, and so $\gamma _{t}(G) \le |X|$. If v and w are distinct vertices of D, and $v' = w$ or $v' = w'$, then $\gamma _{t}(G) \le |X| < 2|D| = 2\gamma (G)$, a contradiction. Therefore, for every pair v and w of vertices in D, the vertices v and w are not adjacent and do not have a neighbor in common; that is, $N_G[v] \cap N_G[w] = \emptyset$. Thus, D is a packing in G. Since $|N_G[v]| = d_G(v) + 1 = k + 1$ for every vertex $v \in D$, and since D is a dominating set of G, the sets $N_G[v]$ where $v \in D$ form a partition V(G), implying that $n = |D|(k+1) = \gamma (G)(k+1)$. $\square$

We wish to determine the connected, k-regular graphs achieving equality in the upper bound of Theorem 2.2 for small values of k. If $k = 1$, then $G = K_2$ and $\gamma _{t}(G) = 2$ and $\gamma (G) = 1$, and so $\gamma _{t}(G)/\gamma (G) = 2$. Hence, it is only of interest to consider the cases when $k \ge 2$.

2.1 2-Regular Graphs

We first consider the case when G is a k-regular graph with $k = 2$. In this case $G \cong C_n$ and $n \ge 3$. It is well known (see, for example, [9, 11, 15]) that $\gamma _{t}(C_n)= \lfloor n/2 \rfloor + \lceil n/4 \rceil - \lfloor n/4 \rfloor$ and $\gamma (C_n) = \lceil n/3 \rceil$. As an immediate consequence of these results, we note that

$$\begin{aligned} \frac{\gamma _{t}(G)}{\gamma (G)} = \frac{3}{2} + \Upsilon (n), \end{aligned}$$

where

$$\begin{aligned} \Upsilon (n) = \left\{ \begin{array}{cl} 0 &{}\quad \text{ if } \quad n \equiv 0,5,10,11 \, (\mathrm{mod}\, 12) \\ -\frac{3}{2(n+2)} &{}\quad \text{ if } \quad n \equiv 1, 7 \, (\mathrm{mod}\, 12) \\ \frac{3}{2(n+1)} &{}\quad \text{ if } \quad n \equiv 2 \, (\mathrm{mod}\, 12) \\ \frac{3}{2n} &{}\quad \text{ if } \quad n \equiv 3, 9 \, (\mathrm{mod}\, 12) \\ -\frac{3}{n+2} &{}\quad \text{ if } \quad n \equiv 4 \, (\mathrm{mod}\, 12) \\ \frac{3}{n} &{}\quad \text{ if } \quad n \equiv 6 \, (\mathrm{mod}\, 12). \\ -\frac{3}{2(n+1)} &{}\quad \text{ if } \quad n \equiv 8 \, (\mathrm{mod}\, 12) \end{array} \right. \end{aligned}$$

Thus, we have the following observations.

Observation 2.4

If G is a connected 2-regular graph of order $n \ge 3$, then

$$\begin{aligned} \frac{\gamma _{t}(G)}{\gamma (G)} = \left\{ \begin{array}{ll} \frac{3}{2} + \frac{3}{2(n+1)} &{}\quad \text{ if } \quad n \equiv 2 \, (\mathrm{mod}\, 12) \\ \frac{3}{2} + \frac{3}{2n} &{}\quad \text{ if } \quad n \equiv 3, 9 \, (\mathrm{mod}\, 12) \\ \frac{3}{2} + \frac{3}{n} &{}\quad \text{ if } \quad n \equiv 6 \, (\mathrm{mod}\, 12) \end{array} \right. \end{aligned}$$

and $\frac{\gamma _{t}(G)}{\gamma (G)} \le \frac{3}{2}$ otherwise.

Observation 2.5

If G is a connected 2-regular graph, then

$$\begin{aligned} \frac{\gamma _{t}(G)}{\gamma (G)} \le 2 \text{ with } \text{ equality } \text{ if } \text{ and } \text{ only } \text{ if } G \in \{C_3,C_6\}. \end{aligned}$$

2.2 3-Regular Graphs

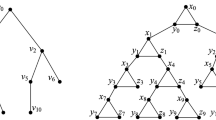
We next consider the case when $k \ge 3$. For this purpose, we shall need a result on the total domination number of a cubic graph. For $\ell \ge 1$, let $G_\ell$ be the graph constructed in [8] as follows. (This construction is also described in Chapter 5, p. 44, of [15].) Consider two copies of the path $P_{2\ell }$ with respective vertex sequences $a_{1}b_{1}a_{2}b_{2} \cdots a_{\ell }b_{\ell }$ and $c_{1}d_{1}c_{2}d_{2} \cdots c_{\ell }d_{\ell }$. For each $i \in [\ell ]$, join $a_{i}$ to $d_{i}$ and $b_{i}$ to $c_{i}$. To complete the construction of the graph $G_\ell$ join $a_{1}$ to $c_{1}$ and $b_{\ell }$ to $d_{\ell }$. Let ${\mathcal {G}}= \{ G_\ell \mid \ell \ge 1\}$. For $\ell \ge 2$, let $H_\ell$ be obtained from $G_\ell$ by deleting the two edges $a_{1}c_{1}$ and $b_{\ell }d_{\ell }$ and adding the two edges $a_{1}b_{\ell }$ and $c_{1}d_{\ell }$. Let ${\mathcal {H}}= \{ H_\ell \mid \ell \ge 2\}$. We note that $G_\ell$ and $H_\ell$ are cubic graphs of order $4\ell$. Further, we note that $G_1 \cong K_4$. The graphs $G_4 \in {\mathcal {G}}$ and $H_4 \in {\mathcal {H}}$, for example, are illustrated in Fig. 1.

Fig. 1

Cubic graphs $G_4 \in {\mathcal {G}}$ and $H_4 \in {\mathcal {H}}$

Let ${\mathcal {H}_{\mathop {\mathrm {even}}}}$ be the subfamily of ${\mathcal {H}}$ consisting of all graphs $H_\ell$ where $\ell$ is even; that is, ${\mathcal {H}_{\mathop {\mathrm {even}}}}= \{ H_\ell \mid \ell \ge 2 \text{ is } \text{ even } \}$.

The following upper bound on the total domination number of a graph with minimum degree at least 3 was established independently by many authors (see, [1, 4, 19]).

Theorem 2.6

[1, 4, 19] If G is a graph of order n with $\delta (G) \ge 3$, then $\gamma _{t}(G) \le \frac{n}{2}$.

The connected graphs that achieve equality in the bound of Theorem 2.6 were characterized in [13].

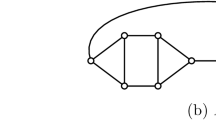
Theorem 2.7

[13] If G is a connected graph of order n with $\delta (G) \ge 3$, then $\gamma _{t}(G)\le \frac{n}{2}$, with equality if and only if $G \in {\mathcal {G}}\cup {\mathcal {H}}$ or G is the generalized Petersen graph shown in Fig. 2.

Fig. 2

The generalized Petersen graph

We are now in a position to characterize the connected, cubic graphs G satisfying $\gamma _{t}(G)/\gamma (G) = 2$.

Theorem 2.8

If G is a connected cubic graph, then $\gamma _{t}(G)/\gamma (G) \le 2$ with equality if and only if the following holds.

• (a) $G \in {\mathcal {G}}\cup {\mathcal {H}_{\mathop {\mathrm {even}}}}$.

• (b) G is the generalized Petersen graph.

Proof

Let G be a connected, cubic graph of order n. By Theorem 2.2, $\gamma _{t}(G)/\gamma (G)\le 2$. Hence it suffices for us to prove that $\gamma _{t}(G)/\gamma (G) = 2$ if and only if (a) or (b) in the statement of the theorem hold. We first prove the sufficiency. Suppose that (a) or (b) in the statement of the theorem holds. If G is the generalized Petersen graph, then $\gamma (G) = 4$ and $\gamma _{t}(G) = 8$, and so $\gamma _{t}(G)/\gamma (G) = 2$. Suppose that $G \in {\mathcal {G}}\cup {\mathcal {H}_{\mathop {\mathrm {even}}}}$. If $G = G_\ell$ for $\ell \ge 2$ even or if $G = H_\ell$ for $\ell \ge 2$ even, then we let

$$\begin{aligned} D = \bigcup _{i=1}^{\ell /2} \{b_{2i-1},c_{2i}\}. \end{aligned}$$

If $G = G_\ell$ for $\ell \ge 1$ odd, then we let

$$\begin{aligned} D = \{b_\ell \} \cup \left( \bigcup _{i=1}^{(\ell - 1)/2} \{b_{2i-1},c_{2i}\} \right) . \end{aligned}$$

In both cases, D is a dominating set of G, implying that $\gamma (G) \le |D| = \ell = n/4$. By Lemma 2.1, $\gamma (G) \ge n/4$. Consequently, $\gamma (G) = n/4$. By Theorem 2.7, $\gamma _{t}(G) = n/2$. Thus, $\gamma _{t}(G)/\gamma (G) = 2$. This proves the sufficiency.

Next, we prove the necessity. Suppose that G is a connected, cubic graph satisfying $\gamma _{t}(G)/\gamma (G) = 2$. By Lemma 2.3, $\gamma (G) = n/4$, implying that $\gamma _{t}(G) = n/2$. By Theorem 2.7, $G \in {\mathcal {G}}\cup {\mathcal {H}}$ or G is the generalized Petersen graph.

It remains for us to show that if $G \in {\mathcal {H}}$, then $G \in {\mathcal {H}_{\mathop {\mathrm {even}}}}$. Suppose, to the contrary, that $G = H_\ell$ for some $\ell \ge 3$, where $\ell$ is odd. For $i \in [\ell ]$, let $V_i = \{a_i,b_i,c_i,d_i\}$. Let D be a minimum dominating set in G. Since $n = 4\ell$ and $\gamma (G) = n/4$, we note that $|D| = \gamma (G) = \ell$ and, by Lemma 2.1, that the set D is a packing in G. In order to dominate the vertex $a_1$, the set D contains exactly one of the vertices $a_1, b_1, b_\ell , d_1$. By symmetry, renaming vertices if necessary, we may assume that either $a_1 \in D$ or $b_1 \in D$.

Suppose that $b_1 \in D$. Since D is a packing, this implies that $D \cap V_1 = \{b_1\}$. Further, $D \cap \{b_\ell ,d_\ell \} = \emptyset$. In order to dominate the vertices $b_\ell$ and $d_\ell$, we note that either $a_\ell \in D$ or $c_\ell \in D$; that is, $D \cap \{a_\ell ,c_\ell \} \ne \emptyset$. In order to dominate the vertex $d_1$, we note that $c_2 \in D$. Since D is a packing, this in turn implies that $D \cap V_2 = \{c_2\}$ and $D \cap \{a_3,c_3\} = \emptyset$. If $\ell = 3$, we contradict our earlier observation that $D \cap \{a_\ell ,c_\ell \} \ne \emptyset$. Therefore, $\ell \ge 5$. In order to dominate the vertices $a_3$ and $c_3$, we note that either $b_3 \in D$ or $d_3 \in D$; that is, $D \cap \{b_3,d_3\} \ne \emptyset$. If $b_3 \in D$, then $c_4 \in D$. If $d_3 \in D$, then $a_4 \in D$. In both cases, since D is a packing, we deduce that $D \cap \{a_5,c_5\} = \emptyset$. Continuing in this way, it therefore holds that $D \cap \{a_{i},c_{i}\} = \emptyset$ for all odd $i \ge 1$ where $i \in [\ell ]$. In particular, noting that $\ell$ is odd, $D \cap \{a_\ell ,c_\ell \} = \emptyset$. This contradicts our earlier observation that $D \cap \{a_\ell ,c_\ell \} \ne \emptyset$.

Suppose that $a_1 \in D$. Since D is a packing, this implies that $D \cap V_1 = \{a_1\}$ and $D \cap \{a_2,c_2\} = \emptyset$, for otherwise $a_1$ would be within distance 2 from some other vertex of D. Further, $D \cap \{a_\ell ,c_\ell \} = \emptyset$ (and $b_\ell \notin D$). In order to dominate the vertices $a_2$ and $c_2$, we note that either $b_2 \in D$ or $d_2 \in D$; that is, $D \cap \{b_2,d_2\} \ne \emptyset$. If $b_2 \in D$, then $c_3 \in D$. If $d_2 \in D$, then $a_3 \in D$. In both cases, $D \cap \{a_3,c_3\} \ne \emptyset$. If $\ell = 3$, we contradict our earlier observation that $D \cap \{a_\ell ,c_\ell \} = \emptyset$. Therefore, $\ell \ge 5$. Since D is a packing and $D \cap \{a_3,c_3\} \ne \emptyset$, we deduce that $D \cap \{a_4,c_4\} = \emptyset$. In order to dominate the vertices $a_4$ and $c_4$, we note that either $b_4 \in D$ or $d_4 \in D$; that is, $D \cap \{b_4,d_4\} \ne \emptyset$. If $b_4 \in D$, then $c_5 \in D$. If $d_4 \in D$, then $a_5 \in D$. In both cases, $D \cap \{a_5,c_5\} \ne \emptyset$. Continuing in this way, it therefore holds that $D \cap \{a_{i},c_{i}\} \ne \emptyset$ for all odd $i \ge 1$ where $i \in [\ell ]$. In particular, noting that $\ell$ is odd, $D \cap \{a_\ell ,c_\ell \} \ne \emptyset$. This contradicts our earlier observation that $D \cap \{a_\ell ,c_\ell \} = \emptyset$.

Since both cases $a_1 \in D$ and $b_1 \in D$ produce a contradiction, we deduce that if $G \in {\mathcal {H}}$, then $G \in {\mathcal {H}_{\mathop {\mathrm {even}}}}$. This proves the necessity. $\square$

3 Upper Domination Versus Upper Total Domination

Dorbec et al. [7] established the following relationship between the upper domination and upper total domination numbers of a graph with no isolated vertex.

Theorem 3.1

[7] For every graph G with no isolated vertex, $\Gamma _{t}(G) \le 2\Gamma (G)$.

As remarked in [7], it remains an open problem to characterize graphs G satisfying $\Gamma _{t}(G) = 2\Gamma (G)$. We wish to determine the connected, k-regular graphs G achieving equality in the upper bound of Theorem 3.1 for small values of k. If $k = 1$, then $G = K_2$ and $\Gamma (G) = 1$ and $\Gamma _{t}(G) = 2$. Hence, it is only of interest to consider the cases when $k \ge 2$.

3.1 2-Regular Graphs

We first consider the case when $k = 2$. The following result determines the upper total domination number of a cycle.

Proposition 3.2

For $n \ge 3$,

$$\begin{aligned} \Gamma _{t}(C_n) = \left\{ \begin{array}{ll} 2\lfloor \frac{n}{3} \rfloor + 1 &{}\quad \text{ if } \quad n \equiv 5 \, (\mathrm{mod}\, 6) \\ 2\lfloor \frac{n}{3} \rfloor &{}\quad \text{ otherwise. }\\ \end{array} \right. \end{aligned}$$

Proof

We proceed by induction on $n \ge 3$. The result is straightforward to check (or use a computer) for small $n \le 9$. Hence we may assume that $n \ge 10$. Let $G \cong C_n$ be the cycle $v_1v_2 \cdots v_n v_1$. We show firstly that $\Gamma _{t}(C_n) \ge 2\lfloor \frac{n}{3} \rfloor + 1$ if $n \equiv 5 \, (\mathrm{mod}\, 6)$ and $\Gamma _{t}(C_n) \ge 2\lfloor \frac{n}{3} \rfloor$, otherwise. If $n \equiv 5 \, (\mathrm{mod}\, 6)$, then the set

$$\begin{aligned} A = \{v_{n-3},v_{n-2},v_{n-1}\} \cup \left( \bigcup _{i=0}^{\frac{n-11}{6}} \left\{ v_{6i+2},v_{6i+3},v_{6i+4},v_{6i+5}\right\} \right) \end{aligned}$$

is a minimal TD-set of G, and so $\Gamma _{t}(G) \ge |A| = 2\lfloor \frac{n}{3} \rfloor + 1$. If $n \equiv 0,1 \, (\mathrm{mod}\, 3)$, let

$$\begin{aligned} B = \bigcup _{i=0}^{\lfloor n/3 \rfloor - 1} \{v_{3i+1},v_{3i+2} \} \end{aligned}$$

while if $n \equiv 2 \, (\mathrm{mod}\, 6)$, let

$$\begin{aligned} B = \left( \bigcup _{i=0}^{\lfloor n/3 \rfloor - 3} \{v_{3i+1},v_{3i+2} \} \right) \cup \{v_{n-6},v_{n-5},v_{n-2},v_{n-1}\}. \end{aligned}$$

In both cases, the set B is a minimal TD-set of G and $|B| = 2\lfloor \frac{n}{3} \rfloor$, and so $\Gamma _{t}(G)\ge 2\lfloor \frac{n}{3} \rfloor$.

We show next that $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor + 1$ if $n \equiv 5 \, (\mathrm{mod}\, 6)$ and $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor$, otherwise. Let S be a $\Gamma _{t}(G)$-set. By the minimality of S, no five consecutive vertices of G all belong to S.

Suppose that S contains four consecutive vertices of G. Renaming vertices if necessary, we may assume that $\{v_3,v_4,v_5,v_6\} \subseteq S$. Since no five consecutive vertices all belong to S, we note that $v_2 \notin S$ and $v_7 \notin S$. If $v_1 \in S$, then $S {\setminus } \{v_3\}$ is a TD-set of G, contradicting the minimality of S. Hence, $v_1 \notin S$. If $v_8 \in S$, then $S {\setminus } \{v_6\}$ is a TD-set of G, contradicting the minimality of S. Hence, $v_8 \notin S$. This implies that $\{v_9,v_{10}\} \subset S$. We now consider the cycle $G'$ obtained from G by deleting the six vertices $v_3,v_4,\cdots ,v_8$ and adding the edge $v_2v_9$. Thus, $G' \cong C_{n'}$ where $n' = n - 6$. Let $S' = S {\setminus } \{v_3,v_4,v_5,v_6\}$. Since S is a minimal TD-set of G, the set $S'$ is a minimal TD-set of $G'$, implying that $|S'| \le \Gamma _{t}(G')$. If $n \equiv 5 \, (\mathrm{mod}\, 6)$, then $n \ge 11$ and $n' \equiv 5 \, (\mathrm{mod}\, 6)$, and by the inductive hypothesis, $\Gamma _{t}(G) = |S| = |S'| + 4 \le \Gamma _{t}(G') + 4 = (2\lfloor \frac{n'}{3} \rfloor + 1) + 4 = (2\lfloor \frac{n-6}{3} \rfloor + 1) + 4= 2\lfloor \frac{n}{3} \rfloor + 1$. If $n \not \equiv 5 \, (\mathrm{mod}\, 6)$, then $n' \not \equiv 5 \, (\mathrm{mod}\, 6)$. By the inductive hypothesis, $\Gamma _{t}(G) = |S| = |S'| + 4 \le \Gamma _{t}(G') + 4 = (2\lfloor \frac{n'}{3} \rfloor ) + 4 = 2\lfloor \frac{n}{3} \rfloor$. Hence, if S contains four consecutive vertices of G, then $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor + 1$ if $n \equiv 5 \, (\mathrm{mod}\, 6)$ and $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor$, otherwise. Hence, we may assume that S contains no four consecutive vertices, for otherwise the desired result follows.

Suppose that S contains three consecutive vertices of G. Renaming vertices if necessary, we may assume that $\{v_3,v_4,v_5\} \subseteq S$. Since no four consecutive vertices all belong to S, we note that $v_2 \notin S$ and $v_6 \notin S$. By the minimality of S, $v_1 \notin S$ and $v_7 \notin S$. This implies that $\{v_n,v_{n-1}\} \subset S$ and $\{v_8,v_{9}\} \subset S$. We now consider the cycle $G'$ obtained from G by deleting the five vertices $v_3,v_4,\ldots ,v_7$ and adding the edge $v_2v_8$. Thus, $G' \cong C_{n'}$ where $n' = n - 5$. Let $S' = S {\setminus } \{v_3,v_4,v_5\}$. Since S is a minimal TD-set of G, the set $S'$ is a minimal TD-set of $G'$, implying that $\Gamma _{t}(G) = |S| = |S'| + 3 \le \Gamma _{t}(G') + 3$.

If $n \equiv 5 \, (\mathrm{mod}\, 6)$, then $n' \equiv 0 \, (\mathrm{mod}\, 6)$, and by the inductive hypothesis, $\Gamma _{t}(G)\le \Gamma _{t}(G') + 3 = 2\lfloor \frac{n'}{3} \rfloor + 3 = 2\lfloor \frac{n-5}{3} \rfloor + 3 = 2\lfloor \frac{n}{3} \rfloor + 1$. If $n \equiv 4 \, (\mathrm{mod}\, 6)$, then $n' \equiv 5 \, (\mathrm{mod}\, 6)$, and by the inductive hypothesis, $\Gamma _{t}(G) \le \Gamma _{t}(G') + 3 = 2\lfloor \frac{n'}{3} \rfloor + 4 = 2\lfloor \frac{n-5}{3} \rfloor + 4 = 2\lfloor \frac{n}{3} \rfloor$. If $n \equiv 0,1,3 \, (\mathrm{mod}\, 6)$, then by the inductive hypothesis, $\Gamma _{t}(G) \le \Gamma _{t}(G') + 3 = 2\lfloor \frac{n'}{3} \rfloor + 3 = 2\lfloor \frac{n-5}{3} \rfloor + 3 \le 2\lfloor \frac{n}{3} \rfloor$.

Suppose that $n \equiv 2 \, (\mathrm{mod}\, 6)$. We show that $\Gamma _{t}(G) \le 2\lfloor \frac{n}{3} \rfloor$. Suppose that $v_{10} \in S$. In this case, $v_{11} \notin S$ and $v_{12} \notin S$. This implies that $\{v_{13},v_{14}\} \subset S$. We now consider the cycle $G''$ obtained from G by deleting the ten vertices $v_3,v_4,\ldots ,v_{12}$ and adding the edge $v_2v_{13}$. Thus, $G'' \cong C_{n''}$ where $n'' = n - 10$. We note that $n'' \equiv 4 \, (\mathrm{mod}\, 6)$. Let $S'' = S {\setminus } \{v_3,v_4,v_5,v_8,v_9,v_{10}\}$. Since S is a minimal TD-set of G, the set $S''$ is a minimal TD-set of $G''$, implying by the inductive hypothesis that $\Gamma _{t}(G) = |S|= |S''| + 6 \le \Gamma _{t}(G'') + 6 \le 2\lfloor \frac{n''}{3} \rfloor + 6 = 2\lfloor \frac{n-10}{3} \rfloor + 6 \le 2\lfloor \frac{n}{3} \rfloor$. Hence, we may assume that $v_{10} \notin S$, for otherwise $\Gamma _{t}(G) \le 2\lfloor \frac{n}{3} \rfloor$ as desired. If $v_{11} \notin S$, then $v_{12} \in S$ and $v_{13} \in S$. In this case, we consider the cycle $G^*$ obtained from G by deleting the four vertices $v_6,v_7,v_8,v_9$ and adding the edge $v_5v_{10}$. Thus, $G^* \cong C_{n^*}$ where $n^* = n - 4$. We note that $n^* \equiv 4 \, (\mathrm{mod}\, 6)$. Let $S^* = S {\setminus } \{v_8,v_9\}$. Since S is a minimal TD-set of G, the set $S^*$ is a minimal TD-set of $G^*$, implying by the inductive hypothesis that $\Gamma _{t}(G) = |S| = |S^*| + 2 \le \Gamma _{t}(G^*) + 2 \le 2\lfloor \frac{n^*}{3} \rfloor + 2 = 2\lfloor \frac{n-4}{3} \rfloor + 2 \le 2\lfloor \frac{n}{3} \rfloor$. Hence, we may assume that $v_{11} \in S$, for otherwise the desired result follows, implying that $v_{12} \in S$. Using analogous and symmetrical arguments, we may assume that $v_{n-2} \notin S$ and $\{v_{n-3},v_{n-4}\} \subset S$, for otherwise the desired upper bound follows. If $n = 14$, then $v_{n-2} = v_{12}$, contradicting the fact that with our current assumptions $v_{12} \in S$ and $v_{n-2} \notin S$. Hence, we note that $n \ge 20$. The set $(S {\setminus } \{v_3,v_4,v_5\}) \cup \{v_2,v_3,v_5,v_6\}$ is a minimal TD-set of G of cardinality $|S| + 1 = \Gamma _t(G) + 1$, a contradiction.

Hence, if S contains three consecutive vertices, then we have shown that $\Gamma _{t}(C_n)\le 2\lfloor \frac{n}{3} \rfloor + 1$ if $n \equiv 5 \, (\mathrm{mod}\, 6)$ and $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor$, otherwise. Hence, we may assume that S contains no three consecutive vertices, for otherwise the desired result follows. With this assumption, $\Gamma _{t}(C_n) \le 2\lfloor \frac{n}{3} \rfloor$ for all $n \ge 10$. This completes the proof of the proposition. $\square$

For $n \ge 3$, we observe that $\Gamma (C_n) = \alpha (C_n) = \lfloor n/2 \rfloor$, where $\alpha (G)$ is the size of a maximum independent vertex set of G. We state this result formally as follows.

Observation 3.3

For $n \ge 3$, $\Gamma (C_n) = \lfloor n/2 \rfloor$.

As an immediate consequence of Proposition 3.2 and Observation 3.3, we note that if $G \cong C_n$ and $n \ge 3$, then

$$\begin{aligned} \frac{\Gamma _{t}(G)}{\Gamma (G)} = \frac{4}{3} + \Phi (n), \end{aligned}$$

where

$$\begin{aligned} \Phi (n) = \left\{ \begin{array}{cl} 0 &{}\quad \text{ if } \quad n \equiv 0,1 \, (\mathrm{mod}\, 6) \\ -\frac{8}{3n} &{}\quad \text{ if } \quad n \equiv 2 \, (\mathrm{mod}\, 6) \\ \frac{4}{3(n-1)} &{}\quad \text{ if } \quad n \equiv 3 \, (\mathrm{mod}\, 6) \\ -\frac{4}{3n} &{}\quad \text{ if } \quad n \equiv 4 \, (\mathrm{mod}\, 6) \\ \frac{2}{3(n-1)} &{}\quad \text{ if } \quad n \equiv 5 \, (\mathrm{mod}\, 6). \\ \end{array} \right. \end{aligned}$$

This yields the following results.

Corollary 3.4

If G is a connected 2-regular graph of order $n \ge 3$, then

$$\begin{aligned} \frac{\Gamma _{t}(G)}{\Gamma (G)} \le \frac{4}{3} + \frac{4}{3(n-1)}. \end{aligned}$$

Corollary 3.5

If G is a connected 2-regular graph, then $\frac{\Gamma _{t}(G)}{\Gamma (G)} \le 2$, with equality if and only if $G \cong C_3$.

3.2 3-Regular Graphs

We next consider the case when $k = 3$. In order to determine the connected 3-regular (cubic) graphs G satisfying $\Gamma _{t}(G)/\Gamma (G) = 2$, we analyse the proof of the upper bound of Theorem 3.1 to obtain the structure of these extremal graphs. For this purpose, we shall need the following key lemma in [7]. For completeness, we provide the proof of this lemma as given in [7].

Lemma 3.6

[7] Every $\Gamma _t(G)$-set contains as a subset a minimal dominating set S such that $|S| \ge \frac{1}{2} \Gamma _t(G)$ and $|\mathrm{epn}(v,S)| \ge 1$ for each $v \in S$.

Proof

Let D be an arbitrary $\Gamma _t(G)$-set, and let

$$\begin{aligned} \begin{array}{lll} A &{} = &{} \left\{ v \in D \mid \mathrm{epn}(v,D) \ne \emptyset \right\} , \\ B &{} = &{} \left\{ v \in D {\setminus } A \mid d_A(v) \ge 1 \right\} , \text{ and } \\ C &{} = &{} D {\setminus } (A \cup B). \end{array} \end{aligned}$$

Then, $D = A \cup B \cup C$. As shown in [7], if $C \ne \emptyset$, then $G[C] = \frac{|C|}{2}K_2$ and each vertex of C has degree 1 in G[D]. Following the notation introduced in [7], we call two adjacent vertices in G[C] partners in C and we let (X, Y) be the partite sets in the graph G[C]. Thus, each vertex in X (resp., in Y) is adjacent in G[D] only to its partner in Y (resp., in X). For each $x \in X$, let $y_x$ be the partner of x in C. As shown in [7], for each vertex $v \in B$, we have $\mathrm{pn}(v,D) = \mathrm{ipn}(v,D) \subseteq A$, implying that

$$\begin{aligned} |A| \ge \sum _{v \in B} |\mathrm{ipn}(v,D)| \ge |B|. \end{aligned}$$

(1)

Following the notation introduced in the proof of Theorem 3.1 given in [7], we let $U = V(G) {\setminus } (D \cup N(A) \cup N(X))$ be the set of vertices in $V(G) {\setminus } D$ not dominated by A or X in G. Since D is a TD-set of G, the set U is dominated by $B \cup Y$. Let $B_Y$ be a minimum subset of $B \cup Y$ that dominates U. Thus for each $v \in B_Y$, we have that $|\mathrm{epn}(v,B_Y) \cap U| \ge 1$.

As observed in [7], the set $S = A \cup B_Y \cup X$ is a dominating set of G, although not necessarily minimal. For each vertex $x \in X$ we systematically delete x from S if $\mathrm{epn}(x,S) = \emptyset$ at each stage in the resulting set S, and let $X^*$ be the resulting subset of vertices of X that belong to the set S upon the completion of this process. Thus, $S = A \cup B_Y \cup X^*$ and, by construction, $|\mathrm{epn}(v,S)| \ge 1$ for each $v \in S$. As observed in [7], the set S is a minimal dominating set of G, and so $\Gamma (G) \ge |S|$. For every vertex $x \in X$, the set S contains at least one of x and its partner in C, noting that if the partner $y_x \in Y$ of x in C is not in S, then $y_x \in \mathrm{epn}(x,S)$, and so x is not deleted from S. Thus, $|S \cap C| \ge |X| = \frac{1}{2}|C|$. As shown earlier, $|A| \ge |B|$. Hence,

$$\begin{aligned} \Gamma (G)\ge & {} |S| \nonumber \\= & {} |S \cap A| + |S \cap B| + |S \cap C| \nonumber \\\ge & {} |A| + |S \cap C| \nonumber \\\ge & {} \frac{1}{2} (2|A| + |C|) \nonumber \\\ge & {} \frac{1}{2} (|A| + |B| + |C|) \nonumber \\= & {} \frac{1}{2} |D| \nonumber \\= & {} \frac{1}{2} \Gamma _t(G), \end{aligned}$$

(2)

or equivalently, $\Gamma _t(G) \le 2\Gamma (G)$. As observed earlier, $S \subset D$ and S is a minimal dominating set of G. Further, $|S| \ge \frac{1}{2} \Gamma _t(G)$ and $|\mathrm{epn}(v,S)| \ge 1$ for each $v \in S$. $\square$

We note that Theorem 3.1 follows as an immediate consequence of Lemma 3.6. We proceed further with the following lemma which gives structural properties of graphs G that achieve equality in the bound of Theorem 3.1. We remark that the following properties of graphs achieving equality in the bound of Theorem 3.1 is implicitly implied in [7], albeit without proof. We provide here a complete proof since we will need these properties in order to characterize the cubic graphs achieving equality in the bound of Theorem 3.1.

Lemma 3.7

If G is a graph with no isolated vertex satisfying $\Gamma _{t}(G) = 2\Gamma (G)$, then the following holds.

• (a) $\Gamma (G) = \alpha (G)$.

• (b) Every $\Gamma _t(G)$-set induces a subgraph that consists of disjoint copies of $K_2$.

• (c) Every vertex that does not belong to an arbitrary $\Gamma _t(G)$-set is contained in a common triangle with two vertices of the set.

Proof

Suppose that G is a graph with no isolated vertex satisfying $\Gamma (G) = \frac{1}{2}\Gamma _t(G)$. Let D be an arbitrary $\Gamma _t(G)$-set. Following exactly the notation introduced in the proof of Lemma 3.6, we must have equality throughout inequality chain (2) in this proof. Hence, $S = A \cup B_Y \cup X^*$ is a $\Gamma (G)$-set, $|A| = |B|$, $S \cap B = \emptyset$ and $|S \cap C| = |C|/2$. Since $|A| = |B|$, we have by inequality chain (1) that $|A| = \sum _{v \in B} |\mathrm{pn}(v,S)| = |B|$. Thus, $|\mathrm{pn}(v,S)| = 1$ for every $v \in B$ and every vertex of A is the (internal) private neighbor of some vertex of B. In particular, $d_S(v) = 1$ for every $v \in A$ and every vertex in B is adjacent to a unique vertex of A, namely to its (internal) private neighbor in S. Hence, A is an independent set and the subgraph $G[A \cup B]$ induced by $A \cup B$ contains a perfect matching. (Note that it is possible that there may be some edges joining vertices of B.)

As observed in the proof of Lemma 3.6, for every vertex $x \in X$, the set S contains at least one of x and its partner in C, and so $|S \cap C| \ge |C|/2$. However, $|S \cap C| = |C|/2$, implying that the set S contains exactly one of x and its partner $y_x$ in C. Renaming vertices of C if necessary, we may assume that $S \cap C = X$. Since A is an independent set and there is no edge between A and C, the set $S = A \cup X$ is an independent set, and so $\alpha (G) \ge |S| = |A| + |C|/2$. Since every maximum independent set in a graph is a minimal dominating set in the graph, we note that $|S| = \Gamma (G) \ge \alpha (G) = |S|$. Consequently, the set $S = A \cup X$ is a maximum independent set in G, and so $\Gamma (G)= \alpha (G) = |S|$. This proves Part (a).

Suppose that $A \ne \emptyset$ and consider an arbitrary vertex $u \in A$. Let v be the neighbor of u in G[D], and so $v \in B$ and $\mathrm{pn}(v,D) = \{u\}$. Further, let $w \in \mathrm{epn}(u,S)$. The vertex w exists since $S\subseteq D$ and $u\in A$ implies that u has an external private neighbor with respect to D. Let $|C| = 2c$ and recall that $G[C] = cK_2$ and each vertex of C has degree 1 in G[D]. In particular, we note that v is adjacent to no vertex of $A \cup C$ different from u. Thus, the set $(S {\setminus } \{u\}) \cup \{v,w\}$ is an independent set in G, implying that $\alpha (G) \ge |S| + 1$, a contradiction. Hence, $A = \emptyset$, which in turn implies that $B = \emptyset$. Thus, $D = C$ and $G[D] = G[C] = cK_2$, where $|C| = 2c$. Since D is an arbitrary $\Gamma _t(G)$-set, we deduce that every $\Gamma _t(G)$-set induces a subgraph isomorphic to $cK_2$. This proves Part (b). By our earlier observations, $\Gamma (G) = \alpha (G) = c$.

To prove Part (c), let v be an arbitrary vertex in $V(G) {\setminus } D$. As observed above, $D = C$ and $G[C] = cK_2$. We show that v is contained in a common triangle with two vertices of C. Suppose, to the contrary, that v does not belong to a common triangle with two vertices of C. If v is adjacent to both x and its partner $y_x$ for some vertex $x \in C$, then $vxy_xv$ is a common triangle containing v and two vertices of C, a contradiction. Hence, v is adjacent to at most one of x and its partner $y_x$ for every vertex $x \in C$. Let $C'$ be a subset of C constructed as follows. Initially, let $C' = \emptyset$. For each pair x and $y_x$ where $x \in C$ (and $xy_x$ is an edge), select one vertex that is not adjacent to v and add it to the set $C'$. Thus, $|C'| = c$ and $C'$ is an independent set. By construction, no vertex of $C'$ is adjacent to v. Hence, $C' \cup \{v\}$ is an independent set on G, and so $\alpha (G) \ge |C'| + 1 = c + 1 > \alpha (G)$, a contradiction. Therefore, the vertex v is adjacent to both x and its partner $y_x$ in C for at least one vertex $x \in C$. $\square$

We are now in a position to characterize the connected cubic graphs achieving equality in Theorem 3.1.

Theorem 3.8

If G is a connected 3-regular graph, then

$$\begin{aligned} \frac{\Gamma _{t}(G)}{\Gamma (G)} \le 2 \, \text{ with } \text{ equality } \text{ if } \text{ and } \text{ only } \text{ if } \,G \cong K_4. \end{aligned}$$

Proof

The inequality follows by Theorem 3.1. Therefore in what follows we assume $\frac{\Gamma _t(G)}{\Gamma (G)}=2$. We adopt the notation introduced in the proof of Lemmas 3.6 and 3.7. Let D be an arbitrary $\Gamma _t(G)$-set. By Lemma 3.7(b), $G[D] \cong cK_2$ for some integer $c \ge 1$. By Lemma 3.7(a), $\Gamma (G) = \alpha (G) = c$. Let G[D] consist of the c edges $x_1y_1, \ldots , x_cy_c$. Let ${\bar{D}} = V(G) {\setminus } D$. By Lemma 3.7(c), each vertex in ${\bar{D}}$ is contained in a common triangle with two vertices from the set D. Since G is a cubic graph, there is therefore a weak partition (where some of the sets in the partition may possibly be empty) of ${\bar{D}}$ into sets $V_1, \ldots , V_c$ such that every vertex in $V_i$ is adjacent to both $x_i$ and $y_i$ in G for all $i \in [c]$. Since G is a cubic graph and $x_i$ and $y_i$ are adjacent to each other and to every vertex in $V_i$, we note that $|V_i| \le 2$ for all $i \in [c]$.

Suppose that $|V_i| \le 1$ for all $i \in [c]$. Let $[D,{\bar{D}}]$ denote the set of edges joining D and ${\bar{D}}$. Since each vertex in D has two neighbors in ${\bar{D}}$ and $|D| = 2c$, we note that $|[D,{\bar{D}}]| = 2|D| = 4c$. By supposition, $|V_i| \le 1$ for all $i \in [c]$, implying that

$$\begin{aligned} |[D,{\bar{D}}]| \le \sum _{i=1}^c 3|V_i| \le 3c, \end{aligned}$$

noting that ${\bar{D}} = (V_1, \ldots , V_c)$ is a partition of ${\bar{D}}$ and each vertex in ${\bar{D}}$ has at most three neighbors in D. Thus, $4c = |[D,{\bar{D}}]| \le 3c$, a contradiction. Therefore, $|V_i| = 2$ for at least one $i \in [c]$. Renaming the sets $V_1, \ldots , V_c$ if necessary, we may assume that $|V_1| = 2$. Let $V_1 = \{u_1,u_2\}$, and so both $u_1$ and $u_2$ are adjacent to $x_1$ and $y_1$. In what follows, let

$$\begin{aligned} D_{\ge i} = \bigcup _{j=i}^c \{x_j,y_j\} \end{aligned}$$

where $i \in [c]$. In particular, we note that $D = D_{\ge 1}$. Suppose that $u_1$ and $u_2$ are not adjacent. Thus, $c \ge 2$. If for every $i \in [c] {\setminus } \{1\}$, there exists a vertex in $\{x_i,y_i\}$ that is adjacent to neither $u_1$ nor $u_2$, then there exists a subset $D_{\ge 2}'$ of $D_{\ge 2}$ such that $|D_{\ge 2}'| = c - 1$ and $D_{\ge 2}' \cup \{u_1,u_2\}$ is an independent set, implying that $\alpha (G)\ge |D_{\ge 2}'| + 2 = c+1$, a contradiction. Hence for some $i \in [c] {\setminus } \{1\}$, the vertex $u_1$ is adjacent to one of $x_i$ and $y_i$, say $y_i$, and the vertex $u_2$ is adjacent to $x_i$. Renaming the sets $V_2, \ldots , V_c$ if necessary, we may assume that $i = 2$. Thus, $u_1$ is adjacent to $y_2$ and $u_2$ is adjacent to $x_2$.

Let $u_3$ be the neighbor of $x_2$ different from $u_2$ and $y_2$. We note that $u_3 \in V_i$ for some $i \in [c] {\setminus } \{1\}$. Suppose that $u_3 \in V_2$. Thus, the vertex $u_3$ is adjacent to both $x_2$ and $y_2$, and is adjacent to at most one vertex from $D_{\ge 3}$. Hence there exists a subset $D_{\ge 3}'$ of $D_{\ge 3}$ such that $|D_{\ge 3}'| = c-2$ and $D_{\ge 3}' \cup \{u_1,u_2,u_3\}$ is an independent set, implying that $\alpha (G) \ge |D_{\ge 3}'| + 3 = c+1$, a contradiction. Therefore, $u_3 \notin V_2$, and so $u_3 \in V_i$ for some $i \in [c] {\setminus } \{1,2\}$. Renaming the sets $V_3, \ldots , V_c$ if necessary, we may assume that $u_3 \in V_3$. Thus, $u_3$ is adjacent to both $x_3$ and $y_3$.

Let $u_4$ be the neighbor of $x_3$ different from $u_3$ and $y_3$. We note that $u_4 \in V_i$ for some $i \in [c] {\setminus } \{1,2\}$. Suppose that $u_4 \in V_3$. Thus, the vertex $u_4$ is adjacent to both $x_3$ and $y_3$, and is adjacent to at most one vertex from $D_{\ge 4}$. Hence there exists a subset $D_{\ge 4}'$ of $D_{\ge 4}$ such that $|D_{\ge 4}'| = c-3$ and $D_{\ge 4}' \cup \{u_1,u_2,u_3,u_4\}$ is an independent set, implying that $\alpha (G) \ge |D_{\ge 4}'| + 4 = c+1$, a contradiction. Therefore, $u_4 \notin V_3$, and so $u_4 \in V_i$ for some $i \in [c] {\setminus } \{1,2,3\}$. Renaming the sets $V_4, \ldots , V_c$ if necessary, we may assume that $u_4 \in V_4$. Thus, $u_4$ is adjacent to both $x_4$ and $y_4$. The graph shown in Fig. 3 is therefore a subgraph of G, where the darkened vertices belong to the set D.

Fig. 3

A subgraph of G

Continuing in this way, there exists a sequence of distinct vertices $u_3,u_4,\ldots ,u_{\ell + 1}$ such that the vertex $u_i$ is adjacent to $x_{i-1}$ and $u_i \in V_i$ for $i \in [\ell ] {\setminus } \{1,2\}$ and $u_{\ell + 1} \in V_{\ell }$. Let $U = \{u_1,u_2,\ldots ,u_{\ell + 1}\}$. If $c = \ell$, then $\alpha (G) \ge |U| = c+1$, a contradiction. Hence, $c \ge \ell + 1$. Noting that $u_{\ell + 1}$ is adjacent to at most one vertex from $D_{\ge \ell + 1}$, there exists a subset $D_{\ge \ell + 1}'$ of $D_{\ge \ell + 1}$ such that $|D_{\ge \ell + 1}'| = c-\ell$ and $U \cup D_{\ge \ell + 1}'$ is an independent set, implying that $\alpha (G) \ge |U| + |D_{\ge \ell + 1}'| = c+1$, a contradiction. We deduce, therefore, that $u_1$ and $u_2$ are adjacent, implying that $G \cong K_4$. Conversely, if $G \cong K_4$, then $\Gamma _{t}(G) = 2$ and $\Gamma (G) = 1$, and so $\Gamma _{t}(G)/\Gamma (G) = 2$. This completes the proof of Theorem 3.8. $\square$

3.3 Closing Questions and Problems

We pose the following two questions that we have yet to settle.

Question 1

Is it true that if $G \ncong K_4$ is a connected 3-regular graph, then

$$\begin{aligned} \frac{\Gamma _{t}(G)}{\Gamma (G)} \le \frac{3}{2}? \end{aligned}$$

Question 2

For $k \ge 2$, if G is a connected k-regular graph, then is it true that

$$\begin{aligned} \frac{\Gamma _{t}(G)}{\Gamma (G)} \le 2 \, \text{ with } \text{ equality } \text{ if } \text{ and } \text{ only } \text{ if } \,G \cong K_{k+1}? \end{aligned}$$

We have shown that Question 2 is true when $k = 2$ (see Corollary 3.5) and when $k = 3$ (see Theorem 3.8). However, we have yet to answer Question 2 when $k \ge 4$.

In summary, our focus in this paper is to characterize the connected cubic graphs G satisfying $\gamma _{t}(G)/\gamma (G) = 2$, and to characterize the connected cubic graphs G satisfying $\Gamma _{t}(G)/\Gamma (G) = 2$. These characterizations are presented in Theorem 2.8 and Theorem 3.8, respectively. It would be interesting to extend these characterizations to connected subcubic graphs. We remark that there are many families of subcubic graphs G that are not cubic graphs satisfying $\gamma _{t}(G)/\gamma (G) = 2$. For example, the 2-corona of a path or a cycle is such a family of subcubic graphs, where we recall that the 2-corona $H \circ P_2$ of a graph H is the graph of order 3|V(H)| obtained from H by attaching a path of length 2 to each vertex of H so that the resulting paths are vertex-disjoint. We close with the following two open problems.

Problem 1

Characterize the subcubic isolate-free graphs G satisfying $\gamma _{t}(G)/\gamma (G)= 2$.

Problem 2

Characterize the subcubic isolate-free graphs G satisfying $\Gamma _{t}(G)/\Gamma (G)= 2$.