Upper Total Domination in Claw-Free Cubic Graphs

Abstract

A set S of vertices in a graph G is a total dominating set if every vertex of G is adjacent to some other vertex in S. A total dominating set S is minimal if no proper subset of S is a total dominating set of G. The upper total domination number, $\Gamma _t(G)$, of G is the maximum cardinality of a minimal total dominating set of G. A claw-free graph is a graph that does not contain a claw $K_{1,3}$ as an induced subgraph. It is known, or can be readily deduced, that if $G \ne K_4$ is a connected claw-free cubic graph of order n, then $\frac{1}{3}n \le \alpha (G) \le \frac{2}{5}n$, and $\frac{1}{3}n \le \Gamma (G) \le \frac{1}{2}n$, and these bounds are tight, where $\alpha (G)$ and $\Gamma (G)$ denote the independence number and upper domination number, respectively, of G. In this paper, we prove that if G is a connected claw-free cubic graph of order n, then $\frac{4}{9}n \le \Gamma _t(G) \le \frac{3}{5}n$.

1 Introduction

An isolate-free graph is a graph that contains no isolated vertex, that is, every vertex has degree at least 1 in the graph. Let G be an isolate-free graph. A set S of vertices in G is a total dominating set, abbreviated TD-set, of G if every vertex in G is adjacent to some other vertex in S. A minimal TD-set in G is a TD-set that contains no TD-set of G as a proper subset. The total domination number, $\gamma _t(G)$, of G is the minimum cardinality of a TD-set of G, while the upper total domination number, $\Gamma _t(G)$, of G is the maximum cardinality of a minimal TD-set in G. By definition, we have $\gamma _t(G) \le \Gamma _t(G)$. A TD-set of cardinality $\gamma _t(G)$ is called a $\gamma _t$-set of G, while a minimal TD-set of cardinality $\Gamma _t(G)$ is called a $\Gamma _t$-set of G. For recent books on domination and total domination in graphs, we refer the reader to [10,11,12, 16].

A graph is F-free if it does not contain F as an induced subgraph. In particular, if $F = K_{1,3}$, then the graph is claw-free, while if $F = K_4-e$, then the graph is diamond-free. An excellent survey of claw-free graphs has been written by Flandrin et al. [7]. Chudnovsky and Seymour recently attracted considerable interest in claw-free graphs due to their excellent series of papers in Journal of Combinatorial Theory on this topic (see, for example, their paper [3]). A cubic graph (also called a 3-regular graph) is a graph in which every vertex has degree 3. Domination and total domination in claw-free cubic graphs has been extensively studied in the literature (see, for example, [5, 6, 8, 9, 13,14,15, 18, 19, 21, 22] and elsewhere). In this paper, we continue the study of total domination in claw-free cubic graphs. Let G be a connected, claw-free, cubic graph of order n. Since $\gamma _t(G) \ge n/\Delta (G)$ for every isolate-free graph, we observe that $\gamma _t(G) \ge \frac{1}{3}n$, and this bound is sharp. Recently, the authors [1, 2] proved that if we exclude four graphs, then $\gamma _t(G) \le \frac{3}{7}n$. In this paper we prove that $\frac{4}{9}n \le \Gamma _t(G) \le \frac{3}{5}n$.

1.1 Graph Theory Notation and Terminology

For notation and graph theory terminology, we in general follow [16]. Specifically, let G be a graph with vertex set V(G) and edge set E(G), and of order $n(G) = |V(G)|$ and size $m(G) = |E(G)|$. A neighbor of a vertex v in G is a vertex u that is adjacent to v, that is, $uv \in E(G)$. The open neighborhood $N_G(v)$ of a vertex v in G is the set of neighbors of v, while the closed neighborhood of v is the set $N_G[v] = \{v\} \cup N_G(v)$. We denote the degree of v in G by $d_G(v) = |N_G(v)|$. As mentioned earlier, a graph is isolate-free if it does not contain an isolated vertex; that is, a vertex of degree 0. For disjoint subsets X and Y of vertices in G, we denote the set of edges between X and Y by [X, Y].

For a set $S \subseteq V(G)$, its open neighborhood is the set $N_G(S) = \cup _{v \in S} N_G(v)$, and its closed neighborhood is the set $N_G[S] = N_G(S) \cup S$. Thus, a set $S \subseteq V(G)$ is a TD-set of G if $N_G(S) = V(G)$. The open S-private neighborhood of v is defined by $\mathrm{pn}_G(v,S) = \{w \in V(G) \, :N_G(w) \cap S = \{v\}\}$. The open S-external private neighborhood of v is the set $\mathrm{epn}_G(v,S) = \mathrm{pn}_G(v,S) \setminus S$, while the open S-internal private neighborhood of v is defined by $\mathrm{ipn}_G(v,S) = \mathrm{pn}_G(v,S) \cap S$. We note that $\mathrm{pn}_G(v,S) = \mathrm{ipn}_G(v,S) \, \cup \, \mathrm{epn}_G(v,S)$. If the graph G is clear from the context, we omit writing it in the above expressions. For example, we simply write $\mathrm{epn}(v,S)$ and $\mathrm{ipn}(v,S)$ rather than $\mathrm{epn}_G(v,S)$ and $\mathrm{ipn}_G(v,S)$, respectively.

A fundamental property of minimal TD-sets was established by Cockayneet al. [4].

Lemma 1

([4]) A TD-set S in a graph G is a minimal TD-set in G if and only if for every vertex $v \in S$, $|\mathrm{epn}(v,S)| \ge 1$ or $|\mathrm{ipn}(v,S)| \ge 1$.

For a set of vertices $S\subseteq V(G)$, the subgraph induced by S is denoted by G[S]. We denote the subgraph obtained from G be deleting a set S of vertices and all edges incident with vertices in S by $G - S$. In particular, if $S = \{v\}$, then we simply denote $G - S$ by $G - v$ (rather than $G - \{v\}$). We denote the path, cycle, and complete graph on n vertices by $P_n$, $C_n$, and $K_n$, respectively, and we denote the complete bipartite graph with partite sets of cardinality n and m by $K_{n,m}$. A triangle in G is a subgraph isomorphic to $K_3$, whereas a diamond in G is an induced subgraph of G isomorphic to $K_4$ with one edge missing, denoted by $K_4 - e$. For $k \ge 1$ an integer, we use the standard notation $[k] = \{1,\ldots ,k\}$.

1.2 A Triangle-Diamond Necklace

We define in this section what we have coined a triangle-diamond-necklace. A triangle-necklace was defined by the authors in [2] as follows.

Definition 1

([2]) For $k \ge 1$ an integer, let $F_{2k}$ be the connected cubic graph constructed as follows. Take 2k disjoint copies $T_1, T_2, \ldots , T_{2k}$ of a triangle, where $V(T_i) = \{x_i,y_i,z_i\}$ for $i \in [2k]$. Let

$$\begin{aligned} E_a &= \{x_{2i-1}x_{2i} :i \in [k] \} \\ E_b &= \{y_{2i-1}y_{2i} :i \in [k] \} \\ E_c &= \{z_{2i}z_{2i+1} :i \in [k] \}, \end{aligned}$$

where addition is taken modulo 2k (and so, $z_1 = z_{2k+1}$). Let $F_{2k}$ be obtained from the disjoint union of these 2k triangle by adding the edges $E_a \cup E_b \cup E_c$. We call the resulting graph $F_{2k}$ a triangle-necklace with 2k triangles. Let ${\mathcal {T}}_\mathrm{cubic}= \{ F_{2k} :k \ge 1\}$. The triangle-necklaces $F_2$ and $F_4$ are shown in Fig. 1a, b, respectively.

Fig. 1

The triangle-necklaces $F_2$ and $F_4$

Definition 2

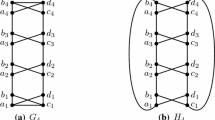
For $k \ge 1$ an integer, let $D_1, \ldots , D_k$ be k disjoint copies of a diamond, where $V(D_i) = \{a_i,b_i,c_i,d_i\}$ where $a_ib_i$ is the missing edge in $D_i$ for $i \in [k]$. Adopting the notation in Definition 1, let $G_{2k}$ be obtained from a triangle-necklace $F_{2k}$ with 2k triangles by deleting the k edges $z_{2i}z_{2i+1}$ from $F_{2k}$ for all $i \in [k]$, adding the k diamonds $D_1, \ldots , D_k$, and adding the edges $a_iz_{2i}$ and $b_iz_{2i+1}$ for all $i \in [k]$ (where addition is taken modulo 2k). We call the resulting graph $G_{2k}$ a triangle-diamond-necklace with k diamonds. Let ${\mathcal {G}}_\mathrm{cubic}= \{ G_{2k} :k \ge 1\}$. The triangle-diamond-necklace $G_2$ and $G_4$ are shown in Fig. 2a, b, respectively.

Fig. 2

The triangle-diamond-necklaces $G_2$ and $G_4$

2 Known Results

Li and Virlouvet [17] established the following upper bound on the independence number of a claw-free graph with minimum degree at least $\delta$.

Theorem 1

([17]) If G is a claw-free graph of order n, then $\alpha (G) \le \frac{2n}{\delta (G) + 2}$.

Southey and Henning [20] established upper bounds on the upper domination number $\Gamma (G)$ and the upper total domination number $\Gamma _t(G)$ of a r-regular graph for all $r \ge 1$.

Theorem 2

([20]) For $r \ge 1$ if G is an r-regular graph of order n, then $\Gamma (G) \le \frac{1}{2}n$ and $\Gamma _t(G) \le \frac{n}{2 - \frac{1}{r}}$.

Both bounds in Theorem 2 are sharp, and the infinite families of graphs that achieve equality in these bounds are characterized in [20].

2.1 The Independence Number and Upper Domination Number

A lower bound on the independence number $\alpha (G)$ of a connected claw-free cubic graph follows from a more general result. For $k \ge 3$, let $G \ne K_{k+1}$ be a connected k-regular graph of order n. By Brooks Coloring Theorem, the chromatic number $\chi (G)$ of G is at most the maximum degree, namely k. Since the independence number $\alpha (G) \ge n/\chi (G)$ for all graphs G, this yields $\alpha (G) \ge n/k$. In the special case when $k = 3$, we have that if $G \ne K_4$ is a connected cubic graph of order n, then $\alpha (G) \ge n/3$. In particular, this yields the following trivial lower bound on the independence number of a claw-free cubic graph, which is certainly known, but we were unable to find a reference.

Observation 1

If $G \ne K_4$ is a connected claw-free graph of order n, then $\alpha (G) \ge \frac{1}{3}n$.

The bound of Observation 1 is tight, as may be seen, for example, by taking a connected claw-free graph that is diamond-free.

As a special case of Theorem 1, we have the following upper bound on the independence number of a connected claw-free cubic graph.

Theorem 3

([17]) If G is a connected claw-free cubic graph of order n, then $\alpha (G) \le \frac{2}{5}n$.

We remark that the bound of Theorem 3 is tight. For example, suppose that $G \in {\mathcal {G}}_\mathrm{cubic}$ is a triangle-diamond-necklace of order n. Thus, $G = G_{2k}$ for some $k \ge 1$, and so G has order $n = 10k$ and $\alpha (G) = 4k = \frac{2}{5}n$. The shaded vertices in Fig. 3a, b are examples of an $\alpha$-set in the graphs $G_2$ and $G_4$, respectively.

Fig. 3

Claw-free cubic graphs G of order n with $\alpha (G) = \frac{2}{5}n$

Since $\Gamma (G) \ge \alpha (G)$ for all graphs G, the following lower bound on the upper domination number of a claw-free cubic graph follows from Observation 1.

Observation 2

If $G \ne K_4$ is a connected claw-free graph of order n, then $\Gamma (G) \ge \frac{1}{3}n$.

As a consequence of the characterizations given in [20], we can readily deduce the extremal family of connected claw-free graphs with largest possible upper domination number. For $k \ge 1$, let $H_1 = kK_3$ and $H_2 = kK_3$ consist of k disjoint copies of $K_3$. Let H be the graph obtained from the disjoint union $H_1 \cup H_2$ by adding a perfect matching between $V(H_1)$ and $V(H_2)$ in such a way that the resulting graph H is connected. We note that H is a claw-free cubic graph of order $n = 6k$. Moreover, the set $V(H_1)$ is a minimal dominating set of H, implying that $\Gamma (H) \ge |V(H_1)| = \frac{1}{2}n$. By Theorem 2, $\Gamma (H) \le \frac{1}{2}n$. Consequently, $\Gamma (H) = \frac{1}{2}n$. Let ${\mathcal {H}}_{\mathrm{cubic}}$ be the family of all such graphs H so constructed.

Theorem 4

([20]) If G is a connected claw-free cubic graph of order n, then $\Gamma (G) \le \frac{1}{2}n$, with equality if and only if $G \in {\mathcal {H}}_{\mathrm{cubic}}$.

Combining the above lower and upper bounds on the independence number and upper total domination number yields the following known result.

Theorem 5

If $G \ne K_4$ is a connected claw-free cubic graph of order n, then the following properties hold.

• (a) $\frac{1}{3}n \le \alpha (G) \le \frac{2}{5}n$, and

• (b) $\frac{1}{3}n \le \Gamma (G) \le \frac{1}{2}n$.

3 Main Result

Our aim in this paper is to provide lower and upper bounds on the upper total domination number of a claw-free connected cubic graph. We shall prove the following theorem.

Theorem 6

If G is a connected claw-free cubic graph of order n, then $\frac{4}{9}n \le \Gamma _t(G) \le \frac{3}{5}n$.

The upper bound in Theorem 6 follows from the more general result given in Theorem 2 that if G is a cubic graph of order n, then $\Gamma _t(G) \le \frac{3}{5}n$. We remark that this bound is tight, even for claw-free cubic graphs. For example, consider a triangle-diamond-necklace $G \in {\mathcal {G}}_\mathrm{cubic}$ of order n. Thus, $G = G_{2k}$ for some $k \ge 1$, and so $n = 10k$. Adopting the notation in Definition 2, let $C = \{c_1,\ldots ,c_k\}$, $D = \{d_1,\ldots ,d_k\}$, $X = \{x_{2i-1} :i \in [k]\}$, $Y = \{y_{2i} :i \in [k]\}$, and $Z = \{z_1,z_2,\ldots ,z_{2k}\}$. The set $C \cup D \cup X \cup Y \cup Z$ is a minimal TD-set of $G_{2k}$, and so $\Gamma _t(G_{2k}) \ge 6k = \frac{3}{5}n$. By Theorem 2, $\Gamma _t(G_{2k}) \le \frac{3}{5}n$. Consequently, $\Gamma _t(G_{2k}) = \frac{3}{5}n$. For example, the shaded vertices in Fig. 4a, b form a $\Gamma _t$-set of $G_2$ and $G_3$, respectively. We state this formally as follows.

Observation 3

If $G \in {\mathcal {G}}_\mathrm{cubic}$ has order n, then $\Gamma _t(G) =\frac{3}{5}n$.

Fig. 4

Claw-free cubic graphs G of order n with $\Gamma _t(G) = \frac{3}{5}n$

4 Proof of Theorem 6

As remarked earlier, the tight upper bound in Theorem 6 follows from Theorem 2. In this section, we establish the lower bound in Theorem 6. In order to prove this lower bound, we need to prove a stronger result. For this purpose, we introduce the concept of a special subcubic graph.

Definition 3

We call a graph G a special subcubic graph if the following three properties hold: (i) G is connected, (ii) $\Delta (G) \le 3$, and (iii) every vertex belongs to a triangle in G.

Every special subcubic graph has minimum degree at least 2, noting that every vertex belongs to a triangle. We note that possibly there are no vertices of degree 2, in which case the special subcubic graph is a claw-free connected cubic graph. Hence, the family of claw-free connected cubic graphs is a subfamily of the family of special subcubic graphs. An identical proof to that presented in [14] yields the following structural property of special subcubic graph.

Lemma 2

If $G \ne K_4$ is a special subcubic graph, then the vertex set V(G) can be uniquely partitioned into sets each of which induces a triangle or a diamond in G.

Adopting the notation in [14] used for claw-free cubic graphs, we refer to the unique partition given in Lemma 2 as a triangle-diamond partition of G, abbreviated $\Delta$-D-partition. Further we call every triangle and diamond induced by a set in our $\Delta$-D-partition a unit of the partition. A unit that is a triangle is called a triangle-unit and a unit that is a diamond is called a diamond-unit. (We note that a triangle-unit is a triangle that does not belong to a diamond.) We say that two units in the $\Delta$-D-partition are adjacent if there is an edge joining a vertex in one unit to a vertex in the other unit. If two triangle-units are joined by two edges, then we call these triangle-units double-bonded. The special subcubic graph $G_9$, for example, shown in Fig. 5 has two-triangle units that are double-bonded.

Fig. 5

The graph $G_9$

If $G \ne K_4$ is a special subcubic graph of order n with $n_t$ triangle-units and $n_d$ diamond-units, then since triangle-unit contributes 3 to the order and every diamond-unit contributes 4 to the order we note that $n = 3n_t + 4n_d$. We are now in a position to present our key result.

Theorem 7

If G is a special subcubic graph of order n, then $\Gamma _t(G) \ge \frac{4}{9}n$.

Proof

We proceed by induction on the order $n \ge 3$ of the special subcubic graph. If $n=3$, then $G = K_3$ and $\Gamma _t(G) = 2 = \frac{2}{3}n > \frac{4}{9}n$. If $n=4$, then either $G = K_4$ or $G = K_4-e$. In both cases, $\Gamma _t(G) = 2 = \frac{1}{2}n > \frac{4}{9}n$. Since there is no special subcubic graph on five vertices, $n \ne 5$. Suppose that $n = 6$. In this case, G is one of the three graphs $G_{6.1}$, $G_{6.2}$ and $G_{6.3}$ shown in Fig. 6a–c, respectively, where the shaded vertices are examples of a $\Gamma _t$-set in the respective graphs. If $G = G_{6.1}$, then $\Gamma _t(G) = 3$, and if $G = G_{6.2}$ or if $G = G_{6.3}$, then $\Gamma _t(G) = 4$. In all cases, $\Gamma _t(G) \ge 3 = \frac{1}{2}n > \frac{4}{9}n$.

If $n = 7$, then G is one of the two graphs $G_{7.1}$ and $G_{7.2}$ shown in Fig. 7a, b, respectively, where the shaded vertices are examples of a $\Gamma _t$-set in the respective graphs. In both cases, $\Gamma _t(G) = 4 = \frac{4}{7}n > \frac{4}{9}n$.

If $n = 8$, then G is one of the two graphs $G_{8.1}$ and $G_{8.2}$ shown in Fig. 7c, d, respectively, where the shaded vertices are examples of a $\Gamma _t$-set in the respective graphs. In both cases, $\Gamma _t(G) = 4 = \frac{1}{2}n > \frac{4}{9}n$.

If $n = 9$, then G consists of three triangle-units, with at least two additional edges between the triangle-units. Either $G = G_9$, in which case $\Gamma _t(G) = 4 = \frac{4}{9}n$, or G is obtained from $G_9$ by removing one or two edges, in which case $\Gamma _t(G) = 6 > \frac{4}{9}n$. This establishes the base cases when $3 \le n \le 9$. Let $n \ge 10$ and assume that if $G'$ is a special subcubic graph of order $n'$ where $n' < n$, then $\Gamma _t(G') \ge \frac{4}{9}n'$. We proceed further with a series of claims.

Claim 1

If G contains a diamond-unit, then $\Gamma _t(G) > \frac{4}{9}n$.

Proof

Suppose that G contains a diamond-unit D. Let $V(D) = \{u_1,u_2,u_3,u_4\}$ where $u_1u_2$ is the missing edge in D. Since $n \ge 10$, at least one of $u_1$ and $u_2$ has degree 3 in G. Let $G' = G - V(D)$, and let $G'$ have order $n'$, and so $n' = n - 4$. We note that either $G'$ is connected, in which case $G'$ is a special subcubic graph, or $G'$ has exactly two components, each of which is a special subcubic graph. Applying the inductive hypothesis to $G'$ if $G'$ is connected, or to the two components of $G'$ if $G'$ is disconnected, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}(n-4)$. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices $u_3$ and $u_4$, implying that $\Gamma _t(G) \ge \Gamma _t(G') + 2 \ge \frac{4}{9}(n-4) + 2 > \frac{4}{9}n$. $\square$

By Claim 1, we may assume that G contains no diamond-unit, that is, every unit in G is a triangle-unit.

Claim 2

If G contains double-bonded triangle-units, then $\Gamma _t(G) \ge \frac{4}{9}n$.

Proof

Suppose that G contains two triangle-units $T_1$ and $T_2$, where $V(T_i) = \{x_i,y_i,z_i\}$ for $i \in [2]$ and where $x_1x_2$ and $y_1y_2$ are edges in G. Thus, $T_1$ and $T_2$ form double-bonded triangle-units. Since $n \ge 10$, at least one of $z_1$ and $z_2$ has degree 3 in G. We may assume that $d_G(z_2) = 3$. Let $z_3$ be the neighbor of $z_2$ not in $T_2$. Let $T_3$ be the triangle-unit that contains $z_3$, and let $V(T_3) = \{x_3,y_3,z_3\}$. Let $G' = G - (V(T_1) \cup V(T_2) \cup V(T_3))$, and let $G'$ have order $n'$, and so $n' = n - 9$. We note that $G'$ contains at most three components, and each component of $G'$ is a special subcubic graph. Applying the inductive hypothesis to the components of $G'$, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}(n-9) = \frac{4}{9}n - 4$. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices $x_1,y_1,z_2$ and $z_3$, implying that $\Gamma _t(G) \ge \Gamma _t(G') + 4 \ge \frac{4}{9}n$. $\square$

By Claim 2, we may assume that G contains no double-bonded triangle-units. Thus, by our earlier assumptions, every unit in G is a triangle-unit and every two triangle-units are joined by at most one edge.

Claim 3

If a triangle-unit of G contains two vertices of degree 2 in G, then $\Gamma _t(G) > \frac{4}{9}n$.

Proof

Suppose that G contains a triangle-unit T that contains two vertices of degree 2 in G. Let $V(T) = \{x,y,z\}$, where x and y have degree 2 in G. Let $G' = G - V(T)$, and let $G'$ have order $n'$, and so $n' = n - 3$. Applying the inductive hypothesis to the special subcubic graph $G'$, we have $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}(n-3)$. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices x and y, implying that $\Gamma _t(G) \ge \Gamma _t(G') + 2 \ge \frac{4}{9}(n-3) + 2 > \frac{4}{9}n$. $\square$

By Claim 3, we may assume that every triangle-unit of G contains at most one vertex of degree 2 in G.

Claim 4

If G contains a vertex of degree 2, then $\Gamma _t(G) \ge \frac{4}{9}n$.

Proof

Suppose that G contains a vertex $z_1$ of degree 2 in G. Let $T_1$ be the triangle-unit in G that contains $z_1$, and let $V(T_1) = \{x_1,y_1,z_1\}$. By assumption, both $x_1$ and $y_1$ have degree 3 in G. Let $x_2$ be a neighbor of $x_1$ not in $T_1$. Let $T_2$ be the triangle-unit in G that contains $x_2$, and let $V(T_2) = \{x_2,y_2,z_2\}$. By assumption, at least one of $y_2$ and $z_2$ have degree 3 in G. Renaming vertices if necessary, we may assume that $y_2$ has degree 3 in G. Let $y_3$ be a neighbor of $y_2$ not in $T_2$. Let $T_3$ be the triangle-unit in G that contains $y_3$, and let $V(T_3) = \{x_3,y_3,z_3\}$. Since G contains no double-bonded triangle-units, the units $T_1$, $T_2$ and $T_3$ are distinct. Let $G' = G - (V(T_1) \cup V(T_2) \cup V(T_3))$, and let $G'$ have order $n'$, and so $n' = n - 9$. We note that $G'$ contains at most four components, and each component of $G'$ is a special subcubic graph. Applying the inductive hypothesis to the components of $G'$, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}(n-9) = \frac{4}{9}n - 4$. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices $x_1,y_2,y_3$ and $z_1$, implying that $\Gamma _t(G) \ge \Gamma _t(G') + 4 \ge \frac{4}{9}n$. $\square$

By Claim 4, we may assume that G is a cubic graph. By our earlier observations, every unit in G is a triangle-unit, and two triangle-units are joined by at most edge. We now construct a graph F from G as follows. For each triangle-unit in G, we associate a vertex of F. If two triangle-units in G are joined by an edge, then add an edge between the corresponding vertices in F. The graph F is called the contraction graph of G. We note that F is a cubic graph of order $n_t$, where recall that $n_t$ denotes the number of triangle-units in G.

Claim 5

If F is a bipartite graph, then $\Gamma _t(G) \ge \frac{1}{2}n$.

Proof

Suppose that F is a bipartite (cubic) graph. Thus, F has two partite sets X and Y, and these two sets have the same cardinality. Let S be the set of all vertices in G that belong to a triangle-unit associated with the set X, and let $\overline{S} = V(G) \setminus S$. We note that $|S| = |\overline{S}| = \frac{1}{2}n$, and $\overline{S}$ is the set of all vertices in G that belong to a triangle-unit associated with the set Y. Reconstructing the graph G from the contraction graph F, the set S is a dominating set of G. Moreover, every vertex in S is adjacent to a unique vertex in $\overline{S}$, and every vertex in $\overline{S}$ is adjacent to a unique vertex in S; that is, the set of edges $[S,\overline{S}]$ between S and $\overline{S}$ induce a perfect matching in G. In particular, $|\mathrm{epn}(v,S)| = 1$ for every vertex $v \in S$. Since G[S] consists of disjoint copies of $K_3$, the graph G[S] is a 2-regular graph and is therefore isolate-free. Thus, S is a TD-set of G. As observed earlier, $|\mathrm{epn}(v,S)| = 1$ for every vertex $v \in S$. Therefore by Lemma 1, the set S is a minimal TD-set of G. Hence, $\Gamma _t(G) \ge |S| = \frac{1}{2}n$. $\square$

Fig. 6

The three special subcubic graphs of order 6

Fig. 7

The four special subcubic graphs of order 7 and 8

By Claim 5, we may assume that F is not a bipartite graph, that is, F contains an odd cycle. Let $g_{\mathrm{odd}}$ denote the odd girth of F, that is, $g_{\mathrm{odd}}$ is the length of a shortest odd cycle in F. We note that $g_{\mathrm{odd}}$ is an odd integer at least 3. Let C be a shortest odd cycle in F (of length $g_{\mathrm{odd}}$), and let C be the cycle

$$ C :v_1v_2 \ldots v_{g_{\mathrm{odd}}} v_1. $$

By the odd girth condition, the cycle C is an induced cycle in F. Let $T_i$ be the triangle-unit in G corresponding to the vertex $v_i$ in F for $i \in [g_{\mathrm{odd}}]$. Further, let $V(T_i) = \{x_i,y_i,z_i\}$ where $x_iy_{i+1}$ is an edge in G for all $i \in [g_{\mathrm{odd}}]$, where addition is taken modulo $g_{\mathrm{odd}}$, and so $x_{g_{\mathrm{odd}}}y_1$ is an edge in G. Let

$$ R = \bigcup _{i=1}^{g_{\mathrm{odd}}} V(T_i), $$

and so $|R| = 3g_{\mathrm{odd}}$. We consider three cases.

Case 1. $g_{\mathrm{odd}} \equiv 3 \, (\mathrm{mod}\, 6)$. In this case, we let $G' = G - R$. Let $G'$ have order $n'$, and so $n' = n - |R| = n - 3g_{\mathrm{odd}}$. We note that $G'$ contains at most $g_{\mathrm{odd}}$ components, and each component of $G'$ is a special subcubic graph. Applying the inductive hypothesis to the components of $G'$, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}(n-3g_{\mathrm{odd}}) = \frac{4}{9}n - \frac{4}{3}g_{\mathrm{odd}}$. Let

$$ S = \bigcup _{i=1}^{\frac{1}{3}g_{\mathrm{odd}}} \{x_{3i-2}, x_{3i}, y_{3i-1}, y_{3i} \}. $$

We note that $|S| = \frac{4}{3}g_{\mathrm{odd}}$. In the special case when $g_{\mathrm{odd}} = 9$, the triangle-units that belong to the set R are illustrated in Fig. 8, and the vertices in the set S are given by the shaded vertices. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices in the set S, implying that

$$ \Gamma _t(G) \ge \Gamma _t(G') + |S| \ge \left( \frac{4}{9}n -\frac{4}{3}g_{\mathrm{odd}}\right) + \frac{4}{3}g_{\mathrm{odd}} = \frac{4}{9}n. $$

Fig. 8

Case 1 when $g_{\mathrm{odd}} = 9$

Case 2. $g_{\mathrm{odd}} \equiv 5 \, (\mathrm{mod}\, 6)$. Let $v_1'$ be the neighbor of $v_1$ in F that does not belong to the cycle C. Let $T_1'$ be the triangle-unit in G corresponding to the vertex $v_1'$ in F, and let $V(T_1') = \{x_1',y_1',z_1'\}$ where $z_1z_1'$ is an edge in G. In this case, let $R' = R \cup V(T_1')$ and let $G' = G - R'$. Let $G'$ have order $n'$, and so $n' = n - |R'| = n - 3(g_{\mathrm{odd}} + 1)$. We note that $G'$ contains at most $g_{\mathrm{odd}} + 1$ components, and each component of $G'$ is a special subcubic graph. Applying the inductive hypothesis to the components of $G'$, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}n - \frac{4}{3}(g_{\mathrm{odd}} +1)$. Let

$$ S = \{z_1,z_1',x_{g_{\mathrm{odd}}},y_{g_{\mathrm{odd}}} \} \cup \bigcup _{i=1}^{\frac{1}{3}(g_{\mathrm{odd}}-2)} \{x_{3i-1}, x_{3i}, y_{3i-1}, y_{3i+1} \}. $$

We note that $|S| = \frac{4}{3}(g_{\mathrm{odd}} - 2) + 4$. In the special case when $g_{\mathrm{odd}} = 5$, the triangle-units that belong to the set $R'$ are illustrated in Fig. 9, and the vertices in the set S are given by the shaded vertices. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices in the set S, implying that

$$ \Gamma _t(G) \ge \Gamma _t(G') + |S| \ge \left( \frac{4}{9}n - \frac{4}{3}(g_{\mathrm{odd}} +1) \right) + \left( \frac{4}{3}(g_{\mathrm{odd}} - 2) + 4 \right) =\frac{4}{9}n. $$

Fig. 9

Case 2 when $g_{\mathrm{odd}} = 5$

Case 3. $g_{\mathrm{odd}} \equiv 1 \, (\mathrm{mod}\, 6)$. By the odd girth condition, there must exists two vertices at distance 2 apart on the cycle C that have no common neighbor in $V(F) \setminus V(C)$. Renaming the vertices of C, if necessary, we may assume that $v_2$ and $v_{g_{\mathrm{odd}}}$ are two such vertices on the cycle. Let $v_2'$ and $v_{g_{\mathrm{odd}}}'$ be the neighbors of $v_2$ and $v_{g_{\mathrm{odd}}}$, respectively, in F that do not belong to the cycle C. By assumption, $v_2' \ne v_{g_{\mathrm{odd}}}'$. Let $T_2'$ and $T_{g_{\mathrm{odd}}}'$ be the triangle-units in G corresponding to the vertices $v_2'$ and $v_{g_{\mathrm{odd}}}'$ in F, and let $V(T_i') = \{x_i',y_i',z_i'\}$ where $z_iz_i'$ is an edge in G for $i \in \{2,g_{\mathrm{odd}}\}$. In this case, let $R' = R \cup V(T_2') \cup V(T_{g_{\mathrm{odd}}}')$ and let $G' = G - R'$. Let $G'$ have order $n'$, and so $n' = n - |R'| = n - 3(g_{\mathrm{odd}} + 2)$. We note that $G'$ contains at most $g_{\mathrm{odd}} + 2$ components, and each component of $G'$ is a special subcubic graph. Applying the inductive hypothesis to the components of $G'$, we have by linearity that $\Gamma _t(G') \ge \frac{4}{9}n' = \frac{4}{9}n - \frac{4}{3}(g_{\mathrm{odd}} + 2)$. Let

$$ S = \{x_1,x_3,y_1,y_3,z_2,z_2',z_{g_{\mathrm{odd}}},z_{g_{\mathrm{odd}}}' \} \cup \bigcup _{i=1}^{\frac{1}{3}(g_{\mathrm{odd}}-4)} \{x_{3i+1}, x_{3i+3}, y_{3i+2}, y_{3i+3} \}. $$

We note that $|S| = \frac{4}{3}(g_{\mathrm{odd}} - 4) + 8$. In the special case when $g_{\mathrm{odd}} = 7$, the triangle-units that belong to the set $R'$ are illustrated in Fig. 10, and the vertices in the set S are given by the shaded vertices. Every $\Gamma _t$-set of $G'$ can be extended to a minimal TD-set of G by adding to it the vertices in the set S, implying that

$$ \Gamma _t(G) \ge \Gamma _t(G') + |S| \ge \left( \frac{4}{9}n -\frac{4}{3}(g_{\mathrm{odd}} + 2) \right) + \left( \frac{4}{3}(g_{\mathrm{odd}} - 4) + 8 \right) = \frac{4}{9}n. $$

Fig. 10

Case 3 when $g_{\mathrm{odd}} = 7$

In all three cases, we have $\Gamma _t(G) \ge \frac{4}{9}n$, which proves the desired lower bound. $\square$

We remark that the lower bound in Theorem 7 is achieved, for example, by the special subcubic graph $G = G_9$ shown in Fig. 5b, noting that in this case $\Gamma _t(G) = 4 = \frac{4}{9}n$.

Recall the statement of the lower bound in Theorem 6: If G is a claw-free connected cubic graph of order n, then $\Gamma _t(G) \ge \frac{4}{9}n$. As observed earlier, every claw-free connected cubic graph is a special subcubic graph. Hence, the lower bound in Theorem 6 is an immediate consequence of Theorem 7.

5 Concluding Remarks

We close with the following problem that we have yet to settle. Let ${\mathcal {F}}_{\mathrm{cubic}}$ denote the family of all connected claw-free cubic graphs.

Problem 1

Determine or estimate the best possible constant $c_{\mathrm{tdom}}$ such that $\Gamma _t(G) \ge c_{\mathrm{tdom}} \cdot n(G)$ for all $G \in {\mathcal {F}}_{\mathrm{cubic}}$.

By Theorem 7, $c_{\mathrm{tdom}} \ge \frac{4}{9}$. One can prove (or use a computer) that the claw-free cubic graph $G = G_{90}$ of order $n = 90$ shown in Fig. 11 satisfies $\Gamma _t(G) = 44 = \frac{22}{45}n$, where the shaded vertices are an example of a $\Gamma _t$-set of G. This yields the following lower and upper bounds on the constant $c_{\mathrm{tdom}}$. It would be interesting to determine the exact value of $c_{\mathrm{tdom}}$.

Theorem 8

$\frac{4}{9} \le c_{\mathrm{tdom}} \le \frac{22}{45}$.

Fig. 11

A claw-free cubic graph $G_{90}$ of order $n = 90$ with $\Gamma _t(G) = 44 = \frac{22}{45}n$