On Upper Total Domination Versus Upper Domination in Graphs

Abstract

A total dominating set of a graph G is a dominating set S of G such that the subgraph induced by S contains no isolated vertex, where a dominating set of G is a set of vertices of G such that each vertex in $V(G){\setminus } S$ has a neighbor in S. A (total) dominating set S is said to be minimal if $S{\setminus } \{v\}$ is not a (total) dominating set for every $v\in S$. The upper total domination number $\varGamma _t(G)$ and the upper domination number $\varGamma (G)$ are the maximum cardinalities of a minimal total dominating set and a minimal dominating set of G, respectively. For every graph G without isolated vertices, it is known that $\varGamma _t(G)\le 2\varGamma (G)$. The case in which $\frac{\varGamma _t(G)}{\varGamma (G)}=2$ has been studied in Cyman et al. (Graphs Comb 34:261–276, 2018), which focused on the characterization of the connected cubic graphs and proposed one problem to be solved and two questions to be answered in terms of the value of $\frac{\varGamma _t(G)}{\varGamma (G)}$. In this paper, we solve this problem, i.e., the characterization of the subcubic graphs G that satisfy $\frac{\varGamma _t(G)}{\varGamma (G)}=2$, by constructing a class of subcubic graphs, which we call triangle-trees. Moreover, we show that the answers to the two questions are negative by constructing connected cubic graphs G that satisfy $\frac{\varGamma _t(G)}{\varGamma (G)}>\frac{3}{2}$ and a class of regular non-complete graphs G that satisfy $\frac{\varGamma _t(G)}{\varGamma (G)}=2$.

1 Introduction

The graphs considered in this paper are finite, undirected and simple. Given a graph G with vertex set V(G) and edge set E(G), the neighborhood of a vertex $v\in V(G)$, which is denoted by $N_G(v)$, is the set of vertices adjacent to v and $N_G[v]=N_G(v)\cup \{v\}$. We say that vdominates vertices in $N_G(v)$. For a subset $S\subseteq V(G)$, let $N_G(S)=(\cup _{v\in S} N_G(v)){\setminus } S$ and $N_G[S]=N_G(S)\cup S$. Denote by $d_G(v)=|N_G(v)|$ and $d_G(S)=|N_G(S)|$ the degrees of v and S in G, respectively. A vertex of degree k is called a k-vertex. A k-regular graph is a graph that contains only k-vertices. We use $\varDelta$ and $\delta$ to denote the maximum degree and minimum degree of G, respectively. A graph is called cubic or subcubic if it is 3-regular or has maximum degree 3, respectively. We use G[S] to denote the subgraph induced by S. We say that GcontainsH if H is an induced subgraph of G. A vertex $v\in V(G)$ or an edge $e\in E(G)$ is incident with H if $v\in V(H)$ or $V(e)\cap V(H)\ne \emptyset$. Let $C_n=c_1c_2\cdots c_nc_1$ be a cycle of length n. We call $C_3$ a triangle. Two triangles are adjacent if they are incident with a common edge. Let $K_n$ be the complete graph on n vertices. For two integers i, j such that $i<j$, we use [i, j] to denote the set $\{i,i+1,\ldots , j\}$.

Let S be a set of vertices of a graph G. If every vertex in $V(G){\setminus } S$ is dominated by a vertex in S, then S is called a dominating set of G, which is abbreviated as a D-set. A D-set S of G is called a total dominating set of G, which is abbreviated as a TD-set, if G[S] contains no isolated vertex. If G has a TD-set, then G contains no isolated vertex. A D-set (TD-set) S of G is minimal if $S{\setminus } \{v\}$ is not a D-set (TD-set) for every vertex $v\in S$. The upper domination number, which is denoted by $\varGamma (G)$, and the upper total domination number, which is denoted by $\varGamma _t(G)$, are the maximum cardinalities of a minimal D-set and TD-set of G, respectively. We refer to a minimal D-set and TD-set of cardinalities $\varGamma (G)$ and $\varGamma _t(G)$ as a $\varGamma (G)$-set and $\varGamma _t(G)$-set, respectively.

Finding a D-set of a graph with the minimum cardinality is a classical NP-complete problem [8], which has been widely studied not only for its intractability in theory [12] but also for its applications in the field of networks [3, 9, 13]. For total domination in graphs, we refer the reader to works [2, 6, 10, 11]. Let G be a graph without isolated vertices. If $\varGamma _t(G)=2\varGamma (G)$, then we call G an upfull graph. Recently, motivated by the result $\frac{\varGamma _t(G)}{\varGamma (G)}\le 2$ [7], scholars [5] have turned to the study of the characterization of upfull graphs. In [5], the authors clarify the structure of connected upfull cubic graphs and propose the following problems and questions:

Problem 1

[5] Characterize the subcubic isolate-free upfull graphs G.

Question 1

[5] Is it true that if $G \not \cong K_4$ is a connected cubic graph, then $\frac{\varGamma _t(G)}{\varGamma (G)} \le \frac{3}{2}\; ?$

Question 2

[5] For $k \ge 2$, if G is a connected k-regular graph, then is it true that G is upfull if and only if $G \cong K_{k+1}?$

In this paper, we solve Problem 1 and show that the answers to Questions 1 and 2 are negative by constructing connected cubic graphs G such that $\frac{\varGamma _t(G)}{\varGamma (G)}>\frac{3}{2}$ and a class of regular non-complete graphs G with $\frac{\varGamma _t(G)}{\varGamma (G)}=2$. For technical convenience, we introduce additional preliminaries as follows:

Let S be a subset of a graph G. For each $v\in S$, pn(v, S)= $\{u\in V(G)|N_G(u)\cap S =\{v\}\}$ is the private neighborhood of v with respect to S, and each vertex in pn(v, S) is called a private neighbor of vwith respect to S. In particular, a vertex $u\in$ pn(v, S) is external if $u\notin S$, and epn(v, S) is used to denote the set of all external private neighbors of v with respect to S, while a vertex $u\in$ pn(v, S) is internal if $u\in S$, and ipn(v, S) is used to denote the set of all internal private neighbors of v with respect to S. It follows that pn(v, S)=epn$(v, S)\cup$ ipn(v, S) and epn$(v, S)\cap$ ipn$(v, S)=\emptyset$. Based on these notations, the minimal total dominating set has the following trivial property: A TD-set S of a graph G without isolated vertices is minimal if and only if either epn$(v,S)\ne \emptyset$ or pn$(v,S)=$ipn(v, S)$\ne \emptyset$ [4].

Let T be a rooted tree with root x. We say that a vertex $y\in V(T)$ is in the $\ell$-level of T if the distance from x to y is $\ell$. In a rooted tree, the parent of a vertex v is the vertex adjacent to v on the path to the root, and a child of a vertex v is a vertex for which v is the parent; every vertex except the root has a unique parent.

For a graph G and a subgraph H of G, we use $G-V(H)$ to denote the subgraph induced by $V(G){\setminus } V(H)$. If there is only one edge between H and $G-V(H)$, say $hh'$, for which $h'\in V(H)$ and $h\in V(G){\setminus } V(H)$, then we refer to H as a pendant subgraph of Gattached at h and we call h the attachment of H and $h'$ a partner of h.

Here, we present some known results that relate to upfull graphs, which will be used in the proof of our results.

Theorem 1

[7] For every graph G without isolated vertices, $\varGamma _t(G)\le 2\varGamma (G)$.

Lemma 2

[5, 7] A connected cubic graph is upfull if and only if the graph is isomorphic to $K_4$.

Lemma 3

[5, 7] Let G be an upfull graph without isolated vertices and D an arbitrary $\varGamma _t(G)$-set of G. Then,

• (a) $\varGamma (G)=\alpha (G)$, where $\alpha (G)$ is the independence number of G, i.e., the number of vertices in a maximum independent set of G;

• (b) the subgraph induced by D is the union of disjoint copies of $K_2$; and

• (c) every vertex in $V(G){\setminus } D$, together with two adjacent vertices in D (two endpoints of a copy of $K_2$), forms a triangle.

2 Connected Subcubic Upfull Graphs

This section is devoted to the characterization of connected upfull subcubic graphs. By Lemma 2, it is sufficient to consider subcubic graphs with a vertex of degree less than 3. For this, we first introduce a class of subcubic graphs, namely, triangle-trees, which will be used as a technical tool to solve Problem 1.

Let T be a rooted tree with root $v_0$ such that $d_{T}(v_0)\le 2$ and $\varDelta (T)\le 3$. Let $V(T)=\{v_0,v_1, \ldots , v_n\}$. We replace each vertex $v_i$ in T with a triangle $T_i=x_iy_iz_ix_i$ such that for each $v_iv_j\in E(T)$, where $v_i$ is the parent of $v_j$, with $i\ne j, i,j\in [0,n]$, we add an edge between $\{y_i,z_i\}$ and $\{x_j\}$ such that each $y_i$ and $z_i$ is incident with at most one such added edge. We refer to the resulting graph as the triangle-tree of T, which is denoted by $T_{\triangle }$, and T as the origin-tree of $T_{\triangle }$. In addition, we call $T_i$, for $i=0,1,\ldots , n$, a triangle of $T_{\triangle }$ and define $T_0$ as the root of $T_{\triangle }$. We say that $T_i$ is in level$\ell$ of $T_{\triangle }$ if $v_i$ is in level $\ell$ of T. $T_0$ is in level 0. In Fig. 1, we present an instance to illustrate the origin-tree (on the left) and its corresponding triangle-tree (on the right).

Fig. 1

Triangle-tree

Based on triangle-tree, we introduce three classes of subcubic graphs as follows:

• 1. $\mathcal {T}_1$. Let $X_1=uv$ be a copy of $K_2$. $\mathcal {T}_1$ consists of $X_1$ and pendant triangle-trees attached at u or v, where the number of triangle-trees attached at each of u and v is at most two; see Fig. 2a.

• 2. $\mathcal {T}_2$. Let $X_2$ be a copy of co-twin-$C_5$ [1] with vertex set $V(X_2)=\{u_i|i=1,2,3,4,5,6\}$ and edge set $E(X_2)=\{u_1u_i|i=2,3,4, u_2u_3,u_2u_6, u_3u_4,u_4u_5, u_5u_6\}$. Then, $\mathcal {T}_2$ consists of $X_2$ and pendant triangle-trees attached at $u_5$ and $u_6$, where the number of triangle-trees attached at each of $u_5$ and $u_6$ is at most one; see Fig. 2b.

• 3. Let $X_3$ be a subcubic graph with vertex set $V(X_3)=\{u_i,v_i,w_i|i=1,2,\ldots ,k\}$ and edge set $E(X_3)=\{u_iv_i,v_iw_i,w_iu_i |i=1,\ldots ,k\} \cup \{v_1u_k, u_iv_{i+1}|i=1,\ldots , k-1\}$. Then, $\mathcal {T}_3$ consists of $X_3$ and pendant triangle-trees attached at $w_i$ for $i\in [1,k]$, where the number of triangle-trees attached at $w_i$ is at most one; see Fig. 2c.

Fig. 2

Illustrations for $\mathcal {T}_1,\mathcal {T}_2,\mathcal {T}_3$

Let $\mathcal {T}=\{T_{\varDelta }\cup \mathcal {T}_1 \cup \mathcal {T}_2 \cup \mathcal {T}_3\}$. Every graph G in $\mathcal {T}$ can be partitioned into vertex-disjoint triangles, copies of $K_2$ and co-twin-$C_5$s. For convenience, we call them t-units, $k_2$-units and co-units of G, respectively.

To solve Problem 1, we will show that a subcubic graph G is upfull if and only if $G\in \mathcal {T}\cup \{K_4\}$. We start with the proof of the sufficiency.

Theorem 4

(Sufficiency) Every graph $G\in \mathcal {T}$ is upfull.

Proof

Let $\ell$ be the number of t-units of G. To prove $\varGamma _t(G)=2\varGamma (G)$, it is sufficient to show that $\varGamma _t(G)\ge 2\varGamma (G)$ by Theorem 1. We address the following two cases:

Case 1G contains no pendant triangle. It follows that either G is isomorphic to a triangle (which satisfies $\varGamma _t(G)\ge 2\varGamma (G)$) or $G\in \mathcal {T}_1\cup \mathcal {T}_2\cup \mathcal {T}_3$. If $G\in \mathcal {T}_1\cup \mathcal {T}_2$, then G is isomorphic to $K_2$ or co-twin-$C_5$, for which $\varGamma _t(G)=2\varGamma (G)$. If $G\in \mathcal {T}_3$, we denote $V(G)=\cup _{i=1}^{\ell } \{u_i,v_i,w_i\}$ and $E(G)=\{u_iv_i,v_iw_i,w_iu_i|i=1,\ldots , \ell \}\cup \{v_1u_{\ell }, u_iv_{i+1}|i=1,\ldots , \ell -1\}$. Let S be a $\varGamma (G)$-set of G. Since S is a minimal D-set, it follows that $1\le |S\cap \{u_i,v_i,w_i\}|\le 2$ for every $i\in [1,\ell ]$, and $w_i\notin S$ when $|S\cap \{u_i,v_i,w_i\}|=2$. Suppose that there exists $i\in [1,\ell ]$, say $i=1$, that satisfies $|S\cap \{u_1,v_1,w_1\}|=2$, i.e., $u_1,v_1\in S$. By the minimality of S, $v_2\in$ epn$(u_1, S)$, which implies that $\{w_2,u_2\}\cap S=\emptyset$ and $w_2$ is not dominated by any vertex in S, which is a contradiction. Therefore, $|S\cap \{u_i,v_i,w_i\}|=1$ for every $i\in [1,\ell ]$, i.e., $|S|=\ell$. Observe that $S'=\{w_i,v_i|i=1,\ldots , \ell \}$ is a minimal TD-set of cardinality $2\ell$. It follows that $\varGamma _t(G)\ge |S'|=2\varGamma (G)$.

Case 2G contains pendant triangles.

Case 2.1 Every pendant triangle-tree of G is a pendant triangle. In this case, if G is a triangle-tree, then G contains two vertex-disjoint triangles and one edge between them. If $G\in \mathcal {T}_1$, then G consists of a copy of $K_2(=uv)$ and pendant triangles attached at u or v such that each u and v is the attachment of at most two pendant triangles. If $G\in \mathcal {T}_2$, then G consists of a copy of co-twin-$C_5$ and pendant triangles attached at $u_5$ or $u_6$ such that each $u_5$ and $u_6$ is the attachment of at most one pendant triangle, where $u_5$ and $u_6$ are the two 2-vertices of the copy of co-twin-$C_5$ (see Fig. 2b). For all these trivial cases, we can readily check that $\varGamma _t(G)=2\varGamma (G)$. In the following, we consider the case of $G\in \mathcal {T}_3$. Let $T_i=u_iv_iw_iu_i$, $i=1,2,\ldots , k$ be the k non-pendant t-units of G, where $\{v_1u_k, u_iv_{i+1}|i=1,2,\ldots , k-1\}\subseteq E(G)$.

Let S be a $\varGamma (G)$-set S of G. Then, S contains exactly one vertex of each pendant triangle (since S is minimal). Hence, any non-pendant t-unit contains at most 2 vertices of S (otherwise, if {$u_i,v_i,w_i$} $\subseteq S$ for some $i\in [1,k]$, then $S{\setminus } \{w_i\}$ is also a D-set, which is a contradiction). If $|S|>\ell$, then there is a non-pendant t-unit, say $T_1$, that contains two vertices of S. Since S is minimal, it follows that $u_1,v_1\in S$, which implies that $v_2\in$ epn$(u_1, S)$ and $u_k\in$ epn$(v_1, S)$. Hence, $V(T_2)\cap S=\emptyset$ and $V(T_k)\cap S=\emptyset$. Thus, by the connectivity among $T_1,\ldots , T_k$, we deduce that every $T_i$ that satisfies $|V(T_i)\cap S|=2$ corresponds uniquely to a $T_j$ that satisfies $V(T_j)\cap S=\emptyset$, $i,j\in [1,k]$ and $i\ne j$. Therefore, $|S\cap (\bigcup _{i=1}^k V(T_i))|\le k$. Hence, $|S|\le k+(\ell -k)=\ell$, i.e., $\varGamma (G)=|S|\le \ell$. In addition, let $S'$ be the set of 2-vertices of G. Observe that each pendant triangle contains two 2-vertices and $T_i$ contains no 2-vertices for all $i\in [1,k]$; we have $|S'|=2|\ell -k|$. It follows that $S'\cup \{v_i,w_i|i=1,2,\ldots , k\}$ is a minimal TD-set of G. Therefore, $\varGamma _t(G)\ge 2\ell \ge 2\varGamma (G)$.

Case 2.2G contains a pendant triangle-tree $T_{\varDelta }$ that includes at least two triangles. Let a be the attachment of $T_{\varDelta }$ and $a'$ the partner of a. We set the triangle of $T_{\varDelta }$ incident with $a'$ as the root of $T_{\varDelta }$. Let $T'$ be a triangle of $T_{\varDelta }$ in the maximum level. Then, $T'$ is a pendant triangle of $T_{\varDelta }$ (also a pendant triangle of G). Let h be the attachment of $T'$ and $h'\in V(T')$ the partner of h. It follows that the vertices in $V(T'){\setminus } \{h'\}$ are 2-vertices in G and h is incident with a triangle, say $hh_1h_2h$.

We proceed by induction on $\ell$. Clearly, $\ell \ge 2$. Let $G'=G-T'$. Then, $G'\in \mathcal {T}$, and the number of t-units in $G'$ is $\ell -1$. If $G'$ contains no pendant triangle or $G'$ contains no pendant triangle-tree with at least two triangles, then by Case 1 and Case 2.1, we have $\varGamma _t(G')\ge 2\varGamma (G')$. If $G'$ contains a pendant triangle-tree that includes at least two triangles, then by the hypothesis, $\varGamma _t(G')\ge 2\varGamma (G')$. Observe that any $\varGamma _t(G')$-set (and $\varGamma (G')$-set) together with $V(T'){\setminus } \{h'\}$ (and one vertex in $V(T'){\setminus } \{h'\}$) is a minimal TD-set (and a minimal D-set) of G. Therefore, $\varGamma _t(G)\ge \varGamma _t(G')+2$ and $\varGamma (G)\ge \varGamma (G')+1$. In the following, we will prove that $\varGamma (G)=\varGamma (G')+1$ and hence $\varGamma _t(G)\ge \varGamma _t(G')+2\ge 2\varGamma (G')+2=2\varGamma (G)$. It is sufficient to prove that $\varGamma (G)\le \varGamma (G')+1$.

Let S be an arbitrary $\varGamma (G)$-set of G, $S_1=S\cap V(T')$ and $S_2=S{\setminus } V(T')$. Since S is a minimal D-set of G, $|S_1|=1$. We suppose that $|S_2|>\varGamma (G')$. In this case, $S_2$ is not a D-set of $G'$ (if $S_2$ were a D-set of $G'$, then $S_2$ would be minimal since S is minimal, a contradiction). This implies that $S_1=\{h'\}$, $h\notin S_2$, and $h\in$epn$(h', S)$, i.e., $\{h_1,h_2\}\cap S_2=\emptyset$. Observe that $S_2\cup \{h\}$ is a D-set of $G'$. Since $|S_2|>\varGamma (G')$, $S_2\cup \{h\}$ is not minimal. Therefore, there exists an $h_3 (\ne h)\in N_{G'}(\{h_1,h_2\})$ such that $(S_2\cup \{h\}){\setminus } \{h_3\}$ is also a D-set of $G'$. Observe that $T'$ is in the maximum level of $T_{\varDelta }$, which implies that $\{h_1,h_2\}$ contains a 2-vertex or a 3-vertex that is the attachment of a pendant triangle. Since S contains exactly one vertex of each pendant triangle, we deduce that S contains only one such vertex $h_3$, i.e., $(S_2\cup \{h\}){\setminus } \{h_3\}$ is minimal. This indicates that $|S_2|\le \varGamma (G')$, a contradiction. Therefore, $|S_2|\le \varGamma (G')$ and $\varGamma (G)=|S|=|S_2|+1\le \varGamma (G')+1$. This completes the proof. $\square$

Now, we turn to the proof of the necessity. First, we present two lemmas, based on which we obtain Theorem 7.

Lemma 5

Let G be a connected upfull subcubic graph, $G\ne K_4$. If G contains no co-twin-$C_5$, then G contains no adjacent triangles.

Proof

Let D be a $\varGamma _t(G)$-set of G. To the contrary, we assume that G contains two adjacent triangles, say $a_1b_1c_1a_1$ and $a_1b_1c_2a_1$. Since $\varDelta (G)\le 3$, by Lemma 3 (b) and (c) we have that $\{a_1,b_1\}\subseteq D$ and $\{c_1,c_2\}\cap D=\emptyset$. According to Lemma 3 (b), we let $D=\{a_i, b_i|i=1,\ldots , \frac{|D|}{2}\}$, where $a_ib_i\in E(G)$ and there is no edge between $\{a_i,b_i\}$ and $\{a_j,b_j\}$ for any $i,j\in [1,\frac{|D|}{2}]$, $i\ne j$.

We claim that both $c_1$ and $c_2$ are 3-vertices. Otherwise, suppose that $c_1$ is a 2-vertex. Then, $D'=(D{\setminus } \{a_1\})\cup \{c_1\}$ is a $\varGamma _t(G)$-set of G, for which $c_2 (\notin D')$ is adjacent to only one vertex in $D'$, which contradicts Lemma 3 (c). Now, let $\{c'_1\}=N_G(c_1){\setminus } \{a_1,b_1\}$ and $\{c'_2\}=N_G(c_2){\setminus } \{a_1,b_1\}$. If $D{\setminus } \{a_1,b_1\}$ contains a subset S such that $|S\cap \{a_i,b_i\}|=1$ for $i=2,3, \ldots , \frac{|D|}{2}$ and $S\cap \{c'_1,c'_2\}=\emptyset$, then $S\cup \{c_1,c_2\}$ is an independent set of G that contains $\frac{|D|}{2}+1$ vertices, which contradicts Lemma 3 (a). Therefore, such an S does not exist. This implies that $c'_1\ne c'_2$, $\{c'_1,c'_2\}\subseteq D$ and $c'_1c'_2\in E(G)$. Then, $G[\{a_1,b_1,c_1,c_2,c'_1, c'_2\}]$ is isomorphic to co-twin-$C_5$, which contradicts the assumption on G. $\square$

Lemma 6

Let G be a connected upfull subcubic graph that contains a co-twin-$C_5$ with vertex set $\{u_i|i=1,2,\ldots , 6\}$, where $u_1,u_2,u_3,u_4$ are the four 3-vertices and $u_2u_4\notin E(G)$ (see Fig. 2b). Then, $G'=G-\{u_1,u_2,u_3,u_4\}$ is upfull, and the restriction of any $\varGamma _t(G)$-set of G to $G'$ is a $\varGamma _t(G')$-set.

Proof

Let D be an arbitrary $\varGamma _t(G)$-set of G. Then, since G is subcubic, by Lemma 3 (b) and (c), we easily deduce that $u_1,u_3\in D$, $u_5,u_6\in D$ and $u_2,u_4\notin D$. $D{\setminus } \{u_1,u_3\}$ is a minimal TD-set of $G'$. Therefore, $\varGamma _t(G')\ge |D|-2$.

Let $S'$ be a $\varGamma (G')$-set of $G'$. We have that $|S'|\le \frac{|D|}{2}-1$. Otherwise, if $|S'|\ge \frac{|D|}{2}$, then $S'\cup \{u_1\}$ is a minimal D-set of G that contains at least $\frac{|D|}{2}+1$ vertices. This shows that $\varGamma (G)\ge \frac{|D|}{2}+1$. However, since G is upfull, it follows that $\varGamma (G)=\frac{\varGamma _t(G)}{2}=\frac{|D|}{2}$, which is a contradiction. Thus, $\varGamma (G')=|S'|\le \frac{|D|}{2}-1$, i.e., $|D|\ge 2\varGamma (G')+2$. This shows that $\varGamma _t(G')\ge |D|-2\ge 2\varGamma (G')$. In addition, by Theorem 1, $\varGamma _t(G')\le 2\varGamma (G')$. Thus, $\varGamma _t(G')= 2\varGamma (G')=|D|-2$. Hence, $D{\setminus } \{u_1,u_3\}$ is a $\varGamma _t$-set of $G'$. $\square$

Theorem 7

Let G be a connected upfull subcubic graph and D a $\varGamma _t(G)$-set of G. If D contains two adjacent vertices $x\in D$ and $x_0\notin D$ such that $xx_0$ is neither an edge of a triangle nor an edge of the co-twin-$C_5$ of G, then the component of $G-xx_0$ that contains vertex $x_0$ is a triangle-tree.

Proof

Let G be a counterexample with |V(G)| as small as possible. That is, the component of $G-xx_0$ that contains vertex $x_0$ is not a triangle-tree. Moreover, for any upfull subcubic graph H with $|V(H)|<|V(G)|$ and any $\varGamma _t(H)$-set $D'$ of H, if there are $x\in D'$ and $x_0\notin D'$ that satisfy $xx_0\in E(H)$ and $xx_0$ is neither an edge of a triangle nor an edge of the co-twin-$C_5$ of H, then the component of $H-xx_0$ that contains vertex $x_0$ is a triangle-tree.

If G contains a co-twin-$C_5$, let H be the graph obtained from G by deleting the four 3-vertices of the co-twin-$C_5$ and their incident edges. Then, by Lemma 6, H is upfull, and $D'=D\cap V(H)$ is a $\varGamma _t(H)$-set of H. Since $x\in D'$ and $x_0\notin D'$ satisfy the conditions of the theorem for H, by the minimality, the conclusion holds for H. Since $xx_0$ is not an edge of the co-twin-$C_5$ of G, it follows that the component of $G-xx_0$ that contains vertex $x_0$ is also a triangle-tree, which contradicts the assumption on G. In the following, we assume that G contains no co-twin-$C_5$. Then, by Lemma 5, G contains no adjacent triangles.

Let $G'$ be the component of $G-xx_0$ that contains $x_0$. By Lemma 3 (c), $x_0$ is incident with a triangle $T_0$ in G. Since $xx_0$ is not an edge of a triangle of G, it follows that $x\notin V(T_0)$. Let $T_0=x_0y_0z_0x_0$, where $y_0,z_0\in D$. Starting with $T_0$ and applying Lemma 3 (b) and (c) repeatedly, we can depict the structure of $G'$ by labeling its vertices as follows:

• 1. Define $T_0$ as the zero level of $G'$.

• 2. Let $N_{G'}(V(T_0))$=$\{x_{1,1}, \ldots , x_{1,\ell _1}\}$. Since G is subcubic, we have $\ell _1\le 2$. When $N_{G'}(V(T_0))$$=\emptyset$, it follows that $G'$ is isomorphic to a triangle, which contradicts $G'$. When $N_{G'}(V(T_0))$$\ne \emptyset$, $N_{G'}(V(T_0))\cap D=\emptyset$. Then, every vertex $x_{1,j}$ for $j\in [1,\ell _1]$ is incident with a triangle $T_{1,j}$. Let $T_{1,j}=x_{1,j}y_{1,j}z_{1,j}x_{1,j}$, where $y_{1,j}, z_{1,j}\in D$. Observe that since G is a subcubic graph that contains no adjacent triangle, there does not exist a $j\in [1,\ell _1]$ such that $\{y_{1,j}, z_{1,j}\}\cap \{y_0,z_0\}\ne \emptyset$ (i.e., $\{y_{1,j}, z_{1,j}\}=\{y_0,z_0\})$, and $\{y_{1,1}, z_{1,1}\} \cap \{y_{1,2}, z_{1,2}\}=\emptyset$ when $\ell _1=2$. Let $T_{1,j}$, $j=1,\ldots , \ell _1$ be the first level of $G'$.

• 3. For $i\ge 1$, define $U_{i+1}=N_{G'}(\cup _{j=1}^{\ell _i} \{y_{i,j}, z_{i,j}\}) {\setminus } \cup _{j=1}^{\ell _i} \{x_{i,j}\},$ and let $U_{i+1} = \{ x_{i+1,1}, \ldots , x_{i+1,\ell _{i+1}} \}$. If $U_{i+1}=\emptyset$, then we stop labeling $V(G')$. If $U_{i+1}\ne \emptyset$, then $U_{i+1}\cap D=\emptyset$. Therefore, every vertex $x_{i+1,j}\in U_{i+1}$, $j\in [1, \ell _{i+1}]$, is incident with a triangle, which is denoted by $T_{i+1, j}=x_{i+1,j}y_{i+1,j}z_{i+1,j}x_{i+1,j}$, where $y_{i+1,j}, z_{i+1,j}\in D$. Let $T_{i+1,j}$, $j=1,\ldots , \ell _{i+1}$, be the $(i+1)$th level of $G'$. Observe that G is finite: There always exists an integer i such that $U_{i+1}$ is empty.

Since $\varDelta (G)\le 3$ and G contains no adjacent triangles, by Lemma 3 (c), every vertex $x_{i+1,j'}\in U_{i+1}$ is adjacent to exactly one vertex in $\{y_{i,j},z_{i,j} | j=1,2,\ldots , \ell _i\}$. This implies that each vertex in $V(G'){\setminus } D$ uniquely corresponds to a pair of adjacent vertices in D, and they form a triangle. Therefore, every vertex in $V(G')$ is incident with a triangle, and every vertex in $V(G'){\setminus } D$ is adjacent to exactly three vertices of D; i.e., $V(G'){\setminus } D$ is an independent set. In addition, $d_{G'}(V(T_{i,j}))\le 3$ for each $j\in [1, \ell _i]$ and $d_{G'}(V(T_0))=2$. Therefore, we deduce that $G'$ is a triangle-tree rooted at $T_0$. This contradicts the assumption on G. $\square$

Based on the above result, we are ready to prove the necessity; prior to this, we show a corollary as follows:

Corollary 8

Let G be a connected upfull subcubic graph and D an arbitrary $\varGamma _t(G)$-set of G. If $V(G){\setminus } D$ contains a 2-vertex, then G is a triangle-tree.

Proof

By Lemma 3 (b), let D=$\{b_i,c_i|i=1,2,\ldots , \frac{|D|}{2}\}$, where $b_ic_i\in E(G)$ for every $i\in [1, \frac{|D|}{2}]$. Let $a_1$ be a 2-vertex in $V(G){\setminus } D$. Then, by Lemma 3 (b) and (c), $a_1$ is incident with a triangle $T'$, say $T'=a_1b_1c_1a_1$. If $N_G(V(T'))=\emptyset$, then G is isomorphic to a triangle, which is a triangle-tree. Suppose that $N_G(V(T'))\ne \emptyset$. Since $d_G(b_1)\le 3$ and $d_G(c_1)\le 3$, it follows that $|N_G(V(T'))|\le 2$. By Lemma 3 (b), $N_G(V(T'))\cap D=\emptyset$.

If $|N_G(V(T'))|=1$, let $N_G(V(T'))=\{b'_1\}$ and assume $b_1b'_1\in E(G)$. Then, we have that $b'_1c_1\notin E(G)$. Otherwise, there exists a set of vertices $S=\{s_i| s_i\in \{b_i,c_i\}, i=2,3,\ldots , \frac{|D|}{2}\}$ such that $S\cap N_G(b'_1)=\emptyset$; hence, $S\cup \{a_1, b'_1\}$ is an independent set of G that contains $\frac{|D|}{2}+1$ vertices, which contradicts Lemma 3 (a). Therefore, $bb'_1$ is not an edge of a triangle or a co-twin-$C_5$ of G. By Theorem 7, $G-T'$ is a triangle-tree. Hence, G is a triangle-tree.

If $|N_G(V(T'))|=2$, let $N_G(V(T'))=\{b'_1, c'_1\}$, where $b_1b'_1\in E(G)$ and $c_1c'_1\in E(G)$. In this case, neither $b_1b'_1$ nor $c_1c'_1$ is an edge of a triangle or a co-twin-$C_5$ of G. Therefore, by Theorem 7, $G-T'$ is the union of two vertex-disjoint triangle-trees. Hence, G is a triangle-tree. $\square$

Theorem 9

(Necessity) Let G be a connected upfull subcubic graph. If $G\ne K_4$, then $G\in \mathcal {T}$.

Proof

By Lemma 2, $\delta (G)\le 2$. Let D be a $\varGamma _t(G)$-set of G. Then, by Lemma 3 (b), we let $D=\{b_i, c_i| i=1,2,\ldots , p\}$, where $b_ic_i\in E(G)$, $p=\frac{|D|}{2}$ and there does not exist any edge between $\{b_{i_1}, c_{i_1}\}$ and $\{b_{i_2}, c_{i_2}\}$ for any $i_1,i_2\in [1,p], i_1\ne i_2$. Let $(V(G){\setminus } D)=\{a_j|j=1,2,\ldots , |V(G)|-2p\}$. By Lemma 3 (c), for every $j\in [1, |V(G)|-2p]$, there is an $i\in [1,p]$ such that $a_jb_ic_ia_j$ is a triangle. For any distinct $j_1,j_2\in [1, |V(G)|-2p]$, $a_{j_1}$ and $a_{j_2}$ are not incident with the identical triangle.

If D contains a vertex, say $b_1$, that is not incident with a triangle, then $N_G(\{b_1, c_1\})\cap D=\emptyset$. By Theorem 7, for every vertex $a\in N_G(\{b_1, c_1\})$, say $ab_1\in E(G)$, if $ab_1$ is not an edge of a co-twin-$C_5$ of G, then the component of $G-ab_1$ that contains a is a triangle-tree. Otherwise, $b_1c_1$ is also an edge of a co-twin-$C_5$ of G. Hence, $G-\{b_1,c_1\}$ is the union of vertex-disjoint triangle-trees and two adjacent triangles. This implies that either $G\in \mathcal {T}_1$ or $G\in \mathcal {T}_2$ (when $b_1c_1$ is an edge of a co-twin-$C_5$ of G).

In what follows, we assume that all vertices in D are incident with triangles. Then, $\delta (G)\ge 2$. If G has a 2-vertex not in D, then by Corollary 8, G is a triangle-tree. Now, we address the case in which all 2-vertices are in D, that is, $d_G(a_i)=3$ for all $i\in [1,|V(G)|-2p]$.

Since $\delta (G)\le 2$, without loss of generality, we let $c_1$ be a 2-vertex. Since $d_{G}(a_1)=3$, $a_1$ is adjacent to a triangle, say $T_2=a_2b_2c_2a_2$. If $a_1a_2\in E(G)$, then $(D{\setminus } \{c_1\})\cup \{a_1\}$ is also a $\varGamma _t(G)$-set that does not contain $c_1$ and G is a triangle-tree by Corollary 8. Therefore, we assume that $a_1b_2\in E(G)$. Then, $a_2$ is also adjacent to a triangle of G, say $T_3$. In this way, we obtain that each $a_i$, for $i\ge 1$, is adjacent to a triangle $T_{i+1}$ of G such that $a_ia_{i+1}\notin E(G)$ (otherwise, $(D{\setminus } \{c_1,b_2, b_3,\ldots , b_{i}\})\cup \{a_1,a_2, \ldots , a_i\}$ is a $\varGamma _t(G)$-set of G that does not contain $c_1$ and G is a triangle-tree by Corollary 8) and $a_ib_{i+1}\in E(G)$.

Note that G is finite. There exists an integer k such that $a_k$ is adjacent to a vertex in $\{b_{i},c_{i}|i=1,2,\ldots , k-1\}$. Here, if necessary, renaming the triangle $T_1, T_2,\ldots , T_k$, we may assume that $a_k$ is adjacent to $b_1$. Thus, by Theorem 7, if $d_G(c_i)=3$, then $c_i$ is adjacent to a triangle-tree for every $i\in [1,k]$; see Fig. 2c.This shows that $G\in \mathcal {T}_3$. $\square$

By Theorems 4 and 9 and Lemma 2, we characterize the upfull subcubic graphs by the following theorem:

Theorem 10

Let G be a connected subcubic graph. Then, G is upfull if and only if $G\in \{K_4\}\cup \mathcal {T}$.

Observe that when a graph G is disconnected, we have that $\varGamma _t(G)=\sum _{i=1}^{\ell } \varGamma _t(G_i)$ and $\varGamma (G)=\sum _{i=1}^{\ell } \varGamma (G_i)$, where $G_1,\ldots , G_{\ell }$ are the $\ell$ components of G. By Theorem 1, $\varGamma _t(G_i)\le 2\varGamma (G_i)$ for any $i\in [1,\ell ]$. Therefore, $\varGamma _t(G)=2\varGamma (G)$ if and only if $\varGamma _t(G_i)=2\varGamma (G_i)$ for any $i\in [1,\ell ]$. Thus, according to Theorem 10, we have the following conclusion:

Theorem 11

Let G be a subcubic graph. Then, G is upfull if and only if each component of G belongs to $\{K_4\}\cup \mathcal {T}$.

3 Answers to Questions 1 and 2

3.1 Question 1

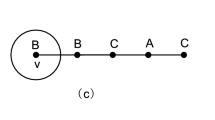
We consider the graph $G_{12}$ in Fig. 3a, which is a cubic graph of order 12 with vertex set $V(G_{12})=\{v_i|i=1,2,\ldots , 12\}$ and edge set $E(G_{12})=\{v_iv_{i+1}|i\in [1,10], v_1v_5, v_1v_{11}, v_2v_{12},v_3v_{12}, v_4v_6,$$v_7v_{12}, v_8v_{10},$$v_9v_{11}\}$.

Let S be a $\varGamma (G_{12})$-set of $G_{12}$. Let $S_1= S\cap \{v_1, v_7, v_8,v_9,v_{10},v_{11}\}$, $S_2=S\cap \{v_4,v_5,v_6\}$, and $S_3=S\cap \{v_2,v_3,v_{12}\}$. One can readily check that $1\le |S_1|\le 3$ and $|S_i|\le 2$ for $i=2,3$. (Otherwise, by symmetry, we assume $|S_2|=3$. Then, $v_3\in$ epn($v_4$, S) and $v_7\in$ epn($v_6$, S). This implies that $\{v_2,v_3,v_{12},v_7\}\cap S=\emptyset$ and $v_{12}$ is not dominated by any vertex in S, which is a contradiction.) In particular, $|S_2|+|S_3|\le 3$. Otherwise, if $|S_2|+|S_3|=4$, then $|S_2|=|S_3|=2$, $S_2=\{v_5,v_6\}$ and $S_3=\{v_2,v_{12}\}$ (observe that if $v_4\in S_2$ or $v_3\in S_3$, then $v_3\in$ epn($v_4$, S) or $v_4\in$ epn($v_3$, S), which implies that $|S_3|=0$ or $|S_2|=0$). Then, $S{\setminus } \{v_{12}, v_5\}$ is also a D-set of $G_{12}$, which is a contradiction.

Now, by symmetry, if $|S_2|+|S_3|=3$, we assume that $S_2\cup S_3=\{ v_5,v_6, v_3\}$. Then, $v_1\in$ epn $(v_5, S)$ and $v_7\in$ epn $(v_6, S)$, which shows that $|S_1\cap S|=1$, i.e., $v_9\in S_1$ or $v_{10}\in S_1$, and $|S|=4$. If $|S_2|+|S_3|=2$, then $|S_1|\le 2$ (since when $|S_1|=3$, $\{v_1,v_7\}\subset S_1$). If $v_5\in S_2$, then epn$(v_1, S)\ne \emptyset$ and epn$(v_5, S)\ne \emptyset$. Clearly, $v_4,v_6\notin S_2$. If $v_2\in$ epn$(v_1, S)$, then $|S_3|=0$ and $|S_2|+|S_3|=1$; if $v_{11}\in$ epn$(v_1, S)$, then $v_8\in S_1$ and $v_{12}\in$ epn $(v_7,S)$, which also implies that $|S_3|=0$ and $|S_2|+|S_3|=1$. Now, we suppose that $\{v_5,v_6,v_2,v_{12}\}\cap S=\emptyset$ (the cases in which $v_2\in S_3$, $v_6\in S_2$ or $v_{12}\in S_3$ are analogous to the case of $v_5\in S_2$). Since only $v_3$ and $v_4$ are not dominated by vertices in $S_1$, we observe that $|S\cap \{v_3,v_4\}|=1$, i.e., $|S_2|+|S_3|=1$. Thus, $|S|\le 4$. If $|S_2|+|S_3|=1$, then $|S|\le 4$. Therefore, $\varGamma (G_{12})\le 4$ ($\varGamma (G_{12})=4$ since $\{v_1,v_9,v_{7}, v_4\}$ is a minimal D-set of $G_{12}$).

In addition, $\{v_1,v_4,v_5,v_6,v_7, v_9,v_{10}\}$ is a minimal TD-set of $G_{12}$. Therefore, $\varGamma _t(G)\ge 7$ and $\frac{\varGamma _t(G_{12})}{\varGamma (G_{12})}\ge \frac{7}{4}>\frac{3}{2}$. This indicates that the answer to Question 1 is negative.

Fig. 3

Three examples that give negative answer to Question 1

Observe that there are many graphs G for which $\frac{\varGamma _t(G)}{\varGamma (G)}>\frac{3}{2}$. Here, we present two additional examples, which are denoted by $G_{14}$ and $G_{18}$, as shown in Fig. 3b, c. With a similar proof (we omit the details here), we can show that $\varGamma (G_{14})=5$ and $\varGamma _t(G_{14})\ge 8$ and that $\varGamma (G_{18})=6$ and $\varGamma _t(G_{18})\ge 10$ (the set of white vertices in each graph is a minimal TD-set of the graphs). Thus, $\frac{\varGamma _t(G_{14})}{\varGamma (G_{14})}\ge \frac{8}{5}>\frac{3}{2}$ and $\frac{\varGamma _t(G_{18})}{\varGamma (G_{18})}\ge \frac{10}{6}>\frac{3}{2}$. Based on these observations, we propose the following conjecture:

Conjecture 1

Let $G \not \cong K_4$ be a connected cubic graph. Then, $\frac{\varGamma _t(G)}{\varGamma (G)} \le \frac{7}{4}.$

3.2 Question 2

We construct a class of graphs as follows: Let n, k be two positive integers that satisfy $k\le \frac{n}{2}$. Let D(n, k) be the graph with vertex set $\{v_0,v_1,\ldots ,v_{n-1}\}$ and edge set $\{v_iv_{i+j}, v_iv_{i-j}|i=0,1,\ldots , n,j=1,2,\ldots , k\}$, where the subscripts read module n. D(n, k) is a 2k-regular graph. The graphs in Fig. 4a, b are D(8, 2) and D(10, 3), respectively.

Theorem 12

Let n be a positive integer such that $n\ge 8$. Then, $\varGamma _t(D(n, \frac{n}{2}-2))=4$ and $\varGamma (D(n, \frac{n}{2}-2))=2$.

Fig. 4

aD(8, 2). bD(10, 3)

Proof

Let $k=\frac{n}{2}$. By the definition of D(n, k), for $i=0,1,\ldots , n-1$, we have that

$$\begin{aligned} N_{D(n, k)}(v_i)=\{v_{i+1}, v_{i+2}, \ldots , v_{i+k-2}, v_{i-1}, v_{i-2}, \ldots , v_{i-k+2}\}. \end{aligned}$$

Then, $V(D(n, k)){\setminus } N_{D(n, k)}[v_i]= \{v_{i+k-1}, v_{i+k}, v_{i+k+1}\}$ since $(i+k+2)\pmod n =(i-k+2)\pmod n$. For each $[0,k-1]$, let $M_i=\{v_iv_{i+1}, v_{i+k}v_{i+1+k}\}$. Each vertex of D(n, k) is adjacent to a vertex in $V(M_i)$. Therefore, for every $i\in [0,n-1]$, $V(M_i)$ is a minimal TD-set of $D(n, \frac{n}{2}-2)$ and $v_i, v_{i+k}$ is a minimal dominating set of $D(n, \frac{n}{2}-2)$, which shows that $\varGamma _t(D(n, \frac{n}{2}-2))\ge 4$ and $\varGamma (D(n, \frac{n}{2}-2))\ge 2$.

Conversely, suppose that $D(n, \frac{n}{2}-2)$ has a minimal dominating set D such that $|D|=3$. Let $D=\{v_i,v_j,v_p\}$, where $i<j<p$. Then, the three vertices not dominated by $v_i$ are dominated by $v_j$ or $v_p$. If $j>i+2 \pmod n$ or $p<i-2\pmod n$, then $\{v_i,v_j\}$ or $\{v_i,v_p\}$ is a dominating set of $D(n, \frac{n}{2}-2)$j; if $j\le i+2 \pmod n$ or $p\ge i-2\pmod n$, then $\{v_j,v_p\}$ is a dominating set. This contradicts the assumption that D is minimal. Therefore, $\varGamma (D(n, \frac{n}{2}-2))\le 2$. Hence, $\varGamma (D(n, \frac{n}{2}-2))=2$. By Lemma 1, $\varGamma _t(D(n, \frac{n}{2}-2))\le 2\varGamma (D(n, \frac{n}{2}-2))=4$. Thus,$\varGamma _t(D(n, \frac{n}{2}-2))=4$. $\square$

By Theorem 12, $D(n, \frac{n}{2}-2)$, for $n\ge 8$, is an upfull $(n-4)$-regular graph, which is not complete. This shows that the answer to Question 2 is also negative.