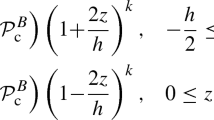Semi-analytical solutions for static and dynamic responses of bi-directional functionally graded nonuniform nanobeams with surface energy effect

Abstract

In this paper, the bending, buckling, and vibration behaviors of bi-directional functionally graded (BDFG) nonuniform micro/nanobeams are investigated. A new Euler–Bernoulli beam model is developed for BDFG tapered micro/nanobeams using Gurtin–Murdoch surface elasticity theory and modified couple stress theory to capture the effects of surface energy and microstructure stiffening, respectively. The present formulation accounts for the physical neutral surface. The material properties of the bulk and surface continuums of the nanobeam are assumed to vary along the thickness and length directions according to power law. Also, the cross section is assumed to vary linearly along the length direction. Hamilton principle is employed to derive the nonclassical equations of motions and boundary conditions. The generalized differential quadrature method (GDQM) is employed to accurately evaluate the variable coefficients of the obtained governing equations. Then after, the Navier’s method is employed for the simply supported BDFG nanobeam for its static bending deflection, critical buckling load, and fundamental frequency. The proposed model is validated by comparing the obtained results with available literature. Effects of different geometrical and material parameters on static and dynamic behaviors of small-scale BDFG nanobeams with the simultaneous effects of microstructure and surface elasticity are comprehensively studied and discussed. Results disclose that the nonuniformity parameters, aspect ratio, dimensionless material length-scale parameter, surface stress, surface elasticity, and gradient indices have a significant effect on the bending, buckling, and free vibration responses of BDFG tapered micro/ nanobeams.

1 Introduction

Functionally graded materials (FGMs) are a subclass of composite materials, which are designed to achieve the optimal distribution of constituent materials suitable for certain applications. The superior properties of FGMs such as designability, lower weight, higher fracture toughness, enhanced thermal properties, lower stress intensity factor, reduced residual thermal stress, reduced interface problems, smaller stress concentration, enhanced corrosion resistance damage resistance, etc., enable them to be suitable candidates for a wide range of different practical fields of engineering and science [1,2,3,4,5,6]. Based on their application, the spatial variations of the mechanical, thermal, electrical, magnetic, etc. of FGMs are tailored to satisfy particular applications in numerous industrial/medical fields such as energy electronics, aerospace, automotive, military, dentistry, and implants, sensors and thermos-generators [7,8,9,10]. In addition, with the rapid advance in nanotechnology, FGMs are currently used in micro/nano-electro-mechanical systems (MEMs/NEMs) such as electrically actuated micro/nano-electromechanical systems [11, 12], atomic force microscopes [13] and also in thin films in the form of shape memory alloys [14]. At small scale, both experimental and molecular dynamics simulation results have invariably shown that the small-scale effects cannot be neglected in the analysis of mechanical properties of micro- and nanostructures, especially in micro- and nanobeams applied as sensors and actuators [15,16,17,18,19,20]. Nowadays, microbeams have been widely used in micro-/nanoelectromechanical systems (MEMS/NEMS) such as micro-engines, micro-turbomachinery, and micro-machining, the ultrasonic piezoelectronic motor, and the development of a micromotor for in vivo medical procedures. However, the classical continuum mechanics theories failed to accurately predict the responses of such small-scale structures.

In the open literature, several size-dependent nonclassical continuum mechanics theories that contain additional material length-scale parameter(s) have been developed to overcome this barrier such as couple stress theory (CST) [21], strain gradient theory (SGT) [22], modified strain gradient theory (MSGT) [20], modified couple stress theory (MCST) [23], nonlocal elasticity theory [24], and nonlocal strain gradient theory (NSGT) [25]. For more details about the nonclassical continuum mechanics theories, the interested readers may refer to the review articles [26,27,28]. Over these nonclassical continuum mechanics theories, MCST has the merit of involving only one additional higher-order material length-scale parameter to simulate the small-scale effect, in addition to classical material Lamé constants. Based on this feature, the MCST has been employed by many researchers to capture the scale effect on the behavior of microstructures. To evaluate the material length-scale parameter of micro-scale structures, some experiment tests have been performed such as torsion test of slim microcylinders having various diameters [29,30,31] and bending test of thin microbeams of various thicknesses [20, 32]. However, experimental results proved that different materials have different material length-scale parameters [20, 33]. Furthermore, the surface elasticity theory proposed by Gurtin and Murdoch [34, 35] is widely used to model the surface energy effect for thin and ultra-thin structures.

Due to the vast applications of FGM micro/nanostructures, many studies have been performed to investigate the static and dynamic behaviors of FG micro/nanobeams with material variation along the thickness, length, or combination of them. In the framework of the modified couple stress theory, a major part of these studies is focused on microbeams made of transverse functionally graded material (TFG) which are graded along the thickness direction [36,37,38,39,40,41,42,43,44,45,46,47,48], and on the axially functionally graded material (AFG) microbeams whose material properties are varied through the length direction [49,50,51,52,53,54,55].

As pointed out by Nemat-Alla [56], in some engineering applications such as aerospace craft and shuttles, distributions of the stress or thermal field in the structural elements of such advanced machines can be in two or three directions and thus, the conventional 1D FGMs are not sufficient. As a consequent, there is a need for multi-directional FGMs whose material properties are tailored in two or three directions to obtain more effective high-temperature resistant materials. However, performance of bi-directional (two-dimensional) functionally graded materials (BD-FGMs) beams whose material properties vary along both the thickness and length directions was modeled and investigated by researchers for different mechanical problems. Lü et al. [57] studied the static bending and thermal deformations of BDFG beams with exponential material variation employing the state-space-based differential quadrature method (DQM). Zhao et al. [58] suggested a symplectic framework using the state-space formulation for the static and free vibration analyses of exponential BDFG beams. Şimşek [59] studied the free and forced vibrations of exponential BDFG Timoshenko beam subjected to a moving load using the Lagrange equations and simple polynomial forms. Şimşek [60] also investigated the buckling behavior of BDFG Timoshenko beams with different boundary conditions using Ritz method. Wang et al. [61] investigated the free vibration of BDFG Euler–Bernoulli beam with clamped-free ends employing semi-analytical and semi-numerical methods. Pydah and Sabale [62] analytically studied the flexural response of curved Euler–Bernoulli beams made of power-law BD-FGM. In another study, Pydah and Batra [63] analyzed the static behavior of BDFG thick circular sandwich beam using the shear deformation beam theory. Karamanlı [64] explored the elastostatic behavior of a BDFG beam with different boundary conditions using various beam theories and the symmetric smoothed particle hydrodynamics method. The flexural behavior of BD-FGM sandwich beams is investigated by Karamanlı [65] using a quasi-3D theory and a meshless method. Based on the third-order beam theory, Karamanlı [66] investigated free vibration response of exponential BDFG beams with various boundary conditions using the Lagrange equations. Nguyen et al. [67] used finite element method (FEM) to compute the vibration response of BDFG Timoshenko beams obeying power-law material distribution under a moving concentrated load. Rajasekaran and Khaniki [68] studied the effect of crack type, position, and depth on the dynamic behavior of BDFG cracked Euler–Bernoulli beams using FEM. Li et al. [69] utilized the meshless total Lagrangian corrective smoothed particle method to study the bending behavior of BDFG beams following power-law and exponential distributions in thickness and length directions, respectively. Tang et al. [70] studied the nonlinear free vibration of BDFG Euler–Bernoulli beams by employing the DQM and the homotopy analysis method. Based on the third-order shear deformation and von Kármán nonlinear theories, postbuckling response of BDFG porous beams was investigated by Lei et al. [71] via the DQM. Huang and Ouyang [72] introduced an exact solution for bending analysis of power-law and exponential BDFG Timoshenko beams based on the classical analysis. The bending and free vibrational behaviors of BDFG cylindrical beams with radially and axially varying material properties based on a high-order beam model are studied by Huang [73]. Chen and Chang [74] studied the free vibration behavior of BDFG Timoshenko beams based on the Chebyshev collocation method. Using the variational iteration method and the Hamiltonian approach, Mohammadian [75] presented closed-form analytical solutions for the nonlinear vibration of damped and undamped BDFG Euler–Bernoulli incorporating higher-order nonlinear terms in the strain field. Using FEM, Nguyen [76] investigated the dynamic behavior of power-law BDFG sandwich beam due to nonuniform motion of a moving point load based on the first-order shear deformation beam theory. Recently, Ghatage et al. [77] presented an exhaustive review on the modeling, analysis, application, and future vision of multi-directional FG structures.

In the framework of nonclassical continuum theories, some studies have been carried for BDFG micro/nanobeams. Using DQM, Nejad et al. [78] and Nejad and Hadi [79] studied the size effects via Eringen’s differential nonlocal elasticity theory (EDNET) on the linear buckling and free vibration responses of BDFG Euler–Bernoulli nanobeams with an arbitrary material variation. Karamanlı and Vo [80] developed a finite element model for studying the flexural behavior of BDFG microbeams based on the quasi-3D theory and modified couple stress theory (MCST). In Karamanlı and Vo [81], the size effects on the structural behaviors of BDFG porous microbeams was captured via the MSGT with three material length-scale parameters. Shafiei et al. [82] and Shafiei and Kazemi [83] employed DQM to investigate the influences of the gradation indices, microscale, nonlocal parameters, and porosity on the free vibration and buckling responses of porous BDFG microbeams and nanobeams, adopting MCST and EDNET, respectively. In the framework of MCST and quasi-3D deformation theory, Trinh et al. [84] studied the free vibration behavior of exponentially varying BDFG microbeams using the state-space concept. Based on the nonlocal strain gradient theory (NSGT), Li et al. [85] investigated the nonlinear bending response of BDFG Euler–Bernoulli nanobeams with power-law material distribution along thickness using DQM. Yang et al. [86] employed DQM to obtain the nonlinear responses of exponentially varying BDFG Euler–Bernoulli nanobeam based on EDNET and von Kármán geometric nonlinearity. Yu et al. [87, 88] adopted the quasi-3D beam theory and MCST to study the size-dependent bending and free vibration of BDFG microbeams using isogeometric finite element analysis. Based on the Euler–Bernoulli theory and MCST, Khaniki and Rajasekaran [89] used FEM to investigate the mechanical behavior of BDFG nonuniform microbeam whose material properties are arbitrary varied. Forced vibration analysis of a general nonuniform varying BDFG Euler–Bernoulli microbeam resting on Winkler elastic foundation subjected to a moving harmonic load is presented by Rajasekaran and Khaniki [90]. Utilizing third-order shear beam theory and MCST, Chen et al. [91] investigated the static and dynamic analysis of postbuckling of BDFG microbeams using DQM. This work was extended by Chen et al. [92] to study the free vibration, buckling, and dynamic stability of BDFG microbeams embedded in an elastic medium. Sahmani and Safaei [93, 94] investigated the size-dependent nonlinear free vibration and resonance behaviors of BDFG nanobeams within the context of the hyperbolic shear deformation beam theory and NSGT employing DQM. In another study, Sahmani and Safaei [95] extended this model to study the effect of homogenization scheme of FGM on the nonlinear bending and postbuckling responses of BDFG nanobeams. Rahmani et al. [96] analyzed the vibration response of power-law BDFG rotating porous nanobeams based on Reddy’s beam theory and a general nonlocal theory employing DQM. Attia and Mohamed [97, 98] developed a microbeam model based on MCST to explore the static and vibration behaviors of thermal buckling and postbuckling of BDFG nonuniform shear deformable microbeam. Barati et al. [99] investigated the transverse vibration of BDFG nanobeams subjected to a longitudinal magnetic field is investigated via the EDNET. The static bending of Euler–Bernoulli nanobeams made of BDFG material with the method of initial values in the frame of gradient elasticity is studied by Çelik and Artan [100]. The free vibration behavior of BDFG nanobeams is analyzed via EDNET by Dangi et al. [101]. Malik and Das [102] studied the free vibration behavior of rotating BDFG Euler–Bernoulli nanobeam based on EDNET.

According to surface elasticity theory (SET) proposed by Gurtin and Murdoch [34, 35], the surface layers of the bulk continuum material are treated as a two-dimensional membrane of zero thickness with different properties from the bulk continuum. This theory can efficiently incorporate the surface energy effect into the mechanical responses of micro/nanostructures. In recent years, Gurtin–Murdoch surface elasticity theory has been adopted in many studies to explore the surface effects on the bending, buckling, vibration, and instability responses of FGM micro/nanobeam, i.e., [103,104,105,106,107,108,109,110,111,112]. Simultaneous effects of surface energy and couple stress have been investigated on the static and dynamic analyses of micro/nanobeams by some authors. Gao and co-workers [113,114,115,116] developed a size-dependent model incorporating microstructure and surface energy effects for homogeneous beams using different beam theories. Attia and Mahmoud [117, 118] investigated the mechanics of elastic and viscoelastic Euler–Bernoulli beam on the basis of nonlocal-couple stress elasticity and surface energy theories. Zhang et al. [119] studied the size-dependent behavior of nanobeams incorporating bulk and surface effects. For FGM micro/nanobeams, Attia [120] and Attia and Rahman [121] explored the mutual effects of microstructure and surface energy on the mechanics of elastic and viscoelastic FG nanobeams. The pull-in stability and freestanding of electromechanically actuated FG nanobeams in the framework of MCST and SET in [122,123,124]. Shanab et al. [125,126,127] and Attia et al. [128] presented a comprehensive investigation of nonlinear bending and vibration of TFG Euler–Bernoulli and Timoshenko nanobeams using an integrated couple stress–surface energy model. On the basis of two-phase local/nonlocal formulation, Hosseini-Hashemi et al. [129] studied the damped vibration behavior of viscoelastic Euler–Bernoulli nanobeams in the presence of surface energy. Yin et al. [130, 131] studied the static bending and free vibration behaviors of the nonclassical Bernoulli–Euler and Timoshenko beams based on MCST and SET using isogeometric FE analysis.

From the above literature review, it is noted that most of the researchers are focused on the mechanical behavior of the BDFG microbeams with uniform cross section and in the absence of surface energy effects. To the best of the author’s knowledge, there is no reported work on the mechanics of BDFG micro/nanobeams accounting for the simultaneous effects of cross-section nonuniformality, microstructure, and surface energy. The present study aims to investigate the static bending, buckling, and free vibration behaviors of tapered BDFG nanobeams based on MCST and Gurtin–Murdoch SET to simulate, respectively, the microstructure and surface energy contributions for the first time. All the material properties of the bulk continuum and surface layers including the material length-scale parameter and surface parameters are varies according to power-law in both thickness and length directions. Hamilton’s energy principle has been used to obtain the equations of motion of Euler–Bernoulli nanobeam on the basis of physical neutral surface concept. To this end, the Navier solution in conjunction with GDQM is employed to solve the nonclassical equations for simply supported nanobeams. To authenticate the preciseness of the developed model and solution procedure, the obtained results are compared with those in the open literature. The influences of different geometrical and material parameters on the static and dynamic responses of nonuniform BDFG micro/ nanobeams are examined and discussed in detail.

2 Theory and formulation

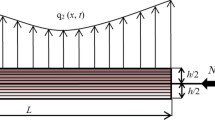
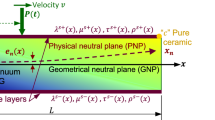
In this section, the size-dependent governing differential equations, and corresponding boundary conditions of a BDFG nonuniform micro/nanoscale beams are exactly derived using the Hamiltonian principle. To model a general micro/nanobeam for mechanical problems, the present formulation considers the simultaneous effect of microstructure and surface energy using the modified couple stress theory and Gurtin–Murdoch surface elasticity theory, respectively, in the framework of continuum mechanics. This is the first time to include the surface energy effects on BDFG tapered nanobeams in the presence of microstructure effect. For this purpose, consider a nonuniform nanobeam whose dimensions with respect to Cartesian coordinate system ($x$, $y$, $z$) are shown in Fig. 1. The middle plane being $z=0$ with origin at $x=0$. Both the thickness and width of the nanobeam are assumed to vary along length $L$ as $h\left(x\right)={h}_{0}\left(1-{\beta }_{h}x/L\right)$ and $b\left(x\right)={b}_{0}\left(1-{\beta }_{b}x/L\right)$, respectively, where ${\beta }_{h}$ and ${\beta }_{b}$ denote the taperness parameters describing the cross-sectional change along thickness and width directions, respectively; and ${h}_{0}$ and ${b}_{0}$ represent, respectively, the thickness and width at $x=0$.

Fig. 1

Schematic sketch of a nonuniform bi-directional functionally graded nanobeam

2.1 Bi-directional functionally graded material

Due to the continuous grading of the material properties of a BDFG beam along both the axial and transverse directions, the effective material properties are defined in terms of the power law in both directions as follows: [59, 60]

$$\mathcal{P}\left(x,z\right)={\mathcal{P}}_{l}+\left({\mathcal{P}}_{r}-{\mathcal{P}}_{l}\right){\mathcal{V}}_{r}\left(x,z\right) , {\mathcal{V}}_{r}\left(z\right)={\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}}, {\mathcal{V}}_{r}\left(x,z\right)+{\mathcal{V}}_{l}\left(x,z\right)=1, $$

(1)

where ${\mathcal{V}}_{r}$ is the volume fraction of the constituent at the upper right corner of the beam, and the subscripts $l$ and $r$ represent, respectively, the phases at the lower left and upper right corners of the BDFG beam. In Eq. (1), ${k}_{x}$ and ${k}_{z}$ stand for non-negative numbers (FGM property gradient indices) that determine the material variation profile through the length and thickness directions, respectively. Following Eq. (1) the variations of the effective Young’s modulus (${E}^{B}$), mass density (${\rho }^{B}$), Poisson’s ratio ($\nu$), and variable microstructure material length-scale ($l$) of the bulk continuum, can be defined as

$${E}^{B}\left(x,z\right)={E}_{l}^{B}+\left({E}_{r}^{B}-{E}_{l}^{B}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}},$$

(2a)

$${\rho }^{B}\left(x,z\right)={\rho }_{l}^{B}+\left({\rho }_{r}^{B}-{\rho }_{l}^{B}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}},$$

(2b)

$$\nu \left(x,z\right)={\nu }_{l}+\left({\nu }_{r}-{\nu }_{l}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} ,$$

(2c)

$$l\left(x,z\right)={l}_{l}+\left({l}_{r}-{l}_{l}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} .$$

(2d)

The effective surface parameters, surface Lamé’s constants (${\lambda }^{s}$ and ${\mu }^{s}$), surface residual stress (${\tau }^{s}$), and surface mass density (${\rho }^{s}$) of the BDFG beam are expressed according to the bi-directional power law in Eq. (1), as follows:

$${\lambda }^{s}\left(x,z\right)={\lambda }_{l}^{s}+\left({\lambda }_{r}^{s}-{\lambda }_{l}^{s}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} ,$$

(3a)

$${\mu }^{s}\left(x,z\right)={\mu }_{l}^{s}+\left({\mu }_{r}^{s}-{\mu }_{l}^{s}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} ,$$

(3b)

$${\tau }^{s}\left(x,z\right)={\tau }_{l}^{s}+\left({\tau }_{r}^{s}-{\tau }_{l}^{s}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} ,$$

(3c)

$${\rho }^{s}\left(x,z\right)={\rho }_{l}^{s}+\left({\rho }_{r}^{s}-{\rho }_{l}^{s}\right){\left(\frac{z}{h\left(x\right)}+\frac{1}{2}\right)}^{{k}_{z}}{\left(\frac{x}{L}\right)}^{{k}_{x}} .$$

(3d)

Herein and throughout the paper, superscripts “$B$” and “$s$” refer to the bulk and surface continuums, respectively, of the nanobeam.

In Eqs. (1–3a, 3b, 3c, 3d), the position of the midplane ($z$) is taken as a reference. It is obvious that the variation of the material properties of a BDFG is non-symmetric about the geometric midplane of the beam. Consequently, the associated physical neutral plane deviates from the midplane counterpart [97]. So, it is defined that ${e}_{n}=z-{z}_{n}$, in which ${z}_{n}$ refers to the $z$-coordinate of the physical neutral plane that can be determined as follows:

$${e}_{n}\left(x\right)=\frac{{\int }_{A(x)} z\left[{\lambda }^{B}\left(x,z\right)+2{\mu }^{B}\left(x,z\right)\right]dA}{{\int }_{A(x)} \left[{\lambda }^{B}\left(x,z\right)+2{\mu }^{B}\left(x,z\right)\right] dA} ,$$

(4)

where ${e}_{n}$ is the distance between the midplane and the neutral plane as shown in Fig. 1. It is clear that the position of physical neutral plane is a function of axial direction due to the variations of both the cross section and the material properties along the axial direction. For symmetric variation of the beam material properties about its midplane, the parameter ${e}_{n}$ is equal to zero. Lamé’s moduli of the bulk material ${\mu }^{B}\left(x,z\right)$ and ${\lambda }^{B}\left(x,z\right)$ are related to Young’s modulus ${E}^{B}\left(x,z\right)$ and Poisson’s ratio $\nu \left(x,z\right)$ of the beam material as follows:

$${\mu }^{B}\left(x,z\right)=\frac{{E}^{B}\left(z\right)}{2\left(\nu \left(z\right)+1\right)}\, \,\,\,\mathrm{and}\,\,\,\, {\lambda }^{B}\left(x,z\right)=\frac{{E}^{B}\left(x,z\right)\nu \left(x,z\right)}{\left(1+\nu \left(x,z\right)\right)\left(1-2\nu \left(x,z\right)\right)} .$$

(5)

It is obvious when the Poisson’s ratio effect is neglected, the term $\left({\lambda }^{B}\left(x,z\right)+2{\mu }^{B}\left(x,z\right)\right)$ yields to ${E}^{B}\left(x,z\right)$, as reported in [59, 60, 93, 94].

2.2 Modified couple stress theory

Based on Euler–Bernoulli beam theory, all applied loads and geometry are such that displacement field of a BDFG micro/nanobeam at an arbitrary point at a height ($z$) measured from the midplane and time ($t$) can be given as

$$\begin{array}{l}U\left(x,z,t\right)=u\left(x,t\right)-{z}_{n}\frac{\partial w\left(x,t\right) }{\partial x}\\ W\left(x,z,t\right)=w\left(x,t\right),\end{array} ,$$

(6)

where $U$ and $W$ represent the displacements in axial and transversal directions, respectively, of an arbitrary point ($x,y,z$) on the beam cross section at time ($t$). $u\left(x,t\right)$ and $w\left(x,t\right)$ are the axial and transverse components of displacement of the point on the physical neutral axis.

In the context of the modified couple stress theory (MCST) proposed by Yang et al. [23], the strain energy of the bulk continuum of deformed micro/nanobeam made of an isotropic linear elastic BDFG is given as

$${\Pi }^{B}=\frac{1}{2}{\int }_{0}^{L}{\int }_{A}\left({\sigma }_{ij}{\varepsilon }_{ij}+{m}_{ij}{\chi }_{ij}\right)dAdx ,$$

(7)

where ${\varepsilon }_{ij}$ and ${\sigma }_{ij}$ are, respectively, the strain tensor and the classical Cauchy stress tensor; and ${\chi }_{ij}$ and ${m}_{ij}$ are, respectively, the symmetric rotation gradient tensor and deviatoric part of the couple stress tensor. These tensors can be expressed as follows [23]:

$${\varepsilon }_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right) ,$$

(8a)

$${\sigma }_{ij}=2\mu \left(x,z\right){\varepsilon }_{ij}+\lambda \left(x,z\right) {\varepsilon }_{kk}{\delta }_{ij} ,$$

(8b)

$${\chi }_{ij}=\frac{1}{2}\left({\theta }_{i,j}+{\theta }_{j,i}\right); {\theta }_{i}=\frac{1}{2}{e}_{ijk}{u}_{k,j} ,$$

(9a)

$${m}_{ij}=2\mu \left(x,z\right) {l}^{2}\left(x,z\right) {\chi }_{ij},$$

(9b)

in which, ${e}_{ijk}$ is the cyclic permutation symbol and ${\delta }_{ij}$ denotes the Kronecker delta. ${u}_{i}$ is the displacement vector given by Eq. (6), ${\theta }_{i}$ is the rotation vector, and $l(x,z)$ denotes the material length-scale parameter which captures the size-effect due to the material microstructures in the nonclassical BDFG beam model. In the aforementioned equations and throughout the paper, the summation convention and standard index notation are used, with the Latin indices running from 1 to 3 and the Greek indices from 1 to 2 unless otherwise indicated.

Based on the kinematic relations of EBBT in Eq. (6), the nonvanishing components of ${\varepsilon }_{ij}$, ${\sigma }_{ij}$, ${\theta }_{i}$, ${\chi }_{ij}$, and ${m}_{ij}$ can be, respectively, obtained as

$${\varepsilon }_{xx}=\frac{\partial u\left(x,t\right) }{\partial x}-{z}_{n}\frac{{\partial }^{2}w\left(x,t\right) }{\partial {x}^{2}} ,$$

(10a)

$${\sigma }_{xx}\equiv \left({\lambda }^{B}\left(x,z\right)+2{\mu }^{B}\left(x,z\right)\right)\left[\frac{\partial u\left(x,t\right) }{\partial x}-{z}_{n}\frac{{\partial }^{2}w\left(x,t\right) }{\partial {x}^{2}}\right] ,$$

(10b)

$${\theta }_{y}=-\frac{\partial w\left(x,t\right) }{\partial x} ,$$

(11a)

$${\chi }_{xy}=-\frac{1}{2}\frac{{\partial }^{2}w\left(x,t\right) }{\partial {x}^{2}} ,$$

(11b)

$${m}_{yx}={m}_{xy}\left(x,t\right)={l\left(x,z\right)}^{2}{\mu }^{B}\left(x,z\right)\left[-\frac{{\partial }^{2}w\left(x,t\right)}{\partial {x}^{2}}\right] .$$

(11c)

2.3 Surface elasticity theory

In this study, Gurtin–Murdoch theory of surface elasticity is employed to model the interactions between the bulk material and elastic surface of nanoscale structures, Gurtin and Murdoch [33, 34]. In this theory, the surface layer of a bulk elastic material satisfies distinct constitutive equations involving surface elastic constants and surface residual stress. According to the Gurtin–Murdoch surface elasticity theory, the strain energy in the surface layers continuum of deformed micro/nanobeam made of an isotropic linear elastic BDFG can be obtained as [113,114,115, 117]

$${\Pi }^{s}=\frac{1}{2}{\int }_{0}^{L}{\oint }_{\partial A}{\sigma }_{ij}^{s}\left(x,t\right) {\varepsilon }_{ij}\left(x,t\right)dSdx.$$

(12)

In accordance with the Gurtin–Murdoch theory of surface elasticity, the surface stress–strain constitutive equations for the surface layers can be introduced as follows [33, 34]:

$${\sigma }_{\alpha \beta }^{s\pm }={\tau }^{s\pm }\left(x,z\right){\delta }_{\alpha \beta }+2\left({\mu }^{s\pm }\left(x,z\right)-{\tau }^{s\pm }\left(x,z\right)\right){\varepsilon }_{\alpha \beta }^{\pm }+\left({\lambda }^{s\pm }\left(x,z\right)+{\tau }^{s\pm }\left(x,z\right)\right){\varepsilon }_{\gamma \gamma }^{\pm }{\delta }_{\alpha \beta }+{\tau }^{s\pm }\left(x,z\right){u}_{\alpha ,\beta }^{\pm } ,$$

(13a)

$${\sigma }_{n\alpha }^{s\pm }={\tau }^{s\pm }\left(x,z\right){u}_{n,\alpha }^{\pm }; \left(\alpha , \beta =x, y\right) , $$

(13b)

where ${\lambda }^{s}$ and ${\mu }^{s}$ are the surface elastic Lame’s constants and ${\tau }^{s}$ is the residual surface stress under unstrained conditions (i.e., the surface stress at zero strain). ${\sigma }_{n\alpha }^{s}$ is the out-of-plane components of the surface stress tensor. Signs ($+$) and ($-$) stand for the upper and lower surface layers at $z=h\left(x\right)/2$ and $z=-h\left(x\right)/2$, respectively, of the BDFG nanobeam. Following Eqs. (6) and (10a), the nonvanishing components of the surface stresses in terms of the displacement field can be obtained as

$${\sigma }_{xx}^{s}={\tau }^{s\pm }\left(x,z\right)+\left({\lambda }^{s\pm }\left(x,z\right)+2{\mu }^{s\pm }\left(x,z\right)\right)\left(\frac{\partial u\left(x,t\right) }{\partial x}-{z}_{n}\frac{{\partial }^{2}w\left(x,t\right) }{\partial {x}^{2}}\right) ,$$

(14a)

$${\sigma }_{nx}^{s}={\tau }^{s\pm }\left(x,z\right){u}_{n,x}^{s}={\tau }^{s\pm }\left(x,z\right)\frac{\partial w}{\partial x}{n}_{z} . $$

(14b)

where ${n}_{z}$ is the $z$-component of the unit outward normal vector to the beam lateral surface.

2.4 The equations of motion of BDFG nanobeam based on the surface elasticity

Hamilton’s principle is used to obtain the nonclassical equations of the motion of BDFG tapered nanobeam considering the simultaneous effect of modified couple stress and surface elasticity. Unlike the existing BDFG beam models, the present model accounts for both axial and transverse deformations and the Poisson’s effect is incorporated.

According to Gurtin–Murdoch surface continuum theory of elasticity and modified couple stress theory, the first variation of the total strain energy, including the bulk and surface continuums of a BDFG tapered nanobeam can be given as

$$\delta {\Pi }^{t}\equiv \delta {\Pi }^{B}+\delta {\Pi }^{s}=\frac{1}{2}\delta {\int }_{0}^{L}\left\{{\int }_{A}\left({\sigma }_{xx}{\varepsilon }_{xx}+2{m}_{xy}{\chi }_{xy}\right)dA+{\oint }_{\partial A}\left({\sigma }_{xx}^{s}{\varepsilon }_{xx}+2{\sigma }_{nx}^{s}{\varepsilon }_{nx}\right)dS\right\}dx ,$$

(15)

where ${\varepsilon }_{nx}=\frac{1}{2}\frac{\partial w}{\partial x}{n}_{z}$. Substitution of Eqs. (10a, 10b), (11a, 11b, 11c), and (14a, 14b), Eq. (15) can be obtained in terms of the stress resultants as follows:

$$\delta {\Pi }^{t}={\int }_{0}^{L}\left[{\mathbb{N}}(x)\frac{\partial \delta u}{\partial x}-{\mathbb{M}}(x)\frac{{\partial }^{2}\delta w}{\partial {x}^{2}}+\left({\mathcal{C}}_{n}^{s}(x)\frac{\partial w}{\partial x}\right)\frac{\partial \delta w}{\partial x}\right]dx$$

(16)

in which,

$${\mathbb{N}}\left(x\right)={N}^{B}\left(x\right)+{N}^{s}\left(x\right)-\frac{1}{2}{\mathcal{C}}_{0}^{s}\left(x\right),$$

(17a)

$${\mathbb{M}}\left(x\right)={M}^{B}\left(x\right)+{M}^{s}\left(x\right)+{\mathrm{Y}}^{B}\left(x\right)-\frac{1}{2}{\mathcal{C}}_{1}^{s}\left(x\right) ,$$

(17b)

The stress and couple-stress resultants of the bulk continuum are given by

$$\left\{\begin{array}{c}{N}^{B}(x)\\ {M}^{B}(x)\\ {\mathrm{Y}}^{B}(x)\end{array}\right\}\equiv {\int }_{A}\left\{\begin{array}{c}{\sigma }_{xx}\\ {z}_{n}{\sigma }_{xx}\\ {m}_{xy}\end{array}\right\}dA=\left\{\begin{array}{c}{A}_{xx}\left(x\right)\frac{\partial u}{\partial x}-{B}_{xx}\left(x\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}\\ {B}_{xx}\left(x\right)\frac{\partial u}{\partial x}-{D}_{xx}\left(x\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}\\ -{A}_{xz}\left(x\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}\end{array}\right\} ,$$

(18)

where

$$\left\{\begin{array}{c}{A}_{xx}(x)\\ {B}_{xx}(x)\\ {D}_{xx}(x)\end{array}\right\}\equiv {\int }_{{b}_{1}\left(x\right)}^{{b}_{2}\left(x\right)}{\int }_{{h}_{1}\left(x\right)}^{{h}_{2}\left(x\right)}\left({\lambda }^{B}\left(x,z\right)+2{\mu }^{B}\left(x,z\right)\right)\left\{\begin{array}{c}1\\ {z}_{n}\\ {{z}_{n}}^{2}\end{array}\right\}dzdy,$$

(19a)

$${A}_{xz}\left(x\right)\equiv {\int }_{{b}_{1}\left(x\right)}^{{b}_{2}\left(x\right)}{\int }_{{h}_{1}\left(x\right)}^{{h}_{2}\left(x\right)}\mu \left(x,z\right) {l}^{2}\left(x,z\right)dzdy.$$

(19b)

The stress resultants of the surface continuum are given by

$$\left\{\begin{array}{c}{N}^{s}(x)\\ {M}^{s}(x)\end{array}\right\}={\oint }_{\partial A}\left\{\begin{array}{c}{\sigma }_{xx}^{s}\\ {z}_{n}{\sigma }_{xx}^{s}\end{array}\right\}dS=\left\{\begin{array}{c}{A}_{xx}^{s}(x)\frac{\partial u}{\partial x}-{B}_{xx}^{s}(x)\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\mathcal{C}}_{0}^{s}(x)\\ {B}_{xx}^{s}(x)\frac{\partial u}{\partial x}-{D}_{xx}^{s}(x)\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\mathcal{C}}_{1}^{s}(x)\end{array}\right\} ,$$

(20)

where

$$\left\{\begin{array}{c}{A}_{xx}^{s}(x)\\ {B}_{xx}^{s}(x)\\ {D}_{xx}^{s}(x)\end{array}\right\}\equiv {\oint }_{\partial A}\left({\lambda }^{s\pm }\left(x,z\right)+2{\mu }^{s\pm }\left(x,z\right)\right)\left\{\begin{array}{c}1\\ {z}_{n}\\ {{z}_{n}}^{2}\end{array}\right\}dS,$$

(21a)

$$\left\{\begin{array}{c}\begin{array}{c}{\mathcal{C}}_{0}^{s}(x)\\ {\mathcal{C}}_{1}^{s}(x)\end{array}\\ {\mathcal{C}}_{n}^{s}(x)\end{array}\right\}\equiv {\oint }_{\partial A}{\tau }^{s}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n}\\ {n}_{z}^{2}\end{array}\right\}dS.$$

(21b)

In Eqs. (18) and (21a, 21b), $dA$ and $dS$ are the differential area and line elements, respectively.

Performing the partial integration over the time interval $[{t}_{0},{t}_{f}$] and after some mathematical manipulations, the first variation of the strain energy can be obtained as

$$\delta {\int }_{{t}_{0}}^{{t}_{f}}{\Pi }^{t}={\int }_{{t}_{0}}^{{t}_{f}}\left\{-{\int }_{0}^{L} \left[\frac{\partial {\mathbb{N}}\left(x\right)}{\partial x}\delta u+\left(\frac{{\partial }^{2}{\mathbb{M}}\left(x\right)}{\partial {x}^{2}}+\frac{\partial }{\partial x}\left({\mathcal{C}}_{n}^{s}\left(x\right)\frac{\partial w}{\partial x}\right)\right)\delta w\right]dx+{ \left[{\mathbb{N}}\left(x\right)\delta u+\left({\mathcal{C}}_{n}^{s}\left(x\right)\frac{\partial w}{\partial x}+\frac{\partial {\mathbb{M}}\left(x\right)}{\partial x}\right)\delta w-{\mathbb{M}}\left(x\right)\frac{\partial \delta w}{\partial x}\right]}_{0}^{L}\right\}dt .$$

(22)

The first variation of the kinetic energy of the BDFG nanobeam incorporating the effect of surface mass density can be obtained as

$$\delta {\Pi }^{k}\equiv \delta {\int }_{0}^{L}\frac{1}{2}\left\{{\int }_{A}\left\{{\rho }^{B}\left(x,z\right)\left({\left(\frac{\partial U}{\partial t}\right)}^{2}+{\left(\frac{\partial W}{\partial t}\right)}^{2}\right)\right\}dA+{\oint }_{\partial A}\left[{\rho }^{s}\left(x,z\right)\left({\left(\frac{\partial U}{\partial t}\right)}^{2}+{\left(\frac{\partial W}{\partial t}\right)}^{2}\right)\right]dS\right\}dx=\delta {\int }_{0}^{L}\frac{1}{2}\left\{{\int }_{A}\left\{{\rho }^{B}\left(x,z\right)\left({\left(\frac{\partial u}{\partial t}-{z}_{n}\frac{{\partial }^{2}w}{\partial x\partial t}\right)}^{2}+{\left(\frac{\partial w}{\partial t}\right)}^{2}\right)\right\}dA+{\oint }_{\partial A}\left[{\rho }^{s}\left(x,z\right)\left({\left(\frac{\partial u}{\partial t}-{z}_{n}\frac{{\partial }^{2}w}{\partial x\partial t}\right)}^{2}+{\left(\frac{\partial w}{\partial t}\right)}^{2}\right)\right]dS\right\}dx .$$

(23)

Proceeding the above integration by parts over the time interval $[{t}_{0},{t}_{f}$], one can obtain the following:

$$\delta {\int }_{{t}_{0}}^{{t}_{f}}{\Pi }^{k}dt=-{\int }_{{t}_{0}}^{{t}_{f}}{\int }_{0}^{L}\left\{\left[{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right]\delta u+\left[{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}w}{\partial {t}^{2}}+{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}+\frac{\partial {\mathrm{I}}_{B}\left(x\right)}{\partial x}\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}-\frac{\partial {\mathrm{I}}_{D}\left(x\right)}{\partial x}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right]\delta w\right\}dxdt+{\int }_{{t}_{0}}^{{t}_{f}}{\left\{\left[{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}-{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}\right]\delta w\right\}}_{0}^{L}dt+{\int }_{0}^{L}{\left\{\left[{\mathrm{I}}_{A}\left(x\right)\frac{\partial u}{\partial t}-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{2}w}{\partial x\partial t}\right]\delta u+\left[{\mathrm{I}}_{A}\left(x\right)\frac{\partial w}{\partial t}\right]\delta w-\left[{\mathrm{I}}_{B}\left(x\right)\frac{\partial u}{\partial t}-{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{2}w}{\partial x\partial t}\right]\delta \frac{\partial w}{\partial x}\right\}}_{{t}_{0}}^{{t}_{f}}dx ,$$

(24)

where the effective mass moments of inertia are given by

$$\left\{\begin{array}{c}{\mathrm{I}}_{A}(x)\\ {\mathrm{I}}_{B}(x)\\ {\mathrm{I}}_{D}(x)\end{array}\right\}={\int }_{{b}_{1}\left(x\right)}^{{b}_{2}\left(x\right)}{\int }_{{h}_{1}\left(x\right)}^{{h}_{2}\left(x\right)}{\rho }_{b}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n}\\ {{z}_{n}}^{2}\end{array}\right\}dzdy+{\oint }_{\partial A}{\rho }_{s}\left(x,z\right)\left\{\begin{array}{c}1\\ {z}_{n}\\ {{z}_{n}}^{2}\end{array}\right\}dS .$$

(25)

From the general expression of the work done by external forces in the modified couple stress theory and in the surface elasticity theory, the virtual work done by the forces applied on the current beam can be written as [46, 113,114,115, 132]

$$\delta {\Pi }^{w}={\int }_{\Omega }\left(\mathbf{f}\bullet \delta {\varvec{u}}+{\mathbf{f}}_{nc}\bullet \delta {\varvec{\uptheta}}\right)d\Omega +{\oint }_{\partial A}\left(\bar{\mathbf{t}}\boldsymbol{ }.\delta \mathbf{u}+\bar{\mathbf{s}}\boldsymbol{ }.\delta {\varvec{\uptheta}}\right)dS+{\int }_{L}P\left(\frac{\partial \delta u}{\partial x}+\frac{\partial w}{\partial x}\frac{\partial \delta w}{\partial x}\right)dx ,$$

(26)

where $\mathbf{f}$ and ${\mathbf{f}}_{nc}$ are, respectively, the body force resultant per unit volume and body couple resultant per unit volume, and $\bar{\mathbf{t}}$ and $\bar{\mathbf{s}}$ are, respectively, the traction resultant per unit area and surface couple resultant per unit area, and $S$ represents the surface of domain $\Omega$. The first variation of work done by the external applied forces on the time interval $[{t}_{0},{t}_{f}$] can be obtained as

$$\delta {\int }_{{t}_{0}}^{{t}_{f}}{\Pi }^{w}={\int }_{{t}_{0}}^{{t}_{f}}{\int }_{0}^{L}\left\{\left(f- \frac{\partial P}{\partial x}\right)\delta u+\left(q-P\frac{{\partial }^{2}w}{\partial {x}^{2}}-\frac{\partial P}{\partial x}\frac{\partial w}{\partial x}+\frac{\partial {f}_{nc}}{\partial x}\right)\delta w\right\}dxdt+{\int }_{{t}_{0}}^{{t}_{f}}{\left\{\left(\bar{N}+P\right)\delta u+\left(\bar{V}+P\frac{\partial w}{\partial x}-{f}_{nc}\right)\delta w-\left({\bar{M}}_{c}+{\bar{M}}_{nc}\right)\frac{\partial \delta w}{\partial x}\right\}}_{0}^{L}dt,$$

(27)

in which, $f$ and $q$ are the distributed axial and transverse loads per unit length along the $x$-axis; $P$ is the applied external compressive axial; and ${f}_{nc}$ is the $y$- component of the body couple per unit length along the $x$-axis. $\bar{N}$ and $\bar{V}$ are the applied axial force and transverse force at the two ends of the beam, respectively; and ${\bar{M}}_{c}$ and ${\bar{M}}_{nc}$ denote the classical and non-classical bending moments due to, respectively, the normal stress component ${\sigma }_{xx}$ and the couple stress component ${m}_{xy}$ at the two ends of the microbeam.

To this end, the Hamilton’s principle states that

$$\delta {\int }_{{t}_{0}}^{{t}_{f}}\left[{\Pi }^{k}-\left({\Pi }^{t}-{\Pi }^{w}\right)\right]dt=0 .$$

(28)

Substituting Eqs. (22), (24) and (27) into Eq. (28), applying the fundamental lemma of calculus of variation and invoking the condition of zero variation at times $t={t}_{0}$ and $t={t}_{f}$, the governing equations of the nonuniform BDFG nanobeam are obtained as the follows:

$$\delta u\Rightarrow -{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\frac{\partial {\mathbb{N}}\left(x\right)}{\partial x}+f-\frac{\partial P}{\partial x}=0 ,$$

(29a)

$$\delta w\Rightarrow -{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}w}{\partial {t}^{2}}-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}-\frac{\partial {\mathrm{I}}_{B}\left(x\right)}{\partial x}\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{\partial {\mathrm{I}}_{D}\left(x\right)}{\partial x}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\frac{{\partial }^{2}{\mathbb{M}}\left(x\right)}{\partial {x}^{2}}+\left({\mathcal{C}}_{n1}\left(x\right)-P\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}+\left(\frac{\partial {\mathcal{C}}_{n1}\left(x\right)}{\partial x}-\frac{\partial P}{\partial x}\right)\frac{\partial w}{\partial x}+\frac{\partial {f}_{nc}}{\partial x}+q=0 ,$$

(29b)

with the following boundary conditions:

$$\delta u: \mathrm{Either} u=\stackrel{\sim }{u} \mathrm{or}-{\mathbb{N}}\left(x\right)+\left(\bar{N}+P\right)=0 ,$$

(30a)

$$\delta w: \mathrm{Either } w=\stackrel{\sim }{w} \mathrm{or} \frac{\partial {\mathbb{M}}\left(x\right)}{\partial x}+{\mathcal{C}}_{n}^{s}\left(x\right)\frac{\partial w}{\partial x}-P\frac{\partial w}{\partial x}-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+{f}_{nc}-\bar{V}=0\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\mathrm{or}\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }w=\stackrel{\sim }{w} ,$$

(30b)

$$\delta \frac{\partial w}{\partial x}: \mathrm{Either} \frac{\partial w}{\partial x}=\stackrel{\sim }{\frac{\partial w}{\partial x}} \mathrm{or} {\mathbb{M}}\left(x\right)-\left({\bar{M}}_{c}+{\bar{M}}_{nc}\right)=0\boldsymbol{ }\boldsymbol{ }.\boldsymbol{ }$$

(30c)

2.5 The equations of motion of BDFG nanobeam in terms of the displacement field

Substitution of Eqs. (17a, 17b), (18) and (20) into Eq. (29a, 29b) gives the following size-dependent governing differential equations in terms of the displacement field:

$$\delta u\Rightarrow -{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+{\mathcal{A}}_{11}\left(x\right)\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{\partial {\mathcal{A}}_{11}\left(x\right)}{\partial x}\frac{\partial u}{\partial x}-{\mathcal{B}}_{11}\left(x\right)\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{\partial {\mathcal{B}}_{11}\left(x\right)}{\partial x}\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{1}{2}\frac{\partial {\mathcal{C}}_{0}^{s}\left(x\right)}{\partial x}+{f}_{u}-\frac{\partial P}{\partial x}=0 ,$$

(31a)

$$\delta w\Rightarrow -{\mathrm{I}}_{A}\left(x\right)\frac{{\partial }^{2}w}{\partial {t}^{2}}-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{3}u}{\partial x\partial {t}^{2}}-\frac{\partial {\mathrm{I}}_{B}\left(x\right)}{\partial x}\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{\partial {\mathrm{I}}_{D}\left(x\right)}{\partial x}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+{\mathcal{B}}_{11}\left(x\right)\frac{{\partial }^{3}u}{\partial {x}^{3}}+2\frac{\partial {\mathcal{B}}_{11}\left(x\right)}{\partial x}\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}{\mathcal{B}}_{11}\left(x\right)}{\partial {x}^{2}}\frac{\partial u}{\partial x}-{\mathcal{D}}_{11}\left(x\right)\frac{{\partial }^{4}w}{\partial {x}^{4}}-2\frac{\partial {\mathcal{D}}_{11}\left(x\right)}{\partial x}\frac{{\partial }^{3}w}{\partial {x}^{3}}+\left({\mathcal{C}}_{n}^{s}\left(x\right)-P-\frac{{\partial }^{2}{\mathcal{D}}_{11}\left(x\right)}{\partial {x}^{2}}\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}+\left(\frac{\partial {\mathcal{C}}_{n}^{s}\left(x\right)}{\partial x}-\frac{\partial P}{\partial x}\right)\frac{\partial w}{\partial x}+\frac{1}{2}\frac{{\partial }^{2}{\mathcal{C}}_{1}^{s}\left(x\right)}{\partial {x}^{2}}+\frac{\partial {f}_{nc}}{\partial x}+q=0 .$$

(31b)

Moreover, the corresponding boundary conditions at $x=0$ and $x=L$ are as follows:

$$\delta u: \mathrm{Either }u=\stackrel{\sim }{u} \mathrm{or } {\mathcal{A}}_{11}\left(x\right)\frac{\partial u}{\partial x}-{\mathcal{B}}_{11}\left(x\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{1}{2}{\mathcal{C}}_{0}^{s}\left(x\right)-\left(\bar{N}+P\right)=0,\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }$$

(32a)

$$\delta w: \mathrm{Either} w=\stackrel{\sim }{w}\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\mathrm{or }\boldsymbol{ }\boldsymbol{ }-{\mathrm{I}}_{B}\left(x\right)\frac{{\partial }^{2}u}{\partial {t}^{2}}+{\mathrm{I}}_{D}\left(x\right)\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+\left({\mathcal{C}}_{n}^{s}\left(x\right)-P\right)\frac{\partial w}{\partial x}+{\mathcal{B}}_{11}\left(x\right)\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{\partial {\mathcal{B}}_{11}\left(x\right)}{\partial x}\frac{\partial u}{\partial x}-{\mathcal{D}}_{11}\left(x\right)\frac{{\partial }^{3}w}{\partial {x}^{3}}-\frac{\partial {\mathcal{D}}_{11}\left(x\right)}{\partial x}\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{1}{2}\frac{\partial {\mathcal{C}}_{1}^{s}\left(x\right)}{\partial x}+{f}_{nc}-\bar{V}=0\boldsymbol{ },\boldsymbol{ }\boldsymbol{ }$$

(32b)

$$\frac{\partial \delta w}{\partial x}: \mathrm{Either }\frac{\partial w}{\partial x}=\stackrel{\sim }{\frac{\partial w}{\partial x}} \mathrm{or} {\mathcal{B}}_{11}\left(x\right)\frac{\partial u}{\partial x}-{\mathcal{D}}_{11}\left(x\right)\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{1}{2}{\mathcal{C}}_{1}^{s}\left(x\right)-\left({\bar{M}}_{c}+{\bar{M}}_{nc}\right)=0 ,$$

(32c)

with

$$\left\{\begin{array}{c}{\mathcal{A}}_{11}\left(x\right)\\ {\mathcal{B}}_{11}\left(x\right)\\ {\mathcal{D}}_{11}\left(x\right)\end{array}\right\}=\left\{\begin{array}{c}{A}_{xx}\left(x\right)+{A}_{xx}^{s}\left(x\right)\\ {B}_{xx}\left(x\right)+{B}_{xx}^{s}\left(x\right)\\ {D}_{xx}\left(x\right)+{D}_{xx}^{s}\left(x\right)+{A}_{xz}\left(x\right)\end{array}\right\} .$$

(33)

When the material gradation is assumed in thickness direction only and by neglecting the axial displacement component, the obtained equation of motion and boundary conditions for the transverse displacement are identical with those reported in [120, 121]. Moreover, without considering surface energy and the material gradation in the axial direction, the obtained governing equations and associated boundary conditions of a uniform transverse functionally graded (TFG) microbeam are the same as those presented in [46].

3 Solution procedure

In general, deriving an analytical solution of the equations of motion (Eqs. 31a, 31b) is quite difficult because of their variable coefficients attributed to the nature of bi-directional material nonhomogeneity and the nonuniform cross section. In addition, accounting for the physical neutral axis as a function of axial direction of the beam and considering the gradation of all the material properties of both the bulk and surface continuums makes the problem more complex. However, obtaining closed form formulas for the governing equations coefficients is quite difficult. To solve this issue, these coefficients are numerically calculated in an accurate way using quadrature method at each point of coordinate $x$. In this circumstance, the generalized differential quadrature method (GDQM) is employed to translate Eqs. (31a, 31b) into a set of coupled fourth-order ordinary differential equations. Besides, with the help of GDQM, the derivative of the discretized calculated coefficients with respect to coordinate $x$ is easily obtained. First, the procedure of GDQM is briefly reviewed.

3.1 Generalized differential quadrature method

The generalized differential quadrature method (GDQM), as an efficient and effective method in differentiating smooth functions, is employed to obtain the derivatives of the coefficients with respect to coordinate $x$ arise in the governing equations, i.e., $\partial {\mathcal{B}}_{11}\left(x\right)/\partial x$, ${\partial }^{2}{\mathcal{B}}_{11}\left(x\right)/\partial {x}^{2}$,…etc. For this purpose, let the nanobeam length ($0\le x\le L$) is discretized to $N$ sampling points along the axial direction according to the Chebyshev–Gauss–Lobatto formula as

$${x}_{i}=\frac{1}{2}\left[1-\mathrm{cos}\left(\frac{i-1}{N-1}\pi \right)\right]\text{, } i=1\text{,} 2\text{,}\dots \text{,}N ,$$

(34)

where the inner sampling points ${x}_{i}$ are not equally spread in the domain.

In the framework of the GDQM, the $r$ th-order derivative vector of any continuously function (coefficient) can be expressed as follows:

$${F}^{(r)}={\mathcal{D}}^{r}F ,$$

(35a)

with

$${F}^{\left(r\right)}={\left[{f}_{1}^{(r)}, {f}_{2}^{(r)}, \dots ,{f}_{n}^{(r)}\right]}^{T}\,\,\,\, \mathrm{and} \,\,\,\,{f}_{i}^{(r)}={\left.\frac{{d}^{r}f}{d{x}^{r}}\right|}_{{x}_{i}},$$

(35b)

where ${\mathcal{D}}^{r}$ is the $r$ th-order derivative weighting coefficient matrix of dimension N × N. If $r=1$, the first-order derivative weighting coefficient matrix $\left({\mathcal{D}}^{1}\right)$ is computed as follows [133, 134]:

$${\mathcal{D}}_{{ij}}^{1} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{x_{i} - x_{j} }}\mathop \prod \limits_{{\begin{array}{*{20}c} {m = 1} \\ {m \ne i,m \ne j} \\ \end{array} }}^{N} \frac{{x_{i} - x_{m} }}{{x_{j} - x_{m} }}~~~~~~~~~~~~~~i \ne j} \\ {\mathop \sum \limits_{{m \ne i,m = 1}}^{N} \frac{1}{{x_{m} - x_{i} }}~~~~~~~~~~~~~~~~~~~~~~~~~~i = j} \\ \end{array} } \right., $$

(36)

and ${\mathcal{D}}^{r}={\mathcal{D}}^{1}{\mathcal{D}}^{r-1}$ for $r\ge 2$.

For simplicity, in the following subsections, the notation of the discretized calculated coefficients at each node will be unchangeable, just dropping $\left(x\right)$. The corresponding vector of the first and second derivates of any coefficient will be noted by subscripts $d$ and $dd$, respectively.

3.2 Semi-analytical solutions

After evaluating the nodal values of the coefficients as well as their derivatives accurately, the Navier-type solution is developed for nonuniform BDFG simply supported nanobeam in the form of power series with $M$ terms. Equations (31a, b) are analytically solved to obtain the static bending, buckling, and free vibration of BDFG nanobeam. The displacement field is assumed as follows:

$$u\left(x,t\right)=\sum_{n=1}^{M}{U}_{n}\mathrm{cos}\left({\alpha }_{n}x\right) {e}^{i\upomega t} \mathrm{and} w\left(x,t\right)=\sum_{n=1}^{M}{W}_{n}\mathrm{ sin}\left({\alpha }_{n}x\right) {e}^{i\upomega t} ,$$

(37)

where $i=\sqrt{-1}, {\alpha }_{n}=n\pi /L$, $\upomega$ is the fundamental linear frequency, and ${U}_{n}$ and ${W}_{n}$ are the unknown Fourier coefficients to be determined.

Substituting Eqs. (37) into Eqs. (31a, 31b) yields

$${e}^{i\upomega t}\sum_{n=1}^{M}-\left[{\mathcal{A}}_{11}{\alpha }_{n}^{2}\mathrm{cos}\left({\alpha }_{n}x\right)+{\mathcal{A}}_{11d}{\alpha }_{n}\mathrm{sin}\left({\alpha }_{n}x\right)-{\upomega }^{2}{\mathrm{I}}_{A}\mathrm{cos}\left({\alpha }_{n}x\right)\right] {U}_{n}+\left[{\mathcal{B}}_{11}{\alpha }_{n}^{3}\mathrm{ cos}\left({\alpha }_{n}x\right)+{\mathcal{B}}_{11d}{\alpha }_{n}^{2}\mathrm{ sin} \left({\alpha }_{n}x\right)-{\upomega }^{2}\left[{\mathrm{I}}_{B}{\alpha }_{n}\mathrm{cos}\left({\alpha }_{n}x\right)\right]\right]{W}_{n}+{\mathcal{C}}_{0d}^{s}+{f}_{u}-\frac{\partial P}{\partial x}=0,$$

(38a)

$${e}^{i\upomega t}\sum_{n=1}^{M}\left[-{\mathcal{D}}_{11}{\alpha }_{n}^{4} \mathrm{sin}\left({\alpha }_{n}x\right)+2{\mathcal{D}}_{11d}{\alpha }_{n}^{3} \mathrm{cos}\left({\alpha }_{n}x\right)-\left({\mathcal{C}}_{n}^{s}-{\mathcal{D}}_{11dd}\right){{\alpha }_{n}}^{2}\mathrm{sin}\left({\alpha }_{n}x\right)+{\mathcal{C}}_{nd}^{s}{\alpha }_{n}\mathrm{cos}\left({\alpha }_{n}x\right)+P{\alpha }_{n}^{2}\mathrm{sin}\left({\alpha }_{n}x\right)+{\upomega }^{2}\left[{\mathrm{I}}_{D}{\alpha }_{n}^{2}\mathrm{ sin}\left({\alpha }_{n}x\right)+{\mathrm{I}}_{A}\mathrm{sin}\left({\alpha }_{n}x\right)-{\mathrm{I}}_{Dd}{\alpha }_{n}\mathrm{cos}\left({\alpha }_{n}x\right)\right]\right]{W}_{n}+\left[{\mathcal{B}}_{11}{\alpha }_{n}^{3} \mathrm{sin}\left({\alpha }_{n}x\right)-2{\mathcal{B}}_{11d}{\alpha }_{n}^{2} \mathrm{cos}\left({\alpha }_{n}x\right)-{\mathcal{B}}_{11dd}{\alpha }_{n} \mathrm{sin}\left({\alpha }_{n}x\right)+{\upomega }^{2}\left[{\mathrm{I}}_{Bd}\mathrm{cos}\left({\alpha }_{n}x\right)-{\mathrm{I}}_{B}{\alpha }_{n}\mathrm{sin}\left({\alpha }_{n}x\right)\right]\right]{U}_{n}+{\mathcal{C}}_{1dd}^{s}+q+\frac{\partial {f}_{nc} }{\partial x}=0 . $$

(38b)

For simplicity, the terms ${\mathcal{C}}_{0d}^{s}$ and ${\mathcal{C}}_{1dd}^{s}\left(x\right)$ are dropped from Eqs. (38a) and (38b), respectively.

3.2.1 Semi-analytical solution for static bending

The static bending problem of simply supported nanobeam is obtained from Eqs. (38a) and (38b) by setting $\upomega$ to zero and the external forces $P$ and $f$ body couple ${f}_{nc}$ are also set to zero. The applied transverse load $q$ is expanded in Fourier series as follows:

$$q\left(x\right)=\sum_{n=1}^{\infty }{Q}_{n}\mathrm{ sin}\left({\alpha }_{n}x\right),$$

(39a)

$${Q}_{n}=2{\int }_{0}^{L}q\left(x\right)\mathrm{ sin}\left({\alpha }_{n}x\right) dx,$$

(39b)

where the coefficient ${Q}_{n}$ is determined according to the applied load, i.e., for a uniform load with load intensity ${q}_{0}$, ${Q}_{n}=4{q}_{0}/n\pi$, $\left(n=\mathrm{1,3},5, \dots \right)$.

Multiplying Eq. (38a) and (38b) by $\mathrm{cos}\left({\alpha }_{m}x\right)$ and$\mathrm{sin}\left({\alpha }_{m}x\right)$, respectively,$m=1, 2 ,3 , \dots M$, and integrating the resulting equations with respect to $x$ from $0$ to$L$, the following system of linear algebraic equations of the unknown vectors of coefficients ${W}_{n}$ and ${U}_{n}$ is obtained:

$$\left[\begin{array}{cc}\left[{\mathbb{K}}_{11}\right]& \left[{\mathbb{K}}_{12}\right]\\ \left[{\mathbb{K}}_{21}\right]& \left[{\mathbb{K}}_{22}\right]\end{array}\right]\left\{\begin{array}{c}{W}_{n}\\ {U}_{n}\end{array}\right\}=\left\{\begin{array}{c}0\\ \left[{\mathbb{Q}}_{2}\right]\end{array}\right\} .$$

(40)

Then, by solving the above algebraic system, the displacement field amplitudes can be obtained as

$$\left\{\begin{array}{c}{W}_{n}\\ {U}_{n}\end{array}\right\}={\left[{\mathbb{K}}\right]}^{-1}{\mathbb{Q}},$$

(41)

in which,

$$\left\{\begin{array}{c}{\mathbb{K}}_{11}(n,m)\\ {\mathbb{K}}_{12}(n,m)\\ {\mathbb{K}}_{21}(n,m)\\ {\mathbb{K}}_{22}(n,m)\end{array}\right\}={\int }_{0}^{L}\left\{\begin{array}{c}\left[{\mathcal{B}}_{11}{\alpha }_{n}^{3}\mathrm{ cos}\left({\alpha }_{n}x\right)+{\mathcal{B}}_{11d}{\alpha }_{n}^{2}\mathrm{ sin} \left({\alpha }_{n}x\right)\right] \mathrm{cos}\left({\alpha }_{m}x\right)\\ \left[-{\mathcal{A}}_{11}{\alpha }_{n}^{2}\mathrm{cos}\left({\alpha }_{n}x\right)-{\mathcal{A}}_{11d}{\alpha }_{n}\mathrm{sin}\left({\alpha }_{n}x\right)\right] \mathrm{cos}\left({\alpha }_{m}x\right)\\ \left[\left\{\left({\mathcal{D}}_{11dd}-{\mathcal{C}}_{n}^{s}\right){\alpha }_{n}^{2}-{\mathcal{D}}_{11}{\alpha }_{n}^{4}\right\}\mathrm{sin}\left({\alpha }_{n}x\right)+\left\{2{\mathcal{D}}_{11d}{\alpha }_{n}^{3}+{\mathcal{C}}_{nd}^{s}{\alpha }_{n}\right\}\mathrm{cos}\left({\alpha }_{n}x\right)\right]\mathrm{ sin}\left({\alpha }_{m}x\right)\\ \left[\left\{{\mathcal{B}}_{11}{\alpha }_{n}^{3}-{\mathcal{B}}_{11dd}{\alpha }_{n}\right\}\mathrm{sin}\left({\alpha }_{n}x\right)-2{\mathcal{B}}_{11d}{\alpha }_{n}^{2}\mathrm{cos}\left({\alpha }_{n}x\right)\right]\mathrm{ sin}\left({\alpha }_{m}x\right)\end{array}\right\}dx,$$

(42)

$${\mathbb{Q}}_{2}\left(n,m\right)={\int }_{0}^{L}\left[{Q}_{n}\mathrm{sin}\left({\alpha }_{n}x\right)\right]\mathrm{sin}\left({\alpha }_{m}x\right)dx.$$

(43)

3.2.2 Semi-analytical solution for buckling

The critical buckling load can be obtained from Eqs. (38a) and (38b) after setting all the external loads except $P$ to zero and $\upomega$ is also set to zero. With some mathematical operations, one gets the following matrix form of coupled system of equations

$$\left[\left[\begin{array}{cc}\left[{\mathbb{K}}_{11}\right]& \left[{\mathbb{K}}_{12}\right]\\ \left[{\mathbb{K}}_{21}\right]& \left[{\mathbb{K}}_{22}\right]\end{array}\right]-\left[\begin{array}{cc}0& 0\\ \left[{\mathbb{P}}_{21}\right]& 0\end{array}\right]\right]\left\{\begin{array}{c}{W}_{n}\\ {U}_{n}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\}\boldsymbol{ }\boldsymbol{ },$$

(44)

with

$${\mathbb{P}}_{21}\left(n,m\right)=P{\int }_{0}^{L}{\alpha }_{n}^{2}\mathrm{ sin}\left({\alpha }_{n}x\right)\mathrm{ sin}\left({\alpha }_{m}x\right)dx,$$

(45)

where the elements of $\left[{\mathbb{K}}\right]$ are pre-defined in Eqs. (42). Equation (44) represents a standard eigenvalue problem and has nontrivial solution only for a critical axial load ${P}_{cr}(n)$, by setting the determinant of its coefficient matrix to zero.

3.2.3 Semi-analytical solution for free vibration

For free vibration analysis, setting all the external forces in Eqs. (38a) and (38b) to zero leads to

$$\left(\left[\begin{array}{cc}\left[{\mathbb{K}}_{11}\right]& \left[{\mathbb{K}}_{12}\right]\\ \left[{\mathbb{K}}_{21}\right]& \left[{\mathbb{K}}_{22}\right]\end{array}\right]+\left[\begin{array}{cc}\left[{\mathbb{M}}_{11}\right]& \left[{\mathbb{M}}_{12}\right]\\ \left[{\mathbb{M}}_{21}\right]& \left[{\mathbb{M}}_{22}\right]\end{array}\right]{\upomega }^{2}\right)\left\{\begin{array}{c}{W}_{n}\\ {U}_{n}\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\} ,$$

(46)

where

$$\left\{\begin{array}{c}{\mathbb{M}}_{11}(n,m)\\ {\mathbb{M}}_{12}(n,m)\\ {\mathbb{M}}_{21}(n,m)\\ {\mathbb{M}}_{22}(n,m)\end{array}\right\}={\int }_{0}^{L}\left\{\begin{array}{c}-{\mathrm{I}}_{B}{\alpha }_{n}\mathrm{cos}\left({\alpha }_{n}x\right)\mathrm{cos}\left({\alpha }_{m}x\right)\\ {\mathrm{I}}_{A}\mathrm{ cos}\left({\alpha }_{n}x\right)\mathrm{cos}\left({\alpha }_{m}x\right)\\ \left[\left\{{\mathrm{I}}_{D}{\alpha }_{n}^{2}+{\mathrm{I}}_{A}\right\}\mathrm{sin}\left({\alpha }_{n}x\right)-{\mathrm{I}}_{Dd}{\alpha }_{n}\mathrm{cos}\left({\alpha }_{n}x\right)\right]\mathrm{sin}\left({\alpha }_{m}x\right)\\ \left[{\mathrm{I}}_{Bd}\mathrm{cos}\left({\alpha }_{n}x\right)-{\mathrm{I}}_{B}{\alpha }_{n}\mathrm{ sin}\left({\alpha }_{n}x\right)\right]\mathrm{sin}\left({\alpha }_{m}x\right)\end{array}\right\}dx .$$

(47)

Equation (47) represents a polynomial eigenvalue problem in the form

$$\left(\left[{\mathbb{K}}\right]+ \left[{\mathbb{M}}\right]{\upomega }^{2}\right)X=0,$$

(48)

which is numerically solved to obtain the fundamental frequency $\upomega$.

To this end, the integrals in Eqs. (42, 43, 45, 47) are implemented via numerical differential integral quadrature method (DIQM) [133, 134].

4 Model verification

Before performing the parametric study, this section is devoted to the validation and accuracy assessment of the developed nonclassical model and the proposed solution procedure. Since there are no published data for BDFG micro/nanobeams including the simultaneous effects of surface energy and modified couple stress, we compared the present Euler–Bernoulli model results for bending, buckling, and free vibration behaviors with those available in the literature for simply supported micro/nanobeams.

The dimensionless center deflection of a simply supported homogeneous microbeam under a uniformly distributed load is presented in Table 1, based on MCST and compared with references [38, 45]. Table 2 shows the validation of the present model by comparing the dimensionless center deflection based on the classical and integrated modified couple stress–surface energy formulations with the reported results in [114, 125].

Table 1 Comparison of the dimensionless center deflection $\bar{w}=100\left(wEI/(q{L}^{4})\right)$ of a homogeneous microbeam under uniform load based on the MCST analysis ($E=1.44\mathrm{ GPa}$, $\nu =0.38$, h = 88 μm, $L=20h$ and $b=2h$)

Table 2 Comparison of dimensionless center deflection $\left(\bar{w}=w/h\right)$ of homogeneous nanobeam under midpoint load based on classical and integrated couple stress–surface energy analyses ($E=90\mathrm{ GPa}$, $\rho =$ 2700$\text{,} \nu =0\text{.}23$, l = 6.58 μm,${ \lambda }^{s}=3\text{.}4939\mathrm{ N}/\mathrm{m}$, ${\mu }^{s}=-5\text{.}4251\mathrm{ N}/\mathrm{m}$, ${\tau }^{s}=0\text{.}5689\mathrm{ N}/\mathrm{m}$, $L=20h$ and $b=2h$)

To check the accuracy of the present buckling analysis, different numerical examples are solved and compared with the available literatures [60, 135, 136]. A comparison of the critical buckling load of a homogeneous microbeam based on surface energy formulation is provided in Table 3, whereas Table 4 validates the predicted critical buckling load of a BDFG uniform beam based on the classical elasticity theory at various gradient indices. Table 5 compares the present classical dimensionless critical buckling load of AFG tapered beam and that reported by Shahba et al. [135].

Table 3 Comparison of the dimensionless critical buckling load ${\bar{P}}_{cr}={10}^{5}\times {P}_{cr}/\left(E{L}^{2}\right)$ of homogeneous nanobeam based on surface energy formulation ($E=210\mathrm{ GPa}$, $\nu =0.24$, $h=\,5\mathrm{nm}$, $L=10\,h$ and $b=h$)

Table 4 Comparison of the dimensionless critical buckling load ${\bar{P}}_{cr}={P}_{cr}\left({L}^{2}/{E}_{L}I\right)$ for BDFG beam based on classical analysis (${E}_{r}/{E}_{L}=2$ and $L/h=50$)

Table 5 Comparison of the dimensionless critical buckling load ${\bar{P}}_{cr}={P}_{cr}\left({L}^{2}/{E}_{0}I\right)$ for AFG tapered beam based on classical analysis, with $E\left(x\right)={E}_{0}(1+x/L)$

Tables 6, 7, 8 are devoted to comparing the fundamental frequency obtained via the current model and those reported in the previous studies. The fundamental frequency are presented and compared in Tables 6, 7, 8 for, respectively, a homogeneous uniform nanobeam including both effects of the modified couple stress and surface energy, a BDFG uniform microbeam based on modified couple stress theory, and an AFG tapered beam based on the classical model. It can be noticed from the comparisons in Tables 1, 2, 3, 4, 5, 6, 7, 8 that the obtained results from the newly developed model and solution procedure are in a good accordance with those in the literature.

Table 6 Comparison of fundamental frequency (MHz) for homogeneous nanobeam based on classical and integrated couple stress–surface energy analyses ($E=90\mathrm{ GPa}$,$\rho =$ 2700$\text{,} \nu =0\text{.}23$, l = 6.58 μm,${\lambda }^{s}=3\text{.}4939\mathrm{ N}/\mathrm{m}$,${\mu }^{s}=-5\text{.}4251\mathrm{ N}/\mathrm{m}$,${\tau }^{s}=0\text{.}5689\mathrm{ N}/\mathrm{m}$, $L=20h$ and$b=2h$)

Table 7 Comparison of the dimensionless fundamental frequency $\bar{\omega }=\omega \left({L}^{2}\sqrt{{\rho }_{r}/{E}_{r}}/h\right)$ for BDFG uniform microbeam based on the classical and couple stress analysis (${l}_{L}$ = 15 μm, ${l}_{r}=22.5$ μm, $h={l}_{r}$$L=100h,b=h$)

Table 8 Convergence of the dimensionless frequency $\left(\bar{\omega }=\omega {L}^{2}\sqrt{{\rho }_{L}A/{E}_{L}I}\right)$ for AFG tapered beam based on classical analysis, with $E\left(x\right)={E}_{0}\left(1+(x/L)\right)$ and $\rho \left(x\right)={\rho }_{0}\left(1+(x/L)+{(x/L)}^{2}\right)$

5 Parametric study

The newly developed nonclassical modified couple stress–surface energy BDFG model incorporating the effects of physical neutral axis and Poisson’s ratio to investigate the mechanical response of simply supported graded non-uniform micro/nanobeams. The effects of various material properties, i.e., gradient indices in thickness and length directions, dimensionless material length-scale parameter, surface residual stress, surface modulus of elasticity, and geometrical parameters, i.e., aspect ratio and taperness ratios, on the mechanics of BDFG tapered simply supported nanobeams are investigated in detail.

In the forthcoming parametric studies, the BDFG beam shown in Fig. 1, is made from aluminum (Al) and silicon (Si) as metallic and ceramic constituent materials, respectively, with the material properties given in Table 9 [105, 109, 114]. The values of geometrical parameters are as follows: thickness $h\left(x\right)={h}_{0}\left(1-{\beta }_{h}x/L\right)$, width $b\left(x\right)={b}_{0}\left(1-{\beta }_{b}x/L\right)$, in which ${h}_{0}=h\left(0\right)$ and ${b}_{0}=b\left(0\right)$ with ${b}_{0}={h}_{0}$, taperness parameters are ${-1\le \beta }_{h}, {\beta }_{b}<1$, and aspect ratio $L/{h}_{0}$=25, unless specifying other material or geometrical parameters. However, due to the lack of experimental data for the material length-scale parameter for silicon (${l}_{\mathrm{Si}}$) or bi-directionally functionally graded materials $l(x,z)$ in the open literature, a range of $h/l$ can be supposed to investigate the effect of the material length-scale parameter on the response of microscale structures [37]. In this study, we avoided the problem of the unknown material length-scale parameter of silicon ${l}_{\mathrm{Si}}$ by assuming ${l}_{\mathrm{Si}}$ as a ratio of that of aluminum ${l}_{\mathrm{AL}}$, [47, 91, 92, 129]. The material length-scale parameter-to-thickness ratio is taken as ${l}_{l}=0.5h$ and ${l}_{r}=(4/3){l}_{l}$, unless other values are mentioned.

Table 9 Material properties of the constituents of BDFG nanobeam

The size-dependent static and dynamic responses of the BDFG nanobeam are explored using different formulations; “CL” which is based on the classical elasticity theory, “SE” incorporating effect of surface energy only ($l=0$), “CS” which is based on the modified couple stress theory, and fully integrated model “CSSER” which is based on the modified couple stress and surface elasticity theories. The predicted results are presented as figures and tables to serve as benchmarks for future analyses of nonuniform BDFG micro/nanobeams. For convenience, the results are presented in terms of the following dimensionless deflection, critical buckling load, and fundamental frequency, respectively:

$$ \bar{w}\left( x \right) = 100\frac{{E_{r} ~I}}{{qL^{4} ~}}w\left( x \right),~~~~~~~\bar{P}_{{cr}} = \frac{{E_{r} L^{2} }}{I}P_{{cr}} ~~~~~{\text{and}}~~~~~\bar{\omega } = \omega \sqrt {\frac{{\rho _{r} A}}{{E_{r} I}}} L^{2} $$

(49)

where ${E}_{r}$ and ${\rho }_{r}$ are, respectively, the Young’s modulus and mass density of the bulk material at the upper right corner of the beam (metallic phase) and $I$ is the second moment of area about the $y$-axis.

5.1 Effect of the taperness parameters

The effect of the rates of cross-section changes along thickness and width directions, ${\beta }_{h}$ and ${\beta }_{b}$, respectively, on the bending, buckling, and vibration responses of BDFG is investigated using classical (CL) and nonclassical (CSSER) analyses. The dimensionless deflection throughout the beam length shows asymmetric curve as shown in Fig. 2, which is attributed to the tapering effect as well as the material gradation in the axial direction. The predicted deflection with positive values of ${\beta }_{h}$ and ${\beta }_{b}$ is much higher than that with negative values, which can be explained in view of Fig. 3. It is depicted from Fig. 3 that the equivalent stiffness ${\mathcal{D}}_{11}\left(x\right)$, defined in Eq. (33), of the nanobeam becomes higher when ${\beta }_{h}$ and ${\beta }_{b}$ are negative. Such asymmetric distribution of the equivalent stiffness through beam length leads to asymmetric deflection.

Fig. 2

The effect of the taperness parameters β_ℎ and β_b on the dimensionless deflection along the length of BDFG nanobeam at k_x = k_z = 1

Fig. 3

Variation of the equivalent stiffness D₁₁(x) (Eq. (33)) along the length of BDFG nanobeam at different taperness parameters and k_x = k_z = 1

Figures 4, 5, 6 demonstrate the simultaneous effects of varying the taperness parameters ${\beta }_{b}$ and ${\beta }_{h}$ on the dimensionless maximum deflection, critical buckling load, and fundamental frequency, respectively, for BDFG nanobeams at ${k}_{x}={k}_{z}=1$. Some numerical values of the dimensionless maximum deflection, critical buckling load, and fundamental frequency are tabulated in Tables 10, 11, 12 at different values of ${\beta }_{b}$ and ${\beta }_{h}$ and different gradation schemes; AFG, TFG, and BDFG. Generally, it is notable that increasing the taperness parameter ${\beta }_{h}$ and/or ${\beta }_{b}$ from negative to positive values significantly increases the dimensionless maximum deflection and decreases the dimensionless critical buckling load and the dimensionless fundamental frequency. For both the static and vibration responses, the influence of varying the thickness parameter ${\beta }_{h}$ is significantly greater than that of the width parameter ${\beta }_{b}$, especially with the classical formulation. As ${\beta }_{h}$ changes from negative to positive values, the influence of ${\beta }_{b}$ rises and vice versa. Generally, the influence of changing the rates of cross section in classical analysis is higher than that for the nonclassical one for all gradation distributions. The mutual contribution of the nonclassical parameters, i.e., material length-scale parameter and surface properties, on the static and vibration responses is greatly increased by increasing ${\beta }_{h}$ and slightly affected by increasing ${\beta }_{b}$. In addition, it is important to emphasize that the maximum impact of the taperness parameters is associated with the deflection response, followed with the buckling, and vibration responses. For both the classical and nonclassical formulations, the highest and lowest effects of the taperness parameters are associated with AFG and homogeneous nanobeams, respectively. The taperness parameters ${\beta }_{h}$ and ${\beta }_{b}$ have the same effect on the classical response of homogeneous and TFG nanobeams. Furthermore, for the same taperness ratio and material gradation, the predicted deflection based on the nonclassical formulation is lower than that predicted using classical elasticity theory, whereas the predicted nonclassical critical load and fundamental frequency are distinctly higher than their corresponding classical values.

Fig. 4

The effect of the taperness parameters on the dimensionless maximum deflection of BDFG nanobeam at k_x = k_z = 1

Fig. 5

The effect of the taperness parameters on the dimensionless critical buckling load of BDFG nanobeam at k_x = k_z = 1

Fig. 6

The effect of the taperness parameters on the dimensionless fundamental frequency of BDFG nanobeam at k_x = k_z = 1

Table 10 Dimensionless maximum deflection of FG nanobeam at different values of taperness parameters and gradient indices

Table 11 Dimensionless critical buckling load of FG nanobeam at different values of taperness parameters and gradient indices

Table 12 Dimensionless fundamental frequency of FG nanobeam at different values of taperness parameters and gradient indices

5.2 Effect of the material gradation

The effect of bi-directional gradient indices along thickness and length directions, ${k}_{z}$ and ${k}_{x}$, respectively, on the response of BDFG nanobeams is investigated, considering both uniform and tapered cross sections. The dimensionless deflection versus the beam length is shown in Fig. 7 at different gradient indices. It is seen that the axial gradient index ${k}_{x}$ as well as the nonuniform cross section can tend the deflection of BDFG nanobeam to asymmetric curves for both classical and nonclassical analyses. Uniform and nonclassical nanobeams give lower dimensionless deflection along the beam length compared with tapered and classical nanobeams, respectively. It is important to emphasize that a homogeneous nanobeam with ${k}_{x}$=${k}_{z}$=0 is made from pure metal constituent and therefore has the smallest stiffness. The variations of the dimensionless maximum deflection, dimensionless critical buckling load, and dimensionless fundamental frequency are plotted in Figs. 8, 9, 10, respectively, and are recorded in Tables 13, 14, 15 versus the gradation indices ${k}_{x}$ and ${k}_{z}$ at different taperness parameters (${\beta }_{b}$=${\beta }_{h}$ = $\beta$). For the considered material properties, it is noticed that inclusion of the microstructure and surface energy effects leads to increasing the beam rigidity. Therefore, the predicted dimensionless deflection using CSSER formulation is always lower than that predicted using CL one, whereas the obtained dimensionless critical buckling load and the dimensionless fundamental frequency based on CSSER are larger than those obtained using CL analysis. Such behavior is observed for all values of the gradient indices and taperness parameters.

Fig. 7

The effect of the gradient indices k_x and k_z on the dimensionless deflection along the length of FG nanobeams with uniform and tapered cross-sections

Fig. 8

The effect of the gradient indices k_x and k_z on the dimensionless maximum deflection of BDFG nanobeam at different taperness parameters

Fig. 9

The effect of the gradient indices k_x and k_z on the dimensionless critical buckling load of BDFG nanobeam at different taperness parameters

Fig. 10

The effect of the gradient indices k_x and k_z on the dimensionless fundamental frequency of BDFG nanobeam at different taperness parameters

Table 13 Dimensionless maximum deflection of BDFG nanobeam at different gradient indices and taperness parameters ${\beta }_{b}$ and ${\beta }_{h}$

Table 14 Dimensionless critical buckling load of BDFG tapered nanobeam at different gradient indices and taperness parameters ${\beta }_{b}$ and ${\beta }_{h}$

Table 15 Dimensionless fundamental frequency of BDFG tapered nanobeam at different gradient indices and taperness parameters ${\beta }_{b}$ and ${\beta }_{h}$

Also, the obtained results reveal that due to the increase in the stiffness of the nanobeam, increasing ${k}_{z}$ and/or ${k}_{x}$ decreases the maximum deflection and increases the dimensionless critical buckling load, and the dimensionless natural frequencies. Further increasing of the gradient indices (almost more than 5), the response converges towards the pure ceramic behavior. The influence of the gradation indices is reduced by incorporating the nonclassical effect and/or nonuniform cross section. Considering BDFG nanobeams, it is notable that the effect of varying ${k}_{z}$ decreases as ${k}_{x}$ increases and being very small as ${k}_{x}$ approach 10. Also, the influence of ${k}_{x}$ is decreased with increasing ${k}_{z}$. Using classical analysis, varying (${k}_{x}$,${k}_{z}$) from (0,0) to (2,2) decreases the dimensionless maximum deflection by 54.6% ($\beta$=0) and 53.2% ($\beta$=0.5), increases the dimensionless critical buckling load by 119.9% ($\beta$=0) and 109.6% ($\beta$=0.5), and increases the dimensionless frequency by 58.5% ($\beta$=0) and 27.2% ($\beta$=0.5). Introducing the nonclassical microstructure and surface energy effects reduces the impact of the gradient indices, i.e., based on CSSER formulation, varying (${k}_{x}$,${k}_{z}$) from (0,0) to (2,2) decreases the dimensionless maximum deflection by 29.3% ($\beta$=0) and 21.7% ($\beta$=0.5), increases the dimensionless critical buckling load by 41.4% ($\beta$=0) and 27.2% ($\beta$=0.5), and increases the dimensionless frequency by 29.6% ($\beta$=0) and 24.3% ($\beta$=0.5). Therefore, ignoring the nonclassical effects leads to a significant error in the predicted static and vibration responses of BDFG micro/nanobeams.

For AFG nanobeams (${k}_{z}=0$), increasing ${k}_{x}$ has a more significant influence on the static and dynamic responses for classical and uniform nanobeams compared with nonclassical and tapered nanobeams, respectively. As ${k}_{x}$ increases from 0 to 2, the dimensionless maximum deflection decreases by 48.7% ($\beta$=0) and 43.9% ($\beta$=0.5) using CL analysis and by 26% ($\beta$=0) and 18.8% ($\beta$=0.5) using CSSER analysis. Whereas, increasing ${k}_{x}$ from 0 to 2, shows an increase in the dimensionless critical buckling load by 93% ($\beta$=0) and 69% ($\beta$=0.5) for CL formulation and by 34.7% ($\beta$=0) and 21.6% ($\beta$=0.5) for CSSER formulation. Rising ${k}_{x}$ of AFG nanobeam from 0 to 2 leads to an increase in the dimensionless fundamental frequency by about 47% ($\beta$=0) and 42% ($\beta$=0.5) based on CL analysis and by 24.4% ($\beta$=0) and 19.9% ($\beta$=0.5) based on CSSER analysis. Again, the highest impact of ${k}_{x}$ is associated with the buckling response. Regarding TFG nanobeams (${k}_{x}=0$), it is depicted that the impact of varying ${k}_{z}$ on the bending, buckling, and vibration responses is independent of the taperness parameters when the classical formulation is employed, i.e. With the rise of ${k}_{z}$ from 0 to 2 based on CL analysis, the dimensionless maximum deflection is reduced by 42.5% and the dimensionless buckling load and dimensionless fundamental frequency are increased by 73.9% and 38.3%, respectively. On the contrary, the effect of ${k}_{z}$ on the nonclassical responses of TFG nanobeam becomes more pronounced with uniform cross section, i.e., as ${k}_{z}$ changes from 0 to 2 based on CSSER analysis, the dimensionless maximum deflection is decreased by 22.3% ($\beta$=0) and 16.9% ($\beta$=0.5) and the dimensionless buckling load and dimensionless fundamental frequency are raised by, respectively, 28.7% and 20.4% ($\beta$=0) and 17% ($\beta$=0.5).

In addition, it is observed that the taperness parameters have a significant influence on the role of ${k}_{x}$ in AFG and have no influence on the role of ${k}_{z}$ in TFG nanobeams. Furthermore, as the gradation indices rise for all the gradation distributions, the impact of the taperness parameters greatly decreases for the classical analysis and slightly increases for the nonclassical analysis.

5.3 Effect of the surface energy

This study is the first attempt to model and investigate the response of BDFG nanobeams in the presence of surface energy. In this section, the effect of the surface residual stress ${\tau }^{s}(x,z)$ and surface elasticity modulus ${E}^{s}(x,z)$, on the static and vibration responses of simply supported nanobeams is explored, considering different gradation schemes. For this purpose, the material properties of bulk continuum and surface layers provided in Table 9 are used, while the microstructure effect is ignored, i.e., ${l}_{l}$=${l}_{r}$=0. The nanobeam dimensions are ${b}_{0}={h}_{0}=5{\text{nm}}$ with equal thickness and width taperness parameters, i.e., $\beta$=${\beta }_{h}$=${\beta }_{b}$. The effect of the surface residual stress ${\tau }_{r}^{s}$ (metallic phase) and ${\tau }_{l}^{s}$ (ceramic phase) of the surface layers on the dimensionless maximum deflection, dimensionless critical buckling load, and dimensionless fundamental frequency is depicted in Figs. 11, 12, 13, respectively, for both uniform and tapered BDFG nanobeams and $L/{h}_{0}$=25 and 50. The reference values are those given in Table 9 (${\tau }_{r0}^{s}$=0.5689 N/m, ${\tau }_{l0}^{s}$=0.6056 N/m). Tables 16, 17, 18 provide, respectively, the dimensionless maximum deflection, dimensionless critical buckling load, and dimensionless fundamental frequency at different values of the residual surface stress, length-to-thickness ratio, and taperness parameters for AFG, TFG, and BDFG nanobeams.

Fig. 11

The effect of the surface residual stress ratios $\tau_{l}^{s}$/$\tau_{l0}^{s}$ and $\tau_{r}^{s}$/$\tau_{r0}^{s}$ on the dimensionless maximum deflection of BDFG nanobeam with k_x = k_z = 1

Fig. 12

The effect of the surface residual stress ratios $\tau_{l}^{s}$/$\tau_{l0}^{s}$ and $\tau_{r}^{s}$/$\tau_{r0}^{s}$ on the dimensionless critical buckling load of BDFG nanobeam with k_x = k_z = 1

Fig. 13

The effect of the surface residual stress ratios $\tau_{l}^{s}$/$\tau_{l0}^{s}$ and $\tau_{r}^{s}$/$\tau_{r0}^{s}$ on the dimensionless fundamental frequency of BDFG nanobeam with k_x = k_z = 1

Table 16 Dimensionless maximum deflection of uniform and tapered FG nanobeams at different surface residual stresses, aspect ratios, and gradation indices (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 17 Dimensionless critical buckling load of uniform and tapered FG nanobeams at different surface residual stresses, aspect ratios, and gradation indices (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 18 Dimensionless fundamental frequency of uniform and tapered FG nanobeams at different surface residual stresses ${\tau }_{r}^{s}$ and ${\tau }_{l}^{s}$ and aspect ratios $L/h$ (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

For the material properties under consideration, it is noticeable that increasing the surface residual stress of the metallic (${\tau }_{r}^{s}$) and/or ceramic (${\tau }_{l}^{s}$) constituent materials significantly decreases the dimensionless deflection and increases both the dimensionless critical buckling load and dimensionless fundamental frequency for all the gradation distributions. Accounting for the residual surface effect induces tension stress in the surface layers, and hence, stiffer surface results in lower deflections. The influence of the surface residual stresses ${\tau }_{r}^{s}$ and ${\tau }_{l}^{s}$ becomes more prominent with the increase of the aspect ratio ($L/h$) and may lead to an increase or a decrease in the equivalent stiffness of nanobeam depending on its material properties. For AFG, TFG, and BDFG nanobeams, rising the residual surface stress ${\tau }_{l}^{s}$ reduces the contribution of ${\tau }_{r}^{s}$, and vice versa. It is also depicted that the highest effects of ${\tau }_{l}^{s}$ and ${\tau }_{r}^{s}$ correspond to BDFG and TFG distributions, respectively. On the other hand, the lowest effects of ${\tau }_{l}^{s}$ and ${\tau }_{r}^{s}$ are associated with, respectively, AFG and BDFG distributions. In other words, the effect of varying the surface residual stress is mainly controlled with the directions of gradation and the geometrical parameters of the beam. Increasing the aspect ratio noticeably rises the effect of surface residual stress on the static and vibration responses, which is attributed to the increase of the surface area-to-bulk volume ratio, and therefore, an increase in surface energy. It is also worth noting that, the impact of the surface residual stress and aspect ratio on the response of tapered nanobeams is much greater than that of uniform nanobeams.

The effect of surface elasticity moduli ${E}_{r}^{s}$ and ${E}_{l}^{s}$ of the metallic and ceramic phases, respectively, of the surface layers is illustrated in Figs. 14, 15, 16 and Tables 19, 20, 21 at different aspect ratios, taperness parameters, and material gradations. The reference values ${E}_{r0}^{s}$ and ${E}_{l0}^{s}$ are taken − 7.3563 N/m and − 10.0497 N/m, respectively, as given in Table 9. It is found that the dimensionless maximum deflection for both uniform and tapered nanobeams is slightly increased by increasing ${E}_{r}^{s}$ and ${E}_{l}^{s}$ individually or simultaneously, whereas the both dimensionless critical buckling load and dimensionless fundamental frequency are decreased. It is observed that the effect of the surface elasticity moduli on the static and vibration responses is reduced with increasing the aspect ratio and taperness parameters. Unlike the surface residual stress, the contribution of ${E}_{r}^{s}$ or ${E}_{l}^{s}$ is almost unaffected by varying ${E}_{l}^{s}$ or ${E}_{r}^{s}$, respectively. Compared with surface residual stress, the bending, buckling, and vibration responses have less sensitivity to surface elasticity modulus.

Fig. 14

The effect of the surface elasticity moduli $E_{l}^{s}$/$E_{l0}^{s}$ and $E_{r}^{s}$/$E_{r0}^{s}$ on the dimensionless maximum deflection of BDFG nanobeam with k_x = k_z = 1

Fig. 15

The effect of the surface elasticity moduli $E_{l}^{s}$/$E_{l0}^{s}$ and $E_{r}^{s}$/$E_{r0}^{s}$ on the dimensionless critical buckling load of BDFG nanobeam with k_x = k_z = 1

Fig. 16

The effect of the surface elasticity moduli $E_{l}^{s}$/$E_{l0}^{s}$ and $E_{r}^{s}$/$E_{r0}^{s}$ on the dimensionless fundamental frequency of BDFG nanobeam with k_x = k_z = 1

Table 19 Dimensionless maximum deflection of uniform and tapered FG nanobeams at different surface elasticity moduli, aspect ratios, and gradation indices (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 20 Dimensionless critical buckling load of uniform and tapered FG nanobeams at different surface elasticity moduli, aspect ratios, and gradation indices (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 21 Dimensionless fundamental frequency of uniform and tapered FG nanobeams at different surface elasticity moduli, aspect ratios, and gradation indices (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

5.4 Effect of the material length-scale parameter

Effect of microstructure effect via MCST on the mechanics of tapered BDFG micro/nanobeams is explored by considering different values of the dimensionless material length-scale parameter (${l}_{r}/h$) and material length-scale parameter ratio (${l}_{l}/{l}_{r}$) for various width and thickness taperness ratios and material gradations. When a constant material length-scale parameter is considered, the ratio ${l}_{l}/{l}_{r}$ is set to unity. To extract a clear investigation of the effect of the material length-scale parameter, the present results are based on the MCST formulation using the material properties in Table 9 with ${l}_{r}=6.58$ μm. In Figs. 17, 18, 19, the dimensionless values of the maximum deflection, critical buckling load, and the fundamental frequency are plotted versus ${l}_{r}/h$ and ${l}_{l}/{l}_{r}$ for uniform and tapered BDFG microbeams with ${k}_{x}={k}_{z}=1$. The mutual effects of ${l}_{r}/h$ and ${l}_{l}/{l}_{r}$ on the microbeam response are recorded in Tables 22, 23, 24, for different gradient indices ${k}_{x}$ and ${k}_{z}$ and taperness ratios ($\beta$=${\beta }_{h}$=${\beta }_{b}$). Based on the obtained results, it is noticeable that introducing the microstructure effect enhances the microbeam rigidity, and consequently, decreases the dimensionless deflection and increases the dimensionless critical buckling load and dimensionless frequency.

Fig. 17

The mutual effect of the dimensionless material length scale parameter (l_r⁄ℎ) and material length scale parameter ratio (l_l⁄l_r) on the dimensionless maximum deflection of BDFG microbeam with k_x = k_z = 1

Fig. 18

The mutual effect of the dimensionless material length scale parameter (l_r⁄ℎ) and material length scale parameter ratio (l_l⁄l_r) on the dimensionless critical buckling load of BDFG microbeam with k_x = k_z = 1

Fig. 19

The mutual effect of the dimensionless material length scale parameter (l_r⁄ℎ) and material length scale parameter ratio (l_l⁄l_r) on the dimensionless fundamental frequency of BDFG microbeam with k_x = k_z = 1

Table 22 Dimensionless maximum deflection of FG nanobeam at different dimensionless material length-scale parameters (${l}_{r}/h$), material length-scale parameter ratios (${l}_{l}/{l}_{r}$), gradation indices, and taperness parameters (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 23 Dimensionless critical buckling load of FG nanobeams at different dimensionless material length-scale parameters (${l}_{r}/h$), material length-scale parameter ratios (${l}_{l}/{l}_{r}$), gradation indices, and taperness parameters (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

Table 24 Dimensionless fundamental frequency of FG nanobeams at different dimensionless material length-scale parameters (${l}_{r}/h$), material length-scale parameter ratios (${l}_{l}/{l}_{r}$), gradation indices, and taperness parameters (${\beta }_{h}$=${\beta }_{b}$=$\beta$)

It is noticeable that as the dimensionless material length-scale parameter (${l}_{r}/h$) increases, the impact of microstructure on the static and vibration responses is distinctly enhanced for all material gradations. For a homogeneous microbeam, there is no effect of the material length-scale parameter by varying ${l}_{r}/h$ and ${l}_{l}/{l}_{r}$ on the dimensionless values of deflection, critical buckling load, and frequency. It is revealed that the impact of ${l}_{r}/h$ rises as ${l}_{l}/{l}_{r}$ increases and the maximum effect of ${l}_{r}/h$ for different gradation distributions depends mainly on the value of ${l}_{l}/{l}_{r}$, i.e., the maximum effect of ${l}_{r}/h$ corresponds to AFG when ${l}_{l}/{l}_{r}$<1 and to BDFG when ${l}_{l}/{l}_{r}\ge$ 1. Also, the predicted responses using a spatially constant material length-scale parameter (${l}_{l}$=${l}_{r}$) are significantly different from those by the spatial-dependent material length-scale parameter (${l}_{l}\ne {l}_{r}$). For a uniform microbeam with ${l}_{r}/h$=0.5, altering the material length-scale parameter ratio ${l}_{l}/{l}_{r}$ from 0.5 to 2, the dimensionless maximum deflection decreases by 49.5, 58.0, and 66.9%, the dimensionless critical buckling load increases by 93.0, 138.2, and 200.9%, and dimensionless frequency increases by 40.5, 54.3, and 73.7% for AFG, TFG, and BDFG distributions, respectively. Therefore, assumption of a constant material length-scale parameter for graded microbeams is unacceptable and leads to distinct error in the predicted response. Also, it is depicted that response of BDFG microbeam is the most sensitive to ${l}_{l}/{l}_{r}$, followed with TFG and AFG. The effect of ${l}_{l}/{l}_{r}$ is enhanced by increasing ${l}_{r}/h$ or taperness parameters towards positive values. The obtained results agree well with those in the previous sections, as rising the taperness parameters, while holding ${l}_{l}/{l}_{r}$ and ${l}_{r}/h$ fixed, leads to a noticeable decrease in the microbeam deflection and an increase in the dimensionless critical buckling load and dimensionless frequency.

5.5 Influence of the slenderness ratio

The effect of the slenderness ratio ($L/h$) on the dimensionless deflection, buckling and frequency of BDFG nanobeam with $h$=15 nm is illustrated in Figs. 20, 21, 22, employing classical “CL” and nonclassical “NC”, i.e., CS, SE, and CSSER, theories. In this section, the results are obtained for FG nanobeams with the material properties provided in Table 9 and the material length-scale parameters are ${l}_{l}$= 10 nm and ${l}_{r}/{l}_{l}$= 3/4. For convenience and better understanding of the effect of slenderness ratio and thickness on the role of nonclassical parameters, the predicted dimensionless maximum deflection, critical buckling load, and free vibration frequency using nonclassical theories are normalized with their corresponding values using the classical theory, i.e., ${\bar{w}}^{N}={\bar{w}}^{NC}/{\bar{w}}^{CL},$ ${\bar{P}}_{cr}^{N}={\bar{P}}_{cr}^{NC}/{\bar{P}}_{cr}^{CL}, {\text{and}} {\bar{\omega }}^{N}={\bar{\omega }}^{NC}/{\bar{\omega }}^{CL}$, respectively. Based on the three different nonclassical theories, Tables 25, 26, 27 record the dimensionless maximum deflection, critical buckling load, and fundamental frequency ratios (${\bar{w}}^{N}, {\bar{P}}_{cr}^{N},$ and ${\bar{\omega }}^{N}$), at various values of the slenderness ratio and thickness, considering different material gradations of both uniform and tapered nanobeams. From these results, it is revealed that for a fixed value of the beam thickness, the ratios ${\bar{w}}^{N}$, ${\bar{P}}_{cr}^{N}$, and ${\bar{\omega }}^{N}$ predicted using the MCST theory are unchanged by varying the slenderness ratio. Employing the SE and CSSE theories and with the increase of $L/h$, the predicted dimensionless maximum deflection ratio decreases, whereas the predicted dimensionless critical buckling load and dimensionless frequency ratios increase. This effect of $L/h$ is observed for different taperness parameters, thicknesses, and material gradations. For the studied ranges of $L/h$ and $h$, the CSSER theory provides the maximum stiffening effect in comparison with CS and SE theories. For low values of $L/h$, the microstructure effect is greater than the surface energy effect. With the increase of $L/h$, the contribution of surface energy rises and the predicted results from SE theory become greater than those from CS theory. For different material gradations, with increasing the beam thickness or varying the taperness from positive to negative values, the effect of the slenderness ratio reduces. Increasing the beam thickness decreases the influence of both the material length-scale parameter and surface energy on the static and vibration behaviors of nanobeams. The effect of the beam thickness on the beam response becomes more pronounced with increasing the slenderness ratio. Amongst the gradation distributions, AFG nanobeam shows the highest sensitivity to the slenderness ratio and thickness.

Fig. 20

Variation of the dimensionless maximum deflection ratio ($\overline{w}N$) with the slenderness ratio (L/ℎ) of BDFG nanobeam using SE, CS, and CSSER theories (ℎ = 15 nm and k_x = k_z = 1.0)

Fig. 21

Variation of the dimensionless critical buckling load ratio ($\overline{P}_{cr}^{N}$) with the slenderness ratio (L/ℎ) of BDFG nanobeam using SE, CS, and CSSER theories (ℎ = 15 nm and k_x = k_z = 1.0)

Fig. 22

Variation of the dimensionless natural frequency ratio ($\overline{\omega }N$) with the slenderness ratio (L/ℎ) of BDFG nanobeam using SE, CS, and CSSER theories (ℎ = 15 nm and k_x = k_z = 1.0)

Table 25 Dimensionless maximum deflection ratio (${\bar{w}}^{N}$) of uniform and tapered FG nanobeams at different values of the slenderness ratio and thickness employing various nonclassical theories

Table 26 Dimensionless critical buckling load ratio (${\bar{P}}_{cr}^{N}$) of uniform and tapered FG nanobeams at different values of the slenderness ratio and thickness, employing various nonclassical theories

Table 27 Dimensionless fundamental frequency ratio (${\bar{\omega }}^{N}$) of uniform and tapered FG nanobeams at different values of the slenderness ratio and thickness, employing various nonclassical theories

6 Conclusion

In this study, a nonclassical integrated modified couple stress–surface elasticity model is developed to explore the size-dependent static bending, buckling, and free vibration responses of BDFG tapered micro/nanobeams, for the first time. All the material properties describing the bulk and surface continuums, including the material length-scale parameter and surface parameters, are assumed to vary along the thickness and length directions according to power-law distribution. The governing equations and boundary conditions of the proposed Euler–Bernoulli nanobeam are exactly derived using Hamilton principle on the basis of the modified couple stress theory and Gurtin–Murdoch surface elasticity theory. Accounting for the physical neutral surface concept, a semi-analytical solution for the static deflection, critical buckling load, and natural frequency of simply supported BDFG tapered nanobeam are derived using the Navier’s method combined with the GDQM. An extensive detailed study on the effect of different characteristic material and geometrical parameters on the static and vibration responses is presented. The main results of this study are summarized as follows:

• Both the microstructure via the MCST and surface residual stress have distinct influences in stiffness-hardening of FG nanobeams, and thus, the static deflection decreases and both the critical buckling load and fundamental frequency increase. In contrast, the surface elastic modulus has a softening effect leading to higher deflection and lower critical buckling load and vibration frequency.

• As the cross section of the nanobeam along the length direction decreases, i.e. (${\beta }_{b}$, ${\beta }_{h}$) changes from (0, 0) to (0.5, 0.5), the predicted deflection increases; whereas, both the critical buckling load and vibration frequency decrease, for all gradation distributions. On the contrary, changing (${\beta }_{b}$, ${\beta }_{h}$) from (0, 0) to (− 0.5, − 0.5) has an opposite effect. The effect of ${\beta }_{b}$ and ${\beta }_{h}$ becomes more pronounced for AFG nanobeams. Employing the CSSE formulation significantly reduces the influence effect of ${\beta }_{h}$, while that of ${\beta }_{b}$ may increase or decrease depending on the gradation distribution. As ${\beta }_{b}$ increases towards positive values, the impact of ${\beta }_{h}$ increases and vice versa.

• Increasing the surface residual stress of the ceramic (${\tau }_{l}^{s}$) and/or metallic (${\tau }_{r}^{s}$) phases shows a distinct reduction in the dimensionless bending deflection and a noticeable increase in the dimensionless critical buckling load and vibration frequency, for all gradation distributions. The buckling response is more sensitive to the surface residual stress than the vibration and bending responses. The highest impact of ${\tau }_{l}^{s}$ and ${\tau }_{r}^{s}$ are, respectively, corresponding to BDFG and TFG nanobeams. Also, the impact of ${\tau }_{l}^{s}$ is reduced as ${\tau }_{r}^{s}$ increases and the opposite is true.

• The surface elasticity moduli ${E}_{l}^{s}$ and ${E}_{r}^{s}$ with negative values slightly enhances the stiffness-softening behavior of FG nanobeams, and accordingly, the dimensionless bending deflection increases and the dimensionless critical buckling load and vibration frequency decrease. BDFG and TFG nanobeams give the highest effect of the surface elasticity moduli ${E}_{l}^{s}$ and ${E}_{r}^{s}$, respectively. It can be concluded that the effect of surface elasticity moduli is very small compared with that of the surface residual stress.

• Increasing the material length-scale parameter-to-thickness ratio (${l}_{r}/h$) and/or the material length-scale parameter ratio (${l}_{r}/{l}_{l}$) improves the stiffness-hardening effect of the microbeam compared with the classical beam model. Compared to the uniform microbeam, the effects of both ${l}_{r}/h$ and ${l}_{r}/{l}_{l}$ increase with positive taperness parameters. The roles of ${l}_{r}/h$ and ${l}_{r}/{l}_{l}$ are significantly influenced by the gradation distribution as the maximum effect of ${l}_{r}/{l}_{l}$ is obtained for BDFG microbeams, followed by TFG and AFG.

• The gradation indices ${k}_{z}$ and ${k}_{x}$ have a significant effect on the response of BDFG tapered micro/nanobeams. Increasing ${k}_{z}$ and/or ${k}_{x}$ increases the stiffness-hardening of the beam and accordingly, the deflection decreases, whereas the critical buckling load and free vibration frequency increase. Both the nonclassical formulation and positive taperness parameters noticeably reduces the effect of ${k}_{z}$ and ${k}_{x}$. Also, the influence of the gradient indices on the bending response is much greater than that on the buckling and vibration responses.

• Increasing the aspect ratio enhances the influence surface energy, whereas the microstructure effect is unchanged. With the increase of aspect ratio, the influences of the surface residual stress increases; whereas, the influence of ${E}_{l}^{s}$ and ${E}_{r}^{s}$ significantly decreases. The impact of the aspect ratio is reduced by increasing the beam thickness or varying the taperness parameters from positive to negative values.

The present results could be helpful in reaching the desired static and free vibration responses of micro/nanobeam. As the beam response can be controlled by appropriate engaging of the gradient indices in thickness and/or length directions and proper selection of the cross section.