Comprehensive investigation of vibration of sigmoid and power law FG nanobeams based on surface elasticity and modified couple stress theories

Abstract

Based on the modified couple stress theory and Gurtin–Murdoch surface elasticity theory, a size-dependent Timoshenko beam model is developed for investigating the nonlinear vibration response of functionally graded (FG) micro-/nanobeams. The model is capable of capturing the simultaneous effects of microstructure couple stress, surface energy, and von Kármán’s geometric nonlinearity. Sigmoid function and power law homogenization schemes are used to model the material gradation of the beam. Hamilton’s principle is exploited to establish the nonclassical nonlinear governing equations and corresponding higher-order boundary conditions. To account for the nonhomogeneity in boundary conditions, the solution of the problem is split into two parts: the nonlinear static response with the nonhomogeneous boundary conditions and the nonlinear dynamic response. The resulting boundary conditions for the dynamic response are homogeneous, and so Galerkin’s approach is applied to reduce the set of PDEs to a nonlinear system of ODEs. The generalized differential quadrature method in terms of spatial variables is applied to obtain the static response and linear vibration mode. Considering the nonlinear system of ODEs in terms of time-related variables, both pseudo-arclength continuation and Runge–Kutta methods are used to obtain the nonlinear free vibration behavior of FG Timoshenko micro-/nanobeams with simply supported and clamped ends. Verification of the proposed model and solution procedure is performed by comparing the obtained results with those available in the open literature. The effects of the nonhomogeneous boundary conditions, surface elasticity modulus, surface residual stress, material length scale parameter, gradient index, and thickness on the characteristics of linear and nonlinear free vibrations of sigmoid function and power law FG micro-/nanobeams are discussed in detail.

1 Introduction

Functionally graded materials (FGMs) are an advanced generation of composite materials fabricated by varying the volume fractions of the constituents along a specific spatial direction, usually over the thickness of a structure. The gradation of material composition can create a nonhomogeneous composite with continuous and smooth properties. Thus, the FGMs have some striking advantages over traditional composite structures such as bearing high temperature gradients, reducing thermal and residual stresses, and eliminating the concentration of stress that occurred in conventional laminated composites [1]. Nowadays, with the development of the material technology, FGMs have been employed in micro-/nanoelectromechanical systems (MEMS/NEMS) such as atomic force microscopes, thin films in the form of shape memory alloys and micro-sensors [2,3,4]. However, the size effect plays a major role in the mechanical behavior of such small-scale structures, and consequently, an accurate mathematical model of FGM structures is a key issue for successful analysis and design of MEMs/NEMs. The effective mechanical properties of the FGMs can be obtained using different homogenization techniques such as exponential, power law, Mori–Tanaka, symmetric power law, and sigmoid function.

At the micro-/nanoscale, the classical continuum mechanics theories cannot correctly predict the experimentally detected size-dependent behavior of structures. To capture this behavior, more general higher-order continuum mechanics theories have been applied, which include strain gradient or couple stress theories that contain additional material constants beside the classical Lamé constants. In the modified couple stress theory (MCST), the stress tensor is symmetric, and only one material length scale parameter is involved to describe the microstructure-dependent size effect, which makes the MCST easier to use than the other higher-order continuum mechanics theories. Since then, the MCST has been widespread applied to investigate the mechanical behavior of micro-/nanoscale structures by researchers [5,6,7,8,9,10,11,12,13,14]. According to these microstructure–dependent models, the couple stress effect leads to an increased stiffness of FG micro-/nanobeams.

In nanoscale structures, there is a significantly increased ratio of surface area to bulk volume, which is considered one of their most important characteristics. In spite of ignoring the surface energy effect in classical mechanics, as it is small compared to the bulk energy, the surface energy should not be neglected due to its significant contribution to the total energy of nanostructures. The presence of surface stress (surface tension) results in nonclassical boundary conditions, which have a significant effect in analyzing the nanostructures. Gurtin and Murdoch [15, 16] presented a surface elasticity model in which the surface energy effect on the elastic behavior of materials is incorporated. Following the Gurtin and Murdoch model, many studies have been developed to model and analyze the effect of size-dependent surface energy on linear/nonlinear bending, buckling, and vibration responses of elastic nanobeams [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36], viscoelastic nanobeams [37, 38], and piezoelectric and cylindrical nanoshells [31, 39,40,41].

Few models have been reported in the literature to investigate the simultaneous effects of couple stress and surface energy on the mechanical behavior of homogeneous nanobeams [22, 23, 42,43,44,45] and nanoplates [46,47,48,49,50,51]. Recently, Attia [20] and Shanab et al. [8] have developed nonclassical continuum models for FG nanobeams considering the combined effects of couple stress and surface energy.

Various approaches exist for solving the governing equations of the nonlinear vibration of nanobeams. Approximate solutions for the nonlinear free and forced vibration of Euler–Bernoulli FG nanobeams were obtained using the multiple scale (MS) method [25, 26, 52, 53], Hamiltonian approach [54], or Jacobi elliptic functions [24, 27]. On the other hand, numerical methods such as FEM, GDQM, pseudo-arclength continuation, and reduced order method are very efficient to obtain the linear and nonlinear responses of nanostructures. For example, Kasirajan et al. [28] used FEM to obtain the nonlinear vibration of a nonlocal Timoshenko beam considering surface effects. Nonlinear free vibration of a homogeneous Timoshenko beam was studied using the pseudo-arclength method by Ansari et al. [18].

It is seen that the nonlinear vibration of sigmoid and power law functionally graded nanobeams incorporating the simultaneous effects of microstructure and surface energy has not been comprehensively studied. Thus, this paper aims to develop a dynamic nonlinear nonclassical continuum model to study the linear and nonlinear free vibration behaviors of sigmoid and power law FG nanobeams based on the von Kármán’s geometric nonlinearity, modified couple stress theory, and surface elasticity theory. The nonlinear nonclassical governing equations and corresponding boundary conditions are derived using Hamilton’s principle in the framework of Timoshenko beam theory. Unlike most previous studies, the present model considers the nonclassical (nonideal) boundary conditions due to the presence of both residual surface stress and the material nonhomogeneity. To solve the resulting equations, the solution is partitioned into static and dynamic responses. The static response accounts for the nonhomogeneous boundary conditions such that the resulting boundary conditions for the dynamic response are homogeneous, and so Galerkin’s approach can be applied. Moreover, a generalized differential quadrature method (GDQM) is used to discretize the developed model without neglecting any of its nonlinearities in governing equations and boundary conditions. After applying Galerkin’s approach, the resulting nonlinear second-order ODE system is solved by two methodologies, namely pseudo-arclength continuation and Runge–Kutta method. The developed model is validated by comparing the present results with the results from the available literature, and good agreement is found. A comprehensive parametric study is presented and discussed in detail to demonstrate the influences of the bulk modulus of elasticity ratio, surface elasticity modulus, surface residual stress, material length scale parameter ratio, dimensionless material length scale parameter, gradient index, nonclassical boundary conditions, and beam thickness on the linear and nonlinear free vibrations of Timoshenko power law and sigmoid FG micro-/nanobeams.

2 Theoretical formulation

2.1 Functionally graded materials

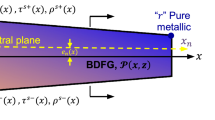
One of the main tasks in material mechanics is to correctly predict the material behavior, which requires estimating (homogenizing) the effective mechanical properties of FGMs. There are different homogenization techniques for FGMs such as exponential, power law, Mori–Tanaka, symmetric power law, and sigmoid function. In the present study, both power law (PL-FG) and sigmoid function (SIG-FG) are adopted as homogenization schemes for the FGM beam under consideration. Considering an FGM nanobeam with a rectangular cross section of length L, width b, and thickness h, the nanobeam is assumed to be made of ceramic and metal. The material at the bottom surface $(z=-h / 2)$ is pure ceramic and at the top surface $(z=h /2)$ is pure metal, as depicted in Fig. 1. Through the beam thickness, the proposed distributions of volume fractions of metal and ceramic follow PL-FG and SIG-FG. Then, the effective local material property of bulk material (${{\mathcal {P}}}^{B}$) such as Young’s modulus ($E^{B}$), Poisson’s ratio ($\nu ^{B}$), mass density ($\rho ^{B}$), and microstructure material length scale (l) of a PL-FG nanobeam can be described as follows:

$$\begin{aligned} {{\mathcal {P}}}^{B}\left( z \right) ={{\mathcal {P}}}_\mathrm{c}^{B}+\left( {{\mathcal {P}}}_\mathrm{m}^{B}-{{\mathcal {P}}}_\mathrm{c}^{B} \right) \left( \frac{1}{2}+\frac{z}{h} \right) ^{k},\quad -\frac{h}{2} \le z \le \frac{h}{2}, \end{aligned}$$

(1)

and for SIG-FG nanobeam, the effective local material property of bulk material can be expressed by (Chi and Chung [55]):

In this study, the effective local material property of surface material (${{\mathcal {P}}}^\mathrm{s}$) such as surface Lamé’s constants ($\lambda ^\mathrm{s}$ and $\mu ^\mathrm{s}$), surface residual stress ($\tau ^\mathrm{s}$), and surface mass density ($\rho ^\mathrm{s}$) of the FG nanobeam is described in terms of PL-FG law as follows:

$$\begin{aligned} {{\mathcal {P}}}^\mathrm{s}\left( z \right) ={{\mathcal {P}}}_\mathrm{c}^\mathrm{s}+\left( {{\mathcal {P}}}_\mathrm{m}^\mathrm{s}-{{\mathcal {P}}}_\mathrm{c}^\mathrm{s} \right) \left( \frac{1}{2}+\frac{z}{h} \right) ^{k}, \quad -\frac{h}{2}\le z\le \frac{h}{2}. \end{aligned}$$

(3)

In Eqs. (1–3), ${{\mathcal {P}}}_\mathrm{c}$ and ${{\mathcal {P}}}_\mathrm{m}$ are the corresponding material properties at the lower (ceramic) and upper (metal) surfaces of the FG beam, respectively. In addition, superscripts “B” and “s” denote the bulk and surface materials, respectively, and k stands for the gradient index which controls the material variation through the beam thickness.

Fig. 1

Schematic of a functionally graded nanobeam with surface layer

2.2 Kinematics and constitutive relations

According to Timoshenko beam theory (TBT), the displacement field for an arbitrary point can be defined as:

$$\begin{aligned} u_{x}\left( x,z,t \right) =u\left( x,t \right) -z\psi \left( x,t \right) ,\quad u_{y}\left( x,z,t \right) =0, \quad u_{z}\left( x,z,t \right) =w\left( x,t \right) \end{aligned}$$

(4)

where u and w are the axial and lateral displacements of any point $\left( x,z \right)$ on the mid-plane, $\psi \left( x,t \right)$ is the rotation of the beam cross section with respect to the vertical direction, and t denotes time.

The nonlinear Green–Lagrangian strain tensor ($E_{ij}$) is defined as follows [56]:

$$\begin{aligned} E_{ij}=\frac{1}{2}\left[ u_{i,j}+u_{j,i}+u_{k,i}u_{k,j} \right] \end{aligned}$$

(5)

where $u_{i}$ are the displacement components given by Eq. (4) Throughout the paper, the summation convention and standard index notation are used, with the Greek indices running from 1 to 2 and the Latin indices from 1 to 3 unless otherwise indicated.

On the basis of von Kármán geometric nonlinearity, i.e., only squares of the slopes $u_{z,x}^{2}$, $u_{z,y}^{2}$, and $u_{z,x}u_{z,y}$ are retained in the Green–Lagrange strain tensor ($E_{ij}$), the only nonzero components of the von Kármán strain tensor ($\varepsilon _{ij}$) for the Timoshenko beam theory are as follows [8, 56]:

$$\begin{aligned} \varepsilon _{xx}=u^{'}+\frac{1}{2}w^{'2}-z\psi ^{'},\quad \varepsilon _{xz}=\varepsilon _{zx}={\begin{array}{cc} \frac{1}{2}\left[ w^{'}-\psi \right] .\\ \end{array} } \end{aligned}$$

(6)

Based on the linear elasticity, the nonzero components of the Cauchy force-stress tensor ($\sigma _{ij}$) for the micro-/nanobeam can be obtained in terms of displacements as [8, 45, 57,58,59]:

$$\begin{aligned} \left\{ {\begin{array}{ll} \sigma _{xx}=Q^{B}\left( z \right) \left[ u^{'}+\frac{1}{2}w^{'2}-z\psi ^{'} \right] , \quad Q^{B}\left( z \right) =2\mu ^{B}\left( z \right) +\lambda ^{B}\left( z \right) , \\ \sigma _{yy}=\sigma _{zz}=\lambda ^{B}\left( z \right) \left[ u^{'}+\frac{1}{2}w^{'2}-z\psi ^{'} \right] ,\\ \sigma _{xz}=\sigma _{zx}=k_{s}\mu ^{B}\left( z \right) \left[ w^{'}-\psi \right] .\\ \end{array} } \right. \end{aligned}$$

(7)

where $k_{s}$ denotes the shear correction coefficient which accounts for the nonuniformity of the shear strain over the beam cross section [60], i.e., $k_{s}={5(1+\nu _{\mathrm {av}})} / {(6+5\nu _{\mathrm {av}})}$, in which the average value of Poisson’s ratios of the metal and ceramic phases is $\nu _{\mathrm {av}}=0.5(\nu _\mathrm{m}+\nu _\mathrm{c})$. $\mu (z)$ and $\lambda (z)$ are the Lamé constants in the classical elasticity.

According to the modified couple stress theory (MCST) presented by Yang et al. [61] and in light of Eq. (4), the nonzero components of the rotation vector ($\theta _{i}$), the symmetric curvature tensor ($\chi _{ij})$, and the corresponding deviatoric part of the symmetric couple stress tensor ($m_{ij}$) can be, respectively, obtained as [8, 45, 57,58,59]:

$$\begin{aligned} \theta _{y}= & {} -\frac{1}{2}\left[ w^{'}+\psi \right] , \end{aligned}$$

(8)

$$\begin{aligned} \chi _{xy}= & {} \chi _{yx}=-\frac{1}{4}\left[ \psi ^{'}+w^{''} \right] , \end{aligned}$$

(9)

$$\begin{aligned} m_{xy}= & {} m_{yx}=-\frac{1}{2}l^{2}\left( z \right) \mu (z)\left[ \psi ^{'}+w^{''} \right] , \end{aligned}$$

(10)

and $l\left( z \right)$ refers to the material length scale parameter measuring the couple stress effect.

To this end, the surface energy effects are incorporated into the developed size-dependent model using the Gurtin–Murdoch surface elasticity theory [15, 16] in which surface stress–strain relations of the FG Timoshenko nanobeam can be formulated as below [8, 20, 37],

$$\begin{aligned} \begin{array}{ll} {\tau _{xx}^{s \pm } = {\tau ^{s \pm }}\left[ {1 - \frac{1}{2}~{{w'}^2}} \right] + {E^{s \pm }}\left[ {u' - z\psi ' + \frac{1}{2}{{w'}^2}} \right] ,\quad {E^{s \pm }} = 2{\mu ^{s \pm }} + {\lambda ^{s \pm }}}, \\ {\tau _{xt}^{s \pm } = \left\{ {\left( {{\mu ^{s \pm }} - {\tau ^{s \pm }}} \right) w' - {\mu ^{s \pm }}\psi } \right\} {n_y} \equiv \tau _{xz}^{s \pm }{n_y}}, \\ {\begin{array}{*{20}{l}} {\tau _{tx}^{s \pm } = \left\{ {{\mu ^{s \pm }}w' - \left( {{\mu ^{s \pm }} - {\tau ^{s \pm }}} \right) \psi } \right\} {n_y} \equiv \tau _{zx}^{s \pm }{n_y}}, \\ {\tau _{nx}^{s \pm } = {\tau ^{s \pm }}{u_{n,x}} = {\tau ^{s \pm }}{n_z}w'}. \end{array}} \end{array} \end{aligned}$$

(11)

Here, $\tau _{xx}^{s\pm }$, $\tau _{xt}^{s\pm }$, $\tau _{tx}^{s\pm }$, and $\tau _{nx}^{s\pm }$ are the only nonzero components of surface stress, $E^{s\pm }$ denotes the surface elastic modulus, $\mu ^{s\pm }$ and $\lambda ^{s\pm }$ are the surface Lamé constants, and $\tau ^{s\pm }$ is the surface residual stress. The subscript n represents the outward unit normal ${{\varvec{n}}}$ to the beam lateral surface, and ${n}_{y}$ and $n_{z}$ represent its y- and z-components, respectively, i.e., and , where $\theta$ is the angle between the normal vector and the y-axis, as shown in Fig. 1. The subscript t denotes the direction of the unit tangent vector ${{\varvec{t}}}$ on the boundary of the beam cross section, i.e., at $\theta =0$, $\tau _{xz}^{s\pm }$ and $\tau _{zx}^{s\pm }$ are the values of $\tau _{xt}^{s\pm }$and $\tau _{tx}^\mathrm{s}$, respectively. The indices “$+$” and “−” represent the upper and lower surfaces of the nanobeam, respectively.

2.3 Size-dependent governing equations

Hamilton’s principle is employed to exactly derive the nonlinear size-dependent governing equations and the associated nonclassical boundary conditions (NCBCs):

$$\begin{aligned} \delta \int _{t{1}}^{t{2}}{\left( {T-U}+{W}\right) \hbox {d}t} =0 \end{aligned}$$

(12)

where U, T, and W are, respectively, the total strain energy, kinetic energy, and work done due to applied external forces.

In the framework of the linear elasticity theory and in accordance with the surface elasticity theory and the modified couple stress theory, the first variation of the total strain energy can be written as [8, 56, 62]:

$$\begin{aligned} \delta \mathrm {U}= & {} \frac{1}{2}\delta \int _0^L \int \limits _A {\left( \sigma _{ij}\varepsilon _{ij}+m_{ij}\chi _{ij} \right) \hbox {d}A\hbox {d}x} +\frac{1}{2}\delta \int _0^L \oint _{\partial A} {\tau _{ij}^\mathrm{s} \varepsilon _{ij}\hbox {d}S \hbox {d}x} \nonumber \\= & {} \frac{1}{2}\delta \int _0^L \left\{ \int \limits _A {\left( \sigma _{xx}\varepsilon _{xx}+2\sigma _{xz}\varepsilon _{xz}+2m_{xy}\chi _{xy} \right) \hbox {d}A}\right. \nonumber \\&\left. + \oint _{\partial A} {\left( \tau _{xx}^\mathrm{s}\varepsilon _{xx}+\left( \tau _{xs}^\mathrm{s}+\tau _{sx}^\mathrm{s} \right) \varepsilon _{xs}+2\tau _{nx}^\mathrm{s}\varepsilon _{nx} \right) \hbox {d}S} \right\} \hbox {d}x \end{aligned}$$

(13)

where

$$\begin{aligned} \varepsilon _{xs}=\varepsilon _{sx}=\frac{1}{2}\left( w^{'}-\psi \right) n_{y}\equiv \varepsilon _{zx}n_{y},\quad \varepsilon _{xn}=\varepsilon _{nx}=\frac{1}{2}w^{'}n_{z}. \end{aligned}$$

(14)

Substituting Eqs. (6, 8–11, 14) into Eq. (13) yields

$$\begin{aligned} \delta \int _{t{1}}^{t{2}} {{U}\text {d}t}= & {} -\int _{t{1}}^{t{2}} \int _0^L \left[ \left\{ N^{'}+N^{s'}+\frac{1}{2}{\mathcal {C}}_{1}w^{'}w^{''} \right\} \delta u\right. \nonumber \\&+\left\{ \frac{1}{2}\left( {\mathcal {Q}}_{1}^{s'}+{\mathcal {Q}}_{2}^{s'} \right) +{\mathcal {Q}}_{xz}^{'}+\frac{1}{2}Y_{xy}^{''}\right. \nonumber \\&\left. +\frac{\hbox {d}}{\hbox {d}x}\left( \left[ N+N^\mathrm{s}+{\mathcal {S}}_{1}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1+u^{'} \right) +\frac{1}{2}{\mathcal {P}}_{1}\psi ^{'} \right] w^{'} \right) \right\} \delta w\nonumber \\&\left. +\left\{ -M_{x}^{'}-\frac{1}{2}Y_{xy}^{'}-M^{s'}+ \frac{1}{2}\left( {\mathcal {Q}}_{s1}+{\mathcal {Q}}_{s2} \right) +{{Q}}_{xz}-\frac{1}{2}{{\mathcal {P}}}_{1}w^{'}w^{''} \right\} \delta \psi \right] \text {d}x\text {d}t \nonumber \\&+\int _{t{1}}^{t{2}} \left[ \left\{ N+N^\mathrm{s}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1-\frac{1}{2}w^{'2} \right) \right\} \delta u\right. \nonumber \\&\left. +\left\{ \left\{ \frac{1}{2}\left( {\mathcal {Q}}_{1}^\mathrm{s}+{\mathcal {Q}}_{2}^\mathrm{s} \right) +{{Q}}_{xz}+\frac{1}{2}Y_{xy}^{'}\right. \right. \right. \nonumber \\&\left. \left. \left. +\left( N+N^\mathrm{s}+{\mathcal {S}}_{1}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1+u^{'} \right) +\frac{1}{2}{{\mathcal {P}}}_{1}\psi ^{'} \right) \right\} w^{'} \right\} \delta w\right. \nonumber \\&\left. -\left\{ \frac{1}{2}Y_{xy} \right\} {\delta w}^{'}-\left\{ M_{x}+\frac{1}{2}Y_{xy}+M^\mathrm{s}-\frac{1}{2}{\mathcal {P}}_{1}\left( 1-\frac{1}{2}w^{'2} \right) \right\} \delta \psi \right] _{0}^{L}\hbox {d}t \end{aligned}$$

(15)

in which the stress and couple stress resultants on the beam cross section are expressed as:

$$\begin{aligned}&\left\{ {\begin{array}{cc} N\\ M_{x}\\ \end{array} } \right\} \equiv \int _A {\left\{ {\begin{array}{cc} 1\\ z\\ \end{array} } \right\} \sigma _{xx}\hbox {d}A} =\left\{ {\begin{array}{cc} A_{xx}\\ B_{xx}\\ \end{array} } \right\} \left[ u^{'}+\frac{1}{2}w^{'2} \right] -\left\{ {\begin{array}{cc} B_{xx}\\ D_{xx}\\ \end{array} } \right\} \psi ^{'}, \end{aligned}$$

(16.1)

$$\begin{aligned}&\left\{ {\begin{array}{cc} Q_{xz}\\ Y_{xy}\\ \end{array} } \right\} \equiv \int _A {\left\{ {\begin{array}{cc} \sigma _{xz}\\ m_{xy}\\ \end{array} } \right\} \hbox {d}A} =\left\{ {\begin{array}{cc} k_{s}S_{xz}\left[ w^{'}-\psi \right] \\ -\frac{1}{2}S_{xy}\left[ \psi ^{'}+w^{''} \right] \\ \end{array} } \right\} , \end{aligned}$$

(16.2)

and the surface stress resultants along the perimeter of the beam cross section are defined as:

$$\begin{aligned}&\left\{ {\begin{array}{cc} N^\mathrm{s}\\ M^\mathrm{s}\\ \end{array} } \right\} \equiv \oint _{\partial A} {\left\{ {\begin{array}{cc} 1\\ z\\ \end{array} } \right\} \tau _{xx}^\mathrm{s}\hbox {d}S} =\left\{ {\begin{array}{cc} {\mathcal {C}}_{1}\\ {\mathcal {P}}_{1}\\ \end{array} } \right\} +\left\{ {\begin{array}{cc} {\mathcal {C}}_{2}\\ {\mathcal {P}}_{2}\\ \end{array} } \right\} u^{'}+\frac{1}{2}\left\{ {\begin{array}{cc} {\mathcal {C}}_{2}-{\mathcal {C}}_{1}\\ {\mathcal {P}}_{2}-{\mathcal {P}}_{1}\\ \end{array} } \right\} w^{'2}-\left\{ {\begin{array}{cc} {\mathcal {P}}_{2}\\ I_{{\mathrm{P}}}\\ \end{array} } \right\} \psi ^{'}, \end{aligned}$$

(16.3)

$$\begin{aligned}&\left\{ {\begin{array}{cc} {\mathcal {Q}}_{1}^\mathrm{s}\\ {\mathcal {Q}}_{2}^\mathrm{s}\\ \end{array} } \right\} \equiv \oint _{\partial A} {n_{y}^{2}\left\{ {\begin{array}{cc} \tau _{xz}^\mathrm{s}\\ \tau _{zx}^\mathrm{s}\\ \end{array} } \right\} \hbox {d}S} =\left\{ {\begin{array}{cc} {\mathcal {L}}_{2}-{\mathcal {L}}_{1}\\ {\mathcal {L}}_{2}\\ \end{array} } \right\} w^{'}-\left\{ {\begin{array}{cc} {\mathcal {L}}_{2}\\ {\mathcal {L}}_{2}-{\mathcal {L}}_{1}\\ \end{array} } \right\} \psi \end{aligned}$$

(16.4)

in which

$$\begin{aligned}&\left\{ {\begin{array}{*{20}{c}} {{A_{xx}}}&{{B_{xx}}}&{{D_{xx}}}&{{S_{xz}}}&{{S_{xy}}} \end{array}} \right\} = \mathop \int \limits _A \left\{ {\begin{array}{*{20}{c}} {{Q^B}(z)}&{z{Q^B}(z)}&{{z^2}{Q^B}(z)}&{{\mu ^B}(z)}&{l{{(z)}^2}} \end{array}{\mu ^B}(z)} \right\} \hbox {d}A \end{aligned}$$

(17.1)

$$\begin{aligned}&\quad \quad \quad \quad \left\{ {\begin{array}{*{20}{c}} {{{{{\mathcal {C}}}}_1}}&{{{{{\mathcal {C}}}}_2}}&{{{{{\mathcal {P}}}}_1}}&{{{{{\mathcal {P}}}}_2}}&{{\mathcal{S}_1}}&{{I_\mathrm{{P}}}}&{{{{{\mathcal {L}}}}_1}}&{{{{{\mathcal {L}}}}_2}} \end{array}} \right\} \nonumber \\&\quad = \mathop \oint \nolimits _{\partial A} \left\{ {\begin{array}{*{20}{c}} {{\tau ^\mathrm{s}}(z)}&{{E^\mathrm{s}}(z)}&{z{\tau ^\mathrm{s}}(z)}&{z{E^\mathrm{s}}(z)}&{n_z^2{\tau ^\mathrm{s}}(z)}&{{z^2}{E^\mathrm{s}}(z)}&{n_y^2{\tau ^\mathrm{s}}(z)}&{n_y^2{\mu ^\mathrm{s}}(z)} \end{array}} \right\} \hbox {d}S. \end{aligned}$$

(17.2)

The first variation of the kinetic energy of the FGM Timoshenko nanobeam accounting for the surface density effect can be written in terms of displacements as:

$$\begin{aligned} \delta \int _{t{1}}^{t{2}} \mathrm {T}= & {} \int _{t{1}}^{t{2}} \frac{1}{2}\delta \int _0^L {\left\{ \int _A {\rho ^{B}(z)\left( {\dot{u}}_{x}^{2}+{\dot{u}}_{y}^{2}+{\dot{u}}_{z}^{2} \right) } \hbox {d}A+\oint _{\partial A} {\rho ^\mathrm{s}(z)\left( {\dot{u}}_{x}^{2}+{\dot{u}}_{y}^{2}+{\dot{u}}_{z}^{2} \right) \hbox {d}S } \right\} \hbox {d}x \hbox {d}t} \nonumber \\= & {} \int _{t{1}}^{t{2}} \left[ \int _0^L {\left\{ \left[ I_{0}{\dot{u}}-I_{1}{\dot{\psi }} \right] \delta {\dot{u}}-\left[ I_{1}{\dot{u}}-I_{2}{\dot{\psi }} \right] \delta {\dot{\psi }}+I_{0}{\dot{w}}\delta {\dot{w}} \right\} \hbox {d}x} \right] \hbox {d}t \end{aligned}$$

(18)

where the mass inertia coefficients ($I_{0}, I_{1}$, and $I_{2}$) including the effect of surface density are defined by:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{I_0}}&{{I_1}}&{{I_2}} \end{array}} \right\} = \mathop \int \nolimits _A \left\{ {\begin{array}{*{20}{c}} {{\rho ^B}(z)}&{z{\rho ^B}(z)}&{{z^2}{\rho ^B}(z)} \end{array}} \right\} \hbox {d}A + \mathop \oint \nolimits _{\partial A} \left\{ {\begin{array}{*{20}{c}} {{\rho ^\mathrm{s}}(z)}&{z{\rho ^\mathrm{s}}(z)}&{{z^2}{\rho ^\mathrm{s}}(z)} \end{array}} \right\} \hbox {d}S. \end{aligned}$$

(19)

Additionally, the variational form of the work done by the external forces applied on the FG nanobeam is given by:

$$\begin{aligned} \delta \int _{t{1}}^{t{2}} {{W}\hbox {d}t}= & {} \int _{t{1}}^{t{2}} {\left[ \int _0^L {\left[ q\delta w+f_\mathrm{c}\delta \theta _{y} \right] \hbox {d}x} \right] \hbox {d}t} +\int _{t{1}}^{t{2}} {\left[ {\bar{N}}\delta u+{\bar{V}}\delta w+{\bar{M}}_\mathrm{m}\delta w^{'}+{\bar{M}}_{\sigma }\delta \psi \right] _{0}^{L}\hbox {d}t} \nonumber \\= & {} \int _{t{1}}^{t{2}} {\int _0^L \left[ \left( q+\frac{1}{2}{f}_\mathrm{c}^{'} \right) \delta w-\frac{1}{2}{f}_\mathrm{c}\delta \psi \right] \text {d}x\text {d}t} \nonumber \\&+\int _{t{1}}^{t{2}} \left[ {\bar{N}}\delta u +\left( {\bar{V}}-\frac{1}{2}{f}_\mathrm{c} \right) \delta w+{\bar{M}}_\mathrm{m}\delta w^{'}+{\bar{M}}_{\sigma }\delta \psi \right] _{0}^{L}\hbox {d}t \end{aligned}$$

(20)

where q is the z-component of body force per unit length along the x-axis and $f_\mathrm{c}$ is the y-component of the body couple imposed on the sections as couple per unit axial length (per unit volume along the x-axis). ${\bar{N}}$, ${\bar{V}}$, ${\bar{M}}_{\sigma }$, and ${\bar{M}}_\mathrm{m}$ denote, respectively, the applied axial resultant force of normal stresses, the transverse resultant force of shear stresses, the resultant external bending moment of normal stresses, and the resultant external bending moment around the y-axis due to couple stresses at the beam ends.

Substituting Eqs. (15, 18, 20) into Eq. (12), applying the fundamental lemma of calculus of variations, and gathering the coefficients of $\delta u$, $\delta w$, and $\delta \psi$, the nonlinear nonclassical governing differential equations of motion of a FG Timoshenko nanobeam can be achieved as:

$$\begin{aligned}&\delta u{:}\, I_{1}\ddot{\psi }-I_{{0}}\ddot{u}+N^{'}+N^{s'}+\frac{1}{2}{\mathcal {C}}_{1}w^{'}w^{''}=0, \end{aligned}$$

(21.1)

$$\begin{aligned}&\delta w{:}\, -I_{0}\ddot{w}+\frac{1}{2}\left( {\mathcal {Q}}_{1}^{s'}+{\mathcal {Q}}_{2}^{s'} \right) +{\mathcal {Q}}_{xz}^{'}+\frac{1}{2}Y_{xy}^{''}+\left( N^{'}+N^{s'}-\frac{1}{2}{\mathcal {C}}_{1}u^{''}+\frac{1}{2}{\mathcal {P}}_{1}\psi ^{''} \right) w^{'}\nonumber \\&\quad +\left( N+N^\mathrm{s}+{\mathcal {S}}_{1}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1+u^{'} \right) +\frac{1}{2}{\mathcal {P}}_{1}\psi ^{'} \right) w^{''}+\left( q+\frac{1}{2}{f}_\mathrm{c}^{'} \right) =0, \end{aligned}$$

(21.2)

$$\begin{aligned}&\delta \psi {:}\, I_{1}\ddot{u}-I_{2}\ddot{\psi }-M_{x}^{'}-\frac{1}{2}Y_{xy}^{'}-M^{s'}+\frac{1}{2}\left( {\mathcal {Q}}_{1}^\mathrm{s}+{\mathcal {Q}}_{2}^\mathrm{s} \right) +{Q}_{xz}-\frac{1}{2}{\mathcal {P}}_ {1}w^{'}w^{''}-\frac{1}{2}{f}_\mathrm{c}=0. \end{aligned}$$

(21.3)

Moreover, the associated nonclassical boundary conditions (NCBCs) at the beam ends ($x=0, L$) can be expressed as:

$$\begin{aligned}&\delta u{:}\,\mathrm {either}\quad u={\bar{u}}\quad \mathrm {or}\quad N+N^\mathrm{s}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1-\frac{1}{2}w^{'2} \right) -{\bar{N}}=0, \end{aligned}$$

(22.1)

$$\begin{aligned}&\delta w{:}\, \mathrm {either }\quad w={\bar{w}} \quad \mathrm {or}\quad \frac{1}{2} \left( {\mathcal {Q}}_{1}^\mathrm{s}+{\mathcal {Q}}_{2}^\mathrm{s} \right) +{{Q}}_{xz}+\frac{1}{2}Y_{xy}^{'}\nonumber \\&\quad +\left( {\mathcal {S}}_{1}+N+N^\mathrm{s}-\frac{1}{2}{\mathcal {C}}_{1}\left( 1+u^{'} \right) +\frac{1}{2}{\mathcal {P}}_{1}\psi ^{'} \right) w^{'}+\frac{1}{2}{f}_\mathrm{c}-{\bar{V}}=0, \end{aligned}$$

(22.2)

$$\begin{aligned}&\delta \psi {:}\, \mathrm {either }\quad \psi =\bar{\psi } \quad \mathrm {or}\quad M_{x}+\frac{1}{2}Y_{xy}+M^\mathrm{s}-\frac{1}{2}{\mathcal {P}}_{1}\left( 1-\frac{1}{2}w^{'2} \right) +{\bar{M}}_{\sigma }=0, \end{aligned}$$

(22.3)

$$\begin{aligned}&\delta w^{'}{:}\, \mathrm {either}\quad w^{'}=\bar{w^{'}} \quad \mathrm {or}\quad \frac{1}{2}Y_{xy}+{\bar{M}}_\mathrm{m}=0. \end{aligned}$$

(22.4)

By inserting the force and moment resultants introduced in Eq. (16.1) into Eqs. (21.1) and (22.1), the size-dependent nonlinear governing equations and the corresponding NCBCs in terms of displacement components can be, respectively, obtained as:

$$\begin{aligned}&I_{1}\ddot{\psi }-I_{0}\ddot{u}+{A}_{11}u^{''}-{B}_{11}\psi ^{''}+{A}_{\mathrm {22}}w^{'}w^{''}=0, \end{aligned}$$

(23.1)

$$\begin{aligned}&-I_{0}\ddot{w}+\left[ \mathrm {{S}}_{11}+{\mathcal {S}}_{1}+ \frac{1}{2}{\mathcal {C}}_{1}+{A}_{\mathrm {22}}u^{'}+ \frac{3}{2}{A}_{\mathrm {33}}w^{'2}-{B}_{\mathrm {22}}\psi ^{'} \right] w^{''}-\frac{1}{4}{{S}}_{xy}w^{''''}\nonumber \\&\quad -\frac{1}{4}{{S}}_{xy}\psi ^{'''}-\mathrm {{S}}_{11}\psi ^{'}+\left[ {A}_{\mathrm {22}}u^{''}-{B}_{\mathrm {22}}\psi ^{''} \right] w^{'}+q+\frac{1}{2}{f}_\mathrm{c}^{'}=0, \end{aligned}$$

(23.2)

$$\begin{aligned}&I_{1}\ddot{u}-I_{2}\ddot{\psi }-{B}_{11}u^{''}+\frac{1}{4}{{S}}_{xy}w^{'''}+\mathrm {{S}}_{11}w^{'}+{D}_{11}\psi ^{''}-\mathrm {{S}}_{11}\psi -{B}_{\mathrm {22}}w^{'}w^{''}-\frac{1}{2}{f}_\mathrm{c}=0, \end{aligned}$$

(23.3)

and

$$\begin{aligned} u= & {} {\bar{u}} \quad \mathrm {or}\quad {A}_{11}u^{'}-{B}_{11}\psi ^{'}+\frac{1}{2}{A}_{\mathrm {22}}w^{'2}-{\bar{N}}+ \frac{1}{2}{\mathcal {C}}_{1}=0, \end{aligned}$$

(24.1)

$$\begin{aligned} w= & {} {\bar{w}} \quad \mathrm {or}\quad -\frac{1}{4}S_{xy}w^{'''}-{S}_{11}\psi -\frac{1}{4}S_{xy}\psi ^{''}\nonumber \\&+\left[ {S}_{11}+{\mathcal {S}}_{1}+\frac{1}{2}{\mathcal {C}}_{1}+{A}_{\mathrm {22}}u^{'}+\frac{1}{2}{A}_{\mathrm {22}}w^{'2}-{B}_{\mathrm {22}}\psi ^{'} \right] w^{'}+\frac{1}{2}{f}_\mathrm{c}-{\bar{V}}=0, \end{aligned}$$

(24.2)

$$\begin{aligned} \psi= & {} {\bar{\psi }} \mathrm {or}\quad {B}_{11}u^{'}-\frac{1}{4}S_{xy}w^{''}-{D}_{11}\psi ^{'}+\frac{1}{2}{B}_{\mathrm {22}}w^{'2} +\frac{1}{2}{\mathcal {P}}_{1}+{\bar{M}}_{\sigma }=0, \end{aligned}$$

(24.3)

$$\begin{aligned} w^{'}= & {} \bar{w^{'}} \mathrm {or}\quad \frac{1}{4}S_{xy}\left( \psi ^{'}+w^{''} \right) -{\bar{M}}_\mathrm{m}=0 \end{aligned}$$

(24.4)

where

$$\begin{aligned}&\left\{ {\begin{array}{cc} {D}_{11} &{} {S}_{11}\\ \end{array} } \right\} =\left\{ {\begin{array}{cc} \left( \frac{S_{xy}}{4}+D_{xx}+I_{{{{\mathrm{P}}}}} \right) &{} \left( k_{s}S_{xz}+{\mathcal {L}}_{2}-\frac{{\mathcal {L}}_{1}}{2} \right) \\ \end{array} } \right\} , \end{aligned}$$

(25.1)

$$\begin{aligned}&\left\{ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{22}}}&{{A_{33}}}&{{B_{11}}}&{{B_{22}}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\left( {{A_{xx}} + {{{\mathcal {C}}}_2}} \right) }&{\left( {{A_{11}} - \frac{{{{{\mathcal {C}}}_1}}}{2}} \right) }&{\left( {{A_{11}} - {{{\mathcal {C}}}_1}} \right) }&{\left( {{B_{xx}} + {{{\mathcal {P}}}_2}} \right) }&{\left( {{B_{11}} - \frac{{{{{\mathcal {P}}}_1}}}{2}} \right) } \end{array}} \right\} . \end{aligned}$$

(25.2)

Up to here, a nonlinear nonclassical functionally graded Timoshenko nanobeam model is developed incorporating the simultaneous effect of microstructure, surface elasticity, surface mass density, surface residual stress, and von Kármán geometric nonlinearity. It is important to mention that the linear equations of motion of a homogeneous Timoshenko nanobeam with the effects of surface energy and modified coupled stress derived by Gao [22] can be recovered from Eq. (23) by dropping the nonlinear terms and setting the gradient index $k=0$. Further, the homogeneous Timoshenko nanobeam model developed by Ansari et al. [18] considering the surface energy effect and von Kármán geometric nonlinearity can be recovered from the present model by setting $k=l=0$, as there are some missed terms in their variation of surface strain energy.

2.4 Dimensionless size-dependent governing equations

We introduce the following dimensionless parameters:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{x^*}}&{{{{u}}^{{*}}}}&{{w^*}}&{{\psi ^*}}&{{{{t}}^{{*}}}}&{{\varOmega }} \end{array}{{~}}} \right\} = \left\{ {\begin{array}{*{20}{c}} {\frac{x}{L}}&{\frac{u}{h}}&{\frac{w}{h}}&\psi&{\frac{t}{\tau }}&{\tau \omega } \end{array}{{~}}} \right\} ,{{~~}}\tau = {L^2}\sqrt{\frac{{{\rho _\mathrm{m}}{A_0}}}{{{E_\mathrm{m}}{I_\mathrm{m}}}}} \end{aligned}$$

(26)

where $A_{0}=bh, I_\mathrm{m}=(bh^{3})/12$. Using Eq. (26) and letting $\xi =L /h$, the nondimensional governing equations for nonlinear free vibration, where all the external forces vanish in Eqs. (23.1) and (24.1), can be obtained as:

$$\begin{aligned}&I_{1}^{*}\ddot{\psi }-I_{0}^{*}\ddot{u}+\xi ^{2}A_{11}^{*}u^{''}-\xi ^{2}B_{11}^{*}\psi ^{''}+\xi A_{22}^{*} w^{'}w^{''}=0, \end{aligned}$$

(27.1)

$$\begin{aligned}&-I_{0}^{*}\ddot{w}+\xi ^{2}\left( {S}_{11}^{*}+{\mathcal {S}}_{1}^{*}+\frac{1}{2}{\mathcal {C}}_{1}^{*} \right) w^{''}-\frac{1}{4}S_{xy}^{*}w^{''''}-\frac{1}{4}\xi S_{xy}^{*}\psi ^{'''}-\xi ^{3}{S}_{11}^{*}\psi ^{'}+\xi {A}_{22}^{*}\left[ u^{''}w^{'}+u^{'}w^{''} \right] \nonumber \\&-\xi {B}_{22}^{*}\left[ \psi ^{''}w^{'}+\psi ^{'}w^{''} \right] +\frac{3}{2}{A}_{33}^{*}w^{\mathrm {'2}}w^{''}=0, \end{aligned}$$

(27.2)

$$\begin{aligned}&I_{1}^{*}\ddot{u}-I_{2}^{*}\ddot{\psi }-\xi ^{2}{B}_{11}^{*}u^{''}+\xi ^{3}{S}_{11}^{*}w^{'}+\frac{1}{4}\xi S_{xy}^{*}w^{'''}-\xi ^{4}{S}_{11}^{*}\psi +\xi ^{2}{D}_{11}^{*}\psi ^{''}-\xi {B}_{22}^{*}w^{'}w^{''}=0. \end{aligned}$$

(27.3)

• (a) Simply supported end support

  $$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\frac{{A_{11}^*}}{\xi }u' - \frac{{B_{11}^*}}{\xi }\psi ' + \frac{1}{2}\frac{{A_{22}^*}}{{{\xi ^2}}}{{~}}{w^{{{'}}2}} + \frac{1}{2}{{{\mathcal {C}}}}_1^* = 0,{{~~~~~~~~}}}\\ {w = 0},\\ {\frac{{B_{11}^*}}{\xi }u' - \frac{1}{4}\frac{{S_{xy}^*}}{{{\xi ^2}}}w'' - \frac{{{{D}}_{11}^*}}{\xi }\psi ' + \frac{1}{2}\frac{{B_{22}^*}}{{{\xi ^2}}}{{~}}{w^{{{'}}2}} + \frac{1}{2}{{{\mathcal {P}}}}_1^* = 0},\\ {\frac{1}{\xi }w'' + \psi ' = 0}. \end{array}} \right. \end{aligned}$$

  (28.1)

• (b) Clamped end support

  $$\begin{aligned} u=w=0, \quad \psi =0, w^{'}=0 \end{aligned}$$

  (28.2)

with

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\left\{ {\begin{array}{*{20}{c}} {I_0^*}&{I_1^*}&{I_2^*} \end{array}} \right\} = \frac{1}{{{\rho _\mathrm{m}}{A_0}}}\left\{ {\begin{array}{*{20}{c}} {{I_0}}&{}{\frac{{{I_1}}}{h}}&{}{\frac{{{I_2}}}{{{h^2}}}} \end{array}} \right\} },\\ {\left\{ {\begin{array}{*{20}{c}} {A_{11}^*}&{}{A_{22}^*}&{}{A_{33}^*}&{}{B_{11}^*}&{}{B_{22}^*} \end{array}} \right\} = \frac{h}{{{E_\mathrm{m}}{I_\mathrm{m}}}}\left\{ {\begin{array}{*{20}{c}} {h{A_{11}}}&{}{h{A_{22}}}&{}{h{A_{33}}}&{}{{B_{11}}}&{}{{B_{22}}} \end{array}} \right\} }, \\ {\left\{ {\begin{array}{*{20}{c}} {S_{xy}^*}&{}{{{S}}_{11}^*}&{}{{{D}}_{11}^*}&{}{{{{\mathcal {S}}}}_1^*}&{}{{{{\mathcal {C}}}}_1^*}&{}{{{{\mathcal {P}}}}_1^*} \end{array}} \right\} = \frac{1}{{{E_\mathrm{m}}{I_\mathrm{m}}}}\left\{ {\begin{array}{*{20}{c}} {{S_{xy}}}&{{h^2}{{{S}}_{11}}}&{{{{D}}_{11}}}&{{h^2}{{{\mathcal {S}}}_1}}&{{h^2}{{{\mathcal {S}}}_1}}&{h{{{\mathcal {P}}}_1}} \end{array}} \right\} .} \end{array}} \right. \end{aligned}$$

(29)

After some mathematical manipulation, the explicit representation of the system given by Eq. (27.1) is as follows:

$$\begin{aligned}&\mathbb {k}_{1}\ddot{u}+\mathbb {k}_{2}u^{''}+\mathbb {k}_{\mathrm {3}}\psi ^{''}+\mathbb {k}_{\mathrm {4}}w^{'}w^{''}+\mathbb {k}_{\mathrm {5}}w^{'}+\mathbb {k}_{\mathrm {6}}w^{'''}+\mathbb {k}_{\mathrm {7}}\psi =0, \end{aligned}$$

(30.1)

$$\begin{aligned}&\mathbb {I}_\mathrm{w}\ddot{w}+\mathbb {c}_{0}w^{''}+\mathbb {c}_{1}w^{''''}+\mathbb {c}_{2}\psi ^{'''}\nonumber \\&\quad +\mathbb {c}_{\mathrm {3}}\psi ^{'}+\mathbb {c}_{\mathrm {4}}\left[ u^{''}w^{'}+u^{'}w^{''} \right] +\mathbb {c}_{\mathrm {5}}\left[ \psi ^{''}w^{'}+\psi ^{'}w^{''} \right] +\mathbb {c}_{\mathrm {6}}w^{'2}w^{''}=0, \end{aligned}$$

(30.2)

$$\begin{aligned}&\mathbb {p}_{1}\ddot{\psi }+\mathbb {p}_{2}\psi ^{''}+\mathbb {p}_{\mathrm {3}}u^{''}+\mathbb {p}_{\mathrm {4}}w^{'}w^{''}+\mathbb {p}_{\mathrm {5}}w^{'}+\mathbb {p}_{\mathrm {6}}w^{'''}+\mathbb {p}_{7}\psi =0 \end{aligned}$$

(30.3)

in which

$$\begin{aligned}&\left\{ {\begin{array}{*{20}{c}} {{\mathbb {k}_1}}\\ {{\mathbb {k}_2}}\\ {\begin{array}{*{20}{c}} {{\mathbb {k}_3}}\\ {{\mathbb {k}_4}}\\ {\begin{array}{*{20}{c}} {{\mathbb {k}_5}}\\ {{\mathbb {k}_6}}\\ {{\mathbb {k}_7}} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} { - I_0^* + {r_1}I_1^*}\\ {{\xi ^2}\left( {A_{11}^* - {r_1}B_{11}^*} \right) }\\ {\begin{array}{*{20}{c}} { - {\xi ^2}\left( {B_{11}^* + {r_1}{{D}}_{11}^*} \right) }\\ {\xi \left( {A_{22}^* - {r_1}B_{22}^*} \right) }\\ {\begin{array}{*{20}{c}} {{\xi ^3}{r_1}{{S}}_{11}^*}\\ {\frac{{\xi {r_1}S_{xy}^*}}{4}}\\ { - {\xi ^4}{r_1}{{S}}_{11}^*} \end{array}} \end{array}} \end{array}} \right\} ,\nonumber \\&\left\{ {\begin{array}{*{20}{c}} {{\mathbb {p}_1}}\\ {{\mathbb {p}_2}}\\ {\begin{array}{*{20}{c}} {{\mathbb {p}_3}}\\ {{\mathbb {p}_4}}\\ {\begin{array}{*{20}{c}} {{\mathbb {p}_5}}\\ {{\mathbb {p}_6}}\\ {{\mathbb {p}_7}} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} { - I_2^* + {r_2}I_1^*}\\ {{\xi ^2}\left( {{{D}}_{11}^* - {r_2}B_{11}^*} \right) }\\ {\begin{array}{*{20}{c}} { - {\xi ^2}\left( {B_{11}^* + {r_2}A_{11}^*} \right) }\\ { - \xi \left( {B_{22}^* + {r_2}A_{22}^*} \right) }\\ {\begin{array}{*{20}{c}} {{\xi ^3}{{S}}_{11}^*}\\ {\xi S_{xy}^*/4}\\ { - {\xi ^4}{{S}}_{11}^*} \end{array}} \end{array}} \end{array}} \right\} ,\nonumber \\&\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{\mathbb {c}_0}}\\ {{\mathbb {c}_1}}\\ {\begin{array}{*{20}{c}} {{\mathbb {c}_2}}\\ {{\mathbb {c}_3}}\\ {\begin{array}{*{20}{c}} {{\mathbb {c}_4}}\\ {{\mathbb {c}_5}}\\ {{\mathbb {c}_6}} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{\xi ^2}\left( {{{S}}_{11}^* + {{{\mathcal {S}}}}_1^* + \frac{1}{2}{{{\mathcal {C}}}}_1^*} \right) }\\ { - S_{xy}^*/4}\\ {\begin{array}{*{20}{c}} { - \xi S_{xy}^*/4}\\ { - {\xi ^3}{{S}}_{11}^*}\\ {\begin{array}{*{20}{c}} {\xi A_{22}^*}\\ { - \xi B_{22}^*}\\ {3A_{33}^*/2} \end{array}} \end{array}} \end{array}} \right\} ,}&{}{\left\{ {\begin{array}{*{20}{c}} {{r_1}}\\ {{r_2}}\\ {{{\mathbb {I}}_w}} \end{array}} \right\} = - \left\{ {\begin{array}{*{20}{c}} {\frac{{I_1^*}}{{I_2^*}}}\\ {\frac{{I_1^*}}{{I_0^*}}}\\ {I_0^*} \end{array}} \right\} }. \end{array} \end{aligned}$$

(31)

It is important to notice that, compared with the clamped end boundary conditions, the simply supported boundary conditions given by Eq. (28.1) are not only nonlinear but also nonhomogeneous (nonideal) due to the presence of the terms ${\mathcal {P}}_{1}^{*}/2$ and $C_{1}^{*}/2$. These terms are nonzero when including the effect of the surface residual stress of the FG nanobeam, i.e., when $\tau _{s}\ne 0$ and $k\ne 0$ as seen from Eq. (17.2). Some recent works [20, 25, 26, 37] have studied FG nanostructures including surface effects and derived the mathematical models with similar nonhomogeneous boundary conditions. However, they solved these models analytically and applied the classical boundary conditions rather than the exact nonhomogeneous ones. In fact, these nonclassical (nonhomogeneous) terms act as self-excitation loading and cause deformation of the microstructure at no external load.

3 Solution strategy

In the present study, the nonlinear governing equations are solved employing the GDQM as one of the most efficient numerical techniques.

3.1 Discretization in ${\varvec{x}}$-direction using GDQM

The normalized beam length $0\le x\le 1$ is discretized to n points: $x_{1}=0, x_{2}=\delta , x_{n-1}=1-\delta , x_{n}=1$, and the other inner nodes $x_{i}$ are calculated using the Chebyshev–Gauss–Lobatto formula:

$$\begin{aligned} x_{i}=\frac{1}{2}\left( 1-\mathrm {cos}\frac{(i-2)\pi }{n-3} \right) i=3, 4,\ldots , n-2. \end{aligned}$$

(32)

Here, $\delta$ is a small number and is taken in this study as $\delta =0.04 x_{3}$.

GDQM is a polynomial-based discretization method that approximates derivatives of a function v(x) as a weighted sum of its values at all discrete nodes in its domain. For a vector $V=\left[ v_{1},v_{2}, \ldots ,v_{n} \right] ^\mathrm{T}$ of nodal values of $v(x), \text {i.e.,} v_{i}=v(x_{i}$), the first-order nodal derivative vector $V^{'}=\left[ v_{1}^{'}, v_{2}^{'}, \ldots ,v_{n}^{'} \right] ^\mathrm{T} , v_{i}^{'}=\left. \frac{\hbox {d}v}{\hbox {d}x} \right| _{x_{i}}$ can be computed as $V^{'}={\mathcal {A}}V$, where ${\mathcal {A}}$ is the first-order derivative weighting coefficient matrix of dimension $n\times n$ and is computed as [63],

(33)

Based on the GDQM, the unknown functions $w\left( x \right) , u(x)$, and $\psi (x)$ in Eq. (30) are discretized to three vectors W, U, and $\varPsi$ where $W=\left[ w_{1}, w_{2}, \ldots ,w_{n} \right] ^\mathrm{T}, U=\left[ u_{1}, u_{2}, \ldots , u_{n} \right] ^\mathrm{T}$, and $\varPsi =\left[ \psi _{1}, \psi _{2}, \ldots , \psi _{n} \right] ^\mathrm{T}$. The associated derivative vectors are approximated as:

$$\begin{aligned}&\left\{ {\begin{array}{*{20}{c}} {W'}\\ {\begin{array}{*{20}{c}} {W''}\\ {\begin{array}{*{20}{c}} {W'''}\\ {{W^{''''}}} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\mathcal {A}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {B}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {C}}}}\\ {{{\mathcal {D}}}} \end{array}} \end{array}} \end{array}} \right\} W, \nonumber \\&{\left\{ {\begin{array}{*{20}{c}} {U'}\\ {\begin{array}{*{20}{c}} {U''}\\ {\begin{array}{*{20}{c}} {U'''} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\mathcal {A}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {B}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {C}}}} \end{array}} \end{array}} \end{array}} \right\} U,} {\left\{ {\begin{array}{*{20}{c}} {{{\Psi '}}}\\ {\begin{array}{*{20}{c}} {{{\Psi ''}}}\\ {\begin{array}{*{20}{c}} {{{\Psi '''}}} \end{array}} \end{array}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{\mathcal {A}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {B}}}}\\ {\begin{array}{*{20}{c}} {{{\mathcal {C}}}} \end{array}} \end{array}} \end{array}} \right\} {{\Psi }}} \end{aligned}$$

(34)

where ${\mathcal {B}}=\mathcal {AA}, {\mathcal {C}}=\mathcal {AB}$, and ${\mathcal {D}}=\mathcal {AC}$.

3.2 Nonlinear vibration of an FG Timoshenko nanobeam

The difficulty encountered in the nonhomogeneous nonlinear boundary conditions (Eq. 28.2) is the fact that in the Galerkin’s approach the solution of a dynamic system is assumed to be a finite sum of products of two functions in space and time variables. The space functions must satisfy the boundary conditions that necessarily should be homogeneous. In order to effectively handle such nonhomogeneous nonlinear boundary conditions, the solution is assumed to consist of two parts, as shown in Eq. (35). The first part is the static solution $\left\{ w_{s},u_{s},\psi _{s} \right\}$, in which the nonhomogeneous boundary conditions are considered during its evaluation. The second part is the dynamic solution $\left\{ w_{d},u_{d},\psi _{d} \right\}$

$$\begin{aligned} w\left( x,t \right)= & {} w_{s}\left( x \right) +w_{d}(x,t),\nonumber \\ u\left( x,t \right)= & {} u_{s}\left( x \right) +u_{d}(x,t),\nonumber \\ \psi \left( x,t \right)= & {} \psi _{s}\left( x \right) +\psi _{d}(x,t). \end{aligned}$$

(35)

3.2.1 Static solution

Dropping the inertia and time-dependent terms in Eq. (30) and substituting Eq. (35), the governing equation for the static response of FG Timoshenko nanobeam can be achieved as:

$$\begin{aligned}&\mathbb {k}_{2} u_{s}^{''}+\mathbb {k}_{\mathrm {3}}\psi _{s}^{''}+\mathbb {k}_{4}w_{s}^{'}w_{s}^{''}+\mathbb {k}_{5} w_{s}^{'}+\mathbb {k}_{6}w_{s}^{'''}+\mathbb {k}_{7}\psi _{s}=0, \end{aligned}$$

(36.1)

$$\begin{aligned}&\mathbb {c}_{0} w_{s}^{''}+\mathbb {c}_{1}w_{s}^{''''}+\mathbb {c}_{2}\psi _{s}^{'''}+\mathbb {c}_{3}\psi _{s}^{'}+\mathbb {c}_{4}\left[ u_{s}^{''}w_{s}^{'}+u_{s}^{'}w_{s}^{''} \right] +\mathbb {c}_{5}\left[ \psi _{s}^{''}w_{s}^{'}+\psi _{s}^{'}w_{s}^{''} \right] +\mathbb {c}_{6}w_{s}^{'2}w_{s}^{''}=0, \end{aligned}$$

(36.2)

$$\begin{aligned}&\mathbb {p}_{2}\psi _{s}^{''}+\mathbb {p}_{3} u_{s}^{''}+\mathbb {p}_{4}w_{s}^{'}w_{s}^{''}+\mathbb {p}_{5} w_{s}^{'}+\mathbb {p}_{6}w_{s}^{'''}+\mathbb {p}_{7}\psi _{s}=0, \end{aligned}$$

(36.3)

and the following nonhomogeneous boundary conditions of a simply supported nanobeam:

$$\begin{aligned} \left\{ \begin{array}{*{20}{l}} {\frac{{A_{11}^*}}{\xi }u_{s}^{'}- \frac{{B_{11}^*}}{\xi }\psi _{s}^{'} + \frac{1}{2}\frac{{A_{22}^*}}{{{\xi ^2}}}{{~}}w_\mathrm{s}^{'2} + \frac{1}{2}{{{\mathcal {C}}}}_1^* = 0,{{~~~~~~~~}}}\\ {{w_\mathrm{s}} = 0},\\ {\frac{{B_{11}^*}}{\xi }u_{s}^{'} - \frac{1}{4}\frac{{S_{xy}^*}}{{{\xi ^2}}}w_\mathrm{s}^{''} - \frac{{{{D}}_{11}^*}}{\xi }\psi _{s}^{'} + \frac{1}{2}\frac{{B_{22}^*}}{{{\xi ^2}}}{{~}}w_\mathrm{s}^{'2} + \frac{1}{2}{{{\mathcal {P}}}}_1^* = 0},\\ {\frac{1}{\xi }w_\mathrm{s}^{''} + \psi _{s}^{'} = 0.{{~~~}}} \end{array} \right. \end{aligned}$$

(37)

Discretization of the governing nonlinear system, Eq. (36), and the nonlinear nonclassical boundary conditions, Eq. (37), by the GDQM result in a nonlinear system of algebraic equations. The Newton method is implemented to approximate the static response $\left\{ w_{s},u_{s},\psi _{s} \right\}$ of the nonlinear system. To improve accuracy and run time, the Jacobian matrix is derived analytically. For more details, refer to the recent work of Shanab et al. [8]

3.2.2 Dynamic solution

By inserting Eq. (35) into the nonlinear system (Eq. 30) and making use of Eq. (36), the nonlinear system of PDEs in the time-dependent variables $w_{d}(x,t)$, $u_{d}( x,t)$, and $\psi _{d}(x,t)$ that describe the dynamic response of an FG Timoshenko nanobeam is obtained as:

$$\begin{aligned}&\mathbb {k}_{1}\ddot{u}_{d}+\mathbb {k}_{2}u_{d}^{''}+\mathbb {k}_{3}\psi _{d}^{''}+\mathbb {k}_{4}\left( w_{s}^{'}w_{d}^{''}+w_{s}^{''}w_{d}^{'}+w_{d}^{'}w_{d}^{''} \right) +\mathbb {k}_{5}w_{d}^{'}+\mathbb {k}_{6} w_{d}^{'''}+\mathbb {k}_{7}\psi _{d}=0, \end{aligned}$$

(38.1)

$$\begin{aligned}&{\mathbb {I}}_\mathrm{w}\ddot{w}_{d}+\mathbb {c}_{0}w_{d}^{''}+\mathbb {c}_{1}w_{d}^{''''}+\mathbb {c}_{2}\psi _{d}^{'''}+\mathbb {c}_{3}\psi _{d}^{'}+\mathbb {c}_{4} \left[ u_{s}^{''}w_{d}^{'}+w_{s}^{'}u_{d}^{''}+u_{s}^{'}w_{d}^{''}+w_{s}^{''}u_{d}^{'}+w_{d}^{'}u_{d}^{''}+w_{d}^{''}u_{d}^{'} \right] ,\nonumber \\&\quad +\mathbb {c}_{5}\left[ \psi _{s}^{''}w_{d}^{'}+w_{s}^{'}\psi _{d}^{''}+\psi _{s}^{'}{w'}_{d}^{'}+w_{s}^{''}\psi _{d}^{'}+w_{d}^{'}\psi _{d}^{''}+w_{d}^{''}\psi _{d}^{'} \right] \nonumber \\&\quad +\mathbb {c}_{6}\left( w_{s}^{'2}w_{d}^{''}+{2w}_{s}^{'}w_{s}^{''} w_{d}^{'}+{2w}_{s}^{'}w_{d}^{'}w_{d}^{''}+w_{s}^{''}w_{d}^{'2}+w_{d}^{''}w_{d}^{'2} \right) =0, \end{aligned}$$

(38.2)

$$\begin{aligned}&\mathbb {p}_{1}\ddot{\psi }_{d}+\mathbb {p}_{2}\psi _{d}^{''}+\mathbb {p}_{3}u_{d}^{''}+\mathbb {p}_{4}\left( w_{s}^{'}w_{d}^{''}+w_{s}^{''}w_{d}^{'}+w_{d}^{'}w_{d}^{''} \right) +\mathbb {p}_{5}w_{d}^{'}+\mathbb {p}_{6}w_{d}^{'''}+\mathbb {p}_{7}\psi _{d}=0. \end{aligned}$$

(38.3)

Similarly, by substituting Eq. (35) into Eq. (28.1) and making use of Eq. (37), the nonlinear boundary conditions at the simply supported end can be obtained as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {\frac{{A_{11}^*}}{\xi }u_{d}^{'} - \frac{{B_{11}^*}}{\xi }\psi _{d}^{'} + \frac{1}{2}\frac{{A_{22}^*}}{{{\xi ^2}}}{{~}}\left( {2w_{s}^{'}{w}_{d}^{'} + {w}_{d}^{'2}} \right) = 0,{{~~~~~~~~}}}\\ {{w_d} = 0},\\ {\frac{{B_{11}^*}}{\xi }u_{d}^{'} - \frac{1}{4}\frac{{S_{xy}^*}}{{{\xi ^2}}}w_d^{''} - \frac{{{{D}}_{11}^*}}{\xi }\psi _{d}^{'} + \frac{1}{2}\frac{{B_{22}^*}}{{{\xi ^2}}}{{~}}\left( {2w_{s}^{'}{w}_{d}^{'} + {w}_{d}^{'2}} \right) = 0},\\ {\frac{1}{\xi }w_d^{''} + \psi _{d}^{'} = 0.{{~~~}}} \end{array}} \right. \end{aligned}$$

(39)

3.3 Fundamental nonlinear frequency

For the nonlinear free vibration analysis, the single-mode and multi-mode Galerkin’s method can be used to convert Eq. (38) to a system of nonlinear ordinary differential equations. At low amplitude ratios, it is found that the number of modes has a minor effect on the nonlinear frequency ratios of nanobeams [64]. Thus, the single-mode Galerkin’s method can provide the nonlinear frequency of nanobeams with good accuracy. Here, the nonlinear dynamics of an FG Timoshenko nanobeam is studied to get the nonlinear free vibration frequency ${\varOmega }_{\mathrm {NL}}$ using the single-mode Galerkin method, such that

$$\begin{aligned} \left\{ \begin{array}{l@{\quad }l} w_{d}(x,t)\\ u_{d}(x,t)\\ \psi _{d}(x,t)\\ \end{array}\right\} =\left\{ \begin{array}{l@{\quad }l} \phi _{w}\left( x \right) q_{w}(t)\\ \phi _{u}(x)q_{u}(t)\\ \phi _{\psi }(x)q_{\psi }(t)\\ \end{array}\right\} \end{aligned}$$

(40)

where $q_{w}(t), q_{u}(t)$, and $q_{\psi }(t)$ are the time response of the beam corresponding to w, u, and $\psi$, respectively. The spatial functions $\phi _{w}(x)$, $\phi _{u}(x)$, and $\phi _{\psi }(x)$ represent the linear first-mode shapes corresponding to w, u, and $\psi$, respectively. These mode shapes are the eigenvectors of the linear eigenvalue problem, which results from discretizing the linear problem obtained after dropping the nonlinear terms in Eqs. (38) and (39).

Substituting Eq. (40) into Eq. (38), multiplying the resulting equations from Eqs. (38.1), (38.2), and (38.3) by $\phi _{u}$, $\phi _{w}$, and $\phi _{\psi }$, respectively, then integrating with respect to x from 0 to 1, the following system of three nonlinear differential equations can be obtained:

$$\begin{aligned}&{{\mathbb {K}}}_{1}\ddot{q}_{u}+{{\mathbb {K}}}_{2}q_{u}+{{\mathbb {K}}}_{3}q_{w}+{{\mathbb {K}}}_{\mathrm {4}}q_{\psi }+{{\mathbb {K}}}_{\mathrm {5}}q_{w}^{2}=0, \end{aligned}$$

(41.1)

$$\begin{aligned}&{\mathbb {M}}_{1}\ddot{q}_{w}+{\mathbb {M}}_{2}q_{w}+{\mathbb {M}}_{\mathrm {3}}q_{\psi }+{\mathbb {M}}_{\mathrm {4}}q_{u}+{\mathbb {M}}_{\mathrm {5}}q_{u}q_{w}+{\mathbb {M}}_{\mathrm {6}}q_{\psi }q_{w}\mathrm {+ }{\mathbb {M}}_{\mathrm {7}}q_{w}^{2}\mathrm {+ }{\mathbb {M}}_{\mathrm {8}}q_{w}^{\mathrm {3}}=0, \end{aligned}$$

(41.2)

$$\begin{aligned}&{\mathbb {P}}_{1}\ddot{q}_{\psi }+{\mathbb {P}}_{2}q_{\psi }+{\mathbb {P}}_{3}q_{u}+{\mathbb {P}}_{\mathrm {4}}q_{w}+{\mathbb {P}}_{5}q_{w}^{2}=0. \end{aligned}$$

(41.3)

The coefficients of Eq. (41) are provided in “Appendix A”. The nonlinear system of ordinary differential equations Eq. (41) is solved using two different techniques. The first one is the Runge–Kutta method, which is preferred to study the transient response of the problem. However, the steady-state nonlinear frequency can be calculated from the three responses $q_{w}\left( t \right) , q_{u}\left( t \right)$, and $q_{\psi }(t)$ obtained after a sufficiently long time. It is found that the three responses oscillate with the same frequency. The other technique composes discretizing the differential equations in Eq. (41) by a spectral collocation method [65]; then, the solution is obtained using the pseudo-arclength continuation method [66]; see “Appendix B”. The later technique is more suitable to study the steady-state response of the problem under consideration, determine the nonlinear frequency, and obtain the frequency–response relationship.

4 Model verification

First of all, let us verify the accuracy of the present model and convergence of the solution procedures by comparing the degenerated results with those reported in the available open literature. For the purpose of comparison with results based on the Euler–Bernoulli beam theory (EBBT), the present TBT model is reduced to the EBBT model by replacing the rotation of the beam cross section $\psi$ in Eq. (4) with $w^{'}$. On the other hand, the comparison with the classical beam theory is obtained from the developed model by setting all nonclassical parameters related to couple stress and surface energy equal to zero (i.e., $\tau ^\mathrm{s}=E^\mathrm{s}=\rho ^\mathrm{s}=l=0$). In addition, results for a homogeneous beam are produced from the present model by setting the gradient index equal to zero (i.e., $k=0$).

Table 1 Convergence and validation of GDQM for the dimensionless fundamental linear frequencies of simply supported and clamped–clamped homogeneous beams based on the classical analysis of EBBT $(L=10$, $L/h=20$, $b=h$, $E=30\,\mathrm {MPa}$, $\rho =1$, $\nu =0.24$)

4.1 Comparison with the available literature

In Table 1, the first three fundamental linear frequencies of simply–simply supported (SS) and clamped–clamped (CC) homogeneous micro-/nanobeams based on EBBT and the classical analysis are validated with the results obtained in [67, 68]. Additionally, the convergence of GDQM is also investigated using different grid points n. It is observed that only nine grid points are sufficient for the convergence of GDQM in this case. Based on the classical theory and EBBT, the dimensionless linear frequencies of a simply supported power law and sigmoid FGM beam are summarized in Tables 2 and 3, respectively. The results are compared with the available literature [20, 69,70,71], and good agreement is found. Based on the fully nonclassical (with the simultaneous effect of surface energy and couple stress) and classical analyses, the fundamental linear frequency of simply supported homogeneous nanobeams is obtained using EBBT and TBT and compared with Gao [22] as reported in Table 4 showing an excellent agreement.

Table 2 Comparison of dimensionless linear classical frequencies of a simply supported power law FG Euler–Bernoulli beam based on the classical analysis ($b=1\,\upmu \text {m}$, $L=10\,\upmu \text {m}$, $E_\mathrm{m}=210\,\mathrm {GPa}$, $E_\mathrm{c}=390\,\mathrm {GPa}$, $k=1$)

Table 3 Comparison of dimensionless linear classical frequencies of a simply supported sigmoid FG Euler–Bernoulli beam based on the classical analysis ($b=1\,\upmu \hbox {m}, h=0.1\,\upmu \hbox {m}, L=10\,\upmu \hbox {m}, E_\mathrm{m}=70\,\mathrm {GPa} , E_\mathrm{c}=380\,\mathrm {GPa},k=1$)

Table 4 Comparison of fundamental linear frequency (MHZ) of a simply supported homogeneous beam based on the classical and fully nonclassical analyses ($E=90\,\mathrm {GPa}$, $\rho =2700, \nu =0.23$, $l=6.58\,\upmu \mathrm {m}$, $\lambda ^\mathrm{s}=3.4939\,\mathrm {N/m}$, $\mu ^\mathrm{s}=-5.4251 \,\mathrm {N/m}$, $\tau ^\mathrm{s}=0.5689\,\mathrm {N/m}$, $L=20\,\hbox {h}$ and $b=2\,\hbox {h}$)

Table 5 Material properties of the constituents of an FGM micro-/nanobeam

4.2 Comparison of Pseudo-arclength and Runge–Kutta methods

In contrast to the linear frequency response of a dynamic system, the nonlinear frequency response depends on the nonlinear amplitude. The solution of the nonlinear system of ordinary differential equations (Eq. (41)) provides the frequency–response relationship of the nonclassical nonlinear free vibration of FG nanobeams. As mentioned in the previous Sect. 3.3, two methodologies have been employed for solving Eq. (41): Runge–Kutta method and pseudo-arclength continuation technique.

Based on the developed integrated model that incorporates the simultaneous effects of couple stress and surface energy (CSSER) and considering the material properties provided in Table 5, the first vibration mode for a simply supported FG Timoshenko beam using Runge–Kutta and pseudo-arclength continuation methods is illustrated in Fig. 2. These results are obtained at $k=1$, $l_\mathrm{c} / {l_\mathrm{m}=1.5}$, $b=h$, $L / h=15$, and $h / l_\mathrm{m}=2$. It is seen that both methods agree with each other for CSSER as well as the classical analyses. Despite this agreement, the computational time of the Runge–Kutta method is larger than that of the pseudo-arclength continuation method. The pseudo-arclength continuation method is only suitable for steady-state responses, as in this study, while the Runge–Kutta method is sufficient for both transient and steady-state responses.

Fig. 2

Comparison of solution methodologies for the frequency response of a simply supported FG nanobeam ($k=1$, $l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $l_\mathrm{c} / {l_\mathrm{m}=1.5}$, $b=h$, $L / h=15$, $h / l_\mathrm{m}=2$)

Fig. 3

Convergence of GDQM with pseudo-arclength and Runge–Kutta methods for the nonlinear frequency of simply supported FG nanobeam based on the CSSER model ($k=1$, $l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $l_\mathrm{c} /{l_\mathrm{m}=1.5}$, $b=h$, $L / h=15$, $h /l_\mathrm{m}=2$)

It should be mentioned that although Eq. (41) governs the response as a function of time (or equivalently, nonlinear frequency), the coefficients of this equation depend on the computed static responses and the linear vibration modes. Thus, the effect of the number of grid points n along the beam length on the convergence of the nonlinear frequency is investigated. Figure 3 shows the dimensionless nonlinear frequency of the simply supported FG Timoshenko nanobeam at different numbers of grid points and nonlinear amplitudes based on the CSSER model. It is clear that the present solution methodologies are well converged for $n\ge 11$. From Table 1 and Fig. 3, it can be concluded that using a considerably smaller number of grid points, GDQM can obtain very accurate numerical results for linear and nonlinear frequencies.

5 Parametric study

In this Section, the proposed model is utilized to figure out the effect of the various bulk and surface material parameters on the frequency response of FG Timoshenko micro-/nanobeams, such as the bulk modulus of elasticity ratio ($E_\mathrm{r}=E_\mathrm{c}^{B}/E_\mathrm{m}^{B}$), dimensionless material length scale parameter $\left( h/l_\mathrm{m},l_\mathrm{c}/l_\mathrm{m} \right)$, surface elastic modulus $\left( E_\mathrm{c}^\mathrm{s},E_\mathrm{m}^\mathrm{s} \right)$, surface residual stress $\left( \tau _\mathrm{c}^\mathrm{s},\tau _\mathrm{m}^\mathrm{s} \right)$, gradient index $\left( k \right)$, and beam thickness $\left( h \right)$. Also, the influence of the nonclassical boundary conditions (NCBCs) is investigated for simply supported beams. Moreover, to explore the effect of the homogenization technique of the functionally graded materials, the results are obtained using power law and sigmoid function schemes.

Fig. 4

Variation of the bulk equivalent stiffness $D_{xx}$ of an FG microbeam with the bulk modulus of elasticity ratio and the gradient index, a SIG-FG and b PL-FG

For this purpose, consider an FGM beam made of aluminum (Al) and silicon (Si) with the bulk and surface material properties tabulated in Table 5 [22, 25, 49, 62, 72, 73]. However, there are no available data of the material length scale parameter for silicon ($l_{\mathrm {Si}}$) or functionally graded materials l(z) in the open literature. In addition, the relation between the bulk and surface material properties and dimensions needs an experimental work, which is also not reported in the open literature. Several studies have been performed to investigate the effect of the material length scale parameter on the response of micro /nanostructures by supposing a range of h/l for homogeneous or FGM beams and plates [9, 74, 75]. To overcome the problem of the unknown value of $l_{\mathrm {Si}}$, it can be assumed as a ratio of $l_{\mathrm {AL}}$ [5, 76,77,78]. In all of the preceding numerical results, the length and width are selected as the ratios of, respectively, $L / h=15$ and $b / h=1$, unless other values of the material or geometrical parameters are mentioned.

5.1 Effect of the bulk modulus of the elasticity ratio

In this study, the effect of the bulk modulus of the elasticity ratio, i.e., $E_\mathrm{r}=E_\mathrm{c}^{B} / E_\mathrm{m}^{B}$, on the linear and nonlinear vibration responses of FG beams based on the classical analysis is investigated, considering both sigmoid function and power law for the material gradation. The following results are obtained by keeping the elastic modulus of the metallic bulk material $E_\mathrm{m}^{B}$ constant at 90 GPa, while that of the ceramic bulk material $E_\mathrm{c}^{B}$ is controlled by the variation of $E_\mathrm{r}$. The dimensions are as follows: $h=2l_\mathrm{m}=13.16 \,{\upmu \hbox {m}}$, $b=h$, and $L=15\,{h}$. It is seen from Fig. 4 that increasing the ratio $E_\mathrm{r}$ increases the bulk equivalent stiffness $D_{xx}$, defined in Eq. (17.1), of both SIG-FG and PL-FG beams. On the other hand, as the gradient index increases, $D_{xx}$ is slightly decreased for SIG-FG and increased for PL-FG beam. However, employing SIG-FG or PL-FG homogenization technique leads to the same beam stiffness at $k=1$, and consequently, they yield an identical vibration response.

Fig. 5

Variation of the dimensionless fundamental linear frequency of a simply supported FG microbeam with $E_\mathrm{r}$ and k based on the classical analysis, a SIG-FG and b PL-FG

Fig. 6

Variation of the dimensionless fundamental nonlinear frequency versus the maximum nonlinear amplitude of a simply supported FG microbeam at different values of $E_\mathrm{r}$ and k based on the classical analysis, a SIG-FG and b PL-FG

Based on the results shown in Fig. 4, increasing the ratio $E_\mathrm{r}$ noticeably increases the dimensionless fundamental linear and nonlinear frequencies of the simply supported FG beam, as figured out in Figs. 5 and  6, respectively. Table 6 tabulates the dimensionless fundamental linear and nonlinear frequencies of the simply supported and clamped–clamped beams for different values of $E_\mathrm{r}$ and k. From these results, it is seen that the effects of $E_\mathrm{r}$ and k on the fundamental linear and nonlinear frequencies show a similar trend as the linear frequency is the starting value for estimating the nonlinear frequency. The fundamental frequencies of the simply supported and clamped–clamped beams are influenced by $E_\mathrm{r}$ and k in a similar way, except that the frequencies of the clamped–clamped beam are larger than those of the simply supported due to the additional stiffness induced by the clamped end. In addition, increasing the gradient index significantly decreases or increases the effect of the ratio $E_\mathrm{r}$ in the case of SIG-FG and PL-FG beams, respectively. For a simply supported beam at $Q_{w}=0.2$, changing $E_\mathrm{r}$ from 1.5 to 4.744, i.e., $E_\mathrm{c}^{B}$ changes from 135 to 427 GPa (SiC), respectively, the fundamental nonlinear frequency of simply supported microbeam is increased by 47.6, 43.2, and 38.2% (SIG-FG) and 33.5, 43.2, and 52.7% (PL-FG) for k of 0.5, 1, and 2, respectively. The effect of the ratio $E_\mathrm{r}$ on the linear vibration response is found to be slightly lower than on the nonlinear response.

Moreover, as the vibration amplitude increases, the fundamental nonlinear frequency of the FG beams increases. In addition, incorporating the geometrical nonlinearity due to von Kármán’s strain increases the frequencies as the beam becomes stiffer. However, the influence of the geometrical nonlinearity on the vibration response of a simply supported beam is higher than that of a clamped–clamped beam as its contribution depends on the structure degree of freedom, i.e., the degree of freedom of a simply supported end is higher than for the clamped–clamped end type.

Table 6 Dimensionless fundamental linear and nonlinear frequencies of simply supported and clamped–clamped SIG-FG and PL-FG microbeams based on the classical analysis ($h=2l_\mathrm{m}$, $b=h$, $L / h=15$)

5.2 Effect of the material length scale parameter

The microstructure length scale parameter introduced in MCST is an inherent material parameter, and thus, it may have different values for different materials. The length scale parameter for specific materials is determined experimentally [79, 80] or using the atomistic simulations method [81]. Since the material length scale parameter is not experimentally determined for all different materials, some developed formulations of functionally graded microbeams were based on the assumption of constant material length scale parameter [9, 74, 75]. The present model treats the material length scale parameter as a variable according to the proposed gradation schemes. The material length scale parameter of the metallic constituent is held constant at $l_\mathrm{m}=6.58\,\upmu \text {m}$, as provided in Table 5, and that of the ceramic constituent is taken as a ratio of $l_\mathrm{m}$ as $\left( l_\mathrm{c} / l_\mathrm{m} \right)$ [5, 76,77,78]. The results in this parametric study are obtained based on incorporating the effect of microstructure only (CS analysis).

Figure 7 demonstrates the variation of the dimensionless fundamental linear frequency of the simply supported FG microbeams versus the material length scale parameter ratio $\left( l_\mathrm{c} /l_\mathrm{m} \right)$ and the gradient index (k). It is depicted that increasing the ratio $l_\mathrm{c} / l_\mathrm{m}$ increases the stiffness–hardening of the microbeam, and hence, the fundamental linear frequency increases. For the same ratio $l_\mathrm{c} / l_\mathrm{m}$, employing the SIG-FG law yields a higher linear frequency compared with PL-FG law when $k<1$, whereas an opposite behavior is detected when $k>1$. Such behavior can be explained in light of the fact that the in-plane shear stiffness coefficient ($S_{xy}$) is the only quantity that depends on l(z), as shown in Eq. (17.1). It is noticed from Fig. 8 that for a certain value of the ratio $l_\mathrm{c} / l_\mathrm{m}$, $S_{xy}$ of SIG-FG is higher than that of PL-FG microbeam for k less than unity and vice versa for k larger than unity. In Fig.  9, the dimensionless fundamental linear frequency of the simply supported FG microbeam is presented as a function of the ratio $l_\mathrm{c} / l_\mathrm{m}$ and $h /l_\mathrm{m}$ at $k=0.5$. For a better illustration, selected numerical values of the dimensionless fundamental linear frequency of the simply supported and clamped–clamped FG nanobeams are tabulated in Tables 7 and 8 for different values of $l_\mathrm{c}\mathrm {/}l_\mathrm{m}$, $h\mathrm {/}l_\mathrm{m}$, and k, considering SIG-FG and PL-FG laws. The results show that the dimensionless linear frequencies predicted by the classical microbeam model are independent of the material length scale parameters, and their values are lower than those computed based on the couple stress analysis. This is attributed to that incorporating the effect of couple stress makes a microbeam stiffer and consequently leads to an increase in the vibration frequencies. Generally, this effect can be ignored when $h /l_\mathrm{m}$ becomes large as demonstrated in Fig. 9. Additionally, it is noticed that as the material length scale parameter of the ceramic component becomes larger compared to that of the metallic component ($l_\mathrm{c} /l_\mathrm{m}$), the vibration frequency of the FG microbeam becomes larger significantly.

Fig. 7

Variation of the dimensionless fundamental linear frequency of a simply supported FG microbeam with $l_\mathrm{c} / l_\mathrm{m}$ and k based on the CS analysis ($l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $b=h$, $L / h=15$, $h / l_\mathrm{m}=2$), a SIG-FG and b PL-FG

Fig. 8

Variation of the in-plane shear stiffness coefficient $S_{xy}$ of an FG microbeam with $l_\mathrm{c} / l_\mathrm{m}$ and k ($l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $b=h$, $L / h=15$, $h / l_\mathrm{m}=2$), a SIG-FG and b PL-FG

Fig. 9

Variation of the dimensionless fundamental linear frequency of a simply supported FG microbeam with $l_\mathrm{c} / l_\mathrm{m}$ and $h / l_\mathrm{m}$ based on the CS analysis ($l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $b=h$, $L / h=15$, $k=0.5$), a SIG-FG and b PL-FG

Table 7 Dimensionless fundamental linear frequency of simply supported SIG-FG and PL-FG microbeams based on CS analysis ($l_\mathrm{m}=6.58\,\upmu \hbox {m}$, $b=h$, $L / h=15$)

Table 8 Dimensionless fundamental linear frequency of clamped–clamped SIG-FG and PL-FG microbeams based on CS analysis ($l_\mathrm{m}=6.58\,\upmu \hbox {m}$, $b=h$, $L / h=15$)

Fig. 10

Variation of the dimensionless fundamental nonlinear frequency versus the maximum nonlinear amplitude of a simply supported FG microbeam at different values of $l_\mathrm{c} / l_\mathrm{m}$ and $h / l_\mathrm{m}$ based on the CS analysis ($l_\mathrm{m}=6.58\,{\upmu \hbox {m}}$, $b=h$, $L / h=15$, $k=0.5$), a SIG-FG and b PL-FG. Solid lines: at $h / l_\mathrm{m}=2$; circle markers: at $h / l_\mathrm{m}=5$

Table 9 Combined effects of $l_\mathrm{m} /l_\mathrm{c}$ and $h / l_\mathrm{m}$ on the dimensionless fundamental nonlinear frequency of simply supported SIG-FG and PL-FG microbeams based on CS analysis ($l_\mathrm{m}=6.58\,\upmu \hbox {m},b=h$, $L / h=15$)

Table 10 Combined effects of $l_\mathrm{m} / l_\mathrm{c}$ and $h / l_\mathrm{m}$ on the dimensionless fundamental nonlinear frequency of clamped–clamped SIG-FG and PL-FG microbeams based on CS analysis ($l_\mathrm{m}=6.58\,\upmu \hbox {m},b=h$, $L /h=15$)

Fig. 11

Variation of the dimensionless fundamental linear frequency of SIG-FG and PL-FG nanobeams with $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$  ($k=0.5$), a simply supported with NCBCs, b simply supported with CBCs, and c clamped–clamped

Fig. 12

Variation of the dimensionless fundamental nonlinear frequency versus the maximum nonlinear amplitude of a simply supported FG nanobeam at different values of $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$ ($k=0.5$), a SIG-FG and b PL-FG

In addition, based on the results in Figs. 8 and  9 and Tables 7 and 8, it is observed that the values of the fundamental linear frequencies based on a position-independent material length scale parameter, i.e., $l_\mathrm{c}=l_\mathrm{m}$, are distinctly different from those predicted based on a position-dependent material length scale parameter, i.e., $l_\mathrm{c}\ne l_\mathrm{m}$, especially with the growth of $l_\mathrm{c}\mathrm {/}l_\mathrm{m}$ or $l_\mathrm{m}/h$. With the increase in $h/l_\mathrm{m}$, the effect of the material length scale parameter ratio becomes inconspicuous. Also, the effect of the material length scale parameter ratio on increasing the fundamental linear frequency of both SIG-FG and PL-FG microbeams becomes more notable as the gradient index increases. For the simply supported FG microbeam with $h/l_\mathrm{m}=2$, increasing $l_\mathrm{c}/l_\mathrm{m}$ from 0.5 to 2 shows an increase in the dimensionless linear frequency by about 49.4, 54, 68.7% (SIG-FG) and 34.3, 54, 96.7% (PL-FG) for a gradient index k of 0.5, 1, 10, respectively. In addition, as the dimensionless material length scale parameter $h/l_\mathrm{m}$ increases from 1 to 5 and at $k=0.5$, the dimensionless linear frequency is decreased by about 42.6, 52.6, 64.1% (SIG-FG) and 45.8, 52.4, 61.8% (PL-FG) for $l_\mathrm{c}/l_\mathrm{m}$ of 0.5, 1, and 2, respectively. In addition, it is noticeable that the effect of the ratio $l_\mathrm{c} /l_\mathrm{m}$ on the fundamental linear frequency of the simply supported and clamped–clamped FG microbeams is similar to a negligible difference.

Fig. 13

Variation of the dimensionless fundamental linear frequency for SIG-FG and PL-FG nanobeams with $\tau _\mathrm{m}^\mathrm{s}$ and $\tau _\mathrm{c}^\mathrm{s}$ ($k=0.5$), a simply supported with NCBCs, b simply supported with CBCs, and c clamped–clamped

Fig. 14

Variation of the dimensionless fundamental nonlinear frequency versus the maximum nonlinear amplitude of a simply supported FG nanobeam at different values of $\tau _\mathrm{m}^\mathrm{s}$ and $\tau _\mathrm{c}^\mathrm{s}$ ($k=0.5$), a SIG-FG and b PL-FG

Fig. 15

Variation of the dimensionless fundamental linear frequency with the thickness of a simply supported FG nanobeam using different analyses ($k=0.5$, $l_\mathrm{m}=0.2\,\mathrm{h}, l_\mathrm{c}=1.5 l_\mathrm{m}$, $L / h=15$), a SIG-FG and b PL-FG

Considering the nonlinear vibration response, the dimensionless fundamental nonlinear frequency ${\varOmega }_{\mathrm {NL}}$ versus the maximum nonlinear vibration amplitude $Q_{w}$ is plotted in Fig. 10 for various values of the ratio $l_\mathrm{c} /l_\mathrm{m}$, two different values of $h /l_\mathrm{m}$ of 2 and 5, and $k=0.5$. Tables 9 and 10 include the values of ${\varOmega }_{\mathrm {NL}}$ at different $Q_{w} ,l_\mathrm{c} / l_\mathrm{m}$, $h/l_\mathrm{m}$, and k. It is noticed that the combined effects of geometric nonlinearity and couple stress result in more hardening for the simply supported FG microbeam when compared with the clamped–clamped one. Also, the influences of $l_\mathrm{c} /l_\mathrm{m}$ and $h/l_\mathrm{m}$ on ${\varOmega }_{\mathrm {NL}}$ of the clamped–clamped FG microbeam are slightly larger than those for a simply supported microbeam, and these influences are much more significant when the gradient index increases. As mentioned before, this is attributed to that the microbeam becomes stiffer as $l_\mathrm{c}$ becomes larger than $l_\mathrm{m}$ or $l_\mathrm{m}$ is smaller than h. One can notice that the dimensionless nonlinear frequency is considerably increased by increasing $l_\mathrm{c} /l_\mathrm{m}$ and significantly reduced by decreasing $h/l_\mathrm{m}$. For $Q_{w}=0.2$ and $h/l_\mathrm{m}=2$, as $l_\mathrm{c}/l_\mathrm{m}$ increases from 0.5 to 2, ${\varOmega }_{\mathrm {NL}}$ increases by about 44.6, 48.6, and 61.4% (SS SIG-FG), 31, 48.6, and 86.3% (SS PL-FG), 47.6, 52.2, and 65.4% (CC SIG-FG), and 33, 52.2, and 92.1% (CC PL-FG) for k of 0.5, 1, and 10, respectively. Also, ${\varOmega }_{\mathrm {NL}}$ of the clamped–clamped FG microbeam changes slightly by varying $Q_{w}$. In addition, comparing the results in Tables 7 , 8, 9, and 10, it is depicted that the effects of $l_\mathrm{c} /l_\mathrm{m}$ and $h/l_\mathrm{m}$ on the nonlinear frequency response are less significant than those on the linear response.

However, the obtained results reveal that the dimensionless linear and nonlinear frequencies are very sensitive to the variations in the ratio $l_\mathrm{c}/l_\mathrm{m}$, especially at $h /l_\mathrm{m}=1$. In addition, the effect of $h/l_\mathrm{m}$ is considerably influenced by $l_\mathrm{c}/l_\mathrm{m}$. At $k=0.5$ and $Q_{w}=0.2$, increasing $h/l_\mathrm{m}$ of a simply supported microbeam from 1 to 5 reduces ${\varOmega }_{\mathrm {NL}}$ by about 39.9, 49.6, and 61.9% (SS SIG-FG), 42.6, 49.5, and 59.5% (SS PL-FG), 41.5, 51.2, and 62.3% (CC SIG-FG), and 44.8, 51, and 60.1% (CC PL-FG) for $l_\mathrm{c}/l_\mathrm{m}$ of 0.5, 1, and 2, respectively. It can be generally concluded that the material length scale parameter should be considered as spatial-dependent function (l(z)) in either a linear or nonlinear analysis of small-scale FG beams, as proposed in the present study.

5.3 Effect of surface energy

The effect of surface parameters, surface elasticity modulus ($E^\mathrm{s}(z)$), and surface residual stress ($\tau ^\mathrm{s}(z)$), on the linear and nonlinear vibration responses is explored for FG simply supported and clamped–clamped nanobeams with $h=20\,\text {nm}$, $b=h$, and $L /h=15$. Both sigmoid and power law gradation schemes are investigated using the bulk and surface material properties provided in Table 5, in the absence of a microstructure effect.

5.3.1 Effect of surface elastic modulus

The influence of the surface elasticity modulus of the metallic and ceramic constituents, $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$, respectively, on the dimensionless linear frequency of FG nanobeams at $k=0.5$ is demonstrated in Fig. 11 when the surface residual stress is ignored. Figure 12 shows the variation of the dimensionless nonlinear frequency of the simply supported FG nanobeams versus the nonlinear amplitude at different values of $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$. The dimensionless fundamental linear and nonlinear frequencies in this study are tabulated in Tables 11 and 12. From these results, it can be easily found that the positive surface modulus of elasticity of the metallic $(E_\mathrm{m}^\mathrm{s})$ or the ceramic material ($E_\mathrm{c}^\mathrm{s}$) increases the first-mode linear frequencies. The main trend is that the fundamental linear and nonlinear frequencies are slightly increased by increasing $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$ simultaneously or individually. The effects of $E_\mathrm{m}^\mathrm{s}$ and $E_\mathrm{c}^\mathrm{s}$, when the bulk material follows SIG-FG, are lower than those when following PL-FG. Also, the surface elasticity moduli have a slight impact on the fundamental nonlinear frequency compared with the linear frequency. Generally, it can be concluded that the positive surface elasticity moduli add stiffness to the system and thus result in larger linear and nonlinear frequencies, whereas an opposite effect is noticed for negative values.

Table 11 Combined effects of $E_\mathrm{m}^\mathrm{s}$, $E_\mathrm{c}^\mathrm{s}$, and k on the dimensionless fundamental linear frequency of FG nanobeams ($h=20\,\mathrm {nm}$, $b=h$, $L / h=15$, $E_{m0}^\mathrm{s}=-7.3563\,\mathrm {N/m}$, $E_{c0}^\mathrm{s}=-10.0497\,\mathrm {N/m}$)

Table 12 Combined effects of $E_\mathrm{m}^\mathrm{s}$, $E_\mathrm{c}^\mathrm{s}$, and k on the dimensionless fundamental nonlinear frequency of FG nanobeams ($h=20\,\mathrm {nm}$, $b=h$, $L /h=15$, $E_{m0}^\mathrm{s}=-7.3563\,\mathrm {N/m}$, $E_{c0}^\mathrm{s}=-10.0497\,\mathrm {N/m}$)

Table 13 Combined effects of $\tau _\mathrm{m}^\mathrm{s}$, $\tau _\mathrm{c}^\mathrm{s}$, and k on the dimensionless fundamental linear frequency of FG nanobeams ($h=20\,\mathrm {nm}$, $b=h$, $L / h=15$, $\tau _{m0}^\mathrm{s}=0.5689\,\mathrm {N/m}$, $\tau _{c0}^\mathrm{s}=0.6056\,\mathrm {N/m}$)

5.3.2 Effect of surface residual stress

The dimensionless fundamental linear frequency of FG nanobeams versus the surface residual stresses ($\tau _\mathrm{m}^\mathrm{s}$ and $\tau _\mathrm{c}^\mathrm{s}$) is shown in Fig. 13 at $k\mathrm {=0.5}$ and $E_\mathrm{c}^\mathrm{s}=E_\mathrm{m}^\mathrm{s}\mathrm {=0}$, while the variation of the dimensionless fundamental nonlinear frequency versus the amplitude of nonlinearity is depicted in Fig. 14 for various values of $\tau _\mathrm{m}^\mathrm{s}$ and $\tau _\mathrm{c}^\mathrm{s}$. The values of the dimensionless linear and nonlinear frequencies of the simply supported and clamped–clamped FG nanobeams are provided in Tables 13 and  14 for different values of $\tau _\mathrm{m}^\mathrm{s} ,\tau _\mathrm{c}^\mathrm{s}$, k, and nonlinear amplitude. In view of these results, it can be seen that the positive values of the surface residual stresses increase the fundamental linear and nonlinear frequencies, and negative values tend to decrease the frequencies. Like the effect of surface elasticity moduli, positive surface residual stresses stiffen the FG nanobeam and in turn lead to higher linear and nonlinear frequencies. The presence of the surface residual stresses dependent terms in simply supported boundary conditions (NCBCs), i.e., ${\mathcal {P}}_{1}^{*}/2$ and $C_{1}^{*}/2$ in Eq. (28.1) acts as self-excitation loading and causes deformation of the FG nanobeam at no external load. As a consequence, the impact of the surface residual stress on the linear and nonlinear frequencies of simply supported FG nanobeams is larger than that of clamped–clamped ends. Comparing between Figs. 11 and 13 as well as Figs. 12 and 14 shows that the effect of the surface residual stress on the frequency response is considerably more pronounced than that of the surface elasticity modulus.

5.4 Effect of the nonclassical boundary conditions

One of the contributions in the developed model and proposed solution procedure is applying the nonclassical (nonideal) boundary conditions (NCBCs) for simply supported FG nanobeams, represented by Eq. (28.1). In NCBCs besides, the nonlinearity in the boundaries’ equations, there is a part of surface energy effect which contributes as an internal excited loading in the case of simply supported FG nanobeams. The effect of NCBCs on the dimensionless linear frequency of simply supported FG nanobeams is presented in Figs. 11a, b and 13a, b based on SE analysis. Also, a comparison between values of the dimensionless linear and nonlinear frequencies employing NCBCs and CBCs is presented in Tables 15 and 16, considering both surface energy (SE) and integrated couple stress-surface energy (CSSER) models. From these results, it can be extracted that for both SIG-FG and PL-FG nanobeams using NCBCs results in linear and nonlinear frequencies lower than those using CBCs for positive $\tau ^\mathrm{s}$, whereas negative $\tau ^\mathrm{s}$ leads to an opposite effect. Varying $E^\mathrm{s}$ from a negative to a positive value has a significant effect on the contribution of NCBCs for negative $\tau ^\mathrm{s}$, and this effect becomes very small to be negligible for positive $\tau ^\mathrm{s}$. Also, the impact of NCBCs on the vibration response increases as the gradient index increases. Moreover, it can be concluded that NCBCs should not be neglected in the formulation of linear and nonlinear vibration problems of simply supported FG nanobeams.

Table 14 Combined effects of $\tau _\mathrm{m}^\mathrm{s}$, $\tau _\mathrm{c}^\mathrm{s}$, and k on the dimensionless fundamental nonlinear frequency of FG nanobeams ($h=20\,\mathrm{nm}$, $b=h$, $L /h=15$, $\tau _{m0}^\mathrm{s}=0.5689\,\mathrm {N/m}$, $\tau _{c0}^\mathrm{s}=0.6056\,\mathrm {N/m}$)

Table 15 Effect of the thickness on the dimensionless fundamental linear frequency of a simply supported FG nanobeam using different analyses with NCBCs and CBCs at various values of k and $h /l_\mathrm{m} (l_\mathrm{c} / l_\mathrm{m}=1.5$, $L / h=15)$

Table 16 Effect of the thickness on the dimensionless fundamental nonlinear frequency of a simply supported FG nanobeam using different analyses with NCBCs and CBCs at various values of k and $Q_{w}$ ($h / l_\mathrm{m}=0.2$, $l_\mathrm{c} /l_\mathrm{m}=1.5$, $L / h=15)$

5.5 Effect of nanobeam thickness

The variation of the dimensionless fundamental linear and nonlinear frequencies for the simply supported nanobeam at different thicknesses is considered in Figs. 15 and  16, respectively, based on the various analyses of SIG-FG and PL-FG distributions. The material parameters are those provided in Table 5 with $k=0.5$, $l_\mathrm{m}=0.2\,\mathrm{h}$, $l_\mathrm{c}=1.5l_\mathrm{m}$, and $L=15\,\mathrm{h}$. Some values of the dimensionless fundamental linear and nonlinear frequencies, respectively, are reported in Tables 15 and 16 at different thicknesses of the simply supported FG nanobeam. It is noticeable that the dimensionless linear and nonlinear frequencies obtained by the classical elasticity (CL) and couple stress (CS) models are unaffected by varying the nanobeam thickness. Also, it is obvious that for surface energy (SE) and integrated couple stress-surface energy (CSSER) models increasing the thickness increases the dimensionless linear and nonlinear frequencies, and their values approach those obtained by the classical elasticity model. Such behavior is due to that the surface layer area-to-the bulk volume ratio is reduced by increasing thickness, and thus, a reduction in surface energy effect is detected.

In addition, the inclusion of NCBCs decreases the contribution of surface energy to the linear and nonlinear responses, especially at large values of the nanobeam thickness, and this effect is decreased by increasing the gradient index or nanobeam thickness. Moreover, increasing the gradient index of SIG-FG and PL-FG nanobeams, respectively, reduces and increases the surface energy effect in both SE and CSSER models. This is observed for all nonlinear vibration amplitudes regardless of employing NCBCs or CBCs.

6 Conclusions

In this article, a continuum mechanics model is developed to study the nonlinear vibration response of FG Timoshenko nanobeams considering the nonlinear von Kármán strains. In order to account for the size-dependent effects, modified couple stress and Gurtin–Murdoch surface elasticity theories are employed. All the bulk and surface properties of the FG nanobeam material are assumed to vary across the thickness based on sigmoid and power law distribution functions. The nonlinear governing equations and corresponding nonideal boundary conditions are exactly derived according to Hamilton’s principle, and then, GDQM was employed to discretize them in the spatial domain with an exact implementation of the nonideal boundary conditions. Runge–Kutta and pseudo-arclength continuation methods are used to obtain the nonlinear free vibration responses. By a comprehensive parametric study, the effects of bulk modulus of elasticity, surface energy, material length scale, and small-scale parameters are investigated for both sigmoid and power law FG micro-/nanobeams. The following main conclusions can be extracted from this study as below.

Fig. 16

Variation of the dimensionless fundamental nonlinear frequency versus the maximum nonlinear amplitude of a simply supported FG nanobeam using different analyses ($k=0.5$, $l_\mathrm{m}=0.2h$, $l_\mathrm{c}=1.5 l_\mathrm{m}L / h=15$), a SIG-FG and b PL-FG

Consideration of classical boundary conditions (CBCs) tends to overestimate the fundamental natural frequencies ${\varOmega }_{\mathrm {L}}$ and ${\varOmega }_{\mathrm {NL}}$ for the simply supported FG nanobeams having positive surface residual stress, while for negative surface residual stress, the natural frequency is underestimated. This effect is increased by increasing or decreasing the gradient index of, respectively, SIG-FG or PL-FG nanobeams. Moreover, the natural frequencies increase with the increase in surface elasticity theory parameters, surface residual stresses, and surface elasticity moduli, due to the induced stiffness-hardening effect, especially for very thin beams. The influence of surface parameters becomes more significant by decreasing or increasing the gradient index of SIG-FG or PL-FG nanobeams, respectively.

The dimensionless material length scale parameter $h /l_\mathrm{m}$ and material length scale parameter ratio $l_\mathrm{c} /l_\mathrm{m}$ have opposite effects; increasing $l_\mathrm{c} /l_\mathrm{m}$ results in the stiffness-hardening effect, while increasing $h /l_\mathrm{m}$ limits the local-microstructure effect. Depending on $h /l_\mathrm{m}$ and the gradient index, $l_\mathrm{c} /l_\mathrm{m}$ can display a dominant or ignored effect for both SIG-FG and PL-FG micro-/nanobeams. Also, spatial variation of the material length scale parameter should be considered in the analysis of FG beams. In addition, the combined effect of nonlinearity, couple stress, and positive surface parameters results in more stiffness-hardening for the FG nanobeam, especially with simply supported ends. For CSSER analysis, the local-microstructure effect becomes the dominant one at larger thicknesses whereas by decreasing the thickness the influence of the surface energy becomes dominant. The effects of the couple stress and surface parameters on the nonlinear vibration response of FG small-scale beams are slightly lower than those on the linear response.

Additionally, increasing the bulk modulus of elasticity ratio $E_\mathrm{r}$ increases the natural frequencies of FG micro-/nanobeams, and this effect is increased as the gradient index of SIG-FG or PL-FG is, respectively, decreases or increases. For all analyses, the frequency of SIG-FG nanobeams is higher than that of PL-FG nanobeams with $k<1$, while the opposite is noticed with $k>1$. Finally, neglecting any of the geometric nonlinearity, local microstructure, surface residual stress, surface elastic modulus, surface mass density, or nonclassical boundary conditions may result in an inaccurate analysis of FG micro-/nanobeams. Also, the vibration response of FG nanobeams can be controlled and optimized by the appropriate selection of the material distribution, i.e., SIG-FG or PL-FG functions, as well as the gradient index.

Appendices

Appendix A: Coefficients of Eq. (41.1)

The coefficients $\mathbb {K}_{1}:\mathbb {K}_{5},\mathbb {P}_{1}:\mathbb {P}_{5}$, and $\mathbb {M}_{1}:\mathbb {M}_{8}$ that appear in Eq. (41.1) are defined as follows:

$$\begin{aligned} \left\{ \begin{array}{c} {{\mathbb {K}}}_{1}\\ {{\mathbb {K}}}_{2}\\ {\begin{array}{l@{\quad }l} {{\mathbb {K}}}_{3}\\ {{\mathbb {K}}}_{4}\\ {{\mathbb {K}}}_{5}\\ \end{array} }\\ \end{array} \right\}= & {} \int _0^1 \left\{ {\begin{array}{c} {\mathbb {k}}_{1}\phi _{u}\\ {\mathbb {k}}_{2}\phi _{u}^{''}\\ {\begin{array}{c} {\mathbb {k}}_{\mathrm {4}}\left( w_{s}^{'}\phi _{w}^{''}+w_{s}^{''}\phi _{w}^{'} \right) +{\mathbb {k}}_{\mathrm {5}}\phi _{w}^{'}+{\mathbb {k}}_{\mathrm {6}}\phi _{w}^{'''}\\ {\mathbb {k}}_{\mathrm {3}}\phi _{\psi }^{''}+{\mathbb {k}}_{\mathrm {7}}\phi _{\psi }\\ {\mathbb {k}}_{\mathrm {4}}\phi _{w}^{'}\phi _{w}^{''}\\ \end{array} }\\ \end{array} } \right\} \phi _{u}\hbox {d}x, \end{aligned}$$

(A.1)

$$\begin{aligned} \left\{ {\begin{array}{c} {\mathbb {P}}_{1}\\ {\mathbb {P}}_{2}\\ {\begin{array}{c} {\mathbb {P}}_{3}\\ {\mathbb {P}}_{4}\\ {\mathbb {P}}_{5}\\ \end{array} }\\ \end{array} } \right\}= & {} \int _0^1 \left\{ {\begin{array}{c} {\mathbb {P}}_{1}\phi _{\psi }\\ {\mathbb {P}}_{2}\phi _{\psi }^{''}+{\mathbb {P}}_{\mathrm {7}}\phi _{\psi }\\ {\begin{array}{c} {\mathbb {P}}_{\mathrm {3}}\phi _{u}^{''}\\ {\mathbb {P}}_{\mathrm {4}}\left( w_{s}^{'}\phi _{w}^{''}+w_{s}^{''}\phi _{w}^{'} \right) +{\mathbb {P}}_{\mathrm {5}}\phi _{w}^{'}+{\mathbb {P}}_{\mathrm {6}}\phi _{w}^{'''}\\ {\mathbb {P}}_{\mathrm {4}}\phi _{w}^{'}\phi _{w}^{''}\\ \end{array} }\\ \end{array} } \right\} \phi _{\psi }\hbox {d}x, \end{aligned}$$

(A.2)

$$\begin{aligned} \left\{ {\begin{array}{c} {\mathbb {M}}_{1}\\ {\mathbb {M}}_{2}\\ {\begin{array}{c} {\mathbb {M}}_{\mathrm {3}}\\ {\mathbb {M}}_{\mathrm {4}}\\ \end{array} }\\ \end{array} } \right\}= & {} \int _0^1 \left\{ {\begin{array}{c} {\mathbb { I}}_{w}\phi _\mathrm{w}\\ \mathbb {c}_{0}\phi _{w}^{''}+\mathbb {c}_{1}\phi _{w}^{'''}+\mathbb {c}_{\mathrm {4}}\left( u_{s}^{''}\phi _{w}^{'}+u_{s}^{'}\phi _{w}^{''} \right) +\mathbb {c}_{\mathrm {5}}\left( \psi _{s}^{''}\phi _{w}^{'}+\psi _{s}^{'}\phi _{w}^{''} \right) +\mathbb {c}_{\mathrm {6}}\left( w_{s}^{\mathrm {'2}}\phi _{w}^{''}+{2w}_{s}^{'}w_{s}^{''}\phi _{w}^{'} \right) \\ {\begin{array}{c} \mathbb {c}_{2}\phi _{\psi }^{'''}+\mathbb {c}_{\mathrm {3}}\phi _{\psi }^{'}+\mathbb {c}_{\mathrm {5}}\left( w_{s}^{''}\phi _{\psi }^{'}+w_{s}^{'}\phi _{\psi }^{''} \right) \\ \mathbb {c}_{\mathrm {4}}\left( w_{s}^{''}\phi _{u}^{'}+w_{s}^{'}\phi _{u}^{''} \right) \\ \end{array} }\\ \end{array} } \right\} \phi _{w}\hbox {d}x, \nonumber \\\end{aligned}$$

(A.3)

$$\begin{aligned} \left\{ {\begin{array}{c} {\mathbb {M}}_{\mathrm {5}}\\ {\mathbb {M}}_{\mathrm {6}}\\ {\begin{array}{c} {\mathbb {M}}_{\mathrm {7}}\\ {\mathbb {M}}_{\mathrm {8}}\\ \end{array} }\\ \end{array} } \right\}= & {} \int _0^1 \left\{ {\begin{array}{c} \mathbb {c}_{\mathrm {4}}\left( \phi _{u}^{''}\phi _{w}^{'}+\phi _{u}^{'}\phi _{w}^{''} \right) \\ \mathbb {c}_{\mathrm {5}}\left( \phi _{\psi }^{''}\phi _{w}^{'}+\phi _{\psi }^{'}\phi _{w}^{''} \right) \\ {\begin{array}{c} \mathbb {c}_{\mathrm {6}}\left( {2w}_{s}^{'}\phi _{w}^{'}\phi _{w}^{''}+w_{s}^{''}\phi _{w}^{{'2}} \right) \\ \mathbb {c}_{\mathrm {6}}\phi _{w}^{\mathrm {'2}}\phi _{w}^{''}\\ \end{array} }\\ \end{array} } \right\} \phi _{w}\hbox {d}x. \end{aligned}$$

(A.4)

Appendix B: Pseudo-arclength continuation

The pseudo-arclength continuation is used to find the steady-state periodic response of a Timoshenko nanobeam, Eq. (41), in a time period $T={2\pi } /{\varOmega }_{\mathrm {NL}}$. In order to obtain this response, we define ${\bar{\tau }}=t /T$; afterward using a spectral collocation method, the system is discretized over the time domain ${\bar{\tau }}$ into an even number of periodic grid points $(N_{t})$ given by Eq. (B.1),

$$\begin{aligned} {\bar{\tau }}=\frac{i}{N_\mathrm{t}}, 0<i<1, \quad i=1,2,\ldots , N_\mathrm{t}. \end{aligned}$$

(B.1)

Then, the discretized system will be

$$\begin{aligned}&\left( \frac{{\varOmega }_{\mathrm {NL}}}{2\pi } \right) ^{2} {{\mathbb {K}}}_{1}D_\mathrm{t}^{\left( 2 \right) }Q_{u}+{{\mathbb {K}}}_{2}Q_{u}+{{\mathbb {K}}}_{3}Q_{w}+{{\mathbb {K}}}_{4}Q_{\psi }+{{\mathbb {K}}}_{5}\left( Q_{w} \right) ^{\circ 2}=0, \end{aligned}$$

(B.2)

$$\begin{aligned}&\left( \frac{{\varOmega }_{\mathrm {NL}}}{2\pi } \right) ^{2}{\mathbb {M}}_{1}D_\mathrm{t}^{\left( 2 \right) }Q_{w}+{\mathbb {M}}_{2}Q_{w}+{\mathbb {M}}_{3}Q_{\psi }+{\mathbb {M}}_{4}Q_{u}+{\mathbb {M}}_{5}\left( Q_{u}\circ Q_{w} \right) \nonumber \\&\quad +{\mathbb {M}}_{6}\left( Q_{\psi }\circ Q_{w} \right) + {\mathbb {M}}_{7}\left( Q_{w} \right) ^{\circ 2}+ {\mathbb {M}}_{8}\left( Q_{w} \right) ^{\circ 3}=0, \end{aligned}$$

(B.3)

$$\begin{aligned}&\left( \frac{{\varOmega }_{\mathrm {NL}}}{2\pi } \right) ^{2}{\mathbb {P}}_{1}D_\mathrm{t}^{(2)}Q_{\psi }+{\mathbb {P}}_{2}Q_{\psi }+{\mathbb {P}}_{3}Q_{u}+{\mathbb {P}}_{4}Q_{w}+{\mathbb {P}}_{5}\left( Q_{w} \right) ^{\circ 2}=0 \end{aligned}$$

(B.4)

where $\left( \circ \right)$ is the Hadamard product operator, ${\varOmega }_{\mathrm {NL}}$ is the nonlinear frequency to be calculated, the column vectors $\left\{ Q_{w},Q_{u},Q_{\psi }\right\}$ are defined as:

$$\begin{aligned} {\begin{array}{lcc} Q_{u}=\left[ q_{u_{1}}, q_{u_{2}}, \ldots q_{u_{N_\mathrm{t}}} \right] ^\mathrm{T}, &{} Q_{w}=\left[ q_{w_{1}}, q_{w_{2}}, \ldots q_{w_{N_\mathrm{t}}} \right] ^\mathrm{T}, &{} Q_{\psi }=\left[ q_{\psi _{1}}, q_{\psi _{2}}, \ldots q_{\psi _{N_\mathrm{t}}} \right] ^\mathrm{T},\\ \end{array} } \end{aligned}$$

(B.5)

and $D_\mathrm{t}^{(2)}$ is spectral differentiation matrix operator [65].

Equations (B.2–B.4) can be rewritten in the form

$$\begin{aligned} {\mathcal {F}}\left( {{\varvec{Q}}},{\varOmega }_{\mathrm {NL}} \right) =0 \end{aligned}$$

(B.6)

where ${\varvec{Q}}={{[}Q_{u}{,}Q_{w}{,}Q_{\psi }{]}}_{3N_\mathrm{t}\times 1}$. In order to employ the pseudo-arclength continuation method, Eq. (B.6) is parameterized by the arclength s, such that

$$\begin{aligned} {\mathcal {F}}\left( {{\varvec{Q}}}(s),{\varOmega }_{\mathrm {NL}}(s) \right) =0. \end{aligned}$$

(B.7)

To obtain a new, fully determined system for the two-vector $\left( {{\varvec{Q}}},{\varOmega }_{\mathrm {NL}} \right)$, a restriction is added such that

$$\begin{aligned} \left\| {\dot{{{\varvec{Q}}}}} \right\| ^{2}+\left\| {\dot{\varOmega }}_{\mathrm {NL}}^{2} \right\| ^{2}=1 \end{aligned}$$

(B.8)

where ${\dot{{{\varvec{Q}}}}}=\frac{\hbox {d}Q}{\hbox {d}s}$ and $\dot{\varOmega }_{\mathrm {NL}}=\frac{\hbox {d}\varOmega }{\hbox {d}s}$. With this restriction, we obtain a new, fully determined system for the two-vector $\left( {{\varvec{Q}}},{\varOmega }_{\mathrm {NL}} \right)$, as a function of s,

$$\begin{aligned} \left\{ {\begin{array}{cc} {\mathcal {F}}_{{{\varvec{Q}}}}{\dot{{{\varvec{Q}}}}}+ {\mathcal {F}}_{{\varOmega }_{\mathrm {NL}}}{\dot{\varOmega }}_{\mathrm {NL}}=0,\\ \left\| {\dot{Q}} \right\| ^{2}+\left\| {\dot{\varOmega }}_{\mathrm {NL}}^{2} \right\| ^{2}=1.\\ \end{array} } \right. \end{aligned}$$

(B.9)

Then, Eq. (B.9) can be solved by a predictor–corrector method, where the Newton-type iterations in the corrector are typically restricted to be perpendicular to the solution curve being continued. Afterward, the frequency response curves, i.e., nonlinear frequency ${\varOmega }_{\mathrm {NL}}$ versus nonlinear amplitude $Q_{w}$, are obtained.