1 Introduction

Knowledge and application of that knowledge are two different sides of the same coin. Recent advances in the application of nanotechnology have resulted in the manufacture of nanoelectromechanical devices. The attractiveness of them is due to their excellent and distinctive mechanical and electrical properties. Among them, carbon nanotubes (CNTs) have been regarded as a class of smart materials and attracted the attention of many researchers for application in optical transparency [1, 2], resonators [3,4,5], diagnosis of gas atoms [6], memory devices [7] and composite material [8].

In the following, it has been proved that the mechanical characteristics of nanostructures such as nanobeams are size dependent [9]. An investigation presented by Eringen and Edelen [9] revealed that the classical continuum theory is longer eligible for studying nanostructures. Thanks to recent advances in the technology of nanostructures, many researchers in their investigations [10,11,12,13,14,15,16] applied the nonlocal elasticity theory proposed and developed by Eringen and Edelen [9, 17]. The results emphasize that nanostructures are size dependent and the considered interaction between atoms should not be ignored.

Many studies have treated the problem with the effect of surface energy. It is well-known that due to increasing the ratio of surface area to bulk, the effect of surface energy becomes crucial and significant. Therefore, it should be taken into consideration. It is worth mentioning that after proposing a new theory of surface effects on nanoscale structures by Gurtin and Murdoch [18, 19], great attention was given to surface effects including high-order and residual surface stress in nanostructures. A two-dimensional theory of piezoelectric plates and shells by surface effects was established by Zhang et al. [20, 21]. Recently, Shaat et al. [22] realized that the effect of surface energy should be taken into consideration using Gurtin and Murdoch theory. Developing a continuum model, Dingreville et al. [23] took free surface energy into account and studied the effects of surface layers on the elastic behavior of nanowires. In another study, applying nonlocal strain gradient theory, Lu and his co-workers [24] found that the surface effects can influence the critical buckling at a high length-to-thickness ratio. To achieve this goal, they developed a size-dependent nanoplate. Effects of surface elasticity and residual surface stress on vibration behavior of microbeams were illustrated by Wang and Feng [25]. Karimi and Shahidi [26] demonstrated the effect of surface energy on buckling analysis of skew nanoplates. It was concluded that by increasing the skew angle, the surface layers have less effect on the buckling of nanoplate. Moreover, emphasizing the surface effects on nonlinear vibration characteristics, Ebrahimi and Hosseini [27] developed a double-layered viscoelastic nanoplate. Flexoelectricity and surface effects on vibration and mechanical behavior of nanoplates were studied by Ebrahimi and Barati [28, 29]. They found that considering the surface effect enhances the stiffness of flexoelectric nanoplate as well as natural frequency. Using couple stress and surface elasticity theories, Shaat and Mohamed [30] investigated the size-dependent results of nonlinear electrostatic model of actuated beams. Mechanical properties and buckling of nanowires incorporating surface elasticity and residual surface tension were investigated by Wang and Feng [31]. Chen et al. [32] modeled a Timoshenko beam to study the effects of surface stresses on the natural frequencies of functionally graded (FG) nanobeams (Table 1).

Table 1 Parameter definitions
Full size table

There are literatures devoted to dynamic instability including linear and nonlinear characteristics. She et al. [33, 34] investigated the effect of nonlinearity on the mechanical characteristics and buckling of FG porous nanobeams. Recently, Krylov and his co-workers [35] concluded that parametric excitation is able to make a stable region larger and instability of the system considerably depends on the damping coefficient. Wang et al. [36] used CNTs to study the effect of parametric excitation on instability. It was found that parametric excitation produces a gap between positive and negative detuning parameters. Other researches [37,38,39] also demonstrated the influence of parametric excitation on energy harvesting system. According to their results, amplitude in energy harvesting systems is considerably affected by parametric excitation. Wang [40] and Yan et al. [41] also explained the effect of parametric excitation on the characteristics of beams including Timoshenko beam model. The influence of thermo-magneto-mechanical loads in nonlinear instability of a short nanobeam exposed to an external parametric was conducted by Ghadiri and Hosseini [42]. The above literature survey in dynamic instability of micro/nanostructures clarifies that dynamic instability of micro- and nanostructures has been untouched in many aspects [43, 44].

Motivated by the lack of sufficient accuracy in the effect of residual surface stress on nonlinear dynamics and instability of double-walled nanobeams caused by an axial force producing parametric excitation, in the present study, the effect of considering residual surface stress on nonlinear dynamics and instability of double-walled nanobeams subjected to an external parametric excitation is investigated. A short double-walled nanobeam is modeled and embedded on a viscoelastic foundation. In the next step, nonlinear governing equation of motion is derived, while the nonlocal elasticity theory and nonlinear von Karman beam theory are applied. To solve the equations, Galerkin technique and multiple time scales method are employed as well. A class of nonlinear Mathieu–Hill equation is established to analyze the nonlinear instability of the system while the emphasis is placed on study of bifurcations.

2 Problem formulation

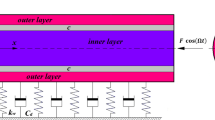
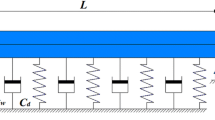
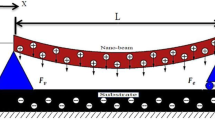
In Fig. 1, the schematic of double-walled nanobeam embedded on a viscoelastic foundation under an axial force is shown. For each layer of nanobeam, an axial force is employed as a function with a harmonic excitation with frequency \( \left( \varOmega \right) \). The thermo-magneto-mechanical loads are applied to expose the outer layer. Besides, the viscoelastic foundation is a combination of viscous damping coefficient \( \left( {c_{d} } \right) \) and Winkler coefficient \( \left( {k_{w} } \right) \). The length of nanobeam taken is \( L \) and the inner and outer diameters of nanobeam are \( d_{i} \) and \( d_{o} \), respectively.

Fig. 1
figure 1

The double-walled nanobeam embedded in a viscoelastic foundation subjected to parametric excitation

Full size image

2.1 Constitutive relations

Referring to the nonlocal elasticity theory presented by Eringen [45, 46], the key idea of the Eringen theory is that the nonlocal stress tensor \( \sigma_{kl,l} \) at point \( X \) can be defined as below:

$$ \sigma_{kl,k} - \rho \ddot{u}_{l} = 0, $$
(1)
$$ \sigma_{kl} \left( X \right) = \mathop \smallint \limits_{V}^{ } K\left( {X, X^{\prime}} \right)\tau_{kl} \left( {X^{\prime}} \right){\text{d}}V\left( {X^{\prime}} \right), $$
(2)
$$ \sigma_{kl} = \frac{1}{2}\left( {u_{k,l} + u_{l,k} } \right), $$
(3)

where \( K\left( {X, X^{\prime}} \right) \) is the Kernel function and represents the nonlocal modulus. Eringen [46] demonstrated that it is possible to represent the integral constitutive relation in an equivalent differential form as:

$$ \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)\sigma = \tau , $$
(4)

where \( \nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} \) is the Laplacian operator. In addition, \( \left( {e_{0} a} \right) \) is the nonlocal parameter in which \( e_{0} \) is a constant determined by experiments and proportionate to each material and \( a \) denotes internal characteristic length. According to nonlocal constitutive relations, it yields for nanobeams as:

$$ \sigma_{xx} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} \sigma_{xx} }}{{\partial x^{2} }} = E\varepsilon_{xx} . $$
(5)

Here we can define new terms as the axial force and the resultant bending moment so that:

$$ \left\{ {N,M} \right\} = \mathop \smallint \limits_{A}^{ } \sigma_{x} \left( {1,z} \right){\text{d}}A, $$
(6)

in which \( z \) depicts the transverse coordinate in the deflection direction. The displacements can be written as below:

$$ u_{1} \left( {x,z,t} \right) = u\left( {x,t} \right) - z\frac{\partial w}{\partial x}, u_{2} = 0, u_{3} \left( {x,z,t} \right) = w\left( {x,t} \right). $$
(7)

Here applying the nonlinear von Karman strain, it yields:

$$ \varepsilon = \varepsilon_{0} + z\kappa . $$
(8)

Using Eqs. (7) and (8), it yields:

$$ \varepsilon_{0} = \frac{\partial u}{\partial x} + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} , \kappa = - \frac{{\partial^{2} w}}{{\partial x^{2} }}. $$
(9)

From Eqs. (6)–(9), it can be written as:

$$ \begin{aligned} \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)N = EA\varepsilon_{0} \hfill \\ \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)M = EI\kappa , \hfill \\ \end{aligned} $$
(10)

where \( I_{i} = \mathop \smallint \limits_{{A_{i} }}^{ } z^{2} {\text{d}}A_{i} \left( {i = 1, 2} \right) \). Finally, the equation of motion is derived as follows [47, 48]:

$$ \begin{aligned} EI_{1} \frac{{\partial^{4} w_{1} }}{{\partial x^{4}}} - \frac{\partial}{\partial x}\left({N_{1} \frac{{\partial w_{1}}}{\partial x}} \right) + \left({e_{0} a} \right)^{2} \frac{{\partial^{3}}}{{\partial x^{3}}}\left({N_{1} \frac{{\partial w_{1}}}{\partial x}} \right) + \rho A_{1} \frac{{\partial^{2}}}{{\partial \mathop t\limits^{2}}}\left[{w_{1} - \left({e_{0} a} \right)^{2} \frac{{\partial^{2} w_{1} }}{{\partial x^{2}}}} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f_{1} - \left({e_{0} a} \right)^{2} \frac{{\partial^{2} f_{1} }}{{\partial x^{2}}}, \hfill \\ \end{aligned} $$
(11a)
$$ \begin{aligned} EI_{2} \frac{{\partial^{4} w_{2} }}{{\partial x^{4}}} - \frac{\partial}{\partial x}\left({N_{2} \frac{{\partial w_{2}}}{\partial x}} \right) + \left({e_{0} a} \right)^{2} \frac{{\partial^{3}}}{{\partial x^{3}}}\left({N_{2} \frac{{\partial w_{2}}}{\partial x}} \right) + \rho A_{2} \frac{{\partial^{2}}}{{\partial \mathop t\limits^{2}}}\left[{w_{2} - \left({e_{0} a} \right)^{2} \frac{{\partial^{2} w_{2} }}{{\partial x^{2}}}} \right] \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f_{2} - \left({e_{0} a} \right)^{2} \frac{{\partial^{2} f_{2} }}{{\partial x^{2}}}, \hfill \\ \end{aligned} $$
(11b)

in Eqs. (11a) and (11b), \( N_{i} \left( {i = 1,2} \right) \) are defined as below:

$$ N_{1} = F_{1} \cos \varOmega \tilde{t} - \left[ {\frac{{EA_{1} }}{2L}} \right]\mathop \int \limits_{0}^{L} \left( {\frac{{\partial w_{1} }}{\partial x}} \right)^{2} {\text{d}}x, $$
(12a)
$$ N_{2} = F_{2} \cos \varOmega \tilde{t} - \left[ {\frac{{EA_{2} }}{2L}} \right]\mathop \int \limits_{0}^{L} \left( {\frac{{\partial w_{2} }}{\partial x}} \right)^{2} {\text{d}}x $$
(12b)

in Eqs. (12a), (12b), the term of axial force \( \left( {F_{i} \cos \varOmega \tilde{t} i = 1,2} \right) \) is the reason of parametric excitation of the nanobeam. In Eqs. (11a) and (11b), \( f_{i} \left( {i = 1,2} \right) \) is defined as below:

$$ f_{1} = c\left( {w_{1} - w_{2} } \right), $$
(13a)
$$ f_{2} = k_{w} w_{2} + c_{d} \frac{{\partial w_{2} }}{{\partial \tilde{t}}}\; + \; c\left( {w_{2} - w_{1} } \right). $$
(13b)

Compared to bulk atoms in nanostructures, surface atoms have different properties and characteristics so that the surface effects should be considered when there is a high ratio of surface to bulk. It is possible to link surface stress \( \left( {\sigma^{s} } \right) \) and axial strain \( \left( {\varepsilon_{xx} } \right) \) by defining the following equation [49]:

$$ \sigma^{s} = \tilde{\tau }_{0} + E^{s} \varepsilon_{xx} . $$
(14)

It can be shown that an effective distributed transverse loading along the nanobeam length can be generated by the effects of the residual surface tensions on the surfaces of the Euler–Bernoulli nanobeam [25] so that:

$$ q = 2\tilde{\tau }_{0} b_{i} \frac{{\partial^{2} w_{i} }}{{\partial x^{2} }}. $$
(15)

Now, for Euler–Bernoulli nanobeam with surface effects, Eq. (10) for the longitudinal force and the nonlocal stress–strain relation can be written as follows [50]:

$$ \begin{aligned} N = \left( {EA_{i} } \right)^{*} \left[ {\mathop \int \limits_{0}^{L} \left( {\frac{{\partial w_{i} }}{\partial x}} \right)^{2} {\text{d}}x} \right] + 2\tilde{\tau }_{0} b_{i} \hfill \\ M - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} M_{ } }}{{\partial x^{2} }} = \left( {EI_{i} } \right)^{*} \frac{{\partial^{2} w}}{{\partial x^{2} }}. \hfill \\ \end{aligned} $$
(16)

Here (EI2)* and (EAi)* can be expressed as follows [51, 52]:

$$ \begin{aligned} \left( {EI_{i} } \right)^{*} = E\left( {\frac{{b_{i} h_{i}^{3} }}{12}} \right) + E^{s} \left[ {\frac{{h_{i}^{3} }}{6} + \frac{{b_{i} h_{i}^{2} }}{2}} \right], \hfill \\ \left( {EA_{i} } \right)^{*} = \frac{{EA_{i} }}{2L} + E^{s} \left[ {\frac{{h_{i} + b_{i} }}{L}} \right], A_{i} = h_{i} b_{i} , i = 1, 2. \hfill \\ \end{aligned} $$
(17)

According to Eqs. (11a, 11b–17), the governing equation of motion of Euler–Bernoulli nanobeam including surface effects is derived as:

$$ \begin{aligned} - \left( {EI_{1} } \right)^{*} \frac{{\partial^{4} w_{1} }}{{\partial x^{4} }}\, & - \left\{ {F_{1} \cos {\varOmega }\bar{t} - \left( {EA_{1} } \right)^{*} \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial w_{1} }}{\partial x}} \right)^{2} {\text{d}}x} \right\}\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} \\ & \quad + \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{1} }}{{\partial x^{4} }}\left\{ {F_{1} \cos {\varOmega }\bar{t} - \left( {EA_{1} } \right)^{*} \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial w_{1} }}{\partial x}} \right)^{2} {\text{d}}x} \right\} \\ & \quad + \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)c\left( {w_{1} - w_{2} } \right) - 2\tilde{\tau }_{0} \left[ {\frac{{\partial^{2} w_{1} }}{{\partial x^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{1} }}{{\partial x^{4} }}} \right] \\ & \quad = \rho A_{1} \left( {\frac{{\partial^{2} w_{1} }}{{\partial \bar{t}^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{1} }}{{\partial \bar{t}^{2} \partial x^{2} }}} \right), \\ \end{aligned} $$
(18a)
$$ \begin{aligned} - \left( {EI_{2} } \right)^{*} \frac{{\partial^{4} w_{2} }}{{\partial x^{4} }} & - \left\{ {F_{2} \cos {\varOmega }\bar{t} - \left( {EA_{2} } \right)^{*} \mathop \int \limits_{0}^{L} \left( {\frac{{\partial w_{2} }}{\partial x}} \right)^{2} {\text{d}}x} \right\}\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} + c_{d} \frac{{\partial w_{2} }}{{\partial \bar{t}}} + k_{w} w_{2} \\ & \quad + \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{2} }}{{\partial x^{4} }}\left\{ {F_{2} \cos {\varOmega }\bar{t} - \left( {EA_{2} } \right)^{*} \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial w_{2} }}{\partial x}} \right)^{2} {\text{d}}x} \right\} \\ & \quad + \left( {1 - \left( {e_{0} a} \right)^{2} \nabla^{2} } \right)c\left( {w_{2} - w_{1} } \right) - 2\tilde{\tau }_{0} \left[ {\frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{2} }}{{\partial x^{4} }}} \right] \\ & \quad - \left( {e_{0} a} \right)^{2} k_{w} \frac{{\partial^{2} w_{2} }}{{\partial x^{2} }} - \left( {e_{0} a} \right)^{2} c_{d} \frac{{\partial^{3} w_{2} }}{{\partial \bar{t}\partial x^{2} }} = \rho A_{2} \left( {\frac{{\partial^{2} w_{2} }}{{\partial \bar{t}^{2} }} - \left( {e_{0} a} \right)^{2} \frac{{\partial^{4} w_{2} }}{{\partial \bar{t}^{2} \partial x^{2} }}} \right). \\ \end{aligned} $$
(18b)

Now, nondimensional parameters can be used for better understanding as follows:

$$ \begin{aligned} X & = \frac{x}{L} , W_{i} = \frac{{w_{i} }}{L} , \gamma = \frac{{e_{0} a}}{L} , K_{w} = \frac{{k_{w} L^{4} }}{{\left( {EI_{i} } \right)^{*} }} , \\ C_{d} & = c_{d} \sqrt {\frac{{L^{4} }}{{\rho A_{i} \left( {EI_{i} } \right)^{*} }}} , \tau_{0} = \frac{{\tilde{\tau }_{0} bL^{2} }}{{\left( {EI_{i} } \right)^{*} }}, t = \frac{{\bar{t}}}{{L^{2} }}\sqrt {\frac{{\left( {EI_{i} } \right)^{*} }}{{\rho A_{i} }}} C = \frac{{cL^{4} }}{{EI_{i} }} i = 1,2. \\ \end{aligned} $$
(19)

In Eqs. (18a) and (18b), the Winkler-type foundation is taken from Ref. [53]. Substituting nondimensional parameters into Eqs. (18a) and (18b), it yields:

$$ \begin{aligned} \frac{{\partial^{4} W_{1} }}{{\partial X^{4} }} & - \left\{ {F_{1} \cos {\varOmega }t - \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial W_{1} }}{\partial X}} \right)^{2} {\text{d}}X} \right\}\frac{{\partial^{2} W_{1} }}{{\partial X^{2} }} + \gamma^{2} \frac{{\partial^{4} W_{1} }}{{\partial X^{4} }}\left\{ {F_{1} \cos {\varOmega }t - \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial W_{1} }}{\partial X}} \right)^{2} {\text{d}}X} \right\} \\ & \quad - 2\tau_{0} \left[ {\frac{{\partial^{2} W_{1} }}{{\partial X^{2} }} - \gamma^{2} \frac{{\partial^{4} W_{1} }}{{\partial X^{4} }}} \right] + C\left( {W_{1} - W_{2} } \right) - C\gamma^{2} \left( {\frac{{\partial^{2} W_{1} }}{{\partial X^{2} }} - \frac{{\partial^{2} W_{2} }}{{\partial X^{2} }}} \right) \\ & \quad = \left( {\frac{{\partial^{2} W_{1} }}{{\partial t^{2} }} - \gamma^{2} \frac{{\partial^{4} W_{1} }}{{\partial t^{2} \partial X^{2} }}} \right) \\ \end{aligned} $$
(20a)
$$ \begin{aligned} \frac{{\partial^{4} W_{2} }}{{\partial X^{4} }} & - \left\{ {F_{2} \cos {\varOmega }t - \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial W_{2} }}{\partial X}} \right)^{2} {\text{d}}X} \right\}\frac{{\partial^{2} W_{2} }}{{\partial X^{2} }} + C_{d} \frac{{\partial W_{2} }}{\partial t} + K_{w} W_{2} \\ & \quad + \gamma^{2} \frac{{\partial^{4} W_{2} }}{{\partial X^{4} }}\left\{ {F_{2} \cos {\varOmega }t - \mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial W_{2} }}{\partial X}} \right)^{2} {\text{d}}X} \right\} - 2\tau_{0} \left[ {\frac{{\partial^{2} W_{2} }}{{\partial X^{2} }} - \gamma^{2} \frac{{\partial^{4} W_{2} }}{{\partial X^{4} }}} \right] \\ & \quad - \gamma^{2} K_{w} \frac{{\partial^{2} W_{2} }}{{\partial X^{2} }} - \gamma^{2} C_{d} \frac{{\partial^{3} W_{2} }}{{\partial t\partial X^{2} }} + C\left( {W_{2} - W_{1} } \right) - C\gamma^{2} \left( {\frac{{\partial^{2} W_{2} }}{{\partial X^{2} }} - \frac{{\partial^{2} W_{1} }}{{\partial X^{2} }}} \right) \\ & \quad = \left( {\frac{{\partial^{2} W_{2} }}{{\partial t^{2} }} - \gamma^{2} \frac{{\partial^{4} W_{2} }}{{\partial t^{2} \partial X^{2} }}} \right). \\ \end{aligned} $$
(20b)

For a simply supported double-walled nanobeam, the corresponding boundary conditions would be:

$$ W_{i} = 0 , \frac{{\partial^{2} W_{i} }}{{\partial X^{2} }} = 0 , \;{\text{at}}\;\; X = 0 , X = L \left( {i = 1,2} \right). $$
(21)

2.2 Galerkin technique

Now, Galerkin technique is employed to solve the equations so that an approximate solution is substituted into Eqs. (20a) and (20b). Therefore, the approximate solution is assumed as follows:

$$ W_{j} \left( {x,t} \right) = \mathop \sum \limits_{k = 1}^{\infty } \psi_{jk} \left( t \right)\sin \frac{k\pi x}{L} $$
(22)

In Eq. (22), \( \psi \left( t \right) \) and \( \sin \frac{k\pi x}{L} \) are time-dependent function and the spatial basis function, respectively. It is noted that for fundamental frequency, we assume \( k = 1 \). Now, substituting Eq. (22) into Eqs. (20a) and (20b), it yields:

$$ \ddot{\psi}_{1} + \omega_{10}^{2} \psi_{1} + \beta_{1} \psi_{1}^{3} - \delta_{1} \cos \left({{\varOmega}t} \right)\psi_{1} - \chi_{1} \psi_{2} = 0 $$
(23a)
$$ \ddot{\psi}_{2} + \omega_{20}^{2} \psi_{2} + 2\mu_{2} \dot{\psi}_{2} + \beta_{2} \psi_{2}^{3} - \delta_{2} \cos \left({{\varOmega}t} \right)\psi_{2} - \chi_{2} \psi_{1} = 0, $$
(23b)

in Eqs. (23a) and (23b), \( \epsilon \left({\epsilon \ll 1} \right) \) is known as scaling parameter. For other parameters, it can be written as:

$$ \begin{array}{lll} \omega_{10}^{2} = \left\{{C + \frac{1}{{\left({1 + \gamma^{2} \left({\frac{\pi}{L}} \right)^{2}} \right)}}\left({\frac{\pi}{L}} \right)^{4}} \right\}, \hfill \\ \omega_{20}^{2} = \left\{{\left[{C + k_{w} + 2\tau_{0}} \right]\left({\frac{\pi}{L}} \right)^{2} + \frac{1}{{\left({1 + \gamma^{2} \left({\frac{\pi}{L}} \right)^{2}} \right)}}\left({\frac{\pi}{L}} \right)^{4}} \right\}, \hfill \\ \beta_{1} = \frac{1}{2}\left({\frac{\pi}{L}} \right)^{4}, \beta_{2} = \frac{1}{2}\left({\frac{\pi}{L}} \right)^{4}, \mu_{2} = \frac{{C_{d}}}{2}, \delta_{1} = F_{1} \left({\frac{\pi}{L}} \right)^{2}, \delta_{2} = F_{2} \left({\frac{\pi}{L}} \right)^{2}, \chi_{1} = \chi_{2} = C. \hfill \\ \end{array} $$
(24)

2.3 Multiple scale method

In this section, to solve Eqs. (23a) and (23b), a set of first-order approximations is applied as [54]. This set of first-order approximations is known as multiple time scales approach and proposed by Nayfeh and Mook [54]. Therefore, it yields:

$$ \psi_{1} \left({t,} \right) = \psi_{10} \left({T_{0},T_{1}} \right) + \psi_{11} \left({T_{0},T_{1}} \right) $$
(25a)
$$ \psi_{2} \left({t,} \right) = \psi_{20} \left({T_{0},T_{1}} \right) + \psi_{21} \left({T_{0},T_{1}} \right). $$
(25b)

For \( T_{0} \) and \( T_{1} \) in Eqs. (25a) and (25b), we have:

$$ T_{0} = t, T_{1} = \epsilon t. $$
(26)

And also, we define operators as:

$$ \frac{d}{{{\text{d}}T}} = \frac{d}{{{\text{d}}T_{0}}} + \frac{d}{{{\text{d}}T_{1}}} + \cdots = D_{0} + \;D_{1} + \cdots, $$
(27a)
$$ \frac{{d^{2}}}{{{\text{d}}T^{2}}} = \frac{{d^{2}}}{{{\text{d}}T_{0}^{2}}} + 2\int \frac{d}{{{\text{d}}T_{0}}}\frac{d}{{{\text{d}}T_{1}}} + \cdots = D_{0}^{2} + 2 \int \;D_{0} D_{1} + \cdots. $$
(27b)

At first, substituting Eqs. (25a), (25b) and (27a), (27b) into Eqs. (23a) and (23b) then, for the coefficients of \( \epsilon^{0} \) and \( \epsilon^{1} \), it can be obtained as:

$$ \epsilon^{0} :D_{0}^{2} \psi_{10} + \omega_{10}^{2} \psi_{10} = 0 $$
(28a)
$$ D_{0}^{2} \psi_{20} + \omega_{20}^{2} \psi_{20} = 0 $$
(28b)
$$ \epsilon^{1} :D_{0}^{2} \psi_{11} + \omega_{10}^{2} \psi_{11} = - 2D_{0} D_{1} \psi_{10} - \beta_{1} \psi_{10}^{3} + \chi_{1} \psi_{20} + \delta_{1} \psi_{10} \cos {\varOmega}T_{0} $$
(29a)
$$ D_{0}^{2} \psi_{21} + \omega_{20}^{2} \psi_{21} = - 2D_{0} D_{1} \psi_{20} - 2\mu_{2} D_{0} \psi_{20} - \beta_{2} \psi_{20}^{3} + \chi_{2} \psi_{10} + \delta_{2} \psi_{20} \cos \varOmega T_{0} . $$
(29b)

To solve Eqs. (28a) and (28b), a general solution may be introduced as:

$$ \psi_{10} = A\left( {T_{1} } \right)e^{{i\omega_{10} T_{0} }} + \bar{A}\left( {T_{1} } \right)e^{{ - i\omega_{10} T_{0} }} , $$
(30a)
$$ \psi_{20} = B\left( {T_{1} } \right)e^{{i\omega_{20} T_{0} }} + \bar{B}\left( {T_{1} } \right)e^{{ - i\omega_{20} T_{0} }} . $$
(30b)

Now, \( A \) and \( B \) are unknown and \( \bar{A} \) and \( \bar{B} \) are the complex conjugate of \( A \) and \( B \). Using Eqs. (30a), (30b) and substituting in Eq. (28a) and (28b), it yields:

$$ \begin{aligned} D_{0}^{2} \psi_{11} + \omega_{10}^{2} \psi_{11} & = - 2i\omega_{10} A^{\prime}e^{{i\omega_{10} T_{0} }} - \beta_{1} A^{3} e^{{3i\omega_{10} T_{0} }} \\ & \quad - 3\beta_{1} A^{2} \bar{A}e^{{i\omega_{10} T_{0} }} + \chi_{1} Be^{{i\omega_{20} T_{0} }} \\ & \quad + \frac{1}{2}\delta_{1} Ae^{{i\left( {\varOmega + 1} \right)T_{0} }} + \frac{1}{2}\delta_{1} Ae^{{i\left( {\varOmega - 1} \right)T_{0} }} + CC, \\ \end{aligned} $$
(31a)
$$ \begin{aligned} D_{0}^{2} \psi_{21} + \omega_{20}^{2} \psi_{21} & = - 2i\omega_{20} B^{\prime}e^{{i\omega_{20} T_{0} }} - i\mu_{2} \omega_{20} Be^{{i\omega_{20} T_{0} }} \\ \,\quad - \beta_{2} B^{3} e^{{3i\omega_{20} T_{0} }} - 3\beta_{2} B^{2} \bar{B}e^{{i\omega_{20} T_{0} }} + \chi_{2} Ae^{{i\omega_{10} T_{0} }} \\ & \quad + \frac{1}{2}\delta_{2} Be^{{i\left( {\varOmega + \omega_{20} } \right)T_{0} }} + \frac{1}{2}\delta_{2} Be^{{i\left( {\varOmega - \omega_{20} } \right)T_{0} }} + CC. \\ \end{aligned} $$
(31b)

It is noted that there will be internal resonance when \( \omega_{20} \approx 1 \). Now, by definition \( \left({{\varOmega} = 2\omega_{20} + \epsilon{\sigma}_{1}, \omega_{20} = 1 + \epsilon{\sigma}_{2}} \right) \) that \( \sigma_{1} \) and \( \sigma_{2} \) are detuning parameters, we eliminate the secular terms in Eqs. (31a) and (31b).

$$ 2i\omega_{10} A^{\prime} + 3\beta_{1} A^{2} \bar{A} - \chi_{1} Be^{{i\sigma_{2} T_{1} }} - \frac{1}{2}\delta_{1} Ae^{{i\left( {\sigma_{1} + 2\sigma_{2} } \right)T_{1} }} = 0, $$
(32a)
$$ 2i\omega_{20} B^{\prime} + i\mu_{2} \omega_{20} B + 3\beta_{2} B^{2} \bar{B} - \chi_{2} Ae^{{ - i\sigma_{2} T_{1} }} - \frac{1}{2}\delta_{2} Be^{{i\sigma_{1} T_{1} }} = 0 $$
(32b)

To define a polar form for \( A \) and \( B \) as below, one can write:

$$ A\left( {T_{1} } \right) = \frac{1}{2}a_{1} \left( {T_{1} } \right)e^{{i\lambda_{1} \left( {T_{1} } \right)}} = \frac{1}{2}a_{1} \left( {\cos \lambda_{1} + i \sin \lambda_{1} } \right), $$
(33a)
$$ B\left( {T_{1} } \right) = \frac{1}{2}a_{2} \left( {T_{1} } \right)e^{{i\lambda_{2} \left( {T_{1} } \right)}} = \frac{1}{2}a_{2} \left( {\cos \lambda_{2} + i \sin \lambda_{2} } \right). $$
(33b)

Substituting Eqs. (33a), (33b) into Eqs. (32a) and (32b), it yields:

$$ a_{1}^{'} = \frac{1}{2}\chi_{1} a_{1} \sin \gamma + \frac{{\delta_{1} }}{{4\omega_{10} }}a_{1} \sin \left( {\sigma T_{1} } \right) $$
(34a)
$$ a_{1} \gamma^{\prime} = a_{1} \lambda_{2}^{'} + a_{1} \sigma_{2} - \frac{3}{{4\omega_{10} }}\beta_{1} a_{1}^{3} + \frac{1}{{2\omega_{10} }}\chi_{1} a_{2} \cos \gamma - \frac{{\delta_{1} }}{{4\omega_{10} }}a_{1} cos\left( {\sigma T_{1} } \right) $$
(34b)
$$ a_{2}^{'} = - \frac{1}{2}\mu_{2} a_{2} + \frac{1}{{2\omega_{20} }}\chi_{2} a_{1} \sin \eta + \frac{{\delta_{2} }}{{4\omega_{20} }}a_{2} \sin \left( {\sigma_{1} T_{1} } \right) $$
(35a)
$$ a_{2} \eta^{\prime} = a_{2} \lambda_{1}^{'} - a_{2} \sigma_{2} - \frac{3}{{4\omega_{20} }}\beta_{2} a_{2}^{3} + \frac{1}{{2\omega_{20} }}\chi_{2} a_{1} \cos \eta + \frac{{\delta_{2} }}{{4\omega_{20} }}a_{2} cos\left( {\sigma_{1} T_{1} } \right) $$
(35b)

where,

$$ \left\{ {\begin{array}{*{20}c} {\gamma = \left( {\lambda_{2} - \lambda_{1} } \right) + \sigma_{2} T_{1} } \\ {\sigma = \sigma_{1} + 2\sigma_{2} } \\ {\eta = \left( {\lambda_{1} - \lambda_{2} } \right) - \sigma_{2} T_{1} } \\ \end{array} } \right.. $$
(36)

According to Eqs. (34a, 34b)–(36), three different cases can occur:

Case I: \( a_{1} = 0, a_{2} \ne 0 \)

$$ 9\beta_{2}^{2} a_{2}^{4} + 24\omega_{20} \sigma_{2} \beta_{2} a_{2}^{2} + 4\omega_{20}^{2} \mu_{2}^{2} + 16\omega_{20}^{2} \sigma_{2}^{2} - \delta_{2}^{2} = 0 $$
(37)

Case II: \( a_{1} \ne 0, a_{2} = 0 \)

$$ 9\beta_{1}^{2} a_{1}^{4} - 24\beta_{1} \sigma_{2} a_{1}^{2} + 16\sigma_{2}^{2} - \delta_{1}^{2} = 0 $$
(38)

Case III: \( a_{1} \ne 0, a_{2} \ne 0 \)

$$ 9\beta_{1}^{2} a_{1}^{6} - 24\beta_{1} \sigma_{2} a_{1}^{4} + \left( {16\sigma_{2}^{2} - \delta_{1}^{2} } \right)a_{1}^{2} - 4\chi_{1} \delta_{1} a_{2} a_{1} - 4\chi_{1}^{2} a_{2}^{2} = 0, $$
(39a)
$$ 9\beta_{2}^{2} a_{2}^{6} + 24\omega_{20} \sigma_{2} \beta_{2} a_{2}^{4} + \left( {4\omega_{20}^{2} \mu_{2}^{2} + 16\omega_{20}^{2} \sigma_{2}^{2} - \delta_{2}^{2} } \right)a_{2}^{2} - 4\chi_{2} \delta_{2} a_{1} a_{2} - 4\chi_{2}^{2} a_{1}^{2} = 0. $$
(39b)

Finally, assuming \( \left( {\mu_{2} > 0} \right) \), the stability of the system can be evaluated. Therefore, defining Cartesian form of the solution \( \left( {A = \frac{1}{2}\left( {p_{1} - iq_{1} } \right)e^{{i\sigma_{1} T_{1} }} , B = \frac{1}{2}\left( {p_{2} - iq_{2} } \right)e^{{i\sigma_{2} T_{1} }} } \right) \) and based on Eqs. (32a) and (32b), it yields:

$$ 2i\omega_{10} A^{\prime} - \chi_{1} Be^{{i\sigma_{2} T_{1} }} - \frac{1}{2}\delta_{1} Ae^{{i\left( {\sigma_{1} + 2\sigma_{2} } \right)T_{1} }} = 0, $$
(40a)
$$ 2i\omega_{20} B^{\prime} + i\mu_{2} \omega_{20} B - \chi_{2} Ae^{{ - i\sigma_{2} T_{1} }} - \frac{1}{2}\delta_{2} Be^{{i\sigma_{1} T_{1} }} = 0. $$
(40b)

Substituting \( A \) and \( B \) in Eqs. (40a) and (40b), we rewrite the process of the solution as below:

$$ p_{1}^{'} - \left( {\sigma_{1} + \frac{{\delta_{1} }}{4}} \right)q_{1} - \frac{{\chi_{1} }}{2}q_{2} = 0 $$
(41a)
$$ q_{1}^{'} + \left( {\sigma_{1} + \frac{{\delta_{1} }}{4}} \right)p_{1} + \frac{{\chi_{1} }}{2}p_{2} = 0 $$
(41b)
$$ p_{2}^{'} + \frac{{\mu_{2} }}{2}p_{2} - \left( {\sigma_{2} + \frac{{\delta_{2} }}{{4\omega_{20} }}} \right)q_{2} - \frac{{\chi_{2} }}{{2\omega_{20} }}q_{1} = 0 $$
(42a)
$$ q_{2}^{'} + \frac{{\mu_{2} }}{2}q_{2} + \left( {\sigma_{2} + \frac{{\delta_{2} }}{{4\omega_{20} }}} \right)p_{2} - \frac{{\chi_{2} }}{{2\omega_{20} }}p_{1} = 0 $$
(42b)

Now, it is assumed and substituted \( \left( {p_{1} = q_{1} = p_{2} = q_{2} = 0} \right) \). Thus, Eqs. (41a), (41b) and Eqs. (42a), (42b) are determined as follows:

$$ \begin{aligned} \Delta & = \frac{1}{{16\omega_{20}^{2} }}\left( {2\delta_{1} \mu_{2}^{2} \sigma_{1} \omega_{20}^{2} + \frac{1}{4}\delta_{1}^{2} \mu_{2}^{2} \omega_{20}^{2} + \delta_{1}^{2} \sigma_{2}^{2} \omega_{20}^{2} + \frac{1}{2}\delta_{2} \delta_{1}^{2} \sigma_{2} \omega_{20} + 8\delta_{1} \sigma_{1} \sigma_{2}^{2} \omega_{20}^{2} } \right. \\ & \quad \omega_{20}^{2} + 4\delta_{2} \delta_{1} \sigma_{1} \sigma_{2} \omega_{20} + 8\delta_{2} \sigma_{1}^{2} \sigma_{2} \omega_{20} + \frac{1}{2}\delta_{2}^{2} \delta_{1} \sigma_{1} + \delta_{2}^{2} \sigma_{1}^{2} + \frac{1}{16}\delta_{2}^{2} \delta_{1}^{2} \\ & \quad \left. { + {\kern 1pt} \,4\mu_{2}^{2} \sigma_{1}^{2} \omega_{20}^{2} + 16\sigma_{1}^{2} \sigma_{2}^{2} \omega_{20}^{2} - \chi_{1}^{2} \chi_{2}^{2} } \right). \\ \end{aligned} $$
(43)

The amplitude response for different cases can be derived from Eqs. (37)–(39a, 39b). In addition, whenever, \( \Delta > 0 \) in Eq. (43), the system is stable and \( \Delta < 0 \) means the system is unstable. Equations (37)–(39a, 39b) and Eq. (43) emphasize that outer layer of nanobeam plays an important role in nonlinear instability of the inner layer in the system.

3 Results and discussion

In this section, numerical results of the present study are presented and discussed in figures. Anterior to the major discussion of this study, the formulation and the numerical should be checked and validated. To achieve this goal, some available literatures are used to have a comparison between results. In the next step, the numerical results for nonlinear dynamics and instability of double-walled nanobeams are presented while it is focused on the effect of residual surface stress on dynamic instability and bifurcations in nonlinear instability of the system. In addition, material properties of the nanobeam is taken as Young’s modulus E = 1100 Gpa, the mass density ρ = 2.3 g/cm3, the residual surface stress τ0 = 0.89 N/m and the surface elasticity Es= 1.22 N/m. Also, the inner and outer diameters of the nanobeam are di= 0.7 nm and do= 1.4 nm, respectively.

3.1 Validation of the study

From Fig. 2, the relation between the amplitude response (ττ) and detuning parameter (σ) in nonlinear instability of a short nanobeam exposed to an external parametric excitation (δ = 6) is observed. It is noted that ττ is the amplitude response of a single layer nanobeam. In fact, it can be equalized with the amplitude response (ττ1)of the double-layered nanobeam in the present study. The results are also compared with the results presented by Ghadiri and Hosseini [42] is observed. There is a good agreement, as can be observed, between the results. It is found from Fig. 2 that due to parametric excitation, stable (solid line) and unstable (dashed line) curves vary for different values of amplitude response. In Fig. 2, bifurcations happen “out of the clear blue sky” for stable and unstable curves. When the amplitude response is equal to zero, we have two trivial solutions before -5. After that, there is one trivial (unstable) and one non-trivial (stable) solutions until 5. After detuning parameter (σ = 6), there are two non-trivial stable and unstable solutions. It should be noted that Fig. 2 is achieved when δ > 2μ which μ represents the damping coefficient of the system of the single layer nanobeam.

Fig. 2
figure 2

The relation between amplitude response \( \left( a \right) \) and detuning parameter \( \left( \sigma \right) \) in nonlinear instability of a nanobeam subjected to an external parametric excitation \( \left( {\delta = 6} \right) \) [42]

Full size image

3.2 Numerical results and discussion

As mentioned, in this section, the numerical results of the effect of residual surface stress on nonlinear dynamics and instability of double-walled nanobeam caused by an external axial force is presented while the emphasis is placed on investigating the effect of parametric excitation, residual surface stress effect, viscoelastic foundation coefficients and damping coefficient. To ensure better understanding of nonlinear instability of the system, bifurcations are discussed and identified in plots. Bifurcations can be supercritical pitchfork, subcritical pitchfork and or saddle node. In fact, bifurcations aid in a good view of stable and unstable situations and regions in nonlinear dynamics of the system.

Figure 3 demonstrates the effect of residual surface stress on bifurcations in nonlinear instability of the system for various values of force amplitude (δ2) and amplitude response (α2). As residual surface stress is increased, a shift in bifurcation points is observed so that for negative values of detuning parameter \( \left( {\sigma_{2} > 0} \right) \), it moves to the left side and for positive values of detuning parameter \( \left( {\sigma_{2} > 0} \right) \), it has a tendency to move toward the right side.

Fig. 3
figure 3

Effect of residual surface stress on bifurcations in nonlinear instability of the system for various values of force amplitude \( \left( {\delta_{2} } \right) \) and amplitude response \( \left( {a_{2} } \right) \)

Full size image

The effect of nonlinear coefficient \( \left( {\beta_{2} } \right) \) on amplitude response \( \left( {a_{2} } \right) \) in nonlinear instability of the system for both with surface stress and without surface stress \( \left( {\tau_{0} } \right) \) is displayed in Fig. 4. It would be clear from Fig. 4 that compared to residual surface stress effect, the effect of nonlinear coefficient is completely effective on amplitude response of the system. As a matter of fact, as the nonlinear coefficient is increased from 1 to 5, the amplitude response considerably grows (Eq. (38). On the other hand, by considering the surface effect, amplitude response gradually grows. In addition, in both plots, the bifurcations come up with three situations including the saddle node, the supercritical pitchfork and the subcritical pitchfork bifurcations.

Fig. 4
figure 4

The effect of the nonlinear coefficient \( \left( {\beta_{2} } \right) \) on the amplitude response \( \left( {a_{2} } \right) \) in the nonlinear instability of the system for both with the surface stress and without the surface stress \( \left( {\tau_{0} } \right) \)

Full size image

From Fig. 5, it is observed that the effect of the foundation coefficients \( \left( {K_{w} , C_{d} } \right) \) on the amplitude response \( \left( {a_{2} } \right) \) of the system is considerable. It is noted that the residual surface stress is taken \( \tau_{0} = 1 \). In Fig. 5a, it can be seen that as the Winkler coefficient increases from 0 to 100, the subcritical pitchfork bifurcations have a considerable shift along to the left side of the force amplitude \( \left( {\delta_{2} } \right) \) axis (Eq. (38)). Therefore, for different values of the Winkler coefficient, different bifurcations include the subcritical pitchfork and the saddle node ones. For Fig. 5b, all explanations of Fig. 5a are valid for Fig. 5b, however, the effects of the viscous damping coefficient are lower than Winkler coefficient on instability of the system. The possible reason of such a behavior is the effect of the foundation coefficients \( \left( {K_{w} , C_{d} } \right) \) on the natural frequency of the system.

Fig. 5
figure 5

The effect of foundation coefficients \( \left( {K_{w} , C_{d} } \right) \) on amplitude response \( \left( {a_{2} } \right) \) in nonlinear instability of the system with residual surface stress \( \left( {\tau_{0} = 1} \right) \)

Full size image

To ensure better understanding of the residual surface stress effect on the nonlinear instability of the system, Fig. 6 presents the emphasis placed on investigating the relation between the amplitude response and the residual surface stress. Figure 6 states the relation between the amplitude response \( \left( {a_{2} } \right) \), the detuning parameter \( \left( {\sigma_{2} } \right) \) and the force amplitude \( \left( {\delta_{2} } \right) \) for different values of the residual surface stress \( \left( {\tau_{0} } \right) \) in the nonlinear instability of the system. As the residual surface stress effect is increased, the amplitude response grows. It is worth mentioning that the supercritical pitchfork bifurcation can be seen for various values of the detuning parameter \( \left( {\sigma_{2} } \right) \). All points on the red line (see, Fig. 6) introduce bifurcation points (the supercritical pitchfork). Figure 6 is derived from Eqs. (39a) and (39b).

Fig. 6
figure 6

Relation between amplitude response \( \left( {a_{2} } \right) \), detuning parameter \( \left( {\sigma_{2} } \right) \) and force amplitude \( \left( {\delta_{2} } \right) \) for different values of residual surface stress \( \left( {\tau_{0} } \right) \) in nonlinear instability of the system

Full size image

In Fig. 7, one of the main results of the present study is observed so that as the force amplitude \( \left( {\delta_{1} } \right) \) is increased while other parameters are held constant, stable and unstable curves (dashed lines and solid lines, respectively) move far away and make the gap between them larger. Also, Fig. 7 is obtained from Eq. (37). It means that the stable region (the region between stable and unstable curves) become larger. At the same time, the supercritical and subcritical pitchfork bifurcations would have a shift towards high values of the detuning parameter \( \left( {\sigma_{2} } \right) \). Moreover, as the force amplitude \( \left( {\delta_{1} } \right) \) is increased, the amplitude response slowly decreases.

Fig. 7
figure 7

The effect of force amplitude \( \left( {\delta_{1} } \right) \) in nonlinear instability of the system for different values of amplitude response \( \left( {a_{1} } \right) \)

Full size image

In contrast to Fig. 7, there is no shift in bifurcations caused by an increase in the nonlinear coefficient \( \left( {\beta_{1} } \right) \) in Fig. 8 (please see, Eq. (37)). From Fig. 8, it can be revealed that the nonlinear coefficient \( \left( {\beta_{1} } \right) \) influences the amplitude response \( \left( {a_{1} } \right) \) in nonlinear instability of the system for different values of detuning parameter \( \left( {\sigma_{2} } \right) \). As nonlinear coefficient \( \left( {\beta_{1} } \right) \) is increased, the amplitude response \( \left( {a_{1} } \right) \) considerably decays. It reveals that nonlinearity can have more influence on the mechanical characteristics of double-walled structures than the residual surface stress effect.

Fig. 8
figure 8

The effect of nonlinear coefficient \( \left( {\beta_{1} } \right) \) in nonlinear instability of the system for different values of amplitude response \( \left( {a_{1} } \right) \)

Full size image

The results of the present study in nonlinear dynamics of double-walled nanobeams illustrate this point that compared to single nanobeams [42], double-walled structures such as nanobeams have different nonlinear behavior and bifurcation properties. Furthermore, as can be seen in derived equations and plots, the outer layer has more effect on instability than the inner layer. It seems that the residual surface stress effect on double-walled nanobeams is inevitable in design of nanoelectromechanical devices.

4 Conclusions

As considering all phenomena associated with nanobeams seems to be necessary, the literature is devoted to considering the effect of residual surface stress on nonlinear dynamics and instability of double-walled nanobeams. A class of nonlinear Mathieu–Hill equation is established to determine the bifurcations and the regions of nonlinear dynamic instability of a short double-walled nanobeam while the emphasis is placed on investigating the effect of residual surface stress on instability. In validation of the numerical results, a good agreement between the results of the present study and the results of the available literatures is observed. Numerical examples are treated which show various discontinuous bifurcations. Also, infinitely stable and unstable solutions are addressed. It is noted that we classify bifurcations as supercritical and subcritical pitchfork and saddle node bifurcations. Some main outcomes of the present study can be enumerated as follows:

  • We classify the bifurcations as discontinuous bifurcations.

  • All the examples show that a discontinuous bifurcation is always accompanied by a jump.

In addition, the numerical results show that as force amplitude \( \left( {\delta_{1} } \right) \) is increased the other parameters are held constant, stable and unstable curves move far away and make the gap between them larger. It means that stable region becomes larger.

At the end, we close this paper by stating that considering the residual surface stress effect on nanoscale structures including beams is inevitable in design of the nanoelectromechanical devices.