1 Introduction

Rock mass normally comprises rock material and rock discontinuities, and this is characterized by discontinuum constitutive models [1]. On the other hand, making a relation between strains and stresses is an important subject in the rock engineering field. Therefore, this study attempts to present the constitutive models for predicting rock fractures. Literature is consisted of lots of studies carried out into this subject (e.g., Azinfar et al. [2]; Ma et al. [3]; Wang and Tian [4]). Though, according to Jing and Stephansson [5], only two approaches exist to modeling the rock fracture behaviors: (1) the empirical approach, and (2) theoretical approach.

The empirical approach tends to develop the models in the shape of empirical functions that can best represent the experimental data through the use of mathematical regression techniques. This approach does not contain any restraint for respecting the thermodynamics second law. This is worth mentioning that in cases where the parameter ranges and loading conditions are taken into consideration in a proper way, these models will be capable of delivering desirable outputs [1]. On the other hand, the theoretical approach consists of thermodynamic considerations; this feature makes assure that the model obeys completely the second law. Though, parameters of the models constructed based on this approach might possess unclear physical meanings or it can be difficult to define the parameters through experiment [5]. Many constitutive models proposed in the literature for rock fractures encompass the key aspects of shear behaviors of rock mass. As a result, there is a need to improve the conventional regression methods and making them more powerful modeling techniques to better capture the nonlinearity of constitutive responses. The tremendous capacity of modern computers together with the high intricacy of shear behaviors of rock joints has made it completely sensible to apply the computational intelligence to the constitutive models formation process. Singh et al. [6] predicted the strength parameters, including uniaxial compressive and shear strength, using artificial neural network (ANN). According to their results, ANN was an acceptable and reliable method in predicting uniaxial compressive and shear strength. Babanouri and Fattahi [1] employed support vector regression (SVM) to present a constitutive model for predicting rock fractures. They indicated the effectiveness of SVM in this field. A new shear strength criterion was presented by Babanouri and Fattahi [7] using a hybrid of teaching–learning-based optimization (TLBO) and neuro fuzzy system. They showed that their proposed model was capable of predicting rock joint shear strength. In another study, Wu et al. [8] offered ANN model to predict peak shear strength for discontinuities, and compared the ANN performance with multivariate regression method. They confirmed the superiority of ANN over regression method in this filed. Furthermore, the use of artificial intelligence methods has been confirmed in some engineering fields [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40], which demonstrates the effectiveness of these methods for predicting aims.

Radial basis function neural network (RBFNN), as one of the most widespread types of ANNs, has been widely employed in several fields of civil and mining engineering [41,42,43]. Although, the literature lacks studies attempting to model the shear behaviors of rock fractures by means of RBFNN. The main contribution of this study is to combine the Genetic Algorithm (GA) and Grey Wolf Optimization (GWO) with the RBFNN model to develop constitutive models for predicting rock fractures.

The rest of this study is organized as follows. In Sect. 2, we mention the research significance. Then, more details regarding the used datasets are stated in Sect. 3. After that, Sects. 4 and 5 explain the implementation of proposed models to predicting rock fractures. Finally, in the sixth and last section, the results of this study and conclusions are provided.

2 Research significance

Determining and predicting the rock fractures is one of the most important issues in rock engineering field. To this end, this study proposes two integrated intelligent computing paradigms for predicting rock fractures. In the proposed models, two optimization algorithms, i.e., GWO and GA are used to improve the performance of RBFNN. To the best of our knowledge, this is the first study that uses the RBFNN-GA and RBFNN-GWO models in the field of rock fractures.

3 Dataset source

The proposed RBFNN-GA and RBFNN-GWO constitutive models were developed based on an experimental database presented in an open source [1]. In this regard, 84 direct shear tests were carried out upon the concrete and plaster replicas of natural rock fractures under various levels of normal stress. The values of joint roughness coefficient (JRC), joint wall compressive strength (JCS), Young’s modulus (E), normal stress (\(\sigma_{n}\)), basic friction angle (\(\phi_{b}\)), dilation angle (d), peak shear displacement (\(\delta_{\text{peak}} )\) and peak shear stress \(\left( {\tau_{p} } \right)\) were measured for all tests. More details regarding the collection of datasets can be found in Babanouri and Fattahi [1]. Table 1 shows the descriptive statistics related to used datasets. Furthermore, a part of datasets used in this study is given in Table 2. To train the RBFNN-GA and RBFNN-GWO models, JRC, JCS, E, \(\sigma_{n}\) and \(\phi_{b}\) were used as input parameters, whereas d, \(\delta_{\text{peak}}\) and \(\tau_{p}\) were used as output parameters. About 80% of the gathered data were employed for constructing the models, while the remaining 20% were used for testing the constructed models.

Table 1 Descriptive statistics for the used datasets
Full size table
Table 2 A part of datasets applied to modeling process in this study
Full size table

4 Models

The present study proposes two optimized RBFNN models for predicting rock fractures using GWO and GA algorithms. In this section, the background of proposed models are briefly explained. In the first subsection, the background of RBFNN is mentioned, and then in the second subsection, the GWO and GA algorithms are briefly explained.

4.1 Radial basis function neural network

A literature survey reveals that radial basis function neural network (RBFNN) is one of the most widespread types of ANNs [44, 45]. ANNs represent a computational intelligence method that can be used for prediction, patterns recognition, and modeling inputs-outputs relationships without putting on any assumption. They are designed based on nervous system of the human brain. The ANN system is constructed of neurons with the aim of processing the information.

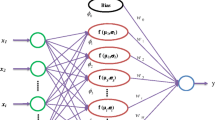
Recently, RBFNN has been largely used in several research areas due to its capacity in obtaining adequate results [46,47,48]. A typical RBFNN model consists of three kinds of layers: input, hidden, and output layers. The input data enter from the input layer. Thereafter, this information is directly transmitted to the hidden layer. This latter represents the principal part of RBFNN; it comprises nodes (nh) and biases (bh). Moreover, each (nh) has a specific radial basis function (RBF) that can be figured with two parameters, the center and the width.

During RBFNN training, a transfer of information from input layer to hidden layer is carried out, where the main goal is to obtain a nonlinear form. Among RBF types, the Gaussian function is mostly used. This function is described by its center (ci) and spread coefficient (σ2). The position of input vector (x) according to the center (ci) is calculated using the Euclidian norm:

$$z_{i} = \sqrt {\mathop \sum \limits_{k = 1}^{d} \left( {x_{k} - c_{ki} } \right)^{2} }$$
(1)

where \(d\) and \(c_{ki}\) indicate the number of variables and the centers, respectively. After that, the obtained distance is introduced into the Gaussian function, and the following formulation is acquired:

$$\varPhi \left( z \right) = { \exp }\left[ {\frac{{z^{2} }}{{2\sigma^{2} }}} \right]$$
(2)

where the parameters \(\varPhi\), \(z\) and \(\sigma^{2}\) denote the Gaussian equation, the Euclidian distance, and the spread coefficient, respectively.

The output layer operates linearly on the basis of the following formula:

$$y_{j} = \mathop \sum \limits_{i = 1}^{{n_{h} }} w_{ij} \varPhi_{i} \left( z \right) + b_{i} ,\quad i\, = \, 1, \ldots ,n_{h} \quad {\text{and}}\quad j\, = \, 1, \ldots ,{\text{N}}$$
(3)

where \(n_{h}\) and N signify the neurons number in the hidden layer and the training samples size, respectively, \(y_{j}\) denotes the jth output of input vector x, \(w_{ij}\) is the weight connecting the hidden node i to the output layer, and \(b_{i}\) is the bias.

The performance of RBFNN is completely related to the spread coefficient and the number of neurons in the hidden layer. Thus, the optimum values of these two parameters should be determined using different metaheuristic algorithms. In the current work, GA and GWO are used for the optimization aim.

4.2 Optimization techniques

4.2.1 Genetic algorithm

Genetic algorithm (GA) is a robust optimization approach first proposed by Holland [49] and Goldberg and Holland [50]. This algorithm was designed to solve different complex optimization problems. It utilizes the principles of natural genetics and natural selection as key operators when dealing with optimizing problems. At the first step of GA, a population of individuals that represent the probable solutions is generated randomly. Different individuals are pointed out in the form of chromosomes. The initialization step is followed by genetic operators, i.e., crossover, reproduction, and mutation. Through the iterative processing of GA, new individuals are produced to replace inappropriate ones according to a fitness function that specifies the objective function to be optimized. The selection operator determines parents from among existing individuals. Then, crossover operator substitutes randomly information between two individuals. The genetic operators are repeated until a stopping criterion is met.

4.2.2 Grey wolf optimization

Grey wolf optimization (GWO) is one of the robust population-based algorithms, which was presented by Mirjalili et al. [51]. The steps followed by GWO during the optimization process are imitated from the group living style and the real behavior of grey wolves. The wolves in a pack are ranked based on their importance into \(\alpha , \beta , \delta\) and \(\omega\), which affects the movements to be made around the prey [51]. The quality of the wolves is assessed with respect to a fitness function. Accordingly, the three fittest individuals are denoted as \(\alpha , \beta\) and \(\delta\), while the rest is considered as \(\omega\).

The algorithm starts by generating an initial population of wolves randomly. The positions of these wolves offer possible solution for to the problem in hand. Then, prior investigation is made, which involves circling around the prey. The wolves surround the prey \(\hbox{``}p\hbox{''}\) based on the following equation [51]:

$$X_{t + 1} = X_{t}^{p} - A.D$$
(4)

where \(\left( {t + 1} \right)\) and \(t\) represent the actual and previous iterations, respectively, \(X_{t}^{p}\) signifies the position of the prey (which is also the position of the best wolf, i.e., \(\alpha\)), and \(D\) is defined as shown below:

$$D = \left| {C.X_{t}^{p} - X_{t} } \right|$$
(5)

where \(X_{t}\) is the position of the wolf, and A and C are known as random relocation terms, and they are formulated as:

$$A = 2a.r_{1} - a$$
(6)
$$C = 2r_{2}$$
(7)

where \(a\) is frequently decreased linearly from 2 to 0; \(r_{1}\) and \(r_{2}\) are random values in the interval of [0, 1].

The wolves \(\left( \omega \right)\) update their positions according to the gained information by the fittest wolves, i.e., \(\alpha , \beta\) and \(\delta\). Therefore, the following equation is applied [51]:

$$X_{t + 1} = \frac{{X^{1} + X^{2} + X^{3} }}{3}$$
(8)

where \(X^{1} , X^{2} and X^{3}\) are defined as follow:

$$X^{1} = X_{t}^{\alpha } - A_{1} .\left| {C_{1} .X_{t}^{\alpha } - X_{t} } \right|$$
(9)
$$X^{2} = X_{t}^{\beta } - A_{2} .\left| {C_{2} .X_{t}^{\beta } - X_{t} } \right|$$
(10)
$$X^{3} = X_{t}^{\delta } - A_{3} .\left| {C_{3} .X_{t}^{\delta } - X_{t} } \right|$$
(11)

where \(X^{\alpha }\), \(X^{\beta }\), and \(X^{\delta }\) are the positions of α, β, and δ, respectively.

After the movement of the wolves, their new positions are evaluated according to the fitness function. Therefore, the new position of the fittest wolf \(\alpha\) is validated only if this latter outperforms the previous one.

5 Model development

Before proceeding to the implementation of the proposed paradigms, the collected database was subjected to a preprocessing that involved: (1) normalization of the database between − 1 and 1, and (2) splitting the data into training and testing sets. The training part covering 80% of the points was used for the models building, while the test set encompassing the rest of the points was applied as blind data to evaluating the reliability of the models with unseen values.

As underlined in the previous sections, GA and GWO were implemented for the aim of optimizing the control parameters of RBFNN, namely the spread coefficient and the number of neurons in the hidden layers. The procedure of the proposed hybridizations is illustrated in Fig. 1. The obtained models are denoted RBFNN-GA and RBFNN-GWO. It is worth noting that mean square error (MSE) was the considered fitness function for both algorithms. This function is defined as shown below:

$$MSE = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {t_{i} - o_{i} } \right)^{2} }}{n}$$
(12)

where \(n\) is the number of training data, \(t_{i}\) and \(o_{i}\) represent the real and the predicted values, respectively.

Fig. 1
figure 1

Workflow of the proposed hybridizations

Full size image

In addition, to gain reliable results using these two nature-inspired algorithms, their control parameters should be well determined, which was done in this study through adopting a tuning procedure. The resultant parameters for GA and GWO are given in Table 3.

Table 3 Setting parameters of GA and GWO
Full size table

6 Analysis of the results

In this study, RBFNN-GA and RBFNN-GWO models were proposed to predict \(\tau_{p}\), \(\delta_{\text{peak}}\), and \(d\) parameters. Table 4 reports the final RBFNN control parameters obtained after the optimization using GA and GWO for the three outputs, i.e., \(\tau_{p}\), \(\delta_{\text{peak}}\), and \(d\). This table reveals that the proposed models for the three outputs yielded their reliable results when the number of nodes was set to a value between 49 and 63; while moderate values for the spread coefficient were noticed in all the models.

Table 4 Final values of the RBFNN control parameters
Full size table

To validate and compare the acquired results from the RBFNN-GA and RBFNN-GWO models, three statistical functions, namely root mean square error (RMSE), coefficient of determination (R2), and mean absolute error (MAE), were used. These statistical functions are expressed by the following formula [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74]:

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} (O_{i} - P_{i} )^{2} }}{n}}$$
(13)
$$R^{2} = \frac{{\left( {\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \bar{O}_{i} } \right)(P_{i} - \bar{P}_{i} )} \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \bar{O}_{i} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} (P_{i} - \bar{P}_{i} )^{2} }}$$
(14)
$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {O_{i} - P_{i} } \right|$$
(15)

where n is the number of data, and Pi and Oi represent the predicted and observed values of the output parameters, respectively. Note that three output parameters were used in the modeling processes. The values of \(R^{2}\), \({\text{MAE}}\), and RMSE obtained from RBFNN-GA and RBFNN-GWO models for each output parameter were calculated, as given in Table 5. According to this Table, for all output parameters, the performance of RBFNN-GWO was better than RBFNN-GA. This clearly indicates the effectiveness of GWO, as an effective optimization algorithm, in combination with RBFNN. Furthermore, Figs. 2, 3, 4, 5, 6 and 7 show the R2 values obtained from the RBFNN-GA and RBFNN-GWO models for all output parameters. Based on these figures, the RBFNN-GWO model can be introduced as a robust machine learning model for the prediction of \(\tau_{p}\), \(\delta_{\text{peak}}\), and \(d\).

Table 5 Statistical functions values obtained from the predictive models
Full size table
Fig. 2
figure 2

The measured \(\delta_{\text{peak}}\) vs predicted \(\delta_{\text{peak}}\) using RBFNN-GA

Full size image
Fig. 3
figure 3

The measured \(\delta_{\text{peak}}\) vs predicted \(\delta_{\text{peak}}\) using RBFNN-GWO

Full size image
Fig. 4
figure 4

The measured \(\tau_{p}\) vs predicted \(\tau_{p}\) using RBFNN-GA

Full size image
Fig. 5
figure 5

The measured \(\tau_{p}\) vs predicted \(\tau_{p}\) using RBFNN-GWO

Full size image
Fig. 6
figure 6

The measured \(d\) vs predicted d using RBFNN-GA

Full size image
Fig. 7
figure 7

The measured \(d\) vs predicted d using RBFNN-GWO

Full size image

For further investigation of the accuracy of the established RBFNN-GWO, Fig. 8 illustrates the relative error distribution between the real values of \(\tau_{p}\), \(\delta_{\text{peak}}\) and \(d\), and predictions of the RBFNN-GWO model. Moreover, Fig. 9 shows the cumulative distribution of the absolute relative deviation of the model for the three outputs. It is worth mentioning that in these two figures, some points having zero value of the output, mainly for the case of \(d\), are not exhibited as these points correspond to an infinite value of relative error. However, the points with a zero-value output are well exhibited in the previous cross plots and are mostly located nearby the unit slope line. As it can be seen in Fig. 9, the predictions of RBFNN-GWO follow a satisfactory distribution nearby the zero-error line. In addition, Fig. 9 clearly shows that a great part of the points is predicted by the established RBFNN-GWO with a low AARD. As a matter of fact, 80% of the points are predicted with AARD values of 0.96%, 9%, and 9.66% for \(\tau_{p}\), \(\delta_{\text{peak}}\) and \(d\), respectively. These two figures confirm the reliability of the proposed RBFNN-GWO in predicting the three outputs.

Fig. 8
figure 8

The relative deviation of the predicted outputs using RBFNN-GWO

Full size image
Fig. 9
figure 9

Cumulative distribution of the absolute relative deviation of RBFNN-GWO

Full size image

As mentioned earlier, the datasets used in this study were borrowed from Babanouri and Fattahi [1]. They have developed the support vector regression (SVR) model in combination with the biogeography-based optimization (BBO) algorithm for the prediction of \(\tau_{p}\), \(\delta_{\text{peak}}\) and \(d\). They predicted the \(\tau_{p}\) with R2 values of 0.890 and 0.902 in training and testing phases, respectively, while, the RBFNN-GWO proposed in this study predicted the \(\tau_{p}\) with R2 values of 1 and 0.960 in training and testing phases, respectively. These results signify superiority of RBFNN-GWO over SVR-BBO in prediction of \(\tau_{p}\) in terms of performance measures. Moreover, Babanouri and Fattahi (2018) predicted the \(\delta_{\text{peak}}\) with R2 values of 0.949 and 0.888 in training and testing phases, respectively, while the proposed RBFNN-GWO predicted the same parameter with R2 values of 0.950 and 0.942 in training and testing phases, respectively. Thus, RBFNN-GWO was confirmed superior to SVR-BBO. On the other hand, the d parameter was predicted by Babanouri and Fattahi (2018) using SVR-BBO model with R2 values of 0.944 and 0.927 in training and testing phases, respectively, while RBFNN-GWO predicted it with R2 values of 0.997 and 0.949 in training and testing phases, respectively. These results showed the higher accuracy of RBFNN-GWO than SVR-BBO in predicting d. Accordingly, it can be concluded that RBFNN-GWO outperforms SVR-BBO in terms of prediction capacity. Additionally, the Taylor diagrams related to three output parameters are shown in Fig. 10. Based on this Fig, the RBFNN-GWO model predicted all output parameters with a better accuracy. In the present study, the sensitivity analysis is also performed using Yang and Zang’s [75] method through the following equation:

$$r_{ij} = \frac{{\mathop \sum \nolimits_{k = 1}^{n} \left( {y_{ik} \times y_{ok} } \right)}}{{\sqrt {\mathop \sum \nolimits_{k = 1}^{n} y_{ik}^{2} \mathop \sum \nolimits_{k = 1}^{n} y_{ok}^{2} } }}.$$
(16)
Fig. 10
figure 10

The obtained Taylor diagrams related to a \(\tau_{p}\), b \(\delta_{\text{peak}}\) and c d

Full size image

The values of \(r_{ij}\) are varied in range of zero to one, and indicate the impact of each input upon the output. In the modeling, five input parameters, i.e., JRC, JCS, E, \(\sigma_{n}\) and \(\phi_{b}\) were used. Also, three parameters, i.e., d, \(\delta_{peak}\) and \(\tau_{p}\) were used as the output parameters. The results of sensitivity analysis are listed below.

  • Regarding the first output (d), the values of \(r_{ij}\) for input parameters (JRC, JCS, E, \(\sigma_{n}\) and \(\phi_{b}\)) were equal to 0.951, 0.794, 0.805, 0.676 and 0.824, respectively. Hence, JRC was the most effective parameter upon d.

  • Regarding the second output (\(\delta_{peak}\)), the values of \(r_{ij}\) for input parameters (JRC, JCS, E, \(\sigma_{n}\) and \(\phi_{b}\)) were equal to 0.834, 0.817, 0.842, 0.801 and 0.960, respectively. Hence, \(\phi_{b}\) was the most effective parameter upon \(\delta_{\text{peak}}\).

  • Regarding the third output (\(\tau_{p}\)), the values of \(r_{ij}\) for input parameters (JRC, JCS, E, \(\sigma_{n}\) and \(\phi_{b}\)) were equal to 0.874, 0.839, 0.855, 0.974 and 0.904, respectively. Hence, \(\sigma_{n}\) was the most effective parameter upon \(\tau_{p}\).

7 Conclusions

Accurate prediction of \(\delta_{peak}\), \(\tau_{p}\), and d is an important challenge in the field of rock discontinuities. The present study proposed two hybrid advanced machine learning models, namely RBFNN-GWO and RBFNN-GA, to predict the above-noted parameters. In other words, GWO and GA were used to optimize RBFNN model to see which one works better. To achieve the objective of this study, the required datasets were collected from an open source in the literature (Babanouri and Fattahi 2018). In this regard, the values of JRC, JCS, E, \(\sigma_{n}\), \(\phi_{b}\), \(\delta_{\text{peak}}\), \(\tau_{p}\), and d were measured for 84 direct shear tests. In modeling process, JRC JCS, E, \(\sigma_{n } {\text{and}} \phi_{b}\) were considered as inputs, while \(\delta_{\text{peak}}\), \(\tau_{p}\), and d were set as outputs. The behaviors of both RBFNN-GWO and RBFNN-GA models were evaluated calculating three statistical functions, i.e., RMSE, R2, and MAE.

The conclusions drawn from this study are as follow. (1) While both proposed constitutive models, i.e., RBFNN-GWO and RBFNN-GA, were capable of predicting the \(\delta_{\text{peak}}\), \(\tau_{p}\), and d, it was found that the RBFNN-GWO prediction performance was more accurate than that of RBFNN-GA. (2) A comparison was made between the performance of RBFNN-GWO presented in this study and SVR-BBO proposed by Babanouri and Fattahi (2018), and according to the obtained results, the performance of RBFNN-GWO model was better than that of SVR-BBO for all output parameters in both training and testing phases. As an example, the SVR-BBO model predicted \(\tau_{p}\) with R2 values of 0.890 and 0.902 in training and testing phases, respectively, while the values of R2 obtained from RBFNN-GWO model in training and testing phases were 1 and 0.960, respectively. (3) The RBFNN-GWO model proposed in this study may be applicable to other prediction problems in the rock mechanic fields. (4) It can be also recommended to use other optimization algorithms such as Gradient Evolution Algorithm, Gravitational Search Algorithm, Interior Search Algorithm, Joint Operations Algorithm, Locust Swarm Algorithm, and Sine Cosine Algorithm to optimize RBFNN model.