Prediction of the inertial permeability of a 2D single rough fracture based on geometric information

Abstract

The apparent permeability of a single rough fracture undergoes complex evolution in a non-Darcy flow regime, making description of the nonlinear flow challenging. The inertial permeability can be used to effectively solve this problem but is very sensitive to the geometric information and difficult to determine directly. Here, a model for predicting the inertial permeability is proposed by considering the geometric information of rough rock fractures. A massive training database of nonlinear flow in single rough fractures was built based on direct numerical simulations. The database consists of 1225 fractures and contains 12 geometric parameters, including 9 morphological and 3 aperture parameters. To predict the inertial permeability, four geometric parameters highly correlated with the inertial permeability were selected by correlation analysis. A robust prediction model was then established based on the support vector machine theory and the artificial bee colony algorithm. Forty-five fractures constructed from Barton's profiles were used to verify the model performance. The validation results show that the proposed method can accurately predict the inertial permeability based on the geometric information of rough fractures. Finally, the proposed prediction model was used to determine the critical Reynolds number.

1 Introduction

Many engineering applications are involved in the characterization of nonlinear flow in single rock fractures, including the construction of underground space [48], the production of oil and gas [31], the design of impermeable curtains [8], and the transport of pollutants [16].

Low-Reynolds-number flow in a fracture follows Darcy’s law, and the apparent permeability of the fracture is a constant equal to the intrinsic permeability [53]. However, with an increasing Reynolds number, the flow will gradually change from linear Darcy flow to non-Darcy flow. The apparent permeability will change in a complicated manner with pressure or velocity, which makes it very challenging to predict fracture permeability. To solve this problem, Ergun [11] proposed the concepts of viscous permeability (k_v) and inertial permeability (k_i) and successfully introduced them into the Forchheimer equation.

$$- \nabla P = \frac{\mu }{{k_{{\text{v}}} }}v + \frac{\rho }{{k_{{\text{i}}} }}v^{2}$$

(1)

where − ∇P is the hydraulic pressure gradient, v is the average velocity of the fracture cross section, μ is the hydrodynamic viscosity coefficient, and ρ is the fluid density. The first and quadratic terms on the right-hand side of the equation represent the pressure gradient caused by the viscous effect and inertial effect, respectively [53, 63]. For a given fracture, k_v and k_i no longer change with v and are controlled only by the geometric information of the fracture [63]. In addition, when v is relatively small, the quadratic term can be ignored, and Eq. (1) is reduced to Darcy's law. The parameter k_v has been fully studied and lies outside the scope of this paper. Therefore, this study is mainly about the quantitative characterization of k_i.

The Forchheimer equation is a semiempirical model [12], whose initial expression is shown in Eq. (2). It has been widely used in many kinds of geological media, such as porous [1, 62], single fracture [34, 38] and fracture networks [28, 46]. Considering the properties of the fluid and the flow medium, Eq. (2) can also be converted into another commonly used form (Eq. 3):

$${ - }\nabla P = AQ + BQ^{2}$$

(2)

$${ - }\nabla P = \frac{12\mu }{{wb_{{\text{h}}}^{3} }}Q + \frac{\rho \beta }{{w^{2} b_{{\text{h}}}^{2} }}Q^{2}$$

(3)

where A and B are the viscous and inertial coefficients, respectively, Q = wb_hv is the volumetric flow rate or discharge, w is the fracture width (in a two-dimensional (2D) fracture, the default value is 1), b_h is the hydraulic aperture, and β is the non-Darcy coefficient. Combining Eqs. (1)–(3), the relationship between k_i and (B and β) can be obtained:

$$k_{{\text{i}}} = \frac{1}{\beta } = \frac{\rho }{{Bw^{2} b_{{\text{h}}}^{2} }}$$

(4)

The quantitative characterization of non-Darcy flow in fractures has been a difficult problem in recent years, attracting the attention of many scholars. Based on a large number of relevant studies, the existing characterization equations of B, β, and k_i are summarized in Table 1. To date, most research has been conducted on B. However, B is related not only to the fracture geometry but also to the fluid properties (ρ) and cannot intrinsically describe the fracture permeability. The inherent parameters of the fracture, k_i and β, do not change with the Reynolds number. However, there have been few reports on the direct study of k_i. Zhou et al. [63] proposed the following universal relationship between k_i and k_v through a collection of 4000 geologic or analogous‐geologic porous medium samples:

$$k_{{\text{i}}} = \omega k_{v}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}}$$

(5)

where ω is a scaling coefficient. However, the value range of ω is very wide (10⁷–10¹³), and it is therefore impossible to accurately determine k_i for fractured media [53].

Table 1 Parametric equation of B, β, and k_i

The inertial permeability is mainly determined by the geometric information of the fracture. The prediction model in Table 1 contains a large number of fracture geometry parameters including the peak asperity height (ξ), the standard deviation of the secondary roughness (σ_Π), the root mean square roughness (R_rms), the root mean square of the first deviation of the profile (Z₂), the joint roughness coefficient (JRC), the average roughness (R_a), the fractal dimension (D_v), the horizontal length (L_c), the fitting coefficient of the cumulative distribution curve of aperture (C), and the average aperture (b_ave). However, only one or two geometric parameters are typically considered in the model. If too few parameters are used to establish the prediction model, then the geometric information of fractures cannot be fully and accurately described, which may lead to a large deviation between the predicted results and the true values. In contrast, if too many parameters are used to establish the model, then the practicality of the model is lost, and the accuracy of the model is impaired because of the information redundancy between input variables. Therefore, correlation analysis and selection of an appropriate combination of geometric parameters are critical to establishing a prediction model for k_i.

Correlation analysis identifies how closely two or more variables are associated with each other [60]. Various methods have been proposed to address this issue, such as the Pearson correlation coefficient [4], Spearman rank correlation coefficient [26] and Kendall’s tau-b rank correlation coefficient methods [60]. However, these classical methods cannot be used for geometric parameters and k_i with highly nonlinear relations. The maximal information coefficient (MIC) provides a good solution to this issue [37]. The MIC is not concerned with the specific functional relationship between two variables, but rather based on mutual information, such that MIC(X, Y) represents the information content of Y that can be explained by X. This method is very sensitive to various relationships between two variables and can detect various relationship types, including both functional and non-functional relationships, as well as supra-functional relationships, among others. Therefore, the MIC is used here to select the input variables of the prediction models for k_i.

The prediction models in Table 1 are mainly established through dimensional analysis or data fitting. There are many undetermined regression coefficients in these equations, making it very challenging to directly determine k_i. In addition, there is a highly nonlinear relationship between the geometric parameters and k_i, which may cause using traditional data fitting methods to fail but can be well accommodated by machine learning (ML). Recent progress in developing various ML techniques has benefitted the study of various problems in porous media and geoscience across disparate scales, such as the prediction of dissipation coefficients [20], fluid flow [19], velocity fields [49] and macroscopic permeability [21]. However, research on nonlinear flow in fractures by ML has not been reported. Since the support vector machine (SVM) algorithm proposed by Vapnik [44] has favorable robustness [40], SVM is used to establish the prediction model of k_i in this paper.

The Reynolds number (Re), as a parameter describing fluid flow behavior, can be used to quantitatively describe the flow regime within fractures. The Reynolds number corresponding to the point where the Darcy flow changes to a non-Darcy flow is called the critical Reynolds number (Re_c). The quantitative characterization of Re_c is of great significance and has been widely studied [35]. Many scholars have used B or β to establish the characterization equation of Re_c [7, 54]. The critical Reynolds number can also be determined by k_i, but this has not yet been reported.

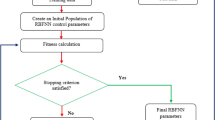
Considering the above issues, the primary motivation of this study is to develop a fracture inertial permeability (k_i) prediction model that utilizes fracture geometric information. First, 1225 two-dimension rough fractures were constructed, and 12 parameters were calculated to describe the geometric information of these fractures. Additionally, numerical simulation and the Forchheimer equation were used to obtain the k_v and k_i values of these fractures. The controlling factors of k_i were selected through the maximal information coefficient (MIC), and a training database with 1225 samples was constructed with the controlling factors as input variables and k_i as input variables. Based on this database, a prediction model for k_i was constructed by combining the artificial bee colony (ABC) algorithm with support vector regression (SVR). The model was then validated using 45 rough fractures constructed from 10 profiles proposed by Barton. The validation results showed that the established model had excellent prediction performance, and further exploration was conducted on how this methodology could be applied to predict k_i in three-dimensional fractures. The global flowchart for developing the inertial permeability prediction model is shown in Fig. 1. Finally, the model was successfully applied to predict the critical Reynold’s number.

Fig.1

Global flowchart for developing the inertial permeability prediction model

2 Theoretical background

2.1 Fracture geometry information characterization method

The inertial permeability is controlled by geometric information such as fracture wall morphology and aperture characteristics and is very sensitive to them. The geometric information of rough fractures can be used to directly predict the inertial permeability; accurate description of the geometric information of rough fractures with strong heterogeneity is essential for prediction accuracy.

The wall morphology of fractures, including the asperity height and asperity inclination angle, tortuosity, and texture structure, has been extensively studied [3, 29, 45, 51]. In this paper, three parameters are selected to describe the asperity height characteristics of the fracture wall, namely, the average relative height (R_ave), the standard deviation of the height (σ_H), and the maximum relative height (R_max). Among them, R_ave is defined as the ratio of the average height of the asperity to the projected length. The parameter σ_H describes the dispersion of the height distribution of the asperities; a larger value corresponds to a rougher fracture wall. R_max represents the asperity height difference of the whole profile line. Then, two parameters, the average inclination angle (θ_ave) and the standard deviation of the inclination angle (σ_θ), are used to describe the asperity inclination angle of the fracture wall. The parameter σ_θ represents the degree of inclination deviation from θ_ave, and the larger σ_θ is, the rougher the wall surface is. In addition, the root mean square of the first deviation of the profile (Z₂) is selected to characterize the spatial structure of the fracture wall, which is defined as the root mean square of the average local slope [30]. The curvature degree of the fracture wall also significantly impacts the flow. The curvature coefficient (R_p) is selected to quantitatively describe the degree of curvature, which is defined as the ratio of the true length to the projected length. Magsipoc et al. [29] noted the difficulty of accurately describing the morphological characteristics of natural fractures with a single statistical parameter. Therefore, the structure function (SF) is used to compensate for this deficiency. SF is a functional proposed by Sayles and Thomas [41] to quantitatively evaluate the texture changes of a profile. Finally, the correlation coefficient (R_{U, D}) of the upper and lower wall surfaces is selected to describe the coincidence degree of fractures [66]. In this way, the combination of 9 parameters can comprehensively describe the morphology of rough fractures. Note that the fracture is composed of upper and lower walls and that all the above parameters except for R_{U, D} are taken as the mean value of the corresponding parameters of the upper and lower walls. Please refer to Eqs. (22)–(33) for the calculation equations of the nine morphological parameters.

The aperture refers to the distance between the upper and lower walls, and its size and distribution characteristics control the flow capacity in the fracture. Two commonly used statistical parameters, including the average aperture (b_ave) and root mean square of aperture (σ_b) of the fracture, are selected to describe the size and discreteness of the rough fracture aperture. The parameter b_ave describes the average fracture aperture, which is defined as the ratio of the area enclosed between the upper and lower profiles to the horizontal projection length of the fracture. The parameter σ_b can be used to evaluate the fluctuation in this value, where a large σ_b corresponds to a large deviation in the aperture from b_ave. The fitting coefficient of the cumulative distribution curve of the aperture (C) is selected to quantify the aperture distribution (please refer to Rong et al. [38]). These three parameters can fully represent the spatial distribution of the fracture aperture. Please refer to Eqs. (34)–(36) for the calculation equations of the three aperture parameters.

Thus, a total of 12 parameters, including 9 morphological parameters and 3 aperture parameters, are selected to describe the geometric information of the fracture.

2.2 Variable selection for the prediction model

A total of 12 fracture geometric parameters are selected to comprehensively describe the fracture geometric information. However, if all the parameters are used as the input variables of the inertial permeability prediction model, then the information redundancy will result in reduced prediction performance as well as the loss of application value of the model. Therefore, it is necessary to reduce the dimensionality and select the main controlling factor of inertial permeability through correlation analysis.

The MIC is used to select the input variable of the k_i prediction model by calculating the correlations among all variables (R_ave, σ_H, R_max, θ_ave, σ_θ, Z₂, R_p, SF, R_{U, D}, b_ave, σ_b, C, k_v, k_i). The calculation steps for MIC values between any two variables X and Y are as follows. Variables X and Y are first combined into a set D = {(X₁, Y₁), (X₂, Y₂),…, (X_n, Y_n)}. Then, c cells and d cells are divided along the horizontal and vertical axes to obtain a grid G by referring to the range of two variables. Different values of c and d correspond to different grid divisions, from which a maximum mutual information value can be obtained:

$$I^{ * } \left( {D,X,Y} \right) = \max I(\left. D \right|_{G} )$$

(6)

where D|_G is the distribution of set D on grid G. After Eq. (6) is standardized, the normalized mutual information value characteristic matrix is obtained:

$$M(D)_{x,y} = \frac{{I^{ * } \left( {D,X,Y} \right)}}{{\log \min \left\{ {x,y} \right\}}}$$

(7)

The MIC value can be obtained by calculating the maximum value of the characteristic matrix of the mutual information value:

$${\text{MIC}}(D){ = }\mathop {\max }\limits_{{xy \le B^{ * } (n)}} \left\{ {M(D)_{x,y} } \right\}$$

(8)

where B^*(n) = n^0.6 is the upper limit of the number of grids. The MIC value corresponds to the determination coefficient of the regression analysis method. The value range of MIC(X, Y) is [0, 1]. In particular, when MIC(X, Y) is 1, it indicates that variable Y is completely correlated with variable X; when MIC(X, Y) is 0, it indicates that the two variables are completely independent. The MIC has the advantages of generality and equitability because the estimations of the Shannon entropy and conditional entropy are robust [43]. The selection of statistical parameters for k_i follows two principles: (1) the variable with a high MIC value with k_i is preferred, and (2) the input variables are mutually independent to the greatest extent possible.

2.3 Prediction model establishment method

Support vector machine (SVM) [44] and the artificial bee colony (ABC) [23] algorithm are used to establish the prediction model for inertial permeability.

The SVM algorithm was proposed based on statistical theory combined with the principle of minimum structural risk. The complexity of an SVM model depends on the number of support vectors rather than the number of samples, which effectively solves the problem of dimensionality. This makes the SVM model suitable for data with high-dimensional and nonlinear characteristics between the fracture geometric information and the inertial permeability. The SVM algorithm has classification and regression functions. The prediction of k_i in this paper is a regression problem, so the classical ε-SVR model is selected. This is mathematically described as follows:

$$k_{{\text{i}}} = \sum\nolimits_{i = 1}^{i = N} {\left( { - \alpha_{i} + \alpha_{i}^{ * } } \right){\text{e}}^{{ - g\left\| {SV_{i} ,{\mathbf{X}}} \right\|}} } + b$$

(9)

where N is the number of support vectors, (− α_i + α_i^*) is the Lagrange multiplier, SV is the support vector, g is the radial basis function (RBF) parameter, and b is the bias constant. A detailed introduction to SVR theory can be found in Sun et al. [42]. There are three parameters to be optimized, which are the sensitive loss coefficient (ε) describing the sparsity of the solution of the model, the penalty factor (c) weighing the error and model complexity, and the RBF parameter (g) controlling the complexity of the mode. The optimization method adopted in this paper is the ABC algorithm, which is a swarm metaheuristic intelligent optimization algorithm based on swarm foraging behavior [23]. This algorithm has the advantages of simple individual behavior, distributed control, strong robustness and scalability. The ABC model consists of four basic elements: hirer bees, follower bees, scout bees, and nectar food sources. Among them, the location of the food source represents the feasible solution to the optimization problem, and the nectar richness of the food source represents the quality of the feasible solution.

When the ABC algorithm is used to optimize the three parameters of SVR based on training data, the mean square error of cross-validation (CVMSE) is taken as the objective function as follows [22]:

$$f_{{\mathbf{u}}} = {\text{CVMSE}}_{{\mathbf{u}}} = \frac{1}{M}\sum\limits_{S = 1}^{S} {\sum\limits_{{i \in G_{S} }} {\left[ {y_{i} - f\left( {{\mathbf{x}}_{i} } \right)\left| {\mathbf{u}} \right.} \right]} }$$

(10)

where u = (ε, c, g) is a solution in the optimization process, M is the number of training data, S is the number of subsets used for cross-validation, G_S is the Sth subset for validation, y_i is the target value, which here represents the value of the numerical test for the inertial permeability, and f(x_i)|u is the value predicted based on SVR when the SVR hyperparameters are set as u. The CVMSE can be obtained directly by opening the cross-validation module of LibSVM [5].

The main steps in optimizing SVR models with the ABC algorithm are summarized as follows (Fig. 2): (1) Determine the ranges of (ε, c, g), the population size (NP), the maximum number of iterations (maxCycle), and a predetermined number (NPD). Next, generate NP/2 solutions u_i = (ε_i, c_i, g_i) through u_ij = L_j + rand(0,1)(D_j− L_j), where L_j and D_j are the lower and upper bounds of (ε, c, g). Calculate the corresponding fitness fit_i of each solution though fit_i = 1/(1 + f_u). (2) Update solutions for employed bees through v_ij = u_ij + θ_ij(u_ij-u_kj), and calculate the corresponding fitness; then, determine new solutions by greedy selection. (3) Calculate the probability p_i of each solution being selected through $p_{i} = {\text{fit}}_{i} /\sum\nolimits_{j = 1}^{NS} {{\text{fit}}_{j} }$, and determine the solution to be updated according to roulette choices. (4) Update solutions for onlookers through v_ij = u_ij + θ_ij(u_ij−u_kj), and calculate the corresponding fitness; then, determine new solutions by greedy selection. (5) Examine whether the number of times the solution has not been updated NNU > NPD. If so, skip to step (6), and if not, skip to step (7). (6) Update the solution u_i = (ε_i, c_i, g_i) for a scout through u_ij = L_j + rand(0,1)(D_j−L_j). (7) Examine whether the number of iteration steps (NIS) has reached maxCycle. If not, then return to step (2). If so, then output the values of (ε, c, g) corresponding to the smallest CVMSE; these values represent the optimal parameter combination.

Fig. 2

Flowchart demonstrating how the ABC algorithm optimizes SVR parameters

3 Fracture model development and direct flow simulation

Focus of this research is to simulate fluid flow in a fracture in 2D instead of 3D, as explained in detail below. The key to building an accurate k_i prediction model using the ML method is to obtain a database containing a large number of fracture samples. There are two substantial problems in conducting numerical experiments on 3D fractures: (1) the grid number for 3D fractures is far more than that for 2D fractures under the condition of ensuring the accuracy of calculation; and (2) the solution of the Navier–Stokes (NS) equations for 3D fractures is very complex and does not readily converge. Based on the above two problems, it is clear that the numerical experiments using 3D fractures would consume considerable time and computer resources. Therefore, building a database containing massive 3D fractures certainly face great challenges. Compared with 3D fractures, the grid number of 2D fractures is greatly reduced to a level that can be easily accommodated by a computer. The solution of 2D NS equations is relatively simple and reliable and has been widely used to study fluid flow or solute transport in rock fractures [6, 52]. The key to the present study is to propose a method that can directly predict the rough fracture k_i based on geometric information. The 2D rough fracture is sufficient to meet our purpose, and the method can be extended to the 3D rough fracture in the future, as discussed in detail in Sect. 4.1.5.

3.1 Rough-walled fracture model development

The construction of a database containing a large number of samples is the key to building a model using machine learning methods. The generation of the rough fracture model mainly includes two parts: determining the top and bottom walls of all fractures, and combining the top and bottom walls to generate rough fractures. The walls of all fractures in this study are selected from 102 profile lines collected by Li and Zhang [25]. The detailed steps to determining the top and bottom walls are as follows. ① Level the profiles. All the profiles need to be levelled, which is very important for the calculation of later morphological parameters. A detailed introduction is given in another article [47]. ② Sort the profiles. These profiles have projected lengths ranging from 72 to 119.6 mm, and a uniform length is needed to eliminate the size effect. Profiles shorter than this length are deleted, and profiles longer than this length are truncated (Fig. 3a). In this study, a uniform length of 99.6 mm was chosen, and a total of 50 profiles were selected as the walls of fractures (please refer to Online Appendix (S1)). Their JRC values are approximately 4.0–20, almost covering the roughness of fractures in nature. ③ Determine the top and bottom walls. Number the 50 profiles from 1 to 50. First, determine the top wall; there are 49 possible cases. Then, determine the bottom wall, which must be determined according to two principles: the top and bottom walls cannot share the same profile (to ensure that the studied objective is an unmatched fracture), and the average JRC value of the top and bottom walls must not be the same. For example, when the top wall is profile No. 1, the bottom wall can accept only the profiles Nos. 2–50. When the top wall is profile No. 2, the bottom wall can accept only profile Nos. 3–50, and so on. Therefore, there are (49 + 48 + ⋯ + 1 = 1225) choices (Fig. 3b).

Fig. 3

Diagram for generating 1225 rough fractures

Since this study deals with 2D fractures, where zero aperture is not admissible, the minimum aperture is uniformly fixed at 0.2 mm. The detailed steps to combine the top and bottom walls into a fracture are as follows. ① Generate coordinate point files for fracture walls with an interpolation spacing of 0.4 mm. Each fracture wall contains 250 coordinate points; ② Fix the bottom profile above and tangent to the x-axis, and place the top profile above the bottom profile (Fig. 3c); ③ Calculate the distance between all points on the lower wall and all points on the upper wall to form a distance matrix D = {dij, i = 1, 2,…, 250; j = 1, 2,…, 250} where d_ij indicates the distance between points i on the bottom wall and j on the top wall: $d_{ij} = \sqrt {\left( {x_{uj} - x_{lx} } \right)^{2} + \left( {y_{uj} - y_{lx} } \right)^{2} }$. The minimum value of matrix D is the minimum distance between the two profiles, namely, b_min. ④ Examine whether the minimum distance satisfies |b_min − b_min0|≤ 10⁻⁷ (b_min0 = 0.2 mm). If so, export the discrete point coordinate files of the top and bottom walls, and if not, move the top wall vertically and return to step ③. In addition, the inlet and outlet coordinate files are generated according to the coordinates of the head and end points of the fracture. A fracture model is composed of four coordinate files: lower wall, upper wall, inlet, and outlet. Additional details regarding the method of fracture model development were provided by Sun et al. [42]. In total, 1225 2D rough fracture models are generated by using the above method.

3.2 Direct numerical simulation

Fluid flow within a fracture at a steady state is governed by the Navier–Stokes equations, which can be expressed as:

$$\begin{aligned} \rho ({\mathbf{u}} \cdot \nabla ){\mathbf{u}} & = - \nabla p + \mu \nabla^{2} {\mathbf{u}} \\ \nabla \cdot {\mathbf{u}} & = 0 \\ \end{aligned}$$

(11)

where ρ and u are the density and velocity vectors of the fluid, respectively. These equations can precisely capture the nonlinear flow characteristics in rough fractures. In this study, FLUENT software is used to solve the Navier–Stokes equations [10, 59, 69].

Before the FLUENT simulations, the mesh of the fracture model needs to be generated. As a powerful mesh generation software, Integrated Computational Engineering and Manufacturing (ICEM) software can generate high-quality meshes [61], which facilitate accurate numerical solutions and good computational convergence [57]. Therefore, the entire fracture medium is covered by a quadrilateral structured mesh, and each fracture wall is further refined using a boundary layer mesh. Mesh independence analysis is carried out to illustrate the rationality of mesh generation. As illustrated in Fig. 4, when the number of cells is 180,000, the value of k_i can be considered unchanged. The number of nodes parallel to the flow direction is 61, and the number of nodes perpendicular to the flow direction is 3001. The thickness of the first layer of mesh near the wall is set to 1e-4 mm, and both parameters that control the mesh size growth rate (ratio 1 and Ratio 2) are set to 1.2. Finally, the structured meshes are converted to unstructured meshes that can be used with FLUENT (as shown in Fig. 5).

Fig. 4

Mesh independence analysis of fracture no. 841

Fig. 5

Two-dimensional fracture mesh of fracture No. 3

When FLUENT is used to solve the NS equations, some appropriate settings are required for nonlinear flow. The number of fractures in this study is large, and the morphology varies greatly, so there may be a large grid area and a narrow calculation area. Therefore, a dual-precision 2D solver was chosen. Considering the effects of the occurrence of recirculation zones [65] and boundary layer separation on the flow field in the fracture media, the realizable k-ε model and the wall surface enhancement function are chosen for the simulation [59]. The direct numerical simulations assume room temperature (approximately 20 °C), so the viscosity and density of water are 1.003 × 10⁻³ kg/m·s and 998.2 kg/m³, respectively. The inlet was modeled as a velocity-inlet, with the velocity magnitude being set as needed. The outlet was modeled as a pressure-outlet with a pressure value of 0. The top and bottom walls were modeled as no-slip boundaries (Fig. 5). In this study, over a thousand fractures needed to be simulated, and each fracture needed to be simulated with 10 different flow velocities. To balance the simulation time and calculation accuracy, the residual convergence criterion was set to the default value of 1e-3 in fluent (Fig. 6). In addition, the simulation duration was also controlled by the geometric characteristics of the fractures. Overall, the simulation duration for most fractures was approximately 1 h, while for some extremely complex fractures, it could exceed 2 h. All the simulations were conducted on a computer equipped with an AMD Ryzen Threadripper PRO 3975WX processor and 128 GB RAM. Before each calculation begins, the entire flow velocity field within the fracture media is initialized based on the given flow velocity value at the input point. After the calculation begins, the pressure value at the input is monitored and recorded for use in the inversion of k_i.

Fig. 6

Convergence profile of the No. 3 fracture with v = 0.082 m/s

ICEM and FLUENT can perform batch processing through journal files. The journal files were generated based on MATLAB to automatically perform all operation steps, including the import of four fracture coordinate files (lower wall, upper wall, inlet, and outlet), the generation and storage of grid files in ICEM, the import of grid files, calculations and the storage of monitoring data in FLUENT. In this study, all fracture calculations are performed by calling journal files, which improves the calculation efficiency and avoids manual operation errors.

4 Results and discussion

4.1 Establishment of the k _i model

Based on the numerical experiment results of FLUENT, the viscous permeability (k_v) and the inertial permeability (k_i) of all fractures were obtained through inversion of the Forchheimer equation, and the geometric information can be obtained based on the point cloud of the fracture wall. In this way, a database with 1225 samples and 14 variables was established. The MIC is used to analyze the correlation of all variables and determine the main controlling factor of k_i. The controlling factors were used as input variables, and k_i was used as the output variable to construct a training database for establishing a prediction model of k_i. Based on this database, a k_i prediction model was established using the ABC-SVR method. Finally, the performance of the established k_i model was validated using 45 rough fractures constructed from 10 Barton standard profiles.

4.1.1 Acquisition of the training dataset

The acquisition of the training dataset is the first step in using SVR to build a prediction model. The training database contains 1225 fractures, and the flow behavior in these fractures is directly simulated by using FLUENT to solve the NS equations. Based on the ICEM journal file, 1225 fractures are meshed, and calculations are performed based on the FLUENT journal file. To reflect the nonlinear relationships of ∇P and v, the inlet boundary conditions of each fracture are set at 10 levels from 0.002 to 0.182 m/s with an interval of 0.02 m/s. Figure 7 shows the streamlines and velocity distribution in the interval x = [0.0 m, 0.4 m] of the No. 3 fracture (Fig. 5) under different inlet velocities. With increasing velocity, the areas of recirculation zones increase gradually, and the width of the mainstream channel decreases gradually. This phenomenon indicates that non-Darcy flow easily occurs in rough fractures and that the non-Darcy effect becomes increasingly significant with increasing velocity.

Fig. 7

Streamlines and velocity distribution in the interval x = [0.0 m, 0.4 m] of the No. 3 fracture under different inlet velocities. a v_inlet = 0.002 m/s; b v_inlet = 0.022 m/s; and c v_inlet = 0.182 m/s

After the calculation and monitoring are carried out, 10 values of ∇P are obtained. The inertial permeability (k_i) is obtained by fitting 10 pairs of ∇P and v values with the Forchheimer equation (Eq. 1). Figure 8 presents the relationship of − ∇P and v for 1225 fractures. The color represents the standard deviation of the asperity height (σ_H). At the same v, the rougher the fracture wall is, the greater the pressure loss, which indicates that the wall morphology has a significant impact on the fracture permeability coefficient. The coefficients of determination (R²) values of all fitting curves are greater than 0.99, which indicates that it is reliable to use the Forchheimer equation to describe nonlinear flow through a single rough fracture.

Fig. 8

Relation between − ∇P and v for 1225 rough fractures. The color represents the value of σ_H

Based on the point cloud of the fracture wall, the geometric parameters of 12 fractures can be calculated by Eqs. (22)–(36). In this way, a database containing 1225 fractures is obtained, and it is composed of 12 statistical parameters related to the fracture geometry and inertial permeability (please refer to Online Appendix (S2)).

4.1.2 Selection of variables based on the MIC

There may be a strong correlation between the geometric parameters of the 12 fractures. For example, there is a highly linear correlation between R_ave and σ_H (R² is 97.3%) (Fig. 9a); the correlation between θ_ave and σ_θ is greater (R² = 99.5%) (Fig. 9b). Using all geometric parameters to establish the k_i prediction model can cause information redundancy, which would reduce model performance. Therefore, it is necessary to carry out correlation analysis on many factors and determine the main controlling factors of inertial permeability. The MIC is used to analyze the correlations between the 12 parameters and k_i. The greater the MIC value is, the greater the correlation between the two variables. Figure 10 shows the MIC analysis results.

Fig. 9

Relationships between geometric parameters: a relationship between R_ave and σ_H and b relationship between θ_ave and σ_θ

Fig. 10

MIC analysis results

The numbers and colors in Fig. 10 represent the size of the MIC. The last column represents the MIC value between all variables and k_i. The correlation between the aperture and k_i is stronger than that between the morphology and k_i. Among all the morphological parameters, the correlation between the asperity height and k_i is stronger than that between the asperity height and the other parameters, such as inclination angle and curvature degree. According to the principle of the MIC method to screen the main control factors, the geometric parameters of 12 fractures are selected as follows. First, the MIC values of two parameters (R_{U, D} and C) and k_i are smaller than other parameters (MIC < 0.25), so they can be discarded. Second, the MIC values between the two asperity height parameters (R_ave and R_max) and σ_H are close to 1, which means that the influence of R_ave and R_max on k_i can be replaced by σ_H. Therefore, only σ_H needs to be selected as the parameter to describe the asperity height. Third, the MIC values of the other five morphological parameters (θ_ave, σ_θ, R_p, Z₂ and SF) are close to 1, so it is sufficient to select only SF with the highest MIC value with k_i. Finally, the MIC values of the two aperture parameters (b_ave and σ_b) and k_i are both large, so b_ave and σ_b are selected as input variables.

In addition, according to previous research results (Table 1), the equivalent hydraulic aperture (b_h) is considered in almost all the prediction models of B and β. Considering the relationship between b_h and k_v (k_v = b_h²/12) and the strong correlation between k_v and k_i (MIC = 0.68), k_v is also selected as the input variable of the k_i prediction model.

Finally, two morphological parameters (σ_H and SF), two aperture parameters (b_ave and σ_b), and k_v are selected to calculate k_i. A training database {(σ_H)_i, (SF)_i, (b_ave)_i, (σ_b)_i, (k_v)_i, (k_i)_i; i = 1,…,1225} serving to build the k_i prediction model is constructed (please refer to Online Appendix (S2)).

4.1.3 SVR-based model establishment

• (1) Normalization of the sample data. There are large differences in units and magnitudes between the input variables and the output variable, which may affect the accuracy and speed of modeling. For example, the magnitude of b_ave is 10¹, while the magnitude of the viscous permeability is 10^–9, with a difference of 10 orders of magnitude. Therefore, it is necessary to normalize the data and eliminate these effects before training and modeling. Normalization and anti-normalization are treated as follows:

  $${\text{Normalization}}:x^{\prime } = {{\left( {x - x_{\min } } \right)} \mathord{\left/ {\vphantom {{\left( {x - x_{\min } } \right)} {\left( {x_{\max } - x_{\min } } \right)}}} \right. \kern-0pt} {\left( {x_{\max } - x_{\min } } \right)}}$$

  (12)
  $${\text{Antinormalization}}:x = x^{\prime } (x_{\max } - x_{\min } ) + x_{\min }$$

  (13)

  where x is the sample value that needs to be normalized and x’, x_max and x_min are normalized values and maximum and minimum values, respectively. All of the samples are normalized to [0, 1] based on Eq. (12), and the normalized data can be reversely normalized through Eq. (13).

• (2) Parameter optimization for the prediction model. The studies discussed in Sect. 2.3 suggested that the SVR hyperparameters (ε, c and g) must be simultaneously optimized. The global optimization of hyperparameters in this paper adopts the LIBSVM library and ABC algorithm. The optimization calculation is performed according to the steps in Sect. 2.3. The population size (NP), the maximum number of iterations (maxCycle), the predetermined number (NPD), the number of subsets used for cross-validation, and the search range of hyperparameters are set to 20, 10 100, 10, and [1e-3, 1e3], respectively. The final optimization result of the SVR hyperparameters (ε, c, and g) is (0.001, 13.5992, and 0.9912).

• (3) Establishment of the prediction model for the inertial permeability. Once the SVR hyperparameters are determined, the prediction model of the inertial permeability can be obtained by combining the whole training database containing 1225 samples:

  $$k_{{\text{i}}} = \sum\limits_{i = 1}^{i = 1211} {\left( { - \alpha_{i} + \alpha_{i}^{ * } } \right){\text{e}}^{{ - 0.9912\left\| {SV_{i} ,{\mathbf{X}}} \right\|}} } + {0}{\text{.4493}}$$

  (14)

In this model, there are 1211 SV and 1211 (-α + α^*) in total, and the bias constant is 0.4493. For a given fracture, the four morphological parameters σ_H, SF, b_ave, and σ_b are easily obtained by using Eqs. (25), (32), (34), and (35), respectively. It is worth emphasizing that there exists a large body of literature proposing various predictive models for k_v. Our previous work has conducted a comprehensive investigation into this topic [42]. Here, we do not discuss the applicability of these models for k_v computation, as this is not the focus of our current study. Once all input variables X = (σ_H, SF, b_ave, σ_b, k_v) are obtained, the k_i of any fracture can be directly determined by Eq. (14), which can further provide an accurate estimation of the permeability of fractures in practical geoengineering. The above modeling process can be easily realized through MATLAB. For the convenience of application, all data and MATLAB codes used in the model are uploaded as supplementary data (please refer to Online Appendix (S3)).

Equation (14) is used to calculate k_i of 1225 fractures, and the results are compared and analyzed with the reverse calculated value of the numerical experiments. The comparison results are shown in Fig. 11, and the R² value is 90.61%.

Fig. 11

Comparison of the predictive and simulation values of k_i in the training database

4.1.4 Validation of the model

To verify the accuracy and generalization performance of the k_i prediction model, 10 profiles (please refer to Online Appendix (S4)) proposed by Barton and Choubey [2] are used to generate the fracture model of the validation database. The 10 profiles at high-frequency are applied to the construction of rough fractures [27, 36], and their JRC values include a wide distribution from smooth (JRC = 0.4) to rough (JRC = 18.7). Two profiles are selected randomly from the 10 standard profiles as the upper and lower wall surfaces of the fractures, and finally, 45 rough fracture models are generated. The experimental values of k_i and k_v of 45 fractures are obtained based on direct numerical simulation, and the geometric parameters (σ_H, b_ave, SF, and σ_b) are calculated based on the coordinate files (please refer to Online Appendix (S5)).

Based on the numerical experimental inversion value of 45 rough fractures, the SVR model is compared with the two models proposed by Zhou et al. [63] and Xing et al. [54]. Two criteria are used to quantitatively evaluate the prediction equation, that is, the normalized objective function (NOF) and the slope γ of the regression line in the plot of the predicted versus experimental values of k_i. The NOF is defined as the ratio of the root mean square error (RMSE) to the mean of the experimental data. The closer to 0 the NOF value is, the higher the accuracy for the predicted value is [64]. The slope γ reflects the model bias for the overestimation (γ > 1) or underestimation (γ < 1) of numerical experimental data [64], which can be obtained with ORIGIN software.

Table 2 and Fig. 12 show the predictive performance of the three models; please refer to “Appendix 2” for the predicted values. The prediction performance of Xing’s model for these 45 fractures is not as good as that of the other two models (NOF = 0.517, γ = 0.876), which may be due to the following two aspects. (1) Xing’s model database is not extensive enough. All 2D fractures serving for the prediction model are collected from the same 3D rough fracture. The range of R_rms, R_a and b_m values is relatively small, and the prediction deviation for fractures beyond this range is large. (2) The geometric parameters of Xing’s model are insufficient. Only the average aperture (b_ave) is selected to describe the aperture distribution characteristics, and the influence of b_ave on k_i may be exaggerated. However, for the study of the non-Darcy effect of complex rough fractures, in addition to b_ave, the root mean square of the aperture (σ_b) will also have a complex and significant impact. Zhou’s model performs better (NOF = 0.186, γ = 0.970), but the predicted values are still more discrete. This is because Zhou's model is a universal model for geologic porous media, not just a single fracture. In addition, Zhou’s model uses only one scale parameter (ω) to describe the geometric information, which makes it inadequate for predicting k_i of 45 rough fractures with strong heterogeneity. The predictive performance of the SVR model is the best (NOF = 0.155, γ = 1.017). The input variable of the SVR model is the main control factor screened through correlation analysis, which can accurately describe the geometric information of rough fractures. In addition, the modeling method adopts the support vector machine methodology that can skillfully handle complex relationships. Crucially, Zhou’s model and Xing’s model contain uncertain parameters that make it impossible to directly determine k_i, while the SVR model can directly obtain k_i of any single rough fracture by using supplementary materials.

Table 2 Comparison results of the prediction model performance

Fig. 12

Comparison of the predictive and simulation values of k_i in the validation database

4.1.5 Extension of the k _i model

To further enable this research to serve practical geoengineering, this section provides an approach on how to establish a predictive model of 3D fracture inertial permeability using the proposed method and outlines the detailed methods. The aim is to provide readers with inspiration and guidance in this field. The specific steps are as follows. (1) Generation of the 3D rough fracture model. Considering the wall morphology, aperture distribution, contact area and other characteristics, Synfrac software [33] is used to generate a large number of 3D fracture models. To facilitate the mesh generation and numerical calculation, the aperture of the contact area is set to 0.01 mm (Fig. 13a). (2) Mesh generation of the 3D fracture model. ICEM CFD software is used to mesh the 3D fractures. The accuracy of the direct simulation is controlled by the quality of the mesh. Therefore, the structured mesh method is used, and the mesh near the boundaries is refined (Fig. 13b). (3) Direct simulation of nonlinear flow. Nonlinear flow in 3D fractures can be directly simulated by solving NS equations with FLUENT (Fig. 13c). The settings of FLUENT are similar to those of 2D fractures. The inlet is modeled as the velocity inlet, and the outlet is modeled as the pressure outlet. By monitoring the pressure at the inlet, a series of pressure gradient and velocity values can be obtained. (4) Acquisition of the database. Based on the numerical calculation results, the inertial permeability can be obtained by fitting the Forchheimer equation. The geometric parameters of 3D fractures can be calculated by referring to 2D fractures through statistical methods [29]. (5) Establishment of the k_i model. Based on the training database composed of a large number of 3D fractures, the main controlling factors of k_i can be selected by the MIC method, and then the prediction model of k_i is established by the ABC-SVR method.

Fig. 13

Modeling and direct simulation of 3D fractures

However, there are two main challenges to the database collection of 3D fractures: (1) The NS equations of 3D fractures may not converge in the calculation [52], which leads to the failure to obtain k_i. (2) The workload of the direct simulation of 3D fractures is tremendous. Compared with 2D fractures, the construction of a 3D fracture database consumes massive amounts of time and computer resources. For the above two problems, further research investment is needed in the future. Once the database is obtained, the method proposed in this paper can be used to establish the k_i prediction model of 3D fractures.

4.2 Application of the k _i model

The Reynolds number (Re), defined as the ratio of inertial forces to viscous forces, can be used to quantitatively describe the flow regime within fractures. The expression for Re is as follows:

$$Re = \frac{{\rho vb_{{\text{h}}} }}{\mu }$$

(15)

When the Re of fluid flow within fractures is sufficient low, the flow within fractures exhibits linear Darcy flow. However, as Re increases, the inertia effect becomes gradually significant, and linear laminar flow gradually transforms into non-Darcy flow. The Reynolds number corresponding to the turning point is called the critical Reynolds number (Re_c). The quantitative characterization of Re_c is very meaningful and has attracted the attention of many scholars. The critical Reynolds number can be determined by the prediction model of k_i (Eq. 14) proposed in this paper.

Similarly to Re, The Forchheimer number (Fo) is also widely pursued in the assessment of the flow regime [15, 54, 58], which is defined as the ratio of the inertial term to the viscous term:

$$Fo = \frac{{\frac{\rho }{{k_{i} }}v^{2} }}{{\frac{\mu }{{k_{v} }}v}} = \frac{{\rho k_{v} v}}{{\mu k_{i} }}$$

(16)

Combining Eqs. (15)–(16), the relationship between Re and Fo can be obtained as follows:

$$Re = \frac{{b_{{\text{h}}} k_{i} }}{{k_{v} }}Fo$$

(17)

Equation (17) includes both the equivalent hydraulic opening (b_h) and viscous permeability (k_v), and the relationship between them can be obtained from Eqs. (1)–(3).

$$b_{{\text{h}}} = (12k_{v} )^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

(18)

An expression of Re can be obtained by introducing Eq. (18) into Eq. (17).

$$Re = \frac{{k_{{\text{i}}} }}{{\sqrt {12k_{v} } }}Fo$$

(19)

According to Eq. (19), Re is connected with k_v, k_i, and Fo, and when Fo attains the critical value Fo_c, the corresponding Re reaches the value Re_c.

In addition to Re_c and Fo_c, the non-Darcy effect factor (E) is a widely used indicator for distinguishing between Darcy flow and non-Darcy flow [18, 46]. E represents the starting point of non-Darcy flow and is defined as the ratio of the pressure gradient caused by inertia effect to the total pressure gradient. By combining the Forchheimer low (Eq. 1), E can be expressed as:

$$E = \frac{{\frac{\rho }{{k_{i} }}v^{2} }}{{\frac{\mu }{{k_{v} }}v + \frac{\rho }{{k_{i} }}v^{2} }} = \frac{Fo}{{Fo + 1}}$$

(20)

For fractures, the widely recognized value of E = 0.1 indicates that when the inertia-effect-caused pressure gradient accounts for 10% of the total pressure gradient, the flow transforms into non-Darcy flow [18, 46]. From the definition, it is evident that E and Re_c are consistent, so the relationship between them can be obtained by solving Eqs. (19) and (20).

$$Re_{{\text{c}}} = \frac{{k_{{\text{i}}} }}{{\sqrt {12k_{v} } }} \cdot \frac{E}{1 - E} = \frac{{k_{{\text{i}}} }}{{18\sqrt {3k_{v} } }}$$

(21)

Based on the numerical experimental inversion value of 45 rough fractures, the performance of Eq. (21) is verified, and the verification results are shown in Fig. 14 and “Appendix 2”. The second to last column of “Appendix 2” is the result obtained by substituting the numerical simulation-obtained k_v and k_i into Eq. (21), and the last column is the result obtained by substituting the numerical simulation-obtained k_v and predicted k_i into Eq. (21).Therefore, the method of using the k_i prediction model to obtain a critical Reynolds number is reliable.

Fig. 14

Comparison of the predictive and simulation values of Re_c in the validation database

5 Conclusions

In this study, we proposed a method for determining the inertial permeability of rough rock fractures by considering their geometric information. A total of 1225 nonmated fractures were generated through the combination of 50 profiles with different roughnesses, and 10 numerical experiments with different flow velocities were carried out for each fracture. A massive database consisting of 9 morphological parameters, 3 aperture parameters and the inertial permeability was obtained. Based on this database, four geometric parameters (σ_H, SF, b_ave, σ_b, k_v) highly correlated with the inertial permeability were selected as input variables by using the MIC method, and a prediction model of the inertial permeability was established through ABC-SVR. The MATLAB program and all data related to solving the model were uploaded as Supplementary data. Forty-five fractures constructed from Barton’s profiles were selected to verify the performance of the prediction model. Two quantitative evaluation criteria (NOF and γ) show that the model has high prediction accuracy and good generalization performance. Finally, the application of the model in the critical Reynolds number was discussed in detail. This work is of great significance for further research on rough 3D fractures. In addition, the methodology in this study could be extended to the study of other engineering geological problems, such as the stability of slopes and underground spaces, the long-term safety of support engineering, and evaluations of underground resources.

Appendices

Appendix

Appendix 1. Calculation of statistical parameters for fracture geometric information

• (1) Average relative height, R_ave

  $$R_{{{\text{ave}}}}\,{=}\,{{h_{{{\text{ave}}}} } \mathord{\left/ {\vphantom {{h_{{{\text{ave}}}} } L}} \right. \kern-0pt} L}$$

  (22)
  $$h_{{{\text{ave}}}} = \frac{1}{L}\int_{x = 0}^{x = L} {\left| y \right|dx} = \sum\nolimits_{i = 1}^{i = N - 1} {\frac{{\left| {y_{i + 1} + y_{i} } \right|\left( {x_{i + 1} - x_{i} } \right)}}{2L}}$$

  (23)
  $$L = \sum\nolimits_{i = 1}^{i = N - 1} {\left( {x_{i + 1} - x_{i} } \right)}$$

  (24)

• (2) Standard deviation of the height, σ_H (mm)

  $$\sigma_{H} = \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {y - h_{{{\text{ave}}}} } \right)^{2} dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \left[ {\frac{1}{L}\sum\nolimits_{i = 1}^{i = N - 1} {\frac{{x_{i + 1} - x_{i} }}{2}\left( {\left( {y_{i} - h_{{{\text{ave}}}} } \right)^{2} + \left( {y_{i + 1} - h_{{{\text{ave}}}} } \right)^{2} } \right)} } \right]$$

  (25)

• (3) Maximum relative height, R_max

  $$R_{\max } = \frac{{h_{p} - h_{v} }}{L}$$

  (26)

• (4) Average inclination angle, θ_ave (°)

  $$\theta_{{{\text{ave}}}} = \tan^{ - 1} \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {\frac{dy}{{dx}}} \right)dx} } \right] = \tan^{ - 1} \left[ {\frac{1}{L}\sum\nolimits_{i = 1}^{i = N - 1} {\frac{{\left| {y_{i + 1} - y_{i} } \right|}}{{x_{i + 1} - x_{i} }}} } \right]$$

  (27)

• (5) Standard deviation of inclination angle, σ_θ (°)

  $$SD_{\theta } = \tan^{ - 1} \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {\frac{dy}{{dx}} - \tan \theta_{{{\text{ave}}}} } \right)^{2} dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} { = }\tan^{ - 1} \left[ {\frac{1}{L}\sum\nolimits_{i = 1}^{i = N - 1} {\left( {\frac{{y_{i + 1} - y_{i} }}{{x_{i + 1} - x_{i} }} - \tan \theta_{{{\text{ave}}}} } \right)^{2} \left( {x_{i + 1} - x_{i} } \right)} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

  (28)

• (6) Root mean square of the first deviation of the profile, Z₂

  $$Z_{2} = \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {\frac{dy}{{dx}}} \right)^{2} dx} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \left[ {\frac{1}{L}\sum\nolimits_{i = 1}^{i = N - 1} {\left( {\frac{{y_{i + 1} - y_{i} }}{{x_{i + 1} - x_{i} }}} \right)^{2} } } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

  (29)

• (7) Roughness profile index, R_p

  $$R_{p} = {{L_{t} } \mathord{\left/ {\vphantom {{L_{t} } L}} \right. \kern-0pt} L}$$

  (30)
  $$L_{t} = \sum\nolimits_{i = 1}^{i = N - 1} {\left[ {\left( {x_{i + 1} - x_{i} } \right)^{2} + \left( {y_{i + 1} - y_{i} } \right)^{2} } \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }$$

  (31)

• (8) Structure function of the profile, SF (mm²)

  $$SF = \frac{1}{L}\int_{x = 0}^{x = L} {\left[ {f\left( {x + dx} \right) - f\left( x \right)} \right]^{2} dx = } \frac{1}{L}\sum\nolimits_{i = 1}^{i = N - 1} {\left( {y_{i + 1} - y_{i} } \right)^{2} \left( {x_{i + 1} - x_{i} } \right)}$$

  (32)

• (9) Correlation coefficient, R_{U, D}

  $$R_{{{\text{U}}{{\mathrm{D}}}}} { = }\frac{{C_{{{\text{U}}{{\mathrm{D}}}}} }}{{\sqrt {C_{{{\text{U}}{{\mathrm{U}}}}} \cdot C_{{{\text{D}}{{\mathrm{D}}}}} } }}$$

  (33)

• (10) Average aperture, b_ave (mm)

  $$b_{{{\text{ave}}}} = \frac{1}{L}\int_{x = 0}^{x = L} {bdx} = \frac{1}{N - 1}\sum\nolimits_{i = 1}^{i = N - 1} {b_{i} }$$

  (34)

• (11) Root mean square of the aperture, σ_b (mm)

  $$\sigma_{b} = \left[ {\frac{1}{L}\int_{x = 0}^{x = L} {\left( {b - b_{{\text{m}}} } \right)^{2} dx} } \right]^{1/2} = \left\{ {\frac{1}{N}\sum\nolimits_{i = 1}^{i = N} {\left( {b_{i} - b_{{\text{m}}} } \right)^{2} } } \right\}^{1/2}$$

  (35)

• (12) Fitting coefficient of the cumulative distribution curve of the aperture, C

  $$A^{ * } = \frac{1}{{1 + \left( {{{b^{ * } } \mathord{\left/ {\vphantom {{b^{ * } } {b_{{{\text{ave}}}} }}} \right. \kern-0pt} {b_{{{\text{ave}}}} }}} \right)^{C} }}$$

  (36)

Appendix 2. Parameters k _i and Re _c of 45 single rough fractures

Number	log10ki (FLUENT)	log10ki v (SVR)	log10ki (Zhou)	log10ki (Xing)	Rec (FLUENT)	Rec (SVR)
F1	− 1.9081	− 1.8758	− 2.4800	− 0.3684	2.7001	2.4468
F2	− 1.8026	− 1.9144	− 2.3058	− 0.6729	3.1067	2.1888
F3	− 2.1712	− 1.7402	− 1.9928	− 0.6788	1.1053	3.2473
F4	− 2.5227	− 2.8670	− 3.0297	− 1.5718	0.9071	0.4763
F5	− 0.5773	− 1.1291	− 1.1108	− 2.4329	25.7858	11.4400
F6	− 1.4278	− 1.8628	− 1.9367	− 1.7447	5.9222	2.1636
F7	− 0.2646	− 1.0972	− 0.9543	− 2.8170	48.2946	12.7399
F8	− 2.7174	− 2.5200	− 2.1607	− 2.0174	0.3469	0.6915
F9	− 2.5062	− 2.9164	− 2.1205	− 1.8695	0.5510	0.2420
F10	− 1.9444	− 1.7195	− 2.2419	− 0.7262	2.1585	3.3593
F11	− 2.5031	− 2.3966	− 1.8897	− 1.0042	0.4843	0.8038
F12	− 2.6747	− 2.9602	− 3.1548	− 1.5507	0.6883	0.3740
F13	− 1.2773	− 1.6026	− 1.3615	− 2.5986	5.9642	4.5248
F14	− 1.8498	− 2.1418	− 2.1369	− 1.8301	2.5220	1.2643
F15	− 0.7680	− 1.0294	− 0.8054	− 2.9889	13.8797	11.2597
F16	− 2.7223	− 2.5305	− 2.0653	− 2.1360	0.3243	0.6507
F17	− 2.6584	− 3.0285	− 2.3197	− 2.0264	0.4366	0.2119
F18	− 2.1776	− 2.0958	− 2.0043	− 1.0829	1.0964	1.4642
F19	− 2.4736	− 2.7813	− 2.7694	− 1.5975	0.8712	0.4499
F20	− 1.5319	− 2.0007	− 1.7905	− 2.5478	4.2751	2.0442
F21	− 2.1862	− 2.1429	− 2.0110	− 2.0134	1.0792	1.3237
F22	− 0.2788	− 0.8360	− 0.7705	− 2.9059	41.9360	18.9416
F23	− 2.8885	− 2.6036	− 2.3860	− 2.0532	0.2673	0.5770
F24	− 2.6491	− 2.7892	− 2.0455	− 2.2981	0.3793	0.3580
F25	− 2.9484	− 2.7185	− 2.5412	− 1.8881	0.2552	0.5243
F26	− 1.3731	− 1.6934	− 1.4605	− 2.4479	5.0721	3.2068
F27	− 2.0928	− 2.2183	− 2.1341	− 1.9788	1.4392	1.0679
F28	− 0.7154	− 0.9723	− 0.7786	− 2.8691	15.4214	9.8367
F29	− 2.8598	− 2.5176	− 2.1069	− 2.2696	0.2421	0.6083
F30	− 2.8156	− 3.2029	− 2.8883	− 2.1543	0.4251	0.1656
F31	− 1.6354	− 2.1963	− 1.7650	− 3.0188	3.3181	0.9924
F32	− 2.0434	− 2.4760	− 2.4250	− 2.1728	1.9145	0.7106
F33	− 0.6266	− 0.9776	− 0.8523	− 3.2617	19.7625	14.6363
F34	− 2.5721	− 2.4068	− 2.0752	− 2.3590	0.4610	0.8229
F35	− 2.3943	− 2.3081	− 1.8430	− 2.3742	0.6053	0.7436
F36	− 3.0202	− 3.4328	− 3.4571	− 3.0608	0.3713	0.1638
F37	− 2.9515	− 3.5877	− 3.4018	− 3.4547	0.4210	0.1034
F38	− 3.8247	− 3.5776	− 3.5717	− 3.3465	0.0623	0.1118
F39	− 3.5064	− 3.2758	− 2.7905	− 3.1292	0.0818	0.1281
F40	− 2.2945	− 2.1279	− 1.7940	− 2.8385	0.7400	1.2674
F41	− 2.6894	− 2.5214	− 2.5775	− 1.9922	0.4732	0.6627
F42	− 3.0921	− 3.0446	− 3.4402	− 3.1810	0.3115	0.2921
F43	− 3.3323	− 3.2255	− 3.5333	− 2.5974	0.1893	0.2992
F44	− 3.9014	− 3.3192	− 3.7300	− 3.9015	0.0573	0.2456
F45	− 2.8595	− 3.1070	− 3.0171	− 2.7746	0.4146	0.2245