1 Introduction

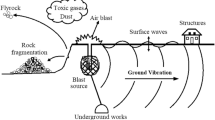
Blasting is considered as the most common method of hard rock fragmentation in mining as well as in civil construction works. Although the primary objective of blasting is to provide proper rock fragmentation and finally facilitating in loading operations, the other environmental side effects of blasting such as airblast, ground vibration, noise and flyrock are inevitable [1,2,3,4,5,6,7]. These phenomena are shown in Fig. 1.

Fig. 1
figure 1

Phenomena of blasting operation

Full size image

Of all the mentioned effects, ground vibration has the most detrimental effect on the surroundings [8,9,10,11,12]. Hence, to reduce environmental effects, the prediction of ground vibration with a high level of accuracy is imperative. According to the literature [13,14,15,16,17], the peak particle velocity (PPV) is accepted as the most important descriptor to determine the blast-induced ground vibration.

A number of researchers have investigated the problem of blast-induced PPV and have provided different empirical models to predict PPV [18,19,20,21,22]. These empirical models are restricted to using maximum charge per delay (W) and distance between monitoring stations and blasting point (D) as the effective parameters on PPV. In the last few years, machine learning methods have been widely employed for solving various engineering problems [23,24,25,26,27,28,29,30,31,32,33,34,35,36]. These methods are being increasingly used to predict blast-induced PPV.

Monjezi et al. [37] used artificial neural network (ANN) to predict PPV. They compared the ANN performance with empirical models. Their results signified the superiority of ANN over empirical models in terms of performance measures. Hasanipanah et al. [10] employed classification and regression tree (CART) to predict PPV. In their study, multiple regression (MR) and several empirical models were also developed. Based on the obtained results, the CART can be introduced as a more suitable model for PPV prediction than the MR and empirical models. Zhang et al. [38] predicted the PPV using extreme gradient boosting machine (XGBoost) combined with particle swarm optimization (PSO). They also used empirical models to check the performance of their proposed model. The results indicated that the PSO-XGBoost was an accurate model to predict PPV and its performance was better than the empirical model. In another study, Bui et al. [39] proposed a combination of fuzzy C-means clustering (FCM) and quantile regression neural network (QRNN) to predict PPV, and compared the results of FCM–QRNN model with ANN, random forest (RF) and empirical models. The results showed that the accuracy of the FCM–QRNN model was higher compared with ANN, RF and empirical models in predicting the PPV.

Jiang et al. [24] explored the use of a neuro-fuzzy inference system to approximate PPV, and compared it with the MR model. They showed the superiority of neuro-fuzzy inference system over MR model in terms of approximations accuracy. The suitability of hybridizing the k-means clustering algorithm (HKM) and ANN to predict PPV was investigated by Nguyen et al. [40]. For comparison aims, support vector regression (SVR), classical ANN, hybrid of SVR and HKM, and empirical models were also employed. According to their results, the HKM–ANN model presented a superior ability to predict PPV and its results were more accurate than the other models. Fang et al. [41] evaluated the application of a hybrid imperialist competitive algorithm (ICA) and M5Rules to predict PPV. They concluded that the ICA–M5Rules method was viable and effective and provided better predictive performance as compared with other models. Recently, Ding et al. [7] hybridized the ICA with XGBoost to forecast PPV. They also applied the ANN, SVR and gradient boosting machine (GBM) to check ICA–XGBoost performance. Their computational result indicated that the ICA–XGBoost model produced better results than ANN, SVR and GBM methods.

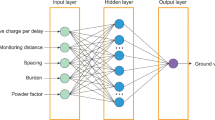
SVR is a well-known artificial intelligence approach which has been widely used for the applications on most of the nonlinear problems in various fields such as mining and civil engineering fields [4, 6]. A view of the SVR structure is shown in Fig. 2. Note that, in the present study, the W and D parameters are the input parameters, and PPV is the output. On the other hand, the use of evolutionary algorithms such as cuckoo search, PSO, genetic algorithm, artificial bee colony and firefly algorithm (FA) in the fields of optimization has been expanding [8, 11, 12, 16]. Among those, FA is the one which has been most widely studied and used to solve various engineering problems, so far. Day by day the number of researchersinterested in FA has increased rapidly. FA proves to be more promising, robust, and efficient in finding both local and global optimum compared to other existing evolutionary algorithms [42,43,44]. A view of the FA flowchart is also shown in Fig. 3.

Fig. 2
figure 2

SVR structure [88]

Full size image
Fig. 3
figure 3

FA flowchart

Full size image

An accurate prediction of PPV can be very practical, especially for drilling engineers to design an optimum blast pattern and to prevent the detrimental effects of blasting. The present study proposes a novel artificial intelligence approach to predict PPV with a high level of accuracy. The proposed approach is based on an improved bagged SVR (BSVR) combined with FA. In other words, the FA was used to modify the weights of the SVR model. For comparison aims, back-propagation neural network (BPNN) and radial basis function network (RBFN) models were also applied.

2 Database source

The used datasets in this study were gathered from Shur River dam region in Iran. For this work, 87 blasting events were monitored and the values of requirement parameters were carefully measured. In this regard, the values of W and D, as the most effective parameters on PPV [45, 46], were measured for all monitored blasts. To measure the D parameter, the GPS (global positioning system) was used. Also, the value of W was measured through controlling the blast-hole charge. For recording the values of PPV, MR2002-CE SYSCOM seismograph was also installed in different locations of sites. More details regarding the used datasets in this study are given in Table 1. Additionally, the frequency histograms of the input (W and D) and output (PPV) parameters are shown in Fig. 4. According to this Fig, in case of the W parameter, 15, 16, 44 and 12 data were varied in the range of 0–500 kg, 500–700 kg, 700–1000 kg and 1000–1500 kg, respectively. Regarding the D parameter, 22, 25, 18 and 22 data were varied in the range of 0–400 m, 400–550 m, 550–700 m and 700–1000 m, respectively. Also, for the PPV parameter, 20, 27, 22 and 18 data were varied in the range of 0–5 mm/s, 5–6.5 mm/s, 6.5–8 mm/s and 8–10 mm/s, respectively. In modeling of BSVR–FA, BPNN and RBFN, the datasets were divided into two phases, namely training and testing phases. In this regard, 80% and 20% of whole data were assigned as training and testing datasets, respectively. In other words, 70 and 17 datasets were used to construct and test the models, respectively.

Table 1 Statistical parameters of the datasets used in this study
Full size table
Fig. 4
figure 4

Frequency histograms of the W, D and PPV parameters

Full size image

3 Methodology

The bagging algorithm and SVR methods were used to develop the hybrid model BSVR, whereas the FA was used for improving the performance of SVR. Bagging depends on the ideas of bootstrapping and aggregating, and was introduced by Breiman [47, 48]. The bagging algorithm has been applied extensively in engineering, economy, and ecology, but is uncommon in the field of PPV prediction. Bagging is one of the vital ensemble algorithms, wherein the randomly sampled approach is used in the training set for n times with substitution [49]. In the bagging model, all training sets are produced with the original training set size. In the proposed model, the training set (TS) consists of n observations TS = {(x1, y1), (x2, y2), …, (xn, yn)}. Hence, the bth bootstrap instance of the training set TS is denoted by the replacement of n elements of TSb (b = 1, 2, …, n). The bagging estimator is denoted as \(\phi = \left( {x,Z} \right)\) which predicts Y with the relative mean and given as follows:

$$Q\left( {y_{i} {|}x} \right) = P\left[ {\phi \left( {x,Z} \right) = y_{i} } \right] T = \left( {x,{ }y} \right).$$
(1)

Let P be the probability input x makes with the class yi. Also, the probability predictor that is correct for the produced state at x is:

$$P_{{{\text{correct}}}} = \mathop \sum \limits_{{y_{i} }} Q\left( {y_{i} {|}x} \right)P\left( {y_{i} {|}x} \right).$$
(2)

Hence, the total probability of correct prediction is indicated as:

$$P = \int \left[ {\mathop \sum \limits_{{y_{i} }} Q\left( {y_{i} {|}x} \right)P\left( {y_{i} {|}x} \right)} \right]P_{x} d\left( x \right),$$
(3)

where the probability distribution of x is determined by \(P_{x} d\left( x \right)\).

In this step, bagging SVR can be exploited to develop the accuracy of the ground vibration prediction. In SVR, the relation between the input variable xi and predicted variable yi is distinguished by f(x) as follows:

$$f\left( x \right) = \mathop \sum \limits_{n = 1}^{N} \omega_{n} \varphi_{n} \left( x \right) + b,$$
(4)

where \(\varphi \left( x \right)\) maps the input variables into a multi-dimensional space as a kernel function, b demonstrates bias, and \(\omega_{n}\) defines the weight of the nth data for input variables [49]. w and b are specified as coefficients for minimizing the convex problem function like the phrase below:

$$P\left( {f\left( x \right)} \right) = \frac{C}{N}\mathop \sum \limits_{n = 1}^{N} G_{\varepsilon } \left( {y_{n} , f\left( {x_{n} } \right)} \right) + \frac{{b\left| {\left| w \right|} \right|}}{2},$$
(5)

where

$$G_{\varepsilon } \left( {y_{n} , f\left( {x_{n} } \right)} \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad {\text{ if}}\, \left| {y - f\left( {x_{n} } \right)} \right| \le \varepsilon } \hfill \\ {\left| {y - f\left( {x_{n} } \right)} \right| - \varepsilon } \hfill & {\quad {\text{otherwise}} } \hfill \\ \end{array} } \right.,$$
(6)

in which C implicates a positive constant with the responsibility of the trade-off between an estimation error and the weight vector, the loss function is determined by \(G_{\varepsilon } \left( {y_{n} , f\left( {x_{n} } \right)} \right)\) which is called ε-insensitive, and ε is the radius of tube size [48].

All essential computations in the input variable are performed by the kernel function without any calculation of the explicit \(\varphi \left( x \right)\). In the current study based on the best performance in the literature, the kernel function is defined by \(K\left( {x_{i} ,x_{j} } \right) = \varphi \left( {x_{i} } \right)\varphi \left( {x_{j} } \right)\), where the Gaussian function is applied as follows [49]:

$$K\left( {x_{i} ,x_{j} } \right) = {\exp}\left( { - \frac{{\left| {\left| {x_{i} - x_{j} } \right|} \right|^{2} }}{{2\sigma^{2} }}} \right),$$
(7)

where \(\sigma\) implicates the kernel function parameter. The parameters of ε, C, and \(\sigma\) must be chosen in advance. In Algorithm 1, the total step of bagging the SVR predictor is indicated.

figure a

.

For improving the performance of BSVR, the importance of parameters in BSVR are justified by the firefly algorithm (FA). The FA, introduced by Yang [50], is fundamentally based on the light intensity variation, which defines the fitness function solution. The light intensity variation fluctuates with any alteration in the interval (r) amongst two fireflies, which is expressed as follows [51]:

$$I\left( r \right) = I_{0} {\text{e}}^{{ - \gamma \times r^{2} }} ,$$
(8)

where \(I\left( r \right)\) signifies the light intensity for r and \(I_{0}\) holds out the light intensity original at r = 0. The coefficient of light absorption is determined by \(\gamma\). Hence, the attractiveness of a firefly is specified as follows [51]:

$$\beta = \beta_{0} {\text{e}}^{{ - \gamma \times r^{2} }} ,$$
(9)

where the attractiveness is represented by \(\beta\), and \(\beta_{0}\). defines the attractiveness with zero distance. The movement of flies from ‘i’ to ‘j’ is represented by the following equation [51]:

$$x_{i} = x_{i} + \beta_{0} {\text{e}}^{{ - \gamma \times r_{ij}^{2} }} \left( {x_{j} - x_{i} } \right) + a\varepsilon_{i} .$$
(10)

In most of the majority, the value of the absorption coefficient is in the interval of 0.1 and 10. In many cases, the value of 1 is chosen for \(\beta_{0}\) and \(a \in \left[ {0,1} \right]\) [52]. In Fig. 5, the flowchart illustrates the modeling of BSVR–FA to the prediction of PPV. Extensive details about the FA can be found in [53,54,55].

Fig. 5
figure 5

Flowchart of BSVR–FA

Full size image

4 Back-propagation neural network (BPNN)

The simple BPNN has three layers that includes an input layer, a hidden layer, and an output layer [56]. Its back-propagation functioning performs the training and testing steps. The topology of the suggested BPNN has been exhibited in Fig. 6.

Fig. 6
figure 6

Structure of BPNN

Full size image

The input data in every layer are adjusted by interconnection weight between the layers (wji), which demonstrates the relation of the ith node of the current layer to the jth node of the next layer [56]. The key role of the hidden layer is to process the input layer information. The sum of total activation is assessed by a sigmoid transfer function. All steps of the BPNN algorithm is represented in Algorithm 2.

figure b

5 Radial basis function network (RBFN)

Fundamentally, the RBFN is compounded by the number of simple and extremely interconnected neurons, which can be organized into many layers [57]. The main idea of RBFN is presented on the basis of the comparison between radial basis function (RBF) and multi-layer perceptron (MLP). For a network with fewer hidden layers, the RBF has much faster convergence than MLP. Also, the RBF network is generally prior to MLP when low-dimensional problem needs to be solved. For better understanding, the RBFN flowchart is shown in Fig. 7. The below steps generally explain the RBFN algorithm:

  1. 1.

    The number of hidden neurons are specified by “K”.

  2. 2.

    Based on the center of K-means clustering, the position of RBF is tuned.

  3. 3.

    Calculate σ using the maximum distance among two hidden neurons.

  4. 4.

    Calculate actions for RBF node closer in the Euclidian space

  5. 5.

    Train the output nodes.

Fig. 7
figure 7

Architecture of a RBFN

Full size image

The activation function in the RBFN model is a Gaussian function. Extensive details about the RBFN can be found in [57].

6 Development of the models

Based on reviewing the literature [58, 59], the principal parameters of FA are the factors of \(\beta_{0}\), \(a\), \(\gamma\), number of iteration (It) and the number of population (Npop). Using the trial and error method, the values of 1, 1 and 1000 were selected for the \(\beta_{0}\),\(a\) and It parameters, respectively. Regarding the best performance of BSVM-FA, the value of Npop is chosen 150 in the event that the values of 10, 20, 30, 40, 50, 100, 150, and 200 were examined in the BSVR–FA model. Besides, the various values of \(\gamma\) in the interval of 0.25–3 were assessed and, based on the best performance, the value of 2 is obtained for the \(\gamma\) in BSVR–FA modeling. Regarding the outcome values in BSVR–FA modeling, the optimized value of C = 257.3, \(\sigma = 1.21\), and ε = 0.69 are obtained for BSVR.

Regarding repetition of the BPNN model, the the best performance with the lowest RMSE and the highest coefficient of determination (R2) was for the 2 × 4 × 1 structure, which was two neurons in the input layer, four neurons in one hidden layer and one neuron in the output layer. Based on the best outcome in the RBFN model, the number of kernel is chosen as three, and the number of K-means iteration is selected as ten.

7 Analysis of the results

In this study, the BSVR–FA, BPNN and RBFN models are employed to predict PPV. This section compares the performance of the proposed models in predicting the PPV. To evaluate the accuracy of models, several well-known statistical indicators, namely R2, root mean square error (RMSE), mean absolute error (MAE), symmetric mean absolute percentage error (SMAPE), Leegate and McCabe index (LM), and variance account for (VAF) are used as follows [28, 60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86]:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {{\text{PPV}}_{{\text{a}}} - {\text{PPV}}_{{\text{p}}} } \right)^{2} } ,$$
(11)
$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {{\text{PPV}}_{{\text{a}}} - {\text{PPV}}_{{\text{p}}} } \right|,$$
(12)
$${\text{SMAPE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \frac{{\left| {{\text{PPV}}_{{\text{a}}} - {\text{PPV}}_{{\text{p}}} } \right|}}{{{\text{PPV}}_{{\text{a}}} + {\text{PPV}}_{{\text{p}}} }} \times 100,$$
(13)
$${\text{LM}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {{\text{PPV}}_{{\text{a}}} - {\text{PPV}}_{{\text{p}}} } \right|}}{{\mathop \sum \nolimits_{i = 1}^{n} \left| {{\text{PPV}}_{{\text{a}}} - \overline{{{\text{PPV}}_{{\text{a}}} }} } \right|}}} \right],$$
(14)
$${\text{VAF}} = \left[ {1 - \frac{{{\text{var}} \left( {{\text{PPV}}_{{\text{a}}} - {\text{PPV}}_{{\text{p}}} } \right)}}{{{\text{var}} \left( {{\text{PPV}}_{{\text{a}}} } \right)}}} \right] \times 100,$$
(15)

where \({\text{PPV}}_{{\text{a}}}\) and \({\text{PPV}}_{{\text{p}}}\) are, respectively, the actual and predicted PPV values, n is the number of data, \(\overline{{{\text{PPV}}_{{\text{a}}} }}\) is the mean of actual PPVs, and var is the variance. The most ideal values for R2, RMSE, MAE, LM, SMAPE and VAF are 1, 0, 0, 1, 0 and 100%, respectively. Table 2 gives the statistical indicator values obtained from BSVR–FA, BPNN and RBFN models for both training and testing phases. From this table, the highest R2, VAF and LM values for both training and testing phases, and the lowest RMSE, MAE and SMAPE values, were obtained from the BSVR–FA model. For observing the accuracy of the BSVR–FA, BPNN and RBFN models in predicting the PPV, Figs. 8, 9 and 10 are also plotted using only testing datasets. Additionally, to demonstrate the model’s reliability and effectiveness, a mathematics-based graphical diagram, namely Taylor diagram, is prepared, as schemed in Fig. 11. From Figs. 8, 9, 10 and 11, it can be found that the BSVR–FA model was the most accurate for the prediction of PPV in the study area. The BPNN and RBFN models were identified as the next categories, respectively. In this study, a sensitivity analysis is also performed to demonstrate the relative influence of the input parameters (W and D) on the output parameter (PPV) using Yang and Zang [87] method:

$$r_{ij} = \frac{{\mathop \sum \nolimits_{k = 1}^{n} \left( {y_{ik} \times y_{{{\text{ok}}}} } \right)}}{{\sqrt {\mathop \sum \nolimits_{k = 1}^{n} y_{ik}^{2} \mathop \sum \nolimits_{k = 1}^{n} y_{{{\text{ok}}}}^{2} } }},$$
(16)
Table 2 Statistical indicators obtained from predictive models
Full size table
Fig. 8
figure 8

Actual vs. predicted PPVs by RBFN

Full size image
Fig. 9
figure 9

Actual vs. predicted PPVs by BPNN

Full size image
Fig. 10
figure 10

Actual vs. predicted PPVs by BSVR–FA

Full size image
Fig. 11
figure 11

Showing Taylor diagram related to the predictive models based on testing datasets

Full size image

where \(y_{ik}\) is the input parameter, \(y_{{{\text{ok}}}}\) is the output parameter, and n is the number of data. The most influential parameter has the highest \(r_{ij}\) value. Using Eq. 10, the values of \(r_{ij}\) for the D and W parameters were obtained as 0.872 and 0.982, respectively. This clearly indicates that the W is the most influential parameter on the PPV in the study area.

8 Conclusion

Precise prediction of blast-induced PPV is an imperative work in the surface mines as well as tunneling projects. This paper aims to propose a BSVR–FA model to predict PPV. To check the validity of the BSVR–FA model, two well-known and classical intelligent models, namely BPNN and RBFN models were also employed. To construct the models, a comprehensive database gathered from Shur River dam region, in Iran, was used. After modeling, several statistical indicators, i.e., R2, RMSE, MAE, VAF, LM and SMAPE were used to compare the models’ performances. Based on the results of this study, we draw some conclusions:

  1. 1.

    The BSVR–FA model yielded an excellent accuracy to predict PPV. A high R2 value of 0.996 was obtained for the BSVR–FA predictions. Further, the BPNN and RBFN results showed R2 value of 0.896 and 0.828, respectively.

  2. 2.

    It was found that the FA is a useful tool to train the BSVR model.

  3. 3.

    The use of BSVR–FA model can be practical in designing an optimum blast pattern and reducing the blast-induced PPV.

  4. 4.

    The BSVR–FA can be also introduced as an accurate model to predict other problems induced by blasting such as airblast and flyrock.