NURBS-augmented finite element method for stability analysis of arbitrary thin plates

Abstract

In the analysis of a plate, the geometry plays a very important role. The non-uniform rational B-spline (NURBS) basis functions are employed for the representation of the geometry and field variables in the isogeometric analysis. These basis functions are able to represent the geometry accurately. They are non-interpolating in nature, and hence do not satisfy the Kronecker-Delta property. Hence, it becomes difficult to enforce the essential boundary conditions at the control variables. A new method called NURBS-augmented finite element method (NAFEM) was proposed (Mishra and Barik, Comput Struct, https://doi.org/10.1016/j.compstruc.2017.10.011, 2017) and arbitrary shaped plates were successfully dealt for bending analysis. In the NAFEM, the authors adopted the finite element basis functions for the field variables as they satisfy the Kronecker-Delta property so that the boundary conditions were enforced with ease and the NURBS basis functions were employed for the geometry, thereby representing the shape of the plate accurately. In the present work, the same is extended for stability analysis of plates having different geometries and boundary conditions and the results are found to be in excellent agreement with the existing ones. Some new shapes have also been considered, and the new results are presented.

1 Introduction

The finite element analysis is a numerical technique to solve various problems in the field of engineering such as structural analysis, heat transfer, fluid flow, etc. In the structural analysis, the geometry plays a vital role which can be achieved with a great accuracy with the help of Computer-aided Design (CAD). The FEA programs developed long before CAD were susceptible to inaccuracies. In order to vanquish this impediment Hughes et al. [7] proposed a concept called isogeometric analysis (IGA) which was successful in integrating the CAD and FEA resulting in representing the geometry accurately; where the non-uniform rational B-splines (NURBS) basis functions were engaged in representing the geometry and the field variables. However, the NURBS basis functions are non-interpolating in nature and do not satisfy the Kronecker-Delta which result in the difficulty in enforcing the essential boundary condition [6, 10] and needed special treatment. A number of methods have been developed to impose the essential boundary conditions. Some of the most popular methods are Lagrange multiplier method [4], penalty method [24] and Nitsche method [6].

The buckling analysis of clamped elliptical plates was first carried out by Woinowsky-Krieger [22] subjected to uniform compression. A semi-analytical semi-numerical method of solution was presented by Zhou et al. [23]) for the stability analysis of simply supported sector plates. The stability analysis of rectangular Mindlin plates having with different boundary conditions have been studied by Liew et al. [8] by using the Levy-type solution method.

Thai et al. [15] presented a new inverse tangent shear deformation theory (ITSDT), layerwise deformation theory [16], higher order shear deformation theory [17] for the bending, free vibration and stability analysis of laminated composite and sandwich plates of arbitrary shapes using isogeometric analysis. The behaviour of laminated composite Reissner–Mindlin plates of various shapes using NURBS based isogeometric analysis under bending, vibration and stability can be found in [18] and [3].

The isogeometric analysis has been used for studying the static, vibration and buckling behaviour of isotropic and laminated composite structures [13, 14, 20, 21], etc. Mishra and Barik [9] coined a new term NURBS-Augmented Finite Element Method (NAFEM) similar to the one used in [12] but with a difference. In this NAFEM the geometry of the plate is represented by NURBS basis functions, whereas the displacement functions for all the elements which include the internal as well as the boundary elements are represented by the classical finite elements.

It is apparent that though IGA is efficient in integrating CAD and FEA, its inherent problem with the imposition of boundary condition makes it a poor choice for the finite element analysis. In the present work, the boundary condition imposition problem is alleviated by replacing the NURBS with classical finite element basis function to represent the field variables.

2 Proposed analysis

2.1 Stability analysis

The equation of equilibrium for the stability analysis is given by

$$\begin{aligned} \left[ K\right] \left\{ \delta \right\} -\lambda \left[ K_{G}\right] \left\{ \delta \right\} =\left\{ 0\right\}, \end{aligned}$$

(1)

where $\left[ K\right]$ and $\left[ K_{G}\right]$ are the global elastic stiffness and geometric stiffness matrices, respectively, $\left\{ \delta \right\}$ is the displacement vector in the global coordinate system.

2.2 NURBS basis function

Given a knot vector $S=\begin{Bmatrix} s_{1},s_{2},s_{3},...s_{n+p+1} \end{Bmatrix}$, the associated set of B-spline basis functions $\begin{Bmatrix} N_{i,p} \end{Bmatrix}_{i=1}^{n}$ are defined recursively by the Cox–de Boor formula, starting with the zeroth order basis function $(p=0)$ as

$$\begin{aligned} N_{i,0}=\left\{ \begin{array}{ll} 1 &{} \quad \text {if }\;s_{i}\le s\le s_{i+1}\\ 0 &{} \quad \text {otherwise} \end{array}\right. \end{aligned}$$

(2)

and for a polynomial order $p\ge 1$

$$\begin{aligned} N_{i,p}(s)=\frac{s-s_{i}}{s_{i+p}-s_{i}}N_{i,p-1}(s)+\frac{s_{i+p+1}-s}{s_{i+p}-s_{i+1}}N_{i+1,p-1}(s), \end{aligned}$$

(3)

where n is the number of basis functions and p is the order of the basis functions. The fractions of the form 0 / 0 are defined as zero.

2.3 Mapping of the plate

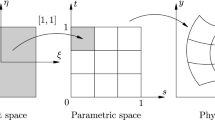
The use of NURBS basis functions for the representation of geometry introduces the concept of parametric space which is absent in the conventional finite element formulation [9, 11]. The consequence of this additional space is that an additional mapping is performed to operate in the parent element coordinates. First, the parent space is mapped to the parametric space and then to the physical space (Fig. 1).

Fig. 1

Mapping parent to physical space through parametric space

The mapping from parametric to physical space is given by

$$\begin{aligned} \left[ \begin{array}{l} X \end{array}\right] =\displaystyle \sum _{i=1}^{n}\sum _{j=1}^{m}P_{i,j}R_{i,j}^{p,q}(s,t), \end{aligned}$$

(4)

where $P_{i,j}$ are the control points and $R_{i,j}^{p,q}(s,t)$ is the bivariate NURBS basis function defined as

$$\begin{aligned} R_{i,j}^{p,q}(s,t)=\frac{N_{i}(s)M_{j}(t)w_{i,j}}{\sum \nolimits _{\bar{i}=1}^{n}\sum \nolimits _{\bar{j}=1}^{m}N_{\bar{i}}(s)M_{\bar{j}}(t)w_{\bar{i},\bar{j}}} \end{aligned}$$

(5)

${N_{i}(s)}$ and $M_{j}(t)$ are the univariate B-spline basis functions of order p and q corresponding to the knot vectors in the respective directions and $\begin{Bmatrix} w_{i,j} \end{Bmatrix}_{i=1,j=1}^{n,m}$, where $w_{i,j}>0$ are the set of NURBS weights. The mapping from parent to parametric space is given by [9, 11]

$$\begin{aligned} s(\xi )=\frac{(s_{i+1}-s_{i})\xi +(s_{i+1}-s_{i})}{2}, \qquad t(\eta )=\frac{(t_{i+1}-t_{i})\eta +(t_{i+1}-t_{i})}{2} \end{aligned}$$

(6)

The geometries in the physical space may also be divided into simple patches and then those patches are mapped to the parent space through the parametric space. As a typical example the physical space defined by the coordinates ACDB is divided into two patches namely ACFE and EFDB as shown in Fig. 2. The parent space is then mapped to two patches in the physical space through the parametric space and the procedure is followed as before to compute the stiffness matrix of each patch. The stiffness matrices of all the patches are assembled to form the global stiffness matrix of the whole plate. Thus the analysis of the plates can be made simpler by subdividing them into more amenable patches which can be dealt with ease [9].

Fig. 2

Mapping parent to the different patches in physical space through parametric space

2.4 Displacement interpolation function

For the proposed element, the four-noded rectangular non-conforming ACM plate bending element with 12$^\circ$ of freedom is taken as the basic element. As the element is in $\xi - \eta$ plane the shape functions and the nodal parameters for the displacements and slopes are expressed in terms of the coordinates $\xi -\eta$ unlike the $x-y$ coordinates of the parent ACM element [2]. Thus the displacement function can be written as [9]:

$$\begin{aligned} w=[N_{w}] \begin{Bmatrix} \delta \end{Bmatrix}, \end{aligned}$$

(7)

where

$$\begin{aligned}{}[N_{w}]=\left[ N_{w}^{1} N_{\theta _{\xi }}^{1} N_{\theta _{\eta }}^{1} \cdots N_{w}^{4} N_{\theta _{\xi }}^{4} N_{\theta _{\eta }}^{4} \right], \end{aligned}$$

(8)

$$\begin{aligned} \begin{Bmatrix} \delta \end{Bmatrix}=\left[ \begin{matrix} w_{1}&\left( \dfrac{\partial w}{\partial \xi }\right) _{1}&\left( \dfrac{\partial w}{\partial \eta }\right) _{1}&\cdots&w_{4}&\left( \dfrac{\partial w}{\partial \xi }\right) _{4}&\left( \dfrac{\partial w}{\partial \eta }\right) _{4} \end{matrix}\right] ^{T}. \end{aligned}$$

(9)

The shape functions for the displacement field for the jth node are given as:

$$\begin{aligned} \left[ \begin{matrix} N_{w}^{j}&N_{\theta _{\xi }}^{j}&N_{\theta _{\eta }}^{j} \end{matrix}\right] =\frac{1}{8}\left[ \begin{matrix} (s_{0}+1)(t_{0}+1)(2+s_{0}+t_{0}-\xi ^{2}-\eta ^{2}) &{} \\ s_{j}(s_{0}+1)^{2}(s_{0}-1)(t_{0}+1) &{} \\ t_{j}(s_{0}+1)(t_{0}+1)^{2}(t_{0}-1) \end{matrix}\right] ^{T}, \end{aligned}$$

(10)

where $s_{0}=\xi s_{j}$ and $t_{0}=\eta t_{j}.$

2.5 Strain–displacement matrix

The displacement functions of the plate element is expressed in terms of the local coordinate system $\xi -\eta,$ whereas strains are in terms of the derivatives of the displacements with respect to $x-y$ coordinates. Hence before establishing the relationship between the strain and displacement, the first- and second-order derivatives of the displacements w with respect to the $x-y$ coordinates are expressed in terms of those of local coordinates $(\xi -\eta )$ using the chain rule of differentiation and are obtained as [9]:

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial w}{\partial \xi } \\ \dfrac{\partial w}{\partial \eta } \end{array}\right\} =\left[ \begin{array}{ll} \dfrac{\partial s}{\partial \xi } &{} \dfrac{\partial t}{\partial \xi }\\ \dfrac{\partial s}{\partial \eta } &{} \dfrac{\partial t}{\partial \eta } \end{array}\right] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial s} \\ \dfrac{\partial w}{\partial t} \end{array}\right\} =[J1]\left\{ \begin{array}{l} \dfrac{\partial w}{\partial s} \\ \dfrac{\partial w}{\partial t} \end{array}\right\}. \end{aligned}$$

(11)

Differentiating Eq. (11) with respect to $\xi$ and $\eta$

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial \xi ^{2}}\nonumber \\ \dfrac{\partial ^{2}w}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2}w}{\partial \xi \partial \eta } \end{array}\right\}& = \left[ \begin{array}{ll} \dfrac{\partial ^{2}s}{\partial \xi ^{2}} &{} \dfrac{\partial ^{2}t}{\partial \xi ^{2}}\\ \dfrac{\partial ^{2}s}{\partial \eta ^{2}} &{} \dfrac{\partial ^{2}t}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2}s}{\partial \xi \,\partial \eta } &{} \dfrac{\partial ^{2}t}{\partial \xi \,\partial \eta } \end{array}\right] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial s}\\ \dfrac{\partial w}{\partial t} \end{array}\right\} \nonumber \\&+\left[ \begin{array}{lll} \left( \dfrac{\partial s}{\partial \xi }\right) ^{2} &{} \left( \dfrac{\partial t}{\partial \xi }\right) ^{2} &{} \left( 2\dfrac{\partial s}{\partial \xi }\,\dfrac{\partial t}{\partial \xi }\right) \\ \left( \dfrac{\partial s}{\partial \eta }\right) ^{2} &{} \left( \dfrac{\partial t}{\partial \eta }\right) ^{2} &{} \left( 2\dfrac{\partial s}{\partial \eta }\dfrac{\partial t}{\partial \eta }\right) \\ \left( \dfrac{\;\partial s}{\partial \xi }\dfrac{\partial s}{\partial \eta }\right) &{} \left( \dfrac{\partial t}{\partial \xi }\dfrac{\partial t}{\partial \eta }\right) &{} \left( \dfrac{\partial s}{\partial \xi }\dfrac{\partial t}{\partial \eta }+ \dfrac{\partial s}{\partial \eta }\dfrac{\partial t}{\partial \xi }\right) \end{array}\right] \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s \, \partial t} \end{array}\right\} \nonumber \\& = [J2][J1]^{-1} \left\{ \begin{array}{l} \dfrac{\partial w}{\partial \xi }\\ \dfrac{\partial w}{\partial \eta } \end{array}\right\} +[J3] \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s \,\partial t} \end{array}\right\} \end{aligned}$$

(12)

Also we have,

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial w}{\partial s}\\ \dfrac{\partial w}{\partial t} \end{array}\right\} =\left[ \begin{array}{ll} \dfrac{\partial x}{\partial s} &{} \dfrac{\partial y}{\partial s}\\ \dfrac{\partial x}{\partial t} &{} \dfrac{\partial y}{\partial t} \end{array}\right] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial x}\\ \dfrac{\partial w}{\partial y} \end{array}\right\} =[J4] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial x}\\ \dfrac{\partial w}{\partial y} \end{array}\right\}. \end{aligned}$$

(13)

Differentiating Eq. (13) with respect to s and t

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\nonumber \\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s\, \partial t} \end{array}\right\}& = \left[ \begin{array}{ll} \dfrac{\partial ^{2}x}{\partial s^{2}} &{} \dfrac{\partial ^{2}y}{\partial s^{2}}\\ \dfrac{\partial ^{2}x}{\partial t^{2}} &{} \dfrac{\partial ^{2}y}{\partial t^{2}}\\ \dfrac{\partial ^{2}x}{\partial s \, \partial t} &{} \dfrac{\partial ^{2}y}{\partial s \, \partial t} \end{array}\right] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial x}\\ \dfrac{\partial w}{\partial y} \end{array}\right\} \nonumber \\&+\left[ \begin{array}{lll} -\left( \dfrac{\partial x}{\partial s}\right) ^{2} &{} -\left( \dfrac{\partial y}{\partial s}\right) ^{2} &{} \left( \dfrac{\partial x}{\partial s}\dfrac{\partial y}{\partial s}\right) \\ -\left( \dfrac{\partial x}{\partial t}\right) ^{2} &{} -\left( \dfrac{\partial y}{\partial t}\right) ^{2} &{} \left( \dfrac{\partial x}{\partial t}\dfrac{\partial y}{\partial t}\right) \\ -\left( \dfrac{\partial x}{\partial s}\dfrac{\partial x}{\partial t}\right) &{} -\left( \dfrac{\partial y}{\partial s}\dfrac{\partial y}{\partial t}\right) &{} \dfrac{1}{2}\left( \dfrac{\partial x}{\partial s}\dfrac{\partial y}{\partial t}+\dfrac{\partial x}{\partial t}\dfrac{\partial y}{\partial s}\right) \end{array}\right] \left\{ \begin{array}{l} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x \,\partial y} \end{array}\right\} \nonumber \\& = [J5]\left\{ \begin{array}{l} \dfrac{\partial w}{\partial x}\\ \dfrac{\partial w}{\partial y} \end{array}\right\} +[J6] \left\{ \begin{array}{l} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x \,\partial y} \end{array}\right\} \end{aligned}$$

(14)

Therefore,

$$\begin{aligned} \left\{ \begin{array}{l} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x \, \partial y} \end{array}\right\} =[J6]^{-1} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s \, \partial t} \end{array}\right\} -[J6]^{-1}[J5] \left\{ \begin{array}{l} \dfrac{\partial w}{\partial x}\\ \dfrac{\partial w}{\partial y} \end{array}\right\}. \end{aligned}$$

(15)

From Eq. (13), we have

$$\begin{aligned} \left\{ \begin{array}{l} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x\, \partial y} \end{array}\right\} =[J6]^{-1} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s\, \partial t} \end{array}\right\} -[J6]^{-1}[J5][J4]^{-1} \left\{ \begin{array}{l} \dfrac{\partial w}{\partial s}\\ \dfrac{\partial w}{\partial t} \end{array}\right\}. \end{aligned}$$

(16)

Again from Eq. (12),

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial s^{2}}\\ \dfrac{\partial ^{2}w}{\partial t^{2}}\\ \dfrac{\partial ^{2}w}{\partial s\, \partial t} \end{array}\right\} =[J3]^{-1} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial \xi ^{2}}\\ \dfrac{\partial ^{2}w}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2}w}{\partial \xi \,\partial \eta } \end{array}\right\} -[J3]^{-1}[J2][J1]^{-1} \left\{ \begin{array}{l} \dfrac{\partial w}{\partial \xi }\\ \dfrac{\partial w}{\partial \eta } \end{array}\right\}. \end{aligned}$$

(17)

Hence Eq. (16) becomes

$$\begin{aligned} \nonumber \left\{ \begin{array}{l} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x \,\partial y} \end{array}\right\}& = [J6]^{-1}[J3]^{-1} \left\{ \begin{array}{l} \dfrac{\partial ^{2}w}{\partial \xi ^{2}}\\ \dfrac{\partial ^{2}w}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2}w}{\partial \xi \,\partial \eta } \end{array}\right\} \nonumber \\&-\left( \begin{array}{l} [J6]^{-1}[J3]^{-1}[J2][J1]^{-1}+[J6]^{-1}[J5][J4]^{-1}[J1]^{-1} \end{array}\right) \left\{ \begin{array}{l} \dfrac{\partial w}{\partial \xi }\\ \dfrac{\partial w}{\partial \eta } \end{array}\right\}, \end{aligned}$$

(18)

where

$$\begin{aligned} \left[ J1\right] =\left[ \begin{array}{lll} \dfrac{\partial s}{\partial \xi } &{} \dfrac{\partial t}{\partial \xi }\\ \dfrac{\partial s}{\partial \eta } &{} \dfrac{\partial t}{\partial \eta } \end{array}\right] , \qquad \left[ J2\right] =\left[ \begin{array}{ll} \dfrac{\partial ^{2}s}{\partial \xi ^{2}} &{} \dfrac{\partial ^{2}t}{\partial \xi ^{2}}\\ \dfrac{\partial ^{2}s}{\partial \eta ^{2}} &{} \dfrac{\partial ^{2}t}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2}s}{\partial \xi \,\partial \eta } &{} \dfrac{\partial ^{2}t}{\partial \xi \,\partial \eta } \end{array}\right], \end{aligned}$$

$$\begin{aligned} \left[ J3\right] =\left[ \begin{array}{lll} \left( \dfrac{\partial s}{\partial \xi }\right) ^{2} &{} \left( \dfrac{\partial t}{\partial \xi }\right) ^{2} &{} \left( 2\dfrac{\partial s}{\partial \xi }\,\dfrac{\partial t}{\partial \xi }\right) \\ \left( \dfrac{\partial s}{\partial \eta }\right) ^{2} &{} \left( \dfrac{\partial t}{\partial \eta }\right) ^{2} &{} \left( 2\dfrac{\partial s}{\partial \eta }\dfrac{\partial t}{\partial \eta }\right) \\ \left( \dfrac{\;\partial s}{\partial \xi }\dfrac{\partial s}{\partial \eta }\right) &{} \left( \dfrac{\partial t}{\partial \xi }\dfrac{\partial t}{\partial \eta }\right) &{} \left( \dfrac{\partial s}{\partial \xi }\dfrac{\partial t}{\partial \eta }+ \dfrac{\partial s}{\partial \eta }\dfrac{\partial t}{\partial \xi }\right) \end{array}\right] ,\qquad \left[ J4\right] =\left[ \begin{array}{ll} \dfrac{\partial x}{\partial s} &{} \dfrac{\partial y}{\partial s}\\ \dfrac{\partial x}{\partial t} &{} \dfrac{\partial y}{\partial t} \end{array}\right], \end{aligned}$$

$$\begin{aligned} \left[ J5\right] =\left[ \begin{array}{ll} \dfrac{\partial ^{2}x}{\partial s^{2}} &{} \dfrac{\partial ^{2}y}{\partial s^{2}}\\ \dfrac{\partial ^{2}x}{\partial t^{2}} &{} \dfrac{\partial ^{2}y}{\partial t^{2}}\\ \dfrac{\partial ^{2}x}{\partial s \, \partial t} &{} \dfrac{\partial ^{2}y}{\partial s \, \partial t} \end{array}\right] ,\qquad \left[ J6\right] =\left[ \begin{array}{lll} -\left( \dfrac{\partial x}{\partial s}\right) ^{2} &{} -\left( \dfrac{\partial y}{\partial s}\right) ^{2} &{} \left( \dfrac{\partial x}{\partial s}\dfrac{\partial y}{\partial s}\right) \\ -\left( \dfrac{\partial x}{\partial t}\right) ^{2} &{} -\left( \dfrac{\partial y}{\partial t}\right) ^{2} &{} \left( \dfrac{\partial x}{\partial t}\dfrac{\partial y}{\partial t}\right) \\ -\left( \dfrac{\partial x}{\partial s}\dfrac{\partial x}{\partial t}\right) &{} -\left( \dfrac{\partial y}{\partial s}\dfrac{\partial y}{\partial t}\right) &{} \dfrac{1}{2}\left( \dfrac{\partial x}{\partial s}\dfrac{\partial y}{\partial t}+\dfrac{\partial x}{\partial t}\dfrac{\partial y}{\partial s}\right) \end{array}\right]. \end{aligned}$$

From Eq. (6) all the elements of the matrix $\left[ J2\right]$ are zeros. Hence Eq. (18) becomes

$$\begin{aligned} \begin{Bmatrix} -\dfrac{\partial ^{2}w}{\partial x^{2}}\\ -\dfrac{\partial ^{2}w}{\partial y^{2}}\\ 2\dfrac{\partial ^{2}w}{\partial x \partial y} \end{Bmatrix}=\left[ \begin{matrix} [T_{F_{1}}]&[T_{F_{2}}] \end{matrix}\right] \begin{Bmatrix} \dfrac{\partial w}{\partial \xi }\\ \dfrac{\partial w}{\partial \eta }\\ \dfrac{\partial ^{2} w}{\partial \xi ^{2}}\\ \dfrac{\partial ^{2} w}{\partial \eta ^{2}}\\ \dfrac{\partial ^{2} w}{\partial \xi \,\partial \eta } \end{Bmatrix} \end{aligned}$$

(19)

or

$$\begin{aligned} \begin{Bmatrix} \epsilon (x,y) \end{Bmatrix}=\left[ \begin{matrix} T \end{matrix}\right] \begin{Bmatrix} \epsilon (\xi ,\eta ) \end{Bmatrix}, \end{aligned}$$

(20)

where $[T_{F_{1}}]=-[J6]^{-1}[J5][J4]^{-1}[J1]^{-1}$ , $[T_{F_{2}}]=[J6]^{-1}[J3]^{-1}$ and $\begin{Bmatrix} \epsilon (x,y) \end{Bmatrix}$ and $\begin{Bmatrix} \epsilon (\xi ,\eta ) \end{Bmatrix}$ denote the strain vectors in the respective coordinate system. The expression for $\begin{Bmatrix} \epsilon (\xi ,\eta ) \end{Bmatrix}$ is given by:

$$\begin{aligned} \left\{ \begin{array}{l} \epsilon (\xi ,\eta ) \end{array}\right\} =\left[ \begin{array}{lllll} \dfrac{\partial w}{\partial \xi }&\dfrac{\partial w}{\partial \eta }&\dfrac{\partial ^{2} w}{\partial \xi ^{2}}&\dfrac{\partial ^{2} w}{\partial \eta ^{2}}&\dfrac{\partial ^{2} w}{\partial \xi \,\partial \eta } \end{array}\right] ^{T}. \end{aligned}$$

(21)

Using Eq. (8)–(9), Eq. (21) can be rewritten as:

$$\begin{aligned} \begin{Bmatrix} \epsilon (\xi ,\eta ) \end{Bmatrix}= [\bar{B}] \begin{Bmatrix} \delta \end{Bmatrix}, \end{aligned}$$

(22)

where $[\bar{B}] =\left[ \begin{array}{l} \dfrac{\partial N_{w}}{\partial \xi } \dfrac{\partial N_{w}}{\partial \eta } \dfrac{\partial ^{2} N_{w}}{\partial \xi ^{2}} \dfrac{\partial ^{2} N_{w}}{\partial \eta ^{2}} \dfrac{\partial ^{2} N_{w}}{\partial \xi \,\partial \eta } \end{array}\right] ^{T}$.

Hence the combination of Eq. (20)–(22), yields

$$\begin{aligned} \begin{Bmatrix} \epsilon (x,y) \end{Bmatrix}=\left[ \begin{matrix} B \end{matrix}\right] \begin{Bmatrix} \delta \end{Bmatrix}, \end{aligned}$$

(23)

where $[B]=[T][\bar{B}]$.

The stress–strain relationship can be expressed as

$$\begin{aligned} \begin{Bmatrix} \sigma \end{Bmatrix}=[D] \begin{Bmatrix} \epsilon \end{Bmatrix} =[D][B]\begin{Bmatrix} \delta \end{Bmatrix}, \end{aligned}$$

(24)

where $\begin{Bmatrix} \sigma \end{Bmatrix}$ is the stress resultant vector given by,

$$\begin{aligned} \begin{Bmatrix} \sigma \end{Bmatrix}=\left[ \begin{matrix} M_{x}&M_{y}&M_{xy} \end{matrix}\right] ^{T} \end{aligned}$$

(25)

2.6 Stiffness matrix

Total potential energy of the plate element is given by [9]

$$\begin{aligned} \Pi _{p}=\dfrac{1}{2}\iint \begin{Bmatrix} \epsilon (x,y) \end{Bmatrix}^{T} \begin{Bmatrix} \sigma (x,y) \end{Bmatrix}\mathrm{{d}}x\;\mathrm{{d}}y-\iint w^{T}\mathrm{{d}}x\;\mathrm{{d}}y. \end{aligned}$$

(26)

Applying the principle of minimum potential energy and making appropriate substitutions for$\begin{Bmatrix} \epsilon (x,y) \end{Bmatrix}$ and$\begin{Bmatrix} \sigma (x,y) \end{Bmatrix}$, we have

$$\begin{aligned}{}[K]_{e} \begin{Bmatrix} \delta \end{Bmatrix}= \begin{Bmatrix} P \end{Bmatrix}_{e}, \end{aligned}$$

(27)

where $\begin{Bmatrix} \delta \end{Bmatrix}$ is the vector of nodal displacements, $\begin{Bmatrix} P \end{Bmatrix}_{e}$ is the vector of nodal forces and $[K]_{e}$ is the plate element stiffness matrix given by

$$\begin{aligned}{}[K]_{e}=\iint [B]^{T}[D][B]\,\mathrm{{d}}x\,\mathrm{{d}}y. \end{aligned}$$

(28)

Since the NURBS basis is a function of s and t, Eq. (28) becomes

$$\begin{aligned}{}[K]_{e}=\iint [B]^{T}[D][B]|J4|\,\mathrm{{d}}s\,\mathrm{{d}}t. \end{aligned}$$

(29)

Again since [B] is a function of $\xi$ and $\eta,$ Eq. (29) becomes

$$\begin{aligned}{}[K]_{e}=\iint [B]^{T}[D][B]|J1||J4|\,\mathrm{{d}}\xi \,\mathrm{{d}}\eta. \end{aligned}$$

(30)

The integration is carried out numerically by adopting $2\times 2$ Gaussian quadrature formula.

2.7 Geometric stiffness matrix

The geometric stiffness matrix is formulated considering the action of the in-plane loads causing the bending strains. The membrane strains associated with the small rotations $\dfrac{\partial w}{\partial x}$ and $\dfrac{\partial w}{\partial y}$ of the plate mid-surface are given by

$$\begin{aligned} \left\{ \epsilon _{G}\right\} = \begin{Bmatrix} \epsilon _{x}\\\epsilon _{y}\\\gamma _{xy} \end{Bmatrix}= \begin{Bmatrix} \dfrac{1}{2}\left( \dfrac{\partial w}{\partial x}\right) ^{2}\\ \dfrac{1}{2}\left( \dfrac{\partial w}{\partial y}\right) ^{2}\\ \left( \dfrac{\partial w}{\partial x}\right) \left( \dfrac{\partial w}{\partial y}\right) \end{Bmatrix}. \end{aligned}$$

(31)

The stresses $\sigma _{x}$, $\sigma _{x}$ and $\tau _{xy}$ are assumed to remain constant, the work done is given by

$$\begin{aligned} W=\int \int \int \left\{ \epsilon _{G}\right\} ^{T}\left\{ \sigma \right\} \;\mathrm{{d}}x\;\mathrm{{d}}y\;\mathrm{{d}}z, \end{aligned}$$

(32)

where

$$\begin{aligned} \left\{ \sigma \right\} = \begin{bmatrix} \sigma _{x}&\sigma _{y}&\tau _{xy} \end{bmatrix}^{T}. \end{aligned}$$

(33)

Now putting the value of $\left\{ \epsilon _{G}\right\}$ from Eq. (31) in Eq. (32), we have

$$\begin{aligned} \nonumber W&=\int \int \int \begin{bmatrix} \dfrac{1}{2}\left( \dfrac{\partial w}{\partial x}\right) ^{2}&\dfrac{1}{2}\left( \dfrac{\partial w}{\partial y}\right) ^{2}&\left( \dfrac{\partial w}{\partial x}\right) \end{bmatrix}\left\{ \sigma \right\} \;\mathrm{{d}}x\;\mathrm{{d}}y\;\mathrm{{d}}z\\&= \int \int \int \dfrac{1}{2}\left\{ \theta \right\} ^{T}\left[ \sigma \right] \left\{ \theta \right\} \;\mathrm{{d}}x\;\mathrm{{d}}y\;\mathrm{{d}}z, \end{aligned}$$

(34)

where

$$\begin{aligned} \left\{ \theta \right\} = \begin{bmatrix} \dfrac{\partial w}{\partial x}&\dfrac{\partial w}{\partial y} \end{bmatrix}^{T} \end{aligned}$$

(35)

and

$$\begin{aligned} \left[ \sigma \right] = \begin{bmatrix} \sigma _{x}&\tau _{xy} \\ \tau _{xy}&\sigma _{y} \end{bmatrix}. \end{aligned}$$

(36)

From Eqs. (13) and (11), Eq. (35) can be expressed in terms of $\xi$ and $\eta$ as

$$\begin{aligned} \left\{ \theta \right\}&= \begin{Bmatrix} \dfrac{\partial w}{\partial x} \nonumber \\ \dfrac{\partial w}{\partial y} \end{Bmatrix}=\left[ J4\right] ^{-1} \begin{Bmatrix} \dfrac{\partial w}{\partial s} \\ \dfrac{\partial w}{\partial t} \end{Bmatrix}\\\nonumber&=\left[ J4\right] ^{-1}\left[ J1\right] ^{-1} \begin{Bmatrix} \dfrac{\partial w}{\partial \xi } \\ \dfrac{\partial w}{\partial \eta } \end{Bmatrix}\\ {}&=\left[ T_{G}\right] \begin{Bmatrix} \dfrac{\partial w}{\partial \xi } \\ \dfrac{\partial w}{\partial \eta } \end{Bmatrix}, \end{aligned}$$

(37)

where

$$\begin{aligned} \left[ T_{G}\right] =\left[ J4\right] ^{-1}\left[ J1\right] ^{-1} \end{aligned}$$

(38)

and

$$\begin{aligned} \begin{Bmatrix} \dfrac{\partial w}{\partial \xi } \\ \dfrac{\partial w}{\partial \eta } \end{Bmatrix}=\left[ \bar{B}_{G}\right] \left\{ \delta \right\}, \end{aligned}$$

(39)

where

$$\begin{aligned} \left[ \bar{B}_{G}\right] = \begin{bmatrix} \begin{bmatrix} \dfrac{\partial N_{w}}{\partial \xi }&\dfrac{\partial N_{w}}{\partial \eta } \end{bmatrix} \end{bmatrix}^{T}. \end{aligned}$$

(40)

Combining Eq. (37) and Eq. (39), $\left\{ \theta \right\}$ can be expressed as

$$\begin{aligned} \left\{ \theta \right\} =\left[ T_{G}\right] \left[ \bar{B}_G\right] \left\{ \delta \right\} =\left[ B_{G}\right] \left\{ \delta \right\}, \end{aligned}$$

(41)

where

$$\begin{aligned} \left[ B_{G}\right] =\left[ T_{G}\right] \left[ \bar{B}_{G}\right]. \end{aligned}$$

(42)

Now substituting the value of $\left\{ \theta \right\}$ from Eq. (41), Eq. (34) becomes

$$\begin{aligned} W&= \int \int \int \dfrac{1}{2}\left\{ \delta \right\} ^{T}\left[ B_{G}\right] ^{T}\left[ \sigma \right] \left[ B_{G}\right] \left\{ \delta \right\} \;\mathrm{{d}}x\;\mathrm{{d}}y\;\mathrm{{d}}z\nonumber \\&=\dfrac{t}{2}\int \int \left\{ \delta \right\} ^{T}\left[ B_{G}\right] ^{T}\left[ \sigma \right] \left[ B_{G}\right] \left\{ \delta \right\} \;\mathrm{{d}}x\;\mathrm{{d}}y\;\mathrm{{d}}z. \end{aligned}$$

(43)

The external work done by the nodal force is given by

$$\begin{aligned} W=\dfrac{1}{2}\left\{ \delta \right\} ^{T}\left[ K_{G}\right] \left\{ \delta \right\}. \end{aligned}$$

(44)

From Eqs. (43) and (44), the geometric stiffness matrix of the plate element can be written as

$$\begin{aligned} \left[ K_{G}\right]&= t \int \int \left[ B_{G}\right] ^{T}\left[ \sigma \right] \left[ B_{G}\right] \; \mathrm{{d}}x\;\mathrm{{d}}y\nonumber \\&= t \int \int \left[ B_{G}\right] ^{T}\left[ \sigma \right] \left[ B_{G}\right] |J4|\;\mathrm{{d}}s\;\mathrm{{d}}t\nonumber \\&= t \int \int \left[ B_{G}\right] ^{T}\left[ \sigma \right] \left[ B_{G}\right] |J1||J4|\;\mathrm{{d}}\xi \;\mathrm{{d}}\eta. \end{aligned}$$

(45)

2.8 Boundary conditions

Reproducing the procedures adopted in [1, 9], as a general case, the stiffness matrix for a curved boundary supported on elastic springs continuously spreads in the directions of all possible displacements and rotations along the boundary line is formulated from which the specific boundary conditions can be obtained by incorporating the appropriate value of spring constants. Considering a local axis system $x_1-y_1$ at a point P on a curved boundary along the direction of the normal to the boundary at that point as shown in Fig. 3, the displacement components along it can be found. Let $\beta$ be the angle made by the local axis $x_1-y_1$ with the global axis $x-y$.

Fig. 3

Coordinate axes at any point of an elastically restrained curved boundary

Hence the relationship between the two axes is given by

$$\begin{aligned} \begin{Bmatrix} x\\ y \end{Bmatrix}= \begin{bmatrix} \cos \beta&-\sin \beta \\ \sin \beta&\cos \beta \end{bmatrix} \begin{Bmatrix} x_1\\ y_1 \end{Bmatrix}. \end{aligned}$$

(46)

The displacements at P which may be restrained can be expressed as

$$\begin{aligned} \{f_{b}\} = \begin{Bmatrix} w\\ \theta _{n}\\ \theta _{t} \end{Bmatrix}= \begin{Bmatrix} w \\ \dfrac{\partial w}{\partial x_{1}} \\ \dfrac{\partial w}{\partial y_{1}} \end{Bmatrix}, \end{aligned}$$

(47)

where $\theta _{n}$ and $\theta _{t}$ represent the slopes which are normal and transverse to the boundaries, respectively. Substituting from Eq. (46), Eq. (47) can be written as

$$\begin{aligned} \{f_{b}\} = \begin{bmatrix} 1&0&0 \\ 0&\cos \beta&\sin \beta \\ 0&-\sin \beta&\cos \beta \end{bmatrix} \begin{Bmatrix} w \\ \dfrac{\partial w}{\partial x} \\ \dfrac{\partial w}{\partial y} \end{Bmatrix}. \end{aligned}$$

(48)

Expressing Eq. (48) in terms of the shape functions, we have

$$\begin{aligned} \{f_{b}\}=[N_{b}]\{\delta \}, \end{aligned}$$

(49)

$$\begin{aligned}{}[N_{b}]= \begin{bmatrix} 1&0&0 \\ 0&\cos \beta&\sin \beta \\ 0&-\sin \beta&\cos \beta \end{bmatrix} \begin{Bmatrix} [N_w] \\ \dfrac{\partial [N_w]}{\partial x}\\ \dfrac{\partial [N_w]}{\partial y} \end{Bmatrix}. \end{aligned}$$

(50)

Let $k_w, k_\alpha ,$ and $k_\beta$ be the spring constants or restraint coefficients corresponding to the direction of $w, \theta _n$and $\theta _t$, respectively. The reaction components per unit length along the boundary line due to the spring constants corresponding to the possible boundary displacements are given by

$$\begin{aligned} \{f_{k}\}= \begin{Bmatrix} f_{kw}\\ f_{k\alpha }\\ f_{k\beta } \end{Bmatrix} = \begin{Bmatrix} k_{w}w\\ k_{\alpha }\theta _{n} \\ k_{\beta } \theta _{t} \end{Bmatrix}. \end{aligned}$$

(51)

Equation (51) can be rewritten by combining Eqs. (47)–(49) as

$$\begin{aligned} \begin{Bmatrix} f_{k} \end{Bmatrix}=\left[ N_{k}\right] \begin{Bmatrix} \delta \end{Bmatrix}, \end{aligned}$$

(52)

where $[N_{k}]=\begin{bmatrix} k_w&0&0 \\ 0&k_\alpha \cos \beta&k_\alpha \sin \beta \\ 0&-k_\beta \sin \beta&k_\beta \cos \beta \end{bmatrix}\begin{Bmatrix} [N_w] \\ \dfrac{\partial [N_w]}{\partial x}\\ \dfrac{\partial [N_w]}{\partial y} \end{Bmatrix}$.

Using Eqs. (48) and (51), the stiffness matrix can be obtained by the virtual work principle and is expressed as

$$\begin{aligned}{}[K_{b}]=\int [N_{b}]^T[N_{k}]|J_b|\,d\lambda _1, \end{aligned}$$

(53)

where $\lambda _1$ is the direction of the boundary line in the $\xi -\eta$ plane and Jacobian $|J_{b}|=\dfrac{\mathrm{{d}} s_{1}}{\mathrm{{d}} \lambda _{1}}$. The value of the Jacobian along a boundary line is considered as a ratio of the actual length to the length on the mapped domain considering any segment of the boundary line. A classical boundary condition can be attained by substituting a high value of the restraint coefficients corresponding to the restraint direction.

3 Numerical examples

The stability analyses of a number of plates having different shapes and boundary conditions are carried out using the simultaneous iteration algorithm of Corr and Jennings [5] and the results obtained are compared with the existing ones. The results are presented in tabular form with a mesh division of $32\times 32$ for the whole plate. Figures of typical plates showing mesh divisions of $8\times 8$ along with the nodes (asterisk) are presented for each case. The abbreviations used in the table for the boundary conditions (S—simply supported, C—clamped, F—free) are depicted in the anti-clockwise direction starting from the left edge of the plate. The ability of NAFEM to analyse some new shapes is showcased by considering a rectangular plate with one side curved edge consisting of a rectangular portion as patch-1 and the remaining as patch-2.

3.1 Circular plate

The buckling loads for the simply supported and the clamped bare circular plates are computed and the results are presented in the form of the parameter $k = \left( N_{r}\right) _{cr}a^2/D,$ where $\left( N_{r}\right) _{cr}$ is the critical compressive force uniformly around the edge of the plate, a is the radius of the circular plate and D is the flexural rigidity of the plate. The results are presented in Table 1 for various mesh divisions of the whole plate to study the convergence of the buckling parameter and they are compared with the analytical values of Timoshenko  and Gere [19]. There is excellent agreement between the results (Fig. 4).

Table 1 Buckling parameter $k = \left( N_{r}\right) _{cr}a^2/D$ for uniformly compressed clamped and simply supported circular plates $(\nu =0.3)$

Fig. 4

A typical circular plate having $8\times 8$ mesh

3.2 Rectangular plate with curved edges

A rectangular plate having curved edges (Fig. 5) is analysed for different boundary conditions and aspect ratios $r_{1}/r_{2}$ (where $r_{1}$ and $r_{2}$ are the semi-major and semi-minor axes of the plate, respectively) that are presented in Tables 2 and 3.

Fig. 5

A typical rectangular plate with curved edges having $8\times 8$ mesh

Table 2 Buckling load parameter $k=\lambda r_{1}^{2}/\pi ^{2} D$ for biaxially compressed rectangular plate with curved edges

Table 3 Buckling load parameter $k=\lambda r_{1}^{2}/\pi ^{2} D$ for uni-axially compressed rectangular plate with curved edges

3.3 Semi-circular semi-elliptical plate

The stability analysis of a plate consisting of a semi-circle and semi-ellipse (Fig. 6) is carried out for different boundary conditions and aspect ratios a / b (where a is the radius of the semi-circle and the semi-minor axis of the semi-ellipse and b is the semi-major axis of the semi-ellipse) and the results are presented in Tables 4 and 5.

Table 4 Buckling load parameter $k=\lambda b^{2}/\pi ^{2} D$ for biaxially compressed semi-circular semi-elliptical plate

Table 5 Buckling load parameter $k=\lambda b^{2}/\pi ^{2} D$ for uni-axially compressed semi-circular semi-elliptical plate

Fig. 6

A typical semi-circular semi-elliptical plate having $8\times 8$ mesh

3.4 Dome-shaped plate

A typical plate resembling the shape of a dome is considered by taking one of the edges straight and its opposite edge as the top of a dome (Fig. 7). The stability analysis of this dome-shaped plate is carried out for different boundary conditions and aspect ratio $r_{1}/r_{2},$ where $r_{1}$ is the length of the straight edge and $r_{2}$ is the semi-minor axis of the dome. The results obtained are presented in Tables 6 and 7.

Table 6 Buckling load parameter $k=\lambda r_{1}^{2}/\pi ^{2} D$ for uni-axially compressed dome-shaped plate

Table 7 Buckling load parameter $k=\lambda r_{1}^{2}/\pi ^{2} D$ for biaxially compressed dome-shaped plate

Fig. 7

A typical dome-shaped plate having $8\times 8$ mesh

3.5 Rectangular plate with one side curved edge

A rectangular plate with one side being curved is analysed by considering the rectangular portion as patch-1 ($32\times 32$ mesh) and the remaining portion as patch-2 ($32\times 32$ mesh) subjected to uniaxial and biaxial compression under different boundary conditions and aspect ratios (a—half of the length of the rectangular portion; b—breadth of the rectangular portion). The nodes of the rectangular portion (patch-1) are represented with asterisk and the remaining portion (patch-2) with circular markers, respectively. The results obtained are presented in Tables 8 and 9. A typical rectangular plate with one side curved edge consisting of a rectangular portion as patch-1 ($4\times 4$ mesh) and the remaining as patch-2 ($4\times 4$ mesh) is shown in Fig. 8.

Table 8 Buckling load parameter $k=\lambda a^{2}/\pi ^{2} D$ for biaxially compressed rectangular plate with one side curved edge

Table 9 Buckling load parameter $k=\lambda a^{2}/\pi ^{2} D$ for uniaxial compressed rectangular plate with one side curved edge

Fig. 8

A typical rectangular plate with one side curved edge consisting of a rectangular portion as patch-1 ($4\times 4$ mesh) and the remaining as patch-2($4\times 4$ mesh)

4 Conclusions

In the present formulation, NURBS basis functions are used to represent the exact shape of the arbitrary thin plates. In contrast to the isogeometric analysis, the use of classical finite element basis functions as field variables helps in imposing the boundary conditions easily which is the main drawback of isogeometric analysis. Further, the knot refinement technique of the NURBS basis function takes care of the mesh generation. The stability analyses of the arbitrary shaped plates are carried out and the results obtained are found to be well in agreement in all the cases. To showcase the robustness of NAFEM some plates of different geometries (semi-circular semi-elliptical, rectangular plate with curved edges and dome-shaped plate) have been considered for the stability analysis and the new results are presented. Further a rectangular plate with one side being curved is analysed by considering the rectangular portion as patch-1 and the remaining potion as patch-2, thereby showing the capability of NAFEM to analyse certain geometries by breaking them into more amenable patches which can be dealt with ease.