Buckling of carbon nanotube (CNT)-reinforced composite skew plates by the discrete singular convolution method

Abstract

A geometric transformation method based on discrete singular convolution (DSC) is firstly applied to solve the buckling problem of a functionally graded carbon nanotube (FG-CNT)-reinforced composite skew plate. The straight-sided quadrilateral plate geometry is mapped into a square domain in the computational space using a four-node DSC transformation method. Hence, the related governing equations of plate buckling and boundary conditions of the problem are transformed from the physical domain into a square computational domain by using the geometric transformation-based singular convolution. The discretization process is achieved via the DSC method together with numerical differential and two different regularized kernels such as regularized Shannon’s delta and Lagrange-delta sequence kernels. The accuracy of the present DSC results is first verified, and then, a detailed parametric study is presented to show the impacts of CNT volume fraction, CNT distribution pattern, geometry of the skew plate and skew angle on the axial and biaxial buckling responses of FG-CNTR composite skew plates with different boundary conditions. Some new results related to critical buckling of an FG-CNT-reinforced composite skew plate are also presented, which can serve as benchmark solutions for future investigations.

1 Introduction

Throughout the history of civilization, materials play a major role in every field of technology such as engineering, biomedicine, computers, sensors, micro- and nano-electro-mechanical systems (MEMS and NEMS), and different industries. From stone up to nanocomposites, all materials have been used to satisfy human needs and to lead to a comfortable life. Carbon nanotube (CNT)- and graphene-reinforced material are two advanced novel materials possessing high strength/stiffness, a very good thermal and electrical performance as well as a high aspect ratio and low density. It is commonly accepted that CNT, fullerene, graphite, and diamond are the main allotropes of carbon. However, CNT-reinforced material has emerged as an effective material, which has many applications in many areas.

It is known that different shapes of plate and shell components are made of a wide range of material properties such as isotropic, orthotropic, laminated composite, anisotropic, and functionally graded composites. Additionally, bending, buckling and vibration behaviors of homogeneous or isotropic and composite plates with rectangular and circular shapes have been widely analyzed in the open literature [1,2,3,4,5,6,7,8,9,10]. Skew plates have also found widespread usages in aerospace and aeronautics, civil, mechanical and marine/ship engineering. Due to their frequent use in many areas of engineering, it is important to define and understand the buckling characteristics of skew plates. Until today many numerical and analytical methods such as Ritz, finite element method, meshless method, differential quadrature, Galerkin and boundary element method have been used for the analysis of buckling and vibration problems of skew plates [11,12,13,14,15,16,17,18]. By using the element-free IMLS-Ritz method, buckling and post-buckling analyses of plates with CNT-reinforced functionally graded materials (FGMs) have been made by Zhang et al. [19]. In this study, they applied the first-order shear deformation theory and von Kármán assumption to take the effects of transverse shear strains, rotary inertia and moderate rotations. Jaberzadeh and Azhari [20] proposed an element-free Galerkin method using meshless formulation for local buckling of moderately thick stepped skew viscoelastic composite plates. Kiani [21] gives some benchmark results for buckling of FG-CNT-reinforced composite plates subjected to parabolic loading. Post-buckling analysis of skew plates subjected to combined in-plane loadings has been analyzed in detail by Upadhyay and Shukla [22]. An higher-order shear deformation theory for isogeometric thermal buckling analysis of FGM plates with temperature-dependent material properties has been discussed by Van Do and Lee [23]. Frikha et al. [24] used efficient shell elements for functionally graded CNT composite shell analysis via finite rotation of three- and four-node shell elements. Mehri et al. [25] introduced the harmonic differential quadrature method for buckling and free vibration solution of a pressurized FG-CNT-reinforced shell under an axial compression load. By using the mesh-free radial basis function method, the linear buckling analysis of arbitrarily shaped shear deformable plates has been investigated by Liew et al. [26]. Huang and Lin [27] introduced a moving least square differential quadrature method for bending and buckling analysis of antisymmetric laminates plates via shear deformable plate theories. Wang et al. [28] also used shear the deformation theory of Mindlin for modeling of buckling problems of plates with internal line supports. The solution was obtained via pb-2 Rayleigh–Ritz method, and detailed benchmark results were provided. Buckling of FG-CNT-reinforced panels under axial compression has been studied using the kernel particle approximation via the Ritz method by Liew et al. [29]. The panels have been reinforced by single-walled carbon nanotubes (SWCNTs) with different types of distributions. Khdeir and Librescu [30] utilized an analytical benchmark solution for buckling and free vibration of symmetric-laminated cross-ply elastic plates based on the higher-order theory. An analysis of arbitrarily shaped FG-CNT-reinforced plates was given by Fantuzzi et al. [31]. In this research, the method of generalized differential quadrature was used for numerical discretization. An analysis of laminated nanocomposite plates using the first-order shear deformation theory and the generalized differential quadrature method was applied for a numerical solution by Tornabene et al. [32]. Buckling of FG-CNT-reinforced composite thick skew plates was studied via the improved moving least squares-Ritz approach by Zhang et al. [33] and Lei et al. [34] with or without elastic foundation. In [33, 34], CNTs were reinforced uniaxially aligned in the axial direction of the plate, and some detailed numerical examples were supplied. Recently, elastic buckling of rectangular and skew plates with FGM with cutout resting on a two-parameter elastic foundation was discussed by Shahrestani et al. [35]. In this study, the isoparametric spline finite strip method has been developed, and detailed results have been listed. In a series of paper, Shen [36, 37] and Shen and Zhang [38] gave a detailed formulation, benchmark results, and the related coefficient for CNT parameters related to the analysis of FG-CNT-reinforced components. An FG-CNT-reinforced composite plate was analyzed using the three-dimensional theory of elasticity and the state-space method by Alibeigloo and Liew [39]. A detailed review on static, vibration and buckling analysis of FG-CNT-reinforced composite structures was given by Liew et al. [40]. Other than that, there are also some other studies that are related to the vibration and buckling analyses of FG-CNT-reinforced composite beams, plates, and shells [41,42,43,44,45,46,47,48,49,50,51].

It is generally known that two main plate theories have been widely used during the past years such as classical or thin plate theories or higher-order deformation theories. The classical plate theory based on Kirchhoff’s hypothesis is not efficient to describe the accurate behavior of thick plates, especially laminated composite plates, because the transverse shear deformation is not considered. Hence, it is necessary to develop some refined and higher-order shear deformation plate theories. The concept of higher-order shear deformation theories has been subsequently proposed to obtain more accurate solutions of the thick and laminated problems [79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106].

In the literature, different numerical and analytical methods such as Ritz, finite element method, differential quadrature methods, and meshless methods have been used for buckling analyses of thin and thick plates. In the method of DSC implementation, boundary conditions are similar for both thin and thick plates. We used the symmetric and antisymmetric extension proposed by Wei [52, 53] and Wei et al. [54, 55] for imposing boundary conditions.

In applications of mechanical, civil, ship, and aerospace engineering areas, skew plates have been widely used as swept wings of aero planes, horizontal and vertical alignments in bridge design, ship hulls and parallelogram slabs in buildings, and reinforced slabs or stiffened plates.

In this study, a buckling analysis of skew plates made of an FG-CNT-reinforced composite has been performed based on the first-order shear deformation and thin plate theory. The skew plate material comprises a mixture of CNTs and the matrix. Also, a nanocomposite skew plate may comprise three different distributions such as uniform distribution of CNTs (UD), O-type functionally graded distributions of CNTs (FG-O) and an X-type functionally graded distribution of CNTs (FG-X). Furthermore, a skew plate is considered to have a linear distribution of the volume fraction of CNTs. Two different singular kernels have been used in conjunction with the discretization of a singular convolution procedure. The straight-sided quadrilateral element is transformed into a square domain in the computational plate domain by using the four-node discrete singular convolution (DSC) mapping. After giving the related governing equations for the buckling of skew plates and boundary conditions, related geometric transformation has been defined via the DSC transformation approach. Then, detailed numerical solutions have been obtained for various FGM and CNT distributions and CNT volume fraction numbers, FGM index, skew angles, load and boundary conditions. To the best of the authors’ knowledge, this is the first instance in which the DSC mapping procedure has been presented for the buckling analysis of FG-CNT-reinforced composite skew plates.

2 Discrete singular convolution (DSC)

Numerical methods for differentiation are of significant interest and important during the numerical discretization of many problems in different engineering problems and applied sciences. The method of DSC has generally become a preferable method by many researchers in recent ten years due to its simplicity and fast convergence characteristics for application. The DSC method was first proposed at the end of the nineties by Wei [52, 53]. This new method has been applied to many mathematical physics and engineering problems by Wei et al. [54, 55] and Ng et al. [56]. It was completely shown and proven by many scientists in different areas via different examples [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71] that the method of DSC has good accuracy, efficiency, and rapid convergence. At the beginning of 2000s, the DSC method was introduced via computer realization of some singular convolutions [45, 52]. Wei [53] used some singular kernels of Hilbert, Abel and delta types in some applications. By the way, the mathematical foundation of the DSC method is older and based on the theory of distributions and the theory of wavelets. In different DSC applications, many DSC kernels such as regularized Shannon’s delta (RSD), regularized Dirichlet, regularized Lagrange, and regularized de la Vallée Poussin kernels were used in [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71]. Such a singular convolution is defined as [52]

$$\begin{aligned} \gamma (t)=(\Gamma *\varphi )(t)=\int \limits _{-\infty }^\infty {\Gamma (t-x)\varphi (x)\mathrm{d}x} \end{aligned}$$

(1)

where $\Gamma (t-x)$ is a singular kernel. Additionally, a delta-type kernel is more suitable and is defined below: [53]

$$\begin{aligned} \Gamma (x)=\delta ^{(n)} (x);\quad (\hbox {n} =0,1,2,\ldots ,). \end{aligned}$$

(2)

Wei gives the final form for practical applications [55],

$$\begin{aligned} \gamma _{\alpha } (t)=\sum \Gamma _{\alpha } (t-x_{k} )g(x_{k} ). \end{aligned}$$

(3)

In Eq. (3), $\gamma _{\alpha }$ (t) is an approximation to $\gamma (t)$, and $\{x_{\mathrm{k}}\}$ is the set of discrete points.

2.1 Regularized Shannon’s Delta (RSD) kernel

Shannon’s kernel is regularized as below:

$$\begin{aligned} \delta _{\Delta ,\sigma } (x-x_{k} )=\frac{\sin [(\pi /\Delta )(x-x_{k} )]}{(\pi /\Delta )(x-x_{k} )}\exp \left[ {-\frac{{(x-x_{k} )}^{2} }{2\sigma ^{2} }} \right] ; \sigma > 0. \end{aligned}$$

(4)

Equation (4) can be used for providing discrete approximations to the singular convolution kernels of the delta type, namely

$$\begin{aligned} g^{(n)} (x)\approx \sum \limits _{k=-M}^M {{\delta }_{\Delta } } (x-x_{k} )f(g_{k}), \end{aligned}$$

(5)

In the method of DSC approach, a discrete partial derivative of a given function is as below [52]:

$$\begin{aligned} {\left. {\frac{d^{n} g(x)}{\mathrm{d}x^{n} }} \right| }_{x=x_{i}} =g^{(n)} (x)\approx \sum \limits _{k=-M}^M {{\delta }_{\Delta ,\sigma }^{(n)} } (x_{i} -x_{k} )g(x_{k} ); \quad (n=0,1,2,\ldots ,). \end{aligned}$$

(6)

A second-order derivative at $x=x_{i}$ is given by:

$$\begin{aligned} {\delta }_{\Delta ,\sigma }^{(2)} (x-x_{j} )=\frac{\mathrm{d}^{2} }{\mathrm{d}x^{2} }{\left. {\left[ {{ \delta }_{\Delta ,\sigma } (x-x_{j} )} \right] } \right| }_{x=x_{i}}. \end{aligned}$$

(7.1)

The discretized form of the second-order derivative can also be written as:

$$\begin{aligned} {\left. {g^{(2)} (x)=\frac{\mathrm{d}^{2} g}{\mathrm{d}x^{2} }} \right| }_{x=x_{i} } \approx \sum \limits _{k=-M}^M {{\delta }_{\Delta ,\sigma }^{(2)} } (k\Delta x_{N} )g_{i+k,\,j} . \end{aligned}$$

(7.2)

For Shannon’s kernel, the related derivatives are defined as: [52, 53]

$$\begin{aligned} \delta _{\pi /\Delta ,\sigma }^{(1)} (x_{m} -x_{k} )= & {} \frac{\cos (\pi /\Delta )(x-x_{k} )}{(x-x_{k} )}\exp [-{(x-x_{k} )}^{2} /2\sigma ^{2} ]\nonumber \\&-\frac{\sin (\pi /\Delta )(x-x_{k} )}{\pi {(x-x_{k} )}^{2} /\Delta }\exp [-({x-x_{k} )}^{2} /2\sigma ^{2} )]\nonumber \\&-\frac{\sin (\pi /\Delta )(x-x_{k} )}{(\pi \sigma ^{2} /\Delta )}\exp [-({x-x_{k} )}^{2} /2\sigma ^{2} )], \end{aligned}$$

(8)

$$\begin{aligned} \delta _{\pi /\Delta ,\sigma }^{(2)} (x_{m} -x_{k} )= & {} -\frac{(\pi /\Delta )\sin (\pi /\Delta )(x-x_{k} )}{(x-x_{k} )}\exp [-{(x-x_{k} )}^{2} /2\sigma ^{2} ]\nonumber \\&-2\frac{\cos (\pi /\Delta )(x-x_{k} )}{{(x-x_{k} )}^{2} }\exp [-({x-x_{k} )}^{2} /2\sigma ^{2} )]\nonumber \\&-2\frac{\cos (\pi /\Delta )(x-x_{k} )}{\sigma ^{2} }\exp [-{(x-x_{k} )}^{2} /2\sigma ^{2} ]\nonumber \\&+2\frac{\sin (\pi /\Delta )(x-x_{k} )}{\pi ({x-x_{k} )}^{3} /\Delta }\exp [-({x-x_{k} )}^{2} /2\sigma ^{2} )]\nonumber \\&+\frac{\sin (\pi /\Delta )(x-x_{k} )}{\pi (x-x_{k} )\sigma ^{2} /\Delta }\exp [-{(x-x_{k} )}^{2} /2\sigma ^{2} ]\nonumber \\&+\frac{\sin (\pi /\Delta )(x-x_{k} )}{\pi \sigma ^{4} /\Delta }(x-x_{k} )\exp [-({x-x_{k} )}^{2} /2\sigma ^{2} )] \end{aligned}$$

(9)

where $\Delta =\uppi /(\hbox {N}-1)$ is the grid spacing and N is the number of grid points. The parameter $\upsigma$ determines the width of the Gaussian envelope and often varies in association with the grid spacing, i.e., $\upsigma = \hbox {rh}$. Here, r is a parameter chosen in computation [52,53,54].

2.2 Lagrange-delta sequence (LDS) kernel

This kernel for $i = 0,1,\ldots , N\,\hbox {--}\,1$ and $j =\hbox {--}M,\ldots ,M$ is given by [57,58,59,60,61]:

$$\begin{aligned} {\mathfrak {R}}_{i,j} (x)=\left\{ {{\begin{array}{lc} \prod \limits _{k=i-M,k\ne i+j}^{i+M} {\frac{x-x_{k}}{x_{i+j} -x_{k} },}&{} \quad x_{i-M} \le \hbox {x}\le x_{i+M,} \\ \\ 0&{} \hbox { otherwise} \\ \end{array} }} \right. \end{aligned}$$

(10)

where $W_{i,j}^{(n)}$ are the weighting coefficients, and these coefficients for the first derivative can be given as:

$$\begin{aligned} W_{i,j}^{(1)}= & {} {\mathfrak {R}}_{i,j}^{(1)} ;\hbox { for }i = 0,1,\ldots , N-1\hbox { and }j =-M,\ldots ,\textit{M, j}\ne 0, \end{aligned}$$

(11.1)

$$\begin{aligned} {W_{i,0} }^{(1)}= & {} -\sum \limits _{j=-M,j\ne 0}^M {{W}_{i,j}^{(1)} } ;\hbox { for }i = 0,1,\ldots , N-1\hbox { and }j=0. \end{aligned}$$

(11.2)

Related to this kernel, the weighting coefficients for any order derivatives can be written as: [58]

$$\begin{aligned} W_{i,j}^{(n)} =n\left[ {W_{i,j}^{(1)} W_{i,j}^{(n-1)} -\frac{W_{i,j}^{(n-1)} }{(x_{i} -x_{i+j} )}} \right] \end{aligned}$$

(12)

for $i = 0,1,\ldots ,N\,\hbox {--}\,1$ and $j =\hbox {--}M,\ldots ,M, j\ne 0$, and $n=2,3,\ldots ,2M$,

$$\begin{aligned} {W_{i,0} }^{(n)} =-\sum \limits _{j=-M,\,j\ne 0}^M {{W}_{i,j}^{(n)} }. \end{aligned}$$

(13)

For a Lagrange kernel, these derivatives are as follows:

$$\begin{aligned} \delta _{\Delta ,\sigma }^{(1)} (x)= & {} \sum \limits _{i=-M;\, i\ne k}^M {\left( {\frac{1}{x_{k} -x_{i} }} \right) } \prod \limits _{i=-M,\, k\ne i}^{i+M} {\frac{x-x_{i} }{x_{k} -x_{i} } }, \end{aligned}$$

(14)

$$\begin{aligned} \delta _{\Delta ,\sigma }^{(2)} (x)= & {} \sum \limits _{\begin{array}{l} i,m=-M;i\ne k \\ m\ne k,i\ne m \\ \end{array}}^M {\left( {\frac{1}{(x-x_{i} )(x-x_{m} )}} \right) } \prod \limits _{i=-M,k\ne i}^{i+M} {\frac{x-x_{i} }{x_{k} -x_{i} }}. \end{aligned}$$

(15)

Fig. 1

Configuration and transformation of quadrilateral plate: a Geometric mapping and b CNT skew plate

3 Geometric mapping for DSC approach

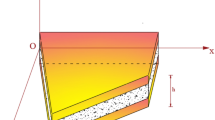
An arbitrary straight-sided quadrilateral CNT plate in the Cartesian $x\text {-}y$ coordinate system is shown in Fig. 1a. The field of this CNT plate can be mapped into a rectangular plate in the natural $\upxi \text {-}\upeta$ plane, as displayed in Fig. 1b. Using the transformation equation, the physical domain can be mapped into the computational domain as:

$$\begin{aligned} x=\sum \limits _{i=1}^N {x_{i} } \Phi _{i} (\xi ,\eta )\quad \hbox { and } \quad y=\sum \limits _{i=1}^N {y_{i} } \Phi _{i} (\xi ,\eta ) \end{aligned}$$

(16)

where $x_{i}$ and $y_{i}$ are the coordinates of node i in the physical domain, N is the number of grid points, $\varPhi _{i} (\xi ,\eta )$; $\hbox {i}= 1,2,3,\ldots ,N$ are the interpolation or shape functions. The interpolation function can be defined as:

$$\begin{aligned} \Phi _{i} (\xi ,\eta )=\frac{1}{4}(1+\xi \,\xi _{i} )(1+\eta \, \eta _{i} ). \end{aligned}$$

(17)

According to After the well-known chain rule, the related differential derivatives of this function can be written as:

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} }} \right\} =[J_{11} ]^{-1}\left\{ {{\begin{array}{*{20}c} {u_{\xi } } \\ {u_{\eta } }\\ \end{array} }} \right\} , \end{aligned}$$

(18.1)

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {u_{xx} } \\ {u_{yy} } \\ {2u_{yx} } \\ \end{array} }} \right\} =[J_{22} ]^{-1}\left\{ {{\begin{array}{*{20}c} {u_{\xi \xi } } \\ {u_{\eta \eta } } \\ {2u_{\xi \eta } } \\ \end{array} }} \right\} -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\left\{ {{\begin{array}{*{20}c} {u_{\xi } } \\ {u_{\eta } } \\ \end{array} }} \right\} \end{aligned}$$

(18.2)

where $\upxi _{\mathrm{i}}$ and $\upeta _{\mathrm{i}}$ are the coordinates of node i in the $\xi \text {-}\eta$ plane, and $J_{ij}$ are the elements of the Jacobian matrix. These are expressed as follows:

$$\begin{aligned} {[}J_{11} ]= & {} \left[ {{\begin{array}{*{20}c} {x_{\xi } } &{} \quad {y_{\xi } }\\ {x_{\eta } } &{} \quad {y_{\eta } }\\ \end{array} }} \right] ;\;\; {[}J_{21} ]=\left[ {{\begin{array}{*{20}c} {x_{\xi \xi } } &{} \quad {y_{\xi \xi } }\\ {x_{\eta \eta } } &{} \quad {y_{\eta \eta } } \\ {x_{\xi \eta } } &{} \quad {y_{\xi \eta }} \\ \end{array} }} \right] ;\nonumber \\ {[}J_{22} ]= & {} \left[ {{\begin{array}{*{20}c} {{x_{\xi } }^{2} } &{} \quad {{y_{\xi } }^{2} } &{} \quad {x_{\xi } y_{\xi } } \\ {{x_{\eta } }^{2} } &{} \quad {{y_{\eta } }^{2} } &{} \quad {x_{\eta } y_{\eta } } \\ {x_{\xi } x_{\eta } } &{} \quad {y_{\xi } y_{\eta } } &{} \quad {\frac{1}{2}(x_{\xi } y_{\eta } +x_{\eta } y_{\xi } )} \\ \end{array} }} \right] . \end{aligned}$$

(19)

Based on these transformation rules, the related derivations are as follows:

$$\begin{aligned} \frac{\partial ^{2}w}{\partial x^{2}}= & {} \sum \limits _{i=-M}^M {\delta ^{(2)}{}_{\Delta ,\sigma } } (k\Delta x)w_{ik}, \end{aligned}$$

(20.1)

$$\begin{aligned} \frac{\partial ^{2}w}{\partial y^{2}}= & {} \sum \limits _{j=-M}^M {\delta ^{(2)}{}_{\Delta ,\sigma } } (k\Delta y)w_{jk} \end{aligned}$$

(20.2)

or

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\frac{\partial ^{2}w}{\partial x^{2}}} \\ {\frac{\partial ^{2}w}{\partial y^{2}}} \\ {\frac{\partial ^{2}w}{\partial x\partial y}} \\ \end{array} }} \right\} =\left[ {J_{22} } \right] ^{-1}\left\{ {{\begin{array}{*{20}c} {\frac{\partial ^{2}w}{\partial \xi ^{2}}} \\ {\frac{\partial ^{2}w}{\partial \eta ^{2}}} \\ {\frac{\partial ^{2}w}{\partial \xi \partial \eta }} \\ \end{array} }} \right\} -\left[ {J_{22} } \right] ^{-1}\left[ {J_{21} } \right] \left[ {J_{11} } \right] ^{-1}\left\{ {{\begin{array}{*{20}c} {\frac{\partial w}{\partial \xi }} \\ {\frac{\partial w}{\partial \eta }} \\ \end{array} }} \right\} . \end{aligned}$$

(21)

The discrete form of these derivatives includes the transformation rule defined by:

$$\begin{aligned} \frac{\partial ^{2}w}{\partial x^{2}}= & {} [J_{22} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(2)}{}_{\Delta ,\sigma } } (k\Delta \xi )w_{ik} -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(1)}{}_{\Delta ,\sigma } } (k\Delta \xi )w_{ik}, \end{aligned}$$

(22)

$$\begin{aligned} \frac{\partial ^{2}w}{\partial y^{2}}= & {} [J_{22} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(2)}{}_{\Delta ,\sigma } } (k\Delta \eta )w_{jk} -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(1)}_{\Delta ,\sigma } } (k\Delta \eta )w_{jk}, \end{aligned}$$

(23)

$$\begin{aligned} \frac{\partial ^{2}w}{\partial x\partial y}= & {} [J_{22} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(1)}{}_{\Delta ,\sigma } } (k\Delta \xi )w_{ik} \sum \limits _{i=-M}^M {\delta ^{(1)}{}_{\Delta ,\sigma } } (k\Delta \eta )w_{jk}\nonumber \\&-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{i=-M}^M {\delta ^{(1)}{}_{\Delta ,\sigma } } (k\Delta \eta )w_{jk}. \end{aligned}$$

(24)

4 Fundamental equation for buckling

In this Section, the related formulations have been presented for CNT skew plates. In order to compare with the literature results, not only thick plate theory but also thin plate equations are presented. So, when the plate is thin, we have used the thin plate formulations; otherwise, thick plate formulations have been used. In order to show the performance of the DSC method, some detailed analyses via thin and thick plate theories have been presented [106] for skew plates. Convergence, comparison, and error analysis related to some DSC parameters and grid numbers have also been supplied [106].

4.1 Thin plate theory

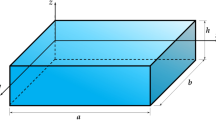
The related governing equation for buckling of a thin CNT plate (Fig. 2) is given as:

$$\begin{aligned}&D\left( {\frac{\partial ^{4}w}{\partial x^{4}}+2\frac{\partial ^{4}w}{\partial x^{2}\partial y^{2}}+\frac{\partial ^{4}w}{\partial y^{4}}} \right) \nonumber \\&\quad \quad \,\, -N_{x} \frac{\partial ^{2}w}{\partial x^{2}}-N_{y} \frac{\partial ^{2}w}{\partial y^{2}}-2N_{xy} \frac{\partial ^{2}w}{\partial x\partial y}=0 \end{aligned}$$

(25)

where D is the bending rigidity of the CNT plate, h is the plate thickness, $N_{x}$ and $N_{y}$ are the applied compressive loads in the respective x and y directions, $N_{xy}$ is the shear force, w is the deflection, and x and y are the mid-plane Cartesian coordinates. We can define the below differential operators for brevity:

$$\begin{aligned} {\mathfrak {R}} =\frac{\partial ^{2}W}{\partial X^{2}} \end{aligned}$$

(26.1)

and

$$\begin{aligned} S=\frac{\partial ^{2}W}{\partial Y^{2}}. \end{aligned}$$

(26.2)

Fourth-order derivatives can be written via Eq. (26),

$$\begin{aligned} \frac{\partial ^{4}W}{\partial X^{4}}= & {} \frac{\partial ^{2}}{\partial X^{2}}\,{\mathfrak {R}}, \end{aligned}$$

(27)

$$\begin{aligned} \frac{\partial ^{4}W}{\partial Y^{4}}= & {} \frac{\partial ^{2}}{\partial Y^{2}}S, \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial ^{4}W}{\partial X^{2}\partial Y^{2}}= & {} \frac{\partial ^{2}}{\partial X^{2}}\left[ {\frac{\partial ^{2}W}{\partial Y^{2}}} \right] =\frac{\partial ^{2}}{\partial X^{2}}S. \end{aligned}$$

(29)

Fig. 2

Different types of loads applied to CNT skew plate: a biaxial and b uniaxial loading

Consequently, the related derivatives in the computational domain can be listed for related derivations:

$$\begin{aligned} \frac{\partial W}{\partial X}= & {} [J_{11} ]^{-1}\frac{\partial W}{\partial \xi }, \end{aligned}$$

(30)

$$\begin{aligned} \frac{\partial W}{\partial Y}= & {} [J_{11} ]^{-1}\frac{\partial W}{\partial \eta }, \end{aligned}$$

(31)

$$\begin{aligned} \frac{\partial ^{2}W}{\partial X^{2}}= & {} [J_{22} ]^{-1}\frac{\partial ^{2}W}{\partial \xi ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial W}{\partial \xi }, \end{aligned}$$

(32)

$$\begin{aligned} \frac{\partial ^{2}W}{\partial Y^{2}}= & {} [J_{22} ]^{-1}\frac{\partial ^{2}W}{\partial \eta ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial W}{\partial \eta }, \end{aligned}$$

(33)

$$\begin{aligned} \frac{\partial ^{4}W}{\partial X^{4}}= & {} \frac{\partial ^{2}{\mathfrak {R}} }{\partial \xi ^{2}}=[J_{22} ]^{-1}\frac{\partial ^{2}{\mathfrak {R}} }{\partial \xi ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial {\mathfrak {R}} }{\partial \xi }, \end{aligned}$$

(34)

$$\begin{aligned} \frac{\partial ^{4}W}{\partial Y^{4}}= & {} \frac{\partial ^{2}S}{\partial \eta ^{2}}=[J_{22} ]^{-1}\frac{\partial ^{2}S}{\partial \eta ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial S}{\partial \eta }, \end{aligned}$$

(35)

$$\begin{aligned} \frac{\partial ^{4}W}{\partial X^{2}\partial Y^{2}}= & {} \frac{\partial ^{2}S}{\partial X^{2}}=[J_{22} ]^{-1}\frac{\partial ^{2}S}{\partial \xi ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial S}{\partial \xi }. \end{aligned}$$

(36)

Equation (25) can be written using the above transformation, such as

$$\begin{aligned}&\frac{\partial ^{2}{\mathfrak {R}} }{\partial X^{2}}+2\frac{\partial ^{2}S}{\partial X^{2}}+\frac{\partial ^{2}S}{\partial Y^{2}}\nonumber \\&\quad \quad \quad -N_{x} \frac{\partial ^{2}w}{\partial x^{2}}-N_{y} \frac{\partial ^{2}w}{\partial y^{2}}-2N_{xy} \frac{\partial ^{2}w}{\partial x\partial y}=0. \end{aligned}$$

(37)

For related coordinates, Eq. (37) then becomes

$$\begin{aligned}&[J_{22} ]^{-1}\frac{\partial ^{2}{\mathfrak {R}} }{\partial \xi ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial {\mathfrak {R}} }{\partial \xi }\nonumber \\&\quad +2\left( {[J_{22} ]^{-1}\frac{\partial ^{2}{\mathfrak {R}} }{\partial \eta ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial {\mathfrak {R}} }{\partial \eta }} \right) \nonumber \\&\quad +\left( {[J_{22} ]^{-1}\frac{\partial ^{2}S}{\partial \eta ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial S}{\partial \eta }} \right) \nonumber \\&\quad -N_{x} \left( {[J_{22} ]^{-1}\frac{\partial ^{2}W}{\partial \xi ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial W}{\partial \xi }} \right) \nonumber \\&\quad -N_{y} \left( {[J_{22} ]^{-1}\frac{\partial ^{2}W}{\partial \eta ^{2}}-[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\frac{\partial W}{\partial \eta }} \right) -2N_{xy} \left( {[J_{22} ]^{-1}\frac{\partial ^{2}W}{\partial \xi \partial \eta }} \right) =0. \end{aligned}$$

(38)

The discretized equations can be written as:

$$\begin{aligned}&[J_{22} ]^{-1}\left[ {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \xi ){\mathfrak {R}}_{kj} +2\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \eta ){\mathfrak {R}}_{ik} +\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \eta )S_{ik} } \right] \nonumber \\&\quad -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\left( {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \xi ){\mathfrak {R}}_{kj} +2\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \eta ){\mathfrak {R}}_{ik} +\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \eta )S_{ik} } \right) \nonumber \\&\quad -N_{x} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \xi )W_{kj} -2[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \xi )W_{kj} } \right) \nonumber \\&\quad -N_{Y} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \eta )W_{ik} -2[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \eta )W_{ik} } \right) \nonumber \\&\quad -2N_{xy} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \xi )\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \eta )W_{ik} } \right) =0. \end{aligned}$$

(39)

Now we introduce

$$\begin{aligned} \nabla ^{2}(\bullet )=\frac{\partial ^{2}(\bullet )}{\partial x^{2}}+\frac{\partial ^{2}(\bullet )}{\partial y^{2}} \end{aligned}$$

(40)

where $\nabla ^{2}$ is the Laplace operator. Thus, the fourth-order equation takes the following simple form:

$$\begin{aligned} \nabla ^{4}(W_{\xi \eta } )=\nabla ^{2}\nabla ^{2}(W_{\xi \eta } ). \end{aligned}$$

(41)

Substituting Eq. (39) in Eq. (41) and using the fourth-order operator, we find

$$\begin{aligned}&\left( {[J_{22} ]^{-1}\left[ {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } {\mathfrak {I}} } \right] -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\left[ {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } \Xi } \right] } \right. \nonumber \\&\quad \left. {\times [J_{22} ]^{-1}\left[ {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } {\mathfrak {I}} } \right] -[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\left[ {\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } \Xi } \right] } \right) \nonumber \\&\quad -N_{x} (G_{\xi } )-N_{y} (G_{\eta } )-2N_{xy} (G_{\xi \eta } )=0. \end{aligned}$$

(42)

For brevity, the below new variables are used in Eq. (42):

$$\begin{aligned} {\mathfrak {I}} (W_{\xi \eta } )= & {} (k\Delta \xi ){{\mathfrak {R}}_{kj}^{2} } +2(k\Delta \xi )S_{kj}^{2} +(k\Delta \eta )S_{kj}^{2}, \end{aligned}$$

(43)

$$\begin{aligned} \Xi (W_{\xi \eta } )= & {} (k\Delta \xi ){\mathfrak {R}}_{kj} +2(k\Delta \xi )S_{kj} +(k\Delta \eta )S_{ik} \end{aligned}$$

(44)

in which the $G_{\xi } ,G_{\eta }$, and $G_{\xi \eta }$ take the following values:

$$\begin{aligned} G_{\xi }= & {} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \xi )W_{kj} -2[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \xi )W_{kj} } \right) ,\nonumber \\ G_{\eta }= & {} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(2)} } (k\Delta \eta )W_{ik} -2[J_{22} ]^{-1}[J_{21} ][J_{11} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \eta )W_{ik} } \right) ,\nonumber \\ G_{\xi \eta }= & {} \left( {[J_{22} ]^{-1}\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \xi )\sum \limits _{k=-M}^M {\delta _{\Delta ,\sigma }^{(1)} } (k\Delta \eta )W_{ik} } \right) . \end{aligned}$$

(45)

We have the following equation for buckling:

$$\begin{aligned} (\hbox {D}_{\xi }^{4} \otimes \hbox {I}_{\eta } +2\hbox {D}_{\xi }^{2} \otimes \hbox {D}_{\eta }^{2} +\hbox {I}_{\xi } \otimes \hbox {D}_{\eta }^{4} )\hbox {W}=\lambda \hbox {W}. \end{aligned}$$

(46)

During the numerical simulation, simply supported, clamped and free edges are used. In the following, the related formulations and their DSC form are given in detail.

(i) For simply supported edge (S)

$$\begin{aligned} W=0, -D\left( \frac{\partial ^{2}W}{\partial n^{2}}+\nu \frac{\partial ^{2}W}{\partial s^{2}}\right) =0. \end{aligned}$$

(47)

(ii) For clamped edge (C)

$$\begin{aligned} W=0, \frac{\partial W}{\partial n}=0. \end{aligned}$$

(48)

(iii) For free edge (F)

$$\begin{aligned} Q_{x} =0,\quad M_{x} =0, \quad M_{xy} =0. \end{aligned}$$

(49)

For imposing boundary conditions, the formulation given by Wei et al. [52, 53, 55] is used. Let us consider a uniform grid distribution,

$$\begin{aligned}&0=X_{0}<X_{1}<\ldots <X_{N_{x} } =1, \end{aligned}$$

(50.1)

$$\begin{aligned}&0=Y_{0}<Y_{1}<\ldots <Y_{N_{y} } =1. \end{aligned}$$

(50.2)

Consider a column vector W given as

$$\begin{aligned} \mathbf{W}=(W_{0,0},\ldots W_{0,N} ,W_{1,0},\ldots W_{N,N} )^{T}. \end{aligned}$$

(51)

For any order derivatives, these can be written as:

$$\begin{aligned} {[}{} \mathbf{D}_{x}^{(n)} ]_{i,j}= & {} \delta _{\sigma ,\Delta }^{(n)} (x_{i} -x_{j} ), \end{aligned}$$

(52.1)

$$\begin{aligned} {[}{} \mathbf{D}_{y}^{(n)} ]_{i,j}= & {} \delta _{\sigma ,\Delta }^{(n)} (y_{i} -y_{j} ). \end{aligned}$$

(52.2)

The related derivation in Eq. (46) can be given by:

$$\begin{aligned} {[}{} \mathbf{D}_{x}^{(n)} ]_{i,j}= & {} \delta _{\sigma ,\Delta }^{(n)} (x_{i} -x_{j} )=\left[ {\left( {\frac{\mathrm{d}}{\mathrm{d}x}} \right) ^{n}\delta _{\sigma ,\Delta } (x-x_{j} )} \right] _{x=x_{i} }, \end{aligned}$$

(53.1)

$$\begin{aligned} {[}{} \mathbf{D}_{y}^{(n)} ]_{i,j}= & {} \delta _{\sigma ,\Delta }^{(n)} (y_{i} -y_{j} )=\left[ {\left( {\frac{\mathrm{d}}{\mathrm{d}y}} \right) ^{n}\delta _{\sigma ,\Delta } (y-y_{j} )} \right] _{y=y_{i} }. \end{aligned}$$

(53.2)

In this stage, we consider the following relation between the inner nodes and outer nodes on the left boundary:

$$\begin{aligned} W(X_{-i} )-W(X_{0} )=a_{i} [W(X_{i} )-W(X_{0} )], \end{aligned}$$

(54.1)

or

$$\begin{aligned} W(X_{-i} )-W(X_{0} )=W(X_{0} )\left( {\sum \limits _{j=0}^J {a_{i} } X_{-i} } \right) [W(X_{i} )-W(X_{0} )]. \end{aligned}$$

(54.2)

After rearrangement, ones obtain

$$\begin{aligned} W(X_{-i} )=a_{i} W(X_{i} )+(1-a_{i} )W(X_{0} ) \end{aligned}$$

(55)

where parameter $a_{i} ,(i=1,2,\ldots ,M)$ can be determined by the boundary conditions. Thus, the first- and second-order derivatives of W on the left boundary are approximated by:

$$\begin{aligned} {W}'(X_{0} )= & {} \left( {\delta _{\sigma ,\Delta }^{(1)} (X_{i} -X_{0} )-\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )} \right) W(X_{0} )\nonumber \\&+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )W(X_{i} ), \end{aligned}$$

(56.1)

$$\begin{aligned} {W}''(X_{0} )= & {} \left( {\delta _{\sigma ,\Delta }^{(2)} (X_{i} -X_{0} )+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )} \right) W(X_{0} )\nonumber \\&+\sum \limits _{j=0}^J {(1+a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )W(X_{i} ). \end{aligned}$$

(56.2)

Similarly, the first- and second-order derivatives of f on the right boundary (at $X_{N\hbox {-}1}$) are approximated by:

$$\begin{aligned} W(X_{N-1+i} )-W(X_{N-1} )=a_{i} [W(X_{N-1-i} )-W(X_{N-1} )] \end{aligned}$$

(57.1)

or

$$\begin{aligned} W(X_{N-1+i} )-W(X_{N-1} )=W(X_{N-1-i} )\left( {\sum \limits _{j=0}^J {a_{i} } X_{-i} } \right) [W(X_{i} )-W(X_{N} )]. \end{aligned}$$

(57.2)

Consequently, we obtain the following relation:

$$\begin{aligned} W(X_{N-1+i} )=a_{i} W(X_{N-1-i} )+W(X_{N-1} )[1-a_{i} ]. \end{aligned}$$

(58)

Hence, the first- and second-order derivatives of f on the right boundary are given by:

$$\begin{aligned} {W}'(X_{N-1} )= & {} \left( {\delta _{\sigma ,\Delta }^{(1)} (X_{i} -X_{N-1} )-\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )} \right) W(X_{N-1} )\nonumber \\&+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )W(X_{i} ), \end{aligned}$$

(59)

$$\begin{aligned} {W}''(X_{N-1} )= & {} \left( {\delta _{\sigma ,\Delta }^{(2)} (X_{i} -X_{N-1} )+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )} \right) W(X_{N-1} )\nonumber \\&+\sum \limits _{j=0}^J {(1+a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )W(X_{i} ). \end{aligned}$$

(60)

For simply supported boundary conditions, the related equations are given by:

$$\begin{aligned} W(X_{0} )=0, {W}''(X_{0} )=0. \end{aligned}$$

(61)

For clamped edge, the antisymmetric extension can be written as:

$$\begin{aligned} W(X_{0} )=0, {W}'(X_{0} )=0, \end{aligned}$$

(62)

Also, these equations given by (62) are satisfied by choosing $a_{i} =1$ for $i=1,2,\ldots ,M,$. This is called symmetric extension. Thus, the DSC form of the related boundary conditions can be given as below:

(i) For simply supported edge (S)

$$\begin{aligned}&W_{ij} =0, \end{aligned}$$

(63)

$$\begin{aligned}&\quad -\left( {\delta _{\sigma ,\Delta }^{(2)} (X_{i} -X_{0} )+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )} \right) W(X_{0})\nonumber \\&\quad +\sum \limits _{j=0}^J {(1+a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (X_{i} -X_{j} )W(X_{i} )\nonumber \\&\quad +\nu \left\{ {\left( {\delta _{\sigma ,\Delta }^{(2)} (Y_{i} -Y_{0} )+\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (Y_{i} -Y_{j} )} \right) W(Y_{0} )} \right. \nonumber \\&\quad +\left. {\sum \limits _{j=0}^J {(1+a_{i} )\delta _{\sigma ,\Delta }^{(2)} } (Y_{i} -Y_{j} )W(Y_{i} )} \right\} =0. \end{aligned}$$

(64)

(ii) For clamped edge (C)

$$\begin{aligned}&W_{ij} =0, \end{aligned}$$

(65)

$$\begin{aligned}&\left( {\delta _{\sigma ,\Delta }^{(1)} (X_{i} -X_{N-1} )-\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )} \right) W(X_{N-1} )\nonumber \\&\quad +\sum \limits _{j=0}^J {(1-a_{i} )\delta _{\sigma ,\Delta }^{(1)} } (X_{i} -X_{j} )W(X_{i} ). \end{aligned}$$

(66)

Finally, Eq. (46) is rewritten as:

$$\begin{aligned} (\hbox {D}_{\xi }^{*4} \otimes \hbox {I}_{\eta } +2\lambda ^{2}\hbox {D}_{\xi }^{*2} \otimes \hbox {D}_{\eta }^{*2} +\lambda ^{4}\hbox {I}_{\xi } \otimes \hbox {D}_{\eta }^{*4} )\hbox {W}=\lambda \hbox {W} \end{aligned}$$

(67)

where ${\mathbf{I}}_{\xi }$ and $\mathbf{I}_{\eta }$ are the $(N_{r}+1)^{2};(r=\xi ,\eta )$ unit matrix and $\otimes$ denotes the tensor product.

$$\begin{aligned} {\mathbf{W}}=(W_{1,1} ,\ldots W_{1,N-2} ,W_{2,1} ,\ldots W_{N-2,N-2} )^{T}. \end{aligned}$$

(68)

4.2 Thick plate theory

Based on the first-order shear deformation theory, the governing equations for buckling of thick plates are given [2, 34]:

$$\begin{aligned}&D_{11} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}+D_{66} \frac{\partial ^{2}\varphi _{x} }{\partial y^{2}}+D_{16} \frac{\partial ^{2}\varphi _{y} }{\partial x^{2}}+D_{26} \frac{\partial ^{2}\varphi _{y} }{\partial y^{2}}+2D_{16} \frac{\partial ^{2}\varphi _{x} }{\partial x\partial y}\nonumber \\&(D_{12} +D_{66} )\frac{\partial ^{2}\varphi _{y} }{\partial x\partial y}-kA_{45} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) -kA_{55} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) =0 \end{aligned}$$

(69.1)

$$\begin{aligned}&D_{16} \frac{\partial ^{2}\varphi _{x} }{\partial x^{2}}+D_{26} \frac{\partial ^{2}\varphi _{x} }{\partial y^{2}}+D_{66} \frac{\partial ^{2}\varphi _{y} }{\partial x^{2}}+D_{22} \frac{\partial ^{2}\varphi _{y} }{\partial y^{2}}+2D_{26} \frac{\partial ^{2}\varphi _{y} }{\partial x\partial y}\nonumber \\&(D_{12} +D_{66} )\frac{\partial ^{2}\varphi _{x} }{\partial x\partial y}-kA_{44} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) -kA_{55} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) =0, \end{aligned}$$

(69.2)

$$\begin{aligned}&\frac{\partial }{\partial x}\left[ {kA_{45} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) +kA_{55} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) } \right] \nonumber \\&\quad +\frac{\partial }{\partial y}\left[ {kA_{44} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) +kA_{55} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) } \right] +q(x,y)\nonumber \\&\quad +N_{x} \frac{\partial ^{2}w}{\partial x^{2}}+2N_{xy} \frac{\partial ^{2}w}{\partial x\partial y}+N_{y} \frac{\partial ^{2}w}{\partial y^{2}}=0 \end{aligned}$$

(69.3)

where $N_{x} ,N_{xy}$, and $N_{y}$ are the in-plane applied forces. The bending moments and shear forces are given as:

$$\begin{aligned} M_{x}= & {} D_{11} \frac{\partial \varphi _{x} }{\partial x}+D_{12} \frac{\partial \varphi _{y} }{\partial y}+D_{16} \frac{\partial \varphi _{y} }{\partial x}+D_{16} \frac{\partial \varphi _{x} }{\partial y}, \end{aligned}$$

(70.1)

$$\begin{aligned} M_{y}= & {} D_{12} \frac{\partial \varphi _{x} }{\partial x}+D_{22} \frac{\partial \varphi _{y} }{\partial y}+D_{26} \frac{\partial \varphi _{y} }{\partial x}+D_{16} \frac{\partial \varphi _{x} }{\partial y}, \end{aligned}$$

(70.2)

$$\begin{aligned} M_{y}= & {} D_{16} \frac{\partial \varphi _{x} }{\partial x}+D_{26} \frac{\partial \varphi _{y} }{\partial y}+D_{66} \frac{\partial \varphi _{y} }{\partial x}+D_{16} \frac{\partial \varphi _{x} }{\partial y}, \end{aligned}$$

(71)

$$\begin{aligned} Q_{x}= & {} kA_{55} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) +kA_{45} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) , \end{aligned}$$

(72)

$$\begin{aligned} Q_{y}= & {} kA_{45} \left( {\varphi _{x} +\frac{\partial w}{\partial x}} \right) +kA_{44} \left( {\varphi _{y} +\frac{\partial w}{\partial y}} \right) . \end{aligned}$$

(73)

As similar to a thin plate, the related Eqs. (69) have also been transformed via the DSC method. For brevity, the DSC form of thick plate equations will not be given.

5 FG-CNT composite

Different structural components made of FGM or CNT-reinforced composite material have attracted enormous attention by researchers and design engineers in many disciplines due to their unique properties such as thermal, electrical, and strength advantage [72,73,74,75,76,77,78].

If two different constituent materials have been used, the volume fraction can be defined as:

$$\begin{aligned} V_{f1} (z)+V_{f2} (z)=1. \end{aligned}$$

(74)

In this study, material properties are assumed to be continuous varying in the z-direction (thickness), namely

$$\begin{aligned} V_{f2} (z)=\left( {\frac{z}{h}+\frac{1}{2}} \right) ^{p}. \end{aligned}$$

(75)

Hence, the related material properties can be easily written. For example, the modulus of elasticity is:

$$\begin{aligned} E(z)=(E_{2} -E_{1} )\left( {\frac{z}{h}+\frac{1}{2}} \right) ^{p}+E_{1}. \end{aligned}$$

(76)

Three different CNTs have been used in the study. The volume fraction of a CNT-reinforced composite is defined below:

$$\begin{aligned} \hbox {UD}: V_{CN}= & {} V_{CN}^{*}, \end{aligned}$$

(77.1)

$$\begin{aligned} \hbox {FG-O}: V_{CN}= & {} 2\left( {1-2\frac{\left| z \right| }{h}} \right) V_{CN}^{*}, \end{aligned}$$

(77.2)

$$\begin{aligned} \hbox {FG-X}: V_{CN}= & {} \left( {4\frac{\left| z \right| }{h}} \right) V_{CN}^{*} \end{aligned}$$

(77.3)

where $V_{CNT}$ is the volume fraction of CNT, and $V_{CNT}^{*}$ is defined by:

$$\begin{aligned} V_{CNT}^{*} =\frac{m_{CNT} }{m_{CNT} +\left( {\rho _{CNT} /\rho _{M} } \right) -\left( {\rho _{CNT} /\rho _{M} } \right) m_{CNT} } \end{aligned}$$

(78)

in which the $m_{CNT}$ represents the mass fraction of CNTs. Also, $\rho _{M}$ and $\rho _{CNT}$ are the densities of the matrix and CNT, respectively. Also, some material properties must be given as

$$\begin{aligned} E_{11}= & {} \eta _{1} V_{CNT} E_{11}^{CNT} +V_{m} E^{m}, \end{aligned}$$

(79)

$$\begin{aligned} \nu _{12}= & {} V_{CNT}^{*} \nu _{12}^{CNT} +(1-V_{CNT}^{*} )\nu ^{m}, \end{aligned}$$

(80)

$$\begin{aligned} E_{22}= & {} \frac{\eta _{2} }{\left( {\frac{V_{CNT} }{E_{22}^{CNT} }+\frac{V_{m} }{E^{m}}} \right) }, \end{aligned}$$

(81)

$$\begin{aligned} G_{12}= & {} \frac{\eta _{3} }{\left( {\frac{V_{CNT} }{G_{12}^{CNT} }+\frac{V_{m} }{G^{m}}} \right) }. \end{aligned}$$

(82)

6 Numerical results

In this Section, a detailed parametric study is performed in order to investigate the buckling behavior of the FG-CNT-reinforced composite skew plates via DSC mapping methodology. During the convergence and comparison, thin and thick plate results have been used. So, we also used the thin and thick plate theories for the related comparison. For FG cases, material properties are summarized in Table 1. Also, material properties of CNT-reinforced composite skew plates are used from the simulated results reported by Shen and Zhang [38]. To study the validity and accuracy of this present DSC geometric mapping approach, Tables 2–5 summarize the comparison of the buckling load for a skew plate under different material and geometry properties.

Table 1 Material properties of FGM cases

Table 2 Convergence of buckling load parameters ($\lambda =N_{cr}b^{2}/D\pi ^{2})$ of an isotropic skew plate with the clamped edge ($\hbox {a/b}=1$; $\hbox {h/b}=0.2$) under uniaxial compression

Table 3 Comparison of the buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of SSSS skew plates with CNT-reinforcement ($\hbox {a/b}=1$; $\hbox {h/a}=0.01$; FG-O) under uniaxial loading

Table 4 Comparison of buckling load ($\lambda =\cos ^{4}(\theta )\cdot N_{cr} b^{2}/D\pi ^{2})$ of SSSS skew plates with FGM ($\hbox {Al/ZrO}_{2}$; $\hbox {a/b}=1$; $\hbox {h/a}=0.001$) under uniaxial loading

Table 5 Comparison of buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of skew plates with CNT-reinforcement ($\hbox {h/a}=0.01$; $\hbox {b/a}=1$; $\alpha =60$) under uniaxial loading

Table 6 Buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of SSSS skew plates with CNT-reinforcement ($\hbox {h/a}=0.01$; $\hbox {b/a}=1$) under biaxial compression loading

Table 7 Buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of SSSS skew plates with CNT-reinforcement (UD-CNT; $\hbox {b/a}=1$; $\hbox {Vcn}=0.11$) under uniaxial loading

Table 2 shows the convergence of buckling load parameters of an isotropic skew plate with clamped edge ($\hbox {a/b}=1$; $\hbox {h/b}=0.2$) under uniaxial compression for two different DSC kernels. The obtained DSC results match well with those presented in the literature given by Kitipornchai et al. [11] and Zhang et al. [33]. Four different skew angles are considered. This comparison demonstrates that the present DSC solution is completely good and reliable. It is also observed that increasing the number of grid points N improves the accuracy of the results and leads to convergent solutions at $N_{x}=N_{y}=11$. Hence, $\hbox {N}=11$ is used in the following numerical calculations in each direction. Buckling loads of SSSS skew plates with CNT-reinforcement ($\hbox {a/b}=1$; $\hbox {h/a}=0.01$; FG-O) under uniaxial loading are compared with the Ritz results given by Zhang et al. [33], which are based on the first-order shear deformation plate theory and element-free approach in Table 3. According to the buckling loads listed in this Table, it can be seen that the results are in excellent agreement with the element-free results.

Table 8 Buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of SSSS skew plates with CNT-reinforcement (FG-X-CNT; $\hbox {h/a}=0.01$; $\hbox {Vcn}=0.11$) under uniaxial loading

Table 9 Buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of skew plates with CNT-reinforcement (UD-CNT; $\hbox {h/a}=0.01$; $\hbox {b/a}=1;\hbox {Vcn}=0.11$) under uniaxial loading

Table 4 shows the comparisons of the buckling loads of SSSS skew plates with FGM (Al/ZrO2; $\hbox {a/b}=1$; $\hbox {h/a}=0.001$) under uniaxial loading with the solutions of Shahrestani et al. [35] using isoparametric spline finite strip method for different skew angles and FGM indexes. The Table also shows that the present DSC results agree well with the buckling loads listed in [35]. Finally, another comparison is made for CNT composite skew plates, and calculated results are listed in Table 5 with the results by Zhang et al. [33]. From the results, one can conclude that the DSC method leads to accurate results even using a few grid points. Furthermore, these convergence and comparison results listed in Tables 2–5 show that as the number of grid points increased, DSC results are rapidly converged to the correct values, which show the fast rate of convergence of the method. Thus, the mesh size of $11\times 11$ is used in the next numerical examples, if otherwise it is not mentioned. In addition to this, the slight difference between our DSC results and the results given by open literature approaches may result from different plate theories or different solution procedures. It is also shown that the convergence of the DSC-Shannon’s delta kernel is much better than that of the DSC-Lagrange-delta kernel.

Table 6 shows the buckling loads of SSSS skew plates with CNT-reinforcement ($\hbox {h/a}=0.01$; $\hbox {b/a}=1$; $\uptheta =60$) under biaxial loading for various skew angles and different values of $\hbox {V}_{\mathrm{CNT}}$ distribution patterns. Results show that as the skew angles increase, buckling loads are increased rapidly. Also, it can be seen that the natural buckling loads increase with the increase in the volume fraction value of CNT. Buckling loads of SSSS skew plates with CNT-reinforcement (UD-CNT; $\hbox {b/a}=1$; $\hbox {V}_{\mathrm{CNT}}=0.11$) under uniaxial loading are presented in Table 7 with different skew angles and thickness-to-side ratio. Results show that as the skew angle increases, buckling of a CNT skew plate decreases. Furthermore, an increase in the plate thickness causes a serious decrease in the buckling loads.

In Table 8, buckling loads of skew plates with CNT-reinforcement (FG-X-CNT; $\hbox {h/a}=0.01$; $\hbox {V}_{\mathrm{CNT}}=0.11$) under uniaxial loading are presented for different skew angles and aspect ratios.

Table 10 Buckling load ($\lambda =N_{cr} b^{2}/E_{m} h^{3})$ of SSSS skew plates with CNT-reinforcement ($\hbox {h/a}=0.01$; $\hbox {b/a}=1$; $\hbox {Vcn}=0.11$) under biaxial compression and tension loading

Table 11 Buckling load ($\lambda =\cos ^{4}(\theta )\cdot N_{cr} b^{2}/D\pi ^{2})$ of CCCC skew plates with FGM ($\hbox {Al/ZrO}_{\mathrm{2}}$; $\hbox {a/b}=1$; $\hbox {h/a}=0.001$) under uniaxial loading

Table 12 Buckling load ($\lambda =N_{cr} b^{2}/D\pi ^{2})$ of SSSS skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {a/b}=1$; $\hbox {h/a}=0.01$) under uniaxial loading

Table 13 Buckling load ($\lambda =N_{cr} b^{2}/D\pi ^{2})$ of SSSS skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {a/b}=2$) under uniaxial loading

Table 14 Buckling load ($\lambda =N_{y} b^{2}/D\pi ^{2})$ of SSSS skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {a/b}=1$; $\hbox {h/a}=0.1$) under biaxial loading

The value of the buckling parameters essentially depends on the CNT types, skew angles, and the boundary conditions.

Buckling loads of skew plates with CNT-reinforcement (UD-CNT; $\hbox {h/a}=0.01$; $\hbox {b/a}=1;\hbox {Vcn}=0.11$) under uniaxial loading for different skew angles and four different boundary conditions are also given in Table 9. Also, buckling loads of SSSS skew plates with CNT-reinforcement ($\hbox {h/a}=0.01$; $\hbox {b/a}=1$; $\hbox {V}_{\mathrm{CNT}}=0.11$) under biaxial loading for two different CNT types are listed in Table 10. Obviously, buckling load parameters decrease with the increase in the skew angles for all considered cases. As clearly shown in these two Tables, an increase in the aspect ratio yields to increasing buckling. It can also be seen that as the skew angles increase, the buckling load decreases.

It is also shown that the aspect ratio plays a major effect in the buckling values of the CNT skew plate. Among the different FG patterns of CNTs across the thickness, FG-X panels feature the maximum values of buckling loads, whereas FG-O panels feature the minimum buckling loads. As also expected, skew plates that are completely clamped show the highest buckling loads due to their higher bending stiffness nearby the clamped edge compared to simply supported and free edges. It is worth noticing that an increased enrichment of CNTs within the matrix from 0.11 to 0.27 yields an increase in the buckling loads, for all boundary conditions.

Table 15 Buckling load ($\lambda =N_{y} b^{2}/D\pi ^{2})$ of SSSS skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {a/b}=2$; $\hbox {h/a}=0.1$) under biaxial loading

Table 16 Buckling load ($\lambda =N_{cr} b^{2}/D\pi ^{2})$ of CCCC skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {h/a}=0.1$; $\hbox {a/b}=1$)

Table 17 Buckling load ($\lambda =N_{cr} b^{2}/D\pi ^{2})$ of CCCC skew plates with FGM ($\hbox {Al/Al}_{2}\hbox {O}_{2}$; $\hbox {h/a}=0.1$; $\hbox {a/b}=1$)

For FGM composites, all results are tabulated in Tables 11–17 for different material and geometric parameters. Buckling loads of CCCC and SSSS skew plates with FGM (Al/ZrO2; $\hbox {a/b}=1$; $\hbox {h/a}=0.001$) under uniaxial loading are obtained and summarized in Tables 11 and 12, respectively. The effect of the FGM index parameters on the non-dimensional buckling loads of FGM skew plates is exhibited in these Tables. It can be seen that as the FGM index parameters increase, the buckling loads decrease rapidly. Further, it can be observed that the buckling load increases monotonically as the skew angle increases.

In order to study the effects of thickness on the buckling loads of SSSS skew plates with FGM (Al/Al2O2; $\hbox {a/b}=2$), a composite material under uniaxial loading with different skew angles and grid numbers is obtained and presented in Table 13. Also, three different FGM index parameters have been studied. It can be concluded that the increase in the FGM index parameters decreases the buckling load parameter for all cases of skew angles under study.

It is also found that the buckling load parameter decreases as the thickness of the plate increases. Buckling loads of SSSS skew plates with FGM (Al/Al2O2; $\hbox {h/a}=0.1$) under biaxial loading for two different aspect ratios are listed in Tables 14 and 15. According to these Tables, it is evident that the buckling loads decrease as the plate aspect ratio increases for all skew angles. The influence of the load cases on the buckling characteristics of FGM skew plates with fully clamped boundary condition under uniaxial and biaxial loads is presented in Tables 16 and 17, respectively. As can be seen, under the same material, geometric and boundary conditions and the buckling loads of uniaxial loading are always higher than of biaxial loading.

7 Conclusions

The main purpose of the present study was to investigate the buckling behavior of FG-CNT-reinforced composite thick skew plates under biaxial and uniaxial loadings. Buckling of shear deformable FG-CNT-reinforced composite thick skew plates was examined by employing geometric transformation DSC method due to their excellent computational efficiency for buckling and vibration problems of beams, plates, and shells. The convergence and accuracy of the present DSC field transformation modeling were validated by comparing its results with those available in the literature. Different material and geometric parameter effects were examined. All parametric studies were performed in detail. The results from the study showed that the method of DSC can provide very good results for buckling of CNT or FGM composite plates of skew shape. Boundary conditions and CNT distributions can significantly influence the buckling load of a CNT skew plate. The CCCC boundary condition and FG-X distribution pattern have given the highest buckling loads. The larger value of skew angles leads to the smallest buckling load of CNT or FGM composite skew plates. Uniaxial buckling case gives larger buckling load than the biaxial loading. Also, results showed that in most cases an increase in the aspect ratio decreases the buckling load, indicating a reduction in the flexural stiffness of FGM/CNT plates. It was also concluded that the buckling load value decreases as the thickness of the plate increases.