A Generalization of Ritz-Variational Method for Solving a Class of Fractional Optimization Problems

Abstract

This paper presents an approximate method for solving a class of fractional optimization problems with multiple dependent variables with multi-order fractional derivatives and a group of boundary conditions. The fractional derivatives are in the Caputo sense. In the presented method, first, the given optimization problem is transformed into an equivalent variational equality; then, by applying a special form of polynomial basis functions and approximations, the variational equality is reduced to a simple linear system of algebraic equations. It is demonstrated that the derived linear system has a unique solution. We get an approximate solution for the initial optimization problem by solving the final linear system of equations. The choice of polynomial basis functions provides a method with such flexibility that all initial and boundary conditions of the problem can be easily imposed. We extensively discuss the convergence of the method and, finally, present illustrative test examples to demonstrate the validity and applicability of the new technique.

1 Introduction

In this article, an efficient approximate method for solving a class of fractional optimization problems is developed. The discussed problem is formulated by a bilinear form, which is a real valued functional of multiple dependent variables with multi-order fractional derivatives. Fractional derivatives are defined in the Caputo sense.

An important type of fractional optimization problems are fractional variational problems (FVPs). General optimality conditions have been developed for FVPs in previous works. For instance, Euler–Lagrange equations for FVPs with Riemann–Liouville and Caputo derivatives are derived in  [1] and  [2], respectively. Optimality conditions for FVPs with functionals containing both fractional derivatives and integrals are presented in  [3]. Such formulas are also developed for FVPs with other definitions of fractional derivatives in  [4, 5]. The general form of the Euler–Lagrange equations for FVPs with Riemann–Liouville, Caputo, Riesz–Caputo and Riesz–Riemann–Liouville derivatives is derived in  [6]. A number of other generalizations of Euler–Lagrange equations for problems with free boundary conditions can be found in [7–10].

Optimal solutions of FVPs should satisfy Euler–Lagrange equations [1–3]. Hence, solving Euler–Lagrange equations leads to optimal solutions to FVPs. Except for some special cases  [11], it is hard to find exact solutions for Euler–Lagrange equations. There exist examples of numerical methods, developed and applied by researchers of the field, for solving various classes of FVPs. Some of them can be found in [12–17].

It is known that for optimization problems with bilinear form operators, there exists an equivalent variational equality  [18]. Building on this existence, we develop a method for solving multidimensional optimization problems with multi-order fractional derivatives and a group of boundary conditions. First, equivalent variational equality of the given multi dimensional optimization problem is derived; then, by expanding unknown functions in terms of special forms of polynomial basis functions and substituting them in the variational equality, a linear system of algebraic equations is achieved. It is proved that the derived system of equations has a unique solution. By approximating fractional derivative operators with Legendre orthonormal polynomial basis functions, the linear system turns into an approximate linear system. By solving the subsequent approximate system of equations, we determine unknown coefficients of the expansions for each variable. Thus, we get polynomial functions as approximate solutions for the problem. The main advantage of our method over the schemes presented in  [12, 13, 15, 16] is that we easily derive a linear system of equations that can be solved instead of the main optimization problem. The existence and uniqueness of the solution for the derived linear system is guaranteed. We also get smooth approximate solutions, in terms of polynomials, that satisfy all initial and boundary conditions of the problem. Examples demonstrate that by applying only few number of approximations we can achieve satisfactory results.

2 Problem Formulation

Operator $\text{ B }$ is defined as follows

$$\begin{aligned}&\text{ B }:\prod _{i=1}^{(m+1)n} L_2[t_0,t_1] \times \prod _{i=1}^{(m+1)n} L_2[t_0,t_1] \rightarrow \mathbb {R},\\&(U,V) \mapsto \text {B}(U,V), \quad U,V \in L_2[t_0,t_1], \end{aligned}$$

where the product space $\prod _{i=1}^{(m+1)n} L_2[t_0,t_1]$ is equipped with the following product norm

$$\begin{aligned} \parallel (f_1,\dots ,f_{(m+1)n})\parallel _{\pi }= & {} \left( \sum _{j=1}^{(m+1)n} \parallel f_j \parallel _{L_2[t_0,t_1]}^2\right) ^{\frac{1}{2}},\nonumber \\ \parallel f_j \parallel _{L_2[t_0,t_1]}= & {} \left( \int _{t_0}^{t_1} f_j^2 {\hbox {d}}t\right) ^{\frac{1}{2}}. \end{aligned}$$

(1)

Assumption 2.1

Operator $\text{ B }$ is considered to have the following properties

• (i) Bilinearity. For all $U, V, W\in \prod _{i=1}^{(m+1)n} L_2[t_0,t_1]$ and $a, b \in \mathbb {R}$

  $$\begin{aligned} \text {B}(aU+bV,W)= & {} a\text {B}(U,W)+b\text {B}(V,W),\\ \text {B}(W,aU+bV)= & {} a\text {B}(W,U)+b\text {B}(W,V). \end{aligned}$$

• (ii) Boundedness. There exists a constant $d>0$ such that

  $$\begin{aligned} \mid \text {B}(U,V) \mid \le d \parallel U \parallel _{\pi } \parallel V \parallel _{\pi }, \quad U,V \in \prod _{i=1}^{(m+1)n} L_2[t_0,t_1]. \end{aligned}$$

• (iii) Symmetry.

  $$\begin{aligned} \text {B}(U,V)=\text {B}(V,U),\quad U,V \in \prod _{i=1}^{(m+1)n} L_2[t_0,t_1]. \end{aligned}$$

• (iv) Strong positivity. There exists $c>0$ such that

  $$\begin{aligned} c\parallel U \parallel _{\pi }^2 \le \text {B}(U,U),\quad U \in \prod _{i=1}^{(m+1)n} L_2[t_0,t_1]. \end{aligned}$$

  Functional J is defined as follows:

  $$\begin{aligned} \quad J[u_1,\dots ,u_n]:= \frac{1}{2}\text {B}(U,U)-\text {L}(U)+C, \end{aligned}$$

  (2)

where $\text{ L }: \prod _{i=1}^{(m+1)n} L_2[t_0,t_1] \rightarrow \mathbb {R}$ is a bounded linear operator, C is a real constant,

$$\begin{aligned} U= & {} (u_1,\dots ,u_n,{^C _{t_0}D^{\alpha _1}_{t}} u_1,\dots ,{^C _{t_0}D^{\alpha _1}_{t}} u_n,\dots ,{^C _{t_0}D^{\alpha _m}_{t}} u_1,\dots ,{^C _{t_0}D^{\alpha _m}_{t}} u_n),\\ t\in & {} [t_0,t_1],\quad \alpha _1<\dots <\alpha _m, \end{aligned}$$

and the fractional derivative is defined in the Caputo sense

$$\begin{aligned} ^C _{t_0}D^{\alpha }_{t}u(t):=\frac{1}{\varGamma (n-\alpha )} \int _{t_0}^{t}(t-\tau )^{n-\alpha -1} u^{(n)}(\tau ), \quad {n-1<\alpha <n}. \end{aligned}$$

In cases for which $\alpha =n$, the Caputo derivative is defined as $^C _{t_0}D^{\alpha }_{t}u(t):=u^{(n)}(t)$. We consider that there exists an element, say $(u_1^*,\dots ,u_n^*)\in \prod _{i=1}^{n} E_i[t_0,t_1]$, that minimizes the functional J on the space $\prod _{i=1}^{n} E_i[t_0,t_1]$,

$$\begin{aligned} E_i[t_0,t_1]:=\{u\in C^{\lceil \alpha _m \rceil }[t_0,t_1] : u^{(k)}(t_0)=u_{i0}^k,u^{(k)}(t_1)=u_{i1}^k, 0 \le k \le \lceil \alpha _m \rceil -1\}. \end{aligned}$$

For this article, our goal was to find approximate minimizing solution for the functional J on $\prod _{i=1}^{n} E_i[t_0,t_1]$.

3 Variational Equality

Without any loss of generality, we let $t_0=0$, $t_1=1$ and $t\in [0,1]$ in problem (2).

Theorem 3.1

The minimization problem of Sect. 2 is equivalent to the following variational problem

$$\begin{aligned} \text {B}(U,V)=\text {L}(V), \end{aligned}$$

(3)

for $(u_1,\dots ,u_n) \in \prod _{i=1}^{(m+1)n} E_i[0,1]$ fixed and $(v_1,\dots ,v_n) \in \prod _{i=1}^{(m+1)n} E^*[0,1]$, where

$$\begin{aligned} U= & {} (u_1,\dots ,u_n,{^C _{0}D^{\alpha _1}_{t}} u_1,\dots ,{^C _{0}D^{\alpha _1}_{t}} u_n,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_1,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_n),\\ t\in & {} [0,1],\\ V= & {} (v_1,\dots ,v_n,{^C _{0}D^{\alpha _1}_{t}} v_1,\dots ,{^C _{0}D^{\alpha _1}_{t}} v_n,\dots ,{^C _{0}D^{\alpha _m}_{t}} v_1,\dots ,{^C _{0}D^{\alpha _m}_{t}} v_n),\\ t\in & {} [0,1],\\ E^*[0,1]= & {} \{u\in C^{\lceil \alpha _m \rceil }[0,1] : u^{(k)}(0)=u^{(k)}(1)=0, 0 \le k \le \lceil \alpha _m \rceil -1\}. \end{aligned}$$

Proof

Let

$$\begin{aligned} \varGamma (t)=J[(u_1,\dots ,u_n)+t(v_1,\dots ,v_n)], \quad t\in \mathbb {R}; \end{aligned}$$

then, we have

$$\begin{aligned} \varGamma (t)= & {} \frac{1}{2}\text {B}(U+tV,U+tV)-\text {L}(U+tV)+C\\= & {} \frac{1}{2}t^2 \text {B}(V,V)+t[\text {B}(U,V)-\text {L}(V)]+\frac{1}{2}\text {B}(U,U)-\text {L}(U)+C. \end{aligned}$$

Since $\text {B}(V,V)$ is positive for all $V\ne 0$, the necessary and sufficient condition of minimality, $\varGamma '(0)=0$, is equivalent with the following condition:

$$\begin{aligned} \text {B}(U,V)=\text{ L }(V), \quad \forall (v_1,\dots ,v_n) \in \prod _{i=1}^{(m+1)n} E^*[0,1], \end{aligned}$$

and the proof is completed. $\square$

Corollary 3.1 shows that variational equality (3) determines a unique solution for minimization problem (2).

Corollary 3.1

Let $(u_1,\dots ,u_n)$ and $(w_1,\dots , w_n)$ be two minimizing solutions for the functional J; then, we have

$$\begin{aligned} \parallel u_j-w_j \parallel _{L_2[0,1]}=0, \quad \parallel {^C _{0}D^{\alpha _i}_{t}} u_j- {^C _{0}D^{\alpha _i}_{t}} w_j \parallel _{L_2[0,1]}=0,\quad 1\le i \le m, \quad 1\le j \le n. \end{aligned}$$

Proof

According to Theorem 3.1, we have

$$\begin{aligned} \text {B}(U,V)=\text{ L }(V),\quad \text {B}(W,V)=\text{ L }(V), \quad \forall (v_1,\dots ,v_n) \in \prod _{i=1}^{n} E_i^*[0,1], \end{aligned}$$

where

$$\begin{aligned} U= & {} (u_1,\dots ,u_n,{^C _{0}D^{\alpha _1}_{t}} u_1,\dots ,{^C _{0}D^{\alpha _1}_{t}} u_n,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_1,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_n),\quad t\in [0,1],\\ W= & {} (w_1,\dots ,w_n,{^C _{0}D^{\alpha _1}_{t}} w_1,\dots ,{^C _{0}D^{\alpha _1}_{t}} w_n,\dots ,{^C _{0}D^{\alpha _m}_{t}} w_1,\dots ,{^C _{0}D^{\alpha _m}_{t}} w_n),\quad t\in [0,1]. \end{aligned}$$

Let $(v_1,\dots ,v_n)=(u_1,\dots ,u_n)-(w_1,\dots ,w_n)$; then, by Assumption 2.1 we get

$$\begin{aligned} c \parallel U- W \parallel _{\pi }^2 \le \text{ B }(U-W,U-W)=0, \end{aligned}$$

and the proof is completed by considering (1). $\square$

4 Approximate Solution of the Variational Equality

In this section, we present an approximate method for solving variational equality (3).

Consider expansions $u_{j,k}(t)$, $1\le j \le n$, in the following form

$$\begin{aligned} u _{j,k}(t)= & {} {C_{j,k}}^T.\varPsi _k(t)+w_j(t), \quad \varPsi _k(t)=\left( \begin{array}{c} \psi _0(t) \\ \psi _1(t) \\ \vdots \\ \psi _k(t) \\ \end{array} \right) , \quad C_{j,k}=\left( \begin{array}{c} c_{j,0} \\ c_{j,1} \\ \vdots \\ c_{j,k} \\ \end{array} \right) , \end{aligned}$$

(4)

$$\begin{aligned} \psi _j(t)= & {} \phi _j(t)t^{\lceil \alpha _m \rceil }(1-t)^{\lceil \alpha _m \rceil },\quad 0\le j \le k. \end{aligned}$$

(5)

Here, $\phi _j$s, $j\in \{0\}\bigcup \mathbb {N}$ are shifted Legendre orthonormal polynomials

$$\begin{aligned} \phi _j(t)=\sqrt{2j+1}\sum _{k=0}^{j}(-1)^{j+k}\frac{(j+k)!t^k}{(j-k)!(k!)^2}, \quad j=0,1,2,... \quad t\in [0,1], \end{aligned}$$

(6)

and each $w_j$ is the Hermit interpolating polynomial that satisfies all initial and boundary conditions of $u_j$. Now let

$$\begin{aligned} U_k:= & {} (u_{1,k},\dots ,u_{n,k},{^C _{0}D^{\alpha _1}_{t}} u_{1,k},\dots ,{^C _{0}D^{\alpha _1}_{t}} u_{n,k},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{1,k},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{n,k}),\\ t\in & {} [0,1],\\ \mu _{i,j}:= & {} (0,\dots ,0,\overbrace{\psi _{j}}^{i th },0,\dots ,0,\overbrace{{^C _{0}D^{\alpha _1}_{t}} \psi _{j}}^{(i+n) th },0,\dots ,0,\overbrace{{^C _{0}D^{\alpha _m}_{t}} \psi _{j}}^{(i+mn)th},0,\dots ,0),\\ t\in & {} [0,1]; \end{aligned}$$

then,

$$\begin{aligned} \text{ B }(U_k,\mu _{i,j})=\text{ L }(\mu _{i,j}), \quad 0 \le j \le k, \quad 1 \le i \le n, \end{aligned}$$

(7)

forms a linear system of $n(k+1)$ equations and unknowns. By solving linear system (7), we achieve coefficients of expansions (4). Thus, we get an approximate solution for minimization problem (2) in terms of polynomials. Note that expansion (4) and consequent approximate solutions satisfy all the boundary conditions of the problem. In Lemma 4.2, we show that linear system (7) has a unique solution. First, we state a lemma, which plays an important role in our discussion in this section and the subsequent section.

Lemma 4.1

Let

$$\begin{aligned} E[0,1]= & {} \{f(t)\in C^n [0,1] : f^{(j)}(0)=f_{0}^j, f^{(j)}(1)=f_{1}^j, j=0,1,\dots ,n-1\},\\ \parallel f \parallel _n= & {} \parallel f \parallel _{\infty }+\parallel f' \parallel _{\infty }+\dots +\parallel f^{(n)} \parallel _{\infty }, \end{aligned}$$

where $f_{0}^j,f_{1}^j$ are given constant values. There exists a sequence of polynomial functions $\{s_l(t)\}_{l\in \mathbb {N}}$ in E[0, 1] such that $s_l \rightarrow f$ with respect to $\parallel . \parallel _n$.

Proof

[14]. $\square$

Lemma 4.2

For any $k\in \mathbb {N}$, linear system (7) has unique solution.

Proof

Let

$$\begin{aligned} \eta _k :=inf \{J[u_1,\dots ,u_n]: (u_1,\dots ,u_n)\in \prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]\}. \end{aligned}$$

$\square$

Here $P_k[0,1]$ denotes the space of polynomials with a degree of at most k. According to Assumption 2.1, we have

$$\begin{aligned} J[u_1,\dots ,u_n]= & {} \frac{1}{2}\text{ B }(U,U)-\text{ L }(U)+C\ge \frac{1}{2}c\parallel U \parallel _{\pi }^2-\parallel \text{ L } \parallel \parallel U \parallel _{\pi }+C,\\ U= & {} (u_{1},\dots ,u_{n},{^C _{0}D^{\alpha _1}_{t}} u_{1},\dots ,{^C _{0}D^{\alpha _1}_{t}} u_{n},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{1},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{n}),\\ t\in & {} [0,1]. \end{aligned}$$

If $\parallel U \parallel _{\pi } \rightarrow \infty$, then $J[u_1,\dots ,u_n] \rightarrow \infty$. Hence, $\eta _k >-\infty$. By the definition of $\eta _k$, there exists a sequence $\{(\gamma _{1,j}^k, \dots , \gamma _{n,j}^k)\}_{j\in \mathbb {N}} \subseteq \prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]$ such that $\lim _{j \rightarrow \infty } J[\gamma _{1,j}^k, \dots , \gamma _{n,j}^k]=\eta _k$. In addition, it can be observed that

$$\begin{aligned} 2\text{ B }(\varGamma _i^k,\varGamma _i^k)+2\text{ B }(\varGamma _j^k,\varGamma _j^k) =\text{ B }(\varGamma _i^k-\varGamma _j^k,\varGamma _i^k-\varGamma _j^k) +\text{ B }(\varGamma _i^k+\varGamma _j^k,\varGamma _i^k+\varGamma _j^k), \end{aligned}$$

where

$$\begin{aligned} \varGamma _j^k:= & {} (\gamma _{1,j}^k,\dots ,\gamma _{n,j}^k,{^C _{0}D^{\alpha _1}_{t}} \gamma _{1,j}^k,\dots ,{^C _{0}D^{\alpha _1}_{t}} \gamma _{n,j}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} \gamma _{1,j}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} \gamma _{n,j}^k),\\ t\in & {} [0,1]. \end{aligned}$$

It is obvious that $(\frac{\gamma _{1,i}^k+\gamma _{1,j}^k}{2},\dots ,\frac{\gamma _{n,i}^k +\gamma _{n,j}^k}{2})$ $\in \prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]$ and $J[\frac{\gamma _{1,i}^k+\gamma _{1,j}^k}{2}$, $\dots , \frac{\gamma _{n,i}^k+\gamma _{n,j}^k}{2}]\ge \eta _k$. Hence

$$\begin{aligned}&J\left[ \gamma _{1,i}^k, \dots , \gamma _{n,i}^k]+J[\gamma _{1,j}^k, \dots , \gamma _{n,j}^k\right] \nonumber \\&\quad =\frac{1}{4}\text{ B }(\varGamma _i^k-\varGamma _j^k,\varGamma _i^k-\varGamma _j^k) +2J[\frac{\gamma _{1,i}^k+\gamma _{1,j}^k}{2}, \dots , \frac{\gamma _{n,i}^k+\gamma _{n,j}^k}{2}]\nonumber \\&\quad \ge \frac{1}{4}c\parallel \varGamma _i^k-\varGamma _j^k \parallel _{\pi } +2 \eta _k. \end{aligned}$$

(8)

Inequality (8) shows that the sequence $\{(\gamma _{1,j}^k, \dots , \gamma _{n,j}^k)\}_{j\in \mathbb {N}}$ is a Cauchy sequence with respect to the product norm $\Vert . \Vert _{\pi }$. On the other hand, according to Lemma 4.1, $P_k[0,1] \bigcap E_i[0,1]$ is a closed subset of the Banach space $(C^{\lceil \alpha _m \rceil }[0,1],\Vert . \Vert _{\lceil \alpha _m \rceil })$. Thus, it is a complete metric space with respect to $\Vert . \Vert _{\lceil \alpha _m \rceil }$. Because $P_k[0,1] \bigcap E_i[0,1]$ is a finite dimensional Banach space, it is complete with respect to any norm. Hence, there exists an element, say $(\gamma _1^k,\dots ,\gamma _n^k)\in \prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]$, such that $(\gamma _{1,j}^k,\dots ,\gamma _{n,j}^k)\rightarrow (\gamma _1^k,\dots ,\gamma _n^k)$. According to Assumption 2.1, bilinear operator $\text{ B }$ and linear operator $\text{ L }$ are bounded. So it can be easily observed that $\eta _k=\lim _{j \rightarrow \infty } J[\gamma _{1,j}^k,\dots ,\gamma _{n,j}^k]=J[\gamma _1^k,\dots ,\gamma _n^k].$ So far we have shown that there exists an element $(\gamma _1^k,\dots ,\gamma _n^k)\in \prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]$ that minimizes the functional J on $\prod _{i=1}^n P_k[0,1] \bigcap E_i[0,1]$. Therefore, according to Theorem 3.1, $\varGamma ^k$ is a solution for the system (7), where

$$\begin{aligned} \varGamma ^k:= & {} (\gamma _{1}^k,\dots ,\gamma _{n}^k,{^C _{0}D^{\alpha _1}_{t}} \gamma _{1}^k,\dots ,{^C _{0}D^{\alpha _1}_{t}} \gamma _{n}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} \gamma _{1}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} \gamma _{n}^k),\\ t\in & {} [0,1]. \end{aligned}$$

Now we are going to show that the solution is unique. Suppose $(u_1^k,\dots ,u_n^k)$ and $(w_1^k,\dots ,w_n^k)$ are two solutions of system (7)

$$\begin{aligned} \text{ B }(U_k,\mu _{i,j})= & {} \text{ L }(\mu _{i,j}), \quad \text{ B }(W_k,\mu _{i,j})=\text{ L }(\mu _{i,j}), \quad 0\le j \le k,\quad 1\le i\le n,\\ U_k= & {} (u_{1}^k,\dots ,u_{n}^k,{^C _{0}D^{\alpha _1}_{t}} u_{1}^k,\dots ,{^C _{0}D^{\alpha _1}_{t}} u_{n}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{1}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{n}^k),\\ t\in & {} [0,1],\\ W_k= & {} (w_{1}^k,\dots ,w_{n}^k,{^C _{0}D^{\alpha _1}_{t}} w_{1}^k,\dots ,{^C _{0}D^{\alpha _1}_{t}} w_{n}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} w_{1}^k,\dots ,{^C _{0}D^{\alpha _m}_{t}} w_{n}^k),\\ t\in & {} [0,1]; \end{aligned}$$

then, we have

$$\begin{aligned} \text{ B }(U_k,V)=\text{ L }(V), \quad \text{ B }(W_k,V)=\text{ L }(V), \end{aligned}$$

where

$$\begin{aligned} V= & {} (v_{1},\dots ,v_{n},{^C _{0}D^{\alpha _1}_{t}} v_{1},\dots ,{^C _{0}D^{\alpha _1}_{t}} v_{n}, \dots ,{^C _{0}D^{\alpha _m}_{t}} v_{1},\dots ,{^C _{0}D^{\alpha _m}_{t}} v_{n}),\quad t\in [0,1],\\&(v_1,\dots ,v_n) \in \prod _{i=1}^n P_k[0,1] \bigcap E^*[0,1]. \end{aligned}$$

Now let $V=U_k-W_k$; then, $c \parallel U_k-W_k \parallel _{\pi } \le \text{ B }(U_k-W_k,U_k-W_k)=0.$

Referring to the definition of $\parallel . \parallel _{\pi }$ in (1), we get $\parallel u_j^k-w_j^k \parallel _{L_2[0,1]}=0$, and the uniqueness is proved given that norms are equivalent in finite dimensional Banach spaces.$\square$

Now we rewrite linear system (7) explicitly in terms of unknown coefficients $c_{i,j}$, $1 \le i \le n$, $0\le j \le k$. First, $U_k$ is decomposed as follows:

$$\begin{aligned} U_k=\sum _{r=1}^n (0,\dots ,0,u_{r,k},0,\dots ,0,{^C_{0}D^{\alpha _1}_{t} u_{r,k}},0,\dots ,0,{^C_{0}D^{\alpha _m}_{t}u_{r,k}},0,\dots ,0). \end{aligned}$$

(9)

Considering expansions (4), we have

$$\begin{aligned}&(0,\dots ,0,u_{r,k},0,\dots ,0,{^C_{0}D^{\alpha _1}_{t}} u_{r,k},0,\dots ,0,{^C_{0}D^{\alpha _m}_{t}}u_{r,k},0,\dots ,0)\nonumber \\&\quad =(0,\dots ,0,{C_{r,k}}^T.\varPsi _k(t)+w_r(t),0,\dots ,0,{C_{r,k}}^T.^C_{0}D^{\alpha _1}_{t}\varPsi _k(t)\nonumber \\&\qquad +\,^C_{0}D^{\alpha _1}_{t}w_r(t),0,\dots \nonumber \\&\quad 0,{C_{r,k}}^T.^C_{0}D^{\alpha _m}_{t}\varPsi _k(t)+{^C_{0}D^{\alpha _m}_{t}}w_r(t),0,\dots ,0)\nonumber \\&\quad =\sum _{l=0}^kc_{r,l}\underbrace{(0,\dots ,0,\overbrace{\psi _l(t)}^{rth},0,\dots ,0,\overbrace{^C_{0}D^{\alpha _1}_{t}\psi _l(t)}^{(n+r)th}, 0,\dots ,0,\overbrace{^C_{0}D^{\alpha _m}_{t}\psi _l(t)}^{(mn+r)th},0,\dots ,0)}_{\lambda _{r,l}}\nonumber \\&\qquad +\underbrace{(0,\dots ,0,w_r(t),0,\dots ,0,\overbrace{^C_{0}D^{\alpha _1}_{t}w_r(t)}^{(n+r)th},0, \dots ,0,\overbrace{^C_{0}D^{\alpha _m}_{t}w_r(t)}^{(mn+r)th},0,\dots ,0)}_{\omega _r}.\nonumber \\ \end{aligned}$$

(10)

By applying (9) and (10), system (7) can be rewritten as follows:

$$\begin{aligned} \sum _{r=1}^{n} \sum _{l=0}^{k} c_{r,l}\text{ B }(\lambda _{r,l},\mu _{i,j})+\sum _{r=1}^{n} \text{ B }(\omega _r,\mu _{i,j})=\text{ L }(\mu _{i,j}), \quad 0\le j \le k, \quad 1\le i \le n. \end{aligned}$$

(11)

We need to solve linear system (11) to find approximate solution for problem (3). In order to simplify the calculation of each $\text{ B }(\lambda _{r,l},\mu _{i,j})$, in Lemma 4.3 we approximate elements $^C_{0}D^{\alpha _r}_{t}\psi _l(t)$, $1\le r \le m$, $0\le l \le k$, by the Legendre orthonormal polynomials $\phi _j$s, $j\in \{0\}\bigcup \mathbb {N}$, utilizing the following theorem.

Theorem 4.1

Let $f\in L^2[0,1]$, $r_m=\sum _{j=0}^m c_j \phi _j$, where $c_{j}=\int _0^1 f(t)\phi _j(t){\hbox {d}}t$; then,

$$\begin{aligned} \lim _{m \rightarrow \infty } \parallel f-r_m\parallel _{L_2[0,1]} =0. \end{aligned}$$

Proof

[19]. $\square$

Lemma 4.3

Consider

$$\begin{aligned} D_{r,\gamma }^{\alpha }= & {} \left( \begin{array}{c} d_0^{\alpha } \\ d_1^{\alpha } \\ \vdots \\ d_{\gamma }^{\alpha } \\ \end{array}\right) ,\quad \Phi _{\gamma }(t)=\left( \begin{array}{c} \phi _0(t) \\ \phi _1(t) \\ \vdots \\ \phi _{\gamma }(t) \\ \end{array} \right) ,\\ d_s^{\alpha }= & {} \sqrt{(2r+1)(2s+1)}\sum _{k=0}^r\sum _{i=0}^ {\lceil \alpha _m \rceil }\sum _{j=0}^s [(-1)^{i+r+k+j+s}{{\lceil \alpha _m \rceil }\atopwithdelims ()i}\\&\frac{(j+s)!(r+k)!\varGamma (2{\lceil \alpha _m \rceil }+k-i+1)}{(s-j)!(j!)^2(r-k)!(k!)^2\varGamma (2{\lceil \alpha _m \rceil }+k-i-\alpha +1)}\delta (\alpha _m ,k,i,\alpha ,j)],\\ 0\le & {} s \le \gamma , \end{aligned}$$

where

$$\begin{aligned} \delta (\alpha _m ,k,i,\alpha ,j)=\frac{1}{2{\lceil \alpha _m \rceil }+k+j-i-\alpha +1}, \end{aligned}$$

for ${\lceil \alpha \rceil \le 2{\lceil \alpha _m \rceil }+k-i}$ and $\delta (\alpha _m ,k,i,\alpha ,j)=0$, for ${\lceil \alpha \rceil >2{\lceil \alpha _m \rceil }+k-i}$; then,

$$\begin{aligned} \lim _{\gamma \rightarrow \infty } \parallel {^C_{0}D^{\alpha }_{t}}\psi _r-{D_{r,\gamma }^{\alpha }}^T. \Phi _{\gamma }\parallel _{L_2[0,1]}=0. \end{aligned}$$

Proof

By utilizing (6), we get

$$\begin{aligned} \psi _r(t)= & {} \phi _r(t)t^{\lceil \alpha _m \rceil }(1-t)^{\lceil \alpha _m \rceil }= t^{\lceil \alpha _m \rceil }(1-t)^{\lceil \alpha _m \rceil }\sqrt{2r+1}\sum _{k=0}^r (-1)^{r+k}\frac{(r+k)!t^k}{(r-k)!(k!)^2}\\= & {} \sqrt{2r+1}\sum _{k=0}^r (-1)^{r+k}\frac{(r+k)!t^{k+{\lceil \alpha _m \rceil }}(1-t)^{\lceil \alpha _m \rceil }}{(r-k)!(k!)^2}\\= & {} \sqrt{2r+1}\sum _{k=0}^r (-1)^{r+k}\frac{(r+k)!t^{k+{\lceil \alpha _m \rceil }}}{(r-k)!(k!)^2}\sum _{i=0}^{\lceil \alpha _m \rceil }{{\lceil \alpha _m \rceil }\atopwithdelims ()i}(-1)^it^{{\lceil \alpha _m \rceil }-i}\\= & {} \sqrt{2r+1}\sum _{k=0}^r\sum _{i=0}^{\lceil \alpha _m \rceil } (-1)^{i+r+k}{{\lceil \alpha _m \rceil }\atopwithdelims ()i}\frac{(r+k)!}{(r-k)!(k!)^2}t^{2{\lceil \alpha _m \rceil }+k-i}. \end{aligned}$$

With respect to the fact that $^C_{0}D^{\alpha }_{t} t^k= \frac{\varGamma (k+1)}{\varGamma (k+1-\alpha )}t^{k-\alpha }$, when ${\lceil \alpha \rceil \le k}$, and $^C_{0}D^{\alpha }_{t} t^k=0$ for ${\lceil \alpha \rceil > k}$  [20], we get the Caputo derivative of $\psi _r(t)$

$$\begin{aligned} ^C_{0}D^{\alpha }_{t}\psi _r(t)= & {} \sqrt{2r+1}\sum _{k=0}^r\sum _{i=0}^{\lceil \alpha _m \rceil } (-1)^{i+r+k}{ \lceil \alpha _m \rceil \atopwithdelims ()i}\nonumber \\&\frac{\varGamma (2{\lceil \alpha _m \rceil }+k-i+1)(r+k)!}{\varGamma (2{\lceil \alpha _m \rceil }+k-i-\alpha +1)(r-k)!(k!)^2}t^{2{\lceil \alpha _m \rceil }+k-i-\alpha }, \end{aligned}$$

(12)

when ${\lceil \alpha \rceil \le 2{\lceil \alpha _m \rceil }+k-i,}$ and $^C_{0}D^{\alpha }_{t}\psi _r(t)=0$ when ${\lceil \alpha \rceil > 2{\lceil \alpha _m \rceil }+k-i}$. Now by applying Theorem 4.1, we approximate $t^{2{\lceil \alpha _m \rceil }+k-i-\alpha }$ for $\lceil \alpha \rceil \le 2{\lceil \alpha _m \rceil }+k-i$ with Legendre orthonormal basis functions $\phi _s$s, and we get

$$\begin{aligned}&t^{2{\lceil \alpha _m \rceil }+k-i-\alpha }\simeq \sum _{s=0}^{\gamma } \beta _s^{\alpha }\phi _s, \end{aligned}$$

(13)

$$\begin{aligned}&\quad \beta _s^{\alpha }=\int _0^1 t^{2{\lceil \alpha _m \rceil }+k-i-\alpha }\phi _s {\hbox {d}}t\nonumber \\&\qquad \quad =\sqrt{2s+1} \sum _{j=0}^s (-1)^{j+s}\frac{(s+j)!}{(s-j)!(j!)^2(2{\lceil \alpha _m \rceil }+k-i-\alpha +j+1)},\nonumber \\&\quad \lim _{\gamma \rightarrow \infty }\parallel t^{2{\lceil \alpha _m \rceil }+k-i-\alpha }- \sum _{s=0}^{\gamma } \beta _s^{\alpha }\phi _s \parallel _{L_2[0,1]}=0. \end{aligned}$$

(14)

Substituting (13) and (14) in (12) we get $d_s^{\alpha }$, and the proof is completed. $\square$

By applying Lemma 4.3 , system (11) is approximated as follows

$$\begin{aligned}&\sum _{r=1}^{n} \sum _{l=0}^{k} c_{r,l}^{\gamma }\text{ B }({\lambda }_{r,l}^{\gamma },{\mu }_{i,j}^{\gamma })+ \sum _{r=1}^{n} \text{ B }(\omega _r,{\mu }_{i,j}^{\gamma })=\text{ L }({\mu }_{i,j}^{\gamma }), \quad 0\le j \le k, \quad 1\le i \le n,\nonumber \\&\quad {\lambda }_{r,l}^{\gamma }={(0,\dots ,0,\overbrace{\psi _l(t)}^{rth}, 0,\dots ,0,\overbrace{D^{\alpha _1}_{l,\gamma }.\Phi _{\gamma }}^{(n+r)th}, 0,\dots ,0,\overbrace{D^{\alpha _m}_{l,\gamma }.\Phi _{\gamma }}^{(mn+r)th},0,\dots ,0)},\nonumber \\&\quad {\mu }_{i,j}^{\gamma }=(0,\dots ,0,\overbrace{\psi _{j}}^{i th },0,\dots ,0,\overbrace{{D^{\alpha _1}_{j,\gamma }} .\Phi _{\gamma }}^{(i+n) th },0,\dots ,0,\overbrace{{D^{\alpha _m}_{j,\gamma }}. \Phi _{\gamma }}^{(i+mn)th},0,\dots ,0),\nonumber \\ t\in & {} [0,1]. \end{aligned}$$

(15)

By solving system (15), the following approximate solution for the problem is achieved:

$$\begin{aligned} u _{j,k}^{\gamma }(t) = {C_{j,k}^{\gamma }}^T.\varPsi _k(t)+w_j(t), \quad C_{j,k}^{\gamma }=\left( \begin{array}{c} c_{j,0}^\gamma \\ c_{j,1}^\gamma \\ \vdots \\ c_{j,k}^\gamma \\ \end{array} \right) . \end{aligned}$$

(16)

5 Convergence

In this section, we discuss the convergence of the method presented in section 4. In Theorem 5.1, we show that, with an increase in values of k and $\gamma$ in (16), the approximate minimizing function $(u_{1,k}^{\gamma },\dots ,u_{n,k}^{\gamma })$ tends to $(u_{1}^{*},\dots ,u_{n}^{*})$. First, we state some basic properties of Caputo fractional derivatives needed in Lemma 5.1 and Theorem 5.1.

Let $f\in C^{n}[0,1]$. For the Caputo fractional derivative of order $\alpha$, $n-1<\alpha \le n$, $^C _{0}D^{\alpha }_{t}f(t) \in C[0,1]$. We also have  [20]

$$\begin{aligned} \parallel {^C_{0}D^{\alpha }_{t}f(t)}\parallel _{\infty } \le \frac{\parallel f^{(n)}\parallel _{\infty } }{\varGamma {(n-\alpha +1)}}, \quad n-1<\alpha \le n. \end{aligned}$$

(17)

Lemma 5.1

Suppose $C_{j,k}$, $1\le j \le n$, $k\in \mathbb {N}$, is the solution of system (11); then, for a sufficiently large value of $\gamma \in \mathbb {N}$, there exists a unique solution $C_{j,k}^{\gamma }$ for the system (15), where

$$\begin{aligned} \lim _{\gamma \rightarrow \infty } \mid C_{j,k}-C_{j,k}^{\gamma }\mid =0. \end{aligned}$$

Proof

By utilizing Lemma 4.3, we get

$$\begin{aligned} \lim _{\gamma \rightarrow \infty } \parallel {\lambda }_{r,l}^{\gamma }-\lambda _{r,l}\parallel _{\pi }=0, \quad \lim _{\gamma \rightarrow \infty } \parallel {\mu }_{i,j}^{\gamma }-\mu _{i,j}\parallel _{\pi }=0. \end{aligned}$$

According to Assumption 2.1, the bilinear operator $\text{ B }$ and the linear operator $\text{ L }$ are bounded. Hence,

$$\begin{aligned}&\lim _{\gamma \rightarrow \infty } \text{ B }({\lambda }_{r,l}^{\gamma },{\mu }_{i,j}^{\gamma })=\text{ B }({\lambda }_{r,l},{\mu }_{i,j}), \end{aligned}$$

(18)

$$\begin{aligned}&\lim _{\gamma \rightarrow \infty } \text{ B }(\omega _r,{\mu }_{i,j}^{\gamma })=\text{ B }(\omega _r,{\mu }_{i,j}), \end{aligned}$$

(19)

$$\begin{aligned}&\lim _{\gamma \rightarrow \infty } \text{ L }({\mu }_{i,j}^{\gamma })=\text{ L }({\mu }_{i,j}). \end{aligned}$$

(20)

Consider linear systems (11) and (15) as follows:

$$\begin{aligned} M_{(k+1)n\times (k+1)n}X=b_{(k+1)n},\quad M_{(k+1)n\times (k+1)n}^{\gamma }X_{\gamma }=b_{(k+1)n}^{\gamma }, \end{aligned}$$

(21)

where

$$\begin{aligned} M_{(k+1)n\times (k+1)n}:= & {} [\text{ B }({\lambda }_{r,l},{\mu }_{i,j})]_{1\le i,r \le n,0\le j,l \le k,}\\ M_{(k+1)n\times (k+1)n}^{\gamma }:= & {} [\text{ B }({\lambda }_{r,l}^{\gamma },{\mu }_{i,j}^{\gamma })]_{1\le i,r \le n,0\le j,l \le k,}\\ b_{(k+1)n}:= & {} [\text{ L }(\mu _{i,j})-\sum _{r=1}^n \text{ B }(\omega _r,\mu _{i,j})]_{1\le i\le n, 0\le j \le k}, \\ b_{(k+1)n}^{\gamma } := & {} [\text{ L }(\mu _{i,j}^{\gamma })-\sum _{r=1}^n \text{ B }(\omega _r,\mu _{i,j}^{\gamma })]_{1\le i\le n, 0\le j \le k},\\ X:= & {} [c_{i,j}]_{1\le i \le n, 0\le j \le k}, \quad X_{\gamma }:=[c_{i,j}^\gamma ]_{1\le i \le n, 0\le j \le k}. \end{aligned}$$

According to Lemma 4.2, linear system (7) has a unique solution. So $\det M_{(k+1)n\times (k+1)n}\ne 0$, and (18) and (19) show us that, for a sufficiently large value of $\gamma$, $\det M_{(k+1)n\times (k+1)n}^{\gamma }\ne 0$. This means that, for a sufficiently large value of $\gamma$, the linear system (15) has a unique solution. Let

$$\begin{aligned} X=M_{(k+1)n\times (k+1)n}^{-1}b_{(k+1)n},\quad X_{\gamma }={{{M^{\gamma }}^{-1}}_{(k+1)n\times (k+1)n}}b_{(k+1)n}^{\gamma }, \end{aligned}$$

for a sufficiently large $\gamma$; then,

$$\begin{aligned} M_{(k+1)n\times (k+1)n}^{-1}= & {} [m_{i,j}]_{1\le i,j \le (k+1)n},\quad {{{M^{\gamma }}^{-1}}_{(k+1)n\times (k+1)n}}=[m_{i,j}^{\gamma }]_{1\le i,j \le (k+1)n},\\ m_{i,j}= & {} (-1)^{i+j}\frac{\det \tilde{M}_{i,j}}{\det M_{(k+1)n\times (k+1)n}}, \quad m_{i,j}^{\gamma }=(-1)^{i+j}\frac{\det \tilde{M}_{i,j}^{\gamma }}{\det M_{(k+1)n\times (k+1)n}^{\gamma }}. \end{aligned}$$

Here $\tilde{M}_{i,j}$ and $\tilde{M}_{i,j}^{\gamma }$ are matrices achieved by deleting the ith row and jth column of matrices $M_{(k+1)n\times (k+1)n}$ and ${M_{(k+1)n\times (k+1)n}^{\gamma }}$, respectively. $0 < \epsilon <1$ is given. Because the determinant of a matrix is a polynomial constructed by matrix entries, considering (18) and (19) it can be observed that, for a sufficiently large value of $\gamma$,

$$\begin{aligned}&\mid m_{i,j}-m_{ij}^{\gamma }\mid < \frac{\epsilon }{2((k+1)n)(\parallel b_{(k+1)n} \parallel _1+1)},\\&\quad \parallel M_{(k+1)n\times (k+1)n}^{-1}-{{{M^{\gamma }}^{-1}}_{(k+1)n \times (k+1)n}}\parallel _1=max_{j=1,\dots ,(k+1)n}\sum _{i=1}^{(k+1)n} \mid m_{i,j}\\&\qquad -m_{i,j}^{\gamma }\mid <\frac{\epsilon }{2(\parallel b_{(k+1)n} \parallel _1+1)}. \end{aligned}$$

By (18)–(20), it is also observed that for a large enough $\gamma$,

$$\begin{aligned} \parallel b_{(k+1)n}-b_{(k+1)n}^{\gamma }\parallel _1= & {} \sum _{i=1}^n \sum _{j=0}^k \mid \text{ L }(\mu _{i,j})-\sum _{r=1}^n \text{ B }(\omega _r,\mu _{i,j})-\text{ L }(\mu _{i,j}^{\gamma })\\&+ \sum _{r=1}^n \text{ B }(\omega _r,\mu _{i,j}^{\gamma })\mid \\ {}\le & {} \sum _{i=1}^n \sum _{j=0}^k \mid \text{ L }(\mu _{i,j})-\text{ L }(\mu _{i,j}^{\gamma })\mid \\&+ \sum _{i=1}^n \sum _{j=0}^k\sum _{r=1}^n \mid \text{ B }(\omega _r,\mu _{i,j}^{\gamma })-\text{ B }(\omega _r,\mu _{i,j}))\mid \\\le & {} \frac{\epsilon }{2 \parallel M_{(k+1)n\times (k+1)n}^{-1} \parallel _1},\\&\parallel b_{(k+1)n}^{\gamma } \parallel _1 < \parallel b_{(k+1)n} \parallel _1+1. \end{aligned}$$

Hence,

$$\begin{aligned}&\parallel X-X_{\gamma }\parallel _1 \le \parallel M_{(k+1)n\times (k+1)n}^{-1}-M_{(k+1)n\times (k+1)n}^{\gamma }\parallel _1 \parallel b_{(k+1)n}^{\gamma } \parallel _1 \\&\quad + \parallel M_{(k+1)n\times (k+1)n}^{-1}\parallel _1 \parallel b_{(k+1)n} - b_{(k+1)n}^{\gamma } \parallel _1 <\epsilon , \end{aligned}$$

and the proof is completed. $\square$

Theorem 5.1

Suppose $\epsilon >0$ is given; then, for sufficiently large values of k and $\gamma$ we have

$$\begin{aligned}&\parallel u_{j,k}^{\gamma }-u_j^* \parallel _{L_2[0,1]}< \epsilon ,\quad \parallel {^C _{0}D^{\alpha _i}_{t} u_{j,k}^{\gamma }}- {^C _{0}D^{\alpha _i}_{t}u_j^* \parallel _{L_2[0,1]}} \\&\quad < \epsilon ,\quad 1\le i \le m, \quad 1\le j \le n. \end{aligned}$$

Proof

Let $(u_{1,k},\dots ,u_{n,k})$ be the solution of system (7):

$$\begin{aligned} \text{ B }(U_k,\mu _{i,j})= & {} \text{ L }(\mu _{i,j}), \quad 0 \le j \le k, \quad 1 \le i \le n,\nonumber \\ U_k= & {} (u_{1,k},\dots ,u_{n,k},{^C _{0}D^{\alpha _1}_{t}} u_{1,k},\dots ,{^C _{0}D^{\alpha _1}_{t}} u_{n,k},\nonumber \\&\quad \dots ,{^C _{0}D^{\alpha _m}_{t}} u_{1,k},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_{n,k}),\quad t\in [0,1]. \end{aligned}$$

(22)

According to Theorem 3.1

$$\begin{aligned} \text{ B }(U^*,\mu _{i,j})= & {} \text{ L }(\mu _{i,j}), \quad 0 \le j \le k,\nonumber \\ 1\le & {} i \le n,\nonumber \\ U^*= & {} (u_1^{*},\dots ,u_n^{*},{^C _{0}D^{\alpha _1}_{t}} u_1^{*},\dots ,{^C _{0}D^{\alpha _1}_{t}} u_n^{*},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_1^{*},\dots ,{^C _{0}D^{\alpha _m}_{t}} u_n^{*}),\nonumber \\ t\in & {} [0,1],\nonumber \\ \mu _{i,j}= & {} (0,\dots ,0,\overbrace{\psi _{j}}^{i th },0,\dots ,0,\overbrace{{^C _{0}D^{\alpha _1}_{t}} \psi _{j}}^{(i+n) th },0,\dots ,0,\overbrace{{^C _{0}D^{\alpha _m}_{t}} \psi _{j}}^{(i+mn)th},0,\dots ,0),\nonumber \\ t\in & {} [0,1]. \end{aligned}$$

(23)

So, considering (22) and (23), it can be observed that

$$\begin{aligned} \text{ B }(U^*-U_k,\mu _{i,j})=0, \quad 0 \le j \le k, \quad 1 \le i \le n. \end{aligned}$$

(24)

By Lemma 4.1, there exists a sequence, say $\{(v_{1,k},\dots ,v_{n,k})\}_{k\in \mathbb {N}}$, $(v_{1,k},\dots ,v_{n,k})\in \prod _{i=1}^{n} P_k[0,1] \bigcap E_i[0,1]$, such that $v_{i,k} \rightarrow u_i^*$, $1\le i \le n$ with respect to $\parallel . \parallel _{\lceil \alpha _m\rceil }$. Considering (24), we get

$$\begin{aligned} \text{ B }(U^*-U_k,U_k-V_k)=0, \end{aligned}$$

(25)

where

$$\begin{aligned} V_k= & {} (v_{1,k},\dots ,v_{n,k},{^C _{0}D^{\alpha _1}_{t}} v_{1,k},\dots ,{^C _{0}D^{\alpha _1}_{t}} v_{n,k},\dots ,{^C _{0}D^{\alpha _m}_{t}} v_{1,k},\dots ,{^C _{0}D^{\alpha _m}_{t}} v_{n,k}),\\ t\in & {} [0,1]. \end{aligned}$$

From (25) we obtain

$$\begin{aligned} \text{ B }(U^*-U_k,U_k)=\text{ B }(U^*-U_k,V_k), \end{aligned}$$

(26)

and

$$\begin{aligned} \text{ B }(U^*-U_k,U^*-U_k)=\text{ B }(U^*-U_k,U^*-V_k). \end{aligned}$$

(27)

Now by referring to Assumption 2.1, we get

$$\begin{aligned}&c\parallel U^*-U_k \parallel _{\pi }^2 \le \text{ B }(U^*-U_k,U^*-U_k)\nonumber \\&\quad =\text{ B }(U^*-U_k,U^*-V_k)\le d \parallel U^*-U_k\parallel _{\pi }\parallel U^*-V_k \parallel _{\pi }. \end{aligned}$$

(28)

$\epsilon >0$ is given. With respect to (17), it can be easily observed that with an increase in the value of k, $\parallel U^*-V_k \parallel _{\pi }$ tends to zero. So inequality (28) shows that for a large enough value of k,

$$\begin{aligned}&\parallel u_{j,k}-u_j^* \parallel _{L_2[0,1]}< \frac{\epsilon }{2}, \quad 1\le j \le n, \end{aligned}$$

(29)

$$\begin{aligned}&\parallel {^C _{0}D^{\alpha _i}_{t}} u_{j,k}- {^C _{0}D^{\alpha _i}_{t}}u_j^* \parallel _{L_2[0,1]} < \frac{\epsilon }{2},\quad 1\le i \le m, \quad 1\le j \le n. \end{aligned}$$

(30)

Now for a fixed value of k that satisfies (29) and (30), according to (17) and Lemma 5.1, $\gamma$ can be set sufficiently large such that

$$\begin{aligned}&\parallel u_{j,k}-u_{j,k}^{\gamma } \parallel _{L_2[0,1]}< \frac{\epsilon }{2}, \quad 1\le j \le n, \end{aligned}$$

(31)

$$\begin{aligned}&\parallel {^C _{0}D^{\alpha _i}_{t}} u_{j,k}- {^C _{0}D^{\alpha _i}_{t}}u_{j,k}^{\gamma } \parallel _{L_2[0,1]} < \frac{\epsilon }{2},\quad 1\le i \le m, \quad 1\le j \le n. \end{aligned}$$

(32)

Hence, by (29)–(32)

$$\begin{aligned} \parallel u_{j,k}^{\gamma }-u_j^* \parallel _{L_2[0,1]}< \epsilon ,\quad \parallel {^C _{0}D^{\alpha _i}_{t}} u_{j,k}^{\gamma }- {^C _{0}D^{\alpha _i}_{t}}u_j^{*} \parallel _{L_2[0,1]} < \epsilon ,\quad 1\le i \le m, \quad 1\le j \le n, \end{aligned}$$

and the proof is completed. $\square$

6 Illustrative Test Problems

In this section, we apply the method presented in section 4 for solving the following test examples. The well-known symbolic software “Mathematica” has been employed for calculations and creating figures.

Fig. 1

Approximate solution $u_{2}^2$ and exact solution $u_{ex}$ for example 6.1

Example 6.1

Consider the following one dimensional problem:

$$\begin{aligned} J[u]= & {} \int _{0}^{1}\left[ (u-t^{\frac{5}{2}})^2+\left( ^C _{0}D^{\frac{1}{4}}_{t}u-\frac{5\sqrt{\pi }\varGamma \left( \frac{7}{4}\right) t^{\frac{9}{4}}}{2\varGamma (\frac{3}{4})\varGamma (\frac{13}{4})}\right) ^2+\left( ^C _{0}D^{\frac{5}{4}}_{t}u-\frac{15\sqrt{\pi }t^{\frac{5}{4}}}{8\varGamma (\frac{9}{4})}\right) ^2\right] {\hbox {d}}t,\\ u(0)= & {} 0,\quad u(1)=1,\quad u'(0)=0, \quad u'(1)=\frac{5}{2}, \end{aligned}$$

with exact solution $u(t)=t^{\frac{5}{2}}$ and $J[u]=0$. For the above problem we have

$$\begin{aligned} \text{ B }(U,U)= & {} 2\int _0^1 [u^2+({^C _{0}D^{\frac{1}{4}}_{t}u})^2+({^C_{0}D^{\frac{5}{4}}_{t}u})^2]{\hbox {d}}t,\\ \text{ L }(U)= & {} \int _0^1 [2t^{\frac{5}{2}}u+\frac{5\sqrt{\pi }t^{\frac{9}{4}}\varGamma (\frac{7}{4})}{\varGamma (\frac{3}{4})\varGamma (\frac{13}{4})}{^C_{0}D^{\frac{1}{4}}_{t}}u+ \frac{15\sqrt{\pi }t^{\frac{5}{4}}}{4\varGamma (\frac{9}{4})}{^C_{0}D^{\frac{5}{4}}_{t}}u]{\hbox {d}}t,\\ U= & {} (u, {^C_{0}D^{\frac{1}{4}}_{t}u},{{^C _{0}D^{\frac{5}{4}}_{t}}u}). \end{aligned}$$

Considering $k=\gamma =2$ in approximation (16), we get

$$\begin{aligned} u_2^2(t)={C_2^2}^T . \varPsi _2(t)+\overbrace{\frac{1}{2}(t^3+t^2)}^{w(t)},\quad {C_{2}^{2}}^T=(-0.200713, 0.0473973,-0.0307623). \end{aligned}$$

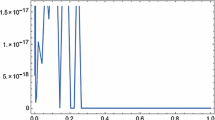
The approximate solution $u_2^2(t)$ and the exact solution $u(t)=t^{\frac{5}{2}}$ are plotted in Fig. 1. The absolute errors in example 6.1 are shown in Table 1.

Table 1 Absolute errors $J[u_{k}^{\gamma }]$, $\parallel u_{k}^{\gamma }-u\parallel _{L_2[0,1]}$ and $r_k^{\gamma }(t)=\mid u_{k}^{\gamma }(t)-u(t)\mid$ in example 6.1

Example 6.2

Consider the following two dimensional problem:

$$\begin{aligned} J[u_1,u_2]= & {} \\&\int _{0}^{1}\left[ (u_1-t^{2.5}-t^2-1)^2+(u_2-t^{4.5})^2+\left( ^C _{0}D^{\frac{1}{2}}_{t}u_1-\frac{8t^{1.5}}{3\sqrt{\pi }}\right. \right. \\&\left. \left. - \frac{15{\pi }t^{2}}{16\sqrt{\pi }}\right) ^2+\left( ^C _{0}D^{\frac{1}{2}}_{t}u_2-\frac{315\sqrt{\pi }t^4}{256}\right) ^2\right] {\hbox {d}}t,\\&u_1(0)=1,\quad u_1(1)=3, \quad u_2(0)=0, \quad u_2(1)=1, \end{aligned}$$

with exact solution ${u}_1(t)=t^{2.5}+t^2+1$, ${u}_2(t)=t^{4.5}$ and $J[u_1,u_2]=0$. For the above problem we have

$$\begin{aligned} \text{ B }(U,U)= & {} 2\int _0^1 [u_1^2+u_2^2+\left( ^C_{0}D^{\frac{1}{2}}_{t}u_1\right) ^2+(^C_{0}D^{\frac{1}{2}}_{t}u_2)^2]{\hbox {d}}t,\\ \text{ L }(U)= & {} 2\int _0^1 \left[ (t^{2.5}+t^2+1)u_1+t^{4.5}u_2+\left( \frac{8t^{1.5}}{3\sqrt{\pi }}+\frac{15{\pi }t^{2}}{16\sqrt{\pi }}\right) {^C _{0}D^{\frac{1}{2}}_{t}}u_1\right. \\&\left. +\frac{315\sqrt{\pi }t^4}{256}{^C _{0}D^{\frac{1}{2}}_{t}u_2}\right] {\hbox {d}}t,\\ U= & {} \left( u_1,u_2, {^C_{0}D^{\frac{1}{2}}_{t}u_1},{^C _{0}D^{\frac{1}{2}}_{t}u_2}\right) . \end{aligned}$$

Fig. 2

Approximate solution $u_{1,4}^5$ and $u_{2,4}^5$ and exact solution ${u}_1$ and ${u}_2$ in example 6.2

Table 2 Absolute errors in example 6.2

Considering $k=4$ and $\gamma =5$ in approximations (16), we get

$$\begin{aligned} u_{1,4}^5(t)= & {} {C_{1,4}^5}^T . \varPsi _4(t)+\overbrace{2t+1}^{w_1(t)},\quad u_{2,4}^5(t)={C_{2,4}^5}^T . \varPsi _4(t)+\overbrace{t}^{w_2(t)},\\ C_{1,4}^{5}= & {} \left( \begin{array}{c} 2.28032 \\ 0.138894 \\ -0.0119808 \\ 0.0022769 \\ -0.00083613\\ \end{array} \right) , \quad C_{2,4}^{5}=\left( \begin{array}{c} 1.96607 \\ 0.711015 \\ 0.127428 \\ 0.00683953 \\ -0.000351182\\ \end{array} \right) . \end{aligned}$$

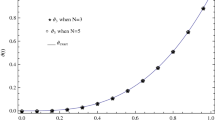
The approximate solution $u_{1,4}^5(t)$ and $u_{2,4}^5(t)$ and the exact solution ${u}_1(t)=t^{2.5}+t^2+1$ and ${u}_2(t)=t^{4.5}$ are plotted in Fig. 2. The absolute errors in example 6.2 are shown in Table 2.

7 Conclusions

An approximate method was developed for solving a class of fractional optimization problems. First, the optimization problem was transformed into a variational equality; then, using a special type of polynomial basis functions, the variational equality was reduced to a linear system of algebraic equations with a unique solution. The approximate solutions are smooth polynomial functions with high flexibility in satisfying all initial and boundary conditions of the problem. The convergence of the method was extensively discussed, and illustrative test examples were presented to demonstrate efficiency of the new technique.