A new operational matrix of fractional order integration for the Chebyshev wavelets and its application for nonlinear fractional Van der Pol oscillator equation

Abstract

In this paper, an efficient and accurate computational method based on the Chebyshev wavelets (CWs) together with spectral Galerkin method is proposed for solving a class of nonlinear multi-order fractional differential equations (NMFDEs). To do this, a new operational matrix of fractional order integration in the Riemann–Liouville sense for the CWs is derived. Hat functions (HFs) and the collocation method are employed to derive a general procedure for forming this matrix. By using the CWs and their operational matrix of fractional order integration and Galerkin method, the problems under consideration are transformed into corresponding nonlinear systems of algebraic equations, which can be simply solved. Moreover, a new technique for computing nonlinear terms in such problems is presented. Convergence of the CWs expansion in one dimension is investigated. Furthermore, the efficiency and accuracy of the proposed method are shown on some concrete examples. The obtained results reveal that the proposed method is very accurate and efficient. As a useful application, the proposed method is applied to obtain an approximate solution for the fractional order Van der Pol oscillator (VPO) equation.

1 Introduction

In recent years, fractional calculus and differential equations have found enormous applications in mathematics, physics, chemistry and engineering because of the fact that, a realistic modeling of a physical phenomenon having dependence not only at the time instant, but also on the previous time history can be successfully achieved by using fractional calculus. The applications of the fractional calculus have been demonstrated by many authors. For example, it has been applied to model the nonlinear oscillation of earthquakes [21], fluid-dynamic traffic [22], frequency dependent damping behavior of many viscoelastic materials [4], continuum and statistical mechanics [38], colored noise [39], solid mechanics [48], economics [5], signal processing [44], and control theory [7]. However, during the last decade fractional calculus has attracted much more attention of physicists and mathematicians. Due to the increasing applications, some schemes have been proposed to solve fractional differential equations. The most frequently used methods are Adomian decomposition method (ADM) [16, 41, 42], homotopy perturbation method [50], homotopy analysis method [20], variational iteration method (VIM) [14, 51], fractional differential transform method (FDTM) [1, 2, 13, 17, 18], fractional difference method (FDM) [40], power series method [43], generalized block pulse operational matrix method [35] and Laplace transform method [45]. Also, recently the operational matrices of fractional order integration for the Haar wavelets [36], Legendre wavelets [23,24,25, 29, 30, 47] and the Chebyshev wavelets of the first kind [26,27,28, 37] and the second kind [53] have been developed to solve the fractional differential equations.

An usual way to solve functional equations is to express the solution as a linear combination of the so-called basis functions. These basis functions can, for instance, be orthogonal or not orthogonal. Approximation by orthogonal families of basis functions has found wide application in science and engineering [30]. The main idea of using an orthogonal basis is that the problem under consideration reduced to a system of linear or nonlinear algebraic equations [30,31,32]. This can be done by truncated series of orthogonal basis functions for the solution of the problem and using the operational matrices [30].

Depending on their structure, the orthogonal functions may be widely classified into four families [49]. The first includes sets of piecewise constant orthogonal functions such as the Walsh functions, block pulse functions, etc. The second consists of sets of orthogonal polynomials such as Laguerre, Legendre, Chebyshev, etc. The third is the widely used sets of sine–cosine functions in Fourier series. The fourth includes orthogonal wavelets such as Haar, Legendre, Chebyshev and CAS wavelets. It is well known that we can approximate any smooth function by the eigenfunctions of certain singular Sturm–Liouville problems such as Legendre or Chebyshev orthogonal polynomials. In this manner, the truncation error approaches zero faster than any negative power of the number of the basis functions used in the approximation [8]. This phenomenon is usually referred to as ‘the spectral accuracy’ [8]. It is worth noting that approximating a continuous function with piecewise constant basis functions results in an approximation that is piecewise constant. On the other hand, if a discontinuous function is approximated with continuous basis functions, the resulting approximation is continuous and can not properly model the discontinuities. In remote sensing, images often have properties that vary continuously in some regions and discontinuously in others. Thus, in order to properly approximate these spatially varying properties it is absolutely necessary to use approximating functions that can accurately model both continuous and discontinuous phenomena. Therefore, neither continuous basis functions nor piecewise constant basis functions taken alone can efficiently or accurately model these spatially varying properties. For these situations, wavelet functions will be more effective. It should be noted that wavelets theory is a relatively new and an emerging area in mathematical research . It has been applied in a wide range of engineering disciplines. Wavelets are localized functions, which are the basis for energy-bounded functions and, in particular, for $L^{2}(R)$, so that localized pulse problems can be easily approached and analyzed [10,11,12]. They are used in system analysis, optimal control, numerical analysis, signal analysis for wave form representation and segmentations, time-frequency analysis and fast algorithms for easy implementation. However, wavelets are another basis functions which offer considerable advantages over alternative basis ones and allow us to attack problems that are not accessible with conventional numerical methods. Some other advantages of these basis functions are that the basis set can be improved in a systematic way, different resolutions can be used in different regions of space, the coupling between different resolution levels is easy, there are few topological constraints for increased resolution regions, the Laplace operator is diagonally dominant in an appropriate wavelet basis, the matrix elements of the Laplace operator are very easy to calculate and the numerical effort scales linearly with respect to the system size [30]. It is worth mentioning that the CWs as a specific kind of wavelets have mutually spectral accuracy, orthogonality and other mentioned useful properties about wavelets. Therefore, in recent years, these orthogonal basis functions have been widely applied for solving different types of differential equations e.g. [26,27,28, 33, 37, 49]. It is also worth noting that a suitable family of orthogonal basis functions which can be used to obtain approximate solutions for fractional functional equations is a family of the Chebyshev polynomials, because the integrals (3) and (5) can be easily computed and the useful property (6) can also be applied. Therefore, due to the fact that the CWs have mutual properties of the Chebyshev polynomials and mentioned properties of wavelets, we believe that these basis functions are suitable for obtaining approximate solutions for fractional functional equations.

In this paper, we first derive a new operational matrix of fractional integration in the Riemann–Liouville sense for the CWs and also present a general procedure based on collocation method and the HFs for constructing this matrix. Then, we prove an useful theorem about the CWs which will be used further in this paper. Next a new computational method based on these bases functions together with their operational matrix of fractional integration is proposed for solving the following NMFDE:

$$\begin{aligned} D_{*}^{\alpha }u(x)+\sum _{i=1}^{s}\gamma _{i}D_{*}^{\alpha _{i}}u(x)+G\left( u(x)\right) =f(x),\quad x\in [0,1], \end{aligned}$$

(1)

with the initial conditions:

$$\begin{aligned} u^{(i)}(0)=d_{i},\,\,\,i=0,1,\ldots ,q-1, \end{aligned}$$

(2)

where $\gamma _{i}\,(i=1,\ldots ,s)$ are real constant coefficients and also $q-1<\alpha \le q$, $0<\alpha _{1}<\alpha _{2}<\ldots<\alpha _{s}<\alpha$ are given real constants. Moreover $D_{*}^{\alpha }u(x)\equiv u^{(\alpha )}(x)$ denotes the Caputo fractional derivative of order $\alpha$ of u(x) which will be described in the next section, the values of $d_{i}\,(i=0,\ldots ,q-1)$ describe the initial state of u(x), G is a known analytic function and f(x) is a given source function. The basic idea of the proposed method is as follows: (i) The NMFDE (1) is converted to a fully integrated form via fractional integration in the Riemann–Liouville sense. (ii) Subsequently, the integrated form of the equation is approximated using a linear combination of the CWs. (iii) Finally, the integrated form of the equation is converted to a nonlinear algebraic equation, by introducing the operational matrix of fractional integration of the CWs.

This paper is organized as follows: In section 2, some necessary definitions and mathematical preliminaries of the fractional calculus are reviewed. In section 3, the CWs and some of their properties are investigated. In section 4, the proposed method is described for solving NMFDE (1). In section 5, the proposed method is applied for some numerical examples. In section 6, the proposed method is applied to obtain approximate solution of the fractional order VPO equation. Finally, a conclusion is drawn in section 7.

2 Preliminaries and notations

In this section, we give some necessary definitions and mathematical preliminaries of the fractional calculus theory which are required for establishing our results.

DEFINITION 2.1

A real function $u(x),~x>0$, is said to be in the space $C_{\mu },~\mu \in \mathbb {R}$ if there exists a real number $p~(>\mu )$ such that $u(x)=x^{p}u_{1}(x)$, where $u_{1}(x)\in C[0,\infty ]$ and it is said to be in the space $C_{\mu }^{n}$ if $u^{(n)}\in C_{\mu },~n\in \mathbb {N}$.

DEFINITION 2.2

The Riemann–Liouville fractional integration operator of order $\alpha \ge 0$ of a function $u\in C_{\mu },~\mu \ge -1$, is defined as [46]

$$\begin{aligned} \left( I^{\alpha }u\right) (x)=\left\{ \begin{array}{ll} \displaystyle \frac{1}{\Gamma (\alpha )}\int _{0}^{x}{(x-t)^{\alpha -1}{u(t)}\mathrm{d}t}, &{} \alpha >0, \\ u(x), &{} \alpha =0. \end{array} \right. \end{aligned}$$

(3)

It has the following properties:

$$\begin{aligned} \begin{array}{ll} \displaystyle \left( I^{\alpha }I^{\beta }u\right) (x)=\left( I^{\alpha +\beta }u\right) (x),&\displaystyle I^{\alpha }x^{\vartheta }=\frac{\Gamma (\vartheta +1)}{\Gamma (\alpha +\vartheta +1)}x^{\alpha +\vartheta }, \end{array} \end{aligned}$$

(4)

where $\alpha ,\,\beta \ge 0$ and $\vartheta >-1$.

DEFINITION 2.3

The fractional derivative operator of order $\alpha >0$ in the Caputo sense is defined as [46]

$$\begin{aligned} \left( D_{*}^{\alpha }u\right) (x)=\left\{ \begin{array}{lll} \displaystyle \frac{d^{n}u(x)}{dx^{n}}, &{}&{} \alpha =n\in \mathbb {N}, \\ \displaystyle \frac{1}{\Gamma (n-\alpha )}\int _{0}^{x}{(x-t)^{n-\alpha -1}u^{(n)}(t)\mathrm{d}t}, &{}&{} n-1<\alpha < n, \end{array}\right. \end{aligned}$$

(5)

where n is an integer $x>0$ and $u\in C_{1}^{n}$. The useful relation between the Riemann–Liouvill operator and Caputo operator is given by the following expression:

$$\begin{aligned} \left( I^{\alpha }D_{*}^{\alpha }u\right) (x)=u(x)-\sum _{k=0}^{n-1}{u^{(k)}(0^{+})}\frac{x^{k}}{k!},\,\,\,x>0, \quad n-1<\alpha \le n, \end{aligned}$$

(6)

where n is an integer, and $u\in C_{1}^{n}$. For more details about fractional calculus, see [46].

3 The CWs and their properties

In this section, we briefly review the CWs and their properties which are used further in this paper.

3.1 Wavelets and the CWs

Wavelets constitute a family of functions constructed from dilation and translation of a single function $\psi (x)$ called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously, we have the following family of continuous wavelets [26]:

$$\begin{aligned} \psi _{ab}(x)=|a|^{-\frac{1}{2}}\psi \left( \frac{x-b}{a}\right) , \quad a,\,b\in \mathbb {R},\,\,a\ne 0. \end{aligned}$$

(7)

If we restrict the parameters a and b to discrete values as $a=a_{0}^{-k}$, $b=nb_{0}a_{0}^{-k}$, where $a_{0}>1$, $b_{0}>0$, we have the following family of discrete wavelets:

$$\begin{aligned} \psi _{kn}(x)=|a_{0}|^{\frac{k}{2}}\psi (a_{0}^{k}x-nb_{0}), \quad k,\,n\in \mathbb {Z}, \end{aligned}$$

(8)

where the functions $\psi _{kn}(x)$ form a wavelet basis for $L^{2}(\mathbb {R})$. In practice, when $a_{0}=2$ and $b_{0}=1$, the functions $\psi _{kn}(x)$ form an orthonormal basis.

The CWs $\psi _{nm}(x)=\psi (k,n,m,x)$ have four arguments, $n=1,2,\ldots ,2^{k}$, k is any arbitrary positive integer, m is the degree of the Chebyshev polynomials and independent variable x is defined on [0, 1]. They are defined on the interval [0, 1] by

$$\begin{aligned} \psi _{nm}(x)=\displaystyle \left\{ \begin{array}{ccc} \displaystyle \frac{\beta _{m}2^{\frac{k}{2}}}{\sqrt{\pi }}T_{m}(2^{k+1}x-2n+1), &{} &{}x\in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] , \\ 0, &{}&{} \mathrm{o.w.}, \end{array}\right. \end{aligned}$$

(9)

where

$$\begin{aligned} \beta _{m}=\left\{ \begin{array}{ccc} \sqrt{2}, &{}&{} m=0, \\ 2, &{}&{} m>0. \end{array}\right. \end{aligned}$$

Here, $T_{m}(x)$ are the well-known Chebyshev polynomials of degree m, which are orthogonal with respect to the weight function $w(x)=\frac{1}{\sqrt{1-x^{2}}}$, on the interval $[-1,1]$ and satisfy the following recursive relation [8]:

$$\begin{aligned} T_{0}(x)=1,\quad T_{1}(x)=x,\quad T_{m+1}(x)=2xT_{m}(x)-T_{m-1}(x),\quad m=1,2,\ldots . \end{aligned}$$

(10)

The set of the CWs is an orthogonal set with respect to the weight function $w_{n}(x)=w(2^{k+1}x-2n+1)$.

3.2 Function approximation

A function u(x) defined over [0, 1] may be expanded by the CWs as

$$\begin{aligned} u(x)=\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }{c_{nm}\psi _{nm}(x)}, \end{aligned}$$

(11)

where

$$\begin{aligned} c_{nm}=\left( u(x),\psi _{nm}(x)\right) _{w_{n}}=\int _{0}^{1}u(x)\psi _{nm}(x)w_{n}(x)\mathrm{d}x, \end{aligned}$$

(12)

in which (., .) denotes the inner product in $L_{w_{n}}^{2}[0,1]$. If the infinite series in (11) is truncated, then it can be written as

$$\begin{aligned} u(x)\simeq \sum _{n=1}^{2^{k}}\sum _{m=0}^{M-1}{c_{nm}\psi _{nm}(x)=C^{T}\Psi (x)}, \end{aligned}$$

(13)

where T indicates transposition, C and $\Psi (x)$ are $\hat{m}=2^{k}M$ column vectors given by

$$\begin{aligned} C\triangleq \left[ c_{10},\ldots ,c_{1M-1}|c_{20}, \ldots ,c_{2M-1}|,\ldots ,|c_{2^{k}0},\ldots ,c_{2^{k}M-1}\right] ^{T} \end{aligned}$$

and

$$\begin{aligned}&\Psi (x)\triangleq \left[ \psi _{10}(x),\ldots ,\psi _{1M-1}(x)|\psi _{20}(x), \ldots ,\psi _{2M-1}(x)|,\right. \nonumber \\&\left. \ldots ,|\psi _{2^{k}0}(x),\ldots ,\psi _{2^{k}M-1}(x)\right] ^{T}. \end{aligned}$$

(14)

By taking the collocation points

$$\begin{aligned} x_{i}=\frac{i}{\hat{m}-1},~~~~i=0,1,\ldots ,\hat{m}-1, \end{aligned}$$

(15)

we define the wavelet matrix $\Phi _{\hat{m}\times \hat{m}}$ as

$$\begin{aligned} \Phi _{\hat{m}\times \hat{m}}\triangleq \left[ \Psi (0),\Psi \left( \frac{1}{\hat{m}-1}\right) ,\ldots ,\Psi (1)\right] . \end{aligned}$$

(16)

For example, for $k=1,\,M=3$, we have

$$\begin{aligned} \Phi _{6\times 6}=\frac{1}{\sqrt{\pi }}\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2&{}2&{}2&{}0&{}0&{}0\\ -2\, \sqrt{2}&{}-\frac{2}{5}\,\sqrt{2}&{}\frac{6}{5}\,\sqrt{2}&{}0&{}0&{}0\\ 2\, \sqrt{2}&{}-{\frac{46}{25}}\,\sqrt{2}&{}-{\frac{14}{25}}\,\sqrt{2}&{}0&{}0 &{}0\\ 0&{}0&{}0&{}2&{}2&{}2\\ 0&{}0&{}0&{}-\frac{6}{5}\, \sqrt{2}&{}\frac{2}{5}\,\sqrt{2}&{}2\,\sqrt{2}\\ 0&{}0&{}0&{}-{ \frac{14}{25}}\,\sqrt{2}&{}-{\frac{46}{25}}\,\sqrt{2}&{}2\,\sqrt{2} \end{array} \right) . \end{aligned}$$

3.3 Convergence of the CWs expansion

The convergence of the CWs expansion in one dimension is investigated in the following theorems:

Theorem 3.1

A function u(x) defined on [0, 1] with bounded first and second derivatives $|u^{\prime }(x)|\le M_{1}$ and $|u^{\prime \prime }(x)|\le M_{2}$, can be expanded as an infinite sum of CWs, and the series converges uniformly to u(x), that is,

$$\begin{aligned} u(x)=\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }{c_{nm}\psi _{nm}(x)}, \end{aligned}$$

where $c_{nm}$’s are defined in (12).

Proof

We consider the following cases:

For m=0 and $n=1,2,\ldots ,2^{k}$, the CWs form an orthonormal system on [0, 1] as

$$\begin{aligned} \displaystyle \psi _{n0}(x)=\left\{ \begin{array}{ccc} \displaystyle \sqrt{\frac{2}{\pi }}2^{\frac{k}{2}},&{} &{} x\in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] , \\ 0, &{} &{}\mathrm{o.w}. \end{array} \right. \end{aligned}$$

(17)

By expanding the function u(x) in terms of these basis functions on [0, 1], we have

$$\begin{aligned} u(x)=\sum _{n=1}^{\infty }c_{n0}\psi _{n0}(x), \end{aligned}$$

(18)

where

$$\begin{aligned} c_{n0}=\sqrt{\frac{2}{\pi }}2^{\frac{k}{2}}\int _{\frac{n-1}{2^{k}}}^{\frac{n}{2^{k}}}u(x)w_{n}(x)\mathrm{d}x. \end{aligned}$$

(19)

By truncating the series in (18), it can be written as

$$\begin{aligned} \tilde{u}(x)\simeq \sum _{n=1}^{2^{k}}c_{n0}\psi _{n0}(x). \end{aligned}$$

(20)

Theorem 3.2

Suppose $\tilde{u}(x)$ be the truncated expansion of the function u(x) in the above basis functions and $\tilde{e}(x)=\tilde{u}(x)-u(x)$ be the corresponding error. Then the expansion will converge in the sense that $\tilde{e}(x)$ approaches zero with the same rate as $2^{k}$, i.e.,

$$\begin{aligned} \Vert \tilde{e}(x)\Vert =O\left( \frac{1}{2^{k}}\right) . \end{aligned}$$

(21)

Proof

By defining the error between u(x) and its expansion over every subinterval as follows:

$$\begin{aligned} e_{n}(x)=c_{n0}\psi _{n0}(x)-u(x),\quad x\in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] ,\,\,\,\,n=1,2,\ldots ,2^{k}, \end{aligned}$$

(22)

we have

$$\begin{aligned} \Vert e_{n}(x)\Vert ^{2}= & {} \int _{\frac{n-1}{2^{k}}}^{\frac{n}{2^{k}}}e_{n}(x)^{2}w_{n}(x)\mathrm{d}x =\int _{\frac{n-1}{2^{k}}}^{\frac{n}{2^{k}}} \left( c_{n0}\psi _{n0}(x)-u(x)\right) ^{2}w_{n}(x)\mathrm{d}x\nonumber \\= & {} \left( c_{n0}\sqrt{\frac{2}{\pi }}2^{\frac{k}{2}}-u(\eta _{n})\right) ^{2}\frac{\pi }{2^{k+1}}, \quad \eta _{n} \in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] , \end{aligned}$$

(23)

where we have used the weighted mean value theorem for integrals. From (19) and the weighted mean value theorem, we also have

$$\begin{aligned} c_{n0}=\sqrt{\frac{2}{\pi }}2^{\frac{k}{2}}\int _{\frac{n-1}{2^{k}}}^{\frac{n}{2^{k}}}u(x)w_{n}(x)\mathrm{d}x =\sqrt{\frac{2}{\pi }}2^{\frac{k}{2}}\frac{\pi }{2^{k+1}}u(\zeta _{n}),\quad \zeta _{n} \in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] . \end{aligned}$$

(24)

By substituting (24) into (23), we obtain

$$\begin{aligned} \Vert e_{n}(x)\Vert ^{2}=\left( u(\zeta _{n})-u(\eta _{n})\right) ^{2}\frac{\pi }{2^{k+1}}. \end{aligned}$$

(25)

Now, since $|u^{\prime }(x)|\le M_{1}$, then it satisfies the Lipschitz condition on each subinterval, i.e.,

$$\begin{aligned} |u(\zeta _{n})-u(\eta _{n})|\le M_{1}|\zeta _{n}-\eta _{n}|, \quad \forall \zeta _{n},\,\eta _{n} \in \left[ \frac{n-1}{2^{k}},\frac{n}{2^{k}}\right] . \end{aligned}$$

(26)

Then from (25) and (26), we have

$$\begin{aligned} \Vert e_{n}(x)\Vert ^{2}\le \frac{\pi M_{1}^{2}}{2^{3k+1}}, \end{aligned}$$

(27)

which leads to

$$\begin{aligned} \Vert \tilde{e}(x)\Vert ^{2}= & {} \int _{0}^{1}\tilde{e}(x)^{2}w_{n}(x)\mathrm{d}x=\int _{0}^{1}\left( \sum _{n=1}^{2^{k}}e_{n}(x)\right) ^{2}w_{n}(x)\mathrm{d}x\nonumber \\= & {} \int _{0}^{1}\left( \sum _{n=1}^{2^{k}}e_{n}(x)^{2}\right) w_{n}(x)\mathrm{d}x+2\sum _{n\le n^{\prime }}\int _{0}^{1}e_{n}(x)e_{n^{\prime }}(x)w_{n}(x)\mathrm{d}x. \end{aligned}$$

(28)

Now, due to disjointness property of these basis functions, we have

$$\begin{aligned} \Vert \tilde{e}(x)\Vert ^{2}=\int _{0}^{1}\left( \sum _{n=1}^{2^{k}}e_{n}(x)^{2}\right) w_{n}(x)\hbox {d}x=\sum _{n=1}^{2^{k}}\Vert e_{n}(x)\Vert ^{2}. \end{aligned}$$

(29)

By substituting (27) into (29), we obtain

$$\begin{aligned} \Vert \tilde{e}(x)\Vert ^{2}\le \frac{\pi M_{1}^{2}}{2^{2k+1}}, \end{aligned}$$

(30)

or, in other words, $\displaystyle \Vert \tilde{e}(t)\Vert =O\left( \frac{1}{2^{k}}\right)$, which completes the proof. $\square$

COROLLARY 3.3

Let $\tilde{u}(x)$ be the expansion of u(x) by the above basis functions, and $\tilde{e}(x)$ be the corresponding error. Then we have

$$\begin{aligned} \Vert \tilde{e}(x)\Vert \le \sqrt{\frac{\pi }{2}}\frac{ M_{1}}{2^{k}}. \end{aligned}$$

(31)

Proof

This is an immediate consequence of Theorem 3.2. $\square$

Remark1

Notice that according to the above information, we have

$$\begin{aligned} \sum _{n=2^{k}+1}^{\infty }c_{n0}^{2}=\Vert \tilde{u}(x)-\sum _{n=1}^{\infty }c_{n0}\psi _{n0}(x)\Vert ^{2}=\Vert \tilde{e}(x)\Vert ^{2}\le \frac{\pi M_{1}^{2}}{2^{2k+1}}. \end{aligned}$$

(32)

In the case $m\ge 1$, it has been proved in [49] that

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \displaystyle |c_{nm}|\le \frac{\sqrt{\pi }M_{1}}{4n^{\frac{3}{2}}}, &{}\quad m=1, \\ |c_{nm}|\le \frac{\sqrt{\pi } M_{2}}{16(n)^\frac{5}{2}(m-1)^{2}}, &{}\quad m>1. \end{array}\right. \end{aligned}$$

(33)

Therefore, the above cases conclude that the series $\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }c_{nm}$ is absolutely convergent, and it follows that $\sum _{n=1}^{\infty }\sum _{m=0}^{\infty }c_{nm}\psi _{nm}(x)$ converges to the function u(x) uniformly. $\square$

Theorem 3.4

Suppose u(x) be a function defined on [0, 1], with bounded first and second derivatives $M_{1}$ and $M_{2}$ respectively, and $C^{T}\Psi (x)$ be its approximation with the CWs. Then for the error bound, we have

$$\begin{aligned} \sigma _{\hat{m}}< & {} \left( \frac{\pi M_{1}^{2}}{2^{2k+1}}+\frac{\pi M_{2}^{2}}{196}\sum _{n=1}^{\infty } \sum _{m=M}^{\infty }a_{nm}+\frac{\pi M_{2}^{2}}{196}\sum _{n=2^{k}+1}^{\infty } \sum _{m=2}^{M-1}a_{nm}\right. \nonumber \\&\left. +\frac{\pi M_{1}^{2}}{16}\sum _{n=2^{k}+1}^{\infty } b_{n}\right) ^{\frac{1}{2}}, \end{aligned}$$

(34)

where

$$\begin{aligned} \sigma _{\hat{m}}= & {} \left( \int _{0}^{1}(u(x)-C^{T}\Psi (x))^{2} w_{n}(x)\mathrm{d}x\right) ^{\frac{1}{2}},\quad a_{nm}=\frac{1}{n^{5}(m-1)^{4}},\\ b_{n}= & {} \frac{1}{n^{3}}. \end{aligned}$$

Proof

By considering definition of $\sigma _{\hat{m}}$, we have

$$\begin{aligned} \sigma ^{2}_{\hat{m}}= & {} \int _{0}^{1}(u(x)-C^{T}\Psi (x))^{2}w_{n}(x)\mathrm{d}x\nonumber \\= & {} \int _{0}^{1}\left( \sum _{n=1}^{\infty } \sum _{m=0}^{\infty }c_{nm}\psi _{nm}(x)- \sum _{n=1}^{2^{k}}\sum _{m=0}^{M-1}c_{nm}\psi _{nm}(x)\right) ^{2}w_{n}(x)\mathrm{d}x\nonumber \\= & {} \int _{0}^{1}\left( \sum _{n=1}^{\infty } \sum _{m=M}^{\infty }c^{2}_{nm}\psi ^{2}_{nm}(x)+\sum _{n=2^{k}+1}^{\infty }\sum _{m=0}^{M-1}c^{2}_{nm}\psi ^{2}_{nm}(x)\right) w_{n}(x)\mathrm{d}x\nonumber \\= & {} \sum _{n=1}^{\infty } \sum _{m=M}^{\infty }c^{2}_{nm}+\sum _{n=2^{k}+1}^{\infty } \sum _{m=0}^{M-1}c^{2}_{nm}=\sum _{n=1}^{\infty } \sum _{m=M}^{\infty }c^{2}_{nm}+\sum _{n=2^{k}+1}^{\infty } \sum _{m=2}^{M-1}c^{2}_{nm}\nonumber \\&+\sum _{n=2^{k}+1}^{\infty }(c^{2}_{n0}+c^{2}_{n1}). \end{aligned}$$

(35)

Now by considering (33), (35) and Remark 1, we achieve the desired result. $\square$

3.4 Operational matrix of fractional order integration

The fractional integration of order $\alpha$ of the vector $\Psi (x)$ defined in (14) can be expressed as

$$\begin{aligned} (I^{\alpha }\Psi )(x)\simeq P^{\alpha }\Psi (x), \end{aligned}$$

(36)

where $P^{\alpha }$ is the $\hat{m}\times \hat{m}$ operational matrix of fractional integration of order $\alpha$. In [37], Li has derived an explicit form of this matrix by employing block pulse functions. In the sequel, we derive a more accurate explicit form of the matrix $P^{\alpha }$. To this end, we need to introduce another family of basis functions, namely hat functions (HFs). An $\hat{m}$-set of these basis functions is defined on the interval [0, 1] as [52]

$$\begin{aligned} \displaystyle \phi _{0}(x)= & {} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{h-x}{h}, &{} 0\le x< h, \\ 0, &{} \mathrm{o.w.}, \end{array} \right. , \end{aligned}$$

(37)

$$\begin{aligned} \displaystyle \phi _{i}(x)= & {} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{x-(i-1)h}{h}, &{} (i-1)h\le x< ih, \\ \displaystyle \frac{(i+1)h-x}{h}, &{} ih\le x< (i+1)h, \\ 0, &{} \mathrm{o.w.}, \end{array}\quad i=1,2,\ldots ,\hat{m}-2,\right. \nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} \displaystyle \phi _{\hat{m}-1}(x)= & {} \left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{x-(1-h)}{h}, &{} 1-h\le x\le 1, \\ 0, &{} \mathrm{o.w.}, \end{array} \right. \end{aligned}$$

(39)

where $h=\frac{1}{\hat{m}-1}$. From the definition of the HFs, we have

$$\begin{aligned} \displaystyle \phi _{i}(jh)=\left\{ \begin{array}{l@{\quad }l} 1, &{} i=j, \\ 0, &{} i\ne j. \end{array} \right. \end{aligned}$$

(40)

An arbitrary function u(x) defined on the interval [0, 1] can be expanded by the HFs as

$$\begin{aligned} u(x)\simeq \sum _{i=0}^{\hat{m}-1}u_{i}\phi _{i}(x)=U^{T}\Phi (x)=\Phi (x)^{T}U, \end{aligned}$$

(41)

where

$$\begin{aligned} U\triangleq [u_{0},u_{1},\ldots ,u_{\hat{m}-1}]^{T} \end{aligned}$$

(42)

and

$$\begin{aligned} \Phi (x)\triangleq [\phi _{0}(x),\phi _{1}(x),\ldots ,\phi _{\hat{m}-1}(x)]^{T}. \end{aligned}$$

(43)

The important aspect of using the HFs in approximating a function u(x) lies in the fact that the coefficients $u_{i}$ in (41) are given by

$$\begin{aligned} u_{i}=u(ih),\,\, i=0,1,\ldots ,\hat{m}-1. \end{aligned}$$

(44)

By considering (41) and (44), it can be simply seen that the CWs can be expanded in terms of an $\hat{m}$-set of HFs as

$$\begin{aligned} \Psi (x)\simeq \Phi _{\hat{m}\times \hat{m}}\Phi (x). \end{aligned}$$

(45)

In [52], the authors have given the HFs operational matrix of fractional integration $F^{\alpha }$ as

$$\begin{aligned} (I^{\alpha }\Phi )(x)\simeq F^{\alpha } \Phi (x), \end{aligned}$$

(46)

where

$$\begin{aligned} \displaystyle F^{\alpha }=\frac{h^{\alpha }}{\Gamma (\alpha +2)}\left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 0 &{} \zeta _{1} &{} \zeta _{2} &{} \ldots &{}\zeta _{\hat{m}-2} &{} \zeta _{\hat{m}-1} \\ 0 &{} 1 &{} \xi _{1} &{} \ldots &{} \xi _{\hat{m}-3} &{} \xi _{\hat{m}-2} \\ 0 &{} 0 &{} 1 &{} \ldots &{} \xi _{\hat{m}-4}&{} \xi _{\hat{m}-3} \\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} \xi _{1} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \end{array}\right) _{\hat{m}\times \hat{m}} \end{aligned}$$

(47)

and

$$\begin{aligned} \displaystyle \left\{ \begin{array}{ll} \displaystyle \zeta _{i}=i^{\alpha }\left( \alpha -i+1\right) +(i-1)^{\alpha +1}, &{} i=1,2,\ldots ,\hat{m}-1, \\ \displaystyle \xi _{i}=(i+1)^{\alpha +1}-2i^{\alpha +1}+(i-1)^{\alpha +1}, &{} i=1,2,\ldots ,\hat{m}-2. \end{array}\right. \end{aligned}$$

(48)

Now by considering (36), and using (45) and (46) we obtain

$$\begin{aligned} \left( I^{\alpha }\Psi \right) (x)\simeq \left( I^{\alpha }\Phi _{\hat{m}\times \hat{m}}\Phi \right) (x)=\Phi _{\hat{m}\times \hat{m}}\left( I^{\alpha }\Phi \right) (x)\simeq \Phi _{\hat{m}\times \hat{m}}F^{\alpha }\Phi (x). \end{aligned}$$

(49)

Moreover, from (36) and (49), we have

$$\begin{aligned} P^{\alpha }\Psi (t)\simeq \Phi _{\hat{m}\times \hat{m}}F^{\alpha }\Phi (t). \end{aligned}$$

(50)

Thus, by considering (45) and (50), we obtain the CWs operational matrix of fractional integration as

$$\begin{aligned} P^{\alpha }\simeq \Phi _{\hat{m}\times \hat{m}}F^{\alpha }\Phi _{\hat{m}\times \hat{m}}^{-1}. \end{aligned}$$

(51)

Therefore, we have found the operational matrix of fractional integration for the CWs. To illustrate the calculation procedure, we choose $\alpha =\frac{1}{2},\,k=1,\,M=3$. Thus we have

$$\begin{aligned}&P^{\left( \frac{1}{2}\right) }=\left( \begin{array}{cccccc} 0.469128&{} 0.250070&{}- 0.0816500&{} 0.454110&{}- 0.108884&{} 0.0224214\\ - 0.0152413&{} 0.191786&{} 0.202564&{} 0.0460971&{}- 0.0403113&{} 0.0119599 \\ - 0.226168&{}- 0.148001&{} 0.0119244&{}- 0.197621&{} 0.0511399&{}- 0.0105525\\ 0.0&{} 0.0&{} 0.0&{} 0.516567&{} 0.224842&{}- 0.0268650\\ 0.0&{} 0.0&{} 0.0&{}- 0.0592536&{} 0.215309&{} 0.109890\\ 0.0&{} 0.0&{} 0.0&{}- 0.146220&{}- 0.144772&{} 0.277383 \end{array} \right) . \end{aligned}$$

3.5 Some useful results for the CWs

In this section, by employing some properties of the HFs, we derive an useful theorem for the CWs, which will be used in this paper. From now on, for any two constant vectors $C^{T}=[c_{1},c_{2},\ldots ,c_{\hat{m}}]$ and $D^{T}=[d_{1},d_{2},\ldots ,d_{\hat{m}}]$, we define $C^{T}\odot D^{T}=[c_{1}d_{1},c_{2}d_{2},\ldots ,c_{\hat{m}}d_{\hat{m}}]$ and $G\left( C^{T}\right) =[G(c_{1}),G(c_{2}),\ldots ,G(c_{\hat{m}})]$ for any analytic function G.

Lemma 3.5

Suppose $\tilde{C}^{T}\Phi (x)$ and $\tilde{D}^{T}\Phi (x)$ be the expansions of u(x) and v(x) by the HFs, respectively. Then we have

$$\begin{aligned} u(x)v(x)\simeq (\tilde{C}^{T}\odot \tilde{D}^{T})\Phi (x). \end{aligned}$$

(52)

Proof

By considering (41) and (44), we have

$$\begin{aligned} u(x)\simeq & {} \sum _{i=0}^{\hat{m}-1}u(ih)\phi _{i}(x)=\tilde{C}^{T}\Phi (x),\\ v(x)\simeq & {} \sum _{i=0}^{\hat{m}-1}v(ih)\phi _{i}(x)=\tilde{D}^{T}\Phi (x) \end{aligned}$$

and

$$\begin{aligned} u(x)v(x)\simeq \sum _{i=0}^{\hat{m}-1}u(ih)v(ih)\phi _{i}(x)=(\tilde{C}^{T}\odot \tilde{D}^{T})\Phi (x), \end{aligned}$$

which completes the proof. $\square$

COROLLARY 3.6

Suppose $\tilde{C}^{T}\Phi (x)$ be the expansion of u(x) by the HFs. Then for any integer $q\ge 2$, we have

$$\begin{aligned}{}[u(x)]^{q}\simeq [\tilde{c}_{0}^{q},\tilde{c}_{1}^{q},\ldots ,\tilde{c}_{\hat{m}-1}^{q}]\Phi (x). \end{aligned}$$

(53)

Proof

From Lemma 3.5, we have

$$\begin{aligned}{}[u(x)]^{2}\simeq [\tilde{c}_{0}^{2},\tilde{c}_{1}^{2},\ldots ,\tilde{c}_{\hat{m}-1}^{2}]\Phi (x), \end{aligned}$$

and by induction, we obtain

$$\begin{aligned}{}[u(x)]^{q}\simeq [\tilde{c}_{0}^{q},\tilde{c}_{1}^{q},\ldots ,\tilde{c}_{\hat{m}-1}^{q}]\Phi (x), \quad q>2. \end{aligned}$$

This completes the proof. $\square$

Theorem 3.7

Suppose G be an analytic function and $\tilde{C}^{T}\Phi (x)$ be the expansion of u(x) by the HFs. Then we have

$$\begin{aligned} G\left( u(x)\right) \simeq G(\tilde{C}^{T})\Phi (x). \end{aligned}$$

(54)

Proof

Since G is an analytic function, by considering Maclaurin expansion of G, i.e. $\displaystyle G(x)=\sum \nolimits _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}x^{q}$, we have

$$\begin{aligned} G\left( u(x)\right) =\sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}\left[ u(x)\right] ^{q}. \end{aligned}$$

(55)

Now, from Corollary 3.6 and relation (55), we have

$$\begin{aligned} G\left( u(x)\right)\simeq & {} \sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}[u_{0}^{q},u_{1}^{q},\ldots ,u_{\hat{m}-1}^{q}]\Phi (x)\\= & {} \left[ \sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}u_{0}^{q},\sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}u_{1}^{q},\ldots ,\sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}u_{\hat{m}-1}^{q}\right] \Phi (x). \end{aligned}$$

Due to the fact that the series in the left-hand side is absolutely and uniformly convergent to G(u), each series in the right-hand side is also absolutely and uniformly convergent to $G\left( u_{i}\right)$, i.e.,

$$\begin{aligned} G\left( u(x)\right)\simeq & {} \left[ \sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}u_{0}^{q},\sum _{q=0}^{\infty }\frac{G^{(q)} (0)}{q!}u_{1}^{q},\ldots ,\sum _{q=0}^{\infty }\frac{G^{(q)}(0)}{q!}u_{\hat{m}-1}^{q}\right] \Phi (x)\\= & {} [G(u_{0}),G(u_{1}),\ldots ,G(u_{\hat{m}-1})]\Phi (x). \end{aligned}$$

Thus we have

$$\begin{aligned} G\left( u(x)\right) \simeq \left[ G(u_{0}),G(u_{1}),\ldots ,G(u_{\hat{m}-1})\right] \Phi (x)=G(\tilde{C}^{T})\Phi (x), \end{aligned}$$

which completes the proof. $\square$

Theorem 3.8

Suppose G be an analytic function and $C^{T}\Psi (x)$ be the expansion of u(x) by the CWs. Then we have

$$\begin{aligned} G\left( u(x)\right) \simeq G(\tilde{C}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (x), \end{aligned}$$

(56)

where

$$\begin{aligned} \tilde{C}^{T}=C^{T}\Phi _{\hat{m}\times \hat{m}}. \end{aligned}$$

Proof

By considering equation (45) and Theorem 3.7, we have

$$\begin{aligned} G\left( u(x)\right)\simeq & {} G(C^{T}\Psi (x))\nonumber \\\simeq & {} G(C^{T}\Phi _{\hat{m}\times \hat{m}}\Phi (x))=G(\tilde{C}^{T}\Phi (x))\simeq G(\tilde{C}^{T})\Phi (x). \end{aligned}$$

(57)

So from (45) and (57), we have

$$\begin{aligned} G\left( u(x)\right) \simeq G(\tilde{C}^{T})\Phi (x)\simeq G(\tilde{C}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (x), \end{aligned}$$

(58)

which completes the proof. $\square$

COROLLARY 3.9

Suppose $C^{T}\Psi (x)$ and $D^{T}\Psi (x)$ be expansions of u(x) and v(x) by the CWs, respectively and also G and H be two analytic functions. Then we have

$$\begin{aligned} G\left( u(x)\right) H\left( v(x)\right) \simeq (G(\tilde{C}^{T})\odot H(\tilde{D}^{T}))\Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (x), \end{aligned}$$

(59)

where

$$\begin{aligned} \tilde{C}^{T}=C^{T}\Phi _{\hat{m}\times \hat{m}},\qquad \tilde{D}^{T}=D^{T}\Phi _{\hat{m}\times \hat{m}}. \end{aligned}$$

Proof

By considering Theorem 3.8 and equation (45) and Lemma 3.5, the proof will be straightforward. $\square$

4 Description of the proposed method

In this section, we apply the operational matrix of fractional integration for the CWs together with the series expansion and useful properties of these basis functions for solving NMFDE (1). The main idea of the proposed method is as follows:

• (1) The NMFDE (1) is converted to a fully integrated form via fractional integration in the Riemann–Liouville sense.

• (2) The integrated form of the equation is approximated using a linear combination of the CWs.

• (3) Finally, the integrated form of the equation is converted to a nonlinear algebraic equation, by introducing the operational matrix of fractional integration for the CWs and employing some useful properties of these basis functions, which were mentioned in the subsection 3.5.

In the following we show the importance of the proposed method. Applying the Riemann–Liouville fractional integration of order $\alpha$ on both sides of (1), yields

$$\begin{aligned}&u(x)-\sum _{j=0}^{q-1}u^{(j)}\left( 0^{+}\right) \frac{x^{j}}{j!}+\sum _{i=1}^{s}\gamma _{i}I^{\alpha -\alpha _{i}}\left[ u(x)-\sum _{j=0}^{q_{i}-1}u^{(j)}\left( 0^{+}\right) \frac{x^{j}}{j!}\right] \nonumber \\&\quad +\,I^{\alpha }G(u(x))=I^{\alpha }f(x), \end{aligned}$$

(60)

where $q_{i}-1<\alpha _{i}\le q_{i}$, $q_{i}\in \mathbb {N}$. By considering (2) and (60), we obtain the following fractional integral equation:

$$\begin{aligned} u(x)+\sum _{i=1}^{s}\gamma _{i}I^{\alpha -\alpha _{i}}u(x)+I^{\alpha }G(u(x))=g(x), \end{aligned}$$

(61)

where

$$\begin{aligned} g(x)=I^{\alpha }f(x)+\sum _{j=0}^{q-1}d_{j}\frac{x^{j}}{j!}+\sum _{i=1}^{s}\gamma _{i}I^{\alpha -\alpha _{i}}\left( \sum _{j=0}^{q_{i}-1}d_{j}\frac{x^{j}}{j!}\right) . \end{aligned}$$

In order to use the Galerkin method with the CWs for solving the integrated problem (61), we approximate u(x) and g(x) by the CWs as follows:

$$\begin{aligned} u(x)\simeq C^{T}\Psi (x) \end{aligned}$$

(62)

and

$$\begin{aligned} g(x)\simeq \tilde{G}^{T}\Psi (x), \end{aligned}$$

(63)

where the vector $\tilde{G}=[g_{1},g_{2},\ldots ,g_{\hat{m}}]$ is given, but $C=[c_{1},c_{2},\ldots ,c_{\hat{m}}]$ is an unknown vector. Also, from Theorem 3.8, we have

$$\begin{aligned} G\left( u(x)\right) \simeq G(\tilde{C}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (x), \end{aligned}$$

(64)

where $\tilde{C}^{T}=C^{T}\Phi _{\hat{m}\times \hat{m}}$. Now, the Riemann–Liouville fractional integration of orders $(\alpha -\alpha _{i})$ and $\alpha$ of the approximate solution (62) and (64) can be written as

$$\begin{aligned} I^{\alpha -\alpha _{i}}u(x)\simeq C^{T}P^{(\alpha -\alpha _{i})}\Psi (x),\quad i=1,2,\ldots ,s \end{aligned}$$

(65)

and

$$\begin{aligned} I^{\alpha }G\left( u(x)\right) \simeq G(\tilde{C}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}P^{\alpha }\Psi (x), \end{aligned}$$

(66)

respectively, where $P^{\alpha }$ is the $\hat{m}\times \hat{m}$ operational matrix of fractional integration of order $\alpha$. By employing equations (62)–(66), we can write the residual function R(x) for equation (61) as follows:

$$\begin{aligned} R(x)=\left( C^{T}+C^{T}\sum _{i=1}^{s}\gamma _{i}P^{(\alpha -\alpha _{i})}+G(\tilde{C}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}P^{\alpha }-\tilde{G}^{T}\right) \Psi (x). \end{aligned}$$

(67)

As in a typical Galerkin method [8], we generate $\hat{m}$ nonlinear algebraic equations by applying

$$\begin{aligned} \left( R(x),\psi _{j}(x)\right) _{w_{n}}=\int _{0}^{1}R(x)\psi _{j}(x)w_{n}(x)\mathrm{d}x=0,\quad j=1,2,\ldots ,\hat{m}, \end{aligned}$$

(68)

where $\psi _{j}(x)=\psi _{nm}(x)$ and the index j is determined by the relation $j=M(n-1)+m+1$. These system of nonlinear equations can be solved for the unknown coefficients of the vector C. Consequently, u(x) given in (62) can be calculated.

5 Numerical examples

In this section, we demonstrate the efficiency and accuracy of the proposed method for some numerical examples in the form (1). To show the accuracy of the proposed method, we use the absolute error in some different points in cases that we have the exact solutions as

$$\begin{aligned} |e(x_{i})|=|u(x_{i})-\tilde{u}(x_{i})|, \end{aligned}$$

where u(x) is the exact solution and $\tilde{u}(x)$ is the approximate solution which is obtained by relation (62).

Example1

First, let us consider the NMFDE:

$$\begin{aligned} D_{*}^{\alpha }u(x)+D_{*}^{\alpha -1}u(x)+\sinh (u(x))=f(x), \quad 1<\alpha \le 2,\,\,\,\,x\in [0,3], \end{aligned}$$

where

$$\begin{aligned} f(x)=-\frac{3}{ 2(1+\,{x}^{2})} +{\frac{4{x}^{2}}{ \left( 1+{ x}^{2} \right) ^{2}}}-{\frac{2x}{1+{x}^{2}}}-\frac{1}{2}-\frac{1}{2}\,{x}^{2}, \end{aligned}$$

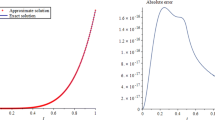
subject to the initial conditions $u(0)=u^{\prime }(0)=0$. Figure 1 shows the behavior of the numerical solution for $\hat{m}=96\,(k=4,\,M=6)$. The exact solution of this problem when $\alpha =2$ is $u(x)=-\ln \left( 1+x^{2}\right)$. From this figure, it can be seen that the numerical solution is in a very good agreement with the exact solution in the case $\alpha =2$. Therefore, we hold that the solutions for $\alpha =1.25,\,1.50$ and $\alpha =1.75$ are also credible.

Fig. 1

Numerical solutions of Example 1 for $\hat{m}=96$ and some values of $1<\alpha \le 2$.

Example2

Consider the NMFDE:

$$\begin{aligned} D_{*}^{\alpha }u(x)+D_{*}^{\beta }u(x)+[u(x)]^{2}=f(x),\quad 1<\alpha \le 2,\,\,\,\,0<\beta \le 1, \end{aligned}$$

where

$$\begin{aligned} f(x)= ( {x}^{2}-x ) ^{2}+{\frac{2{x}^{2-\alpha }}{\Gamma \left( 3-\alpha \right) }}+{\frac{2{x}^{2-{ \beta }}}{\Gamma \left( 3-{ \beta } \right) }}-{\frac{{x}^{1-{ \beta }}}{ \Gamma \left( 2-{ \beta } \right) }}, \end{aligned}$$

subject to the initial conditions $u(0)=0,\,u^{\prime }(0)=-1$. The exact solution for this problem is $u(x)=x^{2}-x$. The behavior of the numerical solutions for $k=2$ and some different values of M with $\alpha =1.75$ and $\beta =0.5$ are shown in figure 2. This figure shows that by increasing M as the degree of the Chebyshev polynomials, the approximate solutions tend to the exact solution faster. Also, in order to show the accuracy of the proposed method (using the new operational matrix of fractional order integration), a comparison between the absolute errors arising by our method via CWs method in [37] for $\alpha =2$, $\beta =0.5$ with $M=4$ and some different values of k in various values of $x_{i}$ is performed in Table 1. From this table, it can be seen that the absolute errors obtained by our method are less than the error obtained by CWs method in [37]. It illustrates that our method is more accurate. From table 1, we also observe that the proposed method can provide numerical results with high accuracy for this problem. Furthermore, it can be seen that as more basis functions are used, we obtain a good approximate solution with higher accuracy. This table also shows that ‘The spectral accuracy’ holds for the proposed method. So, we conclude that our method is suitable for this problem and also by increasing the number of the CWs, the accuracy of the obtained result is improved.

Fig. 2

Comparison between the approximate and exact solutions of Example 2 for some different values of M.

Table 1 The absolute errors of our method and CWs method [37] for some different values of k for Example 2.

Example3

Consider the NMFDE [15, 37]:

$$\begin{aligned}&aD_{*}^{2.0}u(x)+bD_{*}^{\alpha _{2}}u(x)+cD_{*}^{\alpha _{1}}u(x)+e[u(x)]^{3}=f(x),\quad \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \! 0<\alpha _{1}\le 1,\,\,\,\,1<\alpha _{2}\le 2, \end{aligned}$$

where

$$\begin{aligned} f(x)=2\,ax+{\frac{2b}{\Gamma \left( 4-{ \alpha _{2}} \right) }{x}^{3-{ \alpha _{2}}}}+{\frac{2c}{\Gamma \left( 4-{ \alpha _{1}} \right) }{x}^{3-{ \alpha _{1}}}}+\frac{e}{27}{x}^{9}, \end{aligned}$$

subject to the initial conditions $u(0)=u^{\prime }(0)=0$. The exact solution for this problem is $u(x)=\frac{1}{3}x^{3}$. This problem is now solved by the proposed method for $a=b=c=e=1,\,\alpha _{1}=0.333$ and $\alpha _{2}=1.234$. The behavior of the numerical solutions for $M=2$ and some different values of k are shown in figure 3. From this figure, one can see that by increasing the number of the CWs basis functions, the approximate solutions converge to the exact solution with a good speed. In order to show the accuracy of the proposed method, a comparison between the absolute errors arising by our method via CWs method in [37] for different values of k and M in various values of $x_{i}$ is performed in table 2. From this table, it can seen that the absolute errors obtained by our method are less than the error obtained by CWs method in [37]. It illustrates that our method is more accurate. Table 2 also shows that the proposed method can provide approximate solutions with high accuracy for the problem under study. Furthermore, it can be seen that by increasing the number of basis functions a good approximate solution with higher accuracy will be obtained for this problem. This table also shows that ‘The spectral accuracy’ holds for the proposed method. However, it can be concluded that the proposed method is a suitable tool for this problem.

Fig. 3

Comparison between the approximate and exact solutions of Example 3 for some different values of k.

Table 2 The absolute errors of our method and CWs method [37] for some different values of k and M for Example 3.

Example4

Finally, consider the NMFDE [15, 37]:

$$\begin{aligned} D_{*}^{2}u(x)+0.5D_{*}^{1.5}u(x)+0.5[u(x)]^{3}=f(x),\quad x>0, \end{aligned}$$

where

$$\begin{aligned} f(x)=\left\{ \begin{array}{l@{\quad }l} 8,&{} 0\le x\le 1, \\ 0, &{} x>1, \end{array} \right. \end{aligned}$$

subject to the initial conditions $u(0)=u^{\prime }(0)=0$. This is a Bagley–Torvik equation where the nonlinear term $u^{3}(x)$ is introduced. This problem has been solved in [15, 37]. The behavior of the approximate solution for this problem with $\hat{m}=96$ is shown in figure 4 which is in a good agreement with the obtained numerical solutions in [15, 37]. This demonstrates the importance of our method in solving nonlinear multi-order differential equations.

Fig. 4

The behavior of the approximate solution for Example 4.

6 Application for nonlinear fractional order VPO equation

The VPO represents a nonlinear system with an interesting behavior that arises naturally in several applications. In the standard form, it is given by a nonlinear differential equation [9, 34]

$$\begin{aligned} u^{\prime \prime }(t)+\mu (u^{2}(t)-1)u^{\prime }(t)+u(t)=0, \end{aligned}$$

(69)

where $\mu >0$ is the control parameter. Equation (69) is commonly referred to as the unforced VPO equation [19]. The VPO with a forcing term f(t) is given by [19]

$$\begin{aligned} u^{\prime \prime }(t)+\mu (u^{2}(t)-1)u^{\prime }(t)+u(t)=f(t). \end{aligned}$$

(70)

In recent years, the VPO equation and its special properties have been investigated by many authors (for instance, see [3, 6]). A modified version of the classical VPO was proposed by the fractional derivative of order $\alpha$ in the state space formulation of equation (70). It has the following form [34]

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle D_{*}^{\alpha }u_{1}(t)=u_{2}(t),\quad 0<\alpha <1, \\ \displaystyle \frac{du_{2}(t)}{dt}=f(t)-u_{1}(t)-\mu (u_{1}^{2}(t)-1)u_{2}(t), \end{array}\right. \end{aligned}$$

(71)

with the initial conditions $u_{i}(0)=d_{i} \,(i=1,2)$. In order to use the proposed method in section 4, we consider the integral form of (71) as

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle u_{1}(t)=d_{1}+I^{\alpha }u_{2}(t),\quad 0<\alpha <1, \\ \displaystyle u_{2}(t)=d_{2}+If(t)-I\{u_{1}(t)+\mu (u_{1}^{2}(t)-1)u_{2}(t)\}. \end{array}\right. \end{aligned}$$

(72)

Now, we approximate $u_{1}(t)$ and $u_{2}(t)$ by the CWs as

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle u_{1}(t)\simeq U_{1}^{T}\Psi (t), \\ \displaystyle u_{2}(t)\simeq U_{2}^{T}\Psi (t). \end{array}\right. \end{aligned}$$

(73)

Also from Theorem 3.8 and Corollary 3.9, we have

$$\begin{aligned} u_{1}^{2}(t)u_{2}(t)\simeq ( (\tilde{U}_{1}^{T})^{2}\odot \tilde{U}_{2}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1}\Psi (t), \end{aligned}$$

(74)

where

$$\begin{aligned} \begin{array}{ll} \tilde{U}_{1}^{T}=U_{1}^{T}\Phi _{\hat{m}\times \hat{m}},&\tilde{U}_{2}^{T}=U_{2}^{T}\Phi _{\hat{m}\times \hat{m}}. \end{array} \end{aligned}$$

Moreover, we can approximate the function f(t) by the CWs as follows:

$$\begin{aligned} f(t)\simeq \hat{F}^{T}\Psi (t), \end{aligned}$$

(75)

where $\hat{F}$ is a given known vector. Now by substituting (73)–(75) into (72), and using operational matrix of fractional order integration, we obtain

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle U_{1}^{T}\Psi (t)\simeq d_{1}e^{T}\Psi (t)+ U_{2}^{T}P^{\alpha }\Psi (t), \\ \displaystyle U_{2}^{T}\Psi (t)\simeq d_{2}e^{T}\Psi (t)+ \hat{F}^{T}P\Psi (t) \\ \quad -((U_{1}^{T}+\mu ((\tilde{U}_{1}^{T})^{2}\odot \tilde{U}_{2}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1} -\mu U_{2}^{T})P)\Psi (t), \end{array}\right. \end{aligned}$$

(76)

where e is the coefficient vector of unit step function using CWs. Now, from (76), we can write the residual function $R_{1}(t)$ and $R_{2}(t)$ for system (72) as follows:

$$\begin{aligned}&\left\{ \begin{array}{l} R_{1}(t)= (U_{1}^{T}- d_{1}e^{T}- U_{2}^{T}P^{\alpha })\Psi (t), \\ R_{2}(t)=(U_{2}^{T}-d_{2}e^{T}-\hat{F}^{T}P+(U_{1}^{T}+\mu ((\tilde{U}_{1}^{T})^{2}\odot \tilde{U}_{2}^{T})\Phi _{\hat{m}\times \hat{m}}^{-1} -\mu U_{2}^{T})P)\Psi (t) . \end{array}\right. \nonumber \\ \end{aligned}$$

(77)

As in a typical Galerkin method [8], we generate $2\hat{m}$ nonlinear algebraic equations by applying

$$\begin{aligned} \displaystyle \left\{ \begin{array}{c} \displaystyle \left( R_{1}(t),\psi _{j}(t)\right) _{w_{n}}=\int _{0}^{1}R_{1}(t)\psi _{j}(t)w_{n}(t)\mathrm{d}t=0,\quad j=1,2,\ldots , \hat{m},\\ \displaystyle \left( R_{2}(t),\psi _{j}(t)\right) _{w_{n}}=\int _{0}^{1}R_{2}(t)\psi _{j}(t)w_{n}(t)\mathrm{d}t=0,\quad j=1,2,\ldots ,\hat{m}, \end{array}\right. \end{aligned}$$

(78)

where $\psi _{j}(t)=\psi _{nm}(t)$, and the index j is determined by the relation $j=M(n-1)+m+1$. These systems of nonlinear algebraic equations can be solved for the unknown coefficients of the vector $U_{1}$ and $U_{2}$. Consequently, $u_{1}(t)$ and $u_{2}(t)$ given in (73) can be calculated.

Example5

Consider the following fractional Van der Pol equation [34]

Fig. 5

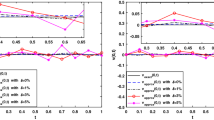
The behavior of the approximate solutions for Example 5.

Fig. 6

The behavior of the approximate solutions for Example 6.

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle D_{*}^{\alpha }u_{1}(t)=u_{2}(t), \\ \displaystyle \frac{du_{2}(t)}{dt}=-u_{1}(t)-0.5u_{1}^{2}(t)u_{2}(t)+0.5u_{2}(t), \end{array}\right. \end{aligned}$$

with the initial conditions

$$\begin{aligned} u_{1}(0)=0,\quad u_{2}(0)=1. \end{aligned}$$

The behavior of the approximate solutions for this problem with $\hat{m}=48$ and two different values of $\alpha$ is shown in figure 5, which is in a good agreement with the numerical solutions in [34]. This demonstrates the importance of our method in solving nonlinear fractional order Van der Pol equation.

Example6

Finally, consider the following fractional Van der Pol equation [34]

$$\begin{aligned} \displaystyle \left\{ \begin{array}{l} \displaystyle D_{*}^{\alpha }u_{1}(t)=u_{2}(t), \\ \displaystyle \frac{\mathrm{d}u_{2}(t)}{\mathrm{d}t}=2\cos (t)-\cos ^{3}(t)-u_{1}(t)-u_{1}^{2}(t)u_{2}(t)-u_{2}(t), \end{array}\right. \end{aligned}$$

with the initial conditions

$$\begin{aligned} u_{1}(0)=0,\quad u_{2}(0)=1. \end{aligned}$$

The exact solution for this problem in the case $\alpha =1$ is $u(t)=\sin (t)$. The behavior of the approximate solutions for this problem with $\hat{m}=48$ and two different values of $\alpha$ is shown in figure 6, which is in a good agreement with the numerical solutions in [34]. This demonstrates the importance of our method in solving nonlinear fractional order Van der Pol equation.

7 Conclusion

In this work, a new operational matrix of fractional order integration for the CWs was derived and applied to solve nonlinear multi-order fractional differential equations. Several examples were given to demonstrate the powerfulness of the proposed method. The underlying problems have been reduced to systems of nonlinear algebraic equations. The obtained results were compared with exact solutions and also with the solutions obtained by the CWs method in [37]. It is worth mentioning that the results obtained by the proposed method were in a good agreement with those obtained using the CWs method in [37]. The numerical results illustrated the efficiency and accuracy of the presented scheme for solving nonlinear multi-order fractional differential equations. Furthermore, as a useful application, the proposed method was applied to obtain approximate solution of the fractional order VPO equation.