Application of quintic B-splines collocation method for solving inverse Rosenau equation with Dirichlet’s boundary conditions

Abstract

In this paper, we discuss a numerical method for solving an inverse Rosenau equation with Dirichlet’s boundary conditions. The approach used is based on collocation of a quintic B-spline over finite elements so that we have continuity of dependent variable and it first four derivatives throughout the solution range. We apply quintic B-spline for spatial variable and derivatives which produce an ill-posed system. We solve this system using Tikhonov regularization method. The accuracy of the proposed method is demonstrated by applying it on a test problem. Figures and comparisons have been presented for clarity. The main advantage of the resulting scheme is that the algorithm is very simple, so it is very easy to implement.

1 Introduction

There has been an overwhelming amount of solutions to the nonlinear evolution equations (NLEEs) obtained in the past few decades using several and newly developed techniques of integration [1,2,3,4]. Some of these nonlinear wave solutions are the cnoidal waves, solitons, solitary waves, shock waves, compactons, stumpons, covatons, cuspons, peakons propeller solitons and several many others; see [5,6,7,8,9,10,11] and references therein. These solutions are all indeed very useful in various areas of applied mathematics and theoretical physics to study the evolution and behavior of the associated solutions (where the exact solution is unlikely to find). In fact, these show up sporadically in plasma physics, nonlinear optics, nuclear physics, fluid dynamics, telecommunications engineering, mathematical biology, mathematical chemistry, mathematical physics just to name a few (see for example [1,2,3,4,5,6,7,8,9,10,11] and references therein).

The Korteweg–de Vries (K-dV) equation is one of the most important problems in nonlinear evolution equations, which models the plane waves with unidirectional propagation in several nonlinear dispersive media. Since the K-dV equation is modelled to describe a unidirectional propagation of waves, it does not treat well wave–wave, wave–wall interactions. Furthermore, because it is derived under the assumption of weakly anharmonic discrete lattice, it may not predict the behavior of high-amplitude waves. To overcome these shortcomings, Rosenau [12, 13] has developed a model called the Rosenau equation, to describe the dynamics of dense discrete systems which leads to a continuum. The equation is expressed as

$$\begin{aligned} u_{t}+u_{xxxxt}=f(u)_{x},\quad (x,t)\in \Omega \times [0,T], \end{aligned}$$

with boundary conditions

$$\begin{aligned} u(x,t)=u_{x}(x,t)=0, \quad (x,t)\in \partial \Omega \times [0,T], \end{aligned}$$

and an initial condition

$$\begin{aligned} u(x,0)=u_{0}(x), \quad x\in \bar{\Omega }, \end{aligned}$$

here $\bar{\Omega }=[0,1]$ and T is a positive real number. The theoretical results on existence, uniqueness and regularity of solutions to this equation have been investigated by Park [14] for more general functions $f \in C^{2}(\mathbb {R})$. A lot of work has been done on the numerical method for the Rosenau equation [15,16,17].

Driven by the needs from applications both in industry and other sciences, the field of inverse problems has undergone a tremendous growth within the last two decades, where recent emphasis has been laid more than before on nonlinear problems. This is documented by the wide current literature on regularization methods for the solution of nonlinear ill-posed problems. Advances in this theory and the development of sophisticated numerical techniques for treating the direct problems allow to address and solve industrial inverse problems on a level of high complexity. Generally these problems belong to the class of problems called the ill-posed problems, i.e., small errors in the measured data can lead to large derivations in the estimated quantities. As a consequence, their solution does not satisfy the general requirement of existence, uniqueness, and stability under small changes to the input data. To overcome such difficulties, a variety of techniques for solving inverse problems have been proposed [18]-[24] and among the most versatile methods the following can be mentioned: Tikhonov regularization [25], iterative regularization [26], mollification [27], base function method (BFM) [28], semi finite difference method (SFDM) [29] and the function specification method (FSM) [30].

Zhou et al. [31] investigated the inverse heat conduction problem in a one-dimensional composite slab with rate-dependent pyrolysis chemical reaction and outgassing flow effects using the iterative regularization approach. They considered the thermal properties of the temperature-dependent composites.

Huang et al. [32] applied an iterative regularization method based inverse algorithm in this study in simultaneously determining the unknown temperature and concentration-dependent heat and mass production rates for a chemically reacting fluid using interior measurements of temperature and concentration.

The theory of spline functions is very active field of approximation theory, boundary value problems and partial differential equations, when numerical aspects are considered. In a series of papers by Caglar et al. [33, 34] boundary value problems are solved using B-splines. In addition, Caglar et al. [35] have used third-degree B-spline functions for the solution of heat equation and Mittal and Jain [36] have used quintic B-spline functions for the solution of Rosenau equation.

In this paper, we consider the mathematical model of nonlinear inverse higher order evolution equation

$$\begin{aligned} u_t+\mu u_{xxxxt}=f(u)_{x}, \quad (x,t)\in \Omega \times [0,T], \end{aligned}$$

(1.1)

where $f(u)_{x}$ is some nonlinear expression in terms of $u,~u_x$ with boundary conditions

$$\begin{aligned} u(0,t)=f_{1}(t), \quad u_{x}(0,t)=f_{2}(t), \quad t\in [0,T], \end{aligned}$$

(1.2)

$$\begin{aligned} u(1,t)=g_{1}(t), \quad u_{x}(1,t)=g_{2}(t), \quad t\in [0,T], \end{aligned}$$

(1.3)

and initial condition

$$\begin{aligned} u(x,0)=u_{0}(x), \quad x\in \bar{\Omega }, \end{aligned}$$

(1.4)

here $\Omega =(0,1), \quad \bar{\Omega }=[0,1]$, $\mu>0$ and the overspecified conditions

$$\begin{aligned} u(\alpha ,t)=p_{1}(t), \quad u_{x}(\alpha ,t)=p_{2}(t), \quad t\in [0,T], \end{aligned}$$

(1.5)

where $0<\alpha <1$ is a fixed point, $g_{1}(x),~ g_{2}(x)$ are continuous known functions, $p_{1}(t),~p_{2}(t)$ and $u_{0}(x)$ are known functions and T represents the final time, while the functions $f_{1}(t),~ f_{2}(t)$ are unknown which remains to be determined from some interior measurements.

This paper is arranged as follows. In Sect. 2, description of the quintic B-splines collocation method is explained. In Sect. 3, procedure for implementation of present method for Eqs. (1.1–1.5) is described. In Sect. 4, procedure to obtain an initial vector which is required to start our method is explained. To regularize the resultant ill-posed linear system of equations, in Sect. 5, we apply the Tikhonov regularization (of second order) method to obtain the stable numerical approximation of our solution and the uniform convergence of the method is provided in Sect. 6. Finally in Sect. 7 numerical experiment is conducted to demonstrate the viability and the efficiency of the proposed method computationally.

2 Description of method

In quintic B-splines collocation method, the approximate solution can be written as a linear combination of basic functions which constitute a basis for the approximation space under consideration.

Let be a uniform partition of interval [0, 1] as follows $0=x_0<x_1<\ldots<x_{N-1}<x_N=1$ where $h=x_{j+1}-x_{j},~ j=0,\ldots ,N-1$. Our numerical treatment for Rosenau equation using the collocation method with quintic B-spline is to find an approximate solution $U_{N}(x,t)$ to the exact solution u(x, t) in the form

$$\begin{aligned} U_{N}(x,t)=\sum _{j=-2}^{N+2}c_j(t)B_j(x), \end{aligned}$$

(2.1)

where $c_j, \quad j=-2, \ldots ,N+2$ are unknown time-dependent quantities to be determined from boundary conditions $g_{1}(t),~ g_{2}(t)$ and the initial condition $u_{0}(x)$ and overspecified conditions $p_{1}(t),~ p_{2}(t)$.

The set of quintic B-spline $\{B_{-2},B_{-1}, \ldots ,B_{N+2}\}$ form a basis over the problem domain [0, 1] [37]. Let ${B_j},j=-2, \ldots ,N+2$,

$$\begin{aligned} B_j(x)= \frac{1}{h^5} {\left\{ \begin{array}{ll} (x-x_{j-3})^5, & \quad {x\in [x_{j-3},x_{j-2})},\\ (x-x_{j-3})^5-6(x-x_{j-2})^5, &\quad {x\in [x_{j-2},x_{j-1})},\\ (x-x_{j-3})^5-6(x-x_{j-2})^5+15(x-x_{j-1})^5, &\quad {x\in [x_{j-1},x_{j})},\\ (x_{j+3}-x)^5-6(x_{j+2}-x)^5+15(x_{j+1}-x)^5, &\quad {x\in [x_{j},x_{j+1})},\\ (x_{j+3}-x)^5-6(x_{j+2}-x)^5, &\quad {x\in [x_{j+1},x_{j+2})},\\ (x_{j+3}-x)^5, &\quad {x\in [x_{j+2},x_{j+3})},\\ 0, &\quad \text {elsewhere}, \end{array}\right. } \end{aligned}$$

(2.2)

be quintic B-splines, which vanish outside interval. Each quintic B-spline covers six elements so that an element is covered by six quintic B-splines.

Using approximate function (2.1) and quintic spline (2.2), the approximate values at the knots of U(x) and its derivatives up to fourth order are determined in terms of the time parameters $c_j$ as

$$\begin{aligned} U_{j}=c_{j-2}+26c_{j-1}+66c_{j}+26c_{j+1}+c_{j+2},\end{aligned}$$

(2.3)

$$\begin{aligned} hU'_{j}=5(c_{j+2}+10c_{j+1}-10c_{j-1}-c_{j-2}),\end{aligned}$$

(2.4)

$$\begin{aligned} h^{2}U''_{j}=20(c_{j-2}+2c_{j-1}-6c_{j}+2c_{j+1}+c_{j+2}),\end{aligned}$$

(2.5)

$$\begin{aligned} h^{3}U'''_{j}=60(c_{j+2}-2c_{j+1}+2c_{j-1}-c_{j-2}),\end{aligned}$$

(2.6)

$$\begin{aligned} h^{4}U^{iv}_{j}=120(c_{j-2}-4c_{j-1}+6c_{j}-4c_{j+1}+c_{j+2}), \end{aligned}$$

(2.7)

where $U_j=U(x_j,t)$.

The values of $B_j(x)$ and its derivatives may be tabulated as in Table 1.

Table 1 Coefficient of quintic B-spline and its derivative at knots $x_j$

Using (2.1) and the boundary conditions (1.3), we get the approximate solution at the boundary point as

$$\begin{aligned} U(x_N,t)=\sum _{j=N-2}^{N+2}c_{j}(t) B_{j}(x_N)=c_{N-2}+26c_{N-1}+66c_{N}+26c_{N+1}+c_{N+2}=g_{1}(t), \end{aligned}$$

(2.8)

$$\begin{aligned} U_{x}(x_N,t)=\sum _{j=N-2}^{N+2}c_{j}(t) B_{j}(x_N)= \left( \frac{5}{h} \right) (c_{N+2}+10c_{N+1}-10c_{N-1}-c_{N-2})=g_{2}(t), \end{aligned}$$

(2.9)

and using overspecified conditions (1.5) where $\alpha =x_s,\;1\le s \le N-1$ and (2.1) we have

$$\begin{aligned} U(x_s,t)=\sum _{j=s-2}^{s+2}c_{j}(t) B_{j}(x_s)=c_{s-2}+26c_{s-1}+66c_{s}+26c_{s+1}+c_{s+2}=p_{1}(t), \end{aligned}$$

(2.10)

$$\begin{aligned} U_{x}(x_s,t)=\sum _{j=s-2}^{s+2}c_{j}(t) B_{j}(x_s)=\left( \frac{5}{h} \right) (c_{s+2}+10c_{s+1}-10c_{s-1}-c_{s-2})=p_{2}(t), \end{aligned}$$

(2.11)

3 Implementation of method

Our numerical treatment for solving Eqs. (1.1–1.5) using the collocation method with quintic B-splines is to find an approximate solution $U_{N}(x,t)$ and $U_{N}(0,t)$, $U_{N_{x}}(0,t)$ to the exact solution u(x, t) and $f_{1}(t)$, $f_{2}(t)$ is given in (2.1), where $c_j(t)$ are time-dependent quantities to be determined from the boundary and overspecific conditions and collocation from the differential equation.

From Eq. (1.1), we get

$$\begin{aligned} u_t+\mu u_{xxxxt}=\phi (x_j,t,u,u_x), \quad v(x,t)\in \Omega \times [0,T], \end{aligned}$$

(3.1)

using (2.1) in (3.1), we have

$$\begin{aligned} U_t+\mu U_{xxxxt}=\phi \left( x_j,t,{ \sum _{j=-2}^{N+2}{c_j(t)}B_j(x)},{\sum _{j=-2}^{N+2}{c_j(t)}B_j'(x)} \right) , \end{aligned}$$

(3.2)

using (2.3), (2.4) in (3.2) then is obtained as follows

$$\begin{aligned} U_t+\mu U_{xxxxt}&=\;\phi (x_j,t,(c_{j-2}+26c_{j-1}+66c_{j}+26c_{j+1}+c_{j+2})\nonumber \\&\quad \left( 5/h \right) (c_{j+2}+10c_{j+1}-10c_{j-1}-c_{j-2}) ), \quad 0\le j\le N. \end{aligned}$$

(3.3)

The time derivative is discretized in a forward finite difference fashion

$$\begin{aligned} (U_t)_j= \; & {} \frac{{U_j}^{(n+1)}-{U_j}^{(n)}}{k},\\ (U_{xxxxt})_j=\; & {} \frac{{(U_{xxxx})_j}^{(n+1)}-{(U_{xxxx})_j}^{(n)}}{k}, \end{aligned}$$

where $k=t^{(n+1)}-t^{(n)}$. In addition, we consider $U=U^{(n)}$, then (3.3) become as

$$\begin{aligned} U_j^{(n+1)}+\mu (U_{xxxx})_j^{(n+1)}&=k\phi \Big (x_j,t^{(n)}, \left( c_{j-2}^{(n)}+26c_{j-1}^{(n)}+66c_{j}^{(n)}+26c_{j+1}^{(n)}+c_{j+2}^{(n)}\right) ,\nonumber \\&\quad (5/h) \left( c_{j+2}^{(n)}+10c_{j+1}^{(n)}-10c_{j-1}^{(n)}-c_{j-2}^{(n)} \right) \Big )\nonumber \\&\quad +U_j^{(n)}+\mu (U_{xxxx})_j^{(n)}, \quad 0\le j\le N. \end{aligned}$$

(3.4)

Introducing (2.3–2.7) into (3.4) yields

$$\begin{aligned} \delta c_{j-2}^{(n+1)}+\beta c_{j-1}^{(n+1)}+\sigma c_{j}^{(n+1)}+\beta c_{j+1}^{(n+1)}+\delta c_{j+2}^{(n+1)}=\rho _j^{(n)}, \end{aligned}$$

(3.5)

where

$$\begin{aligned} \delta=\; & {} (h^4+120 \mu ),\\ \beta= \;& {} (26h^4-480 \mu ),\\ \sigma=\; & {} (66h^4+720 \mu ),\\ \rho _j^{(n)}= \;& {} kh^4 \Big [\phi (x_j,t^{(n)},\left( c_{j-2}^{(n)}+26c_{j-1}^{(n)}+66c_{j}^{(n)}+26c_{j+1}^{(n)}+c_{j+2}^{(n)}\right) ,\\&(5/h)\left( c_{j+2}^{(n)}+10c_{j+1}^{(n)}-10c_{j-1}^{(n)}-c_{j-2}^{(n)} \right) \Big ]\\&+(h^4) \left( c_{j-2}^{(n)}+26c_{j-1}^{(n)}+66c_{j}^{(n)}+26c_{j+1}^{(n)}+c_{j+2}^{(n)} \right) \\&+120 \mu \left( c_{j-2}^{(n)}-4c_{j-1}^{(n)}+6c_{j}^{(n)}-4c_{j+1}^{(n)}+c_{j+2}^{(n)}\right) ,~~~~0\le j\le N, \end{aligned}$$

where k is time step and the superscripts n and n+1 denote the adjacent time levels.

Therefore, we have a system as follows

$$\begin{aligned} AC=\rho , \end{aligned}$$

(3.6)

where

$$\begin{aligned}&A[1,s-2]=A[1,s+2]=A[N+5,N+1]=A[N+5,N+5]=1,\\&A[1,s-1]=A[1,s+1]=A[N+5,N+2]=A[N+5,N+4]=26,\\&A[1,s]=A[N+5,N+3]=66,\\&A[2,s-2]=-A[2,s+2]=A[N+4,N+1]=-A[N+4,N+5]=-(5/h),\\&A[2,s-1]=-A[2,s+1]=A[N+4,N+2]=-A[N+4,N+4]=-(50/h),\\&A[2,s]=A[N+4,N+3]=0, \end{aligned}$$

by (2.8–2.11).

Thus

$$\begin{aligned} A= \begin{pmatrix} 0&{} \ldots &{} \lambda &{} \varepsilon &{} \zeta &{} \varepsilon &{}\lambda &{}\ldots &{}\ldots &{}0 \\ 0&{} \ldots &{}- \nu &{} -\eta &{} 0 &{} \eta &{}\nu &{}\ldots &{}\ldots &{}0 \\ \delta &{} \beta &{} \sigma &{}\beta &{}\delta &{} &{} &{} &{} &{} \vdots \\ &{} \delta &{} \beta &{}\sigma &{}\beta &{} \delta &{} &{} \\ &{} &{} \cdots &{}\cdots &{}\cdots &{} \cdots &{} \cdots &{} \\ &{} &{} &{}\cdots &{}\cdots &{}\cdots &{} \cdots &{}\cdots &{} \\ &{} &{} &{} &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{} \cdots &{} \\ &{} &{} &{} &{} &{} \delta &{} \beta &{}\sigma &{}\beta &{} \delta \\ \vdots &{} &{} &{} &{} &{}-\nu &{}-\eta &{}0&{}\eta &{} \nu \\ 0 &{} \cdots &{} &{} &{} &{} \lambda &{}\varepsilon &{}\zeta &{}\varepsilon &{} \lambda \\ \end{pmatrix}, \end{aligned}$$

that $\lambda =1$, $\varepsilon =26$, $\zeta =66$, $\nu =\frac{5}{h}$, $\eta =\frac{50}{h}$,

$$\begin{aligned} {C}= \begin{pmatrix} {c_{-2}^{(n+1)}}\\ {c_{-1}^{(n+1)}}\\ {c_{0}^{(n+1)}}\\ {c_{1}^{(n+1)}}\\ \vdots \\ {c_{N-1}^{(n+1)}}\\ {c_{N}^{(n+1)}}\\ {c_{N+1}^{(n+1)}}\\ {c_{N+2}^{(n+1)}}\\ \end{pmatrix} ,\ \rho = \begin{pmatrix} {\rho _{-2}^{(n)}}\\ {\rho _{-1}^{(n)}}\\ {\rho _{0}^{(n)}}\\ {\rho _{1}^{(n)}}\\ \vdots \\ {\rho _{N-1}^{(n)}}\\ {\rho _{N}^{(n)}}\\ {\rho _{N+1}^{(n)}}\\ {\rho _{N+2}^{(n)}}\\ \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \rho _{-2}^{(n)}= \; &{} p_{1}(t^{(n)}),\\ \rho _{-1}^{(n)}=\; &{} p_{2}(t^{(n)}),\\ \rho _{j}^{(n)}=\; &{} kh^4 \Big [\phi (x_j,t^{(n)}, \left( c_{j-2}^{(n)}+26c_{j-1}^{(n)}+66c_{j}^{(n)}+26c_{j+1}^{(n)}+c_{j+2}^{(n)} \right) ,\\&(5/h) \left( c_{j+2}^{(n)}+10c_{j+1}^{(n)}-10c_{j-1}^{(n)}-c_{j-2}^{(n)} \right) \Big ]\\&+(h^4) \left( c_{j-2}^{(n)}+26c_{j-1}^{(n)}+66c_{j}^{(n)}+26c_{j+1}^{(n)}+c_{j+2}^{(n)} \right) \\&+120\mu \left( c_{j-2}^{(n)}-4c_{j-1}^{(n)}+6c_{j}^{(n)}-4c_{j+1}^{(n)}+c_{j+2}^{(n)} \right) ,~~~~0\le j\le N,\\ \rho _{N+1}^{(n)}= \;&{} g_{2}(t^{(n)}),\\ \rho _{N+2}^{(n)}=\; &{} g_{1}(t^{(n)}), \end{aligned}$$

here A is $(N+5)\times (N+5)$ matrix, C and $\rho$ are $(N+5)$ order vectors, which depend on the overspecified and boundary conditions (1.5), (1.3). Now we solve (3.6) for vector C and finally

$$ \begin{gathered} f_{1} (t^{{(n)}} ) = c_{{ - 2}}^{{(n)}} + 26c_{{ - 1}}^{{(n)}} + 66c_{0}^{{(n)}} + 26c_{1}^{{(n)}} + c_{2}^{{(n)}} ,\quad n = 0,1, \ldots , \hfill \\ f_{2} (t^{{(n)}} ) = \left( {\frac{5}{h}} \right)(c_{2}^{{(n)}} + 10c_{1}^{{(n)}} - 10c_{{ - 1}}^{{(n)}} - c_{{ - 2}}^{{(n)}} ,\quad n = 0,1, \ldots , \hfill \\ U(x_{j} ,t^{{(n)}} ) = c_{{j - 2}}^{{(n)}} + 26c_{{j - 1}}^{{(n)}} + 66c_{j}^{{(n)}} + 26c_{{j + 1}}^{{(n)}} + c_{{j + 2}}^{{(n)}} ,\quad n = 0,1, \ldots ,\quad j = 0,1, \ldots ,N. \hfill \\ \end{gathered} $$

For start we need an initial vector $C^0$ which can be obtained to follow the procedure of section.

4 The initial vector $C^0$

The initial vector $C^0$ can be obtained from the initial condition (1.4) and boundary and overspecified conditions (1.3, 1.5) as the following expression

$$\begin{aligned} u(x_s,0)= & {} c_{s-2}^{(0)}+26c_{s-1}^{(0)}+66c_{s}^{(0)}+26c_{s+1}^{(0)}+c_{s+2}^{(0)}=p_{1}(0),\\ u_{x}(x_s,0)= & {} (\dfrac{5}{h})(c_{s+2}^{(0)}+10c_{s+1}^{(0)}-10c_{s-1}^{(0)}-c_{s-2}^{(0)},=p_{2}(0),\\ u(x_j,0)= & {} c_{j-2}^{(0)}+26c_{j-1}^{(0)}+66c_{j}^{(0)}+26c_{j+1}^{(0)}+c_{j+2}^{(0)}=u_0(x_j), \quad 0\le j \le N,\\ u_{x}(x_N,0)= & {} (\dfrac{5}{h})(c_{N+2}^{(0)}+10c_{N+1}^{(0)}-10c_{N-1}^{(0)}-c_{N-2}^{(0)},=g_{2}(0),\\ u(x_N,0)= & {} c_{N-2}^{(0)}+26c_{N-1}^{(0)}+66c_{N}^{(0)}+26c_{N+1}^{(0)}+c_{N+2}^{(0)}=g_{1}(0). \end{aligned}$$

This yield a $(N+5)\times (N+5)$ system of equations, of the form

$$\begin{aligned} \Delta C^0=b, \end{aligned}$$

(4.1)

where

$$\begin{aligned}&\Delta [1,s-2]=\Delta [1,s+2]=\Delta [N+5,N+1]=\Delta [N+5,N+5]=1,\\&\Delta [1,s-1]=\Delta [1,s+1]=\Delta [N+5,N+2]=\Delta [N+5,N+4]=26,\\&\Delta [1,s]=\Delta [N+5,N+3]=66,\\&\Delta [2,s-2]=-\Delta [2,s+2]=\Delta [N+4,N+1]=-\Delta [N+4,N+5]=-(5/h),\\&\Delta [2,s-1]=-\Delta [2,s+1]=\Delta [N+4,N+2]=-\Delta [N+4,N+4]=-(50/h),\\&\Delta [2,s]=\Delta [N+4,N+3]=0, \end{aligned}$$

by (2.8–2.11).

Thus

$$\begin{aligned} \Delta = \begin{pmatrix} 0&{} \ldots &{} \lambda &{} \varepsilon &{} \zeta &{} \varepsilon &{}\lambda &{}\ldots &{}\ldots &{}0 \\ 0&{} \ldots &{}- \nu &{} -\eta &{} 0 &{} \eta &{}\nu &{}\ldots &{}\ldots &{}0 \\ 1 &{} 26 &{} 66 &{} 26 &{}1 &{} &{} &{} &{} &{} \vdots \\ &{} 1 &{}26 &{} 66 &{}26 &{} 1 &{} &{} \\ &{} &{} \cdots &{}\cdots &{}\cdots &{} \cdots &{} \cdots &{} \\ &{} &{} &{}\cdots &{}\cdots &{}\cdots &{} \cdots &{}\cdots &{} \\ &{} &{} &{} &{}\cdots &{}\cdots &{}\cdots &{}\cdots &{} \cdots &{} \\ &{} &{} &{} &{} &{} 1 &{}26 &{} &{}26 &{} 1 \\ \vdots &{} &{} &{} &{} &{}-\nu &{}-\eta &{}0&{}\eta &{} \nu \\ 0 &{} \cdots &{} &{} &{} &{} \lambda &{}\varepsilon &{}\zeta &{}\varepsilon &{} \lambda \\ \end{pmatrix}, \end{aligned}$$

that $\lambda =1$, $\varepsilon =26$, $\zeta =66$, $\nu =\frac{5}{h}$, $\eta =-\frac{50}{h}$,

$$\begin{aligned} C^0= \begin{pmatrix} {c_{-2}^0}\\ {c_{-1}^0}\\ {c_{0}}^0\\ {c_{1}}^0\\ \vdots \\ {c_{N-1}}^0\\ {c_{N}}^0\\ {c_{N+1}}^0\\ {c_{N+2}}^0\\ \end{pmatrix} ,\ b= \begin{pmatrix} {p_{1}(0)}\\ {p_{2}(0)}\\ u_0(x_{0})\\ u_0(x_{1})\\ \vdots \\ u_0(x_{N-1})\\ u_0(x_{N})\\ {g_{2}(0)}\\ {g_{1}(0)}\\ \end{pmatrix}, \end{aligned}$$

the solution of (4.1) can be found by Tikhonov regularization method.

5 Tikhonov regularization method

The singular matrix $\Delta$ is ill-posed and the estimate of $C^0$ by (4.1) will be unstable so that the Tikhonov regularization method must be used to control this singularity. The Tikhonov regularized solution ([38, 39] and [40]) to the system of linear algebraic equations (3.6) and (4.1) is given by

$$\begin{aligned} \digamma _\omega (C^0)=\Vert \Delta C^0 - b \Vert _2^2 + \omega \Vert R^{(2)}C^0 \Vert _2^2. \end{aligned}$$

On the case of $M=N+5$ the second-order Tikhonov regularization method, the matrix $R^{(2)}$ is given by, see e.g. [41]

$$\begin{aligned} R^{(2)}= \begin{pmatrix} 1 &{} -2 &{} 1 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 0 &{} 1 &{} -2 &{} 1 &{} 0 &{} \ldots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} 0 &{} \ldots &{} 1 &{} -2 &{} 1 &{} 0 \\ 0 &{} 0 &{} \ldots &{} 0 &{} 1 &{} -2 &{} 1 \\ \end{pmatrix}\in \mathbb {R}^{(M-2)\times M}. \end{aligned}$$

Therefore, we obtain the Tikhonov regularized solution of the regularized equation as

$$\begin{aligned} {C^0}_\omega = \bigl [\Delta ^T\Delta +\omega (R^{(2)})^T R^{(2)}\bigr ]^{-1}\Delta ^T b, \end{aligned}$$

(5.1)

in our computation, we use gcv scheme to determine a suitable value of $\omega$ [42, 43].

6 Convergence analysis

Let u(x) be the exact solution of the Eq. (1.1) with the boundary conditions (1.3) and initial condition (1.4) and overspecific conditions (1.5) and also $U(x)=\sum _{j=-2}^{N+2}c_j(t)B_j(x)$ be the B-splines collocation approximation to u(x). Due to round off errors in computations we assume that $\hat{U}(x)$ be the computed spline for U(x) so that $\hat{U}(x)=\sum _{j=-2}^{N+2}\hat{c}_j(t)B_j(x)$ where $\hat{C}=(\hat{c}_{-2}, \hat{c}_{-1}, \hat{c}_{0}, \dots , \hat{c}_N, \hat{c}_{N+1}, \hat{c}_{N+2})$. To estimate the error $\Vert u(x)-U(x)\Vert _{\infty }$ we must estimate the errors $\Vert u(x)-\hat{U}(x)\Vert _{\infty }$ and $\Vert \hat{U}(x)-U(x)\Vert _{\infty }$ separately.

Following (3.6) for $\hat{U}$ we have

$$\begin{aligned} A\hat{C}=\hat{\rho }, \end{aligned}$$

(6.1)

where

$$\begin{aligned} \hat{\rho }=(p_{1}(t), p_{2}(t), \hat{\phi _{0}},\hat{\phi _{1}},\ldots ,\hat{\phi _{N}},g_{2}(t),g_{1}(t)), \end{aligned}$$

and

$$\begin{aligned} \hat{\phi }_{j}= \;& {} kh^4[\phi (x_j,t,(\hat{c}_{j-2}+26\hat{c}c_{j-1}+66\hat{c}_{j}+26\hat{c}_{j+1}+\hat{c}_{j+2}),\\&\times \, (5/h)(\hat{c}_{j+2}+10\hat{c}_{j+1}-10\hat{c}_{j-1}-\hat{c}_{j-2})]\\&+ \; h^4(\hat{c}_{j-2}+26\hat{c}_{j-1}+66\hat{c}_{j}+26\hat{c}_{j+1}+\hat{c}_{j+2})\\&+\; 120\mu (\hat{c}_{j-2}-4\hat{c}_{j-1}+6\hat{c}_{j}-4\hat{c}_{j+1}+\hat{c}_{j+2}), \quad 0\le j\le N, \end{aligned}$$

by subtracting (6.1) and (3.6) we have

$$\begin{aligned} A(C-\hat{C})=(\rho -\hat{\rho }). \end{aligned}$$

(6.2)

Now, first we need to recall some theorems.

Theorem 6.1

Suppose that $f(x)\in C^{6} \, [0,1]$ and $|f^{6}(x)|\le L,\forall x\in [0,1]$ and $\Upsilon =\{0=x_{0}<x_{1}< \cdots <x_{N}=1\}$ be the equality spaced partition of [0, 1] with step size h. If $S_{\Upsilon }(x)$ be the unique spline function interpolate f(x) at nodes , then there exist a constant $x_{0},x_{1}, \ldots ,x_{N}\in \Upsilon$ $\lambda _{j}$ such that $\forall x\in [0,1]$, where

$$\begin{aligned} \Vert f^{j}(x)-S_{\Upsilon }^{j}(x)\Vert \le \lambda _{j}Lh^{6-j}, \quad j=0,1,\ldots ,5, \end{aligned}$$

( 6.3)

$\Vert \cdot \Vert$ represents the $\infty$ -norm.

Proof

For the proof see [44, 45]. $\square$

Now we want to find a bound on $\Vert \rho -\hat{\rho }\Vert _{\infty }$, we have

$$\begin{aligned} |\rho (x_j)-\hat{\rho }(x_{j})|= & {} |kh^4[\phi (x_j,U(x_j),{U^{\prime }}(x_j))-\phi (x_j,\hat{U}(x_j),{\hat{U}}^{\prime }(x_j))]\\&\quad +&h^4[U(x_j)-\hat{U}(x_j)]+120 \mu [U^{iv}(x_j)-\hat{U}^{iv}(x_j)]|, \end{aligned}$$

by following theorem (6.1) and [46] (p. 218), we obtain

$$\begin{aligned} \Vert \rho -\hat{\rho }\Vert _{\infty }\le Mkh^4(|U(x)-\hat{U}(x)|+|U^{\prime }(x)-{\hat{U}}^{\prime }(x)|)+h^4(\lambda _{0}Lh^6)+120\mu \lambda _{4}Lh^{2} \nonumber \\ \le MkL\lambda _{0}h^{10}+MkL\lambda _{1}h^{9}+\lambda _{0}Lh^{10}+120\mu \lambda _{4}Lh^{2}, \end{aligned}$$

(6.4)

where $\Vert \phi ^{\prime }(z)\Vert _{\infty }\le M$. Thus, we can rewrite (6.4) as follows

$$\begin{aligned} \Vert \rho -\hat{\rho }\Vert _{\infty }\le M_{1}h^{2}, \end{aligned}$$

(6.5)

where $M_{1}= MkL\lambda _{0}h^{8}+MkL\lambda _{1}h^7+\lambda _{0}Lh^8+120\mu \lambda _{4}L$.

It is obvious that the matrix A in (6.2) is a nonsingular matrix, thus we have

$$\begin{aligned} (C-\hat{C})=A^{-1}(\rho -\hat{\rho }), \end{aligned}$$

(6.6)

taking the infinity norm and then using (6.5), we find

$$\begin{aligned} \Vert C-\hat{C}\Vert _{\infty }\le \Vert A^{-1}\Vert _{\infty }\Vert \rho -\hat{\rho }\Vert _{\infty }\le M_{2}h^{2}, \end{aligned}$$

(6.7)

where $M_{2}=M_{1} \Vert \ A^{-1}\Vert _{\infty }$. Now we will be able to prove the convergence of our present method. Therefore, we recall a following lemma first

Lemma 6.1

The B-splines $\{B_{-2},B_{-1}, \ldots ,B_{N+2}\}$ satisfies the following inequality

$$\begin{aligned} \Bigg |\sum _{j=-2}^{N+2}B_j(x) \Bigg |\le 186, \quad (0\le x\le 1). \end{aligned}$$

(6.8)

Proof

We know that

$$\begin{aligned} \Bigg |\sum _{j=-2}^{N+2}B_j(x)|\le \sum _{j=-2}^{N+2}|B_j(x) \Bigg |. \end{aligned}$$

At any node $x_{i}$, we have

$$\begin{aligned} \sum _{j=-2}^{N+2}|B_j|=|B_{j-2}|+|B_{j-1}|+|B_j|+|B_{j+1}|+|B_{j+2}|=120 <186. \end{aligned}$$

Also, we have

$$\begin{aligned} |B_j(x)|\le 66 \; \text {and} \; |B_{j-1}(x)|\le 66, \quad x_{j-1}\le x<x_{j}. \end{aligned}$$

Similarly,

$$\begin{aligned}& |B_{j-2}(x)|\le 26 \; \text {and} \; |B_{j+1}(x)|\le 26, & \quad x_{j-1}\le x < x_{j},\\& |B_{j-3}(x)| < 1 \; \text {and} \;|B_{j+2}(x)|\le 1, & \quad x_{j-1}\le x < x_{j}. \end{aligned}$$

Now for any point $x_{j-1}\le x<x_{j}$, we have

$$\begin{aligned} \sum _{j=-2}^{N+2}|B_j(x)|=|B_{j-3}|+|B_{j-2}|+|B_{j-1}|+|B_j|+|B_{j+1}|+|B_{j+2}|\le 186. \end{aligned}$$

Hence, this proves the lemma. $\square$

Now observe that we have

$$\begin{aligned} U(x)-\hat{U}(x)=\sum _{j=-2}^{N+2}(c_{j}-\hat{c}_{j})B_j(x), \end{aligned}$$

thus taking the infinity norm and using (6.7) and (6.8), we get

$$\begin{aligned} \Vert U(x)-\hat{U}(x)\Vert _{\infty }=\Big \Vert \sum _{j=-2}^{N+2}(c_{j}-\hat{c}_{j})B_j(x) \Big \Vert _{\infty }\le \Big \Vert (c_{j}-\hat{c}_{j}) \Big \Vert _{\infty } \quad \times \Big |\sum _{j=-2}^{N+2}B_j(x) \Big |\le 186M_{2}h^{2}. \end{aligned}$$

(6.9)

Theorem 6.2

Let u(x) be the exact solution of the Eq. (1.1) with the boundary conditions (1.3) and initial condition (1.4) and overspecific conditions (1.5) and also U(x ) be the B-spline collocation approximation to u(x) then the method has second order convergence

$$\begin{aligned} \Vert u(x)-U(x)\Vert \le \Gamma h^2, \end{aligned}$$

where $\Gamma =\lambda _{0}L h^4+186M_{2}$ is some finite constant.

Proof

From theorem (6.1), we have

$$\begin{aligned} \Vert u(x)-\hat{U}(x)\Vert \le \lambda _{0}L h^{6}, \end{aligned}$$

(6.10)

thus substituting from (6.9) and (6.10), we have

$$\begin{aligned} \Vert u(x)-U(x)\Vert \le \Vert u(x)-\hat{U}(x)\Vert +\Vert \hat{U}(x)-U(x)\Vert \le \lambda _{0}L h^{6}+186M_{2}h^{2}=\Gamma h^2, \end{aligned}$$

(6.11)

where $\Gamma =\lambda _{0}L h^4+186M_{2}$. $\square$

Theorem 6.3

The time discretization process ( 3.4) that we use to discretize equation (1.1) in time variable is of the one order convergence.

Proof

See [48]. $\square$

We suppose that u(x, t) be the solution of Eq. (1.1) and U(x, t) be the approximate solution by our present method, then we have

$$\begin{aligned} \Vert u(x,t^{(n)})-U(x,t^{(n)})\Vert \le \rho (k+h^2), \end{aligned}$$

($\rho$ is some finite constant), thus the order of convergence of our process is $O(k+h^2)$.

7 Numerical experiments and discussion

In this section, we are going to study numerically the inverse problems (1.1) with the unknown boundary conditions. The main aim here is to show the applicability of the present method for solving the inverse problems (1.1). As expected the inverse problems are ill-posed and therefore it is necessary to investigate the stability of the present method by giving a test problem, thus we compute $L_{\infty }$ and $L_{2}$ error norms, using following formula

$$\begin{aligned} L_{\infty }=\text {max}|(u_{\text {exact}})_{i}-(U_{\text {num}})_{i}|, ~~~~~~~i=0,1,...,n, \end{aligned}$$

$$\begin{aligned} L_{2}=\sqrt{k\left(\sum _{i=0}^{n}|(u_{\text {exact}})_{i}-(U_{\text {num}})_{i}|^2\right)}, \end{aligned}$$

where $u_{i}=u(x_j,t_i)$, $t_n=T$.

Example 7.1

We consider the following generalized Rosenau equation given in [49]

$$\begin{aligned} 2u_{t}+u_{xxxxt}+3u_{x}-60u^{2}u_{x}+120u^{4}u_{x}=0, \quad 0\le x \le 1, \quad 0\le t \le T, \end{aligned}$$

(7.1)

with the boundary conditions

$$\begin{aligned} u(1,t)=\text {sec}h(1-t), \quad 0\le t \le T, \end{aligned}$$

$$\begin{aligned} u_x(1,t)=-\text {sin}h(1 - t)/\text {cos}h(1 - t)^2, \quad 0\le t \le T, \end{aligned}$$

and initial condition

$$\begin{aligned} u(x,0)=\text {sec}h(x), \quad 0\le x \le 1. \end{aligned}$$

The exact solution for the Rosenau equation (7.1) is known to be a soliton-type solution $u(x,t)=sech(x-t)$ (see also [5,6,7,8,9,10,11]). The Eq. (7.1) can be rewritten as

$$\begin{aligned} u_t+0.5u_{xxxxt}=f(u)_{x}, \end{aligned}$$

where $f(u)=10u^3-12u^5-1.5u$.

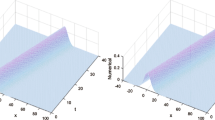
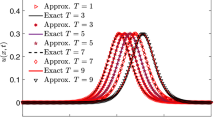
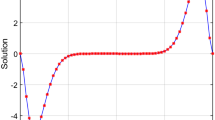
For numerical computation, we take $T=1,3$ with $k = 0.002,$ and $h=0.1$ for estimate $u(0,t)=f_{1}(t),$ $u_x(0,t)=f_{2}(t),$ u(x, t) with noisy data and results are reported in Tables 2, 3, 4, 5, 6, 7 and Figs. 1, 2, 3, 4, 5, 6.

Table 2 The comparison between exact solution and numerical solutions for $f_{1}(t)$ with the noisy data using quintic B-spline method when $\alpha =0.4$

Fig. 1

The comparison between the exact and numerical results for $f_{1}(t)$ of the problem (7.1) with the noisy data using quintic B-spline method and Tikhonov 2nd when $\alpha =0.4$

Table 3 The comparison between exact solution and numerical solutions for $f_{2}(t)$ with the noisy data using quintic B-spline method when $\alpha =0.4$

Fig. 2

The comparison between the exact and numerical results for $f_{2}(t)$ of the problem (7.1) with the noisy data using quintic B-spline method and Tikhonov 2nd when $\alpha =0.4$

Table 4 The comparison between exact solution and numerical solutions for u(0.7, t) with the noisy data using quintic B-spline method when $\alpha =0.4$

Fig. 3

The comparison between the exact and numerical results for u(x, t) of the problem (7.1) with the noisy data by using quintic B-spline method and Tikhonov 2nd when $\alpha =0.4$

Table 5 The comparison between exact solution and numerical solutions for $f_{1}(t)$ with the noisy data using quintic B-spline method when $\alpha =0.2$

Fig. 4

The comparison between the exact and numerical results for $f_{1}(t)$ of the problem (7.1) with the noisy data using quintic B-spline method and Tikhonov 2nd when $\alpha =0.2$

Table 6 The comparison between exact solution and numerical solutions for $f_{2}(t)$ with the noisy data using quintic B-spline method when $\alpha =0.2$

Fig. 5

The comparison between the exact and numerical results for $f_{2}(t)$ of the problem (7.1) with the noisy data using quintic B-spline method and Tikhonov 2nd when $\alpha =0.2$

Table 7 The comparison between exact solution and numerical solutions for u(0.5, t) with the noisy data using quintic B-spline method when $\alpha =0.2$

Fig. 6

The comparison between the exact and numerical results for u(x, t) of the problem (7.1) with the noisy data using quintic B-spline method and Tikhonov 2nd when $\alpha =0.2$

8 Conclusion

The following results are obtained:

• 1. The present study, successfully applies the numerical method to inverse problems.

• 2. Unlike some previous techniques using various transformations to reduce the equation in to more simple equation, the current method does not require extra effort to deal with the nonlinear terms. Therefore, the equations are solved easily and elegantly using the present method.

• 3. Numerical results show that our approximations of unknown functions using the quintic B-spline method combined with second order Tikhonov regularization, are almost accurate with noisy data.

• 4. Numerical results show that an excellent estimation can be obtained within a couple of minutes CPU time at pentium(R) 4 CPU 2.10 GHz.