Numerical solution by quintic B-spline collocation finite element method of generalized Rosenau–Kawahara equation

Abstract

In this study, numerical solution of generalized Rosenau–Kawahara equation with quintic B-spline collocation finite element method has been obtained. First, the generalized Rosenau–Kawahara equation is converted into a coupled differential equation system by the change of variable for the derivative with respect to space variable. Then, the numerical integrations of the resulting system according to time and space were obtained using the Crank–Nicolson-type formulation and quintic B-spline functions, respectively. The obtained numerical scheme has been applied to four model problems. It is seen that the results obtained from the presented scheme are compatible with the analytical solution, the error norms are smaller than those given in the literature, and conservation constants remain virtually unchanged.

Introduction

Some nonlinear physical properties such as diffusion, dispersion, dissipation, reaction and convection, especially fluid dynamics, nonlinear optics, plasma physics and many other areas, are represented by nonlinear evolution equations. Nonlinear waves, one of the nonlinear evolution equations, is one of the important scientific research topics. Some of the partial differential equations that define the motion of nonlinear waves are KdV (Korteweg-de Vries) [1,2,3,4], RLW (regularized long wave) [5,6,7] and Rosenau-type equations [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

Waves moving in one direction on the water surface are defined by the KdV equation, but since the KdV equation is insufficient to represent wave-wave and wave-wall interactions, the following equation

$$\begin{aligned} U_{t}+U_{xxxxt}+U_{x}+\gamma \left( U^{p}\right) _{x}=0, \end{aligned}$$

(1)

was developed for $p=2$ by Rosenau [19]. Equation (1) is called as Rosenau equation. Then, the following Rosenau type of equations

$$\begin{aligned} U_{t}+U_{xxxxt}=F(U,U_{x},U_{xx},U_{xxx},U_{xxt},U_{xxxxx}) \end{aligned}$$

(2)

appeared in the literature. The Kawahara equation representing plasma waves is given in the following form:

$$\begin{aligned} U_{t}+U_{x}+\alpha U_{xxx}-\beta U_{xxxxx}+\gamma \left( U^{p}\right) _{x}=0, \end{aligned}$$

(3)

[23, 24]. Korkmaz and Dağ [25] presented the differential quadrature method for the numerical solution of the Kawahara equation. Dereli and Dağ [26] obtained the numerical solution of some Kawahara-type equations by collocation method using radial base functions. Bagherzadeh [27] presented the numerical solution of Kawahara and modified Kawahara equations using the sextic B-spline collocation finite element method. Ak and Karakoç [28] gave the numerical solution of the modified Kawahara equation with the septic B-spline collocation method. The Rosenau–Kawahara equation is of the following form:

$$\begin{aligned}&U_{t}+U_{xxxxt}+U_{x}+\alpha U_{xxx}-\beta U_{xxxxx}+\gamma U^{p} U_{x}\nonumber \\&\quad =0,\,\,\left( x,t\right) \in \left[ x_{L},x_{R}\right] \times \left( 0,T\right] \end{aligned}$$

(4)

with the initial condition

$$\begin{aligned} U\left( x,0\right) =U_{0}\left( x\right) ,\;x\in \left[ x_{L} ,x_{R}\right] , \end{aligned}$$

(5)

and boundary conditions

$$\begin{aligned} \left. \begin{array} [c]{c} U\left( x_{L},t\right) =U\left( x_{R},t\right) =0\\ U_{x}\left( x_{L},t\right) =U_{x}\left( x_{R},t\right) =0\\ U_{xx}\left( x_{L},t\right) =U_{xx}\left( x_{R},t\right) =0 \end{array} \right\} \ t\in \left[ 0,T\right] . \end{aligned}$$

(6)

Here, U(x, t) shows the profile of the wave, and the x and t are position and time variables. p is known as the nonlinearity parameter and is an integer such that $p\ge 1$. Equation (4) is called Rosenau–Kawahara for $p=1$, modified Rosenau–Kawahara for $p=2$ and generalized Rosenau–Kawahara for $p>2$. $U_{0}\left( x\right)$ is a predefined smooth function, $\alpha ,\beta$ and $\gamma$ are real numbers taking different values depending on the physical conditions of the problem. Rosenau–Kawahara equation is obtained by coupling the Rosenau equation (1) and Kawahara equation (3). The Rosenau–Kawahara equation often arises in fluid dynamics whose solutions are solitons known as solitary waves. It is pointed out that this a result of a fine balances between nonlinearity and dispersion.

The exact solution of the Rosenau–Kawahara equation was obtained by Zuo [22] using the sine-cosine and tanh methods. The exact solution of the generalized Rosenau–Kawahara equation was given by Biswas et al. [10] using the solitary wave ansatz method. Labidi and Biswas [15] used variational iteration and homotopy perturbation methods to find the exact solution of the generalized Rosenau–Kawahara equation. Hu and his colleagues [14] obtained the numerical solution of the Rosenau–Kawahara equation using two-level nonlinear and three-level linear finite difference approaches. He [13] presented the numerical solution of the Rosenau–Kawahara equation with the three level linear implicit finite difference method. Chen and his colleagues [11] gave the numerical solution of the generalized Rosenau–Kawahara equation by applying the semi-implicit linearized finite difference approach. Manorot et al. [16] obtained the numerical solution of the Rosenau–Kawahara equation using two linear schemes based on the finite difference method. Wongsaijai et al. [29] presented the numerical solution of the Rosenau–Kawahara equation with the compact finite difference schemes.

As far as we know, there are very few articles about the numerical solutions of the generalized Rosenau–Kawahara equation in the literature. One of the main aims of the present article is to make a contribution to the limited number of approximate solutions of the problem. In this study, in order to obtain the numerical solution of the initial and boundary value problem given by Eqs. (4)–(6) using quintic B-spline collocation finite element method, in Rosenau–Kawahara equation (4), $V=U_{xxx}$ was taken and converted into a coupled differential equation system. Then, for the numerical integrations of the obtained differential equation system according to time and location, the numerical scheme was obtained using the Crank–Nicolson formulation and quintic B-spline functions, respectively. Mass and energy conservation constants with error norms $L_{2}$, ${L}_{{\infty }}$ were calculated by applying the obtained numerical scheme to four model problems. Fourier stability analysis of the presented method was performed, and the method was found to be unconditionally stable.

Quintic B-spline collocation finite element method

By using $V=U_{xxx}$, the generalized Rosenau–Kawahara equation (4 ) is converted into coupled system of differential equations as follows:

$$\begin{aligned}&U_{t}+V_{xt}+\left( 1+\gamma U^{p}\right) U_{x}+\alpha V-\beta V_{xx}=0, \end{aligned}$$

(7)

$$\begin{aligned}&V-U_{xxx}=0. \end{aligned}$$

(8)

The initial and boundary conditions for U are as given in Eqs. (5) and (6), respectively. For V; the initial and boundary conditions are, respectively, taken as

$$\begin{aligned} V\left( x,0\right) =U_{0}^{^{\prime \prime \prime }}\left( x\right) ,\;x\in \left[ x_{L},x_{R}\right] \end{aligned}$$

(9)

and

$$\begin{aligned} \left. \begin{array} [c]{c} V\left( x_{L},t\right) =V\left( x_{R},t\right) =0\\ V_{x}\left( x_{L},t\right) =V_{x}\left( x_{R},t\right) =0\\ V_{xx}\left( x_{L},t\right) =V_{xx}\left( x_{R},t\right) =0 \end{array} \right\} \ t\in \left[ 0,T\right] . \end{aligned}$$

(10)

Let the uniform partition of space domain $\left[ x_{L},x_{R}\right]$ and time domain [0, T] be $P_{1}=\left\{ x_{0},x_{1},\ldots ,x_{M-1} ,x_{M}\right\}$ and $P_{2}=\left\{ t_{0},t_{1},\ldots ,t_{N-1} ,t_{N}\right\}$, respectively, where $P_{1}$ and $P_{2}$ are given as $\left\| P_{1}\right\| =$ $h=x_{m+1}-x_{m}$, $m=0(1)M-1$, $\left\| P_{2}\right\| =k=t_{n+1}-t_{n}$, $n=0(1)N-1$. The quintic B-spline base functions $\phi _{i}\left( x\right)$, $i=-2(1)M+2$ over the domain $\left[ x_{L},x_{R}\right]$ are given as [30]

$$\begin{aligned} \phi _{i}\left( x\right) =\frac{1}{h^{5}}\left\{ \begin{array} [c]{ll} q_{0}=\left( x-x_{i-3}\right) ^{5}, &{} \left[ x_{i-3},x_{i-2}\right] \\ q_{1}=q_{0}-6\left( x-x_{i-2}\right) ^{5}, &{} \left[ x_{i-2},x_{i-1}\right] \\ q_{2}=q_{1}+15\left( x-x_{i-1}\right) ^{5}, &{} \left[ x_{i-1},x_{i}\right] \\ q_{3}=q_{2}-20\left( x-x_{i}\right) ^{5}, &{} \left[ x_{i},x_{i+1}\right] \\ q_{4}=q_{3}+15\left( x-x_{i+1}\right) ^{5}, &{} \left[ x_{i+1},x_{i+2}\right] \\ q_{5}=q_{4}-6\left( x-x_{i+2}\right) ^{5}, &{} \left[ x_{i+2},x_{i+3}\right] \\ 0, &{} otherwise. \end{array} \right. \end{aligned}$$

Since under these conditions a function defined on the interval, $\left[ x_{L},x_{R}\right]$ can be expressed as a linear combination of quintic B-spline bases functions $\left\{ \phi _{-2}\left( x\right) ,\phi _{-1}\left( x\right) ,\ldots ,\phi _{M+2}\left( x\right) \right\}$, the approximate solutions $U_{A}(x,t)$ and $V_{A}(x,t)$ corresponding to the exact solutions U(x, t) and V(x, t) given by Eqs. (7) and (8) are of the following form:

$$U_{A} \left( {x,t} \right) = \sum\limits_{{i = - 2}}^{{M + 2}} {\delta _{i}} \left( t \right)\phi _{i} \left( x \right)\;{\text{and}}\;V_{A} \left( {x,t} \right) = \sum\limits_{{i = - 2}}^{{M + 2}} {\sigma _{i} }\left( t \right)\phi _{i} \left( x \right).$$

(11)

Here, $\delta _{i}\left( t\right)$ and $\sigma _{i}\left( t\right)$ for $i=-2(1)M+2$ are time-dependent parameters to be sought for. Since on a typical element given on $\left[ x_{m},x_{m+1}\right]$ all of the quintic B-spline bases functions except for $\phi _{m-2},$ $\phi _{m-1},$ $\phi _{m}$, $\phi _{m+1},$ $\phi _{m+2}$ and $\phi _{m+3}$ are identically zero, the solutions $U_{A}(x,t)$ and $V_{A}(x,t)$ given by Eq. (11) can be written as:

$$U_{A} \left( {x,t} \right) = \sum\limits_{{i = m - 2}}^{{m + 3}} {\delta _{i} \left( t \right)\phi _{i} \left( x \right)\;{\text{and}}\;V_{A} \left( {x,t} \right) = \sum\limits_{{i = m - 2}}^{{m + 3}} {\sigma _{i} \left( t \right)\phi _{i} \left( x \right)} },$$

(12)

respectively. Thus, when the local transformation $h\xi =x-x_{m},\;0\le \xi \le 1$ is applied on the interval $\left[ x_{m},x_{m+1}\right]$, quintic B-spline basis functions in terms of local variable $\xi$ on the interval $\left[ 0,1\right]$ are given in the following form:

$$\begin{aligned} \phi _{m-2}&=1-5\xi +10\xi ^{2}-10\xi ^{3}+5\xi ^{4}-\xi ^{5},\\ \phi _{m-1}&=26-50\xi +20\xi ^{2}+20\xi ^{3}-20\xi ^{4}+5\xi ^{5},\\ \phi _{m}&=66-60\xi ^{2}+30\xi ^{4}-10\xi ^{5},\\ \phi _{m+1}&=26+50\xi +20\xi ^{2}-20\xi ^{3}-20\xi ^{4}+10\xi ^{5},\\ \phi _{m+2}&=1+5\xi +10\xi ^{2}+10\xi ^{3}+5\xi ^{4}-5\xi ^{5},\\ \phi _{m+3}&=\xi ^{5}. \end{aligned}$$

Under these conditions, the values of functions $U_{A}\left( x,t\right)$ and $V_{A}\left( x,t\right)$ and their derivatives with respect to the variable x up to the third order at the nodal points $\left( x_{m},t\right)$ $(m=0(1)M)$ in terms of parameters $\delta _{m}$ and $\sigma _{m}$ are obtained as:

$$\begin{aligned} U_{A}\left( x_{m},t\right)&=\delta _{m-2}+26\delta _{m-1}+66\delta _{m}+26\delta _{m+1}+\delta _{m+2},\nonumber \\ U_{A}^{^{\prime }}\left( x_{m},t\right)&=\dfrac{5}{h}\left[ -\delta _{m-2}-10\delta _{m-1}+10\delta _{m+1}+\delta _{m+2}\right] ,\nonumber \\ U_{A}^{^{\prime \prime }}\left( x_{m},t\right)&=\dfrac{20}{h^{2}}\left[ \delta _{m-2}+2\delta _{m-1}-6\delta _{m}+2\delta _{m+1}+\delta _{m+2}\right] ,\nonumber \\ U_{A}^{^{\prime \prime \prime }}\left( x_{m},t\right)&=\dfrac{60}{h^{3} }\left[ -\delta _{m-2}+2\delta _{m-1}-2\delta _{m+1}+\delta _{m+2}\right] \end{aligned}$$

(13)

and

$$\begin{aligned} V_{A}\left( x_{m},t\right)&=\sigma _{m-2}+26\sigma _{m-1}+66\sigma _{m}+26\sigma _{m+1}+\sigma _{m+2},\nonumber \\ V_{A}^{^{\prime }}\left( x_{m},t\right)&=\dfrac{5}{h}\left[ -\sigma _{m-2}-10\sigma _{m-1}+10\sigma _{m+1}+\sigma _{m+2}\right] ,\nonumber \\ V_{A}^{^{\prime \prime }}\left( x_{m},t\right)&=\dfrac{20}{h^{2}}\left[ \sigma _{m-2}+2\sigma _{m-1}-6\sigma _{m}+2\sigma _{m+1}+\sigma _{m+2}\right] ,\nonumber \\ V_{A}^{^{\prime \prime \prime }}\left( x_{m},t\right)&=\dfrac{60}{h^{3} }\left[ -\sigma _{m-2}+2\sigma _{m-1}-2\sigma _{m+1}+\sigma _{m+2}\right] . \end{aligned}$$

(14)

Now, by taking $Z=1+\gamma U^{p}$ and writing forward difference approximation in place of derivatives with respect to time t and Crank–Nicolson-type finite difference approximation in Eqs. (7) and (8), the following system of equations is obtained

$$\begin{aligned}&\frac{U^{n+1}-U^{n}}{k}+\frac{V_{x}^{n+1}-V_{x}^{n}}{k}+Z\frac{U_{x} ^{n+1}+U_{x}^{n}}{2}+\alpha \frac{V^{n+1}+V^{n}}{2}\nonumber \\&\quad -\,\beta \frac{V_{xx} ^{n+1}+V_{xx}^{n}}{2}=0,\ \end{aligned}$$

(15)

$$\begin{aligned}&\frac{V^{n+1}+V^{n}}{2}-\frac{U_{xxx}^{n+1}+U_{xxx}^{n}}{2}=0. \end{aligned}$$

(16)

When these newly obtained equations are reorganized such that $(n+1)^{th}$ time level variables are on the left side and $n^{th}$ time level variables for are on the right side for U and V, then the following system of equations results in

$$\begin{aligned}&U^{n+1}+V_{x}^{n+1}+\dfrac{Zk}{2}U_{x}^{n+1}+\dfrac{\alpha k}{2}V^{n+1} \nonumber \\&\quad -\,\dfrac{\beta k}{2}V_{xx}^{n+1}=U^{n}+V_{x}^{n}\ -\dfrac{Zk}{2}U_{x} ^{n}\nonumber \\&\quad -\,\dfrac{\alpha k}{2}V^{n}+\dfrac{\beta k}{2}V_{xx}^{n}, \end{aligned}$$

(17)

$$\begin{aligned}&V^{n+1}-U_{xxx}^{n+1}=-V^{n}+U_{xxx}^{n}. \end{aligned}$$

(18)

When the pointwise values given by Eqs. (13) and (14) are written in their places in Eqs. (17) and (18), the following system of algebraic equations is obtained

$$\begin{aligned}&{{A}}{_{1}\delta }_{m-2}^{n+1}+{A}_{2}{\delta }_{m-1}^{n+1}+{A}_{3}{\delta }_{m}^{n+1}+{A}_{4}{\delta }_{m+1}^{n+1}+{A}_{5}{\delta }_{m+2}^{n+1}\nonumber \\&\quad {+B_{1}\sigma }_{m-2}^{n+1}+{B}_{2}{\sigma }_{m-1}^{n+1}+{{B}_{3}\sigma } _{m}^{n+1}+{B}_{4}{\sigma }_{m+1}^{n+1}+{B}_{5}{\sigma }_{m+2}^{n+1} \ = \nonumber \\&{{A}_{5}\delta }_{m-2}^{n}+{A}_{4}{\delta }_{m-1}^{n}+{A}_{3}{\delta }_{m} ^{n}+{A}_{2}{\delta }_{m+1}^{n}+{A}_{1}{\delta }_{m+2}^{n}\nonumber \\&\quad -\,B_{5}{\sigma } _{m-2}^{n}-B_{4}{\sigma }_{m-1}^{n}-{B_{3}\sigma }_{m}^{n}-B_{2}{\sigma } _{m+1}^{n}-B_{1}{\sigma }_{m+2}^{n}, \end{aligned}$$

(19)

$$\begin{aligned}&{C_{1}\delta }_{m-2}^{n+1}+C_{2}{\delta }_{m-1}^{n+1}+C_{3}{\delta }_{m} ^{n+1}+C_{4}{\delta }_{m+1}^{n+1}+{C_{5}\delta }_{m+2}^{n+1}\nonumber \\&\quad +D_{1}{\sigma } _{m-2}^{n+1}+D_{2}{\sigma }_{m-1}^{n+1}+D_{3}{\sigma }_{m}^{n+1}+D_{4}{\sigma }_{m+1}^{n+1}+{D_{5}\sigma }_{m+2}^{n+1}=\nonumber \\&{C_{5}\delta }_{m-2}^{n}+C_{4}{\delta }_{m-1}^{n}+C_{3}{\delta }_{m}^{n} +C_{2}{\delta }_{m+1}^{n}+C_{1}{\delta }_{m+2}^{n}\nonumber \\&\quad -\,D_{5}{\sigma }_{m-2} ^{n}-D_{4}{\sigma }_{m-1}^{n}-D_{3}{\sigma }_{m}^{n}-D_{2}{\sigma }_{m+1} ^{n}-D_{1}{\sigma }_{m+2}^{n}. \end{aligned}$$

(20)

The coefficients ${A}_{i}$, ${B}_{i}$, ${C}_{i}$, $D_{i}$ for $(i=1\left( 1\right) 5)$ and $Z_{m}$ in these algebraic equations system are as follows:

$$\begin{aligned} \begin{array} [c]{llll} A_{1}=1-\dfrac{5kZ_{m}}{2h}, &{} B_{1}=-\dfrac{5}{h}+\dfrac{k\alpha }{2} -\dfrac{20k\beta }{2h^{2}}, &{} C_{1}=\dfrac{60}{h^{3}}, &{} D_{1}=1,\\ A_{2}=26-\dfrac{50kZ_{m}}{2h}, &{} B_{2}=-\dfrac{50}{h}+\dfrac{26k\alpha }{2}-\dfrac{40k\beta }{2h^{2}}, &{} C_{2}=-\dfrac{120}{h^{3}}, &{} D_{2}=26,\\ A_{3}=66, &{} B_{3}=\dfrac{66k\alpha }{2}+\dfrac{120k\beta }{2h^{2}}, &{} C_{3}=0, &{} D_{3}=66,\\ A_{4}=26+\dfrac{50kZ_{m}}{2h}, &{} B_{4}=\dfrac{50}{h}+\dfrac{26k\alpha }{2}-\dfrac{40k\beta }{2h^{2}}, &{} C_{4}=\dfrac{120}{h^{3}}, &{} D_{4}=26,\\ A_{5}=1+\dfrac{5kZ_{m}}{2h}, &{} B_{5}=\dfrac{5}{h}+\dfrac{k\alpha }{2} -\dfrac{20k\beta }{2h^{2}}, &{} C_{5}=-\dfrac{60}{h^{3}}, &{} D_{5}=1,\\ Z_{m}=1+\gamma U_{m}^{p}. &{} &{} &{} \end{array} \end{aligned}$$

(21)

Each of the algebraic equations given by Eqs. (19) and (20) consists of $2M+10$ unknowns and $M+1$ equations. The number of unknowns in each of the algebraic equations become $2M+2$ for $m=0,1,M-1,M$ by eliminating the unknowns ${\delta }_{-2}$, ${\delta }_{-1}$, ${\delta }_{M+1}$, ${\delta }_{M+2}$ using the boundary conditions $U\left( x_{L},t\right) =0$, $U_{x}\left( x_{L},t\right) =0$, $U\left( x_{R},t\right) =0$, $U_{x}\left( x_{R},t\right) =0$ and the unknowns $\ {\sigma }_{-2}$, ${\sigma }_{-1}$, ${\sigma }_{M+1}$, ${\sigma }_{M+2}$ using the boundary conditions $V\left( x_{L},t\right) =U_{0}^{^{\prime \prime \prime }}\left( x_{L}\right)$, $V_{x}\left( x_{L},t\right) =U_{0}^{^{(4)}}\left( x_{L}\right)$, $V\left( x_{R},t\right) =U_{0}^{^{\prime \prime \prime } }\left( x_{R}\right)$, $\ V_{x}\left( x_{R},t\right) =U_{0}^{^{(4)} }\left( x_{R}\right)$. By rearranging the unknowns as ${\mathbf {D}}=\;\left[ {\delta }_{0}\text { }{\sigma }_{0}\;{\delta }_{1}\text { }{\sigma }_{1}\cdots {\delta }_{M}\text { }{\sigma }_{M}\right] ^{T}$, and the coefficient matrices as ${\mathbf {A}}$ and $\mathbf {B,}$ the system of algebraic equations given by Eqs. (19) and (20) can be written as follows:

$$\begin{aligned} {{\mathbf {A}}}{{\mathbf {D}}}^{n+1}={{\mathbf {B}}}{{\mathbf {D}}}^{n}. \end{aligned}$$

(22)

Here ${\mathbf {A}}$ and ${\mathbf {B}}$ are $2M+2$ type square matrices and are given as follows, respectively:

$$\begin{aligned} {\mathbf {A}}={\left[ \begin{array} [c]{ccccccccccccc} {\widehat{A}}_{3} &{} {\widehat{B}}_{3} &{} {\widehat{A}}_{4} &{} {\widehat{B}}_{4} &{} {\widehat{A}}_{5} &{} {\widehat{B}}_{5} &{} &{} &{} &{} &{} &{} &{} \\ {\widehat{C}}_{3} &{} {\widehat{D}}_{3} &{} {\widehat{C}}_{4} &{} {\widehat{D}}_{4} &{} {\widehat{C}}_{5} &{} {\widehat{D}}_{5} &{} 0 &{} &{} &{} &{} &{} &{} \\ {\overline{A}}_{2} &{} {\overline{B}}_{2} &{} {\overline{A}}_{3} &{} {\overline{B}}_{3} &{} {\overline{A}}_{4} &{} {\overline{B}}_{4} &{} A_{5} &{} B_{5} &{} &{} &{} &{} &{} \\ {\overline{C}}_{2} &{} {\overline{D}}_{2} &{} {\overline{C}}_{3} &{} {\overline{D}}_{3} &{} {\overline{C}}_{4} &{} {\overline{D}}_{4} &{} C_{5} &{} D_{5} &{} 0 &{} &{} &{} &{} \\ A_{1} &{} B_{1} &{} A_{2} &{} B_{2} &{} A_{3} &{} B_{3} &{} A_{4} &{} B_{4} &{} A_{5} &{} B_{5} &{} &{} &{} \\ C_{1} &{} D_{1} &{} C_{2} &{} D_{2} &{} C_{3} &{} D_{3} &{} C_{4} &{} D_{4} &{} C_{5} &{} D_{5} &{} 0 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} 0 &{} A_{1} &{} B_{1} &{} A_{2} &{} B_{2} &{} A_{3} &{} B_{3} &{} A_{4} &{} B_{4} &{} A_{5} &{} B_{5}\\ &{} &{} &{} C_{1} &{} D_{1} &{} C_{2} &{} D_{2} &{} C_{3} &{} D_{3} &{} C_{4} &{} D_{4} &{} C_{5} &{} D_{5}\\ &{} &{} &{} &{} 0 &{} A_{1} &{} B_{1} &{} {\widetilde{A}}_{2} &{} {\widetilde{B}}_{2} &{} {\widetilde{A}}_{3} &{} {\widetilde{B}}_{3} &{} {\widetilde{A}}_{4} &{} {\widetilde{B}} _{4}\\ &{} &{} &{} &{} &{} C_{1} &{} D_{1} &{} {\widetilde{C}}_{2} &{} {\widetilde{D}}_{2} &{} {\widetilde{C}}_{3} &{} {\widetilde{D}}_{3} &{} {\widetilde{C}}_{4} &{} {\widetilde{D}} _{4}\\ &{} &{} &{} &{} &{} &{} 0 &{} {\underline{A}}_{1} &{} {\underline{B}}_{1} &{} {\underline{A}}_{2} &{} {\underline{B}}_{2} &{} {\underline{A}}_{3} &{} {\underline{B}}_{3}\\ &{} &{} &{} &{} &{} &{} &{} {\underline{C}}_{1} &{} {\underline{D}}_{1} &{} {\underline{C}}_{2} &{} {\underline{D}}_{2} &{} {\underline{C}}_{3} &{} {\underline{D}}_{3} \end{array} \right] } \end{aligned}$$

and

$$\begin{aligned} {\mathbf {B}}={\left[ \begin{array} [c]{ccccccccccccc} {\underline{A}}_{3} &{} -{\underline{B}}_{3} &{} {\underline{A}}_{2} &{} -{\underline{B}} _{2} &{} {\underline{A}}_{1} &{} -{\underline{B}}_{1} &{} &{} &{} &{} &{} &{} &{} \\ {\underline{C}}_{3} &{} -{\underline{D}}_{3} &{} {\underline{C}}_{2} &{} -{\underline{D}} _{2} &{} {\underline{C}}_{1} &{} -{\underline{D}}_{1} &{} 0 &{} &{} &{} &{} &{} &{} \\ {\widetilde{A}}_{4} &{} -{\widetilde{B}}_{4} &{} {\widetilde{A}}_{3} &{} -{\widetilde{B}} _{3} &{} {\widetilde{A}}_{2} &{} -{\widetilde{B}}_{2} &{} A_{1} &{} -B_{1} &{} &{} &{} &{} &{} \\ {\widetilde{C}}_{4} &{} -{\widetilde{D}}_{4} &{} {\widetilde{C}}_{3} &{} -{\widetilde{D}} _{3} &{} {\widetilde{C}}_{2} &{} -{\widetilde{D}}_{2} &{} C_{1} &{} -D_{1} &{} 0 &{} &{} &{} &{} \\ A_{5} &{} -B_{5} &{} A_{4} &{} -B_{4} &{} A_{3} &{} -B_{3} &{} A_{2} &{} -B_{2} &{} A_{1} &{} -B_{1} &{} &{} &{} \\ C_{5} &{} -D_{5} &{} C_{4} &{} -D_{4} &{} C_{3} &{} -D_{3} &{} C_{2} &{} -D_{2} &{} C_{1} &{} -D_{1} &{} 0 &{} &{} \\ &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \\ &{} &{} 0 &{} A_{5} &{} -B_{5} &{} A_{4} &{} -B_{4} &{} A_{3} &{} -B_{3} &{} A_{2} &{} -B_{2} &{} A_{1} &{} -B_{1}\\ &{} &{} &{} C_{5} &{} -D_{5} &{} C_{4} &{} -D_{4} &{} C_{3} &{} -D_{3} &{} C_{2} &{} -D_{2} &{} C_{1} &{} -D_{1}\\ &{} &{} &{} &{} 0 &{} A_{5} &{} -B_{5} &{} {\overline{A}}_{4} &{} -{\overline{B}}_{4} &{} {\overline{A}}_{3} &{} -{\overline{B}}_{3} &{} {\overline{A}}_{2} &{} -{\overline{B}}_{2}\\ &{} &{} &{} &{} &{} C_{5} &{} -D_{5} &{} {\overline{C}}_{4} &{} -{\overline{D}}_{4} &{} {\overline{C}}_{3} &{} -{\overline{D}}_{3} &{} {\overline{C}}_{2} &{} -{\overline{D}}_{2}\\ &{} &{} &{} &{} &{} &{} 0 &{} {\widehat{A}}_{5} &{} -{\widehat{B}}_{5} &{} {\widehat{A}}_{4} &{} -{\widehat{B}}_{4} &{} {\widehat{A}}_{3} &{} -{\widehat{B}}_{3}\\ &{} &{} &{} &{} &{} &{} &{} {\widehat{C}}_{5} &{} -{\widehat{D}}_{5} &{} {\widehat{C}}_{4} &{} -{\widehat{D}}_{4} &{} {\widehat{C}}_{3} &{} -{\widehat{D}}_{3} \end{array} \right] } \end{aligned}$$

where

$$\begin{aligned}&{\widehat{A}}_{3}=\frac{165}{4}A_{1}-\frac{33}{8}A_{2}+A_{3},\;{\widehat{A}} _{4}=\frac{130}{4}A_{1}-\frac{18}{8}A_{2}+A_{4},\nonumber \\&\quad \;{\widehat{A}}_{5}=\frac{9}{4}A_{1}-\frac{1}{8}A_{2}+A_{5}, \\&{\widehat{B}}_{3}=\frac{165}{4}B_{1}-\frac{33}{8}B_{2}+B_{3},\;{\widehat{B}} _{4}=\frac{130}{4}B_{1}-\frac{18}{8}B_{2}+B_{4},\nonumber \\\nonumber&\quad \;{\widehat{B}}_{5}=\frac{9}{4}B_{1}-\frac{1}{8}B_{2}+B_{5}, \\&{\widehat{C}}_{3}=\frac{165}{4}C_{1}-\frac{33}{8}C_{2}+C_{3},\;{\widehat{C}} _{4}=\frac{130}{4}C_{1}-\frac{18}{8}C_{2}+C_{4},\nonumber \\&\quad \;{\widehat{C}}_{5}=\frac{9}{4}C_{1}-\frac{1}{8}C_{2}+C_{5}, \\&{\widehat{D}}_{3}=\frac{165}{4}D_{1}-\frac{33}{8}D_{2}+D_{3},\;{\widehat{D}} _{4}=\frac{130}{4}D_{1}-\frac{18}{8}D_{2}+D_{4},\nonumber \\&\quad \;{\widehat{D}}_{5}=\frac{9}{4}D_{1}-\frac{1}{8}D_{2}+D_{5},\\&{\overline{A}}_{2}=-\frac{33}{8}A_{1}+A_{2},\;{\overline{A}}_{3}=-\frac{18}{8}A_{1}+A_{3},\nonumber \\&\quad \;{\overline{A}}_{4}=-\frac{1}{8}A_{1}+A_{4}, \\&{\overline{B}}_{2}=-\frac{33}{8}B_{1}+B_{2},\;{\overline{B}}_{3}=-\frac{18}{8}B_{1}+B_{3},\nonumber \\&\quad \;{\overline{B}}_{4}=-\frac{1}{8}B_{1}+B_{4}, \\&{\overline{C}}_{2}=-\frac{33}{8}C_{1}+C_{2},\;{\overline{C}}_{3}=-\frac{18}{8}C_{1}+C_{3},\nonumber \\&\quad \;{\overline{C}}_{4}=-\frac{1}{8}C_{1}+C_{4}, \\&{\overline{D}}_{2}=-\frac{33}{8}D_{1}+D_{2},\;{\overline{D}}_{3}=-\frac{18}{8}D_{1}+D_{3},\nonumber \\&\quad \;{\overline{D}}_{4}=-\frac{1}{8}D_{1}+D_{4}, \end{aligned}$$

$$\begin{aligned} &{\widetilde{A}}_{2}=A_{2}-\frac{1}{8}A_{5},\;{\widetilde{A}}_{3}=A_{3}-\frac{18}{8}A_{5},\nonumber \\&\quad \;{\widetilde{A}}_{4}=A_{4}-\frac{33}{8}A_{5}, \\&{\widetilde{B}}_{2}=B_{2}-\frac{1}{8}B_{5},\;{\widetilde{B}}_{3}=B_{3}-\frac{18}{8}B_{5},\nonumber \\&\quad \;{\widetilde{B}}_{4}=B_{4}-\frac{33}{8}B_{5}, \\&{\widetilde{C}}_{2}=C_{2}-\frac{1}{8}C_{5},\;{\widetilde{C}}_{3}=C_{3}-\frac{18}{8}C_{5},\nonumber \\&\quad \;{\widetilde{C}}_{4}=C_{4}-\frac{33}{8}C_{5}, \\&{\widetilde{D}}_{2}=D_{2}-\frac{1}{8}D_{5},\;{\widetilde{D}}_{3}=D_{3}-\frac{18}{8}D_{5},\nonumber \\&\quad \;{\widetilde{D}}_{4}=D_{4}-\frac{33}{8}D_{5}, \\&{\underline{A}}_{1}=A_{1}-\frac{1}{8}A_{4}+\frac{9}{4}A_{5},\;{\underline{A}} _{2}=A_{2}-\frac{18}{8}A_{4}+\frac{130}{4}A_{5},\nonumber \\&\quad \;{\underline{A}}_{3} =A_{3}-\frac{33}{8}A_{4}+\frac{165}{4}A_{5}, \\&{\underline{B}}_{1}=B_{1}-\frac{1}{8}B_{4}+\frac{9}{4}B_{5},\;{\underline{B}} _{2}=B_{2}-\frac{18}{8}B_{4}+\frac{130}{4}B_{5},\nonumber \\&\quad \;{\underline{B}}_{3} =B_{3}-\frac{33}{8}B_{4}+\frac{165}{4}B_{5}, \\&{\underline{C}}_{1}=C_{1}-\frac{1}{8}C_{4}+\frac{9}{4}C_{5},\;{\underline{C}} _{2}=C_{2}-\frac{18}{8}C_{4}+\frac{130}{4}C_{5},\nonumber \\&\quad \;{\underline{C}}_{3} =C_{3}-\frac{33}{8}C_{4}+\frac{165}{4}C_{5}, \\&{\underline{D}}_{1}=D_{1}-\frac{1}{8}D_{4}+\frac{9}{4}D_{5},\;{\underline{D}} _{2}=D_{2}-\frac{18}{8}D_{4}+\frac{130}{4}D_{5},\nonumber \\&\quad \;{\underline{D}}_{3} =D_{3}-\frac{33}{8}D_{4}+\frac{165}{4}D_{5}. \end{aligned}$$

Thus, using the obtained solutions with Thomas algorithm of algebraic equations system given by Eq. (22) for $n=0,1,\ldots ,N-1$, the values of ${\mathbf {D}}^{n+1}$ are found for any desired time level T and the required parameters for finding out the solution of generalized Rosenau–Kawahara equation are obtained. In order to obtain the solutions of equations given by Eq. (22) recursively, there is a need for finding the initial condition ${\mathbf {D}}^{0}$. These initial values of ${\mathbf {D}}^{0}$ are found by the solution of the following systems of equations

$$\begin{aligned} \begin{array} [c]{ll} \delta _{-2}^{0}+2\delta _{-1}^{0}-6\delta _{0}^{0}+2\delta _{1}^{0}+\delta _{2}^{0} &{} =U_{0}^{^{\prime \prime }}\left( x_{L}\right) ,\\ -\delta _{-2}^{0}-10\delta _{-1}^{0}+10\delta _{1}^{0}+\delta _{2}^{0} &{} =U_{0}^{^{\prime }}\left( x_{L}\right) ,\\ \delta _{m-2}^{0}+26\delta _{m-1}^{0}+66\delta _{m}^{0}+26\delta _{m+1}^{0} +\delta _{m+2}^{0} &{} =U_{0}\left( x_{m}\right) ,\text { }m=0\left( 1\right) N,\\ -\delta _{N-2}^{0}-10\delta _{N-1}^{0}+10\delta _{N+1}^{0}+\delta _{N+2}^{0} &{} =U_{0}^{^{\prime }}\left( x_{R}\right) ,\\ \delta _{N-2}^{0}+2\delta _{N-1}^{0}-6\delta _{N}^{0}+2\delta _{N+1}^{0} +\delta _{N+2}^{0} &{} =U_{0}^{^{\prime \prime }}\left( x_{R}\right) , \end{array} \end{aligned}$$

(23)

$$\begin{aligned} \begin{array} [c]{ll} \sigma _{-2}^{0}+2\sigma _{-1}^{0}-6\sigma _{0}^{0}+2\sigma _{1}^{0}+\sigma _{2}^{0} &{} =U_{0}^{(5)}\left( x_{L}\right) ,\\ -\sigma _{-2}^{0}-10\sigma _{-1}^{0}+10\sigma _{1}^{0}+\sigma _{2}^{0} &{} =U_{0}^{(4)}\left( x_{L}\right) ,\\ \sigma _{m-2}^{0}+26\sigma _{m-1}^{0}+66\sigma _{m}^{0}+26\sigma _{m+1}^{0} +\sigma _{m+2}^{0} &{} =U_{0}^{^{\prime \prime \prime }}\left( x_{m}\right) ,\text { }m=0\left( 1\right) N,\\ -\sigma _{N-2}^{0}-10\sigma _{N-1}^{0}+10\sigma _{N+1}^{0}+\sigma _{N+2}^{0} &{} =U_{0}^{(4)}\left( x_{R}\right) ,\\ \sigma _{N-2}^{0}+2\sigma _{N-1}^{0}-6\sigma _{N}^{0}+2\sigma _{N+1}^{0} +\sigma _{N+2}^{0} &{} =U_{0}^{^{(5)}}\left( x_{R}\right) . \end{array} \end{aligned}$$

(24)

Besides, due to the nonlinear term $\left( 1+\gamma U^{p}\right) U_{x}$ in order to improve the approximate solutions, an inner iteration in the following form

$$\begin{aligned} {\delta }_{m}^{*}={\delta }_{m}^{n}+\frac{1}{2}\left( {\delta }_{m} ^{n+1}-{\delta }_{m}^{n}\right) \end{aligned}$$

(25)

has been applied.

Stability analysis

In this section, the stability analysis of the difference equations (19) and (20) obtained by applying the quintic B-spline finite element method has been carried out by von Neumann method [31]. For this purpose, in Eq. (7) in place of nonlinear term $U^{p}$ in $U^{p}U_{x}$ a local constant ${\widehat{Z}}$ is taken and in Eq. (19) the term $Z_{m}$ is taken a local constant as $1+\gamma {\widehat{Z}}_{m}^{\,}$. Here, $i=\sqrt{-1}$, $\varphi$ is an arbitrary real number, $q=q\left( \varphi \right)$ is the amplification factor. When the special solutions ${\delta }_{m}^{n}=Pq^{n}e^{im\varphi }$, ${\sigma }_{m}^{n}=Wq^{n}e^{im\varphi }$ are written in their places in difference equations given by Eqs. (19) and (20) and the Euler formula $e^{i\varphi }=\cos \varphi +i\sin \varphi$ is used, the following system of homogenous algebraic equations is obtained

$$\begin{aligned}&\left[ \left( 2A+iZB\right) q-\left( 2A-iZB\right) \right] P+\left[ \left( E+i\frac{2B}{k}\right) q \right. \nonumber \\&\quad \left. +\left( E-i\frac{2B}{k}\right) \right] W=0, \end{aligned}$$

(26)

$$\begin{aligned}&\left( q+1\right) \left( iDP+2AW\right) =0 \end{aligned}$$

(27)

where

$$\begin{aligned}&A=26\cos \varphi +\cos 2\varphi +33,\text { }\\&\quad B=\frac{5k}{h}\left( 10\sin \varphi +\sin 2\varphi \right) , \\&C=\frac{20k\beta }{h^{2}}\left( 2\cos \varphi +\cos 2\varphi -3\right) ,\text { }\\&\quad D=\frac{120}{h^{3}}\left( 2\sin \varphi -\sin 2\varphi \right) , \\&E=k\alpha A-C,\text { }Z=\max Z_{m}. \end{aligned}$$

To have at least one solution different from zero of this homogeneous algebraic equation system, the determinant of the coefficient matrix must be zero. For this, the equality

$$\begin{aligned}&\left[ 4A^{2}+\frac{2BD}{k}+i\left( 2ABZ-DE\right) \right] \nonumber \\&q-\left[ 4A^{2}+\frac{2BD}{k}-i\left( 2ABZ-DE\right) \right]&=0\text { } \end{aligned}$$

(28)

$$\begin{aligned}&\text {or }q+1&=0 \end{aligned}$$

(29)

should be satisfied. Under these conditions, the amplification factor is found as

$$\begin{aligned} q=\frac{4A^{2}+\dfrac{2BD}{k}-i\left( 2ABZ-DE\right) }{4A^{2}+\dfrac{2BD}{k}+i\left( 2ABZ-DE\right) }\text { or }q=-1. \end{aligned}$$

(30)

For stability, the condition $\left| q\right| \le 1$ should be satisfied. Clearly, since $\left| q\right| =1$ is obtained, the proposed scheme is unconditionally stable.

Numerical calculations and comparisons

In this section, the numerical results obtained by applying the above numerical scheme to the examples with known exact solutions are given in tables and graphs. In order to test the efficiency and accuracy of the proposed scheme, the conservation constants known as mass $\left( Q\right)$ and energy $\left( E\right)$ for generalized Rosenau–Kawahara equation

$$\begin{aligned}&Q(t)=\int _{x_{L}}^{x_{R}}u\left( x,t\right) \hbox {d}x=\int _{x_{L}}^{x_{R}}u\left( x,0\right) \hbox {d}x=Q\left( 0\right) , \end{aligned}$$

(31)

$$\begin{aligned}&E\left( t\right) =\int _{x_{L}}^{x_{R}}\left[ u^{2}\left( x,t\right) +u_{xx}^{2}\left( x,t\right) \right] \hbox {d}x=E\left( 0\right) \end{aligned}$$

(32)

together with the error norms $L_{2}$ and $L_{{\infty }}$

$$\begin{aligned} L_{2}=\sqrt{h\sum _{i=1}^{N}\left| U_{i}-\left( U_{A}\right) _{i}\right| },\qquad L_{{\infty }}=\underset{1\le i\le N}{\hbox {max}}\left| U_{i}-\left( U_{A}\right) _{i}\right| \end{aligned}$$

are calculated [10, 13, 14, 29].

Example 1

For parameter values of $p=1$, $\alpha =1$, $\beta =1$ and $\gamma =1,$ Eq. (4) becomes

$$\begin{aligned}&U_{t}+U_{xxxxt}+U_{x}+U_{xxx}-U_{xxxxx}+UU_{x}=0,\left( x,t\right) \nonumber \\&\quad \in \left[ x_{L},x_{R}\right] \times \left( 0,T\right] . \end{aligned}$$

(33)

The exact solution of this problem [14, 22] is

$$\begin{aligned} U(x,t)=k_{1}sech^{4}\left[ k_{2}\left( x-k_{3}t\right) \right] . \end{aligned}$$

(34)

Here, $k_{1}=-\dfrac{35}{12}+\dfrac{35}{156}\sqrt{205}$, $k_{2}=\dfrac{1}{12}\sqrt{-13+\sqrt{205}}$ and $k_{3}=\dfrac{1}{13}\sqrt{205}$. When $t=0$ is taken in Eq. (34), the initial condition for Rosenau–Kawahara equation (33) is obtained as follows:

$$\begin{aligned} U(x,0)=k_{1}\hbox {sech}^{4}\left( k_{2}x\right) \end{aligned}$$

and the boundary conditions are as given by Eq. (6). The error norms $L_{2}$ and $L_{\infty }$ are calculated on the interval $[x_{L},x_{R} ]=[-40,100]$ for values of $h=k=0.1$, 0.05, 0.025 at times $T=10,20,30,40$ and these calculated norms are compared with those of Hu et al. [14] and presented in Tables 1 and 2. It is seen from Tables 1 and 2 that the error norms of the presented method are smaller than theirs. In addition, it is observed that the error norms decrease as the space and time steps decrease.

Table 1 Comparison of $L_{2}$ error norm for various h = k in $x\in \left[ -40,100\right]$

Table 2 Comparison of $L_{\infty }$ error norm for various h = k in $x\in \left[ -40,100\right]$

The conservation constants mass and energy are calculated by the proposed method on the interval $[x_{L},x_{R}]=[-40,100]$ for values of $h=k=0.1$, 0.05, 0.025 at times $T=10,20,30,40$ and compared with those of Hu et al. [14] and compared in Tables 3 and 4. At time $T=0$ the conservation constants mass and energy in Tables 3 and 4 are calculated by the equations given by (31) and (32), respectively. It is observed from Tables 3 and 4 that the proposed method preserves the conservation constants mass and energy as time goes on.

Table 3 Comparison of the mass $\left( Q\right)$ conservation for various h = k in $x\in \left[ -40,100\right]$

Table 4 Comparison of the energy $\left( E\right)$ conservation for various h = k in $x\in \left[ -40,100\right]$

The graphs of analytical and numerical solutions on the interval $\left[ -40,100\right]$ for $h=0.5,\;k=0.05$ are given in Figure 1, respectively. From Figure 1, it is seen that the numerical solutions are in agreement with analytical ones. In addition, the height of each wave remains almost constant as time goes on. For example, for the analytical solution given in Figure 1 while the wave heights are $u(0,0)=0.2956650$, $u(11,10)=0.2956640$, $u(22,20)=0.2956609$, $u(33,30)=0.2956558$, $u(44,40)=0.2956487$ those of the numerical solution are $u_{A}(11,10)=0.2956621$, $u_{A}(22,20)=0.2956573$, $u_{A}(33,30)=0.2956504$, $u_{A}(44,40)=0.2956430$. Thus, it is evident that the wave exhibits its physical behavior that it must act accordingly and preserves its conservation properties.

Fig. 1

Graphs of the exact and the numerical solutions ($h=0.5,\;k=0.05$) of Example 1

Example 2

When $p=2$, $\alpha =1$, $\beta =1$ and $\gamma =1$ are taken in Eq. (4), the following

$$\begin{aligned}&U_{t}+U_{xxxxt}+U_{x}+U_{xxx}-U_{xxxxx}+U^{2}U_{x}=0,\left( x,t\right) \nonumber \\&\quad \in \left[ x_{L},x_{R}\right] \times \left( 0,T\right] \end{aligned}$$

(35)

modified Rosenau–Kawahara equation is obtained. The exact solution of this equation is [10, 13]

$$\begin{aligned} U(x,t)=k_{1}\hbox {sech}^{2}\left[ k_{2}\left( x-k_{3}t\right) \right] \end{aligned}$$

(36)

where $k_{1}=\dfrac{3\sqrt{2}\sqrt{\sqrt{29}-5}}{4}$, $k_{2}=\dfrac{\sqrt{\sqrt{29}-5}}{4}$ and $k_{3}=\dfrac{4}{5\left( \sqrt{29}-5\right) }-1$ . In Eq. (36) when $t=0$ is taken, the initial condition for modified Rosenau–Kawahara equation (35) is obtained as follows:

$$\begin{aligned} U(x,0)=k_{1}\hbox {sech}^{2}\left( k_{2}x\right) \end{aligned}$$

and the boundary conditions are as given in Eq. (6). The error norms $L_{2}$ and $L_{\infty }$ are calculated using the proposed method on the interval $[x_{L},x_{R}]=[-40,200]$ for values of $k=0.1,0.01$, $h=0.8,0.4,0.2$ at time $T=10$ and presented in Table 5. Moreover, it is seen that it is less for $k=0.01$. The results are compared with those in the study of He [13]. From Table 5, it is seen that both of the error norms of the proposed method for values of $k=0.1,0.01$ are less than theirs. The error norms $L_{2}$ and $L_{\infty }$ of the proposed method on the interval $[x_{L},x_{R}]=[-40,200]$ for values of $h=0.1$, $k=0.8,0.4,0.2$ at time $T=10$ are calculated and given in Table 6. Moreover, in the same table they are compared with the study of He [13]. From Table 6, it is seen that although the space step size is larger, the error norms are smaller. The error norms $L_{2}$ and $L_{\infty }$ at time $T=10$ on the interval $[x_{L},x_{R}]=[-40,200]$ for values of $h=k=0.5,0.25,0.125,0.0625$ are calculated and given in Table 7. From Table 7, it is seen that as the value of $h=k$ decreases, the error norms $L_{2}$ and $L_{\infty }$ also decrease. The conservation constants mass and energy are calculated using the proposed method on the interval $[x_{L},x_{R}]=[-50,200]$ for values of $h=k=0.125$ at times $T=10,20,30,40$ and given in Table 8. The conservation constants mass and energy at time $T=0$ given in Table 8 are calculated by Eqs. (31) and (32), respectively. From Table 8, it is seen that the conservation constants mass and energy remain almost constant as time goes on. The graphs of analytical solution on the region $[-40,200]\times \left[ 0,40\right]$ and those of numerical solution for values of $h=0.5$, $k=0.05$ are illustrated in Figure 2. From Figure 2, it is seen that the numerical solutions are in agreement with analytical ones. In addition, the height of each wave remains almost constant as time goes on. For example, for the analytical solution given in Figure 2 while the wave heights are $u(0,0)=$ 0.6582631754, $u(11,10)=0.6574280174$, $u(21.5,20)=0.6582369795$, $u(32.5,30)=0.6576973895$, $u(43,40)=0.6581584002$ those of the numerical solution are$\ u_{A}(11,10)=0.6574154826$, $u_{A}(21.5,20)=0.6582360818$, $u_{A}(32.5,30)=0.6576886499$, $u_{A} (43,40)=0.6581362681$. Thus, it is evident that the wave exhibits its physical behavior properly and preserves its conservation properties.

Table 5 Comparison of $L_{2}$ and $L_{\infty }$ errors norms for $k=0.1,0.01$, $h=0.8,0.4,0.2$, in $x\in \left[ -40,200\right]$ at $T=10.$

Table 6 Comparison of $L_{2}$ and $L_{\infty }$ errors norms for $h=0.1$, $k=0.8,0.4,0.2$ in $x\in \left[ -40,200\right]$ at $T=10.$

Table 7 $L_{2}$ and $L_{\infty }$ error norms for various $h=k$ at $T=10$

Table 8 The mass $\left( Q\right)$ and the energy $\left( E\right)$ conservative constants for $h=k=0.125$ in $[-50,200]$ at $T=10,20,30,40$

Fig. 2

Graphs of the exact and the numerical solution ($h=0.5$, $k=0.05$) of Example 2

Example 3

When $p=4$, $\alpha =1$, $\beta =1$ and $\gamma =1$ are taken in Eq. (4)

$$\begin{aligned}&U_{t}+U_{xxxxt}+U_{x}+U_{xxx}-U_{xxxxx}+U^{4}U_{x}=0,\left( x,t\right) \nonumber \\&\quad \in \left[ x_{L},x_{R}\right] \times \left( 0,T\right] \end{aligned}$$

(37)

the generalized Rosenau–Kawahara equation is obtained. The exact solution for this problem is [10, 13]

$$\begin{aligned} U(x,t)=k_{1}sech\left[ k_{2}\left( x-k_{3}t\right) \right] . \end{aligned}$$

(38)

Here $k_{1}=\root 4 \of {\dfrac{4\sqrt{109}-10}{3}}$, $k_{2}=\dfrac{\sqrt{\sqrt{109}-10}}{3}$ and $k_{3}=\dfrac{9}{10\left( \sqrt{109}-10\right) } -1$. By taking $t=0$ in Eq. (38), the initial condition for Rosenau–Kawahara (37) is obtained as follows:

$$\begin{aligned} U(x,0)=k_{1}sech\left( k_{2}x\right) \end{aligned}$$

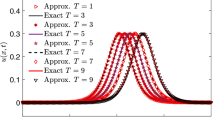
and the boundary conditions are as given by Eq. (6). The error norms $L_{2}$ and $L_{\infty }$on the interval $[x_{L},x_{R}]=[-70,130]$ for values of $h=k=0.5,0.25,0.125,0.0625$ at time $T=10$ using the proposed method are calculated and given in Table 9. From the table, it is seen that the error norms $L_{2}$ and $L_{\infty }$ of the proposed method decrease as the values of $h=k$ decreases. The conservation constants mass and energy are calculated by the proposed method on the interval $[x_{L},x_{R}]=[-60,200]$ for values of $h=0.5$, $k=0.01$ at times $T=10,20,30,40$ and presented in Table 10. The conservation constants mass and energy at time $T=0$ given in Table 10 have been calculated by using Eqs. (31) and (32), respectively. From Table 10, it is seen that the conservation constants mass and energy of the proposed method remain almost constant as time goes on. The graphs of the analytical and numerical solutions on the interval $[x_{L},x_{R}]=[-60,200]$ at times $T=0,10,20,30,40$ for values of $h=0.5$, $k=0.01$ are illustrated in Figure 3. From Figure 3 it is seen that the analytical and numerical solutions are in agreement with each other. In addition, the height of each wave remains almost constant as time goes on. For example, from Figure 3 while the amplitudes of analytical solution are $u(0,0)=$ 0.8753333202, $u(10.5,10)=0.8752570283$, $u(21,20)=0.8750282191$, $u(31.5,30)=0.8746470918$, $u(42,40)=0.8741139782$ those of numerical solution are$\ u_{A} (10.5,10)=0.8752619732$, $u_{A}(21,20)=0.8750280477$, $u_{A} (31,30)=0.8746531157$, $u_{A}(42,40)=0.8741136720$. Thus, it is evident that the wave exhibits physical behavior accordingly and preserves its conservation properties.

Table 9 $L_{2}$ and $L_{\infty }$ error norms for various $h=k$ at $T=10$

Table 10 The mass $\left( Q\right)$ and the energy $\left( E\right)$ conservative constants for $h=0.5$, $k=0.01$ in $[-60,200]$ at $T=10,20,30,40$

Fig. 3

The analytical and numerical solutions ($h=0.5$, $k=0.01$) of Example 3 at various times

Example 4

When $p=7$, $\alpha =1$, $\beta =1$ and $\gamma =8$ are taken in Eq. (4), the following form of the generalized Rosenau–Kawahara

$$\begin{aligned}&U_{t}+U_{xxxxt}+U_{x}+U_{xxx}-U_{xxxxx}+8U\,^{7}U_{x}=0,\left( x,t\right) \nonumber \\&\quad \in \left[ x_{L},x_{R}\right] \times \left( 0,T\right] \end{aligned}$$

(39)

is obtained. The exact solution of this equation is [10, 11]

$$\begin{aligned} U(x,t)=k_{1}\hbox {sech}^{\frac{4}{7}}\left[ k_{2}\left( x-k_{3}t\right) \right] \,\, \end{aligned}$$

(40)

where $k_{1}=\root 7 \of {\frac{55\left( -85+\sqrt{7549}\right) }{1224}}$, $k_{2}=\frac{7\sqrt{-85+\sqrt{7549}}}{36}$ and $k_{3}=\frac{\sqrt{7549}}{85}$. When $t=0$ is taken in Eq. (40), the initial condition of the generalized Rosenau–Kawahara equation given by Eq. (39) is obtained as:

$$\begin{aligned} U(x,0)=k_{1}\hbox {sech}^{\frac{4}{7}}\left( k_{2}x\right) \end{aligned}$$

and the boundary conditions are as in Eq. (6). The error norms $L_{2}$ and $L_{\infty }$ of the proposed method on the interval $[x_{L},x_{R}]=[-80,120]$ for values of $h=k=0.5,0.25,0.125,0.0625$ at time $T=10$ are calculated and presented in Table 11. From Table 11, it is seen that the error norms decrease as the values of $h=k$ decrease. The error norm $L_{\infty }$ of the proposed method on the interval $[-80,120]$ for $h=k=0.1,0.05,0.025$ at times $T=10,20,30,40$ is calculated and compared with those of Chen et al. [11] and compared in Table 12. It is seen from Table 12 the error norm of proposed method is smaller than theirs. The conservation constants mass and energy have been calculated on the interval $[x_{L},x_{R}]=[-80,120]$ for values of $h=k=0.125$ at times $T=10,20,30,40$ and given in Table 13. From Table 13 it is seen that the conservation constants mass and energy are conserved as times goes on. The conservation constants mass and energy in Table 13 at time $T=0$ have been calculated by Eqs. (31) and (32), respectively, using rectangle rule. The graphs of numerical solution on interval $[x_{L},x_{R}]=[-80,120]$ for values of $h=k=0.125$ at times $T=10,20,30,40$ and those of analytical solutions at times $T=0,10,20,30,40$ are given in Figure 4. From Figure 4 it is seen that analytical and numerical solutions are in agreement with each other. In addition, the height of each wave remains almost constant as time goes on. For example, while the heights of the wave for analytical solution given in Figure 4 are $u(0,0)=0.7028152766$, $u(10.25,10)=0.7028038659$, $u(20.5,20)=0.7027696359$, $u(30.625,30)=0.7027920494$, $u(40.875,40)=0.7028131986$ those of numerical solutions are$\ u_{A}(10.25,10)=0.7027708948$, $u_{A}(20.5,20)=0.7026977472$, $u_{A}(30.625,30)=0.7027079356$, $u_{A}(40.875,40)=0.7026906363$. Thus, it is evident that the wave exhibits its physical behavior in a proper way and preserves its conservation properties.

Table 11 $L_{2}$ and $L_{\infty }$ error norms for various $h=k$ at $T=10$

Table 12 Comparison of $L_{\infty }$ error norm

Table 13 The mass $\left( Q\right)$ and the energy $\left( E\right)$ conservative constants for $h=k=0.125$ in $[-80,120]$ at $T=10,20,30,40$

Conclusion

Fig. 4

Graphs of the analytical and the numerical solutions ($h=k=0.125$) of Example 4 at various times

In this study, an efficient numerical scheme is proposed to obtain the numerical solution of the Rosenau–Kawahara equation by quintic B-spline collocation finite element method. The error norms $L_{2}$ and $L_{{\infty }}$ are calculated by applying the proposed numerical scheme to four model of problems with an analytical solution. The error norms obtained were compared with the studies available in the literature, and it was concluded that the error norms of the proposed numerical scheme were smaller. The numerical solutions obtained for each problem were plotted, and analytical solutions were compatible with the graphics. In addition, it was observed that the main conservation properties of the Rosenau–Kawahara equation, mass and energy, were preserved by the proposed numerical scheme. Although it is found out that the method is easy to use and well suited for computer programming, and also produces better results for sufficiently large values of space and time step sizes, in this study, since a coupled form of Rosenau–Kawahara equation is solved, the storage capacity and computational cost have increased naturally. As a result, the numerical solution of high-order nonlinear partial differential equations frequently arising in science and mathematical physics for a wide range of phenomena encountered in the nature can be obtained easily and effectively with the proposed method.