Mixed Poisson INAR(1) processes

Abstract

Overdispersion is a phenomenon commonly observed in count time series. Since Poisson distribution is equidispersed, the INteger-valued AutoRegressive (INAR) process with Poisson marginals is not adequate for modelling overdispersed counts. To overcome this problem, in this paper we propose a general class of first-order INAR processes for modelling overdispersed count time series. The proposed INAR(1) processes have marginals belonging to a class of mixed Poisson distributions, which are overdispersed. With this, our class of overdispersed count models have the known negative binomial INAR(1) process as particular case and open the possibility of introducing new INAR(1) processes, such as the Poisson-inverse Gaussian INAR(1) model, which is discussed here with some details. We establish a condition to our class of overdispersed INAR processes is well-defined and study some statistical properties. We propose estimators for the parameters and establish their consistency and asymptotic normality. A small Monte Carlo simulation to evaluate the finite-sample performance of the proposed estimators is presented and one application to a real data set illustrates the usefulness of our proposed overdispersed count processes.

1 Introduction

Count time series arise naturally in many practical situations and due to this an increased interest in the modelling of such data have been observed. Some areas where we observe count time series data are economy, medicine, epidemiology, natural and social sciences, just to name a few. For example, in this paper we will deal with monthly counting of sex offences registered in the 21st police car beat in Pittsburgh from January 1990 and ending in December 2001.

The most common way for dealing with this type of data is to consider a ARMA-type model or an INteger-valued AutoRegressive (INAR) process. These models can be seen as parameter-driven and observation-driven models, respectively. We here focus on the observation-driven approach based on the INAR structure.

The Poisson INAR(1) (first-order INAR) model is the most popular INAR process for modelling count time series data. This process is based on the binomial thinning operator; this operator was introduced by Steutel and van Harn (1979). Pionering works on the Poisson INAR (in short PINAR) process are due to McKenzie (1985), Al-Osh and Alzaid (1987) and McKenzie (1988). After these works, some papers have dealt with inferential and forescasting aspects of the PINAR(1) process. For instance, see Freeland and McCabe (2004a), Freeland and McCabe (2004b) and Freeland and McCabe (2005).

An important variant of the PINAR(1) process was considered by Ristić et al. (2009). They introduced an INAR(1) process with geometric marginals by using a negative binomial thinning operator (Aly and Bouzar (1994)). The literature about INAR processes is very rich and the interest in this topic has increased in the last years. Some recent contributions on INAR processes are given by Nastić and Ristić (2012), Jazi et al. (2012), Ristić et al. (2013), Weiß (2013), Weiß and Kim (2013), Meintanis and Karlis (2014), Schweer and Weiß (2014), Andersson and Karlis (2014), Barreto-Souza and Bourguignon (2015), Barreto-Souza (2015), Weiß (2015), Bisaglia and Canale (2016), Nastić et al. (2016a), Nastić et al. (2016b), Nastić et al. (2016c), Yang et al. (2016) and Weiß et al. (2016). For a good review on INAR processes we recommend the papers by McKenzie (2003), Weiß (2008b) and Scotto et al. (2015).

Overdispersion is a phenomenon commonly observed in count time series. Since Poisson distribution is equidispersed, the PINAR process is not adequate for modelling overdispersed counts. Overdispersion can be caused by excess of zeros. In this direction, Jazi et al. (2012) and Barreto-Souza (2015) proposed INAR processes with zero-inflated Poisson innovations and zero-modified geometric marginals, respectively; both models are also able for dealing with underdispersion. Another important work on this issue is due to Schweer and Weiß (2014). They proposed a class of compound Poisson INAR(1) models and in particular obtained an overdispersion testing.

There are many different causes of overdispersion rather than excess of zeros. For example, the non-observation of significant covariates. A common way for treating overdispersion in count data is to use the mixed Poisson distributions, which is obtained by introducing a latent random effect on the mean of a Poisson distribution. For an account on mixed Poisson distributions, we recommend the paper by Karlis and Xekalaki (2005). With this in mind, in this paper we propose a class of overdispersed INAR(1) processes with marginals belonging to a general class of mixed Poisson distributions. With this approach, our class of INAR models includes the known negative binomial INAR(1) process as particular case and open the possibility of introducing new INAR(1) processes, such as the Poisson-inverse Gaussian INAR(1) model.

The paper is organized as follows. In Sect. 2 we define our class of mixed Poisson INAR(1) processes and derive some basic statistical properties. We also establish a condition to our class is well defined. In Sect. 3 we present the Poisson-inverse Gaussian INAR(1) model with some details. We propose estimators for the parameters and establish their consistency and asymptotic normality in Sect. 4. Further, we present a small Monte Carlo simulation to evaluate the finite-sample performance of the proposed estimators. An empirical illustration of our class of overdispersed INAR(1) processes is given in Sect. 5. Concluding remarks and future research are discussed in Sect. 6.

2 Definition and basic properties

In order to present our class of mixed Poisson INAR(1) processes and make this paper self-contained, we begin this section speaking about mixed Poisson distributions and self-decomposable random variables.

Definition 1

A random variable Y follows a mixed Poisson distribution if satisfies the stochastic representation $Y|Z=z\sim \text{ Poisson }(\mu z)$, for $\mu >0$, where Z is some non-negative random variable.

The probability function of a mixed Poisson random variable Y takes the form

$$\begin{aligned} P(Y=y)=\int _0^\infty \frac{e^{-\mu z}(\mu z)^y}{y!}d G_\phi (z), \end{aligned}$$

for $y\in \mathbb {N}_0\equiv \{0,1,\ldots \}$, where $G_\phi (\cdot )$ is the distribution function of Z and $\phi$ denotes the parameter vector associated to the distribution of Z; we denote $Y\sim \text{ MP }(\mu ,\phi )$. Let $\Psi _Z(t)=E(e^{tZ})$ be the moment generating function (mgf) of Z, for t belonging to some interval containing the value zero.

We have that the mgf of Y, say $\Psi _Y(\cdot )$, can be expressed by

$$\begin{aligned} \Psi _Y(t)=\Psi _Z(\mu (e^t-1)), \end{aligned}$$

for t belonging some interval containing the value zero. Assume that Z has the finite second moment. Then, the mean and variance of Y are given by $E(Y)=\mu E(Z)$ and $\text{ Var }(Y)=\mu \{E(Z)+\mu \text{ Var }(Z)\}$. As we can see, Y is overdispersed for any choice of distribution for Z (with finite second moment).

Definition 2

A random variable X is said to be self-decomposable if, for all $\alpha \in [0,1)$, there is a random variable $X_{\alpha }$ independent of X such that the following stochastic representation holds: $X\mathop {=}\limits ^{d}\alpha X+X_{\alpha }$, where “$\mathop {=}\limits ^{d}$” means equality in distribution.

Remark 1

A non-degenerate random variable X that is self-decomposable according Definition 2 is necessarily absolutely continuous.

Definition 3

(Steutel and van Harn (1979)) A random variable X assuming values on $\mathbb N_0$ is said to be discrete self-decomposable if, for all $\alpha \in [0,1)$, there is a random variable $X_{\alpha }$ independent of X such that the following stochastic representation holds: $X\mathop {=}\limits ^{d}\alpha \circ X+X_{\alpha }$, where $\circ$ is the thinning operator defined by $\alpha \circ X=\sum _{i=1}^XB_i$, where $\{B_i\}_{i=1}^\infty$ is a sequence of iid Bernoulli random variables with $P(B_1=1)=1-P(B_1=0)=\alpha$ and $\alpha \circ 0\equiv 0$.

In what follows, we present some results that will be important to define our class of overdispersed INAR processes.

Proposition 1

Let $Y\sim \text{ MP }(\mu ,\phi )$. Then, $\alpha \circ Y\sim \text{ MP }(\alpha \mu ,\phi )$, for $\alpha \in [0,1)$.

Proof

Using the fact that $\alpha \circ Y|Z=z$ follows a Poisson distribution with parameter $\alpha \mu z$, we obtain that

$$\begin{aligned} \Psi _{\alpha \circ Y}(t)\equiv & {} E\left( \exp \{t (\alpha \circ Y)\}\right) =E[E(\exp \{t (\alpha \circ Y)\}|Z)]=E\left( \exp \left\{ \mu \alpha Z\left( e^t-1\right) \right\} \right) \\= & {} \Psi _Z\left( \mu \alpha \left( e^t-1\right) \right) , \end{aligned}$$

that is the mgf of a $\text{ MP } (\alpha \mu ,\phi )$ random variable. $\square$

Proposition 2

Let Z be a non-negative self-decomposable random variable according Def. 2 with mgf $\Psi _Z(\cdot )$ and $\Psi (\cdot )$ be a function defined as

$$\begin{aligned} \Psi (t)=\frac{\Psi _Z\left( \mu \left( e^t-1\right) \right) }{\Psi _Z\big (\alpha \mu \big (e^t-1\big )\big )}, \end{aligned}$$

(1)

for t belonging some interval containing the value 0. Then $\Psi (t)$ is a proper mgf for all $\alpha \in [0,1)$. Moreover, this is a mgf of a mixed Poisson distribution.

Proof

Since Z is self-decomposable, there is a random variable $Z_\alpha$ independent of Z such that $Z\mathop {=}\limits ^{d} \alpha Z+Z_\alpha$. Hence, we have that the function $\Psi _Z(t)/\Psi _Z(\alpha t)$ is a proper mgf for all $\alpha \in [0,1)$; this function is the mgf of $Z_\alpha$. Let W be a random variable with this mgf. We now show that the function (1) is a mgf of mixed Poisson random variable, denoted by $\epsilon$, which satisfies the following stochastic representation: $\epsilon |W=w\sim \text{ Poisson }(\mu w)$, with W as defined above. It follows that

$$\begin{aligned} E(\exp \{\epsilon t\})= & {} E\left[ E\left( \exp \left\{ \epsilon t\right\} |W\right) \right] =E\left[ \exp \left\{ \mu \left( e^t-1\right) W\right\} \right] \\= & {} \frac{\Psi _Z\left( \mu \left( e^t-1\right) \right) }{\Psi _Z\big (\alpha \mu \big (e^t-1\big )\big )}=\Psi (t), \end{aligned}$$

so proving the desired result. $\square$

With the results above, we now are ready to define our class of mixed Poisson INAR(1) processes as follows.

Definition 4

We said that a sequence $\{X_n\}_{n=0}^\infty$ is a Mixed Poisson INAR(1) process, named in short by $\text{ MPINAR }(1)$ process, if $X_n\sim \text{ MP }(\mu ,\phi )$ for all n and if it admits the following stochastic representation:

$$\begin{aligned} X_n=\alpha \circ X_{n-1}+\epsilon _n, \end{aligned}$$

(2)

for $n\ge 1$, with $\{\epsilon _n\}_{n=1}^\infty$ being a sequence of iid random variables and $\epsilon _n$ independent of $X_j$, for $j<n$, for all n.

Remark 2

Proposition 2 gives us that the self-decomposability of Z is a sufficient condition to the MPINAR(1) process is well-defined. In fact, this condition also is necessary. Forst (1979) (see also Alamatsaz (1983)) showed that a mixed Poisson random variable is discrete self-decomposable if and only if its associated random effect (denoted in this paper by Z) is self-decomposable (in the sense of Def. 2). Therefore, in order to define an INAR process with mixed Poisson marginals, it is sufficient and necessary to restrict to the cases where Z (the random effect) is self-decomposable.

An INAR(1) process $\{X_n\}_{n=0}^\infty$ satisfying (2) has 1-step transition probabilities given by

$$\begin{aligned} p_{l,k}\equiv P\left( X_n=k|X_{n-1}=l\right) =\sum _{j=0}^{\min (k,l)}\left( {\begin{array}{c}l\\ j\end{array}}\right) \alpha ^j(1-\alpha )^{l-j}P(\epsilon _n=k-j), \end{aligned}$$

(3)

for $k,l\in \mathbb N$. Further, the autocorrelation function is given by $\rho (k)=\alpha ^k$. For more general properties on INAR processes, see Weiß (2008a).

The following result will be important to establish the asymptotic properties of the estimators which will be proposed in the Sect. 4.

Proposition 3

Let $\{X_n\}_{n=0}^\infty$ be a mixed Poisson INAR(1) process. If $E(X_n)<\infty$, then it is a geometrically ergodic, irreducible and aperiodic Markov chain.

Proof

The Markovian property of $\{X_n\}_{n=0}^\infty$ follows from (2). We now argue that $P(\epsilon _n=k)>0$ for all $k\in \mathbb N$. This and (3) implies that the MPINAR(1) processes are irreducible Markov chains.

Since $\{X_n\}_{n=0}^\infty$ is a MPINAR(1) process, we have that the random latent effect Z is an absolutely continuous random variable (see Remarks 1 and 2). With this, we have that W defined in proof of Proposition 2 is an absolutely continuous random variable. Denote by $f(\cdot )$ its density function. Further, from proof of Proposition 2 we have that the innovations $\epsilon _n$ satisfies the stochastic representation $\epsilon _n|W=w\sim \text{ Poisson }(\mu w)$. Therefore, we have that $P(\epsilon _n=k)=\int _0^\infty \frac{e^{-\mu w}(\mu w)^k}{k!}f(w)dw>0$. The aperiodicity of $\{X_n\}_{n=0}^\infty$ follows from the fact (due to the above arguments) $p_{k,k}>0$ for all $k\in \mathbb N$.

Now, since $E(X_n)<\infty$, we obtain that $E(\epsilon _n)<\infty$. With this, by following the same steps of proof of Theorem 3.4.1 from Schweer and Weiß (2014), we conclude that $\{X_n\}_{n=0}^\infty$ is geometrically ergodic. $\square$

We now discuss about the joint and conditional mgfs and moments. Using standard manipulations, it can be checked that the conditional and joint mgfs are given by

$$\begin{aligned} \Psi _{X_n|X_{n-1}}(t)\equiv E(\exp \{t X_n\}|X_{n-1})=\left( 1-\alpha +\alpha e^t\right) ^{X_{n-1}}\dfrac{\Psi _Z(\mu (e^t-1))}{\Psi _Z(\alpha \mu (e^t-1))} \end{aligned}$$

and

$$\begin{aligned} \Psi _{X_n,X_{n-1}}(t,s)\equiv & {} E(\exp \{t X_n+sX_{n-1}\})\nonumber \\= & {} \Psi _Z\left( \mu e^s\left( 1-\alpha +\alpha e^t\right) -1\right) \dfrac{\Psi _Z\left( \mu \left( e^t-1\right) \right) }{\Psi _Z\big (\alpha \mu \big (e^t-1\big )\big )}, \end{aligned}$$

(4)

respectively, where t belongs some interval containing the value 0 in both cases.

Remark 3

From now on, we assume that $E(Z)=1$ and $Var(Z)=\phi ^{-1}$. The condition $E(Z)=1$ is commonly adopted in mixed Poisson distributions in order to avoid non-identifiability problems.

The conditional mean and variance of $X_n$ given $X_{n-1}$ are respectively

$$\begin{aligned} E(X_n|X_{n-1})=\alpha X_{n-1}+\mu (1-\alpha ) \end{aligned}$$

and

$$\begin{aligned} \text{ Var }(X_n|X_{n-1})=\alpha (1-\alpha )X_{n-1}+\mu (1-\alpha )[1+\mu \phi ^{-1}(1+\alpha )]. \end{aligned}$$

We now define the jump process by $J_n=X_n-X_{n-1}$, for $n\ge 2$. This process is generally used for diagnostic checking of fitted INAR models. For instance, see Weiß (2008b, 2009). The mgf of $J_n$ can be obtained from (4). More specifically, we have that $\Psi _{J_n}(t)\equiv E(\exp \{tJ_n\})=\Psi _{X_n,X_{n-1}}(t,-t)$. From this, in particular, we obtain the two first moments of $J_n$, that are $E(J_n)=0$ and $E(J_n^2)=2\mu (1-\alpha )(1+\mu \phi ^{-1})$.

In the subsequent section we introduce and study the Poisson-inverse Gaussian INAR(1) process with some details. Another process that belongs to our class of overdispersed INAR(1) models is the negative binomial INAR(1) process. This model is already known in the literature (under a different parametrization) and therefore we do not present it here; for instance, see McKenzie (1986) and Ristić et al. (2012). We call attention that the Poisson INAR(1) process is obtained as a limiting case of our proposed class by taking $\phi \rightarrow \infty$.

3 Poisson inverse-Gaussian INAR(1) process

We now present a particular model of our class that yet is unknown in the literature. Let Z be a random variable with inverse Gaussian distribution with mean 1 and dispersion parameter $\phi >0$. More specifically, assume that the moment generating function of Z is given by

$$\begin{aligned} \Psi _Z(t)\equiv E(\exp \{tZ\})=\exp \left\{ \phi \left[ 1-\sqrt{1-2\phi ^{-1}t}\right] \right\} , \end{aligned}$$

for $t<\phi /2$.

Let X be a discrete random variable following a Poisson inverse-Gaussian (PIG) distribution with parameters $\mu >0$ and $\phi >0$. It is well known that X satisfies the following stochastic representation $X|Z=z\sim \text{ Poisson }(\mu z)$, where Z is defined above. We denote $X\sim \text{ PIG }(\mu ,\phi )$. The moment generating function of X is given by

$$\begin{aligned} \Psi _X(t)\equiv E(\exp \{t X\})=\exp \left\{ \phi \left[ 1-\sqrt{1-2\phi ^{-1}\mu (e^t-1)}\right] \right\} , \end{aligned}$$

for $t<\log (1+\phi /(2\mu ))$. The mean and variance of X are $E(X)=\mu$ and $\text{ Var }(X)=\mu (1+\phi ^{-1}\mu )$, respectively.

The probability function of X can be expressed by

$$\begin{aligned} p(k)\equiv P(X=k)=\sqrt{\dfrac{2}{\pi }}[\phi (\phi +2\mu )]^{-(k-1/2)/2}\dfrac{e^\phi (\mu \phi )^k}{k!}\mathcal K_{k-1/2}\left( \sqrt{\phi (\phi +2\mu )}\right) , \end{aligned}$$

for $k=0,1,\ldots$, where $\mathcal K_\lambda (t)=\frac{1}{2}\int _0^\infty u^{\lambda -1}\exp \bigg \{-\frac{t}{2}\bigg (u+\frac{1}{u}\bigg )\bigg \}du$ is the modified Bessel function of third kind, which can be computed in softwares such as R program, Maple and Mathematica.

We have that the inverse-Gaussian distribution is self-decomposable; for instance, Pillai and Satheesh (1992) and Abraham and Balakrishna (2002). With this and using Proposition 2, we obtain that the Poisson inverse-Gaussian distribution is discrete self-decomposable. Hence, we can define our INAR process with PIG marginals as follows.

Definition 5

We said that a sequence $\{X_n\}_{n=0}^\infty$ is a Poisson-inverse Gaussian INAR(1) process, named in short by $\text{ PIG }\text{ INAR }(1)$ process, if $X_n\sim \text{ PIG }(\mu ,\phi )$ for all n and if it admits the stochastic dynamics given in Definition 4.

The mgf of the innovations is given by

$$\begin{aligned} \Psi (t)= & {} \frac{\Psi _Z(\mu (e^t-1))}{\Psi _Z(\alpha \mu (e^t-1))}\\= & {} \exp \left\{ \phi \left[ \sqrt{1-2\phi ^{-1}\mu \alpha (e^t-1)}-\sqrt{1-2\phi ^{-1}\mu (e^t-1)}\right] \right\} , \end{aligned}$$

for $t<\log (1+\phi /(2\mu ))$. The first four cumulants of the innovations are

$$\begin{aligned}&\displaystyle E(\epsilon _n)=\mu (1-\alpha ),\\&\displaystyle \text{ Var }(\epsilon _n)=\mu (1-\alpha )[1+\mu \phi ^{-1}(1+\alpha )],\\&\displaystyle E\left[ (\epsilon _n-E(\epsilon _n))^3\right] =3\mu ^3\phi ^{-2}(1-\alpha ^3)+3\mu ^2\phi ^{-1}(1-\alpha ^2)+\mu (1-\alpha ) \end{aligned}$$

and

$$\begin{aligned} E\left[ (\epsilon _n-E(\epsilon _n))^4\right]= & {} 15\mu ^4\phi ^{-3}(1-\alpha ^4)+18\mu ^3\phi ^{-2}(1-\alpha ^3)\\&+\,7\mu ^2\phi ^{-1}(1-\alpha ^2)+\mu (1-\alpha ). \end{aligned}$$

We are naturally interested in the distribution of the innovations since we need to simulate the $\epsilon _n$’s in order to construct simulated trajectories and to study the finite-sample behaviour of the estimators we will propose. On the other hand, it is very difficult to obtain an explicit form for the probability function of the innovations.

More specifically, our innovations satisfy the following stochastic representation: $\epsilon |W=w\sim \text{ Poisson }(\mu w)$, where W has the distribution of an innovation of an inverse-Gaussian AR(1) process [see Pillai and Satheesh (1992); Abraham and Balakrishna (2002)], which has not explicit density function. Therefore, we do not have an explicit form for the probability function of our innovations $\epsilon _n$.

To overcome this problem, we use a method for generating random variables based on the moment generating function given by Ridout (2009). With this, we generate observations of the distribution of W and use the above stochastic representation for generating from the distribution of the innovations.

4 Estimation and asymptotic properties

We discuss here estimation methods of the parameter vector $\theta \equiv (\mu ,\alpha ,\phi )^\top$ and establish consistency and asymptotic normality. We begin with the conditional least squares (CLS) method. The function we need to minimize in order to find the conditional least squares estimator for $\theta$ is given by

$$\begin{aligned} Q(\theta )=\sum _{i=2}^n(X_i-E(X_i|X_{i-1}))^2=\sum _{i=2}^n(X_i-\alpha X_{i-1}-\mu (1-\alpha ))^2, \end{aligned}$$

where n is the sample size of the count time series. The above estimating equation does not depend on $\phi$ and therefore an alternative method to estimate it is necessary; this point will be discussed in the sequence. By solving the nonlinear system of equations $\left( \partial Q(\theta )/\partial \mu ,\partial Q(\theta )/\partial \alpha \right) ^\top =(0,0)^\top$, we get

$$\begin{aligned} {\widehat{\alpha }}_{cls}=\dfrac{(n-1)\sum _{i=2}^nX_iX_{i-1}-\sum _{i=2}^nX_i\sum _{i=2}^nX_{i-1}}{(n-1)\sum _{i=2}^nX_{i-1}^2-(\sum _{i=2}^nX_{i-1})^2} \end{aligned}$$

and

$$\begin{aligned} {\widehat{\mu }}_{cls}=\dfrac{\sum _{i=2}^nX_i-{\widehat{\alpha }}_{cls}\sum _{i=2}^nX_{i-1}}{(n-1)(1-{\widehat{\alpha }}_{cls})}. \end{aligned}$$

The above estimators based on the CLS method estimation assume the same form as the corresponding ones in the Poisson INAR(1) process; see Al-Osh and Alzaid (1987) and Freeland and McCabe (2005).

The additional equation for estimating $\phi$ is based on the $Q^*$ function given by

$$\begin{aligned} Q^*(\theta ^*)= & {} \sum _{i=2}^n(X_i^2-E(X_i^2|X_{i-1}))^2\\= & {} \sum _{i=2}^n(X_i^2-g({\widehat{\mu }}_{cls},{\widehat{\alpha }}_{cls},X_{i-1})-\phi ^{-1}h({\widehat{\mu }}_{cls},{\widehat{\alpha }}_{cls}))^2, \end{aligned}$$

where $\theta ^*=({\widehat{\mu }}_{cls},{\widehat{\alpha }}_{cls},\phi )^\top$, $g(\mu ,\alpha ,x)=(\alpha x+\mu (1-\alpha ))^2+\alpha (1-\alpha )x$ and $h(\mu ,\alpha )=\mu ^2(1-\alpha ^2)$.

The above method we using here, that is, by using two conditional least squares equations, it is known as two-step CLS estimation and was introduced by Karlsen and Tjostheim (1988). Solving the equation $\partial Q^*(\theta ^*)/\partial \phi =0$, we get

$$\begin{aligned} \widehat{\phi }_{cls}=\dfrac{(n-1){\widehat{\mu }}_{cls}^2(1-{\widehat{\alpha }}_{cls}^2)}{\displaystyle \sum \nolimits _{i=2}^n\left\{ X_i^2-(1-{\widehat{\alpha }}_{cls})({\widehat{\mu }}_{cls}+{\widehat{\alpha }}_{cls} X_{i-1})-({\widehat{\alpha }}_{cls} X_{i-1}+{\widehat{\mu }}_{cls}(1-{\widehat{\alpha }}_{cls}))^2\right\} }. \end{aligned}$$

We obtain now the Yule-Walker estimators. Since $E(X_t)=\mu$, $\text{ Var }(X_t)=\mu (1+\mu /\phi )$ and $\text{ corr }(X_{t-1},X_t)=\alpha$, we get the following Yule-Walker estimators:

$$\begin{aligned} {\widehat{\alpha }}_{yw}=\dfrac{\sum _{i=2}^n(X_i-\bar{X}_n)(X_{i-1}-\bar{X}_n)}{\sum _{i=1}^n(X_i-\bar{X}_n)^2}, \end{aligned}$$

(5)

$$\begin{aligned} {\widehat{\mu }}_{yw}=\bar{X}_n \end{aligned}$$

(6)

and

$$\begin{aligned} \widehat{\phi }_{yw}=\dfrac{\bar{X}_n}{S_n^2-\bar{X}_n}, \end{aligned}$$

(7)

where $\bar{X}_n=\frac{1}{n}\sum \nolimits _{t=1}^nX_t$ is the sample mean and $S^2_n=\dfrac{1}{n}\sum \nolimits _{t=1}^nX_t^2-\bar{X}_n^2$ is the sample variance.

We perform now a small Monte Carlo simulation in order to study the finite-sample behaviour of the proposed estimators and to compare the CLS and Yule-Walker estimation methods. We generate the PIGINAR(1) process, which was introduced and studied with some details in the previous section, under four configurations. In the Configurations I, II, III and IV we set $(\mu ,\alpha ,\phi )=(0.5,0.7,0.2)$, $(\mu ,\alpha ,\phi )=(2,0.5,1)$, $(\mu ,\alpha ,\phi )=(1,0.25,0.5)$ and $(\mu ,\alpha ,\phi )=(0.5,0.1,1.5)$, respectively. We consider the sample sizes $n=100,200,300,400,500,1000$ and the number of loops of the Monte Carlo simulation equals to 10000.

The results based on the Configurations I, II, III and IV are presented in Tables 1, 2, 3 and 4, respectively. These tables give us the empirical mean of the estimates of the parameters and also the standard errors.

Table 1 Empirical mean and standard errors (in parentheses) of the estimates of the parameters for $(\mu ,\alpha ,\phi )=(0.5,0.7,0.2)$ and some values of n under the PIGINAR(1) process

Table 2 Empirical mean and standard errors (in parentheses) of the estimates of the parameters for $(\mu ,\alpha ,\phi )=(2,0.5,1)$ and some values of n under the PIGINAR(1) process

Table 3 Empirical mean and standard errors (in parentheses) of the estimates of the parameters for $(\mu ,\alpha ,\phi )=(1,0.25,0.5)$ and some values of n under the PIGINAR(1) process

Table 4 Empirical mean and standard errors (in parentheses) of the estimates of the parameters for $(\mu ,\alpha ,\phi )=(0.5,0.1,1.5)$ and some values of n under the PIGINAR(1) process

Looking at these tables, we see that the bias and standard error of the estimates of the parameters decreases as the sample size increases for all cases considered, as expected. We also observe that the parameters $\mu$ and $\alpha$ are in general well estimated and that the CLS and Yule-Walker estimators yield very similar results for these parameters. The explanation for this is that $(\widehat{\mu }_{cls},\widehat{\alpha }_{cls})$ and $(\widehat{\mu }_{yw},\widehat{\alpha }_{yw})$ are asymptotically equivalent. More specifically, we have that $(\widehat{\mu }_{cls}-\widehat{\mu }_{yw},\widehat{\alpha }_{cls}-\widehat{\alpha }_{yw})=o_p(n^{-1/2})$. This can be checked by following the same steps that in Proof of Theorem 3 by Freeland and McCabe (2005). We now concentrate our attention to the estimation of the parameter $\phi$. Under the Configurations II ($\phi =1$) and III ($\phi =0.5$), we observe that the estimators $\widehat{\phi }_{cls}$ and $\widehat{\phi }_{yw}$ yield similar results with a slightly advantage for the Yule-Walker estimator that presents smaller bias and standard error with respect to the CLS estimator. Now, with respect to the Configurations I ($\phi =0.2$) and IV ($\phi =1.5$), we see that there is a considerable bias under both CLS and Yule-Walker estimation methods for estimating $\phi$ with $n=100,200,300$. Anyway, this bias is smaller under the Yule-Walker approach. We also see that the standard error of the Yule-Walker estimator is smaller than that one based on the CLS estimation. For $n\ge 400$, both methods work similarly. Overall, we see that the Yule-Walker estimation method works better that the CLS one for our mixed Poisson INAR(1) process considered. With this, we suggest the use of the Yule-Walker approach. This method will be considered in our application to a real dataset.

We establish now the consistency and asymptotic normality of the estimators (5), (6) and (7).

Proposition 4

Assume that $E(X_n^4)<\infty$. Then, the estimators ${\widehat{\mu }}_{yw}$, $\widehat{\phi }_{yw}$ and ${\widehat{\alpha }}_{yw}$ are strongly consistent for $\mu$, $\phi$ and $\alpha$ respectively and satisfy the asymptotic normality

$$\begin{aligned} \sqrt{n}\{({\widehat{\mu }}_{yw},\widehat{\phi }_{yw},{\widehat{\alpha }}_{yw})-(\mu ,\phi ,\alpha )\}\mathop {\longrightarrow }\limits ^{d} N(0,B\Sigma B^\top ), \end{aligned}$$

as $n\rightarrow \infty$, where

$$\begin{aligned} B= \left( \begin{array}{ccc} 1 &{} 0 &{} \quad 0\\ \mu \dfrac{2(\kappa _2+\mu ^2)-\mu }{(\kappa _2-\mu )^2} &{} \quad -\dfrac{\mu ^2}{(\kappa _2-\mu )^2}&{}\quad 0\\ \quad -2\mu \dfrac{1-\alpha }{\kappa _2} &{} -\dfrac{\alpha }{\kappa _2}&{} \quad \dfrac{1}{\kappa _2}\\ \end{array} \right) \end{aligned}$$

and $\Sigma$ being a $3\times 3$ symmetric matrix with entries given by

$$\begin{aligned}&\displaystyle \Sigma _{11}=\kappa _2\dfrac{1+\alpha }{1-\alpha },\\&\displaystyle \Sigma _{12}=\kappa _3+2\mu \kappa _2+(\kappa _3-\kappa _2)\dfrac{\alpha ^2}{1-\alpha ^2}+\dfrac{\alpha }{1-\alpha }(\kappa _2+4\mu \kappa _2+\kappa _3), \end{aligned}$$

$$\begin{aligned} \Sigma _{13}= & {} \alpha (1+\alpha )(\kappa _3-\kappa _2)+2\kappa _2(\alpha +\mu (1+\alpha ))+\dfrac{\alpha ^3}{1-\alpha ^2}(\kappa _3-\kappa _2)\\&+\dfrac{\alpha }{1-\alpha }\{\alpha ^2(\kappa _3-\kappa _2)+2\kappa _2[\mu +\alpha (1+\mu )]\},\\ \Sigma _{22}= & {} \mu _4-\mu _2^2+\dfrac{2\alpha ^2}{1-\alpha ^2}\left\{ \kappa _4+\kappa _3(2\mu -1)-\kappa _2^2-2\mu \kappa _2\right\} \\&+\dfrac{2\alpha }{1-\alpha }(1+2\mu )(\kappa _3+2\mu \kappa _2), \end{aligned}$$

$$\begin{aligned} \Sigma _{23}= & {} \alpha (1+\alpha ^2)(\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2))+(\kappa _3-\kappa _2)\left\{ 3\alpha \left( 1+\alpha \right) \left( 1+\mu \right) +2\mu \right\} \\&+\,2\mu ^2\kappa _2+4\kappa _2^2\alpha +2\kappa _2(1+\mu )(\alpha +\mu (1+2\alpha ))\\&+ \dfrac{\alpha ^3}{1-\alpha ^2}\left\{ \kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2) +2(\kappa _3-\kappa _2)(1+\mu )+2\kappa _2^2\right\} \\&+\dfrac{\alpha ^2}{1-\alpha ^2}\left\{ \alpha ^3(\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2))+\alpha ^2(\kappa _3-\kappa _2)(2+\mu )\right. \\&\left. +\,2\alpha \kappa _2^2+\mu (\kappa _3-\kappa _2)\right\} \\&+\dfrac{\alpha }{1-\alpha }\left\{ (\kappa _3-\kappa _2)\left( \alpha ^2(1+2\mu )+\alpha (1+\mu )+\mu \right) \right. \\&\left. +\,2\alpha \kappa _2(1+\mu )^2+2\mu \kappa _2(\mu +(1+\mu )(1+\alpha ))\right\} \end{aligned}$$

and

$$\begin{aligned} \Sigma _{33}= & {} \dfrac{2\alpha ^3}{1-\alpha ^2}\left\{ \alpha ^3(\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2))+\alpha ^2(\kappa _3-\kappa _2)(2+\mu )\right. \\&\left. +2\alpha \kappa _2^2+\mu (\kappa _3-\kappa _2)\right\} \\&+\dfrac{2\alpha }{1-\alpha }\left\{ \alpha ^3(\kappa _3-\kappa _2)(1+\mu )+\alpha ^2\mu (\kappa _3-\kappa _2)+\alpha ^2\kappa _2(1+\mu )^2\right. \\&\left. +2\alpha \mu \kappa _2(1+\mu )+\mu ^2\kappa _2\right\} \\&+\alpha ^2(1+2\alpha ^2)\left\{ \kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2)\right\} \\&+\alpha (\kappa _3-\kappa _2)\left\{ \alpha +(1+\alpha )(1+4\mu )+2\alpha ^2(3+2\mu )\right\} +\alpha \kappa _2(1+\mu )(5\mu \\&+2\alpha (1+\mu )+1)+(4+\alpha )\mu ^2\kappa _2+5\alpha ^2\kappa _2^2+\kappa _2(\kappa _2-2\alpha \mu ^2). \end{aligned}$$

Proof

Since $E(X_n)<\infty$ by assumption, it follows from Proposition 3 that the stationary process $\{X_n\}_{n=0}^\infty$ is ergodic. With this, we can apply the Law of Large Numbers for stationary and ergodic processes to obtain the strong consistency of the estimators; for instance, see Proposition 7.1 by Hamilton (1994).

In order to show the asymptotic normality of the estimators, we define $Y_n=\sum \nolimits _{t=1}^n X_t$, $Z_n=\sum \nolimits _{t=1}^n X_t^2$ and $W_n=\sum \nolimits _{t=1}^n X_{t-1}X_t$, for $n\ge 1$. Note that the estimators $({\widehat{\mu }}_{yw},\widehat{\phi }_{yw},{\widehat{\alpha }}_{yw})$ are asymptotically equivalent to $g(Y_n/n,Z_n/n,W_n/n)$, where $g(y,z,w)=\left( y,\dfrac{y}{z-y^2-y},\dfrac{w-y^2}{z-y^2}\right)$, for $(y,z,w)\in \mathbb R^+$, $z\ne y(y+1)$ and $z\ne y^2$.

By using the Central Limit Theorem for stationary and ergodic processes (see Chapter 7 from Anderson (1971)), we obtain that $\sqrt{n}\{(Y_n/n,Z_n/n,W_n/n)-(\mu ,\mu ^2+\kappa _2,\mu ^2+\alpha \kappa _2)\}\mathop {\longrightarrow }\limits ^{d} N(0,\Sigma )$ as $n\rightarrow \infty$, where $\mu =E(X_n)$, $\kappa _2=\text{ Var }(X_n)$ and $\Sigma$ is some asymptotic covariance matrix. With the results above and by applying the Delta Method with the function $g(\cdot ,\cdot ,\cdot )$ as defined above, we obtain that $\sqrt{n}\{({\widehat{\mu }}_{yw},\widehat{\phi }_{yw},{\widehat{\alpha }}_{yw})-(\mu ,\phi ,\alpha )\}\mathop {\longrightarrow }\limits ^{d} N(0,B\Sigma B^\top )$, where $B=\partial g(\theta )/\partial \theta$. The point that remains to be proven is the form of the covariance matrix $\Sigma$, which is done in the Appendix. $\square$

5 Empirical illustration

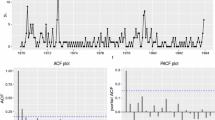
In this section we illustrate the usefulness of the proposed class of mixed Poisson INAR(1) processes. We consider a sex offence count time series data, which can be found at site www.forecastingprinciples.com. For this count time series, an observation corresponds to a monthly count of sex offences reported in the 21st police car beat in Pittsburgh. These data contain 144 observations starting in January 1990 and ending in December 2001 and was firstly used by Ristić et al. (2009). The plots of the data and the associated ACF and PACF are presented in Fig. 1. From these plots, we see that the first sample autocorrelation is more significant than the other and there exists a cutoff after lag 1 in the partial autocorrelations. These facts indicate that an INAR process of order 1 can be suitable for modelling the monthly count of sex offences.

Fig. 1

Plots of the monthly count of sex offences reported in the 21st police car beat in Pittsburgh from January 1990 up to December 2001 and the associated ACF and PACF

We begin this application performing an overdispersion test proposed by Schweer and Weiß (2014), which the test statistic is based on the empirical index of dispersion $\widehat{I}_d\equiv S_n^2/\bar{X}_n$. The null hypothesis is $H_0{\text {:}}\, X_1,\ldots ,X_n$come from a Poisson INAR(1) process against the alternative hypothesis $H_1{\text {:}}\, X_1,\ldots ,X_n$come from an overdispersed INAR(1) process. For the count time series considered here, we have that $\widehat{I}_d=1.7394$. The associated p-value is $2.55\times 10^{-12}$, that is, by using any usual significance level (for instance at 5%) we reject the null hypothesis in favor of the alternative hypothesis that states that an overdispersed INAR(1) process is more adequate for modelling this count data.

In Table 5 we present the estimates of the parameters based on the Yule-Walker estimation method given in Sect. 4. We also present in this table the associated standard errors and confidence intervals for the parameters with significance level at 5%. We consider the PIGINAR(1) and NBINAR(1) (negative binomial) processes and call attention that the estimates of the parameters are the same in both case since the estimation depends only on the first moments that are equal for these models. We see that the standard error for the estimates of $\mu$ are equal for both models (as expected) and that the standard errors of the estimates of $\alpha$ and $\phi$ are smaller under the negative binomial assumption with respect to the PIG-based model.

Table 5 Estimates of the parameters and their associated standard errors under the MPINAR(1) processes based on the Yule-Waker estimation method for the monthly count of sex offences time series data

We also fit a Poisson INAR(1) process and compare with our fitted mixed Poisson INAR(1) processes. In Table 6 we provide some empirical and estimated quantities based on the Poisson, negative binomial and Poisson-inverse Gaussian INAR(1) models. We consider the following quantities: mean, variance, skewness, kurtosis, index of dispersion (ratio of the variance to the mean), probability of zero and the first higher-order moment, denoted by $\kappa _1$, $\kappa _2$, skew., kurt., $I_d$, $p_0$ and $\mu (1)$, respectively.

Table 6 Comparison among the models based on empirical and estimated quantities under the PIG, NB and Poisson INAR(1) processes

From the results presented in Table 6, it is very clear that the Poisson INAR(1) process is not adequate for modelling the monthly count of sex offences considered here. On the other hand, we observe a good agreement among the empirical quantities and the estimated quantities based on our mixed Poisson INAR(1) processes, with a slight advantage of the PIGINAR(1) process over the NBINAR(1) process.

We now discuss the goodness-of-fit of the models based on the residuals $R_t\equiv X_t-\widehat{E}(X_t|X_{t-1})=X_t-{\widehat{\alpha }}_{yw} X_{t-1}-{\widehat{\mu }}_{yw}(1-{\widehat{\alpha }}_{yw})$ and on the jumps $J_t$ defined in the final of Sect. 2, for $t=2,\ldots ,n$. In the Fig. 2, we present the ACF of the residuals based on the MPINAR(1) process. This figure indicates that the residuals $R_2,\ldots ,R_n$ are not correlated, so our fitted models seem to have captured well the dependence of the count time series. In this figure we also plot the jumps against the time with $\pm 3\sigma _J$ bounds chosen as benchmark chart, where $\sigma _J=\sqrt{\text{ Var }(J_t)}$; this graphic is also known in the literature as Shewhart control chart and was proposed by Weiß (2009) as a diagnostic checking of fitted INAR(1) models. We plot the bounds based on our mixed Poisson INAR processes and also the corresponding to the Poisson INAR process. We see that the bounds based on the mixed INAR process accommodate adequately the points (around 97% of them) in contrast with the benchmark chart related to the Poisson INAR process, where many points are out of the bounds (around 16% of them).

Fig. 2

Sample autocorrelation function (ACF) of the residuals and jumps against time with bounds based on the mixed Poisson INAR(1) and Poisson INAR(1) processes

As suggested by one referee, we also use the standardized Pearson residual (for instance, see Harvey and Fernandes (1989) and Jung and Tremayne (2011))

$$\begin{aligned} r_t\equiv & {} \dfrac{X_t-\widehat{E}(X_t|X_{t-1})}{\sqrt{\widehat{\text{ Var }}(X_t|X_{t-1})}}\\= & {} \dfrac{X_t-{\widehat{\alpha }}_{yw} X_{t-1}-{\widehat{\mu }}_{yw}(1-{\widehat{\alpha }}_{yw})}{\sqrt{{\widehat{\alpha }}_{yw}(1-{\widehat{\alpha }}_{yw})X_{t-1}+{\widehat{\mu }}_{yw}(1-{\widehat{\alpha }}_{yw})[1+{\widehat{\mu }}_{yw}\widehat{\phi }_{yw}^{-1}(1+{\widehat{\alpha }}_{yw})]}}, \end{aligned}$$

for $t=2,\ldots ,n$, in order to check the variance, which should be close to 1. According to Harvey and Fernandes (1989), a sample variance greater than 1 indicates overdispersion with respect to the model that is being considered. We compute the sample variance of the standardized Pearson Residual and obtain that it is equal to 0.9539, so giving evidence that our mixed Poisson INAR(1) processes have captured with success the overdispersion of the count time series considered.

With the results and discussion presented above, we conclude that the INAR process based on the Poisson assumption is not adequate for modelling the present count time series data and that the mixed Poisson INAR processes provide an adequate approach.

6 Conclusions and future research

A common way for treating overdispersion in count data is to use the mixed Poisson distributions, which is obtained by introducing a latent random effect on the mean of a Poisson distribution. With this motivation, we introduced a class of INAR(1) processes with mixed Poisson marginals. We established a condition to our class is well-defined and discussed statistical properties. The INAR(1) process with Poisson-inverse Gaussian marginals was introduced and presented with some details. We discussed estimation of the parameters and gave conditions to have consistency and asymptotic normality of the estimators. Simulated results showed that the estimators work well for the scenarios considered. An empirical example illustrated the importance in considering our overdispersed INAR processes for analyzing count time series data.

Possible points of future research are: (a) multivariate extension of our mixed Poisson INAR(1) process; (b) to define and study a mixed Poisson INAR process of p-order; (c) to explore more particular cases of our class of overdispersed INAR processes such as an INAR model with Poisson-log normal marginals.

Appendix

We here derive the asymptotic covariance matrix of the weak convergence given in Proposition 4. For this, we will use joint moments, which are defined by

$$\begin{aligned} \mu (s_1,\ldots ,s_r)\equiv E(X_tX_{t+s_1}\ldots X_{t+s_r}), \end{aligned}$$

where $0\le s_1\le \ldots \le s_r$ and r belongs to $\mathbb N$. Expressions of joint moments up to fourth order for INAR(1) processes were obtained by Schweer and Weiß (2014) (Theorem 3.3.1). We will use these expressions for computing the desired asymptotic covariance matrix.

Let $Y_n$, $Z_n$ and $W_n$ be as defined in Sect. 4 and define $g_n(i,j)=n{-}i{-}\frac{\alpha ^j}{1-\alpha ^j}\big (1-\alpha ^{j(n-i)}\big )$, for $i,j\in \mathbb N$. Using joint moments and their expressions given in Theorem 3.3.1 from Schweer and Weiß (2014), after some manipulations we obtain that

$$\begin{aligned} \text{ Var }(Y_n)= & {} n\text{ Var }(X_t)+2\sum _{t=1}^n\sum _{k=t+1}^n\text{ cov }(X_k,X_t)= n\kappa _2{+}2\sum _{t=1}^n\sum _{k=t+1}^n\big \{\mu (k-t){-}\mu ^2\big \}\\= & {} n\kappa _2\left\{ 1+2\dfrac{\alpha }{1-\alpha }-2\alpha ^2\dfrac{1-\alpha ^n}{n(1-\alpha )^2}\right\} , \end{aligned}$$

$$\begin{aligned} \text{ Var }(Z_n)= & {} n\text{ Var }(X_t^2)+2\sum _{t=1}^n\sum _{k=t+1}^n\text{ cov }\left( X_k^2,X_t^2\right) \\= & {} n(\mu _4-\mu _2^2)+2\sum _{t=1}^n\sum _{k=t+1}^n\left\{ \mu (0,k-t,k-t)-\left( \kappa _2+\mu ^2\right) ^2\right\} \\= & {} n\left( \mu _4-\mu _2^2\right) +2\dfrac{\alpha ^2}{1-\alpha ^2}g_n(1,2)\left\{ \kappa _4+\kappa _3(2\mu -1)-\kappa _2^2-2\mu \kappa _2\right\} \\&+\,2\dfrac{\alpha }{1-\alpha }g_n(1,1)(1+2\mu )(\kappa _3+2\mu \kappa _2), \end{aligned}$$

$$\begin{aligned} \text{ Var }(W_n)= & {} n\text{ Var }(X_{t-1}X_t)+2\sum _{t=1}^{n-2}\sum _{k=t+2}^n\text{ cov }(X_{k-1}X_k,X_{t-1}X_t)\\&+\,2\sum _{t=1}^{n-1}\text{ cov }(X_{t-1}X_t,X_tX_{t+1})\\= & {} \,n\left\{ \mu (0,1,1)-\mu (1)^2\right\} +2\sum _{t=1}^{n-2}\sum _{k=t+2}^n\left\{ \mu (1,k-t,k-t+1)-\mu (1)^2\right\} \\&+\,2\sum _{t=1}^{n-1}\left\{ \mu (1,1,2)-\mu (1)^2\right\} \\= & {} 2g_n(2,2)\dfrac{\alpha ^3}{1-\alpha ^2}\left\{ \alpha ^3(\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2))\right. \\&\left. +\,\,\alpha ^2(\kappa _3-\kappa _2)(2+\mu )+2\alpha \kappa _2^2+\mu (\kappa _3-\kappa _2)\right\} \\&+ 2g_n(2,1)\dfrac{\alpha }{1-\alpha }\left\{ \alpha ^3(\kappa _3-\kappa _2)(1+\mu )+\alpha ^2\mu (\kappa _3-\kappa _2)\right. \\&\left. +\,\,\alpha ^2\kappa _2(1+\mu )^2+2\alpha \mu \kappa _2(1+\mu )+\mu ^2\kappa _2\right\} \\&+ \,\alpha ^2\{\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2)\}(n+2\alpha ^2(n-1))\\&+\,\alpha (\kappa _3-\kappa _2)\{n(\alpha +(1+\alpha )(1+2\mu ))\\&+ \,2(n-1)(\mu (1+\alpha )+\alpha ^2(3+2\mu ))\}+\alpha \kappa _2\{n(1+\mu )(1+3\mu )\\&+\,2(n-1)(1+\mu )(2\mu +\alpha (1+\mu ))\}\\&+\, \mu ^2\kappa _2(n(4+\alpha )-2)+\alpha ^2\kappa _2^2(5n-2)+n\kappa _2(\kappa _2-2\alpha \mu ^2), \end{aligned}$$

$$\begin{aligned} \text{ cov }(Y_n,Z_n)= & {} nE(X_t^3)+\sum _{t=1}^{n-1}\sum _{k=t+1}^nE(X_tX_k^2)\\&+\,\sum _{k=1}^{n-1}\sum _{t=k+1}^nE(X_tX_k^2)-n^2E(X_t)E(X_t^2)\\= & {} n\mu _3+\sum _{t=1}^{n-1}\sum _{k=t+1}^n\mu (k-t,k-t)+\sum _{k=1}^{n-1}\sum _{t=k+1}^n\mu (0,t-k)-n^2\mu \mu _2\\= & {} n(\kappa _3+2\kappa _2\mu )+(\kappa _3-\kappa _2)\dfrac{\alpha ^2}{1-\alpha ^2}g_n(1,2)\\&+\dfrac{\alpha }{1-\alpha }g_n(1,1)(\kappa _2+4\mu \kappa _2+\kappa _3), \end{aligned}$$

$$\begin{aligned} \text{ cov }(Y_n,W_n)= & {} nE(X_{t-1}X_t^2)+(n-1)E(X^2_{t-1}X_t)+\sum _{t=1}^{n-2}\sum _{k=t+2}^nE(X_tX_{k-1}X_k)\\&+\,\sum _{k=1}^{n-1}\sum _{t=k+1}^nE(X_tX_{k-1}X_k)-n^2E(X_t)E(X_{t-1}X_t)\\= & {} n\mu (1,1)+(n-1)\mu (0,1)+\sum _{t=1}^{n-2}\sum _{k=t+2}^n\mu (k-t-1,k-t)\\&+\,\sum _{k=1}^{n-1}\sum _{t=k+1}^n\mu (1,t-k+1)-n^2\mu \mu (1)\\= & {} \,\alpha (n\alpha +n-1)(\kappa _3-\kappa _2)+(2n-1)\kappa _2(\alpha +\mu (1+\alpha ))\\&+\,(\kappa _3-\kappa _2)\dfrac{\alpha ^3}{1-\alpha ^2}g_n(2,2)\\&+\,\kappa _2\dfrac{\alpha }{1-\alpha }g_n(2,1)(\mu +\alpha (1+\mu ))\\&+\,\dfrac{\alpha }{1-\alpha }g_n(1,1)\{\alpha ^2(\kappa _3-\kappa _2) +\,\alpha \kappa _2(1+\mu )+\mu \kappa _2\}, \end{aligned}$$

and

$$\begin{aligned} \text{ cov }(Z_n,W_n)= & {} nE(X_{t-1}X_t^3)+(n-1)E(X^3_{t-1}X_t)+\sum _{t=1}^{n-2}\sum _{k=t+2}^nE(X_t^2X_{k-1}X_k)\\&+\,\sum _{k=1}^{n-1}\sum _{t=k+1}^nE(X_{k-1}X_kX_t^2)-n^2E(X_t^2)E(X_{t-1}X_t)\\= & {} n\mu (1,1,1)+(n-1)\mu (0,0,1)+\sum _{t=1}^{n-2}\sum _{k=t+2}^n\mu (0,k-t-1,k-t)\\&+\,\sum _{k=1}^{n-1}\sum _{t=k+1}^n\mu (1,t-k+1,t-k+1)-n^2\mu _2\mu (1)\\= & {} \alpha (n\alpha ^2+n-1)\{\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2)\}\\&+\,\alpha (n\alpha +n-1)(\kappa _3-\kappa _2)(3+2\mu )\\&+\,\mu \{n(\alpha (1+\alpha )+2)-(1+\alpha )\}(\kappa _3-\kappa _2)\\&+\,(2n-1)\kappa _2\{\mu ^2+2\alpha \kappa _2+(1+\mu )(\alpha +\mu (1+2\alpha ))\}\\&+\,\dfrac{\alpha ^3}{1-\alpha ^2}g_n(2,2)\{\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2)\\&+\,2(\kappa _3-\kappa _2)(1+\mu )+2\kappa _2^2\}\\&+\,\dfrac{\alpha }{1-\alpha }g_n(2,1)\{(\kappa _3-\kappa _2)(\mu +\alpha (1+\mu ))\\&+\,\alpha \kappa _2(1+\mu )^2+\kappa _2\mu (1+\mu )(1+\alpha )+\mu ^2\kappa _2\}\\&+\,\dfrac{\alpha ^2}{1-\alpha ^2}g_n(1,2)\{\alpha ^3(\kappa _4-3\kappa _3+\kappa _2(2-3\kappa _2))\\&+\,\alpha ^2(\kappa _3-\kappa _2)(2+\mu )+2\alpha \kappa _2^2+\mu (\kappa _3-\kappa _2)\}\\&+\,\dfrac{\alpha }{1-\alpha }g_n(1,1)\{\alpha ^2(\kappa _3-\kappa _2)(1+2\mu )+\alpha \kappa _2(1+\mu )^2\\&+\,\mu \kappa _2(\mu +(1+\mu )(1+\alpha ))\}, \end{aligned}$$

where $\mu =E(X_n)$, $\kappa _j=E((X_n-\mu )^j)$ and $\mu _j=E(X_n^j)$, for $j=2,3,4$.

Let $\Sigma _n$ be the covariance matrix with the above terms. Hence, it follows that the covariance matrix $\Sigma$ of the Proposition 4 can be obtained by $\Sigma =\displaystyle \lim _{n\rightarrow \infty }\Sigma _n/n$.