Modelling of low count heavy tailed time series data consisting large number of zeros and ones

Abstract

In this paper, we construct a new mixture of geometric INAR(1) process for modeling over-dispersed count time series data, in particular data consisting of large number of zeros and ones. For some real data sets, the existing INAR(1) processes do not fit well, e.g., the geometric INAR(1) process overestimates the number of zero observations and underestimates the one observations, whereas Poisson INAR(1) process underestimates the zero observations and overestimates the one observations. Furthermore, for heavy tails, the PINAR(1) process performs poorly in the tail part. The existing zero-inflated Poisson INAR(1) and compound Poisson INAR(1) processes have the same kind of limitations. In order to remove this problem of under-fitting at one point and over-fitting at others points, we add some extra probability at one in the geometric INAR(1) process and build a new mixture of geometric INAR(1) process. Surprisingly, for some real data sets, it removes the problem of under and over-fitting over all the observations up to a significant extent. We then study the stationarity and ergodicity of the proposed process. Different methods of parameter estimation, namely the Yule-Walker and the quasi-maximum likelihood estimation procedures are discussed and illustrated using some simulation experiments. Furthermore, we discuss the future prediction along with some different forecasting accuracy measures. Two real data sets are analyzed to illustrate the effective use of the proposed model.

1 Introduction

Time series of count data arise in various fields of science, especially in social science, medicine and epidemiology. For example, monthly reported cases of a particular water-borne disease, and monthly cases of kidnapping in a city are some examples of count time series data. If the counts are large, data can be well approximated by some continuous distributions and hence the well-known Box-Jenkins’ ARMA model can be used. The main justification behind this approximation is that many common discrete distributions, e.g., binomial, Poisson and negative binomial can be well approximated by normal distribution when the means of these distributions are large. However, in practice, it is often observed that the counts are small. For example, for the monthly cases of poliomyelitis data (see Zeger 1988), almost 80% of the total observations lie between 0 and 2. Therefore, in such scenarios, it is not desirable to approximate the data by some continuous time series models. Furthermore, it is very important to use a model that preserves the count property of the data.

In this regard, the most well-known model is the integer-valued auto-regressive process of first order (or INAR(1)) based on binomial thinning operator introduced by McKenzie (1985). This class of models is constructed based on the binomial thinning operator of Steutel and Van Harn (1979) defined as follows. Given a discrete random variable X and a constant $\alpha$ lying between 0 and 1, the binomial thinning operator “$\circ$” is defined as $\alpha \circ X = \sum _{i=1}^{X}B_{i},$ where $B_{i}$’s are independent and identically distributed (i.i.d.) Bernoulli($\alpha$) random variables. Given the above definition of the thinning operator, McKenzie’s class of INAR(1) process has the form $Y_{t} = \alpha \circ Y_{t-1} + \varepsilon _{t}$, where $\alpha \in (0,1)$, and $\{\varepsilon _{t}\}$ is a sequence of i.i.d. discrete random variables. It is also assumed that $\varepsilon _{t}$ is independent of the past lag values of $Y_t$, i.e, $Y_{t-k}$ for $k \ge 1$. Given the above class of INAR(1) process, it has been shown that all distributions of $Y_{t}$ that are discrete self-decomposable (DSD) in the sense of Steutel and Van Harn (1979) are stationary solutions of the above equation. For example, Poisson and geometric distributions are stationary solutions of the above INAR(1) process. However, distributions that are defined on a finite support space, e.g., binomial distribution, are not stationary solutions of the above class.

Based on this idea, Al-Osh and Alzaid (1987) introduced the Poisson INAR(1) or PINAR(1) process which was subsequently studied by Freeland and McCabe (2004, 2005), McCabe and Martin (2005), Silva et al. (2009) and many others. This model is widely used in various scientific disciplines because of its nice closed mathematical form. However, when data in practice are under-dispersed (variance is smaller than mean) or over-dispersed (variance is larger than mean), such class of PINAR(1) models does not fit the data well. In such cases, over-dispersed INAR(1) models like geometric INAR(1) (GINAR(1) in short), negative binomial INAR(1) (NBINAR(1) in short) process proposed by McKenzie (1986), compound Poisson INAR(1) (CPINAR(1) in short) process proposed by Schweer and Weiß (2014) are very useful. However, this over-dispersed class of INAR(1) models also fails when data contains a large number of zeros. For example, the skin lesions data used by Jazi et al. (2012) contains a large number zeros. In such cases, the PINAR(1), GINAR(1) and other over-dispersed models do not fit the data well. As an alternative, Jazi et al. (2012) proposed a class of zero-inflated Poisson INAR(1) (ZINAR(1) in short) models whose innovation distribution is zero-inflated Poisson. Such models can also be used for zero-deflated data. However, the marginal distribution of their model is very complicated and does not have any closed form expression. Recently, Maiti et al. (2015) proposed an another class of zero-inflated Poisson INAR(1) models based on binomial thinning operator for which the marginal distribution of $Y_t$ is zero-inflated Poisson. Such models perform better than the usual over-dispersed models like GINAR(1) in capturing the large number of zeros.

On the other hand, Latour (1998) extended the binomial thinning operator to generalized thinning operator which is defined as follows. Given a discrete random variable X and a constant $\alpha$ lying between 0 and 1, the generalized thinning operator “$\bullet$” is defined as $\alpha \bullet X = \sum _{i=1}^{X}B_{i},$ where $B_{i}$’s are i.i.d. non-negative random variables with mean $\alpha$. Using this operator, Ristić et al. (2009) proposed a new geometric INAR(1) (or NGINAR(1)) process assuming $B_{i}$’s follow i.i.d. geometric distribution with mean $\alpha$ and they named it negative binomial thinning operator. Several other thinning operators and consequent INAR processes can be found in Weiß (2008) and Scotto et al. (2015). In order to accommodate a large number of zeros, Barreto-Souza (2015) proposed a zero-modified geometric INAR(1) or ZMGINAR(1) process based on the negative binomial thinning operator. They showed that the marginal distribution of such models follows a zero-inflated geometric distribution. In addition, such models can be used for both zero-inflation and zero-deflation. However, when a count time series data contains a large number of zeros along with a large number of ones which often arise in practice [e.g., poliomyelitis data used by Zeger (1988)], both the over-dispersed [e.g., GINAR(1)] and zero-inflated Poisson INAR(1) models fail. In such scenarios, it demands some adjustment of probability mass on zero and one observations.

In order to fill this gap, here we propose a new class of one-modified geometric INAR(1) (or OMGINAR(1)) process, extending the idea articulated in Maiti et al. (2015). The applications studied in this article demand a theoretical study of the newly proposed process. We study some structural properties of the proposed model such as mean, variance, dispersion index, autocorrelation function, marginal and joint distributions. We show that the proposed model is strongly stationary and ergodic. We study the parameter estimation using Yule-Walker (YW) and quasi-maximum likelihood estimation (QMLE) methods. We also provide a mathematical proof of consistency of the YW estimators. Furthermore, the robustness of the proposed model is studied in great details with respect to various forecasting measures of accuracy using simulated data from various INAR(1) models like PINAR(1), GINAR(1) and ZINAR(1). Finally, we illustrate the proposed model using two real data sets, namely the monthly cases of poliomyelitis in the US and monthly cases of assault data reported in Pittsburgh, US.

We present the article as follows. In Sect. 2, we describe the proposed model along with its different distributional properties like marginal distribution and autocorrelation. Joint and conditional distributions along with its h-step ahead forecasting distribution are discussed in Sect. 3. In Sect. 4, we discuss two estimation methods, namely the YW and the QMLE to estimate the model parameters. Simulation experiments are presented in Sect. 5. In Sect. 6, we illustrate the methodology using two real data sets. Sect. 7 concludes with some discussions. All the proofs and derivations are relegated to “Appendix”.

2 The model

Let $\{Y_t\}_{t \in \mathbb {N}}$ be a PINAR(1) process of Al-Osh and Alzaid (1987) based on binomial thinning operator and can be written as $Y_{t} = \alpha \circ Y_{t-1} + \varepsilon _{t}, \;\; t = 0,1,\ldots$, where $Y_t$ has the Poisson marginal distribution with mean $\lambda$. Let $\{X_{t}\}_{t \in \mathbb {N}}$ be a sequence of i.i.d. random variables with $P(X_t = 1) = p = 1-P(X_t = 0)$. Then the ZIPINAR(1) process of Maiti et al. (2015), $\{Z_{t}\}_{t \in \mathbb {N}}$, based on the idea of allocating extra weight at 0 in PINAR(1) process, can be written as $Z_{t} = X_{t}Y_{t}$. Using the similar idea, here we propose a new OMGINAR(1) process. We allocate an extra weight at 1 in the GINAR(1) process of McKenzie (1986). Our proposed process can be defined as follows.

Let $\{Y_t\}_{t \in \mathbb {N}}$ be a GINAR(1) process as defined in McKenzie (1986) where $Y_t$ has the geometric marginal distribution in the form $P(Y_t = i) = (1-\theta )\theta ^{i},\; i = 0,1,\ldots ;$ and let $\{X_t\}$ be a sequence of i.i.d. Bernoulli random variables defined above. Then, the proposed process OMGINAR(1) can be written as follows

$$\begin{aligned} Z_{t} = {\left\{ \begin{array}{ll} Y_t &{} \text{ with } \text{ probability } p \\ 1 &{} \text{ with } \text{ probability } 1-p. \end{array}\right. } \end{aligned}$$

(1)

Assuming that $Y_{t}^{0}=1$ when $Y_{t}=0$, we can write the above process (1) as

$$\begin{aligned} Z_{t}=Y_{t}^{X_{t}}. \end{aligned}$$

(2)

Unlike ZMGINAR(1) process of Barreto-Souza (2015) which is based on negative binomial thinning operator defined by Ristić et al. (2009), our proposed process is based on binomial thinning operator of Steutel and Van Harn (1979). Under the above setup, we can obtain the following result.

Proposition 1

The marginal distribution of $\{Z_t\}$ can be written as

$$\begin{aligned} P(Z_{t}=i)= {\left\{ \begin{array}{ll} 1-p+p \theta (1-\theta ), &{}\qquad \text{ for } \qquad i=1 \\ p(1-\theta )\theta ^{i}, &{} \qquad \text{ for } \qquad i=0,2,3,\ldots . \end{array}\right. } \end{aligned}$$

(3)

Proof

Proof is given in Appendix A. $\square$

Corollary 1

Using the above result, the marginal mean and marginal variance of $\{Z_t\}$ can be obtained as $E(Z_{t})= 1-p+p\theta ^{*}$ and $Var(Z_{t}) = 1-p + p \theta ^{*}(1+2\theta ^{*}) - (1-p+p\theta ^{*})^2$, respectively. Hence, the dispersion-index (DI) can be computed as

$$\begin{aligned} DI = \dfrac{Var(Z_{t})}{E(Z_{t})} = p(1-\theta ^{*}) + \dfrac{2p\theta ^{*}}{1-p+p\theta ^{*}} \end{aligned}$$

where $\theta ^{*} = \dfrac{\theta }{1-\theta }$.

Unlike the GINAR(1) process (for which $DI=\dfrac{1}{1-\theta } >1$), here DI can take any value between 0 and $\infty$ depending on the values of $\theta$ and p. Therefore, the proposed process can be used for both under- and over-dispersed time series data. However, in this article, we use the process for over-dispersed time series data.

3 Joint and conditional distributional properties

3.1 Auto-correlation structure and weak stationarity

The auto-covariance function (ACVF) of the process can be routinely derived, and is given by

$$\begin{aligned} \gamma _{z}(h)={\left\{ \begin{array}{ll} p^{2}\theta ^{*}(1+\theta ^{*})\alpha ^h, &{}\qquad \text{ if } \qquad h=1,2,\ldots \\ 1-p + p \theta ^{*}(1+2\theta ^{*}) - (1-p+p\theta ^{*})^2 &{}\qquad \text{ if } \qquad h=0, \end{array}\right. } \end{aligned}$$

(4)

where $\gamma _{z}(h) = Cov(Z_{t+h}, Z_{t})$. This implies that the auto-correlation function of the process decays exponentially to 0 as $h \rightarrow \infty$. This phenomena can be used to characterize the process.

From equations (3) and (4), we can see that the marginal mean of $Z_t$ and the auto-covariance function between $Z_t$ and $Z_{t+h}$ do not depend on the time index t. Hence, the proposed process OMGINAR(1) is at least covariance (weakly) stationary.

3.2 Strong stationarity and ergodicity

Under the above setup, it can be shown that the proposed OMGINAR(1) process is strongly stationary. For proof, see Appendix B.

Proposition 2

The joint distribution of $Z_{t+h}$ and $Z_{t}$ for the proposed process can be derived as

$$\begin{aligned} P_{Z_{t+h}, Z_{t}}(i,j)={\left\{ \begin{array}{ll} (1-p)^{2}+2p\bar{p}\theta \bar{\theta }+p^{2} \theta \bar{\theta }P_{Y_{t+h}|Y_{t}}(i|j), &{}\qquad \text{ if } \qquad i=j=1 \\ \\ p\theta ^j\bar{\theta }\left\{ \bar{p}+p P_{Y_{t+h}|Y_{t}}(i|j)\right\} &{}\qquad \text{ if } \qquad i=1, j\ne 1 \\ \\ p \bar{p} \bar{\theta } \theta ^{i} + p^{2} \theta \bar{\theta } P_{Y_{t+h}|Y_{t}}(i|j) &{}\qquad \text{ if } \qquad i\ne 1, j=1 \\ \\ p^2 \bar{\theta } \theta ^j P_{Y_{t+h}|Y_{t}}(i|j) &{}\qquad \text{ if } \qquad i,j \ne 1 \\ \\ \end{array}\right. } \end{aligned}$$

(5)

where

$$\begin{aligned}&P_{Y_{t+h}|Y_{t}}(i|j)\nonumber \\&\quad = {\left\{ \begin{array}{ll} (1-\alpha ^h)(1-\theta )\theta ^{i-j}\displaystyle \sum _{k=0}^i{{j}\atopwithdelims (){k}}\alpha ^{hk}\{(1-\alpha ^h)\theta \}^{j-k}\\ \qquad +{{j}\atopwithdelims (){i}}\alpha ^{h(i+1)}(1-\alpha ^h)^{j-i}, &{}\qquad i=0,1,\ldots , j\\ (1-\alpha ^h)(1-\theta )\theta ^{i-j}\{\alpha ^h+(1-\alpha ^h)\theta \}^j, &{}\qquad i=j+1,j+2,\ldots . \end{array}\right. }\nonumber \\ \end{aligned}$$

(6)

Proof

Derivation of the above result is given in Appendix C. $\square$

The joint probability generating function (pgf) of $Z_{t+1}$ and $Z_{t}$ can be derived as

$$\begin{aligned} \begin{array}{lcl} \Phi _{Z_{t+1},Z_{t}}(u,v) &{}=&{} (1-p)^{2} uv + p(1-p) \left( \dfrac{1-\theta }{1-\theta u}\right) + p(1-p) \left( \dfrac{1-\theta }{1-\theta v}\right) \\ &{} &{} + p^{2} \dfrac{\lambda (\lambda +\alpha u)}{(\lambda +u)(\lambda + \alpha u +v-\alpha u v)}, \end{array} \end{aligned}$$

(7)

which is not symmetric in u and v. Hence the process is not time-reversible. This is also because the hidden process $\{Y_{t}\}$ is not time-reversible.

Using the joint distribution result of $Z_{t+h}$ and $Z_{t}$ in (5), we can prove that the proposed OMGINAR(1) process is ergodic. See Appendix D for the proof.

3.3 Conditional distribution

Even though the latent process $\{Y_{t}\}$ is a Markov Chain of order one, i.e., given $(Y_{t}, \ldots , Y_{1})$, $Y_{t+1}$ depends only on the most present observation $Y_{t}$, the observed process $\{Z_{t}\}$ may not be a Markov chain of order one. In fact, the order of the process $\{Z_{t}\}$ cannot be assured. For example, suppose $Z_{t} \ne 1$, then the conditional distribution of $Z_{t+1}$ given $(Z_{t}, Z_{t-1}, \ldots , Z_{1})$ is equivalent to the conditional distribution of $Z_{t+1}$ given $Z_{t}$. However, if $Z_{t} = 1$ and $Z_{t-1} \ne 1$, then the conditional distribution of $Z_{t+1}$ given $(Z_{t}, Z_{t-1}, \ldots , Z_{1})$ is equal to the conditional distribution of $Z_{t+1}$ given $(Z_{t}, Z_{t-1})$. In general, if $Z_{t}=1, \ldots , Z_{t-k+1}=1$ but $Z_{t-k}\ne 1$, then the conditional distribution of $Z_{t+1}$ given $(Z_{t}, Z_{t-1}, \ldots )$ is equal to the conditional distribution of $Z_{t+1}$ given $(Z_{t}, Z_{t-1}, \ldots , Z_{t-k})$.

Again the above result can be generalized to $Z_{t+h}$ from $Z_{t+1}$, i.e., for any given integer $h\ge 1$, the conditional distribution of $Z_{t+h}$ given $(Z_{t} = 1, Z_{t-1}=1, \ldots , Z_{t-k+1} = 1, Z_{t-k}\ne 1, \ldots )$ is equal to the conditional distribution of $Z_{t+h}$ given $(Z_{t} = 1, Z_{t-1}=1, \ldots , Z_{t-k+1} = 1, Z_{t-k}\ne 1).$

Since the process is not a Markov Chain, the conditional distribution of $Z_t$ given past observations does not have any closed form expression. Thus the run distribution of zeros and ones, and expected length of those runs do not have any closed mathematical formula. Therefore, results related to expected length of runs of zeros and ones for the proposed process are difficult to compute.

4 Parameter estimation

4.1 Yule-Walker estimation

Given a data set $\{Z_1, Z_2, \ldots , Z_n\}$ of size n, we can write the following three moment equations to obtain the YW estimates of $\alpha$, $\theta$ and p:

$$\begin{aligned} \hat{\mu }_{1}^{\prime }= & {} 1-p+p\theta ^{*} \end{aligned}$$

(8)

$$\begin{aligned} \hat{\mu }_{2}^{\prime }= & {} p\theta ^{*}(1+2\theta ^{*}) + (1-p) \end{aligned}$$

(9)

$$\begin{aligned} \hat{\gamma }_{z}(1)= & {} p^2 \theta ^{*}(1+\theta ^{*})\alpha \end{aligned}$$

(10)

where $\hat{\mu }_{1}^{\prime } = \dfrac{1}{n} \displaystyle \sum _{t=1}^{n}Z_{t}$, $\hat{\mu }_{2}^{\prime } = \dfrac{1}{n} \displaystyle \sum _{t=1}^{n}Z_{t}^{2}$, and $\hat{\gamma }_{z}(1) = \dfrac{1}{n}\displaystyle \sum _{t=2}^{n} (Z_{t} - \hat{\mu }_{1}^{\prime }) (Z_{t-1} - \hat{\mu }_{1}^{\prime })$.

After solving the first two equations, we can obtain the YW estimates of p from the following quadratic equation

$$\begin{aligned} 2p^2 + (5\hat{\mu }_{1}^{\prime } - \hat{\mu }_{2}^{\prime } - 4)p + 2(\hat{\mu }_{1}^{\prime } - 1)^2 = 0. \end{aligned}$$

(11)

Suppose $\hat{p}_{yw}$ be the YW estimate of p, then from the first equation (89) we can get

$$\begin{aligned} \hat{\theta }^{*}_{yw} = \dfrac{\mu _{1}^{\prime } - 1 + \hat{p}_{yw}}{\hat{p}_{yw}} \end{aligned}$$

which implies

$$\begin{aligned} \hat{\theta }_{yw} = \dfrac{\mu _{1}^{\prime }-1+2\hat{p}_{yw}}{\mu _{1}^{\prime }-1+2\hat{p}_{yw}}. \end{aligned}$$

(12)

From the third moment Eq. (10), we get

$$\begin{aligned} \hat{\alpha }_{yw} = \dfrac{ \hat{\gamma }_{z}(1)}{ \hat{p}_{yw}^2 \hat{\theta }^{*}_{yw} (1+\hat{\theta }^{*}_{yw})}. \end{aligned}$$

(13)

Proposition 3

Under the above setup, the YW estimators of $\alpha , \theta$ and p are consistent, i.e.,

$$\begin{aligned} \hat{\alpha }_{yw} \overset{p}{\rightarrow } \alpha , \qquad \hat{\theta }_{yw} \overset{p}{\rightarrow } \theta , \qquad \hat{p}_{yw} \overset{p}{\rightarrow } p, \end{aligned}$$

where $`\overset{p}{\rightarrow }'$ denotes the convergence in probability.

Proof

Proof is given in Appendix F. $\square$

4.2 Quasi-maximum likelihood estimation

Suppose $\{Z_{1}, Z_{2}, \ldots , Z_{n}\}$ be set of n observations. In order to obtain the maximum likelihood estimates of OMGINAR(1) process, we have to maximize the log likelihood function

$$\begin{aligned} \ell _{n}(\alpha , \theta , p)= & {} \ln p(Z_{1}, Z_{2}, \ldots , Z_{n})\\= & {} \ln \Big (p(Z_{1}) p(Z_{2}\mid Z_{1}) p(Z_{3}\mid Z_{2}, Z_{1})\ldots p(Z_{n}\mid Z_{n-1}, \ldots , Z_{1})\Big ) \end{aligned}$$

subject to the constraint $0<\alpha , \theta , p<1$, where for the proposed process, the conditional distribution of $Z_{t}$ given the past observations can be written as

$$\begin{aligned} p(Z_{t}| Z_{t-1}, Z_{t-2}, \ldots ) = {\left\{ \begin{array}{ll} p(Z_{t}| Z_{t-1}) &{} \text{ if } Z_{t-1} \ne 1 \\ p(Z_{t}| Z_{t-1}, Z_{t-2}) &{} \text{ if } Z_{t-1}=1, Z_{t-2} \ne 1\\ p(Z_{t}| Z_{t-1}, Z_{t-2}, Z_{t-3}) &{} \text{ if } Z_{t-1}=1, Z_{t-2}=1, Z_{t-3}\ne 1\\ \vdots \end{array}\right. } \end{aligned}$$

In practice, beyond $k=1$, $p(Z_{t}| Z_{t-1}=1, Z_{t-2}=1, \ldots , Z_{t-k+1}=1, Z_{t-k}\ne 1)$ has a very cumbersome expression. For example, for $k=2$, we will have $2^3=8$ different cumbersome expressions for the conditional distribution of $p(Z_{t}| Z_{t-1}, Z_{t-2})$. To avoid that, here we propose to use one-step QMLE where we maximize $\ell ^{*}(\alpha , \theta , p) = \ln p(Z_{1}) + \displaystyle \sum _{t=2}^{n} \ln p(Z_{t}| Z_{t-1})$ instead of maximizing the actual likelihood function. In the next section, using some simulated data sets we study the consistency of this one-step QMLE method both with respect to bias and standard error.

5 Simulation study

In this section, we carried out some simulation experiments to compare the proposed model with some other existing INAR(1) models, namely the PINAR(1), GINAR(1), CPINAR(1) with $\text{ Poisson }_{2}$, and ZINAR(1) models. For model validation, we generated samples from the proposed model, and compared the fit of the proposed model to the data with the above five models with respect to AIC and some h-step ahead forecasting accuracy measures, namely predicted root mean squared error or PRMSE(h), predicted mean absolute error or PMAE(h) and percentage of true prediction PTP(h) which can be obtained using the following formulas:

$$\begin{aligned} \text{ PRMSE }(h) = E\left( (Y_{n+h} - \hat{Y}_{n+h})^{2}\mid \mathbf {Y}_{n:1}\right) \hat{=} \sqrt{\dfrac{1}{m} \displaystyle \sum _{i=1}^{m} (Y_{n+i} - \hat{Y}^{(h)}_{mean,n+i})^{2}}; \; \; h=1,2,\ldots , \end{aligned}$$

where $\hat{Y}^{(h)}_{mean,n+i} = \widehat{\text{ mean }}(Y_{n+i}|Y_{n-h+i})$ be the h-step ahead conditional mean of the fitted process;

$$\begin{aligned} \text{ PMAE }(h) = E\left( \left| Y_{n+h} - \hat{Y}_{n+h}\right| \mid \mathbf {Y}_{n:1}\right) \hat{=} \dfrac{1}{m} \displaystyle \sum _{i=1}^{m} \left| Y_{n+i} - \hat{Y}^{(h)}_{median,n+i}\right| ; \; \; h=1,2,\ldots , \end{aligned}$$

where $\hat{Y}^{(h)}_{median,n+i} = \widehat{\text{ median }}(Y_{n+i}|Y_{n-h+i})$ be the h-step ahead conditional median of the fitted process; and

$$\begin{aligned} \text{ PTP }(h) = E\Big (I(Y_{n+h} = \hat{Y}_{n+h})\mid \mathbf {Y}_{n:1}\Big ) \hat{=} \dfrac{1}{m} \displaystyle \sum _{i=1}^{m} I(Y_{n+i} = \hat{Y}^{(h)}_{mode,n+i}) \times 100; \; \; h=1,2,\ldots , \end{aligned}$$

where $\hat{Y}^{(h)}_{mode,n+i} = \widehat{\text{ mode }}(Y_{n+i}|Y_{n-h+i})$ be the h-step ahead conditional mode of the fitted process, and $\mathbf {Y}_{n:1} = (Y_{n}, Y_{n-1}, \ldots , Y_{1})$. To study the robustness of the proposed model, we generated samples from the PINAR(1), GINAR(1), CPINAR(1) with with $\text{ Poisson }_{2}$, and ZINAR(1) models.

Table 1 Parameter estimates of the OMGINAR(1) model using quasi maximum-likelihood method along with its bias and standard error

To begin with, we generated samples from the OMGINAR(1) process. We set the parameter values $\alpha = 0.3, 0.6$, $\theta = 0.6$, and $p = 0.5, 0.7, 0.9$ and sample sizes $n = 100, 500, 1000, 5000$. Note that $\alpha$, the first order ACF of the hidden process GINAR(1), can take any value between 0 and 1. Therefore, we set $\alpha =0.3$ for the class of lower ACF values and $\alpha = 0.6$ for the class of higher ACF values. Here $\theta =0.6$ was chosen based on some real data examples. However, the mixture parameter p that plays the main role in differentiating the proposed model from the GINAR(1) process was varied between 0.5 and 1. Here p close to 1 implies the process almost equals to the GINAR(1) process and close to 0 implies that the resulting process coincides with a degenerate process at 1. So we decided to set p not very close to 0. Besides, samples of size 100 were used to study the small-sample properties, samples of size 5000 were used to get an idea about the large-sample properties, and samples of sizes 500 and 1000 were used for moderate-sample properties. For a fixed sample size and fixed set of parameter values, we generated the samples 500 times and obtained the average estimates of parameters along with their biases and standard errors. The estimated parameters with their biases and standard errors are presented in Table 1. As we can see, there is very little effect on the biases of the QMLE estimates whereas standard errors converge to zero, as the sample size increases.

Table 2 Selection percentages of various models under study through AIC where the data are generated from the OMGINAR(1) process with various sets of parameter values

For model validation, first we performed a comparison between our proposed model and other competing models mentioned earlier with respect to AIC. We repeated the above simulation experiment and computed the AIC for all the models under comparison. Based on 500 Monte Carlo replications, we reported the percentage of times AIC selects a particular model among the set of six models in Table 2. It turns out that as the sample size increases, AIC selects the OMGINAR(1) model almost all the time. In other words, the proposed model is consistent with respect to AIC.

We also performed a similar study with respect to point forecasting accuracy measures, namely PRMSE(h), PMAE(h) and PTP(h). In this case, we fixed the sample size $n=400$ and repeated the above simulation experiment for all the above set of parameter values. To compute the accuracy measures, we divided each sample into two parts. The first part consisting of 300 (training set) observations were used to fit the models under comparison and the remaining 100 observations (validation set) were used to calculate the above three accuracy measures for $h=1, 2, 3, 4, 5$. Based on 500 Monte Carlo replications, we computed the average values of these measures and reported them in Tables 3, 4 and 5. As we can see, our proposed model performs better than the competing models considered in this study, as the mixture parameter decreases. In other words, as the mixture parameter decreases, the proposed model deviates from the GINAR(1) model, resulting in higher forecasting accuracy than the GINAR(1) and other four competing models. Furthermore, it is observed that as $\alpha$ increases, the forecasting accuracy also increases across all the models. This is because the mean and variance of the innovation process $\varepsilon _{t}$ of the hidden process GINAR(1) decreases to zero as $\alpha$ increases to one (i.e., the innovation process converges to a degenerate process degenerated at 0). On the other hand, as we can see from Tables  3, 4 and 5, the forecasting accuracy decreases across all the models as h increases; this finding is in conformity with our intuitive expectation that as one goes far ahead from the present, chances of making an accurate forecast will decrease.

Table 3 Values of PRMSE(h) for different models and for varying h where the data were simulated from the OMGINAR(1) process with various sets of parameter values

Table 4 Values of PMAE(h) for varying h where the data were simulated from the OMGINAR(1) process with various sets of parameter values

Table 5 Values of PTP(h) for varying h where the data were simulated from the OMGINAR(1) process with various sets of parameter values

Table 6 Values of PRMSE(h) for varying h where the data were simulated from the PINAR(1) process with various sets of parameter values

Table 7 Values of PMAE(h) for varying h where the data were simulated from the PINAR(1) process with various sets of parameter values

Table 8 Values of PTP(h) for varying h where the data were simulated from the PINAR(1) process with various sets of parameter values

Table 9 Values of PRMSE(h) for varying h where the data were simulated from the GINAR(1) process with various sets of parameter values

Table 10 Values of PMAE(h) for varying h where the data were simulated from the GINAR(1) process with various sets of parameter values

Table 11 Values of PTP(h) for varying h where the data were simulated from the GINAR(1) process with various sets of parameter values

To study the robustness of the OMGINAR(1) model, we simulated data from different models, viz, PINAR(1), GINAR(1), CPINAR(1) with $\text{ Poisson }_{2}$, ZINAR(1) and ZMGINAR models, and computed the percentage of times the model is selected by AIC and how it performs with respect to the above forecasting accuracy measures. However, we could not include the ZMGINAR(1) model in the simulation study because for some simulated data sets, the estimated value of $\alpha$ for the ZMGINAR(1) model was out of the parametric space $(\max \{0, \dfrac{\pi \mu }{1+\pi \mu }\}, \dfrac{\mu }{1+\mu })$. However, for the Poliomyelitis and assault data analyses in Sect. 6, the estimated parameter $\alpha$ for the ZMGINAR(1) model lies in the above restricted interval. So, we included this important model in the data analysis section but not here. For all the data generating models, we set $\alpha =0.3, 0.6$ for all the models. Individually, we set $\lambda =1, 1.5$ for the PINAR(1) and CPINAR(1) models, $\theta = 0.5, 0.6$ for the GINAR(1) model, and $\lambda =1.5, \rho = 0.1, 0.3, 0.5$ for the ZINAR(1) model. For each data generating process (DGP), we repeated the above procedure to compute the h-step ahead forecasting accuracy measures. We only reported the results based on DGP PINAR(1) in Tables 6, 7 and 8; and on DGP GINAR(1) in Tables 9, 10 and 11. For other DGPs, similar kind of observations are observed. So we skipped those results here. As we can see from all those results, our model performs at least as good as (often better than) the GINAR(1) process in terms of the forecasting accuracy measures. Irrespective of whether the data were generated from PINAR(1) or GINAR(1) or CPINAR(1) or ZINAR(1), our proposed model always has lower forecasting errors compared to the GINAR(1) process. This is because the proposed process is a more generalized version of the GINAR(1) process; more specifically, when the mixing parameter p is 1, the proposed process reduces to the GINAR(1) process. While we are considering a more complicated process compared to the GINAR(1) process by introducing an extra parameter p, the added complexity of our proposed process is offset by the improved fitting and forecasting accuracy measures. In addition, note that, here our objective is to improve the fitting of the data, not the inference of the model parameters. In that respect, our approach is quite successful.

Fig. 1

Monthly cases of poliomyelitis in US during 1970 to 1983, and its ACF and PACF plots

Fig. 2

Observed vs expected frequency distribution for the monthly poliomyelitis data

Table 12 Estimated parameters, AIC, $\chi ^2$-goodness of fit, and different h-step ahead forecasting accuracy measures for the monthly US poliomyelitis data set where $h=1$

6 Data analysis

6.1 Poliomyelitis data

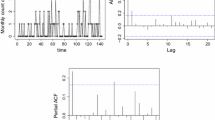
We consider the monthly cases of poliomyelitis data in the US for a period of 14 years from 1970 to 1983. This data set was first analyzed by Zeger (1988). In particular, it has 168 observations; out of which 64 (38%) observations are zero, 55 (32%) observations are one, and remaining 49 (30%) observations have monthly cases more than one. The marginal mean and marginal variance are computed as 1.33 and 3.50, and hence the dispersion index which is defined as the ratio of variance and mean is given as 2.63. It indicates that the data is over-dispersed. The raw data along with its ACF and PACF are plotted in Fig. 1 to see the characteristic of the data.

Since first lag of PACF plot in Fig. 1 is significant, we fitted most of the existing INAR(1) models, namely Poisson INAR(1), over-dispersed models like GINAR(1) and CPINAR(1), zero-inflated models like ZINAR(1) and ZMGINAR(1), and our proposed OMGINAR(1) model to the data to facilitate model comparison. Based on these fitted models, we computed the respective expected frequencies and plotted them in Fig. 2 with the observed frequencies. As we can see, while the PINAR(1) process underestimates the zero cases, the GINAR(1) process overestimates the zero observations and underestimates the one observations. This kind of limitations is seen with the other existing models under consideration. However, as we can see from Fig. 2 and $\chi ^2$-goodness of fit statistic from Table 12, our proposed OMGINAR(1) model outperforms the other models with respect to the observed-expected frequency distributions comparison.

Furthermore, we examined the effectiveness of the proposed model over other existing INAR(1) models mentioned above with respect to some forecasting accuracy measures. To compute the forecasting accuracy measures, we divided the data set into two parts, the first part consisting of the first 148 observations (training set) were used to fit the models under comparison and the remaining 20 observations (validation set) were used to compute all the three forecasting accuracy measures. We presented the results based on the forecasting accuracy measures and AIC in Table 12. The results show that except PINAR(1) model, other models have same forecasting accuracy measures. However, our proposed model has the lowest AIC value which indicates that it fits the data best among all the existing models considered in this study.

Fig. 3

Monthly cases of aggravated assault data reported in Pittsburgh, and its ACF and PACF plots

Fig. 4

Observed vs expected frequency distribution for the monthly assault data

6.2 Aggravated assault data

In our second application, we analyzed a monthly aggravated assault data set that gives the monthly cases of aggravated assault reported in the 34th police car beat in Pittsburgh, US. The data was first analyzed by Barreto-Souza (2015) using a zero-mixture of geometric INAR(1) process. The marginal mean and variance for the data set are 0.845 and 0.997, and hence the dispersion index was computed as 1.179. The data set contains 144 observations from January 1990 to December 2000. We presented the data along with its ACF and PACF in Fig. 3.

We fitted all the six models mentioned above and reported their respective estimated parameter values along with AIC, PRMSE, PMAE and PTP. As we can see, the ZMGINAR(1) model has the lowest AIC value, however our newly proposed model has the second lowest AIC value. Also to see the difference more closely, we used pairwise bar plot for all the models against the observed data; these plots are displayed in Fig. 4. As like the poliomyelitis data, here also PINAR(1) process underestimates zero, and overestimates one, whereas both CPINAR(1) and GINAR(1) processes overestimate zero and underestimate one. However, ZINAR(1) and ZMGINAR(1) processes estimate zeros and ones better than the other existing processes but poorly perform on the other observations. In contrast, our proposed model fits all the observations better than its competitors. This is also clear from the $\chi ^2$-goodness of fit statistic given in Table 13.

To compute the forecasting accuracy measures, we divided the data set into two parts, the first part consisting of the first 124 observations (training set) were used to fit the models under comparison and the remaining 20 observations (validation set) were used to compute all the three forecasting accuracy measures. From Table 13, we see that there is not much difference among these models in terms of the forecasting measures except the ZMGINAR(1) model. The ZMGINAR(1) model has the highest forecasting accuracy in terms of the PTP measure but it has the lowest forecasting accuracy with respect to both PRMSE and PMAE measures. On the other hand, our proposed model along with PINAR(1) and ZINAR(1) models jointly perform better than the others in terms of the PRMSE and PMAE measures. Therefore, the proposed model can be an alternative choice in this case as well.

Table 13 Estimated parameters, AIC, $\chi ^2$-goodness of fit, and different h-step ahead forecasting accuracy measures for the monthly aggravated assault data set where $h=1$

7 Discussion

In this paper, we proposed a new mixture of geometric INAR(1) process for modeling under and over-dispersed count time series data. We studied the stochastic properties, such as stationarity and ergodicity of the proposed process. We also discussed the h-step ahead coherent forecasting for the proposed model. Some simulated experiments and two real data analyses showed that the proposed model performs at least as good as (and often better than) the GINAR(1) and some other existing over-dispersed and zero-inflated processes.

In particular, we studied two different methods of parameter estimation, namely YW and QMLE for the proposed model. Mathematically we proved the consistency of the YW estimators. While the consistency of the QMLE estimators are not proved theoretically, we empirically illustrated their consistency via extensive simulation experiments.

Although, our study is restricted to the allocating of weight (or probability mass) at one point, the proposed method can easily be extended for more than one points depending on the nature of the data. Here, we made our weight distribution using an i.i.d. Bernoulli process, however a data-driven structure can also be employed by replacing the i.i.d. Bernoulli process with a two-state Markov chain on $\{0,1\}$ to potentially improve the forecasting performance even better. Since we wanted to keep things relatively simple, we did not pursue this in this current article. However, we recognize this as a promising future research direction.