A new estimation for INAR(1) process with Poisson distribution

Abstract

The first-order Poisson autoregressive model may be suitable in situations where the time series data are non-negative integer valued. In this article, we propose a new parameter estimator based on empirical likelihood. Our results show that it can lead to efficient estimators by making effective use of auxiliary information. As a by-product, a test statistic is given, testing the randomness of the parameter. The simulation values show that the proposed test statistic works well. We have applied the suggested method to a real count series.

1 Introduction

Owen (1988) first proposed an empirical likelihood (EL) as a way to extend likelihood-based inference ideas to certain nonparametric situations. The advantages of the empirical likelihood are now recognized. For more details and further studies, we refer to the book or the papers by Owen (1991), Qin and Lawless (1994), Qin and Lawless (1995), and Zhang et al. (2011b) among others.

In many different fields, for example, economics, medicine, actuarial statistics etc, lots of interesting variables are integer-valued. Recently, there has been an increasing attention in modeling non-negative integer-valued time series. Some models have been proposed in the literature. See, for instance, (Weiss 2017) and (Steutel and Van Harn 1979) proposed a thinning operator “$\circ$”, which is defined as

$$\begin{aligned} \phi \circ X=\sum \limits _{i=1}^X B_i, \end{aligned}$$

where $\phi \in [0,1),$ X is an integer-valued random variable and $\{B_i\}$ is an independent and identically distributed Bernoulli random sequence with $P(B_i=1)=1-P(B_i=0)=\phi$ and is independent of X. With the operator, the first-order integer-valued autoregressive model (INAR(1)) is defined as follows

$$\begin{aligned} X_t=\phi \circ X_{t-1}+Z_t,\qquad t\ge 1, \end{aligned}$$

(1)

where the innovations $\{Z_t\}$ is a sequence of i.i.d. non-negative integer-valued random variables with mean $\lambda$ and variance $\sigma _Z^2$. Here all thinning operations are performed independently of each other and of $\{Z_t\}$ and the thinning operations at each time t as well as $Z_t$ are independent of $\{X_s\}_{s<t}.$ The model has some similar properties as the ordinary AR(1) model and it has been discussed by Al-Osh and ALZAID (1987), Alzaid and Al-Osh (1988), and Al-Osh and Aly (1992). If the $\{Z_t\}$ are assumed to be Poisson distributed, $Z_t\sim Poi(\lambda )$ with $\lambda >0,$ then $\{X_t\}$ is a stationary and ergodic Markov chain with a Poisson marginal distribution, such that mean and variance are equal to each other, $\mu _X=\sigma _X^2=\lambda /(1-\phi ),$ and all moments exist. For conditional mean and variance, we have (Alzaid and Al-Osh (1988)): $E[X_t|X_{t-1}]=\phi \cdot X_{t-1}+\lambda , \mathrm{Var}[X_t|X_{t-1}]=\phi (1-\phi )\cdot X_{t-1}+\lambda .$

In this article, based on empirical likelihood, we provide a novel estimator which has small bias and is efficient by making use of auxiliary information shown in the following section. (Keith Freeland and McCabe 2005) derived the asymptotic properties of the conditional least squares (CLS) estimators in this model. (Bourguignon and Vasconcellos 2015) proposed a bias-adjusted estimator.

Note that the parameter $\phi$ may vary with time and it may be random. Zheng et al. (2007) proposed the following first-order random coefficient integer-valued autoregressive (RCINAR(1)) model:

$$\begin{aligned} X_t=\phi _t\circ X_{t-1}+Z_t,\qquad t\ge 1, \end{aligned}$$

(2)

where $\{\phi _t\}$ is an i.i.d. sequence with cumulative distribution function on [0, 1),  with $E[\phi _t]=\phi$ and $\mathrm{Var}(\phi _t)=\sigma _\phi ^2$; $\{Z_t\}$ is an i.i.d non-negative integer-valued sequence as the same in the model (1). Moreover, $\{\phi _t\}$ and $\{Z_t\}$ are independent. The process $\{X_t\}$ is also a stationary and ergodic Markov chain. For conditional mean and variance, we have $E[X_t|X_{t-1}]=\phi \cdot X_{t-1}+\lambda , \mathrm{Var}[X_t|X_{t-1}]=\sigma _\phi ^2\cdot X_{t-1}^2+(\phi (1-\phi )-\sigma _\phi ^2)\cdot X_{t-1}+\sigma _Z^2.$ In Zheng et al. (2007), the authors consider two methods, conditional least squares and the modified quasi-likelihood (MQL). Zhang et al. (2011a) studied the empirical likelihood method for the model (2). Kang and Lee (2009) considered the problem of testing for a parameter change in the model (2). There is one of the problems of interest, given the data $\{x_1,x_2,\ldots ,x_n\}$, test the hypothesis that there is no time variation for the thinning parameter $\phi$ (the series is INAR(1)) against that it varies randomly across the time (it is RCINAR(1)). This is essentially same as testing $H_0:\sigma _\phi ^2=0$ against $H_1:\sigma _\phi ^2>0.$

In this article, we give a test statistic for testing this hypothesis. Zhao and Hu (2015) have proposed a test for randomness of the coefficient of an RCINAR(1) process, but using the least squares estimates of the parameter $\sigma _\phi ^2.$Awale et al. (2019) developed a locally most powerful-type testing the hypothesis that the thinning parameter is constant across the time depended on the distribution of the innovation $Z_t$.

The rest of the paper is organized as follows. In Sect. 2, we introduce the methodology and the main results. In Sect. 3, simulation results are reported. In Sect. 4, an empirical example is discussed.

Throughout the paper, we use the notation “${\mathop {\longrightarrow }\limits ^{d}}$” to denote convergence in distribution, “$'$” to denote the transpose operator and $\Vert \cdot \Vert$ to denote the Euclidean norm of the matrix.

2 Methodology and main results

Al-Osh and ALZAID (1987) defined the Poisson AR(1) model by

$$\begin{aligned} X_t=\phi \circ X_{t-1}+Z_t,\quad t\ge 1, \end{aligned}$$

(3)

where $\phi \circ X_{t-1}=\sum _{i=1}^{X_{t-1}}B_{i,t}, B_{1,t},B_{2,t},\cdots ,B_{X_{t-1},t}$ are i.i.d. Bernoulli random variables with $P(B_{it}=1)=1-P(B_{it}=0)=\phi$;  $\{Z_t\}$ are i.i.d. with a Poisson distribution having mean $\lambda$ and are independent of the Bernoulli variables $B_{it}$.

Remark 1

$\{X_t\}$ is a Markov chain on $\{0,1,2\ldots \}$ with the transition probability,

$$\begin{aligned} p_{ij}=P(X_t=j|X_{t-1}=i)=\sum \limits _{k=0}^{\min \{i,j\}} C_i^k\phi ^k(1-\phi )^{i-k}\frac{\lambda ^{(j-k)}e^{-\lambda }}{(j-k)!}. \end{aligned}$$

For PINAR(1) process (3), let ${\varvec{\theta }}=[\phi ,\lambda ]'$, we can construct estimation equations:

$$\begin{aligned} {{\varvec{m}}}_t(\theta )= {\left( \begin{array}{c} m_{1t}({{\varvec{\theta }}})\\ m_{2t}({{\varvec{\theta }}}) \\ m_{3t}({{\varvec{\theta }}})\\ \end{array} \right) ={\varvec{0}}, } \end{aligned}$$

where $m_{1t}({{\varvec{\theta }}})=X_t-\phi X_{t-1}-\lambda , m_{2t}({{\varvec{\theta }}})=(X_t-\phi X_{t-1}-\lambda )X_{t-1}, m_{3t}({{\varvec{\theta }}})=(X_t-\phi X_{t-1}-\lambda )^2-\phi (1-\phi ) X_{t-1}-\lambda .$

The profile empirical likelihood ratio function is (Owen 1991)

$$\begin{aligned} R({{\varvec{\theta }}})=\max \left\{ \prod \limits _{t=1}^n np_t\Big | p_t\ge 0,\sum \limits _{t=1}^n p_t=1,\sum \limits _{t=1}^n p_tm_t({{\varvec{\theta }}})=0\right\} . \end{aligned}$$

(4)

The maximum may be obtained via Lagrange multipliers. Let

$$\begin{aligned} H=\sum \limits _{t=1}^n\log (np_t)-n{\varvec{\beta }}'\left( \sum \limits _{t=1}^np_tm_t({{\varvec{\theta }}})\right) +\gamma \left( 1- \sum \limits _{t=1}^np_t\right) , \end{aligned}$$

where $\gamma$ and ${\varvec{\beta }}=(\beta _1,\beta _2,\beta _3)'$ are Lagrange multipliers. Taking the partial derivative of H with respect to $p_t$ to be zero, we have $\frac{\partial H}{\partial p_t}=\frac{1}{p_t}-n{{\varvec{\beta }}}'m_t({{\varvec{\theta }}})-\gamma =0,$ so

$$\begin{aligned} 0=\sum \limits _{t=1}^n p_t\frac{\partial H}{\partial p_t}=n-\gamma ,\quad p_t=\frac{1}{n}\frac{1}{1+{{\varvec{\beta }}}'m_t(\theta )},\quad t=1,2,\ldots ,n. \end{aligned}$$

Here, being a function of ${{\varvec{\theta }}}$, ${\varvec{\beta }}={\varvec{\beta }}({{\varvec{\theta }}})$ is with the restriction that

$$\begin{aligned} \frac{1}{n}\sum \limits _{t=1}^n\frac{m_t({{\varvec{\theta }}})}{1+{\varvec{\beta }}'m_t({{\varvec{\theta }}})}=0. \end{aligned}$$

The empirical log-likelihood ratio (ELR) is

$$\begin{aligned} \ell ({{\varvec{\theta }}})=\log R({{\varvec{\theta }}})=\sum \limits _{t=1}^n \log (1+\beta 'm_t({{\varvec{\theta }}})). \end{aligned}$$

(5)

The asymptotic distribution of the ELR was derived by Qin and Lawless (1994) for general estimating equations and by Zhang et al. (2011b) for RCINAR(p) model. Basing on their results, it is possible to proved an asymptotic chi-squared distribution for (5) as shown in the following theorem.

Theorem 1

As $n\rightarrow \infty ,$ we have $2\ell ({\varvec{\theta }}_0) {\mathop {\longrightarrow }\limits ^{d}} \chi ^2(2),$ where $\ell ({{\varvec{\theta }}})$ is defined in (5).

So, it is easy to obtain the confidence region for the parameter ${{\varvec{\theta }}}$. The result is as follows:

Corollary 1

For the parameter ${{\varvec{\theta }}}$, the $100(1-\alpha )\%$ confidence region is $C_{\alpha ,n}=\{{{\varvec{\theta }}}|2\ell ({{\varvec{\theta }}})\le \chi _{1-\alpha }^2(2)\},$ where $1-\alpha$ is the confidence level and $\chi _{1-\alpha }^2(2)$ is the upper $1-\alpha -$quantile of the chi-squared distributed with 2 degrees of the freedom.

Then, we may find the maximum empirical likelihood estimator (MELE) $\check{{{\varvec{\theta }}}}$ for the parameter ${{\varvec{\theta }}}$ by minimizing $\ell ({{\varvec{\theta }}})$ over ${\varvec{\theta }}$.

Theorem 2

For the MELE $\check{{{\varvec{\theta }}}},$ we have

$$\begin{aligned} \sqrt{n}(\check{{{\varvec{\theta }}}}-{{\varvec{\theta }}}_0) {\mathop {\longrightarrow }\limits ^{d}} N({\varvec{0}}, V), \end{aligned}$$

where ${\varvec{V}}=[{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}{\varvec{\Omega }}]^{-1}, {\varvec{\Omega }}=E \left( \displaystyle \frac{\;\partial {\varvec{m}}_t({{\varvec{\theta }}})\;}{\;\partial {{\varvec{\theta }}}\;} \right) , {\varvec{\Sigma }}=E\left[ {\varvec{m}}_t(\theta ){\varvec{m}}_t({{\varvec{\theta }}})'\right]$.

Remark 2

If we don’t consider the third equation and only use  $m_{1t}=0, m_{2t}=0$ as the estimation equations, the maximum empirical likelihood estimator is consistent with the conditional least squares estimator.

Remark 3

The conditional least squares estimator (CLE) of the model’s parameters can be calculated by the following expression

$$\begin{aligned} \hat{\phi }=\frac{n\sum _{t=1}^nX_tX_{t-1}-\left( \sum _{t=1}^nX_{t-1}\right) \left( \sum _{t=1}^nX_t\right) }{n\sum _{t=1}^nX_{t-1}^2-\left( \sum _{t=1}^nX_{t-1}\right) ^2},\quad \hat{\lambda }=\frac{1}{n}\left( \sum \limits _{t=1}^nX_t-\hat{\phi }\sum \limits _{t=1}^nX_{t-1}\right) . \end{aligned}$$

The CLS estimator is consistent and asymptotically normal, see  (Keith Freeland and McCabe 2005).

Remark 4

Note that the conditional variance is

$$\begin{aligned} V_{{\varvec{\theta }}}(X_t|X_{t-1}):=\mathrm{Var}(X_t|X_{t-1}) =\phi (1-\phi )X_{t-1}+\lambda , \end{aligned}$$

then the maximum quasi-likelihood (MQL) estimator of the parameters are:

$$\begin{aligned} \begin{aligned} \left( \begin{array}{c} \tilde{\phi } \\ \tilde{\lambda } \\ \end{array} \right) =&\left( \begin{array}{cl} \sum _{t=1}^nX_{t-1}^2V_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1}) &{}\sum _{t=1}^nX_{t-1}V_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1})\\ \sum _{t=1}^nX_{t-1}V_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1}) &{}\sum _{t=1}^nV_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1}) \end{array}\right) ^{-1} \\&\times \left( \begin{array}{l} \sum _{t=1}^nX_{t-1}X_tV_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1})\\ \sum _{t=1}^nX_tV_{{\varvec{\hat{\theta }}}}^{-1}(X_t|X_{t-1}) \end{array}\right) , \end{aligned} \end{aligned}$$

where $\hat{{\varvec{\theta }}}$ is its consistent estimator, in practice, we can use the conditional least squares estimator of ${{\varvec{\theta }}}$. Similar to the proof of theorem 3.2 in Zheng et al. (2007), it can be proved that the estimator is also consistent and asymptotically normal.

Remark 5

The conditional maximum likelihood (CML) estimator of the parameter ${\varvec{\bar{\theta }}}$ is

$$\begin{aligned} {\varvec{\bar{\theta }}}=\arg \max \sum \limits _{t=1}^n \log p_{x_t|x_{t-1}}({\varvec{\theta }}), \end{aligned}$$

where

$$\begin{aligned} p_{x_t|x_{t-1}}({\varvec{\theta }}):=P(X_t=x_t|X_{t-1}=x_{t-1}) =\sum _{k=0}^{\min (x_t,x_{t-1})}\left( \begin{array}{c} x_{t-1}\\ k \end{array} \right) \phi ^k(1-\phi )^{x_{t-1}-k}{\frac{\lambda ^{x_t-k}}{(x_t-k)!}}. \end{aligned}$$

The CML estimator is consistent and asymptotically normal, see Freeland and Mccabe (2004).

In order to test $H_0: \sigma _\phi ^2=0,$ we may consider the following theorem.

Theorem 3

Under $H_0,$ we have $2\ell ( \check{{\varvec{\theta }}}) {\mathop {\longrightarrow }\limits ^{d}} \chi ^2(1),$ as $n\rightarrow \infty ,$where $\ell ({{\varvec{\theta }}})$ is defined in (5).

Then, it follows that the null hypothesis $H_0: \sigma _\phi ^2=0$ may be tested using the statistic $T=2\ell (\check{{\varvec{\theta }}})$ and the rejection region $\{T>\chi _{1-\alpha }^2(1)\}.$

3 Simulation study

Simulation studies are reported in the section to evaluate the finite sample performance of the proposed maximum empirical likelihood estimator (MELE). We computed the empirical bias and root of the mean squared errors (RMSE) based on 1000 replications for each parameter combination. These values are reported within parenthesis in Tables 1. For succinctness, we only report here partial results, to illustrate the effect of parameter $\phi$ while holding the other parameter $\lambda$ identical. Other results are available from the authors upon request. In the following Table 1, the format (Bias, RMSE) is used; for example, (0.0142,0.1204) means that the bias is 0.0142 and RMSE is 0.1204.

Table 1 Estimates for parameter $\phi$ and $\lambda =1$

From the above results, we can see that MELE is a good estimation method producing estimators whose biases and RMSEs are overall comparable to the CML method. As expected, the CML performs best which has the smallest bias and RMSE and there are almost no differences between the MELE and CML. The CLS and QML have the same performance in terms of both bias and the RMSE. Howerver, when the sample size is small or the parameters are large, the MELE works better than the CLS and QML.

In order to assess the performance of the suggested test statistic, we have done a lot of simulation studies. We simulate observations from the Poisson INAR(1) model various combinations of the parameters, as shown in 2. In each case, the sizes of samples are 100, 300, 500, 1000, 5000 and 1000 simulations were carried out. The distribution of $\phi _t$ is assumed to Beta(a, b) under the alternative hypothesis. The empirical level and power of the test statistic is reported in Tables 2 and 3, respectively.

Table 2 Empirical level of the test at nominal level 0.05 for Poisson INAR(1) model

Table 3 Empirical power of the test at nominal level 0.05 for Poisson RCINAR(1) model with $\phi _t\sim Beta(a,b)$

Table 4 Empirical level of the Awale et al. (2019) test at nominal level 0.05 for Poisson INAR(1) model

Table 5 Empirical power of the Awale et al. (2019) test at nominal level 0.05 for Poisson RCINAR(1) model with $\alpha _t\sim Beta(a,b)$

It can be seen that the test maintains the level and the power tends to one as sample size increase. We also perform the test proposed by Awale et al. (2019), since it is better than the test given by Zhao and Hu (2015). The results are reported in Tables 4 and 5.

From comparison with level and power of the the suggested test from Tables 2 and 3, it can be seen that the test is not as good as the proposed test using the probability distribution function, as accepted. However, the suggested test in this article is competitive and convenient as opposed to that of Awale et al. (2019).

4 Real data example

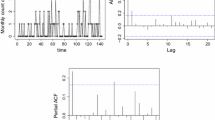
In this section, we employ the programme suggested in the previous section a real time series data. The data set consists of monthly counts of claimants collecting short-term wage loss benefit for born-related injuries received in workplace. The data set contains 120 observations for the period January 1985 to December 1994. These data were previously studied by Freeland and Mccabe (2004) and Bourguignon and Vasconcellos (2015). Table 6 provides some descriptive statistics. The series and its sample autocorrelation function are shown in Fig. 1.

Fig. 1

The time plot, the sample autocorrelation and partial autocorrelation functions of the series of the burns claims

From mean, variance and correlation plots given in Fig. 1, it can be seen that the data can be modeled by a Poisson INAR(1) model and the constancy of the thinning parameter may be suspected. Therefore it is of interest to test the hypothesis of constancy of the thinning parameter. The value of the test statistic for testing $H_0: \sigma _\phi ^2=0$ against $H_1:\sigma _\phi ^2>0$ turned out to be 0.1035 , with p-value 0.7477, indicating that one did not reject the null hypothesis at $5\%$ level of significance. Consequently, it is better to model this data with a Poisson INAR(1) model rather than the RCINAR(1) model. Table 7 display the estimates. Two goodness-of-fit statistics are also shown: the root mean-squared error (RMSE) and mean absolute deviation (MAD). Those statistics defined as follows. For $t=2,\ldots ,n,$ consider the expected value of the observation at the previous time, $E[X_t|X_{t-1}]=\phi X_{t-1}+\lambda$. Let $\epsilon _t^\star =X_t-\phi ^\star X_{t-1}-\lambda ^\star ,$ where $\phi ^\star$ and $\lambda ^\star$ are any estimates of $\phi$ and $\lambda$. Define

$$\begin{aligned} \text {RMSE}=\sqrt{\frac{1}{n-1}\sum \limits _{t=2}^n(\epsilon _t^\star )^2},\quad \text {MAD}=\frac{1}{n-1}\sum \limits _{t=2}^n|\epsilon _t^\star |. \end{aligned}$$

Table 6 Descriptive statistic

Table 7 Estimates of the parameters (standard errors in parentheses), RMSE and MAD for burns claims

From Table 7, it can be found that the CML and MELE are competitive and superior in terms of RMSE and MAD. We also plot the confidence region of the parameter as shown in Fig. 2. This is an indication that our proposed estimator can be indeed a good choice in practice.

Fig. 2

Estimates and 95% confidence regions for $(\phi ,\lambda )$, based on CLS($\vartriangle$, dotted line), CML($\bullet$, dashed line), EL($*$, solid line)

We can also compare the estimators in terms of predictive power. Let $\phi _n^\star$ and $\lambda _n^\star$ be any estimators of $\phi$ and $\lambda$, obtained from n observations. Then, at any given time n, we can forecast the next observation as

$$\begin{aligned} X_{n+1}^\star =\langle \phi _n^\star X_n+\lambda _n^\star \rangle , \end{aligned}$$

where $\langle \cdot \rangle$ represents the nearest integer. The one-step ahead absolute forecast deviation is then given by

$$\begin{aligned} \left| X_{n+1}^\star -X_{n+1}\right| , \end{aligned}$$

where $X_{n+1}^\star$ is the one-step ahead forecast.

Table 8 $\left| X_{n+1}^\star -X_{n+1}\right|$ for counts of burns claim

Table 8 shows that all four estimators produce a correct forecast or a small forecast error in all the time interval here studied $(n=111,\ldots ,120).$ This confirms that the PINAR(1) process is a good model for this data, at least in this interval. We observe that the CLS and MQL provide the worst forecasting performance. On the other hand, the MELE and CML provide the same forecasting and predict better than CLS and MQL. This is an indication that our proposed MELE estimator can be indeed a good choice for forecasting purposes.

5 Conclusions

In this article, we considered the empirical likelihood inference for the Poisson INAR(1) process by making effective use of auxiliary information and found a test statistic of testing the randomness of the parameter. A straightforward question is to ask this point is whether similar results as shown here could be obtained in the other models. This is our further work.

Appendix

Proof of Theorem 1 The proof follows essentially the lines of the classical proof of Owen (2001) for the i.i.d. case, which may be applied when the following three conditions are satisfied. Let $S({{\varvec{\theta }}})=\frac{1}{n}\sum _{t=1}^n {\varvec{m}}_t({{\varvec{\theta }}})m_t({{\varvec{\theta }}})'.$

(C1) $S({{\varvec{\theta }}}_0) \rightarrow {\varvec{\Sigma }}$ in probability and ${\varvec{\Sigma }}$ positive definite.

(C2) $m_n^\star =\max _{1\le t\le n}\Vert {\varvec{m}}_t({{\varvec{\theta }}}_0)\Vert =o_p(n^{1/2})$.

(C3) $\frac{1}{n}\sum _{t=1}^n \Vert {\varvec{m}}_t({{\varvec{\theta }}}_0)\Vert ^3=o_p(n^{1/2}),$ where ${{\varvec{\theta }}}_0$ is the true value of the parameter.

For the first condition, let $\mathcal F_n=\sigma (X_0,X_1,\ldots ,X_n), A_n=\sum _{t=1}^n m_{1t}(\theta _0)=\sum _{t=1}^n(X_t-\phi _0 X_{t-1}-\lambda _0),A_0=0,$ then,

$$\begin{aligned} E(A_n|\mathcal F_{n-1})=A_{n-1}+E(X_n-\phi _0 X_{n-1}-\lambda _0)=A_{n-1}, \end{aligned}$$

so, $\{A_n, \mathcal F_n, n\ge 0\}$ is a martingale. For $E|X_t|^2<\infty ,$ $\{(X_t-\phi _0 X_{t-1}-\lambda _0)^2, n\ge 1\}$ is square integrable. By the strictly stationary and ergodic theorem,

$$\begin{aligned} \displaystyle \frac{\;1\;}{\;n\;}\sum \limits _{t=1}^n(X_t-\phi _0 X_{t-1}-\lambda _0)^2 {\mathop {\longrightarrow }\limits ^{a.s}} E(X_1-\phi _0 X_0-\lambda _0)^2. \end{aligned}$$

Similarly, we can proof that $B_n=\sum _{t=1}^nm_{2t}({{\varvec{\theta }}}_0), C_n=\sum _{t=1}^n m_{3t}(\theta _0)$ are martingale. Then the first condition holds. To check the second condition, we note that $E\{{\varvec{m}}_t({{\varvec{\theta }}}_0)/{\varvec{m}}_t({{\varvec{\theta }}}_0)\}<\infty ,$ then, $\sum _{n=1}^\infty P({\varvec{m}}_t({{\varvec{\theta }}}_0)'$ ${\varvec{m}}_t({{\varvec{\theta }}}_0)>n)<\infty .$ By the Borel-Cantelli lemma, $\Vert {\varvec{m}}_t({{\varvec{\theta }}}_0)\Vert >\sqrt{n}$ happens with probability 1 only for finitely many n, since $\{X_t\}$ is a strictly stationary process. This implies that there are only finitely many n for which $m_n^\star >\sqrt{n}.$ Similarly, for any $\varepsilon >0,$ there are only finitely many n for which $m_n^\star >\varepsilon \sqrt{n},$ hence $\lim \sup _{n\rightarrow \infty }m_n^\star /\sqrt{n}\le \varepsilon$ holds with probability 1, so $m_n^\star =o_p(\sqrt{n}).$ From the (C1) and (C2), we have $\frac{\;1\;}{\;n\;}\sum _{t=1}^n \Vert {\varvec{m}}_t({{\varvec{\theta }}}_0)\Vert ^3\le m_n^\star \frac{\;1\;}{\;n\;}\sum _{t=1}^n {\varvec{m}}_t({{\varvec{\theta }}}_0){\varvec{m}}_t({{\varvec{\theta }}}_0)' = o_p(\sqrt{n})O_p(1)=o_p(n^{1/2}).$ See Zhang et al. (2011a) and Zhao and Yu (2016) also.

Proof of Theorem 2 The proof is similar to that of Theorem 6.2 of Zhang et al. (2011a) and that of Theorem 1 of Qin and Lawless (1994). Let

$$\begin{aligned} Q_{1n}({{\varvec{\theta }}},{\varvec{\beta }})=\frac{1}{n}\sum \limits _{t=1}^n \frac{{\varvec{m}}_t({{\varvec{\theta }}})}{1+{\varvec{\beta }}'{\varvec{m}}_t({{\varvec{\theta }}})},\quad Q_{2n}({{\varvec{\theta }}},{\varvec{\beta }})=\frac{1}{n}\sum \limits _{t=1}^n \frac{{\varvec{\beta }}({{\varvec{\theta }}})}{1+{\varvec{\beta }}'{\varvec{m}}_t({{\varvec{\theta }}})}\left( \frac{\partial {\varvec{m}}_t({{\varvec{\theta }}})}{\partial {{\varvec{\theta }}}}\right) '. \end{aligned}$$

Expanding $Q_{1n}(\check{{\varvec{\theta }}}, \check{{\varvec{\beta }}}),Q_{2n}(\check{{\varvec{\theta }}},\check{{\varvec{\beta }}})$ at $({{\varvec{\theta }}}_0,0),$ we have

$$\begin{aligned} 0= & {} Q_{1n}(\check{{\varvec{\theta }}},\check{{\varvec{\beta }}})=Q_{1n}({{\varvec{\theta }}}_0,0)+\frac{\partial Q_{1n}({{\varvec{\theta }}}_0,0)}{\partial {{\varvec{\theta }}}}(\check{{\varvec{\theta }}}-{{\varvec{\theta }}}_0)+\frac{\partial Q_{1n}({{\varvec{\theta }}}_0,0)}{\partial {\varvec{\beta }}'}(\check{{\varvec{\beta }}}-0)+o_p(\delta _n), \\ 0= & {} Q_{2n}(\check{{\varvec{\theta }}},\check{{\varvec{\beta }}})=Q_{2n}({{\varvec{\theta }}}_0,0)+\frac{\partial Q_{2n}({{\varvec{\theta }}}_0,0)}{\partial {{\varvec{\theta }}}}(\check{{\varvec{\theta }}}-{{\varvec{\theta }}}_0)+\frac{\partial Q_{2n}({{\varvec{\theta }}}_0,0)}{\partial {\varvec{\beta }}'}(\check{{\varvec{\beta }}}-0)+o_p(\delta _n), \end{aligned}$$

where $\delta _n=\Vert \check{{\varvec{\theta }}}-{{\varvec{\theta }}}_0\Vert +\Vert \check{{\varvec{\beta }}}\Vert =O_p(n^{-1/2}).$ So, we have

$$\begin{aligned} S_n\left( \begin{array}{c} \check{{\varvec{\beta }}}\\ \check{{\varvec{\theta }}}-{{\varvec{\theta }}}_0 \end{array}\right) =\left( \begin{array}{c} -Q_{1n}({{\varvec{\theta }}}_0,0)+o_p(\delta _n)\\ o_p(\delta _n) \end{array}\right) . \end{aligned}$$

where

$$\begin{aligned} S_n=\left( \begin{array}{cc} \frac{\partial Q_{1n}}{\partial {\varvec{\beta }}'} &{}\frac{\partial Q_{1n}}{\partial {{\varvec{\theta }}}}\\ \frac{\partial Q_{2n}}{\partial {\varvec{\beta }}'} &{}0 \end{array}\right) _{({{\varvec{\theta }}}_0,0)} \rightarrow \left( \begin{array}{cc} -E(m_{t}m_{t}') &{}E\left( \frac{\partial {\varvec{m}}_t}{\partial {{\varvec{\theta }}}}\right) \\ E\left( \frac{\partial {\varvec{m}}_t}{\partial {{\varvec{\theta }}}}\right) ' &{}0 \end{array}\right) = \left( \begin{array}{cc} -{\varvec{\Sigma }}&{}{\varvec{\Omega }}\\ {\varvec{\Omega }}'&{}0 \end{array}\right) . \end{aligned}$$

since $\{X_t\}$ is strictly stationary and ergodic and note that $\sqrt{n} Q_{1n}({{\varvec{\theta }}}_0,0)=\frac{1}{\sqrt{n}}\sum _{t=1}^n m_{t}({{\varvec{\theta }}}_0){\mathop {\longrightarrow }\limits ^{d}} N(0,{\varvec{\Sigma }}).$ Then, we have

$$\begin{aligned} \sqrt{n}(\check{{\varvec{\theta }}}-{{\varvec{\theta }}}_0)=({\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}{\varvec{\Omega }})^{-1}{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}\sqrt{n} Q_{1n}({{\varvec{\theta }}}_0,0)+o_p(1). \end{aligned}$$

The proof of the theorem is completed.

Proof of Theorem 3: The proof is similar to that of Theorem 2 and Corollary 4 of Qin and Lawless (1994) and will be only sketched here.

Note that

$$\begin{aligned} \ell (\check{{\varvec{\theta }}},\check{{\varvec{\beta }}}) =\sum \limits _{t=1}^n\log [1+\check{{\varvec{\beta }}}{\varvec{m}}_t(\check{{{\varvec{\theta }}}})] =\frac{n}{2}\left[ \frac{1}{n}\sum \limits _{t=1}^n {{\varvec{m}}_t({{\varvec{\theta }}}_0)'}\right] {\varvec{A}} \left[ \frac{1}{n}\sum \limits _{t=1}^n {{\varvec{m}}_t({{\varvec{\theta }}}_0)}\right] +o_p(1), \end{aligned}$$

where ${\varvec{A}}={\varvec{\Sigma }}^{-1}[{\varvec{I}}-{\varvec{\Omega }}[{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}{\varvec{\Omega }}]^{-1}{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}].$ Thus,

$$\begin{aligned} 2\ell (\check{{\varvec{\theta }}})&=[{\varvec{\Sigma }}^{-1/2}\sqrt{n} Q_{1n}({{\varvec{\theta }}}_0,0)]' [{\varvec{I}}-{\varvec{\Sigma }}^{-1/2}{\varvec{\Omega }}[{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}{\varvec{\Omega }}]^{-1}{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1/2}] [{\varvec{\Sigma }}^{-1/2}\\&\quad \sqrt{n} Q_{1n}({{\varvec{\theta }}}_0,0)]+o_p(1), \end{aligned}$$

Note that $({\varvec{\Sigma }})^{-1/2}{\sqrt{n}}Q_{1n}({{\varvec{\theta }}}_0,0)$ converges to a standard multivariate normal distribution and the matrix ${\varvec{I}}-{\varvec{\Sigma }}^{-1/2}{\varvec{\Omega }}[{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1}{\varvec{\Omega }}]^{-1}{\varvec{\Omega }}'{\varvec{\Sigma }}^{-1/2}$ is symmetric and idempotent, with trace equal to 1. Hence the test statistic $2\ell (\check{{{\varvec{\theta }}}})$ converges to $\chi ^2(1).$