Nonparaxial propagation of Lorentz-Gauss vortex beams in uniaxial crystals orthogonal to the optical axis

Abstract

Analytical expressions for the components of the nonparaxial propagation a Lorentz-Gauss vortex beam in uniaxial crystals orthogonal to the optical axis are derived. The intensity and the phase distributions of the components of a Lorentz-Gauss vortex beam propagating in a uniaxial crystal orthogonal to the optical axis are shown by numerical examples. Even though one of the two transversal components of a Lorentz-Gauss vortex beam in the source plane is equal to zero, it emerges upon propagation inside the uniaxial crystal. Moreover, the beam profile of a Lorentz-Gauss vortex beam in the uniaxial crystal becomes twisted and tilted. The three components are completely different and have their respective evolution laws. The intensity distribution and the phase distribution of a Lorentz-Gauss vortex beam can be modulated by the uniaxial crystal, which is beneficial to the optical trapping and nonlinear optics involving in the special beam profile.

1 Introduction

Due to the highly angular spreading, Lorentz-Gauss beams have been introduced to describe the radiation emitted by a single-mode diode laser [1, 2]. The properties of Lorentz-Gauss beams have been extensively investigated [3–11]. If the radiation emitted by a single-mode diode laser goes through a spiral phase plate, it becomes a Lorentz-Gauss vortex beam. The spiral phase plate can modulate the wave-front phase of the Lorentz-Gauss vortex beam. The characteristics of a Lorentz-Gauss vortex beam is that it has a twisted phase front and an intensity of zero in the center of the beam profile. Due to carrying the orbital angular momentum, the Lorentz-Gauss vortex beam can be applied in the fields of optical micro-manipulation, nonlinear optics, and quantum information processing, etc. [12–14]. Many applications such as the design of the polarizer and the compensator are involved in laser beams propagating in uniaxial crystals. The propagation of various kinds of laser beams in uniaxial crystals has been widely examined [15–22]. In the remainder of this paper, therefore, the propagation of a Lorentz-Gauss vortex beam in uniaxial crystals orthogonal to the optical axis is to be investigated. As the far-field divergence angle of the radiation emitted by a single-mode diode laser is large, the paraxial theory is no longer valid. Accordingly, here we consider the nonparaxial propagation of a Lorentz-Gauss vortex beam in uniaxial crystals orthogonal to the optical axis.

2 Theoretical derivation

In the Cartesian coordinate system, the z-axis is taken to be the propagation axis. The optical axis of the uniaxial crystal coincides with the x-axis. The input plane is z = 0 and the observation plane is z. The dielectric tensor of the uniaxial crystal is described by

$$ \varepsilon = \left( {\begin{array}{*{20}c} {n_{\text{e}}^{2} } & 0 & 0 \\ 0 & {n_{\text{o}}^{2} } & 0 \\ 0 & 0 & {n_{\text{o}}^{2} } \\ \end{array} } \right), $$

(1)

where n _o and n _e are the ordinary and extraordinary refractive indices, respectively. The Lorentz-Gauss vortex beam considered here is linearly polarized in the x-direction and is incident on a uniaxial crystal in the plane z = 0. The Lorentz-Gauss vortex beam in the input plane z = 0 takes the form as [1, 2]

$$ \left[ {\begin{array}{*{20}c} {E_{x} (\rho_{0} ,0)} \\ {E_{y} (\rho_{0} ,0)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{w_{0x} w_{0y} (x_{0} + iy_{0} )}}{{(w_{0x}^{2} + x_{0}^{2} )(w_{0y}^{2} + y_{0}^{2} )}}\exp \left( { - \frac{{x_{0}^{2} + y_{0}^{2} }}{{w_{0}^{2} }}} \right)} \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 & {} \\ \end{array} } & {} & {} & {} \\ \end{array} } & {} \\ \end{array} } & {} & {} \\ \end{array} } & {} & {} & {} \\ \end{array} } \\ \end{array} } \right], $$

(2)

where ρ ₀ = x ₀ e _x  + y ₀ e _y . e _x and e _y are the unit vectors in the x- and y-directions, respectively. w ₀ is the waist of the Gaussian part. w _0x and w _0y are the width parameters of the Lorentzian part in the x- and y-directions, respectively. The propagation of the Lorentz-Gauss vortex beam in uniaxial crystals orthogonal to the optical axis obeys the following equations [23]:

$$ \begin{aligned} E(\rho ,z) & = \int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {d^{2} k\exp (ik \cdot \rho )\exp (ik_{{{\text{e}}z}} z)\left( {\begin{array}{*{20}c} {\tilde{E}_{x} (k)} \\ { - \frac{{k_{x} k_{y} }}{{k_{0}^{2} n_{\text{o}}^{2} - k_{x}^{2} }}\tilde{E}_{x} (k)} \\ { - \frac{{k_{{{\text{e}}z}} k_{x} }}{{k_{0}^{2} n_{\text{o}}^{2} - k_{x}^{2} }}\tilde{E}_{x} (k)} \\ \end{array} } \right)} } \\ & \quad + \int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {d^{2} k\exp (ik \cdot \rho )\exp (ik_{{{\text{o}}z}} z)\left( {\begin{array}{*{20}c} 0 \\ {\frac{{k_{x} k_{y} }}{{k_{0}^{2} n_{\text{o}}^{2} - k_{x}^{2} }}\tilde{E}_{x} (k) + \tilde{E}_{y} (k)} \\ { - \frac{{k_{y} }}{{k_{{{\text{o}}z}} }}\left[ {\frac{{k_{x} k_{y} }}{{k_{0}^{2} n_{\text{o}}^{2} - k_{x}^{2} }}\tilde{E}_{x} (k) + \tilde{E}_{y} (k)} \right]} \\ \end{array} } \right)} } , \\ \end{aligned} $$

(3)

where k = k _x e _x  + k _y e _y , ρ = xe _x  + ye _y , and k ₀ = 2π/λ is the wave number with λ being the optical wavelength. $\tilde{E}_{\text{s}} (k)$ is the two-dimensional Fourier transform of the transverse components of the optical field in the plane z = 0 and is given by

$$ \tilde{E}_{\text{s}} (k) = \frac{1}{{(2\pi )^{2} }}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{\text{s}} (\rho_{0} ,0)\exp \left[ { - i(k_{x} x_{0} + k_{y} y_{0} )} \right]dx_{0} dy_{0} } } ,\quad s = x,y. $$

(4)

k _ez and k _oz are defined by

$$ k_{{{\text{e}}z}} = [k_{\text{o}}^{2} n_{\text{e}}^{2} - (n_{\text{e}}^{2} /n_{\text{o}}^{2} )k_{x}^{2} - k_{y}^{2} ]^{1/2} ,k_{{{\text{o}}z}} = \left(k_{\text{o}}^{2} n_{0}^{2} - k_{x}^{2} - k_{y}^{2} \right)^{1/2}. $$

(5)

To describe the nonparaxial field in a uniaxial crystal, (3) can be expressed as the sum of the paraxial field and a nonparaxial correction term [23]:

$$ \begin{aligned} E(\rho ,z) & = \exp (ik_{0} n_{\text{e}} z)\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {d^{2} k\exp (ik \cdot \rho )\exp \left( { - i\frac{{n_{\text{e}}^{2} k_{x}^{2} + n_{\text{o}}^{2} k_{y}^{2} }}{{2k_{0} n_{\text{e}} n_{\text{o}}^{2} }}z} \right)\left( {\begin{array}{*{20}c} {\tilde{E}_{x} (k)} \\ { - \frac{{k_{x} k_{y} }}{{k_{0}^{2} n_{\text{o}}^{2} }}\tilde{E}_{x} (k)} \\ { - \frac{{n_{\text{e}} k_{x} }}{{k_{0}^{{}} n_{\text{o}}^{2} }}\tilde{E}_{x} (k)} \\ \end{array} } \right)} } \\ & \quad + \exp (ik_{0} n_{\text{o}} z)\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {d^{2} k\exp (ik \cdot \rho )\exp \left( { - i\frac{{k_{x}^{2} + k_{y}^{2} }}{{2k_{0} n_{\text{o}} }}z} \right)\left( {\begin{array}{*{20}c} 0 \\ {\frac{{k_{x} k_{y} }}{{k_{0}^{2} n_{\text{o}}^{2} }}\tilde{E}_{x} (k) + \tilde{E}_{y} (k)} \\ { - \frac{{k_{y} }}{{k_{\text{o}} n_{\text{o}} }}\tilde{E}_{y} (k)} \\ \end{array} } \right)} } \,. \\ \end{aligned} $$

(6)

By using the property of the Fourier transforms [24], the components of the nonparaxial field in the uniaxial crystal orthogonal to the optical axis can also be rewritten as

$$ E_{x} (\rho ,z) = \frac{{k_{0} n_{\text{o}} }}{2\pi iz}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{x} (\rho_{0} ,0)\Uplambda_{\text{e}} (\rho ,\rho_{0} )dx_{0} dy_{0} } } , $$

(7)

$$ \begin{aligned} E_{y} (\rho ,z) & = \frac{{ik_{0} n_{\text{o}} }}{{2\pi z^{3} }}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{x} (\rho_{0} ,0)(x - x_{0} )(y - y_{0} )[\Uplambda_{\text{e}} (\rho ,\rho_{0} ) - \Uplambda_{\text{o}} (\rho ,\rho_{0} )]dx_{0} dy_{0} } } \\ & \quad + \frac{{k_{0} n_{\text{o}} }}{2\pi iz}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {E_{y} (\rho_{0} ,0)\Uplambda_{\text{o}} (\rho ,\rho_{0} )dx_{0} dy_{0} } } , \\ \end{aligned} $$

(8)

$$ E_{z} (\rho ,z) = \frac{{ik_{0} n_{\text{o}} }}{{2\pi z^{2} }}\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {\left[ {E_{x} (\rho_{0} ,0)(x - x_{0} )\Uplambda_{\text{e}} (\rho ,\rho_{0} ) + E_{y} (\rho_{0} ,0)(y - y_{0} )\Uplambda_{\text{o}} (\rho ,\rho_{0} )} \right]dx_{0} dy_{0} } } , $$

(9)

where Λ_e(ρ, ρ ₀) and Λ_o(ρ, ρ ₀) being given by

$$ \Uplambda_{\text{e}} (\rho ,\rho_{0} ) = \exp (ik_{0} n_{\text{e}} z)\exp \left\{ { - \frac{{k_{0} }}{{2izn_{\text{e}} }}\left[ {n_{\text{o}}^{2} (x - x_{0} )^{2} + n_{\text{e}}^{2} (y - y_{0} )^{2} } \right]} \right\}, $$

(10)

$$ \Uplambda_{\text{o}} (\rho ,\rho_{0} ) = \exp (ik_{0} n_{\text{o}} z)\exp \left\{ { - \frac{{k_{0} n_{\text{o}} }}{2iz}\left[ {(x - x_{0} )^{2} + (y - y_{0} )^{2} } \right]} \right\}. $$

(11)

Inserting (2) into (7) and performing the integrals, the components of the Lorentz-Gauss vortex beam in the uniaxial crystal orthogonal to the optical axis are found to be

$$ \begin{aligned} E_{x} (\rho ,z) & = \frac{{k_{0} \pi n_{\text{o}} }}{8z}\exp \left[ {\frac{{kn_{\text{o}} (1 - a)x^{2} }}{2ieaz} + \frac{{ken_{\text{o}} (1 - b)y^{2} }}{2ibz} + ik_{0} n_{\text{e}} z} \right]\left\{ {w_{0x} [U_{x}^{ + } (x,z) - U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z)} \right. \\ & \left. {\quad + V_{y}^{ - } (y,z)] + iw_{0y} [U_{x}^{ + } (x,z) + U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) - V_{y}^{ - } (y,z)]} \right\}, \\ \end{aligned} $$

(12)

$$ \begin{aligned} E_{y} (\rho ,z) & = \frac{{ik_{0} \pi n_{\text{o}} }}{{8z^{3} }}\exp \left[ {\frac{{kn_{\text{o}} (1 - a)x^{2} }}{2ieaz} + \frac{{ken_{\text{o}} (1 - b)y^{2} }}{2ibz} + ik_{0} n_{\text{e}} z} \right]\left\{ {w_{0x} (w_{0y}^{2} + ixy)[U_{x}^{ + } (x,z) - U_{x}^{ - } (x,z)]} \right. \\ & \quad \times [V_{y}^{ + } (y,z) + V_{y}^{ - } (y,z)] + w_{0x} w_{0y} (x + iy)[U_{x}^{ + } (x,z) - U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) - V_{y}^{ - } (y,z)] - w_{0y} (iw_{0x}^{2} + xy) \\ & \quad \times [U_{x}^{ + } (x,z) + U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) - V_{y}^{ - } (y,z)] + (iw_{0y}^{2} x + w_{0x}^{2} y)[U_{x}^{ + } (x,z) + U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) \\ & \left. {\quad + V_{y}^{ - } (y,z)]} \right\} - \frac{{k_{0} \sqrt {\pi (a - 1)} n_{\text{o}} w_{0} w_{0x} }}{{4\sqrt a z^{3} }}\exp \left[ { - \frac{{x^{2} }}{{aw_{0}^{2} }} + \frac{{ken_{\text{o}} (1 - b)y^{2} }}{2ibz} + ik_{0} n_{\text{e}} z} \right]\left[ {(w_{0y} + iy)} \right. \\ & \left. {\quad \times V_{y}^{ + } (y,z) + (iy - w_{0y} )V_{y}^{ - } (y,z)} \right] + \frac{{k_{0} \sqrt {\pi (b - 1)} n_{\text{o}} w_{0} w_{0y} }}{{4\sqrt b z^{3} }}\exp \left[ {\frac{{kn_{\text{o}} (1 - a)x^{2} }}{2eiaz} - \frac{{y^{2} }}{{bw_{0}^{2} }} + ik_{0} n_{\text{e}} z} \right] \\ & \quad \times \left[ {(x - iw_{0x} )U_{x}^{ + } (x,z) + (x + iw_{0x} )U_{x}^{ - } (x,z)} \right] - \frac{{ik_{0} \pi n_{\text{o}} }}{{8z^{3} }}\exp \left[ {\frac{{kn_{\text{o}} (1 - c)(x^{2} + y^{2} )}}{2icz} + ik_{0} n_{\text{o}} z} \right] \\ & \quad \times \left\{ {w_{0x} (w_{0y}^{2} + ixy)[\Upomega_{x}^{ + } (x,z) - \Upomega_{x}^{ - } (x,z)]} \right.[\Upomega_{y}^{ + } (y,z) + \Upomega_{y}^{ - } (y,z)] + w_{0x} w_{0y} (x + iy)[\Upomega_{x}^{ + } (x,z) - \Upomega_{x}^{ - } (x,z)] \\ & \quad \times [\Upomega_{y}^{ + } (y,z) - \Upomega_{y}^{ - } (y,z)] - w_{0y} (iw_{0x}^{2} + xy)[\Upomega_{x}^{ + } (x,z) + \Upomega_{x}^{ - } (x,z)][\Upomega_{y}^{ + } (y,z) - \Upomega_{y}^{ - } (y,z)] \\ & \quad + (iw_{0y}^{2} x + w_{0x}^{2} y)[\Upomega_{x}^{ + } (x,z) + \Upomega_{x}^{ - } (x,z)][\Upomega_{y}^{ + } (y,z)\left. { + \Upomega_{y}^{ - } (y,z)]} \right\} + \frac{{k_{0} \sqrt {\pi (c - 1)} n_{\text{o}} w_{0} w_{0x} }}{{4\sqrt c z^{3} }} \\ & \quad \times \exp \left[ { - \frac{{x^{2} }}{{cw_{0}^{2} }} + \frac{{kn_{\text{o}} (1 - c)y^{2} }}{2icz} + ik_{0} n_{\text{o}} z} \right]\left[ {(w_{0y} + iy)\Upomega_{y}^{ + } (y,z) + (iy - w_{0y} )\Upomega_{y}^{ - } (y,z)} \right] \\ & \quad - \frac{{k_{0} \sqrt {\pi (c - 1)} n_{\text{o}} w_{0} w_{0y} }}{{4\sqrt c z^{3} }}\exp \left[ {\frac{{kn_{\text{o}} (1 - c)x^{2} }}{2icz} - \frac{{y^{2} }}{{cw_{0}^{2} }} + ik_{0} n_{0} z} \right]\left[ {(x - iw_{0x} )\Upomega_{x}^{ + } (x,z)} \right. \\ & \quad + \left. {(x + iw_{0x} )\Upomega_{x}^{ - } (x,z)} \right], \\ \end{aligned} $$

(13)

$$ \begin{aligned} E_{z} (\rho ,z) & = - \frac{{k_{0} \pi n_{\text{o}} }}{{8z^{2} }}\exp \left[ {\frac{{kn_{\text{o}} (1 - a)x^{2} }}{2ieaz} + \frac{{ken_{\text{o}} (1 - b)y^{2} }}{2ibz} + ik_{0} n_{\text{e}} z} \right]\left\{ {w_{0x} x[U_{x}^{ + } (x,z) - U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z)} \right. \\ & \quad + V_{y}^{ - } (y,z)] + iw_{0y} x[U_{x}^{ + } (x,z) + U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) - V_{y}^{ - } (y,z)] + w_{0x} w_{0y} [U_{x}^{ + } (x,z) - U_{x}^{ - } (x,z)] \\ & \left. {\quad \times [V_{y}^{ + } (y,z) - V_{y}^{ - } (y,z)] - iw_{0x}^{2} [U_{x}^{ + } (x,z) + U_{x}^{ - } (x,z)][V_{y}^{ + } (y,z) + V_{y}^{ - } (y,z)]} \right\} - \frac{{ik_{0} \sqrt {\pi (a - 1)} n_{\text{o}} w_{0} w_{0x} }}{{4\sqrt a z^{2} }} \\ & \quad \times \exp \left[ { - \frac{{x^{2} }}{{aw_{0}^{2} }} + \frac{{ken_{\text{o}} (1 - b)y^{2} }}{2ibz} + ik_{0} n_{\text{e}} z} \right][V_{y}^{ + } (y,z) + V_{y}^{ - } (y,z)], \\ \end{aligned} $$

(14)

with $U_{x}^{ \pm } (x,z)$, $V_{y}^{ \pm } (y,z)$, $\Upomega_{x}^{ \pm } (x,z)$, and $\Upomega_{y}^{ \pm } (y,z)$ being given by

$$ U_{x}^{ \pm } (x,z) = \exp \left[ {\frac{{kn_{\text{o}} a}}{2iez}\left( {w_{0x} \pm i\frac{x}{a}} \right)^{2} } \right]\text{erfc}\left[ {\sqrt {\frac{{kn_{\text{o}} a}}{2iez}} \left( {w_{0x} \pm i\frac{x}{a}} \right)} \right], $$

(15)

$$ V_{y}^{ \pm } (y,z) = \exp \left[ {\frac{{ken_{\text{o}} b}}{2iz}\left( {w_{0y} \pm i\frac{y}{b}} \right)^{2} } \right]\text{erfc}\left[ {\sqrt {\frac{{ken_{\text{o}} b}}{2iz}} \left( {w_{0y} \pm i\frac{y}{b}} \right)} \right], $$

(16)

$$ \Upomega_{\text{s}}^{ \pm } (s,z) = \exp \left[ {\frac{{kn_{\text{o}} c}}{2iz}\left( {w_{{0{\text{s}}}} \pm i\frac{s}{c}} \right)^{2} } \right]\text{erfc}\left[ {\sqrt {\frac{{kn_{\text{o}} c}}{2iz}} \left( {w_{{0{\text{s}}}} \pm i\frac{s}{c}} \right)} \right],\quad s = x,y, $$

(17)

where erfc (·) is the complementary error function. The auxiliary parameters are defined by

$$ e = \frac{{n_{\text{e}} }}{{n_{\text{o}} }},\;a = 1 + \frac{iez}{{n_{0} z_{\text{r}} }},\;b = 1 + \frac{iz}{{en_{\text{o}} z_{\text{r}} }}, $$

(18)

$$ c = 1 + \frac{i}{{n_{0} z_{\text{r}} }},\;z_{\text{r}} = kw_{0}^{2} /2, $$

(19)

where z _r is the Rayleigh length of the Gaussian part.

3 Numerical results and analyses

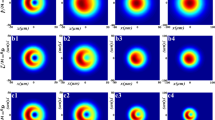
Based on the analytical formulae derived in the last section, here we investigate the propagation properties of a Lorentz-Gauss vortex beam in the uniaxial crystals orthogonal to the optical axis. Here we mainly pay attention to the influence of the uniaxial crystals on the propagation of a Lorentz-Gauss vortex beam. The calculation parameters are chosen as n _o = 2.616, e = 1.5, w ₀ = 10λ, w _0x  = w _0y  = 5λ. Figures 1, 2 and 3 represent the contour graph of the intensity distribution of the components of a Lorentz-Gauss vortex beam propagating in the uniaxial crystals orthogonal to the optical axis at several observation planes. The observation planes are z = 0.01z _r, z = 0.4z _r, z = z _r, and z = 3z _r. The intensity is proportional to the scale of 1/λ ², which is omitted in the figures. If the label of the intensity along the vertical axis in all the subfigures of one figure is same, we only mark it in the subfigures (b) and (d) to make the figure compact. The equality of w _0x and w _0y results in the symmetry of the beam profile of the x-component in the x- and y-directions of the source plane. Upon propagation in the uniaxial crystals orthogonal to the optical axis, however, the above symmetry of the beam profile of the x-component in the transversal directions will be lost. The outcome of the anisotropic effect of the crystals, which results in the spreading of the beam profile in the y-direction is far slower than that in the x-direction, and the optical vortex is the twisted profile of the x-component. The beam profile of the x-component is dark hollow. Though the y-component of Lorentz-Gauss vortex beam in the source plane is zero, it is no longer equal to zero upon propagation in the uniaxial crystals, which can be interpreted as follows: The y-component is affected by the x-component because of the dependence on $\tilde{E}_{x} (k),$ and this corresponds to a change of polarization state of the radiation that occurs during propagation in the uniaxial crystals [23]. Compared with the magnitude of the x-component, the magnitude of the y-component is very small. However, the y-component can not be negligible. Upon propagation in the uniaxial crystals, the beam profile of the y-component will finally spilt into four lobes. Moreover, the four lobes can be divided into two groups, and the lobe in each group can be obtained by rotating the other lobe. There also exists a central dark region in the beam profile of the y-component. The magnitude of the longitudinal component is far smaller than that of the x-component but far larger than that of the y-component, which is caused by the calculated values of the beam parameters being far larger than the wavelength. When the values of the beam parameters are smaller than or of the order of the wavelength, the magnitude of the longitudinal component is of the order of that of the x-component. Upon propagation in the uniaxial crystals, the beam profile of the longitudinal component splits into two lobes. The contour graph of the intensity distribution of a Lorentz-Gauss vortex beam propagating in the uniaxial crystals orthogonal to the optical axis at several observation planes is shown in Fig. 4. As |E _x |² ≫ |E _z |² ≫ |E _y |² ≫, the beam profile of a Lorentz-Gauss vortex beam is close to that of the x-component. However, the details in the edge of the beam profile between the Lorentz-Gauss vortex beam and its x-component are different.

Fig. 1

Contour graph of the intensity of the x-component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Fig. 2

Contour graph of the intensity of the y-component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Fig. 3

Contour graph of the intensity of the longitudinal component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Fig. 4

Contour graph of the intensity of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Figures 5, 6 and 7 represent the contour graph of the phase of the components of a Lorentz-Gauss vortex beam propagating in the uniaxial crystals. Just as their different intensity distributions, the phase distributions of the three components of a Lorentz-Gauss vortex beam propagating in the uniaxial crystals are also completely different. With the increase of the axial propagation distance, the phase distribution of the x-component gradually takes on spiral shape. The phase distributions of the y-component in the observation planes z = 0.01z _r and 0.4z _r are irregular. When the axial propagation distance is far enough, the phase distribution of the y-component is regular and takes on the distribution of back to the font. When in the observation plane z = 0.01z _r, the phase distribution of the longitudinal component is composed of two petals. With the increase of the axial propagation distance, the phase distribution of the longitudinal component experiences combination, rotation, and finally takes on a ring distribution.

Fig. 5

Contour graph of the phase of the x-component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Fig. 6

Contour graph of the phase of the y-component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Fig. 7

Contour graph of the phase of the longitudinal component of a Lorentz-Gauss vortex beam in several observation planes of the uniaxial crystal. e = 1.5. (a) z = 0.01z _r, (b) z = 0.4z _r, (c) z = z _r and (d) z = 3z _r

Figure 8 represents the contour graph of the intensity of a Lorentz-Gauss vortex beam in the observation plane z = z _r of different uniaxial crystals. When e = 1, the beam profile of the Lorentz-Gauss vortex beam is nearly symmetric and slightly leans toward the right. When e < 1, the beam profile becomes twisted and slants to the right. When e > 1, the beam profile is also twisted and slants to the left. With increasing the deviation of e from unity, the twisting and the tilt of the beam profile both become larger.

Fig. 8

Contour graph of the intensity of a Lorentz-Gauss vortex beam propagating in the observation plane z = z _r of different uniaxial crystals. (a) e = 0.6, (b) e = 0.8, (c) e = 1.0 and (d) e = 1.2

4 Conclusions

The analytical nonparaxial formula of a Lorentz-Gauss vortex beam propagating in a uniaxial crystal orthogonal to the optical axis has been derived. The intensity and the phase distributions of the components of a Lorentz-Gauss vortex beam propagating in a uniaxial crystal orthogonal to the optical axis have been demonstrated by numerical examples. Though the y-component of Lorentz-Gauss vortex beam in the source plane is zero, the y-component emerges upon propagation in the uniaxial crystals. The patterns of the intensity and the phase distribution of the three components are completely different, and the intensity and the phase distribution of the three components have their respective evolution laws. The uniaxial crystal can modulate the intensity distribution and the phase distribution of a Lorentz-Gauss vortex beam. With increasing the deviation of e from unity, the twisting and the tilt of the beam profile of a Lorentz-Gauss vortex beam both become larger. This research is beneficial to the optical trapping and nonlinear optics involving in the special beam profile.