Propagation properties of the partially coherent asymmetric vortex beams in uniaxial crystal orthogonal to the optical axis

Abstract

The propagation properties of partially coherent asymmetric vortex (PCAV) beams in uniaxial crystal orthogonal to the optical axis are studied. Propagation expression for the cross-spectral density of the PCAV beams propagating in a uniaxial crystal is derived. Based on the formulas derived, we study the propagation properties, such as the spectral density, the spectral degree of coherence, and the effective beam width of the PCAV beams inside uniaxial crystals in detail. The results show that the evolution properties of a PCAV beam in a uniaxial crystal are much different from its evolution properties in free space and are closely determined by the initial beam parameters and the parameters of the uniaxial crystal. The uniaxial crystal can modulate the distributions of the intensity and the degree of the polarization for PCAV beams, which is beneficial to the optical trapping and nonlinear optics involving in the special beam profile.

Introduction

Asymmetric beams are this kind of laser beams with decentered field profile with a dark area in the middle. Namely, the radiation field is non-symmetry, and the position of the center of gravity of the beams deviates from the propagation z-axis [1]. Recently, the asymmetric Laguerre–Gaussian beams are proposed and can be used in optical trapping and moving [2, 3]. In Kotlyar et al. [4], the asymmetric Bessel modes are introduced, and it can be used instead of conventional Gaussian beam for trapping and transferring live cells without thermal damage [5]. In Kotlyar et al. [6], the asymmetric vortex Gaussian beams are studied and generated experimentally. Up to now, few papers have addressed the propagation of the asymmetrical laser beams propagating in medium [1, 7].

Uniaxial crystals exhibiting some interesting optical properties, such as double refraction, optical rotation or polarization effects, are required in some applications, including the design of the polarizer and the compensator [8], simple modulation of light [9], fiber Bragg gratings [10], polarization conversion [11], and generation of white-light optical vortices [12, 13] and vector bottle beams [14]. During the past years, the propagation of many other kinds of laser beams through uniaxial crystals has received much more attention, such as Hermite–Gauss [15], Laguerre–Gauss and Bessel–Gauss beams [16], flat-topped beams [17, 18], dark hollow Gaussian beams [19], beams generated by Gaussian mirror resonator in uniaxial crystals [20], partially polarized and partially coherent beam [21], higher-order cosh-Gaussian beams [22, 23], four-petal Gaussian vortex beam [24, 25], Laguerre–Gaussian correlated Schell model beam [26], three-dimensional flattened Gaussian beams [27], elliptical Gaussian vortex beam [28],sine beams [29], and hyperbolic sinusoidal Gaussian beams [30]. However, most studies are restricted to the laser beams with axis symmetry field. In this paper, our aim is to study the propagation of partially coherent asymmetric vortex beams in uniaxial crystals orthogonal to the optical axis. Analytical formulas for partially coherent asymmetric beams propagating in uniaxial crystals are derived, and some numerical illustrations are given. The results obtained in this work are beneficial to the optical trapping and nonlinear optics involving in the special beam profile.

Propagation expression for the cross-spectral density of the PCAV beams

In the rectangular coordinate system, the electric field of asymmetric optical vortex beams at z = 0 can be expressed as [6]

$$E_{0}^{\prime } \left( {{{\varvec{\uprho}}}^{\prime } ,0} \right) = \left[ {\frac{{\left( {x^{\prime } - x_{0} } \right) + iy^{\prime } }}{w}} \right]^{N} \exp \left( { - \frac{{x^{\prime 2} + y^{\prime 2} }}{{w^{2} }}} \right),$$

(1)

where ρ′≡(x′,y′) is the two-dimensional position vector at the z = 0 plane. w is the waist radius, N is the topological charge, and x₀ is a distance the embeded optical vortex shifted from the Gaussian beam center along the x-axis.

In the Cartesian coordinate system, the cross-spectral density function of a PCAV beam at the source plane z = 0 can be expressed as

$$W^{\left( 0 \right)} \left( {{\mathbf{\rho^{\prime}}}_{1} ,{\mathbf{\rho^{\prime}}}_{2} ,0} \right) = \sqrt {I\left( {{\mathbf{\rho^{\prime}}}_{1} ,0} \right)I\left( {{\mathbf{\rho^{\prime}}}_{2} ,0} \right)} g\left( {x^{\prime}_{1} - x^{\prime}_{2} ,y^{\prime}_{1} - y^{\prime}_{2} } \right),$$

(2)

where $g\left( {x^{\prime}_{1} - x^{\prime}_{2} ,y^{\prime}_{1} - y^{\prime}_{2} } \right)$ is the spectral degree of coherence

$$g\left( {x^{\prime}_{1} - x^{\prime}_{2} ,y^{\prime}_{1} - y^{\prime}_{2} } \right) = \exp \left[ { - \frac{{\left( {x^{\prime}_{1} - x^{\prime}_{2} } \right)^{2} }}{{2\sigma_{0}^{2} }} - \frac{{\left( {y^{\prime}_{1} - y^{\prime}_{2} } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right],$$

(3)

where σ₀ is the coherence length.

Substituting Eq. (3) into Eq. (2), and I(ρ′,0) =|E′₀(ρ′,0)|², the cross-spectral density of the PCAV beams at z = 0 plane can be expressed as

$$\begin{aligned} W^{\left( 0 \right)} \left( {{\mathbf{\rho^{\prime}}}_{1} ,{\mathbf{\rho^{\prime}}}_{2} ,0} \right) = & \left[ {\frac{{\left( {x_{1}^{\prime } - x_{0} } \right) - iy_{1}^{\prime } }}{w}} \right]^{N} \left[ {\frac{{\left( {x_{2}^{\prime } - x_{0} } \right) + iy_{2}^{\prime } }}{w}} \right]^{M} \\ & \; \times \exp \left( { - \frac{{x_{1}^{\prime 2} + y_{1}^{\prime 2} + x_{2}^{\prime 2} + y_{2}^{\prime 2} }}{{w^{2} }}} \right)\exp \left( { - \frac{{\left( {x_{1}^{\prime } - x_{2}^{\prime } } \right)^{2} }}{{2\sigma_{0}^{2} }} - \frac{{\left( {y_{1}^{\prime } - y_{2}^{\prime } } \right)^{2} }}{{2\sigma_{0}^{2} }}} \right), \\ \end{aligned}$$

(4)

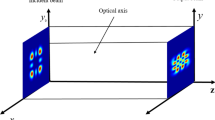
We assumed that the PCAV beams propagate along the z-axis and the optical axis of the uniaxial crystal coincides with the x-axis. The ordinary and extraordinary refractive indices of the uniaxial crystal are n_o and n_e, respectively. Within the framework of a paraxial approximation, the components of the laser beam in uniaxial crystals orthogonal to the optical axis can be treated by the following integral formulas [8]

$$E_{x} \left( {{{\varvec{\uprho}}},z} \right) = \exp \left( {ikn_{e} z} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\tilde{E}_{x} \left( {k_{x} ,k_{y} } \right)} } \exp \left[ {i\left( {k_{x} x + k_{y} y} \right) - i\frac{{n_{e}^{2} k_{x}^{2} + n_{o}^{2} k_{y}^{2} }}{{2kn_{o}^{2} n_{e} }}z} \right]dk_{x} dk_{y} ,$$

(5)

$$E_{y} \left( {{{\varvec{\uprho}}},z} \right) = \exp \left( {ikn_{o} z} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\tilde{E}_{y} \left( {k_{x} ,k_{y} } \right)} } \exp \left[ {i\left( {k_{x} x + k_{y} y} \right) - i\frac{{k_{x}^{2} + k_{y}^{2} }}{{2kn_{0} }}z} \right]dk_{x} dk_{y} ,$$

(6)

with the two-dimensional Fourier transform $\tilde{E}_{x} \left( {k_{x} ,k_{y} } \right)$ and $\tilde{E}_{y} \left( {k_{x} ,k_{y} } \right)$ being given by

$$\tilde{E}_{x} \left( {{{\varvec{\uprho}}},z} \right) = \frac{1}{{4\pi^{2} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{x} } } \left( {{\mathbf{\rho^{\prime}}},0} \right)\exp \left[ { - i\left( {k_{x} x + k_{y} y} \right)} \right]dk_{x} dk_{y} ,$$

(7)

$$\tilde{E}_{y} \left( {{{\varvec{\uprho}}},z} \right) = \frac{1}{{4\pi^{2} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{y} } } \left( {{\mathbf{\rho^{\prime}}},0} \right)\exp \left[ { - i\left( {k_{x} x + k_{y} y} \right)} \right]dk_{x} dk_{y} ,$$

(8)

In the paraxial approximation, the longitudinal component of the field can be neglected as long as the transversal beam radius w₀ is larger compared with the wavelength [31]. Equations (7) and (8) indicate that the x component of the optical field is only a superposition of extraordinary plane waves and the y component uniquely contains ordinary plane waves, and can be rewritten as

$$\begin{aligned} E_{x} \left( {{{\varvec{\uprho}}},z} \right) = & - \frac{{ikn_{o} }}{2\pi z}\exp \left( {ikn_{e} z} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{x} \left( {{\mathbf{\rho^{\prime}}},0} \right)} } \\ & \; \times \exp \left\{ {\frac{ik}{{2zn_{e} }}\left[ {n_{o}^{2} \left( {x - x^{\prime}} \right)^{2} + } \right.\left. {n_{e}^{2} \left( {y - y^{\prime}} \right)^{2} } \right]} \right\}dx^{\prime}dy^{\prime}, \\ \end{aligned}$$

(9)

$$\begin{aligned} E_{y} \left( {{{\varvec{\uprho}}},z} \right) = & - \frac{{ikn_{o} }}{2\pi z}\exp \left( {ikn_{o} z} \right)\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {E_{y} \left( {{\mathbf{\rho^{\prime}}},0} \right)} } \\ & \; \times \exp \left\{ {\frac{{ikn_{o} }}{2z}\left[ {\left( {x - x^{\prime}} \right)^{2} + } \right.\left. {\left( {y - y^{\prime}} \right)^{2} } \right]} \right\}dx^{\prime}dy^{\prime}, \\ \end{aligned}$$

(10)

where k = 2π /λ is the wave number with λ being the optical wavelength.

In this work, the propagation of partially coherent beams passing through uniaxial crystals orthogonal to the optical axis will be studied. Here, we only consider the incidence extraordinary laser beam (x-polarized) propagating through uniaxial crystals orthogonal to the optical axis. The cross-spectral density of a laser beam propagating in uniaxial crystals can be expressed as

$$\begin{aligned} W\left( {{{\varvec{\uprho}}}_{1} ,{{\varvec{\uprho}}}_{2} ,z} \right) = & \left\langle {E\left( {{{\varvec{\uprho}}}_{1} ,{{\varvec{\uprho}}}_{2} ,z} \right)E^{ * } \left( {{{\varvec{\uprho}}}_{1} ,{{\varvec{\uprho}}}_{2} ,z} \right)} \right\rangle \\ = & \frac{{k_{0}^{2} n_{o}^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {\exp \left\{ {\frac{{ik_{0} }}{{2zn_{e} }}\left[ {n_{o}^{2} \left( {x_{1} - x^{\prime}_{1} } \right)^{2} + n_{e}^{2} \left( {y_{1} - y^{\prime}_{1} } \right)^{2} } \right]} \right\}} } } } \\ & \; \times \exp \left\{ { - \frac{{ik_{0} }}{{2zn_{e} }}\left[ {n_{o}^{2} \left( {x_{1} - x^{\prime}_{2} } \right)^{2} + n_{e}^{2} \left( {y_{1} - y^{\prime}_{2} } \right)^{2} } \right]} \right\}W^{\left( 0 \right)} \left( {{\mathbf{\rho^{\prime}}}_{1} ,{\mathbf{\rho^{\prime}}}_{2} ,0} \right)dx^{\prime}_{1} dx^{\prime}_{2} dy^{\prime}_{1} dy^{\prime}_{2} , \\ \end{aligned}$$

(11)

Using the following formulas [32]

$$\left( {a + b} \right)^{n} = \sum\limits_{l = 0}^{n} {\frac{n!}{{l!\left( {n - l} \right)!}}a^{n - l} b^{l} } ,$$

(12)

$$\int\limits_{ - \infty }^{\infty } {x^{2n} \exp \left( { - bx^{2} + 2cx} \right)dx = \left( {2n} \right)!\sqrt {\frac{\pi }{b}} \left( \frac{c}{b} \right)^{2n} \exp \left( {\frac{{c^{2} }}{b}} \right)\sum\limits_{s = 0}^{n} {\frac{1}{{s!\left( {2n - 2s} \right)!}}\left( {\frac{b}{{4c^{2} }}} \right)^{s} } } ,$$

(13)

Substituting Eq. (4) into Eq. (11), after a tedious but straightforward integration, the cross-spectral density of the PCAV beams polarized along the x axis through uniaxial crystals can be obtained as

$$\begin{aligned} W\left( {{{\varvec{\uprho}}}_{1} ,{{\varvec{\uprho}}}_{2} ,z} \right) = & \frac{{k_{0}^{2} n_{o}^{2} }}{{4\pi^{2} z^{2} }}\frac{1}{{w^{N} }}\frac{1}{{w^{M} }}\exp \left[ {\frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }}\left( {x_{2}^{2} + y_{2}^{2} } \right) - \frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }}\left( {x_{1}^{2} + y_{1}^{2} } \right)} \right] \\ & \; \times \sum\limits_{m = 0}^{M} {\frac{{M!i^{m} }}{{m!\left( {M - m} \right)!}}} \sum\limits_{q = 0}^{M - m} {\frac{{\left( {M - m} \right)!}}{{q!\left( {M - m - q} \right)!}}} \sum\limits_{n = 0}^{N} {\frac{{N!\left( { - i} \right)^{n} }}{{n!\left( {N - n} \right)!}}} \sum\limits_{p = 0}^{N - n} {\frac{{\left( {N - n} \right)!}}{{p!\left( {N - n - p} \right)!}}} \\ & \; \times \left( { - x_{0} } \right)^{p + q} \left( {N - n - p} \right)!\left( {\frac{1}{{\alpha_{1} }}} \right)^{N - n - p} \sqrt {\frac{\pi }{a1}} \sum\limits_{k1 = 0}^{{\left[ {\frac{N - n - p}{2}} \right]}} {\frac{1}{{k1!\left( {N - n - p - 2k1} \right)}}} \\ & \; \times \left( {\frac{{\alpha_{1} }}{4}} \right)^{k1} \sum\limits_{s1 = 0}^{N - n - p - 2k1} {\frac{{\left( {N - n - p - 2k1} \right)!}}{{s1!\left( {N - n - p - 2k1 - s1} \right)!}}} \left( {\frac{{k_{0} n_{o}^{2} x_{1} }}{{i2zn_{e} }}} \right)^{N - n - p - 2k1 - s1} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s1} \\ & \; \times \exp \left( {\frac{1}{{\alpha_{1} }}\left( {\frac{{k_{0} n_{o}^{2} x_{1} }}{{i2zn_{e} }}} \right)^{2} } \right)\left( {M - m - q + s1} \right)!\exp \left( {\frac{{\gamma_{1}^{2} }}{{\beta_{1} }}} \right)\left( {\frac{{\gamma_{1} }}{{\beta_{1} }}} \right)^{M - m - q + s1} \sqrt {\frac{\pi }{{\beta_{1} }}} \\ & \; \times \sum\limits_{s2 = 0}^{{\left[ {\frac{M - m - q + s1}{2}} \right]}} {\frac{1}{{s2!\left( {M - m - q + s1 - 2s2} \right)}}} \left( {\frac{{\beta_{1} }}{{4\gamma_{1}^{2} }}} \right)^{s2} n!\left( {\frac{1}{{\alpha_{2} }}} \right)^{n} \sqrt {\frac{\pi }{{\alpha_{2} }}} \\ & \; \times \sum\limits_{k2 = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{1}{{k2!\left( {n - 2k2} \right)!}}} \left( {\frac{{\alpha_{2} }}{4}} \right)^{k2} \sum\limits_{s3 = 0}^{{\left[ {\frac{n - 2k2}{2}} \right]}} {\frac{{\left( {n - 2k2} \right)!}}{{s3!\left( {n - 2k2 - s3} \right)!}}} \left( {\frac{{k_{0} n_{e} }}{2iz}y_{1} } \right)^{n - 2k2 - s3} \\ & \; \times \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s3} \exp \left( {\frac{1}{{\alpha_{2} }}\left( {\frac{{k_{0} n_{e} }}{2iz}} \right)^{2} y_{1}^{2} } \right)\left( {m + s3} \right)!\exp \left( {\frac{{\gamma_{2}^{2} }}{{\beta_{2} }}} \right)\left( {\frac{{\gamma_{2} }}{{\beta_{2} }}} \right)^{m + s3} \sqrt {\frac{\pi }{{\beta_{2} }}} \\ & \; \times \sum\limits_{s4 = 0}^{{\left[ {\frac{m + s3}{2}} \right]}} {\frac{1}{{s4!\left( {m + s3 - 2s4} \right)}}} \left( {\frac{{\beta_{2} }}{{4\gamma_{2}^{2} }}} \right)^{s4} , \\ \end{aligned}$$

(14)

where

$$\alpha_{1} = \frac{1}{{w^{2} }} + \frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }} + \frac{1}{{2\sigma_{0}^{2} }}$$

(15)

$$\beta_{1} = \frac{1}{{w^{2} }} - \frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }} + \frac{1}{{2\sigma_{0}^{2} }} - \frac{1}{{4\alpha_{1} \sigma_{0}^{4} }}$$

(16)

$$\gamma_{1} = \frac{{k_{0} n_{o}^{2} }}{{4i\alpha_{1} zn_{e} \sigma_{0}^{2} }}x_{1} - \frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }}x_{2}$$

(17)

$$\alpha_{2} = \frac{1}{{w^{2} }} + \frac{1}{{2\sigma_{0}^{2} }} + \frac{{k_{0} n_{e} }}{2iz}$$

(18)

$$\beta_{2} = \frac{1}{{w^{2} }} - \frac{{k_{0} n_{e} }}{2iz} + \frac{1}{{2\sigma_{0}^{2} }} - \frac{1}{{4\alpha_{2} \sigma_{0}^{4} }}$$

(19)

$$\gamma_{2} = \frac{{k_{0} n_{e} }}{{4iz\alpha_{2} \sigma_{0}^{2} }}y_{1} - \frac{{k_{0} n_{e} }}{2iz}y_{2}$$

(20)

Equations (14)–(20) are the analytical expression for the cross-spectral density of the PCAV beams propagating in uniaxial crystals orthogonal to the optical axis and indicates that W(ρ₁, ρ₂,z) at the z plane depends on the beam parameters, such as topological charge, the coherence width σ₀, waist width w, and the refractive indices of the uniaxial crystal n_o, n_e. Substituting ρ₁ = ρ₂ = ρ into Eq. (14), the spectral density at any point (ρ, z) can be obtained

$$\begin{aligned} S\left( {{{\varvec{\uprho}}},z} \right) = & \frac{{k_{0}^{2} n_{o}^{2} }}{{4\pi^{2} z^{2} }}\frac{1}{{w^{N} }}\frac{1}{{w^{M} }}\sum\limits_{m = 0}^{M} {\frac{{M!i^{m} }}{{m!\left( {M - m} \right)!}}} \sum\limits_{q = 0}^{M - m} {\frac{{\left( {M - m} \right)!}}{{q!\left( {M - m - q} \right)!}}} \\ & \; \times \sum\limits_{n = 0}^{N} {\frac{{N!\left( { - i} \right)^{n} }}{{n!\left( {N - n} \right)!}}} \sum\limits_{p = 0}^{N - n} {\frac{{\left( {N - n} \right)!}}{{p!\left( {N - n - p} \right)!}}} \left( { - x_{0} } \right)^{p + q} \left( {N - n - p} \right)! \\ & \; \times \left( {\frac{1}{{\alpha_{1} }}} \right)^{N - n - p} \sqrt {\frac{\pi }{{\alpha_{1} }}} \sum\limits_{k1 = 0}^{{\left[ {\frac{N - n - p}{2}} \right]}} {\frac{1}{{k1!\left( {N - n - p - 2k1} \right)}}\left( {\frac{{\alpha_{1} }}{4}} \right)^{k1} } \\ & \; \times \sum\limits_{s1 = 0}^{N - n - p - 2k1} {\frac{{\left( {N - n - p - 2k1} \right)!}}{{s1!\left( {N - n - p - 2k1 - s1} \right)!}}} \left( {\frac{{k_{0} n_{o}^{2} x}}{{i2zn_{e} }}} \right)^{N - n - p - 2k1 - s1} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s1} \\ & \; \times \exp \left( {\frac{1}{{\alpha_{1} }}\left( {\frac{{k_{0} n_{o}^{2} x}}{{i2zn_{e} }}} \right)^{2} } \right)\left( {M - m - q + s1} \right)!\exp \left( {\frac{{\delta_{1}^{2} }}{{\beta_{1} }}x^{2} } \right)\left( {\frac{{\delta_{1} }}{{\beta_{1} }}x} \right)^{M - m - q + s1} \\ & \; \times \sqrt {\frac{\pi }{{\beta_{1} }}} \sum\limits_{s2 = 0}^{{\left[ {\frac{M - m - q + s1}{2}} \right]}} {\frac{1}{{s2!\left( {M - m - q + s1 - 2s2} \right)}}} \left( {\frac{{\beta_{1} }}{{4\delta_{1}^{2} x^{2} }}} \right)^{s2} n!\left( {\frac{1}{{\alpha_{2} }}} \right)^{n} \sqrt {\frac{\pi }{{\alpha_{2} }}} \\ & \; \times \sum\limits_{k2 = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{1}{{k2!\left( {n - 2k2} \right)!}}\left( {\frac{{\alpha_{2} }}{4}} \right)^{k2} } \sum\limits_{s3 = 0}^{{\left[ {n - 2k2} \right]}} {\frac{{\left( {n - 2k2} \right)!}}{{s3!\left( {n - 2k2 - s3} \right)!}}} \\ & \; \times \left( {\frac{{k_{0} n_{e} }}{2iz}y} \right)^{n - 2k2 - s3} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s3} \exp \left( {\frac{1}{{\alpha_{2} }}\left( {\frac{{k_{0} n_{e} }}{2iz}y} \right)^{2} } \right)\left( {m + s3} \right)!\exp \left( {\frac{{\delta_{2}^{2} }}{{\beta_{2} }}y^{2} } \right) \\ & \; \times \left( {\frac{{\delta_{2} }}{{\beta_{2} }}y} \right)^{m + s3} \sqrt {\frac{\pi }{{\beta_{2} }}} \sum\limits_{s4 = 0}^{{\left[ {\frac{m + s3}{2}} \right]}} {\frac{1}{{s4!\left( {m + s3 - 2s4} \right)}}} \left( {\frac{{\beta_{2} }}{{4\delta_{2}^{2} y^{2} }}} \right)^{s4} , \\ \end{aligned}$$

(21)

with

$$\delta_{1} = \frac{{k_{0} n_{o}^{2} }}{{4i\alpha_{1} zn_{e} \sigma_{0}^{2} }} - \frac{{k_{0} n_{o}^{2} }}{{2izn_{e} }},$$

(22)

$$\delta_{2} = \frac{{k_{0} n_{e} }}{{4i\alpha_{2} z\sigma_{0}^{2} }} - \frac{{k_{0} n_{e} }}{2iz}.$$

(23)

The degree of coherence of the PCAV beams at a pair of points ρ and − ρ can be given by

$$\mu \left( {{{\varvec{\uprho}}}, - {{\varvec{\uprho}}},z} \right) = \frac{{W\left( {{{\varvec{\uprho}}}, - {{\varvec{\uprho}}},z} \right)}}{{\sqrt {S\left( {{{\varvec{\uprho}}},z} \right)S\left( { - {{\varvec{\uprho}}},z} \right)} }},$$

(24)

where W(ρ, − ρ, z) can be obtained by setting ρ₁ = − ρ₂ = ρ in Eq. (14), S(− ρ, z) can be obtained by replacing ρ with − ρ in Eq. (21).

The effective beam width of the PCAV beams at plane z is defined as

$$W_{j} = \sqrt {\frac{{2\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {j^{2} S\left( {x,y,z} \right)dxdy} } }}{{\int\limits_{ - \infty }^{\infty } {\int\limits_{ - \infty }^{\infty } {S\left( {x,y,z} \right)dxdy} } }}} \left( {j = x,y} \right),$$

(25)

where W_x and W_y are the effective beam widths of the PCAV beams in the x and y directions, respectively.

Substituting Eq. (21) into Eq. (25), the effective beam width of the PCAV beams yields

$$W_{j} = \sqrt {\frac{{2A_{1j} }}{{A_{2j} }}} \left( {j = x,y} \right),$$

(26)

with A_1j and A_2j given by

$$\begin{aligned} A_{sx} = & \sum\limits_{m = 0}^{M} {\frac{{M!i^{m} }}{{m!\left( {M - m} \right)!}}} \sum\limits_{q = 0}^{M - m} {\frac{{\left( {M - m} \right)!}}{{q!\left( {M - m - q} \right)!}}} \sum\limits_{n = 0}^{N} {\frac{{N!\left( { - i} \right)^{n} }}{{n!\left( {N - n} \right)!}}} \sum\limits_{p = 0}^{N - n} {\frac{{\left( {N - n} \right)!}}{{p!\left( {N - n - p} \right)!}}} \\ & \; \times \left( { - x_{0} } \right)^{p + q} \left( {N - n - p} \right)!\left( \frac{1}{a1} \right)^{N - n - p} \sqrt {\frac{\pi }{a1}} \sum\limits_{k1 = 0}^{{\left[ {\frac{N - n - p}{2}} \right]}} {\frac{1}{{k1!\left( {N - n - p - 2k1} \right)}}\left( \frac{a1}{4} \right)^{k1} } \\ & \; \times \sum\limits_{s1 = 0}^{N - n - p - 2k1} {\frac{{\left( {N - n - p - 2k1} \right)!}}{{s1!\left( {N - n - p - 2k1 - s1} \right)!}}} \left( {\frac{{k_{0} n_{o}^{2} }}{{i2zn_{e} }}} \right)^{N - n - p - 2k1 - s1} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s1} \left( {M - m - q + s1} \right)! \\ & \; \times \left( {\frac{d1}{{b1}}} \right)^{M - m - q + s1} \sqrt {\frac{\pi }{b1}} \sum\limits_{s2 = 0}^{{\left[ {\frac{M - m - q + s1}{2}} \right]}} {\frac{1}{{s2!\left( {M - m - q + s1 - 2s2} \right)}}} \left( {\frac{b1}{{4d1^{2} }}} \right)^{s2} D_{sx} n!\left( \frac{1}{a2} \right)^{n} \\ \;\;\sqrt {\frac{\pi }{a2}} \sum\limits_{k2 = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{1}{{k2!\left( {n - 2k2} \right)!}}\left( \frac{a2}{4} \right)^{k2} } \sum\limits_{s3 = 0}^{{\left[ {n - 2k2} \right]}} {\frac{{\left( {n - 2k2} \right)!}}{{s3!\left( {n - 2k2 - s3} \right)!}}} \left( {\frac{{k_{0} n_{e} }}{2iz}} \right)^{n - 2k2 - s3} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s3} \\ & \; \times \left( {m + s3} \right)!\left( {\frac{d2}{{b2}}} \right)^{m + s3} \sqrt {\frac{\pi }{b2}} \sum\limits_{s4 = 0}^{{\left[ {\frac{m + s3}{2}} \right]}} {\frac{1}{{s4!\left( {m + s3 - 2s4} \right)}}} \left( {\frac{b2}{{4d2^{2} }}} \right)^{s4} D_{2y} , \\ \end{aligned}$$

(27)

$$\begin{aligned} A_{sy} = & \sum\limits_{m = 0}^{M} {\frac{{M!i^{m} }}{{m!\left( {M - m} \right)!}}} \sum\limits_{q = 0}^{M - m} {\frac{{\left( {M - m} \right)!}}{{q!\left( {M - m - q} \right)!}}} \sum\limits_{n = 0}^{N} {\frac{{N!\left( { - i} \right)^{n} }}{{n!\left( {N - n} \right)!}}} \sum\limits_{p = 0}^{N - n} {\frac{{\left( {N - n} \right)!}}{{p!\left( {N - n - p} \right)!}}} \\ & \; \times \left( { - x_{0} } \right)^{p + q} \left( {N - n - p} \right)!\left( \frac{1}{a1} \right)^{N - n - p} \sqrt {\frac{\pi }{a1}} \sum\limits_{k1 = 0}^{{\left[ {\frac{N - n - p}{2}} \right]}} {\frac{1}{{k1!\left( {N - n - p - 2k1} \right)}}\left( \frac{a1}{4} \right)^{k1} } \\ & \; \times \sum\limits_{s1 = 0}^{N - n - p - 2k1} {\frac{{\left( {N - n - p - 2k1} \right)!}}{{s1!\left( {N - n - p - 2k1 - s1} \right)!}}} \left( {\frac{{k_{0} n_{o}^{2} }}{{i2zn_{e} }}} \right)^{N - n - p - 2k1 - s1} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s1} \left( {M - m - q + s1} \right)! \\ & \; \times \left( {\frac{d1}{{b1}}} \right)^{M - m - q + s1} \sqrt {\frac{\pi }{b1}} \sum\limits_{s2 = 0}^{{\left[ {\frac{M - m - q + s1}{2}} \right]}} {\frac{1}{{s2!\left( {M - m - q + s1 - 2s2} \right)}}} \left( {\frac{b1}{{4d1^{2} }}} \right)^{s2} D_{2x} n!\left( \frac{1}{a2} \right)^{n} \sqrt {\frac{\pi }{a2}} \\ & \; \times \sum\limits_{k2 = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{1}{{k2!\left( {n - 2k2} \right)!}}\left( \frac{a2}{4} \right)^{k2} \sum\limits_{s3 = 0}^{{\left[ {n - 2k2} \right]}} {\frac{{\left( {n - 2k2} \right)!}}{{s3!\left( {n - 2k2 - s3} \right)!}}} \left( {\frac{{k_{0} n_{e} }}{2iz}} \right)^{n - 2k2 - s3} \left( {\frac{1}{{2\sigma_{0}^{2} }}} \right)^{s3} } \\ & \; \times \left( {m + s3} \right)!\left( {\frac{d2}{{b2}}} \right)^{m + s3} \sqrt {\frac{\pi }{b2}} \sum\limits_{s4 = 0}^{{\left[ {\frac{m + s3}{2}} \right]}} {\frac{1}{{s4!\left( {m + s3 - 2s4} \right)}}} \left( {\frac{b2}{{4d2^{2} }}} \right)^{s4} D_{sy} , \\ \end{aligned}$$

(28)

where

$$D_{1x} = \left[ { - \frac{{d1^{2} }}{b1} - \frac{1}{a1}\left( {\frac{{k_{0} n_{o}^{2} }}{{i2zn_{e} }}} \right)^{2} } \right]^{{\left[ { - {{\left( {3 + M + N - m - n - q - p - 2k1 - 2s2} \right)} \mathord{\left/ {\vphantom {{\left( {3 + M + N - m - n - q - p - 2k1 - 2s2} \right)} 2}} \right. \kern-0pt} 2}} \right]}} \Gamma \left( {\frac{3 + M + N - m - n - q - p - 2k1 - 2s2}{2}} \right),$$

(29)

$$D_{2x} = \left[ { - \frac{{d1^{2} }}{b1} - \frac{1}{a1}\left( {\frac{{k_{0} n_{o}^{2} }}{{i2zn_{e} }}} \right)^{2} } \right]^{{\left[ { - {{\left( {1 + M + N - m - n - q - p - 2k1 - 2s2} \right)} \mathord{\left/ {\vphantom {{\left( {1 + M + N - m - n - q - p - 2k1 - 2s2} \right)} 2}} \right. \kern-0pt} 2}} \right]}} \Gamma \left( {\frac{1 + M + N - m - n - q - p - 2k1 - 2s2}{2}} \right),$$

(30)

$$D_{1y} = \left[ { - \frac{{d2^{2} }}{b2} - \frac{1}{a2}\left( {\frac{{k_{0} n_{e} }}{2iz}} \right)^{2} } \right]^{{\left[ {{{ - \left( {3 + m + n - 2k2 - 2s4} \right)} \mathord{\left/ {\vphantom {{ - \left( {3 + m + n - 2k2 - 2s4} \right)} 2}} \right. \kern-0pt} 2}} \right]}} \Gamma \left( {\frac{3 + m + n - 2k2 - 2s4}{2}} \right),$$

(31)

$$D_{2y} = \left[ { - \frac{{d2^{2} }}{b2} - \frac{1}{a2}\left( {\frac{{k_{0} n_{e} }}{2iz}} \right)^{2} } \right]^{{\left[ {{{ - \left( {1 + m + n - 2k2 - 2s4} \right)} \mathord{\left/ {\vphantom {{ - \left( {1 + m + n - 2k2 - 2s4} \right)} 2}} \right. \kern-0pt} 2}} \right]}} \Gamma \left( {\frac{1 + m + n - 2k2 - 2s4}{2}} \right).$$

(32)

with s = 1 or 2 and Γ(·) is a Gamma function. As a result, the calculations of the spectral degree of coherence and the effective beam width are convenient by using the derived formulas.

Numerical examples

According to the obtained analytical expressions, the properties of the x linearly polarized PCAV beam propagating in uniaxial crystals orthogonal to the x-axis are numerically demonstrated. The calculation parameters are set as follows: λ = 632.8 nm (He–Ne laser), w = 20 μm, σ₀ = 10 μm, x = 0.1w, n_o = 2.616 (rutile crystal) [33], and M = N = 1, unless specified in captions.

First, let us consider the effects of the coherent length on the evolution properties of the PCAV beams propagating in free space (n_o = n_e = 1). Figure 1 represents the spectral density distributions of the PCAV beam at several propagation distances for different values of the coherence length. It can be seen that the distribution of spectral density from a hollow profile of source plane becomes a Gaussian profile with the increase of propagation distance (see the upper row of Fig. 1). It is also found that the beam profile changes from asymmetric to symmetrical distribution. This is due to the diffraction effect of the beam itself. As the coherence length increases, the increasing evolution distances are needed to form Gaussian profile (see the middle row of Fig. 1) and the PCAV beam keeping hollow profile propagates farther (see the lower row of Fig. 1). This is because for the partially coherent beams the longer the coherence length is, the smaller the diffraction effect is. Therefore, we can adjust the spectral density distribution of the PCAV beams through the change of the coherence length. It should be noted that the spreading of PCAV beams decreases with the increasing the coherence length, which can be observed from the results presented in [25].

Fig. 1

Spectral density distributions of a PCAV beam propagating in free space at several propagation distances for different values of the coherence length

The spectral density distribution of a PCAV beam propagating in uniaxial crystals with n_e/n_o = 1.2 at several propagation distances for different shifted values of x₀ is given in Fig. 2. In the case of x₀ = 0, the PCAV beam reduces to partially coherent symmetric vortex beam. One can see from a1–a4 of Fig. 1 the partially coherent symmetric vortex beam can keep hollow profile at the short propagation distance, and will lose circularly symmetric profile upon propagation. Finally it will evolve into asymmetric elliptical profile. This phenomenon is in line with the existing results [34]. The physical reason of the asymmetric distribution is due to the effect of anisotropic crystals (n_e > n_o), the effect of uniaxial crystals on the distribution of x-direction is more obvious than y-direction. In uniaxial crystals, the propagation properties of the PCAV beam are very different from that of partially coherent symmetric vortex beam. From Fig. 1 it can be also seen that propagation distance of the PCAV beam keeping hollow profile in uniaxial crystals is larger than that in free space (see b2 of Fig. 1 and b2 of Fig. 2). As shifted distance x₀ increases, beam gravity is further away from the beam centre, and the worse non-uniformity of laser beams is, however, the position of the intensity maximum is changeless.

Fig. 2

Spectral density distributions of a PCAV beam at several propagation distances for different shifted values

Figure 3 gives the spectral density distributions of a PCAV beam with M = N = 2 at several propagation distances for different values of e. The case of n_e = n_o (see the upper row of Fig. 3) represents the evolution properties of the spectral density distribution of the PCAV beam propagating in isotropic crystals. The condition of n_e ≠ n_o means the evolution properties of the PCAV beam propagating in anisotropic crystals. It is evident that from Fig. 3 the hollow profile increases with increase of topological charge. The intensity distribution will rotate anticlockwise 45°in isotropic crystals and 90° in anisotropic crystals of n_e/n_o = 1.2 with the increase of transmission distances. For the anisotropic crystals of n_e/n_o = 1.5, the intensity distribution will rotate clockwise during short propagation distance (see c1 and c2 of Fig. 3), and then rotate counterclockwise at far field. This physical reason for the inconsistent rotation between near and far field is that the strong anisotropic effect restrains the rotation properties of vortex beam and plays an leading role for the PCAV beam propagating in anisotropic crystals of n_e/n_o = 1.5. Because of the refractive index n_e > n_o, the beam spreads faster along the x direction than the y direction when the propagation distance increases. The propagation properties of a PCAV beam propagating through a negative crystal is shown in Figs.3 (d1)-(d4). It is obvious from Fig. 3 that for the case e < 1, i.e., negative crystal, the beam profile of a PCAV beam is elongated in the y direction; for the case e > 1, i.e., positive crystal, the beam profile of a PCAV beam is elongated in the x direction.

Fig. 3

Spectral density distributions of a PCAV beam at several propagation distances for different different values of the extraordinary and ordinary refractive indices

Next, let us turn to study the coherence properties of PCAV beam propagating in free space or inside uniaxial crystals orthogonal to the optical axis. Figure 4 gives the evolution of the modulus of the spectral degree of coherence of a PCAV beam propagating in free space at several propagation distances for different shifted values. One can find from Fig. 4 that profiles of |μ(ρ,–ρ, z)| in the initial source plane are all Gaussian distributions. The profiles of |μ(ρ,–ρ, z)| of a partially coherent symmetric vortex beam (see the upper row of Fig. 4), consisting of a concentric ring with a central bright spot during propagation, are much different from that of a PCAV beam with x₀ = 0.3w. The larger propagation distance, the bigger profiles of |μ(ρ,–ρ, z)|. When x₀ = 0.1w, the profile of |μ(ρ,–ρ, z)| of a PCAV beam is similar to that of a partially coherent symmetric vortex beam after certain propagation distance, however, the outer ring and the inner spot are incompletely separated at a short propagation distance. This is because, after a certain propagation distance, a PCAV beam will evolve into a symmetric Gaussian beam similar to the distribution of a partially coherent symmetric vortex beam. From the lower row of Fig. 4, we can find that the patterns of the spectral degree of coherence of a PCAV beam with longer shifted distance consist of a central bright spot with two dark areas and rotate anticlockwise during the propagation. This rotation phenomenon meets with the above results.

Fig. 4

Modulus of the spectral degree of coherence of a PCAV beam propagating in free space at several propagation distances for different shifted values

Figure 5 gives the modulus of the spectral degree of coherence of a PCAV beam propagating inside uniaxial crystals orthogonal to the optical axis at several propagation distances for different values of the extraordinary and ordinary refractive indices. Under the condition of n_e/n_o = 1 (see the upper row of Fig. 5), it represents the modulus of the spectral degree of coherence of the PCAV beam propagating in isotropic crystals. It is observed that evolution of the spectral degree of coherence of the PCAV beam propagating in isotropic crystals is similar to that in free space. As propagation distance increases, the patterns of |μ(ρ,–ρ, z)| of the PCAV beam propagating in anisotropic crystals will evolve into an elliptical ring with a central bright ellipse spot. The larger the n_e/n_o value, the more elliptical the beam shape.

Fig. 5

Modulus of the spectral degree of coherence of a PCAV beam at several propagation distances for different different values of the extraordinary and ordinary refractive indices

Finally, we turn to discuss the evolution properties of the effective beam width of the PCAV beams from Eq. (24). Figure 6 shows the dependence of the effective beam width of the PCAV beam propagating in uniaxial crystals orthogonal to the optical axis on propagation distance z for different values of n_e/n_o and coherence length. We can see from (a) and (b) of Fig. 4 that the effective beam width along x axis is the same as that along y axis for n_e/n_o = 1. With increasing the value of n_e/n_o, the effective beam width in the x-direction increases and the effective beam width in the y-direction decreases.The reason is that the anisotropic effect along x-direction is more stronger than that along y-direction. From (c) and (d) of Fig. 4, one can see that the effective beam width of the PCAV beam increases more rapidly during the propagation as the coherence length decreases, it is larger in x direction than in y-direction at a given propagation distance due to the anisotropic effect. This phenomenon is in line with the reported results [17, 26, 35].

Fig. 6

The dependence of the effective beam width of the PCAV beam propagating in uniaxial crystals orthogonal to the optical axis on propagation distance z for different values of n_e/n_o and coherence length

Conclusion

We have derived the analytical expressions for the cross-spectral density function of the PCAV beams propagating in uniaxial crystals orthogonal to the optical axis, and the simulation is done by considering the effects of crystal factor (the ratio of extraordinary and ordinary refractive indices) and source parameters (such as the coherence length, and topological charge), as well as the propagation distance in detail. It is found that the distribution of spectral density becomes from a decentered profile of source plane to a Gaussian profile at a far field, and with increasing the coherence length, the increasing distances are needed for the form of Gaussian profile. The PCAV beam will rotate π/2 along counterclockwise during the propagation. The obtained results show that the profiles of the PCAV beams can be modulated by the uniaxial crystals, which will be useful in optical trapping and nonlinear optics in which the special profile is required.