Propagation of vortex cosine-hyperbolic-Gaussian beams in uniaxial crystals orthogonal to the optical axis

Abstract

In this paper, we investigate theoretically the properties of a vortex cosine-hyperbolic-Gaussian beam (vChGB) propagating in uniaxial crystals orthogonal to the optical axis. Analytical expressions for the vChGB propagating through a uniaxial crystal orthogonal to the optical axis are derived. From the obtained formulas the evolution properties of the intensity and phase distributions of the output beam are analyzed with numerical examples. It is shown that a vChGB propagating in the uniaxial crystal keeps its initial profile nearly invariant for a small propagation distance, whereas, during the beam propagation the anisotropy of the uniaxial crystal influences strongly the beam properties. The output beam becomes astigmatic, and the intensity and phase distributions are dependent on the ratio of refractive indices of the crystal and the initial beam parameters. The present study may provide a convenient way to generate astigmatic vortex hollow beams.

1 Introduction

The propagation of laser beams in a uniaxial crystal has been investigated extensively in the last years due to their applications in the design of wave plates, polarizers, compensators, and optical modulation devices. The theoretical model for light beams propagating in uniaxial crystal orthogonal to the optical axis has firstly been proposed and developed by Ciattoni and coworkers (Ciattoni et al. 2001a, b; Cincotti et al. 2002; Ciattoni and Palma 2003). Since then, many studies on the propagation properties of coherent and partially coherent light beams in uniaxial crystals have been reported, including dark hollow beams (Deng et al. 2008; Liu and Zhou 2008; Li et al. 2019), flat-topped beams (Lü and Luo 2004; Liu et al. 2016a, b; Liu and Zhou 2010), higher-order cosh-Gaussian beams (Li et al. 2010), four-petal Gaussian vortex beams (Liu et al. 2015a, b), Lorentz and Lorentz-Gauss beams(Zhao and Cai 2010; Liu et al. 2017, 2019), Airy and Airy related beams (Deng and Deng 2016; Zheng et al. 2017; Li et al. 2017; zhou et al. 2019), Laguerre-Gaussian correlated Schell-model beams (Zhu et al. 2015), partially coherent multi-Gaussian Schell-model vortex beams (Liu et al. 2016b; Lu et al. 2016; Ma et al 2020a; Mao and Mei 2017), random electromagnetic multi-Gaussian Schell-model vortex beams (Ma et al 2020b), and hyperbolic sinusoidal Gaussian beams (Bayraktar 2021a, b).

On other hand, a new dark hollow beam called vortex cosine-hyperbolic-Gaussian beam (vChGB) has been recently introduced, and its propagation characteristics in different optical media have been reported (Hricha et al. 2020, 2021a, b, c, d; Lazrek et al. 2021a; Lazrek et al. 2022). From the previous works, it is found that the vChGB has a flexible shaped profile, which is assured by two control key parameters, namely the decentered parameter and the vortex charge number M. Indeed, by choosing appropriate values of the beam parameters the profile of a vChGB in the initial plane may be a hollow vortex Gaussian-like or a four-petal vortex Gaussian-like. The profile of the vChGB is preserved upon propagation in the near-field, and its stability range can be controlled by adjusting the parameters b and M. In the far-field, the vChGB evolves into a multi-lobe structure whose pattern is closely connected to the beam parameters. Such beam propagation properties may be beneficial to practical applications in optical trapping, micromanipulation, beam splitting, and optical communications.

To the best of our knowledge, no results have been reported up to now on the propagation of vChGBs in uniaxial crystals. The present paper is aimed at studying theoretically the paraxial propagation of a vChGB in uniaxial crystals orthogonal to the optical axis. The influences of the ratio of refractive index n_e/n_o of the uniaxial crystal and the initial beam parameters on the propagation characteristics of the output beam are illustrated graphically with numerical examples. The rest of the paper is organized as follows. In the forthcoming section, the propagation formula for a vChGB passing through a uniaxial crystal is derived by using the Huygens–Fresnel diffraction integral. In the third section, the influence of the ratio of refractive index n_e/n_o as well as the initial beam parameters such as the decentered parameter b and topological charge on the intensity and phase distributions of the output beam are analyzed with illustrative numerical examples. In Sect. 4, a summary of the main results concludes this paper.

2 Theory model for a vChGB propagating in a uniaxial crystal

For a coherent vChGB in a rectangular coordinates system, its electric field at the initial plane z = 0 is defined as (Hricha et al. 2020)

$$ E\left( {x_{0} ,y_{0} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega_{0} }}} \right)e^{{ - \left( {\frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)}} \left( {x_{0} + iy_{0} } \right)^{M} , $$

(1)

where $\left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)$ are the transverse Cartesian coordinates at the plane z = 0, and $\omega_{0}$ is the waist radius of the Gaussian part. b is the decentered parameter associated with the cosh part, and M is a positive integer that denotes the topological charge of the beam.

Let us assume that a vChGB linearly polarized is incident on a uniaxial crystal at the plane z = 0, and propagates along the z-axis that is orthogonal to the optical axis (see Fig. 1).

Fig. 1

Geometry for the propagation of a vChGB in a uniaxial crystal

In this frame of reference, the relative dielectric tensor of the uniaxial crystal can be expressed as (Ciattoni et al. 2001b)

$$ \varepsilon = \left( \begin{gathered} n_{e}^{2} \,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,\,\,n_{0}^{2} \,\,\,\,\,\,\,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,0\,\,\,\,\,\,\,\,\,\,\,\,n_{0}^{2} \hfill \\ \end{gathered} \right), $$

(2)

where $n_{0}$ and $n_{e}$ are the ordinary and extraordinary refractive indices of the uniaxial crystal. Within the approximation of paraxial propagation, the x- and y-components of the beam propagating in the uniaxial crystal at the output plane z obey the Huygens-Fresnel diffraction integral and can be expressed as (Ciattoni et al. 2001b; Collins 1970):

$$ E_{x} \left( {\vec{r},z} \right) = \frac{{kn_{0} }}{2\pi \,iz}\exp \left( {ikn_{e} z} \right)\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\exp \left\{ {\frac{ - k}{{2izn_{e} }}\left[ {n_{0}^{2} \left( {x - x_{0} } \right)^{2} + n_{e}^{2} \left( {y - y_{0} } \right)^{2} } \right]} \right\}} E_{x} \left( {\vec{r}_{0} ,0} \right)dx_{0} dy_{0} } $$

(3a)

$$ E_{y} \left( {\vec{r},z} \right) = \frac{{kn_{0} }}{2\pi \,iz}\exp \left( {ikn_{0} z} \right)\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {\exp \left\{ {\frac{{ - kn_{0} }}{2iz}\left[ {\left( {x - x_{0} } \right)^{2} + \left( {y - y_{0} } \right)^{2} } \right]} \right\}} E_{y} \left( {\vec{r}_{0} ,0} \right)dx_{0} dy_{0} } $$

(3b)

where $k = \frac{2\pi }{\lambda }$ is the wavenumber in a vacuum with λ is the wavelength; $\vec{r} = \left( {x,y} \right)$ and $\vec{r}_{0} = \left( {x_{0} ,y_{0} } \right)$ are the position vectors at the output and input planes, respectively. $E_{\alpha } \left( {\overrightarrow {{r_{0} }} ,0} \right)$ and $E_{\alpha } \left( {\overrightarrow {r} ,z} \right)$ (with α = x or y) are the electric fields at the input and output planes.

Because of the presence of both refractive indexes n₀ and n_e in the integrand function in Eq. (3a), the x-component of the field (i.e., $E_{x} \left( {\vec{r},z} \right)$) will spread along the x- and y-directions in an asymmetrical manner. In contrast, one finds from Eq. (3b) that the y-component of the field is identical to the Fresnel integral for the paraxial propagation in the isotropic medium. The spreading behavior of $E_{y} \left( {\vec{r},z} \right)$ is then similar to that of a vChGB propagating in free space (Hricha et al. 2020). For the sake of convenience, we will consider hereafter an initial x-polarized vChGB propagating in a uniaxial crystal orthogonal to the optical axis.

By substituting from Eq. (1) into Eq. (3a), and using the binomial formula (Gradshteyn and Ryzhik 1994)

$$ \left( {x{\kern 1pt} + {\kern 1pt} iy{\kern 1pt} } \right)^{M} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{M} {C_{l}^{M} } x^{l} \left( {iy} \right)^{{_{M - l} }} , $$

(4a)

with

$$ C_{l}^{M} = {\kern 1pt} \frac{M!}{{l!\left( {M - l} \right)!}}, $$

(4b)

then, recalling the integral formula (Belafhal et al. 2020)

$$ \int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} } dx = \sqrt {\frac{\pi }{p}} \,e^{{\frac{{q^{2} }}{p}}} \left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right), $$

(5)

and after tedious integral calculations, one can obtain

$$ \begin{aligned} E_{x} \left( {r,z} \right)& = \frac{{kn_{0} }}{8\pi \,iz}\sqrt {\frac{\pi }{{a_{x} }}} \sqrt {\frac{\pi }{{a_{y} }}} \exp \left( {ikn_{e} z} \right)\exp \left( { - \frac{{kn_{0}^{2} }}{{2izn_{e} }}x^{2} - \frac{{kn_{e} }}{2iz}y^{2} } \right)\sum\limits_{l = 0}^{M} {} C_{l}^{M} \left( i \right)^{M - l} \hfill \\ & \times \left( {\frac{1}{{2i\sqrt {a_{x} } }}} \right)^{l} \left[ {\exp \left\{ {\frac{{\left( {q_{x}^{ + } } \right)^{2} }}{{a_{x} }}} \right\}H_{l} \left( {\frac{{iq_{x}^{ + } }}{{\sqrt {a_{x} } }}} \right) + \exp \left\{ {\frac{{\left( {q_{x}^{ - } } \right)^{2} }}{{a_{x} }}} \right\}H_{l} \left( {\frac{{iq_{x}^{ - } }}{{\sqrt {a_{x} } }}} \right)} \right] \hfill \\ & \times \left( {\frac{1}{{2i\sqrt {a_{y} } }}} \right)^{M - l} \left[ {\exp \left\{ {\frac{{\left( {q_{y}^{ + } } \right)^{2} }}{{a_{y} }}} \right\}H_{M - l} \left( {\frac{{iq_{y}^{ + } }}{{\sqrt {a_{y} } }}} \right) + \exp \left\{ {\frac{{\left( {q_{y}^{ - } } \right)^{2} }}{{a_{y} }}} \right\}H_{M - l} \left( {\frac{{iq_{y}^{ - } }}{{\sqrt {a_{y} } }}} \right),} \right] \hfill \\ \end{aligned} $$

(6)

with

$$ a_{x} = \frac{1}{{\omega_{0}^{2} }} + \frac{{kn_{0}^{2} }}{{2izn_{e} }}, $$

(7a)

$$ q_{x}^{ \pm } = \frac{{kn_{0}^{2} x}}{{2izn_{e} }} \pm \frac{b}{{2\omega_{0} }}, $$

(7b)

$$ a_{y} = \frac{1}{{\omega_{0}^{2} }} + \frac{{kn_{e} }}{2iz}, $$

(7c)

and

$$ q_{y}^{ \pm } = \frac{{kn_{e} y}}{2iz} \pm \frac{b}{{2\omega_{0} }}. $$

(7d)

Equation (6) is the analytical expression of a vChGB propagating in uniaxial crystals orthogonal to the optical axis. It indicates that the output beam depends explicitly on the crystal refractive indices (n_o, n_e) and the initial beam parameters (b, M, $\omega_{0}$), and this will provide a convenient way for studying the evolution properties of the vChGB in uniaxial crystals.

From the main formula above, one can distinguish the following special cases:

• When b = 0, Eq. (6) will give the propagation formula of a hollow Gaussian vortex beam in uniaxial crystals, which can be expressed as

  $$ \begin{aligned} E_{x} \left( {r,z} \right) &= \frac{{kn_{0} }}{8\pi \,iz}\sqrt {\frac{\pi }{{a_{x} }}} \sqrt {\frac{\pi }{{a_{y} }}} \exp \left( {ikn_{e} z} \right)\exp \left( { - \frac{{kn_{0}^{2} }}{{2izn_{e} }}x^{2} - \frac{{kn_{e} }}{2iz}y^{2} } \right)\sum\limits_{l = 0}^{M} {} C_{l}^{M} \left( i \right)^{M - l} \hfill \\ & \times \left( {\frac{1}{{i\sqrt {a_{x} } }}} \right)^{l} \left( {\frac{1}{{i\sqrt {a_{y} } }}} \right)^{M - l} \left[ {\exp \left\{ {\frac{{\left( {q_{x} } \right)^{2} }}{{a_{x} }}} \right\}H_{l} \left( {\frac{{i\left( {q_{x} } \right)}}{{\sqrt {a_{x} } }}} \right)} \right]\left[ {\exp \left\{ {\frac{{\left( {\left( {q_{y} } \right)} \right)^{2} }}{{a_{y} }}} \right\}H_{M - l} \left( {\frac{{i\left( {q_{y} } \right)}}{{\sqrt {a_{y} } }}} \right)} \right], \hfill \\ \end{aligned} $$

  (8)

  where

  $$ q_{x} = \frac{{kn_{0}^{2} x}}{{2izn_{e} }}, $$

  (9a)

  and

  $$ q_{y} = \frac{{kn_{e} y}}{2iz}. $$

  (9b)

• When M = 0 (i.e., in the absence of the vortex charge), Eq. (6) will reduce to

  $$ \begin{aligned} E_{x} \left( {r,z} \right) &= \frac{{kn_{0} }}{8\pi \,iz}\sqrt {\frac{\pi }{{a_{x} }}} \sqrt {\frac{\pi }{{a_{y} }}} \exp \left( {ikn_{e} z} \right)\exp \left( { - \frac{{kn_{0}^{2} }}{{2izn_{e} }}x^{2} - \frac{{kn_{e} }}{2iz}y^{2} } \right) \hfill \\ & \times \left[ {\exp \left\{ {\frac{{\left( {q_{x}^{ + } } \right)^{2} }}{{a_{x} }}} \right\} + \exp \left\{ {\frac{{\left( {q_{x}^{ - } } \right)^{2} }}{{a_{x} }}} \right\}} \right] \times \left[ {\exp \left\{ {\frac{{\left( {q_{y}^{ + } } \right)^{2} }}{{a_{y} }}} \right\} + \exp \left\{ {\frac{{\left( {q_{y}^{ - } } \right)^{2} }}{{a_{y} }}} \right\}} \right], \hfill \\ \end{aligned} $$

  (10)

  which describes the electric field of a cosine-hyperbolic-Gaussian beam (ChGB) propagating in a uniaxial crystal.

• Under the condition of n_o = n_e = 1, Eq. (6) will describe a vChGB propagating in free space, and the obtained result will be consistent with Ref. (Hricha et al. 2020).

3 Numerical examples and analysis

In this section, the intensity and phase distributions of a vChGB propagating in uniaxial crystals orthogonal to the optical axis are analyzed numerically by calculating Eq. (6). As was reported in the introduction part, the profile of initial vChGBs depends crucially on the value of the parameter b, i.e., the initial beam profile is hollow vortex Gaussian-like when the value of b is small (saying typically b is 0.1), and it is four-petal vortex Gaussian-like when the value of b is large (saying b = 4), so, in the following numerical calculations, we will consider vChGBs with small b and large b configurations. The calculation parameters are chosen as $\omega_{0} = 5\mu m$$\lambda = 632nm$, n_o = 2.616 (for a rutile crystal), and $z_{R} = \frac{{n_{o} \pi \omega_{0}^{2} }}{\lambda } = 324.58\mu m$.

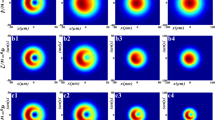
Figure 2 displays the 3D-normalized intensity distribution and the corresponding contour graph for an incident vChGB propagating in uniaxial crystals at several propagation distances, with M = 1 and ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{o} }}} \right. \kern-\nulldelimiterspace} {n_{o} }}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1.1$. It can be seen that the beam can keep its initial profile almost invariant at short propagation distances.

Fig. 2

3D-Normalized intensity and the corresponding contour graph for circular vChGB propagating in uniaxial crystals with ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.1$, M = 1. a, e $z = 0$, b, f $z = 0.1\,z_{R}$, c, g $z = z_{R}$, d, h $z = 5\,z_{R}$

For the small b configuration, the beam at a small propagation distance has a dark central region surrounded by a circular bright ring spot, and with increasing further the propagation distance, the bright spot loses its initial circular symmetry and evolves into an elliptical shape (sees Fig. 2b–d). For the incident beam with large b, one can see that the four beam lobes gradually overlap as the propagation distance increases, and in the far-field, the beam evolves into a hollow multi-lobes pattern with several faint lobes around four main petals (see Fig. 2g–h). By comparing the beam behavior in the uniaxial crystal with the one in free space, one can easily see that in the far-field the profile of the beam becomes elliptical due to the crystal anisotropy.

For further analyzing the crystal anisotropy on the propagation properties of a vChGB, we have depicted in Fig. 3 the intensity distribution of the output beam under a larger index ratio ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{o} }}} \right. \kern-\nulldelimiterspace} {n_{o} }}{\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} 1.5$.

Fig. 3

3D-Normalized intensity and corresponding contour graph for circular vChGB propagating in uniaxial crystals with ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.5$, M = 1. a, e $z = 0$, b, f $z = 0.1\,z_{R}$, c, g $z = z_{R}$, d, f $z = 5\,z_{R}$

From comparing Figs. 2 and 3, one can find that for larger value of ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{o} }}} \right. \kern-\nulldelimiterspace} {n_{o} }}$ the beam propagating in the uniaxial crystal will evolve into elliptical symmetry, and spread faster along the x-axis than the y-axis. In addition, we depicted in Figs. 4 and 5 the beam intensity (in the x- and y- direction) in the near field ($z = z_{R}$) and far-field ($z = 5\,z_{R}$). These figures show that the central lobe size of the intensity distribution along the x-direction increases with the increase ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{o} }}} \right. \kern-\nulldelimiterspace} {n_{o} }}$, this means that the beam spreads faster along the x-axis than on the y-axis. The central lobe behavior in the y-direction is the opposite of that in the x-direction. In addition, one can observe that the ring is deformed at a short propagation distance ($z < z_{R}$) but can regain its initial shape during propagation ($z > z_{R}$).

Fig. 4

Cross sections (y = 0) of normalized intensity of a vChGB propagating in uniaxial crystal for different values of n_e/n_0, with M = 1 a–c $z = z_{R}$, b–d $z = 5\,z_{R}$

Fig. 5

Cross sections (x = 0) of normalized intensity of a vChGB propagating in uniaxial crystal for different values of n_e/n_0, with M = 1 a–c $z = z_{R}$, b–d $z = 5z_{R}$

Figures 6 and 7 show the contour graphs of intensity evolution for a vChGB propagating in the uniaxial crystal, with different values of the topological charge M. It is seen from the plots of these figures that for an incident beam with a small b configuration, the beam shape remains the same and its central dark region becomes larger as M is increased. For a vChGB with large b, it is seen that the structure of intensity distribution in the far-field depends strongly on the value of M.

Fig. 6

The contour graphs of normalized intensity for circular vChGB propagating in uniaxial crystals for different values of M, with b = 0.1 ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.5$

Fig. 7

The contour graphs of normalized intensity for circular vChGB propagating in uniaxial crystals for different values of M, with b = 4 and ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.5$

Figures 8 and 9 illustrate the phase distribution of the output beams given in Figs. 5 and 6. One can see that the phase distribution has a clockwise spiral pattern, and the number of phase spirals remains unchanged upon propagation.

Fig. 8

The phase of vChGB propagating in uniaxial crystals for different values M with b = 0.1 and ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.5$

Fig. 9

The phase of vChGB propagating in uniaxial crystals for different values of M with b = 4 and ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{0} }}} \right. \kern-\nulldelimiterspace} {n_{0} }} = 1.5$

When the propagation distance increases, the phase pattern becomes more asymmetrical as ${{n_{e} } \mathord{\left/ {\vphantom {{n_{e} } {n_{o} }}} \right. \kern-\nulldelimiterspace} {n_{o} }}{\kern 1pt}$ it increased. Furthermore, one can notice that for large b, the phase shape is almost circular at short propagation distances but when the propagation distance increases the phase shape changes. The above results indicate that the output beam profile of vChGB in the uniaxial crystal can be controlled by adjusting properly the ratio of refractive index n_o/n_e, this provides a convenient way to generate an astigmatic vChGB.

4 Conclusion

In this study, the propagation equation for a vChGB in a uniaxial crystal orthogonal to the optical axis is derived based on the Huygens–Fresnel integral. The evolution properties of both intensity and phase distributions of the beam in a uniaxial crystal are analyzed numerically as a function of the uniaxial crystal factor and initial beam parameters. It is found that the beam loses its initial symmetry and evolves from a circular shape into an elliptical shape in the far field due to the influence of crystal anisotropy. In addition, it is shown that the incident beam parameters affect the profile of the output field. Our results have shown that the beam profile of a vChGB in a uniaxial crystal can be controlled by the ratio of refractive index n_o/n_e and the incident beam parameters. This study may provide a convenient way to generate astigmatic vortex hollow beams with variable profiles.