The Derivative Nonlinear Schrödinger Equation with Zero/Nonzero Boundary Conditions: Inverse Scattering Transforms and N-Double-Pole Solutions

Abstract

In this paper, we report a rigorous theory of the inverse scattering transforms (ISTs) for the derivative nonlinear Schrödinger (DNLS) equation with both zero boundary conditions (ZBCs) and nonzero boundary conditions (NZBCs) at infinity and double zeros of analytical scattering coefficients. The scattering theories for both ZBCs and NZBCs are addressed. The direct scattering problem establishes the analyticity, symmetries, and asymptotic behaviors of the Jost solutions and scattering matrix, and properties of discrete spectra. The inverse scattering problems are formulated and solved with the aid of the matrix Riemann–Hilbert problems, and the reconstruction formulae, trace formulae and theta conditions are also posed. In particular, the IST with NZBCs at infinity is proposed by a suitable uniformization variable, which allows the scattering problem to be solved on a standard complex plane instead of a two-sheeted Riemann surface. The reflectionless potentials with double poles for the ZBCs and NZBCs are both carried out explicitly by means of determinants. Some representative semi-rational bright–bright soliton, dark–bright soliton, and breather–breather solutions are examined in detail. These results and idea can also be extended to other types of DNLS equations such as the Chen–Lee–Liu-type DNLS equation, Gerdjikov–Ivanov-type DNLS equation, and Kundu-type DNLS equation and will be useful to further explore and apply the related nonlinear wave phenomena.

1 Introduction

As a fundamental and important nonlinear physical model, the derivative nonlinear Schrödinger (DNLS) equation (alias the DNLSI)

$$\begin{aligned} \mathrm {i}q_t+q_{xx}+\mathrm {i}\sigma (\left| q\right| ^2q)_x=0, \quad \sigma =\pm 1, \end{aligned}$$

(1)

where the subscripts denote the partial derivatives, admits some physical applications, such as the wave propagation of circular polarized nonlinear Alfvén waves in plasmas (Rogister 1971; Mjølhus 1976; Mio et al. 1976; Mjølhus 1989; Mjølhus and Hada 1997), weak nonlinear electromagnetic waves in ferromagnetic (Nakata 1991), antiferromagnetic (Daniel and Veerakumar 2002) or dielectric (Nakata et al. 1993) systems under external magnetic fields. Moreover, Eq. (1) was shown by Kaup and Newell (1978) to be completely integrable. The parameter $\sigma$ stands for the relative magnitude of the derivative nonlinearity term. Without loss of generality, one can take $\sigma =-1$ (since the case $\sigma =1$ can be transformed into $\sigma =-1$ by means of $x\rightarrow -x$). Eq. (1) can be transformed into the modified NLS equation (also called generalized DNLS equation or NLS-KN equation) (Wadati et al. 1979)

$$\begin{aligned} \mathrm {i}u_{\tau }+u_{\xi \xi }+g_1|u|^2u+\mathrm {i}g_2(|u|^2u)_{\xi }=0, \quad g_{1,2}\in {\mathbb {R}},\quad g_2\ne 0, \end{aligned}$$

(2)

in terms of the gauge transform (Ichikawa et al. 1980)

$$\begin{aligned} q(x, t)=u(\tau , \xi )\mathrm {e}^{-\mathrm {i}(kx+k^2t)}, \quad x=\frac{g_2}{\sigma }\xi -\frac{2g_1}{\sigma }\tau ,\quad t=\frac{g_2^2}{\sigma ^2}\tau ,\quad k=\frac{\sigma g_1}{g_2^2}, \end{aligned}$$

(3)

where the Kerr nonlinear coefficient $\lambda$ and derivative nonlinear coefficient $\gamma$ both depend on nonlinear refractive index $n_2$. The modified NLS equation (2) describes transmission of femtosecond pulses in optical fibers (Tzoar and Jain 1981; Anderson and Lisak 1983; Ohkuma et al. 1987).

To conveniently discuss the connections between Eq. (2) and other types of DNLS equations, one can take $g_1=\pm \beta ,\, g_2=\pm \alpha$ with $\alpha >0,\,\beta \ge 0$ such that Eq. (2) can be rewritten as

$$\begin{aligned} \mathrm {i}u_{\tau }+u_{\xi \xi }\pm \beta |u|^2u\pm \mathrm {i}\alpha (|u|^2u)_{\xi }=0. \end{aligned}$$

(4)

Inspiring by the idea of the gauge transforms connecting various (integrable) nonlinear wave equations (see, e.g., Lamb 1976; Lakshmanan 1977; Wadati and Sogo 1983 and references therein), Kundu (1984) changed the generalized DNLS Eq. (4) to the Kundu-type DNLS equation

$$\begin{aligned} \mathrm {i}U_{\tau }+U_{\xi \xi }\pm \beta |U|^2U\pm \mathrm {i}\alpha (|U|^2U)_{\xi }+\gamma (4\gamma +\beta )|U|^4U\pm 4\mathrm {i}\gamma (|U|^2)_{\xi }U=0,\nonumber \\ \end{aligned}$$

(5)

by means of the U(1)-gauge transform $U(\xi ,\tau )=u(\xi ,\tau )e^{2\mathrm {i}\vartheta (\xi ,\tau )}$ with $\vartheta (\xi ,\tau )$ satisfying

$$\begin{aligned} \vartheta _{\xi }=\mp \gamma |u|^2, \quad \vartheta _{\tau }=\pm \mathrm {i}\gamma (uu_{\xi }^*-u^*u_{\xi })+\frac{3}{2}\alpha \gamma |u|^4, \quad \gamma \in {\mathbb {R}}, \end{aligned}$$

(6)

which are called the ‘particle’ and ‘current’ densities of Eq. (4), respectively, and consistent with the condition $\vartheta _{\xi \tau }=\vartheta _{\tau \xi }$ due to the modified NLS Eq. (4) (Kundu 1984, 1987). The Kundu-type DNLS equation (5) has these special forms for the distinguish parameters:

• For $\alpha =-4\gamma ,\,\, \beta =0$, it reduces to the Chen–Lee–Liu-I (CLL-I) DNLS equation (alias DNLSII) (Chen et al. 1979)

  $$\begin{aligned} \mathrm {i}U_{\tau }+U_{\xi \xi }+\mathrm {i}\alpha |U|^2U_{\xi }=0. \end{aligned}$$

  (7)

• For $\alpha =-4\gamma ,\,\, \beta \ne 0$, it is the Chen–Lee–Liu-II (CLL-II) DNLS equation (Kundu 1984)

  $$\begin{aligned} \mathrm {i}U_{\tau }+U_{\xi \xi }\pm \beta |U|^2U+\mathrm {i}\alpha |U|^2U_{\xi }=0. \end{aligned}$$

  (8)

• For $\alpha =-2\gamma ,\, \, \beta =0$, it becomes the Gerdjikov–Ivanov-I (GI-I) DNLS equation (alias DNLSIII) (Gerdjikov and Ivanov 1983a)

  $$\begin{aligned} \mathrm {i}U_{\tau }+U_{\xi \xi }+\frac{1}{2}\alpha ^2|U|^4U\mp \mathrm {i}\alpha U^2U^*_{\xi }=0. \end{aligned}$$

  (9)

• For $\alpha =-2\gamma ,\,\, \beta \ne 0$, it becomes the Gerdjikov–Ivanov-II (GI-II) DNLS equation (Gerdjikov and Ivanov 1983b)

  $$\begin{aligned} \mathrm {i}U_{\tau }+U_{\xi \xi }\pm \beta |U|^2U+\frac{1}{2}\alpha ^2|U|^4U\mp \mathrm {i}\alpha U^2U^*_{\xi }=0. \end{aligned}$$

  (10)

• For $\gamma =0$, it reduces to the modified NLS (or generalized DNLS) equation (4) (Wadati et al. 1979).

• For $\alpha \beta \ne 0$, it can reduce to the Painlevé integrable combination of the CLL-I equation and GI-I equation (Clarkson and Cosgrove 1987)

  $$\begin{aligned} \mathrm {i}W_{\tau }+W_{\zeta \zeta }+(\gamma _0-1)(\gamma _0-2)|W|^4W\pm 2\mathrm {i}\gamma _0 |W|^2W_{\zeta }\pm 2\mathrm {i}(\gamma _0-1)W^2W_{\zeta }^*=0\nonumber \\ \end{aligned}$$

  (11)

  by the gauge transform (Kakei et al. 1995)

  $$\begin{aligned}&W(\zeta ,\tau )=U(\xi ,\tau )\sqrt{\frac{\alpha }{2}}\exp \left[ -\frac{\mathrm {i}\beta }{\alpha }(\xi +\beta /\alpha \tau )\right] ,\nonumber \\&\zeta =\xi +\frac{2\beta }{\alpha }\tau , \quad \gamma _0=\frac{4\gamma }{\alpha }+2. \end{aligned}$$

  (12)

Remark 1

• (i) Wadati and Sogo (1983) even established a gauge transform between the DNLSI (1) and DNLSII (7);

• (ii) If one takes $U(\xi ,\tau )={\hat{U}}({\hat{\xi }},\tau ),\,\, {\hat{\xi }}=\xi$ in Eq. (8), then the Chen–Lee–Liu-II DNLS equation (8) can reduce to the Chen–Lee–Liu-II DNLS equation (7) in terms of the gauge transform

  $$\begin{aligned} U(\xi ,\tau )={\hat{U}}({\hat{\xi }}, \tau )\exp \left( \mp \frac{\mathrm {i}\beta }{\alpha }\xi -\frac{\mathrm {i}\beta ^2}{\alpha ^2}\tau \right) ,\quad {\hat{\xi }}=\xi \pm \frac{2\beta }{\alpha }\tau . \end{aligned}$$

  (13)

• (iii) If one chooses $U(\xi ,\tau )={\hat{U}}({\hat{\xi }},\tau ),\,\, {\hat{\xi }}=\xi$ in Eq. (10), then the Gerdjikov–Ivanov-II DNLS equation (10) can reduce to the Gerdjikov–Ivanov-II DNLS equation (9) in terms of the gauge transform

  $$\begin{aligned} U(\xi ,\tau )={\hat{U}}({\hat{\xi }}, \tau )\exp \left( -\frac{\mathrm {i}\beta }{\alpha }\xi -\frac{\mathrm {i}\beta ^2}{\alpha ^2}\tau \right) ,\quad {\hat{\xi }}=\xi +\frac{2\beta }{\alpha }\tau . \end{aligned}$$

  (14)

• (iv) Since there are equivalent relations: DNLSI (1) $\rightleftharpoons$ modified NLS Eq. (2) (or Eq. (4)) $\rightleftharpoons$ the Kundu Eq. (5) under some gauge transforms, and the Kundu Eq. (5) can reduce to other many types of DNLS equations containing the DNLSII (7) and DNLSIII (9), that is, all aforementioned other types of the DNLS equations can be transformed into the DNLSI (1), thus, one only needs to study the properties of the DNLSI (1), and corresponding ones of other types of DNLS equations can be found via some transforms.

The solutions of nonlinear wave equations with ZBCs and NZBCs are always physically interesting subjects. The inverse scattering transform (IST) due to Gardner et al. (1967) provides a powerful approach to discover solutions and properties of some integrable nonlinear partial differential equations with initial value problems. The IST for the DNLS equation (1) with ZBCs was studied to find its one-soliton solution (Kaup and Newell 1978) and N-soliton solutions (Zhou and Huang 2007). The ISTs of the DNLS equation (1) with NZBCs at infinity were also developed (Kawata and Inoue 1978; Chen and Lam 2004; Chen et al. 2006; Lashkin 2007; Zhou 2012). The long-time leading-order asymptotics of Eqs. (1) and (2) were studied in Kitaev and Vartanian (1999); Xu et al. (2013) by the Deift–Zhou method (Deift and Zhou 1993). Recently, the global existence was shown for the DNLS equation (1) via the IST (Liu et al. 2016). Besides, the modified NLS equation (2) with NZBCs was studied (Kawata et al. 1980). However, to the best of our knowledge, these IST works on the DNLS equation (1) only focus on the case that all discrete spectra are simple. A natural problem is whether the explicit double-pole solutions can be found for the DNSL equation (1) with ZBCs/NZBCs by the approximate ISTs based on the matrix Riemann–Hilbert problems (Prinari et al. 2006; Demontis et al. 2013, 2014; Biondini and Kovačič 2014; Prinari 2015; Pichler and Biondini 2017).

In this paper, we present the ISTs of the DNLS equation (1) with ZBCs/NZBCs in terms of the matrix Riemann–Hilbert problems (RHPs), and their double-pole solutions by solving the corresponding RHPs. It should pointed out that the DNLS equation (1) is associated with the modified Zakharov–Shabat eigenvalue problem (Kaup and Newell 1978), not the usual Zakharov–Shabat eigenvalue problem related to the NLS-type equations (Shabat and Zakharov 1972; Ablowitz et al. 1973; Prinari et al. 2006; Demontis et al. 2013, 2014; Biondini and Kovačič 2014; Prinari 2015; Pichler and Biondini 2017; Zhang and Yan 2020a, b) such that the discrete spectrum and solving Riemann–Hilbert problems are more complicated.

The DNLS equation (1) is completely integrable and associated with the following modified Zakharov–Shabat eigenvalue problem (Kaup and Newell 1978):

$$\begin{aligned} \varPhi _x&=X\varPhi , \quad X=X(x,t; k)=k(\mathrm {i}k\sigma _3+Q), \end{aligned}$$

(15)

$$\begin{aligned} \varPhi _t&=T\varPhi , \quad \,\,T=T(x,t; k)=-\left( 2k^2+Q^2\right) X-\mathrm {i}kQ_x\sigma _3, \end{aligned}$$

(16)

that is, Eq. (1) is as the compatibility condition (or zero-curvature condition) $X_t-T_x+[X, T]=0$ of system (15, 16), where $\psi =\psi (x,t; k)$ is a 2$\times$2 matrix-valued eigenfunction, $k\in {\mathbb {C}}$ is a spectral parameter, the potential matrix $Q=Q(x,t)$ is written as

$$\begin{aligned} Q(x,t)=\begin{bmatrix} 0&{} q(x,t) \\ \sigma q^*(x,t)&{}0 \end{bmatrix}, \end{aligned}$$

(17)

the asterisk $(*)$ denotes the complex conjugate, and $\sigma _3$ is one of the Pauli’s spin matrices given by

$$\begin{aligned} \sigma _1=\begin{bmatrix} 0&{}1 \\ 1&{}0 \end{bmatrix},\qquad \sigma _2=\begin{bmatrix} 0&{}-\mathrm {i} \\ \mathrm {i}&{}0 \end{bmatrix},\qquad \sigma _3=\begin{bmatrix} 1&{}0 \\ 0&{}-1 \end{bmatrix}. \end{aligned}$$

(18)

The rest of this paper is arranged as follows. In Sec. 2, the IST for the DNLS equation (1) with ZBCs at infinity is introduced and solved for the double zeros of analytically scattering coefficients by means of the matrix Riemann–Hilbert problem. As a consequence, we present a formula of the explicit double-pole N-soliton solutions. In Sec. 3, we give a detailed theory of the IST for the DNLS equation (1) with NZBCs at infinity and the double zeros of analytically scattering coefficients, which is more complicated than the case of ZBCs since more symmetries and a two-sheeted Riemann surface are required. As a result, we present an explicit expression for the double-pole N-solitons for the case of NZBCs. Particularly, we discuss the special double-pole solitons. Finally, some conclusions and discussions are carried out in Sec. 4.

2 The IST with ZBCs and Double Poles

In this section, we will seek the solution q(x, t) for the DNLS equation (1) with $\sigma =-1$ (without loss of generality) and ZBCs at infinity given by

$$\begin{aligned} \lim _{x\rightarrow \pm \infty }q(x, t)=0. \end{aligned}$$

(19)

The IST for DNLS equation (1) with ZBCs (19) was first presented by Kaup and Newell (1978), where the simple poles were required. In what follows, we will further present the IST and double-pole solitons for Eq. (1) with ZBCs by solving a matrix Riemann–Hilbert problem.

2.1 The Direct Scattering with ZBCs

2.1.1 Jost Solutions, Analyticity, and Continuity

Considering the asymptotic scattering problem ($x\rightarrow \pm \infty$) of the modified Zakharov–Shabat eigenvalue problem (15, 16)

$$\begin{aligned} \varPhi _x=X_0 \varPhi , \quad \varPhi _t=T_0\varPhi , \end{aligned}$$

(20)

where $X_0=\mathrm {i}k^2\sigma _3$ and $T_0=-2\mathrm {i}k^4\sigma _3=-2k^2X_0$, one can find that the fundamental matrix solution $\varPhi ^{\mathrm {bg}}(x, t; k)$ of system (20) as

$$\begin{aligned} \varPhi ^{\mathrm {bg}}(x, t; k)=\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}, \quad \theta (x, t; k)=k^2(x-2k^2 t). \end{aligned}$$

Let $\Sigma :={\mathbb {R}}\cup \mathrm {i}{\mathbb {R}}$. Then, one can seek for the Jost solutions $\varPhi _{\pm }(x, t; k)$ such that

$$\begin{aligned} \varPhi _{\pm }(x, t; k)=\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}+o\left( 1\right) , \quad k\in \Sigma , \quad \mathrm {as} \quad x\rightarrow \pm \infty . \end{aligned}$$

(21)

Consider the modified Jost solutions $\mu _{\pm }(x, t; k)$ in the form

$$\begin{aligned} \mu _{\pm }(x, t; k)=\varPhi _{\pm }(x, t; k)\,\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}, \end{aligned}$$

(22)

which leads to $\mu _{\pm }(x, t; k)\rightarrow I$ as $x\rightarrow \pm \infty$. Then, we know that $\mu _{\pm }(x,t;k)$ satisfy the Volterra integral equations

$$\begin{aligned} \mu _{\pm }(x, t; k)=I+k\int _{\pm \infty }^x \mathrm {e}^{\mathrm {i}k^2(x-y){{\widehat{\sigma }}}_3}\left( Q(y, t)\,\mu _{\pm }(y, t; k)\right) \,\mathrm {d}y, \end{aligned}$$

(23)

where $\mathrm {e}^{\alpha {{\widehat{\sigma }}}_3}A:=\mathrm {e}^{\alpha \sigma _3}A\mathrm {e}^{-\alpha \sigma _3}$ with A being a $2\times 2$ matrix. The Volterra integral equation (23) differs from one for the NLS equation with ZBCs related to the Zakharov–Shabat eigenvalue problem.

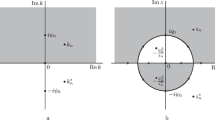
Let $D^{\pm }:=\left\{ k\in {\mathbb {C}}\,|\,\pm \mathrm {Re}(k)\mathrm {Im}(k)>0\right\}$ (see Fig. 1). One has the following Proposition.

Fig. 1

Complex k-plane. Region $D^+$ (grey region), region $D^-$ (white region), discrete spectrum, and orientation of the contours for the matrix Riemann–Hilbert problem in the inverse scattering problem

Proposition 1

Suppose that $q(x,t)\in L^1\left( {\mathbb {R}}\right)$ and $\varPhi _{\pm j}(x, t; k)$ is the jth column of $\varPhi _{\pm }(x, t; k)$. Then, the Jost solutions $\varPhi _\pm (x, t; k)$ possess the properties:

• Eq. (15) has the unique Jost solutions $\varPhi _{\pm }(x, t; k)$ satisfying (21) on $\Sigma$;

• The column vectors $\varPhi _{+1}(x, t; k)$ and $\varPhi _{-2}(x, t; k)$ can be analytically extended to $D^{+}$ and continuously extended to $D^{+}\cup \Sigma$;

• The column vectors $\varPhi _{-1}(x, t; k)$ and $\varPhi _{+2}(x, t; k)$ can be analytically extended to $D^{-}$ and continuously extended to $D^-\cup \Sigma$.

Proof

The proposition was reported in Refs. Kaup and Newell (1978), Zhou and Huang (2007). One can refer to Refs. Biondini and Kovačič (2014), Zhang and Yan (2020a) for more details. Similarly, the analyticity and continuity for the modified Jost solutions $\mu _{\pm }(x, t; k)$ can be simply shown from ones of $\varPhi _{\pm }(x, t; k)$ and the relation (22). $\square$

Proposition 2

The Jost solutions $\varPhi _{\pm }(x, t; k)$ satisfy both parts of the modified Zakharov–Shabat eigenvalue problem (15, 16) simultaneously.

Proof

This Proposition can be easily shown via a direct calculation. The Liouville’s formula leads to

$$\begin{aligned} \mathrm {det}\,\varPhi _{\pm }(x, t; k)=\lim _{x\rightarrow \pm \infty }\mathrm {det}\,\varPhi _{\pm }(x, t; k)=\lim _{x\rightarrow \pm \infty }\mathrm {det}\,\mu _{\pm }(x, t; k)=1, \end{aligned}$$

that is, $\varPhi _{\pm }(x, t; k)$ are the fundamental matrix solutions on $\Sigma$. By the compatibility condition, $X_t-T_x+[X, T]=0$, of the modified Zakharov–Shabat eigenvalue problem (15, 16), one can find that $\varPhi _{\pm t}(x, t; k)-T\varPhi _{\pm }(x, t; k)$ also solve the x-part (15). Thus, there exist the two matrices $G_{\pm }(t; k)$ such that

$$\begin{aligned} \varPhi _{\pm t}(x, t; k)-T\varPhi _{\pm }(x, t; k)=\varPhi _{\pm }(x, t; k)\,G_{\pm }(t; k),\quad \mathrm {as}\quad k\in \Sigma . \end{aligned}$$

Multiplying both sides by $\mathrm {e}^{-i\theta (x, t; k)\sigma _3}$ and letting $x\rightarrow \pm \infty$, one can find $G_{\pm }(t; k)=0$, that is, $\varPhi _{\pm }(x, t; k)$ also solve the t-part (16). This completes the proof. One can refer to Ref. Zhang and Yan (2020a) for the technique of the proof. $\square$

2.1.2 Scattering Matrix and Reflection Coefficients

As usual, since the fundamental matrix solutions $\varPhi _{\pm }(x, t; k)$ solve the both parts of the modified Zakharov–Shabat eigenvalue problem (15, 16), there is a constant scattering matrix $S(k)=\left( s_{ij}(k)\right) _{2\times 2}$ (not dependent on x and t) Ablowitz and Clarkson (1991) such that

$$\begin{aligned} \varPhi _+(x, t; k)=\varPhi _-(x, t; k)\,S(k), \quad k\in \Sigma , \end{aligned}$$

(24)

where $s_{ij}(k)$’s are called the scattering coefficients. It follows from Eq. (24) that $s_{ij}(k)'s$ have the Wronskian representations:

$$\begin{aligned} \begin{aligned} s_{11}(k)&={\mathrm{Wr}}(\varPhi _{+1}(x, t; k), \varPhi _{-2}(x, t; k)),\quad s_{22}(k)={\mathrm{Wr}}(\varPhi _{-1}(x, t; k), \varPhi _{+2}(x, t; k)),\\ s_{12}(k)&={\mathrm{Wr}}(\varPhi _{+2}(x, t; k), \varPhi _{-2}(x, t; k)),\quad s_{21}(k)={\mathrm{Wr}}(\varPhi _{-1}(x, t; k), \varPhi _{+1}(x, t; k)). \end{aligned}\nonumber \\ \end{aligned}$$

(25)

Proposition 3

Suppose that $q(x,t)\in L^1\left( {\mathbb {R}}\right)$. Then, $s_{11}(k)$ can be analytically extended to $D^+$ and continuously extended to $D^+\cup \Sigma$, while $s_{22}(k)$ can be analytically extended to $D^-$ and continuously extended to $D^-\cup \Sigma$. Moreover, both $s_{12}(k)$ and $s_{21}(k)$ are continuous in $\Sigma$.

Proof

The proposition can be directly deduced via Proposition 1 and the relations given by Eq. (25) between $s_{ij}(k)$ and $\varPhi _{\pm j}(x, t; k),\, i,j=1,2.$ $\square$

Note that one cannot rule out the possible presence of zeros for $s_{11}(k)$ and $s_{22}(k)$ along $\Sigma$. To study the Riemann–Hilbert problem in the inverse process, we focus on the potential without spectral singularities (Zhou 1989). As usual, the reflection coefficients $\rho (k)$ and ${{\tilde{\rho }}}(k)$ are defined in the form

$$\begin{aligned} \rho (k)=\frac{s_{21}(k)}{s_{11}(k)},\quad {{\tilde{\rho }}}(k)=\frac{s_{12}(k)}{s_{22}(k)}, \quad k\in \Sigma . \end{aligned}$$

(26)

2.1.3 Symmetry Properties

Proposition 4

(Symmetry reduction) X(x, t; k), T(x, t; k), Jost solutions, scattering matrix, and reflection coefficients have two symmetry reductions:

• The first symmetry reduction

  $$\begin{aligned} \begin{aligned} X(x, t; k)&=\sigma _2\,X(x, t; k^*)^*\sigma _2, \quad T(x, t; k)=\sigma _2\,T(x, t; k^*)^*\sigma _2, \\ \varPhi _{\pm }(x, t; k)&=\sigma _2\,\varPhi _{\pm }(x, t; k^*)^*\,\sigma _2,\quad S(k)=\sigma _2\,S(k^*)^*\,\sigma _2, \quad \rho (k)=-{{\tilde{\rho }}}(k^*)^*. \end{aligned}\nonumber \\ \end{aligned}$$

  (27)

• The second symmetry reduction

  $$\begin{aligned} \begin{aligned} X(x, t; k)&=\sigma _1X(x, t; -k^*)^*\sigma _1,\quad T(x, t; k)=\sigma _1T(x, t; -k^*)^*\sigma _1, \\ \varPhi _{\pm }(x, t; k)&=\sigma _1\,\varPhi _{\pm }(x, t; -k^*)^*\,\sigma _1, \quad S(k)=\sigma _1\,S(-k^*)^*\,\sigma _1, \quad \rho (k)={{\tilde{\rho }}}(-k^*)^*. \end{aligned}\nonumber \\ \end{aligned}$$

  (28)

Proof

The similar properties were reported in Refs. Kaup and Newell (1978), Zhou and Huang (2007). Besides, one can also refer to Refs. Demontis et al. (2013), Biondini and Kovačič (2014), Zhang and Yan (2020a) for more details. $\square$

2.1.4 Discrete Spectrum with Double Zeros

The discrete spectrum of the studied scattering problem is the set of all values $k\in {\mathbb {C}}\backslash \Sigma$ such that the scattering problem possesses eigenfunctions in $L^2({\mathbb {R}})$. As was shown in Biondini and Kovačič (2014), there are exactly the values of k in $D^+$ such that $s_{11}(k)=0$ and those values in $D^-$ such that $s_{22}(k)=0$. Differing from the previous results with simple poles (Kaup and Newell 1978; Zhou and Huang 2007), we here suppose that $s_{11}(k)$ has N double zeros in $K_0=\left\{ k\in {\mathbb {C}}:\mathrm {Re} \,k>0, \mathrm {Im}\, k>0\right\}$ denoted by $k_n$, $n=1, 2, \cdots , N$, that is, $s_{11}(k_n)=s'_{11}(k_n)=0$ and $s''_{11}(k_n)\not =0$. It follows from the symmetries of the scattering matrix that

$$\begin{aligned} \left\{ \begin{array}{l} s_{11}(k_n)=s_{11}(-k_n)=s_{22}(k_n^*)=s_{22}(-k_n^*)=0, \\ s'_{11}(k_n)=s'_{11}(-k_n)=s'_{22}(k_n^*)=s'_{22}(-k_n^*)=0. \end{array} \right. \end{aligned}$$

(29)

Therefore, the corresponding discrete spectrum is defined by the set

$$\begin{aligned} K=\left\{ k_n,\, k_n^*,\, -k_n^*, \,-k_n\right\} _{n=1}^{N}, \end{aligned}$$

(30)

whose distributions are shown in Fig. 1. For a given $k_0\in K\cap D^+$, it follows from the Wronskian representations (25) and $s_{11}(k_0)=0$ that $\varPhi _{+1}(x, t; k_0)$ and $\varPhi _{-2}(x, t; k_0)$ are linearly dependent. Similarly, for a given $k_0\in K\cap D^-$, it follows from the Wronskian representations (25) and $s_{22}(k_0)=0$ that $\varPhi _{+2}(x, t; k_0)$ and $\varPhi _{-1}(x, t; k_0)$ are linearly dependent. For convenience, we introduce the norming constant $b[k_0]$ such that

$$\begin{aligned} \begin{aligned} \varPhi _{+1}(x, t; k_0)&=b[k_0]{\varPhi _{-2}(x, t; k_0)},\quad k_0\in K\cap D^+, \\ \varPhi _{+2}(x, t; k_0)&=b[k_0]{\varPhi _{-1}(x, t; k_0)},\quad k_0\in K\cap D^-. \end{aligned} \end{aligned}$$

(31)

Given $k_0\in K\cap D^+$, it follows from the Wronskian representations (25) and $s'_{11}(k_0)=0$ that $\varPhi _{+1}'(x, t; k_0)-b[k_0]\,\varPhi _{-2}'(x, t; k_0)$ and $\varPhi _{-2}(x, t; k_0)$ are linearly dependent, where $\varPhi _j'(x, t; k)=\partial \varPhi _j(x, t; k)/(\partial k),\, j=+1,\,-2$. In the same manner, as $k_0\in K\cap D^-$, $\varPhi _{+2}'(x, t; k_0)-b[k_0]\,\varPhi _{-1}'(x, t; k_0)$ and $\varPhi _{-1}(x, t; k_0)$ are linearly dependent. For convenience, we define another norming constant $d[k_0]$ such that

$$\begin{aligned} \begin{aligned} {\varPhi _{+1}'(x, t; k_0)-b[k_0]\,\varPhi _{-2}'(x, t; k_0)}&=d[k_0]{\varPhi _{-2}(x, t; k_0)},\quad k_0\in K\cap D^+, \\ {\varPhi _{+2}'(x, t; k_0)-b[k_0]\,\varPhi _{-1}'(x, t; k_0)}&=d[k_0]{\varPhi _{-1}(x, t; k_0)},\quad k_0\in K\cap D^-. \end{aligned}\quad \end{aligned}$$

(32)

Moreover, let

$$\begin{aligned} \begin{aligned} A[k_0]&=\left\{ \begin{aligned} \frac{2\,b[k_0]}{s_{11}''(k_0)},\quad k_0\in K\cap D^+,\\ \frac{2\,b[k_0]}{s_{22}''(k_0)},\quad k_0\in K\cap D^-, \end{aligned}\right. \\ B[k_0]&=\left\{ \begin{aligned} \frac{d[k_0]}{b[k_0]}-\frac{s_{11}'''(k_0)}{3\,s_{11}''(k_0)},\quad k_0\in K\cap D^+,\\ \frac{d[k_0]}{b[k_0]}-\frac{s_{22}'''(k_0)}{3\,s_{22}''(k_0)},\quad k_0\in K\cap D^-. \end{aligned}\right. \end{aligned} \end{aligned}$$

(33)

Then, one has the compact form

$$\begin{aligned} \begin{aligned} \mathop {\mathrm {L_{-2}}}\limits _{k=k_0}\left[ \frac{\varPhi _{+1}(x, t; k)}{s_{11}(k)}\right]&=A[k_0]\,\varPhi _{-2}(x, t; k_0), \quad k_0\in K\cap D^+,\\ \mathop {\mathrm {L_{-2}}}\limits _{k=k_0}\left[ \frac{\varPhi _{+2}(x, t; k)}{s_{22}(k)}\right]&=A[k_0]\,\varPhi _{-1}(x, t; k_0), \quad k_0\in K\cap D^-,\\ \mathop {\mathrm {Res}}\limits _{k=k_0}\left[ \frac{\varPhi _{+1}(x, t; k)}{s_{11}(k)}\right]&=A[k_0]\left[ \varPhi _{-2}'(x, t; k_0)+B[k_0]\, \varPhi _{-2}(x, t; k_0)\right] , \quad k_0\in K\cap D^+,\\ \mathop {\mathrm {Res}}\limits _{k=k_0}\left[ \frac{\varPhi _{+2}(x, t; k)}{s_{22}(k)}\right]&=A[k_0]\left[ \varPhi _{-1}'(x, t; k_0)+B[k_0]\, \varPhi _{-1}(x, t; k_0)\right] , \quad k_0\in K\cap D^-, \end{aligned} \end{aligned}$$

(34)

where $\mathop {\mathrm {L_{-2}}}\limits _{k=k_0}\left[ \textit{\textbf{f}}(x,t; k)\right]$ denotes the coefficient of $O\left( \left( k-k_0\right) ^{-2}\right)$ term in the Laurent series expansion of $\textit{\textbf{f}}(x, t ; k)$ at $k=k_0$.

Proposition 5

Given $k_0\in K$, the two symmetry relations for $A[k_0]$ and $B[k_0]$ are given as follows:

• The first symmetry relation $A[k_0]=-A[k_0^*]^*, \quad B[k_0]=B[k_0^*]^*.$

• The second symmetry relation $A[k_0]=A[-k_0^*]^*, \quad B[k_0]=-B[-k_0^*]^*.$

Proof

One can use two symmetry reductions of X and T, and one can derive the two symmetries for the Jost solution and scattering matrix given in Proposition 4 and combine with the definitions of $A[k_0]$ and $B[k_0]$ given by Eq. (33). As a result, the symmetry relations in this Proposition can be verified. $\square$

By the two symmetry relations in Proposition 5, one obtains the constraints of discrete spectrum

$$\begin{aligned} A[k_n]= & {} A[-k_n^*]^*=-A[k_n^*]^*=-A[-k_n],\nonumber \\ B[k_n]= & {} -B[-k_n^*]^*=B[k_n^*]^*=-B[-k_n],\quad k_n\in K_0. \end{aligned}$$

(35)

2.1.5 Asymptotic Behaviors

To propose and solve the matrix Riemann–Hilbert problem presented in the inverse problem, one has to determine the asymptotic behaviors of the modified Jost solutions and scattering matrix as $k\rightarrow \infty$. The usual Wentzel–Kramers–Brillouin (WKB) expansion can be used to derive the asymptotic behaviors of the modified Jost solutions.

Proposition 6

The asymptotic behaviors of the modified Jost solutions are

$$\begin{aligned} \mu _{\pm }(x, t; k)=\mathrm {e}^{\mathrm {i}v_{\pm }(x, t)\sigma _3}+O\left( 1/k\right) , \quad \mathrm {as}\quad k\rightarrow \infty . \end{aligned}$$

(36)

Proof

We consider the expansions of the modified Jost solutions $\mu _{\pm }(x, t; k)$ as $k\rightarrow \infty$ as

$$\begin{aligned} \mu _{\pm }(x, t; k)=\sum _{j=0}^n\frac{\mu _{\pm }^{[j]}(x, t)}{k^j}+O\left( \frac{1}{k^{n+1}}\right) , \quad \mathrm {as}\quad k\rightarrow \infty , \end{aligned}$$

(37)

and substitute $\varPhi _{\pm }(x, t; k)=\mu _{\pm }(x, t; k)\,\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}$ with these expansions into Eq. (15). By matching the $O\left( k^2\right)$ term, one obtains the off-diagonal parts $\left( \mu _{\pm }^{[0]}(x, t)\right) ^{\mathrm {off}}=0$. It follows by matching the $O\left( k\right)$ term that $\left( \mu _{\pm }^{[1]}(x, t)\right) ^{\mathrm {off}}=\frac{\mathrm {i}}{2}\,\sigma _3Q(x, t)\,\mu _{\pm }^{[0]}(x, t)$. By matching the $O\left( 1\right)$ term, one yields that $\mu _{\pm }^{[0]}(x, t)=C^{\mathrm {diag}}\,\mathrm {e}^{\mathrm {i}v_{\pm }(x,t)\sigma _3}$, where

$$\begin{aligned} v_{\pm }(x, t)=\frac{1}{2}\int _{\pm \infty }^x\left| q(y, t)\right| ^2\,\mathrm {d}y. \end{aligned}$$

(38)

Combining with the asymptotic behaviors of the modified Jost solutions $\mu _{\pm }(x, t; k)$ as $x\rightarrow \pm \infty$, one deduces the asymptotic behavior as $k\rightarrow \infty$. $\square$

Proposition 7

The asymptotic behavior for the scattering matrix is given by

$$\begin{aligned} S(k)=\mathrm {e}^{-\mathrm {i}v\sigma _3}+O\left( 1/k\right) , \quad \mathrm {as}\quad k\rightarrow \infty , \end{aligned}$$

(39)

where the constant v reads as

$$\begin{aligned} v=\frac{1}{2}\int _{-\infty }^{+\infty }\left| q(y, t)\right| ^2\,\mathrm {d}y. \end{aligned}$$

(40)

Proof

From the definition or Wronskian presentations of scattering matrix given by Eq. (25) and the asymptotic behaviors of the modified Jost solutions given by Eq. (36), one can yield the asymptotic behaviors (39) of the scattering matrix.

Substituting $\varPhi _{\pm }(x, t; k)=\mu _{\pm }(x, t; k)\,\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}$ with these expansions into Eq. (16) and matching the $O\left( k^4\right)$, $O\left( k^3\right)$, $O\left( k^2\right)$, $O\left( k\right)$ and $O\left( 1\right)$ in order can yield $v_{t}=0$ as $x\rightarrow \mp \infty$. That is, v does not depend on the variable t. $\square$

2.2 Inverse Problem with ZBCs and Double Poles

2.2.1 The Matrix Riemann–Hilbert Pproblem

As usual (Ablowitz and Clarkson 1991), according to the relation (24) of two fundamental solutions $\varPhi _{\pm }(x, t; k)$, we can study the inverse problem via a Riemann–Hilbert problem. To pose and solve the Riemann–Hilbert problem conveniently, we define

$$\begin{aligned} \eta _n=\left\{ \begin{aligned}&k_n,&n&=1, 2, \cdots , N,\\ -{}&k_{n-N},&n&=N+1, N+2, \cdots , 2N. \end{aligned}\right. \end{aligned}$$

(41)

Then, a matrix Riemann–Hilbert problem is proposed as follows.

Proposition 8

Let the sectionally meromorphic matrix be

$$\begin{aligned} M(x, t; k)=\left\{ \begin{aligned} \left( \frac{\mu _{+1}(x, t; k)}{s_{11}(k)},\, \mu _{-2}(x, t; k)\right) ,\quad k\in D^+, \\ \left( \mu _{-1}(x, t; k),\, \frac{\mu _{+2}(x, t; k)}{s_{22}(k)}\right) , \quad k\in D^-, \end{aligned}\right. \end{aligned}$$

(42)

and

$$\begin{aligned} M^{\pm }(x, t; k)=\displaystyle \lim _{\begin{array}{c} k'\rightarrow k\\ k'\in D^{\pm } \end{array}}M(x, t; k'), \quad k\in \Sigma . \end{aligned}$$

(43)

Then, the multiplicative matrix Riemann–Hilbert problem is given below:

• Analyticity: M(x, t; k) is analytic in $\left( D^+\cup D^-\right) \backslash K$ and has the double poles in K, whose principal parts of the Laurent series at each double pole, $\eta _n$ or $\eta _n^*$, are determined as

  $$\begin{aligned} \begin{aligned} \mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n}M&=\left( A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\mu _{-2}(x, t; \eta _n),\, 0\right) , \\ \mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n^*}M&=\left( 0,\, A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; \eta _n^*)}\mu _{-1}(x, t; \eta _n^*)\right) , \\ \mathop {\mathrm {Res}}\limits _{k=\eta _n}M&=\left( A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\left\{ \mu _{-2}'(x, t; \eta _n)\right. \right. \\&\quad \left. \left. +\Big [B[\eta _n]-2\,\mathrm {i}\,\theta '(x, t; \eta _n)\Big ]\mu _{-2}(x, t; \eta _n)\right\} ,\, 0 \right) , \\ \mathop {\mathrm {Res}}\limits _{k=\eta _n^*}M&=\left( 0,\, A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; \eta _n^*)}\left\{ \mu _{-1}'(x, t; \eta _n^*)\right. \right. \\&\quad \left. \left. +\Big [B[\eta _n^*]+2\,\mathrm {i}\,\theta '(x, t; \eta _n^*)\Big ]\mu _{-1}(x, t; \eta _n^*)\right\} \right) , \end{aligned} \end{aligned}$$

  (44)

  where the prime denotes the partial derivative with respect to k.

• Jump condition:

  $$\begin{aligned} M^-(x, t; k)=M^+(x, t; k)\left( I-J(x, t; k)\right) , \quad k\in \Sigma , \end{aligned}$$

  (45)

  where J(x, t; k) is given by

  $$\begin{aligned} J(x, t; k)=\mathrm {e}^{\mathrm {i}\theta (x, t; k){{\widehat{\sigma }}}_3} \begin{bmatrix} 0&{}-{{\tilde{\rho }}}(k)\\ \rho (k)&{}\rho (k)\,{{\tilde{\rho }}}(k) \end{bmatrix}. \end{aligned}$$

  (46)

• Asymptotic behavior:

  $$\begin{aligned} M(x, t; k)=\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}+O\left( 1/k\right) , \quad k\rightarrow \infty . \end{aligned}$$

  (47)

Proof

The analyticity of M(x, t; k) can follow from the analyticity of the modified Jost solutions and scattering data in Propositions 1 with Eq. (22) and Proposition 3. It follows from Eqs. (22), (34), and (42) that for each double pole $\eta _n\in D^+$ or $\eta _n^*\in D^-$, we have

$$\begin{aligned} \begin{aligned} \mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n}\left[ \frac{\mu _{+1}(x, t; k)}{s_{11}(k)}\right]&=A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\mu _{-2}(x, t; \eta _n),\\ \mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n^*}\left[ \frac{\mu _{+2}(x, t; k)}{s_{22}(k)}\right]&=A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; \eta _n^*)}\mu _{-1}(x, t; \eta _n^*),\\ \mathop {\mathrm {Res}}\limits _{k=\eta _n}\left[ \frac{\mu _{+1}(x, t; k)}{s_{11}(k)}\right]&=A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\left\{ \mu _{-2}'(x, t; \eta _n).\right. \\&\quad \left. +\Big [B[\eta _n]-2\,\mathrm {i}\,\theta '(x, t; \eta _n)\Big ]\mu _{-2}(x, t; \eta _n)\right\} , \\ \mathop {\mathrm {Res}}\limits _{k=\eta _n^*}\left[ \frac{\mu _{+2}(x, t; k)}{s_{22}(k)}\right]&=A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; \eta _n^*)}\left\{ \mu _{-1}'(x, t; \eta _n^*)\right. \\&\quad \left. +\Big [B[\eta _n^*]+2\,\mathrm {i}\,\theta '(x, t; \eta _n^*)\Big ]\mu _{-1}(x, t; \eta _n^*)\right\} , \end{aligned} \end{aligned}$$

(48)

which can generate the principal parts of the Laurent series of M(x, t; k) at each double pole, that is, Eq. (44) holds. As usual, it follows from Eqs. (22) and (24) that

$$\begin{aligned} \left\{ \begin{aligned} \frac{\varPhi _{+1}(x, t; k)}{s_{11}(k)}\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}&=\varPhi _{-1}(x, t; k)\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}+\rho (z)\,\varPhi _{-2}(x, t; k)\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3},\\ \frac{\varPhi _{+2}(x, t; k)}{s_{22}(k)}\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}&={{\tilde{\rho }}}(k)\,\varPhi _{-1}(x, t; k)\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}+\varPhi _{-2}(x, t; k)\mathrm {e}^{-\mathrm {i}\theta (x, t; k)\sigma _3}, \end{aligned}\right. \end{aligned}$$

(49)

which can easily generate

$$\begin{aligned} \left( \mu _{-1}(x, t; k),\, \frac{\mu _{+2}(x, t; k)}{s_{22}(k)}\right) =\left( \frac{\mu _{+1}(x, t; k)}{s_{11}(k)},\, \mu _{-2}(x, t; k)\right) (I-J(x, t; k)), \end{aligned}$$

(50)

where J is given by Eq. (46). This completes the proof of the jump condition (45). The asymptotic behaviors of the modified Jost solutions $\mu _{\pm }(x,t;k)$ and scattering matrix S(k) given in Propositions 6 and 7 can easily lead to that of M(x, t; k). $\square$

By subtracting out the asymptotic values as $k\rightarrow \infty$ and the singularity contributions, one can regularize the Riemann–Hilbert problem as a standard form. Then, combining with Cauchy projectors and Plemelj’s formulae (Biondini and Kovačič 2014), one can establish the solutions of the corresponding matrix Riemann–Hilbert problem via an integral equation.

Proposition 9

The solution of the above-mentioned matrix Riemann–Hilbert problem can be expressed as

$$\begin{aligned} \begin{aligned} M(x, t; k)&=\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}+\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{(M^+J)(x, t; \zeta )}{\zeta -k}\,\mathrm {d}\zeta \\&\quad +\sum _{n=1}^{2N}\left( C_n(k)\left[ \mu _{-2}'(\eta _n)+\left( D_n +\frac{1}{k-\eta _n}\right) \mu _{-2}(\eta _n)\right] ,\right. \\&\quad \left. \,{{\widehat{C}}}_n(k)\left[ \mu _{-1}'(\eta _n^*)+\left( {{\widehat{D}}}_n +\frac{1}{k-\eta _n^*}\right) \mu _{-1}(\eta _n^*)\right] \right) , \end{aligned} \end{aligned}$$

(51)

where $k\in {\mathbb {C}}\backslash \Sigma$,  $\int _\Sigma$ an integral along the oriented contour exhibited in Fig. 1,

$$\begin{aligned} \begin{aligned} C_n(k)&=\frac{A[\eta _n]}{k-\eta _n}\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}, \quad D_n=B[\eta _n]-2\,\mathrm {i}\,\theta '(x, t; \eta _n), \\ {{\widehat{C}}}_n(k)&=\frac{A[\eta _n^*]}{k-\eta _n^*}\,\mathrm {e}^{2\mathrm {i}\theta (x, t; \eta _n^*)}, \quad {{\widehat{D}}}_n=B[\eta _n^*]+2\,\mathrm {i}\,\theta '(x, t; \eta _n^*), \end{aligned} \end{aligned}$$

(52)

$\mu _{-s}$ and $\mu _{-s}'\,\, (s=1,2)$ satisfy

$$\begin{aligned} \mu _{-1}(\eta _n^*)= & {} \mathrm {e}^{\mathrm {i}v_-\sigma _3} \begin{bmatrix} 1\\ 0 \end{bmatrix} +\sum _{k=1}^{2N}C_k(\eta _n^*)\left[ \mu _{-2}'(\eta _k) +\left( D_k+\frac{1}{\eta _n^*-\eta _k}\right) \mu _{-2}(\eta _k)\right] \\&+\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _1(\zeta )}{\zeta -\eta _n^*}\,\mathrm {d}\zeta ,\\ \mu _{-1}'(\eta _n^*)= & {} -\sum _{k=1}^{2N}\frac{C_k(\eta _n^*)}{\eta _n^*-\eta _k}\left[ \mu _{-2}'(\eta _k)+\left( D_k+\frac{2}{\eta _n^*-\eta _k}\right) \mu _{-2}(\eta _k)\right] \\&+\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _1(\zeta )}{\left( \zeta -\eta _n^*\right) ^2}\,\mathrm {d}\zeta , \\ \mu _{-2}(\eta _k)= & {} \mathrm {e}^{\mathrm {i}v_-\sigma _3}\begin{bmatrix}0\\ 1 \end{bmatrix} +\sum _{j=1}^{2N}{{\widehat{C}}}_j(\eta _k)\left[ \mu _{-1}'(\eta _j^*)+\left( {{\widehat{D}}}_j+\frac{1}{\eta _k-\eta _j^*}\right) \mu _{-1}(\eta _j^*)\right] \\&+\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _2(\zeta )}{\zeta -\eta _k}\,\mathrm {d}\zeta , \\ \mu _{-2}'(\eta _k)= & {} -\sum _{j=1}^{2N}\frac{{{\widehat{C}}}_j(\eta _k)}{\eta _k-\eta _j^*}\left[ \mu _{-1}'(\eta _j^*)+\left( {{\widehat{D}}}_j+\frac{2}{\eta _k-\eta _j^*}\right) \mu _{-1}(\eta _j^*)\right] \\&+\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _2(\zeta )}{\left( \zeta -\eta _k\right) ^2}\,\mathrm {d}\zeta . \end{aligned}$$

Proof

To regularize the Riemann–Hilbert problem, one has to subtract out the asymptotic values as $k\rightarrow \infty$ given by Eq. (47) and the singularity contributions. Then, the jump condition becomes

$$\begin{aligned} \begin{aligned}&M^--\mathrm {e}^{\mathrm {i}v_-\sigma _3}-\sum _{n=1}^{2N}\left[ \frac{\mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n}[M]}{\left( k-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n}[M]}{k-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n^*}[M]}{\left( k-\eta _n^*\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n^*}[M]}{k-\eta _n^*}\right] \\&\quad =M^+-\mathrm {e}^{\mathrm {i}v_-\sigma _3}-\sum _{n=1}^{2N}\left[ \frac{\mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n}[M]}{\left( k-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n}[M]}{k-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n^*}[M]}{\left( k-\eta _n^*\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n^*}[M]}{k-\eta _n^*}\right] -M^+\,J, \end{aligned} \end{aligned}$$

(53)

where

$$\begin{aligned}&\displaystyle \mathop {{\mathrm{L}}_{-2}}_{k=\eta _n}[M]=\left( \mathop {{\mathrm{L}}_{-2}}_{k=\eta _n}\left[ \frac{\mu _{+1}(x,t;k)}{s_{11}(k)}\right] ,\, 0\right) ,\quad \mathop {{\mathrm{Res}}}_{k=\eta _n}[M]=\left( \mathop {{\mathrm{Res}}}_{z=\eta _n}\left[ \frac{\mu _{+1}(x,t;k)}{s_{11}(k)}\right] ,\, 0\right) , \\&\displaystyle \mathop {{\mathrm{L}}_{-2}}_{k=\eta _n^*}[M]=\left( 0,\, \mathop {{\mathrm{L}}_{-2}}_{k=\eta _n^*}\left[ \frac{\mu _{+2}(x,t;k)}{s_{22}(k)}\right] \right) ,\quad \mathop {{\mathrm{Res}}}_{k=\eta _n^*}[M]=\left( 0,\, \mathop {{\mathrm{Res}}}_{k=\eta _n^*}\left[ \frac{\mu _{+2}(x,t;k)}{s_{22}(k)}\right] \right) , \end{aligned}$$

which are given by Eq. (44). By the Cauchy projectors defined by

$$\begin{aligned} P^{\pm }\left[ f\right] (z)=\frac{1}{2\pi i}\int _{\Sigma }\frac{f(\zeta )}{\zeta -(z\pm i0)}\,d\zeta , \end{aligned}$$

(54)

where the notation $z\pm i0$ represents the limit taken from the left/right of z, the Plemelj’s formulae (see, e.g., Biondini and Kovačič 2014) to Eq. (53), one can show the proposition. The technique of the proof is fairly standard and one can also refer to Refs. Pichler and Biondini (2017), Zhang and Yan (2020a) for more details. $\square$

2.2.2 Reconstruction Formula of the Potential

It follows from the solution of the matrix Riemann–Hilbert problem that one can obtain

$$\begin{aligned} M(x, t; k)=\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}+\frac{M^{[1]}(x, t)}{k}+O\left( \frac{1}{k^2}\right) , \quad \mathrm {as} \quad k\rightarrow \infty , \end{aligned}$$

(55)

where

$$\begin{aligned} M^{[1]}(x, t)&=-\frac{1}{2\pi \mathrm {i}}\int _\Sigma M^+(x, t; \zeta )\,J(x, t; \zeta )\,\mathrm {d}\zeta \\&\quad +\sum _{n=1}^{2N}\left[ A[\eta _n]\,\mathrm {e}^{-2\mathrm {i} \theta (\eta _n)}\left( \mu _{-2}'(\eta _n)+D_n\mu _{-2}(\eta _n)\right) ,\right. \\&\quad \left. A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (\eta _n^*)}\left( \mu _{-1}'(\eta _n^* )+{{\widehat{D}}}_n\mu _{-1}(\eta _n^*)\right) \right] . \end{aligned}$$

Substituting $\varPhi (x, t; k)=M(x, t; k)\,\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}$ into Eq. (15) and matching $O\left( k\right)$ term, one can find the reconstruction formula of the solution (potential) of the DNLS equation with ZBCs and double poles as

$$\begin{aligned} q(x, t)=-2\,\mathrm {i}\,\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\alpha ^\mathrm {T}\gamma , \end{aligned}$$

(56)

where the column vectors $\alpha =(\alpha ^{(1)},\,\alpha ^{(2)})^\mathrm {T}$ and $\gamma =(\gamma ^{(1)},\,\gamma ^{(2)})^\mathrm {T}$ are given by

$$\begin{aligned} \begin{array}{ll} \alpha ^{(1)}=\left( A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (\eta _n^*)}{{\widehat{D}}}_n\right) _{1\times 2N},&{} \alpha ^{(2)}=\left( A[\eta _n^*]\,\mathrm {e}^{2\mathrm {i}\theta (\eta _n^*)}\right) _{1\times 2N},\\ \gamma ^{(1)}=\big (\mu _{-11}(\eta _n^*)\big )_{1\times 2N}, &{} \gamma ^{(2)}=\left( \mu _{-11}'(\eta _n^*)\right) _{1\times 2N}. \end{array} \end{aligned}$$

(57)

2.2.3 Trace Formulae

The so-called trace formulae are that the scattering coefficients $s_{11}(k)$ and $s_{22}(k)$ are formulated in terms of the discrete spectrum K and reflection coefficients $\rho (k)$ and ${{\tilde{\rho }}}(k)$. Recall that $s_{11}(k)$ is analytic in $D^+$ and $s_{22}(k)$ is analytic in $D^-$. The discrete spectral points $\eta _n$’s are the double zeros of $s_{11}(k)$, while $\eta _n^*$’s are the double zeros of $s_{22}(k)$. Define

$$\begin{aligned} \begin{aligned} \beta ^+(k)=s_{11}(k)\prod _{n=1}^{2N}\left( \frac{k-\eta _n^*}{k-\eta _n}\right) ^2\mathrm {e}^{\mathrm {i}v}, \qquad \beta ^-(k)=s_{22}(k)\prod _{n=1}^{2N}\left( \frac{k-\eta _n}{k-\eta _n^*}\right) ^2\mathrm {e}^{-\mathrm {i}v}. \end{aligned} \end{aligned}$$

(58)

Then, $\beta ^+(k)$ and $\beta ^-(k)$ are analytic and have no zero in $D^+$ and $D^-$, respectively. Moreover, $\beta ^{\pm }(k)\rightarrow 1$ as $k\rightarrow \infty$. Besides, one has $-\log \beta ^+(k)-\log \beta ^-(k)=\log \left[ 1-\rho (k)\,{{\tilde{\rho }}}(k)\right]$, which is employed by the Cauchy projectors and Plemelj’s formulae Biondini and Kovačič (2014) such that one has

$$\begin{aligned} \log \beta ^{\pm }(k)=\mp \frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\log \left[ 1-\rho (\zeta ) \,{{\tilde{\rho }}}(\zeta )\right] }{\zeta -k}\,\mathrm {d}\zeta , \quad k\in D^{\pm }. \end{aligned}$$

(59)

Therefore, it follows from Eqs. (58) and (59) that the trace formulae are derived as

$$\begin{aligned} \begin{aligned} s_{11}(k)&=\exp \left( -\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\log \left[ 1-{{\tilde{\rho }}}(\zeta )\,\rho (\zeta )\right] }{\zeta -k}\,\mathrm {d}\zeta \right) \prod _{n=1}^{2N} \left( \frac{k-\eta _n}{k-\eta _n^*}\right) ^2\mathrm {e}^{-\mathrm {i}v},\\ s_{22}(k)&=\exp \left( \frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\log \left[ 1-{{\tilde{\rho }}}(\zeta )\,\rho (\zeta )\right] }{\zeta -k}\,\mathrm {d}\zeta \right) \prod _{n=1}^{2N} \left( \frac{k-\eta _n^*}{k-\eta _n}\right) ^2 \mathrm {e}^{\mathrm {i}v}. \end{aligned} \end{aligned}$$

(60)

2.2.4 Reflectionless Potential: Double-Pole Solitons

We consider a special kind of solution with $\rho (k)={{\tilde{\rho }}}(k)=0$: reflectionless potential. From the Volterra integral equation (23), one obtains $\varPhi _{\pm }(x, t; 0)=\mu _{\pm }(x, t; 0)=I$. Thus, $s_{11}(0)=1$. Combining the trace formula, one obtains that there exists an integer $j\in {\mathbb {Z}}$ such that $v=8\displaystyle \sum _{n=1}^{N}\mathrm {arg}(k_n)+2j\,\pi .$

Theorem 1

The explicit formula for the double-pole solution of the DNLS equation (1) with ZBCs is given by

$$\begin{aligned} q(x, t)=2\mathrm {i}\left( \frac{\mathrm {det}\left( {{\widehat{G}}}\right) }{\mathrm {det}\left( I-{{\widehat{H}}}\right) }\right) ^2\frac{\mathrm {det} \left( I-H\right) }{\mathrm {det}\left( G\right) }, \end{aligned}$$

(61)

where

$$\begin{aligned} G= & {} \begin{bmatrix} I-H &{}\beta \\ \alpha ^T&{}0\end{bmatrix}, \quad {{\widehat{G}}}=\begin{bmatrix} I-{{\widehat{H}}}&{}\beta \\ \alpha ^T&{}0\end{bmatrix}, \quad \beta =\begin{bmatrix}\beta ^{(1)}\\ \beta ^{(2)} \end{bmatrix}, \nonumber \\ \beta ^{(1)}= & {} \left( 1\right) _{2N\times 1},\quad \beta ^{(2)}=\left( 0\right) _{2N\times 1}, \end{aligned}$$

(62)

the $4N\times 4N$ matrix $H=\begin{bmatrix} H^{(1, 1)}&{} H^{(1, 2)}\\ H^{(2, 1)}&{} H^{(2, 2)} \end{bmatrix}$ with $H^{(i, m)}=\left( H^{(i, m)}_{n, j}\right) _{2N\times 2N}\, (i, m=1, 2)$ given by

$$\begin{aligned} H^{(1, 1)}_{n, j}&=\sum _{k=1}^{2N}C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k) \left[ -\frac{1}{\eta _k-\eta _j^*}\left( {{\widehat{D}}}_j+\frac{2}{\eta _k-\eta _j^*}\right) \right. \\&\quad \left. +\left( D_k+\frac{1}{\eta _n^*-\eta _k}\right) \left( {{\widehat{D}}}_j+\frac{1}{\eta _k-\eta _j^*}\right) \right] , \\ H^{(1, 2)}_{n, j}&=\sum _{k=1}^{2N}C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)\left[ -\frac{1}{\eta _k-\eta _j^*}+\left( D_k+\frac{1}{\eta _n^*-\eta _k}\right) \right] , \\ H^{(2, 1)}_{n, j}&=\sum _{k=1}^{2N}C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)\left[ \frac{1}{\eta _k-\eta _j^*}\left( {{\widehat{D}}}_j+\frac{2}{\eta _k-\eta _j^*}\right) \right. \\&\quad \left. -\left( D_k+\frac{2}{\eta _n^*-\eta _k}\right) \left( {{\widehat{D}}}_j+\frac{1}{\eta _k-\eta _j^*}\right) \right] , \\ H^{(2, 2)}_{n, j}&=\sum _{k=1}^{2N}C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)\left[ \frac{1}{\eta _k-\eta _j^*}-\left( D_k+\frac{2}{\eta _n^*-\eta _k}\right) \right] , \end{aligned}$$

and the $4N\times 4N$ matrix ${{\widehat{H}}}=\begin{bmatrix} {{\widehat{H}}}^{(1, 1)}&{} {{\widehat{H}}}^{(1, 2)}\\ {{\widehat{H}}}^{(2, 1)}&{} {{\widehat{H}}}^{(2, 2)} \end{bmatrix}$ with ${{\widehat{H}}}^{(i, m)}=\left( {{\widehat{H}}}^{(i, m)}_{n, j}\right) _{2N\times 2N}\, (i, m=1, 2)$ given by

$$\begin{aligned} {{\widehat{H}}}^{(1, 1)}_{n, j}&=\eta _n^*\sum _{k=1}^{2N}\frac{C_k(\eta _n^*) \,{{\widehat{C}}}_j(\eta _k)}{\eta _k}\left[ -\frac{1}{\eta _k-\eta _j^*} \left( {{\widehat{D}}}_j+\frac{2}{\eta _k-\eta _j^*}\right) \right. \\&\quad \left. +\frac{\eta _k}{\eta _j^*}\left( D_k+\frac{1}{\eta _n^*-\eta _k}-\frac{1}{\eta _k}\right) \left( {{\widehat{D}}}_j+\frac{1}{\eta _k-\eta _j^*}-\frac{1}{\eta _j^*}\right) \right] , \\ {{\widehat{H}}}^{(1, 2)}_{n, j}&=\eta _n^*\sum _{k=1}^{2N}\frac{C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)}{\eta _k}\left[ -\frac{1}{\eta _k-\eta _j^*}+\frac{\eta _k}{\eta _j^*}\left( D_k+\frac{1}{\eta _n^*-\eta _k}-\frac{1}{\eta _k}\right) \right] , \\ {{\widehat{H}}}^{(2, 1)}_{n, j}&=\sum _{k=1}^{2N}\frac{C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)}{\eta _n^*-\eta _k}\left[ \frac{1}{\eta _k-\eta _j^*}\left( {{\widehat{D}}}_j+\frac{2}{\eta _k-\eta _j^*}\right) \right. \\&\quad \left. -\frac{\eta _k}{\eta _j^*}\left( D_k+\frac{2}{\eta _n^*-\eta _k}\right) \left( {{\widehat{D}}}_j+\frac{1}{\eta _k-\eta _j^*}-\frac{1}{\eta _j^*}\right) \right] , \\ {{\widehat{H}}}^{(2, 2)}_{n, j}&=\sum _{k=1}^{2N}\frac{C_k(\eta _n^*)\,{{\widehat{C}}}_j(\eta _k)}{\eta _n^*-\eta _k}\left[ \frac{1}{\eta _k-\eta _j^*}-\frac{\eta _k}{\eta _j^*}\left( D_k+\frac{2}{\eta _n^*-\eta _k}\right) \right] . \end{aligned}$$

Proof

From the reconstruction formula (56), the reflectionless potential is deduced by determinants:

$$\begin{aligned} q(x, t)=2\mathrm {i}\,\frac{\mathrm {det}\left( G\right) }{\mathrm {det}\left( I-H\right) }\,\mathrm {e}^{2\mathrm {i}v_-(x, t)}. \end{aligned}$$

(63)

However, this formula (63) is implicit since $v_-(x, t)$ is included. One needs to derive an explicit form for the reflectionless potential. From the trace formulae (60) and Volterra integral equation (23), one derives that

$$\begin{aligned} M=I+k\sum _{n=1}^{2N}\left( \frac{\mathop {\mathrm {L_{-2}}} \limits _{k=\eta _n}\left[ M/k\right] }{\left( k-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n}\left[ M/k\right] }{k-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{k=\eta _n^*}\left[ M/k\right] }{\left( k-\eta _n^*\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{k=\eta _n^*}\left[ M/k\right] }{k-\eta _n^*}\right) , \end{aligned}$$

(64)

which can yield the $\gamma$ given by Eq. (57) explicitly. Then, substituting $\gamma$ into the formula of the potential, one yields

$$\begin{aligned} q(x, t)=2\mathrm {i}\,\frac{\mathrm {det}\left( {{\widehat{G}}}\right) }{\mathrm {det}(I-{{\widehat{H}}})}\,\mathrm {e}^{\mathrm {i}v_-(x, t)}. \end{aligned}$$

(65)

Combining Eq. (63) with Eq. (65), we can complete the proof. $\square$

For example, it follows from Eq. (61) that we have the single double-pole solution of Eq. (1) with ZBCs for parameters $N=1, k_1=\frac{1}{2}\left( 1+\mathrm {i}\right) , A[k_1]=1, B[k_1]=1$ as $q(x,t)=P_1(x,t)/P_2(x,t)$, where

$$\begin{aligned} P_1(x,t)&=\dfrac{\mathrm {i}}{4}\Big \{[4(\mathrm {i}-1)t^3+[1-2i-2(1 +\mathrm {i})x]t^2+[(13i-11)/8\\&\quad +(\mathrm {i}-1)x^2+(2-\mathrm {i})x]t+(10-\mathrm {i})/32 \\&\quad -(1+\mathrm {i})x^3/2+(3+2i)x^2/4-(7+\mathrm {i})x/16]\mathrm {e}^{4x}\\&\quad +[(1+\mathrm {i})t^3+((1-\mathrm {i})x-3)t^2/4 \\&\quad +[(1+\mathrm {i})x^2/4+ix/4+(11+5i)/32]t+(1-\mathrm {i})x^3/8\\&\quad -x^2/16-(1 +\mathrm {i})x/64-7i/128]\mathrm {e}^{2x} \\&\quad +[(1-\mathrm {i})x/2-(1+\mathrm {i})t+(2\mathrm {i}-1)/4]\mathrm {e}^{6x} +(1-\mathrm {i})t/64\\&\quad -[1+2(1+\mathrm {i})x]/256\Big \}^2e^{x+it},\\ P_2(x,t)&=\Big \{[t^4-t^3/2+(2x^2-x+2)t^2/4-(2x^2-x+7)t/16\\&\quad +(x^2-x/2+5/8)(x^2 -x/2+1/8)/16]\mathrm {e}^{4x} \\&\quad +(1-8t)\mathrm {e}^{2x}/512+(8t-1)\mathrm {e}^{6x}/32+\mathrm {e}^{8x}/16 +1/4096\Big \}\\&\quad \Big \{[4(\mathrm {i}-1)t^3+(5+2i-2(1+\mathrm {i})x)t^2 \\&\quad +[(\mathrm {i}-1)x^2+ix-(3+11i)/8]t+(2+7i)/32-(1+\mathrm {i})x^3/2\\&\quad +(3+2i)x^2/4-(7+9i)x/16]\mathrm {e}^{4x} \\&\quad +[(1+\mathrm {i})t^3+(1-4i+2(1-\mathrm {i})x)t^2/4+(5(\mathrm {i}-1)+8(1 +\mathrm {i})x^2\\&\quad -8(2+\mathrm {i})x)t/32+\mathrm {i}/128 \\&\quad +(1-\mathrm {i})x^3/8-x^2/16+(7-\mathrm {i})x/64]\mathrm {e}^{2x} +[(1+\mathrm {i})t\\&\quad +(\mathrm {i}-1)x/2+(1-2i)/4]\mathrm {e}^{6x} \\&\quad +(\mathrm {i}-1)t/64+[1+2(1+\mathrm {i})x]/256\Big \}. \end{aligned}$$

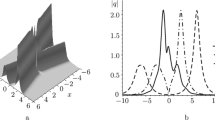
Figure 2a, b exhibits the dynamical structures of the exact double-pole soliton of the DNLS equation with ZBCs, which is equivalent to the elastic collisions of two bright–bright solitons. Figure 2c displays the distinct profiles of the exact double-pole soliton for $t=\pm 2, 0$.

Notice that the general expression of the single double-pole solution for $N=1$ from Eq. (61) is very complicated and is not given explicitly. However, with the aid of computer softwares such as Maple and Matlab, one can easily get the corresponding double-pole solution for different parameters by using Eq. (61).

Fig. 2

Double-pole soliton solution of DNLS equation (1) with ZBCs and $N=1, k_1=(1+\mathrm {i})/2, A[k_1]=B[k_1]=1$. (a) 3D profile; (b) intensity profile; (c) profiles for $t=-2$ (solid line), $t=0$ (dashed line), and $t=2$ (dash-dot line)

3 The IST with NZBCs and Double Poles

Recently, the ISTs of integrable nonlinear systems with NZBCs have attracted more and more attention (Prinari et al. 2006; Demontis et al. 2013, 2014; Biondini and Kovačič 2014; Prinari 2015; Pichler and Biondini 2017; Zhang and Yan 2020a, b). In this section, we will find a double-pole solution q(x, t) for the DNLS equation (1) with $\sigma =-1$ and the NZBCs

$$\begin{aligned} \lim _{x\rightarrow \pm \infty }q(x, t)= q_{\pm },\quad \left| q_{\pm }\right| =q_0> 0, \end{aligned}$$

(66)

with the aid of the IST. The ISTs for DNLS equation (1) with NZBCs (66) were also studied (Kawata and Inoue 1978; Chen and Lam 2004; Chen et al. 2006; Lashkin 2007), but they only considered the case of simple poles by solving the corresponding Gel’fand–Levitan–Marchenko integral equations. In what follows, we try to present the IST of the DNLS equation (1) with NZBCs (66) and double poles based on another approach, that is, the Riemann–Hilbert problem.

3.1 Direct Scattering with NZBCs and Double Poles

3.1.1 Jost Solutions, Analyticity, and Continuity

As $x\rightarrow \pm \infty$, we consider the asymptotic scattering problem of the modified Zakharov–Shabat eigenvalue problem (15, 16):

$$\begin{aligned} \begin{aligned} \varPhi _x&=X_{\pm }\varPhi ,\quad \varPhi _t=T_{\pm }\varPhi ,\quad X_{\pm }=k\left( ik\sigma _3+Q_{\pm }\right) , \\ T_{\pm }&=-\left( 2k^2-q_0^2\right) X_{\pm },\quad Q_{\pm }= \begin{bmatrix} 0&{}q_{\pm } \\ -q_{\pm }^*&{}0 \end{bmatrix}. \end{aligned} \end{aligned}$$

(67)

such that the fundamental matrix solution of Eq. (67) is given as

$$\begin{aligned} \varPhi _{\pm }^{\mathrm {bg}}(x, t; k)= \left\{ \begin{array}{ll} E_{\pm }(k)\,\mathrm {e}^{\mathrm {i}\theta (x, t; k)\sigma _3}, &{}\quad k\ne \pm \mathrm {i}q_0,\\ I+\left( x+3\,q_0^2\,t\right) X_{\pm }(k),&{}\quad k=\pm \mathrm {i}q_0, \end{array}\right. \end{aligned}$$

(68)

where

$$\begin{aligned}&E_{\pm }(k)= \begin{bmatrix} 1&{}\dfrac{\mathrm {i}q_{\pm }}{k+\lambda (k)} \\ \dfrac{\mathrm {i}q_{\pm }^*}{k+\lambda (k)}&{}1 \end{bmatrix},\nonumber \\&\theta (x, t; k)=k \lambda (k)\left[ x-\left( 2k^2-q_0^2\right) t\right] , \quad \lambda ^2(k)=k^2+q_0^2. \end{aligned}$$

(69)

Since $\lambda (k)$ stands for a two-sheeted Riemann surface, for convenience, taking a new variable: $z=k+\lambda ,$ which was first introduced in Faddeev and Takhtajan (1987), we will illustrate the scattering problem on a standard z-plane instead of the two-sheeted Riemann surface by the inverse mapping:

$$\begin{aligned} k=\frac{1}{2}\left( z-\frac{q_0^2}{z}\right) ,\quad \lambda =\frac{1}{2}\left( z+\frac{q_0^2}{z}\right) . \end{aligned}$$

Fig. 3

Complex z-plane, exhibiting the region $D^+$ (grey region), the region $D^-$ (white region), the discrete spectrum, and the orientation of the contours for the matrix Riemann–Hilbert problem in the inverse scattering problem

Define $\Sigma$ and $D^{\pm }$ on the z-plane as $\Sigma :={\mathbb {R}}\cup \mathrm {i}{\mathbb {R}}\backslash \left\{ 0\right\} , \, D^{\pm }:=\left\{ z\in {\mathbb {C}}\, | \pm (\mathrm {Re}\,z)\,(\mathrm {Im}\,z)>0\right\} .$ From the mapping relation between the k-plane and z-plane under the uniformization variable, one finds that $\mathrm {Im}\,(k\lambda )=0\, \mathrm {when}\, z\in \Sigma ; \, \mathrm {Im}\,(k\lambda )>0\,\mathrm {when}\, z\in D^+;\, \mathrm {Im}\,(k\lambda )<0\, \mathrm {when}\, z\in D^-.$ According to the IST technique (Demontis et al. 2013, 2014; Biondini and Kovačič 2014; Pichler and Biondini 2017), one needs to define the Jost solutions $\varPhi _{\pm }(x, t; z)$ with

$$\begin{aligned} \varPhi _{\pm }(x, t; z)=E_{\pm }(z)\,\mathrm {e}^{\mathrm {i}\theta (x, t; z)\sigma _3}+o\left( 1\right) ,\quad z\in \Sigma _0,\quad \mathrm {as}\,\, x\rightarrow \pm \infty , \end{aligned}$$

(70)

and the modified Jost solutions $\mu _{\pm }(x, t; z)$ via dividing by the transform

$$\begin{aligned} \mu _{\pm }(x, t; z)=\varPhi _{\pm }(x, t; z)\,\mathrm {e}^{-\mathrm {i}\theta (x, t; z)\sigma _3}, \end{aligned}$$

(71)

such that $\lim _{x\rightarrow \pm \infty }\mu _{\pm }(x, t; z)=E_{\pm }(z).$ It follows from Eq. (15) that the modified Jost solutions $\mu _{\pm }(x, t; z)$ satisfy the Volterra integral equations

$$\begin{aligned}&\mu _{\pm }(x, t; z)=E_{\pm }(z)\nonumber \\&\quad +\left\{ \begin{array}{ll} k(z)\int _{\pm \infty }^xE_{\pm }(z)\,\mathrm {e}^{\mathrm {i}k(z) \lambda (z)(x-y){{\widehat{\sigma }}}_3}\left[ {E_{\pm }^{-1}(z)}\Delta Q_{\pm }(y, t)\,\mu _{\pm }(y, t; z)\right] \,\mathrm {d}y, &{}\quad z\ne 0,\, \pm \mathrm {i}q_0,\\ k(z)\int _{\pm \infty }^x\left[ I+\left( x-y\right) X_{\pm }(z)\right] \Delta Q_{\pm }(y, t)\,\mu _{\pm }(y, t; z)\,\mathrm {d}y, &{}\quad z=\pm \mathrm {i}q_0, \end{array}\right. \end{aligned}$$

(72)

which are used to deduce the following analyticity of the (modified) Jost solution.

Proposition 10

Suppose $\left( 1+\left| x\right| \right) \left( q(x,t)-q_{\pm }\right) \in L^1\left( \mathbb {R^{\pm }}\right)$. Then, $\varPhi _\pm (x, t; z)$ have the following properties:

• Eq. (15) has the unique solution $\varPhi _{\pm }(x, t; z)$ satisfying Eq. (70) on $\Sigma$;

• $\varPhi _{+1, -2}(x, t; z)$ can be analytically extended to $D^{+}$ and continuously extended to $D^{+}\cup \Sigma$;

• $\varPhi _{-1, +2}(x, t; z)$ can be analytically extended to $D^{-}$ and continuously extended to $D^-\cup \Sigma$.

Proof

The proposition is reported in Refs. Kawata and Inoue (1978), Chen and Lam (2004); Chen et al. (2006), Lashkin (2007). Besides, one can refer to Refs. Demontis et al. (2013), Biondini and Kovačič (2014), Zhang and Yan (2020a) for the standard technique of the proof. The analyticity and continuity for $\mu _{\pm }(x, t; z)$ can be deduced from those of $\varPhi _{\pm }(x, t; z)$. $\square$

Similarly to the case of ZBCs in Sec. 2, one can also confirm that the Jost solutions $\varPhi _{\pm }(x, t; z)$ are the simultaneous solutions for both parts of the modified Zakharov–Shabat eigenvalue problem (15, 16).

3.1.2 Scattering Matrix, Analyticity, and Continuity

Liouville’s formula implies $\varPhi _{\pm }$ are the fundamental matrix solutions in $z\in \Sigma _0=\Sigma \backslash \left\{ \pm \mathrm {i}q_0\right\}$, so one can define the constant scattering matrix $S(z)=(s_{ij}(z))_{2\times 2}$ such that

$$\begin{aligned} \varPhi _+(x, t; z)=\varPhi _-(x, t; z)\,S(z),\quad z\in \Sigma _0. \end{aligned}$$

(73)

Then, one has the scattering coefficients as

$$\begin{aligned} \begin{aligned} s_{11}(z)&=\frac{{\mathrm{Wr}}(\varPhi _{+1}(x, t; z), \varPhi _{-2}(x, t; z))}{s(z)},\quad s_{22}(z)=\frac{{\mathrm{Wr}}(\varPhi _{-1}(x, t; z), \varPhi _{+2}(x, t; z))}{s(z)},\\ s_{12}(z)&=\frac{{\mathrm{Wr}}(\varPhi _{+2}(x, t; z), \varPhi _{-2}(x, t; z))}{s(z)},\quad s_{21}(z)=\frac{{\mathrm{Wr}}(\varPhi _{-1}(x, t; z), \varPhi _{+1}(x, t; z))}{s(z)}, \end{aligned} \end{aligned}$$

(74)

where ${\mathrm{Wr}}(\varvec{\cdot }, \varvec{\cdot })$ denotes the Wronskian determinant and $s(z):=1+q_0^2/z^2$. From these Wronskian representations, one can extend the analytical regions of $s_{11}(z)$ and $s_{22}(z)$.

Proposition 11

Suppose $q(x,t)-q_{\pm }\in L^1\left( \mathbb {R^{\pm }}\right)$. Then, $s_{11}(z)$ can be analytically extended to $D^+$ and continuously extended to $D^+\cup \Sigma _0$, while $s_{22}(z)$ can be analytically extended to $D^-$ and continuously extended to $D^-\cup \Sigma _0$. Moreover, both $s_{12}(z)$ and $s_{21}(z)$ are continuous in $z\in \Sigma _0$.

Proof

The proposition can be verified by using Proposition 10 and Eq. (74). $\square$

Proposition 12

Suppose $\left( 1+\left| x\right| \right) \left( q-q_{\pm }\right) \in L^1\left( \mathbb {R^{\pm }}\right)$. Then, $\lambda (z)\,s_{11}(z)$ can be analytically extended to $D^+$ and continuously extended to $D^+\cup \Sigma$, while $\lambda (z)\,s_{22}(z)$ can be analytically extended to $D^-$ and continuously extended to $D^-\cup \Sigma$. Moreover, both $\lambda (z)\,s_{12}(z)$ and $\lambda (z)\,s_{21}(z)$ are continuous in $\Sigma$.

Proof

The proposition can be verified by using Proposition 10 and Eq. (74). $\square$

To further solve the matrix Riemann–Hilbert problem established in the inverse process, we focus on the potential without spectral singularities (Zhou 1989). Besides, we suppose $s_{ij}(z)\, (i, j=1,2)$ are continuous in the branch points $\left\{ \pm \mathrm {i}q_0\right\}$. The reflection coefficients $\rho (z)$ and ${{\tilde{\rho }}}(z)$ are defined as

$$\begin{aligned} \rho (z)=\frac{s_{21}(z)}{s_{11}(z)},\quad {{\tilde{\rho }}}(z)=\frac{s_{12}(z)}{s_{22}(z)}, \quad z\in \Sigma , \end{aligned}$$

(75)

which will be used in the inverse scattering problem.

3.1.3 Symmetry Structures

The symmetries of X(x, t; z), T(x, t; z), Jost solutions, scattering matrix and reflection coefficients in the case of NZBCs are more complicated than ones in the ZBCs.

Proposition 13

(Symmetry reductions) For the case of NZBCs, X(x, t; z) and T(x, t; z) in the modified Zakharov–Shabat eigenvalue problem (15, 16), Jost solutions, scattering matrix and reflection coefficients admit three reduction conditions on the z-plane:

• The first symmetry reduction

  $$\begin{aligned} \begin{aligned} X(x, t; z)&=\sigma _2\,X(x, t; z^*)^*\,\sigma _2, \quad T(x, t; z)=\sigma _2\,T(x, t; z^*)^*\,\sigma _2, \\ \varPhi _{\pm }(x, t; z)&=\sigma _2\,\varPhi _{\pm }(x, t; z^*)^*\,\sigma _2, \quad S(z)=\sigma _2\,S(z^*)^*\,\sigma _2, \quad \rho (z)=-{{\tilde{\rho }}}(z^*)^*. \end{aligned}\nonumber \\ \end{aligned}$$

  (76)

• The second symmetry reduction

  $$\begin{aligned} \begin{aligned} X(x, t; z)&=\sigma _1\,X(x, t; -z^*)^*\,\sigma _1,\quad T(x, t; z)=\sigma _1\,T(x, t; -z^*)^*\,\sigma _1,\\ \varPhi _{\pm }(x, t; z)&=\sigma _1\,\varPhi _{\pm }(x, t; -z^*)^*\sigma _1,\quad S(z)=\sigma _1\,S(-z^*)^*\sigma _1, \quad \rho (z)={{\tilde{\rho }}}(-z^*)^*. \end{aligned}\nonumber \\ \end{aligned}$$

  (77)

• The third symmetry reduction

  $$\begin{aligned} \begin{aligned}&X(x, t; z)=X\left( x, t; -\frac{q_0^2}{z}\right) ,\quad T(x, t; z)=T\left( x, t; -\frac{q_0^2}{z}\right) ,\\&\varPhi _{\pm }(x, t; z)=\frac{\mathrm {i}}{z}\,\varPhi _{\pm }\left( x, t; -\frac{q_0^2}{z}\right) \sigma _3Q_{\pm }, \,\,\, S(z)=\left( \sigma _3Q_-\right) ^{-1}S\left( -\frac{q_0^2}{z}\right) \sigma _3Q_+,\\&\rho (z)=\frac{q_-^*}{q_-}\,{{\tilde{\rho }}}\left( -\frac{q_0^2}{z}\right) . \end{aligned}\nonumber \\ \end{aligned}$$

  (78)

Proof

The similar properties are reported in Refs. Kawata and Inoue (1978), Chen and Lam (2004); Chen et al. (2006), Lashkin (2007), Zhou (2012). Besides, one can also refer to Refs. Demontis et al. (2013), Biondini and Kovačič (2014), Zhang and Yan (2020a) for more details of the standard technique of the proof. $\square$

3.1.4 Discrete Spectrum with Double Zeros

The previous works on the DNLS equation (1) with NZBCs focused on the simple zeros of the scattering coefficients (Kawata and Inoue 1978; Chen and Lam 2004; Chen et al. 2006; Lashkin 2007). Here, we consider the case of $s_{11}(z)$ with double zeros and suppose that $s_{11}(z)$ has $N_1$ double zeros in $Z_0=\left\{ z\in {\mathbb {C}}\,|\,\mathrm {Re} \,z>0, \mathrm {Im}\, z>0, \left| z\right| >q_0\right\}$ denoted by $z_n$, and $N_2$ double zeros in $W_0=\left\{ z\in {\mathbb {C}}\,|\, z=q_0\,\mathrm {e}^{\mathrm {i}\phi },\, 0<\phi <\frac{\pi }{2}\right\}$ denoted by $w_m$, that is, $s_{11}(z_0)=s'_{11}(z_0)=0$ and $s''_{11}(z_0)\not =0$ if $z_0$ is a double zero of $s_{11}(z)$. From the symmetries of the scattering matrix presented in Proposition 13, the discrete spectrum is the set

$$\begin{aligned} Z=\left\{ \pm z_n,\, \pm z_n^*, \, \pm \frac{q_0^2}{z_n},\, \pm \frac{q_0^2}{z_n^*}\right\} _{n=1}^{N_1} \bigcup \Big \{\pm w_m, \,\pm w_m^*\Big \}_{m=1}^{N_2}, \end{aligned}$$

(79)

whose distributions are displayed in Fig. 3.

For convenience, we introduce the norming constants $b[z_0]$ and $d[z_0]$ such that

$$\begin{aligned} \begin{array}{ll} {\varPhi _{+1}(x, t; z_0)}=b[z_0]{\varPhi _{-2}(x, t; z_0)}, &{} \quad z_0\in Z\cap D^+, \\ {\varPhi _{+2}(x, t; z_0)}=b[z_0]{\varPhi _{-1}(x, t; z_0)}, &{} \quad z_0\in Z\cap D^-, \\ {\varPhi _{+1}'(x, t; z_0)-b[z_0]\,\varPhi _{-2}'(x, t; z_0)}=d[z_0]{\varPhi _{-2}(x, t; z_0)}, &{} \quad z_0\in Z\cap D^+,\\ {\varPhi _{+2}'(x, t; z_0)-b[z_0]\,\varPhi _{-1}'(x, t; z_0)}=d[z_0]{\varPhi _{-1}(x, t; z_0)}, &{} \quad z_0\in Z\cap D^-, \end{array} \end{aligned}$$

(80)

and define $A[z_0]$ and $B[z_0]$ as

$$\begin{aligned} A[z_0]&=\left\{ \begin{aligned} \frac{2\,b[z_0]}{s_{11}''(z_0)},\quad z_0\in Z\cap D^+,\\ \frac{2\,b[z_0]}{s_{22}''(z_0)},\quad z_0\in Z\cap D^-, \end{aligned}\right. \nonumber \\ B[z_0]&=\left\{ \begin{aligned} \frac{d[z_0]}{b[z_0]}-\frac{s_{11}'''(z_0)}{3\,s_{11}''(z_0)},\quad z_0\in Z\cap D^+,\\ \frac{d[z_0]}{b[z_0]}-\frac{s_{22}'''(z_0)}{3\,s_{22}''(z_0)},\quad z_0\in Z\cap D^-. \end{aligned}\right. \end{aligned}$$

(81)

Then, one can pose the compact forms:

$$\begin{aligned} \begin{aligned} \mathop {\mathrm {L_{-2}}}\limits _{z=z_0}\left[ \frac{\varPhi _{+1}(x, t; z)}{s_{11}(z)}\right]&=A[z_0]\,\varPhi _{-2}(x, t; z_0), \quad z_0\in Z\cap D^+,\\ \mathop {\mathrm {L_{-2}}}\limits _{z=z_0}\left[ \frac{\varPhi _{+2}(x, t; z)}{s_{22}(z)}\right]&=A[z_0]\,\varPhi _{-1}(x, t; z_0), \quad z_0\in Z\cap D^-,\\ \mathop {\mathrm {Res}}\limits _{z=z_0}\left[ \frac{\varPhi _{+1}(x, t; z)}{s_{11}(z)}\right]&=A[z_0]\left[ \varPhi _{-2}'(x, t; z_0)+B[z_0]\, \varPhi _{-2}(x, t; z_0)\right] , \quad z_0\in Z\cap D^+,\\ \mathop {\mathrm {Res}}\limits _{z=z_0}\left[ \frac{\varPhi _{+2}(x, t; z)}{s_{22}(z)}\right]&=A[z_0]\left[ \varPhi _{-1}'(x, t; z_0)+B[z_0]\, \varPhi _{-1}(x, t; z_0)\right] , \quad z_0\in Z\cap D^-, \end{aligned} \end{aligned}$$

(82)

where $\mathop {\mathrm {L_{-2}}}\limits _{z=z_0}\left[ f(x,t;z)\right]$ stands for the coefficient of $O\left( \left( z-z_0\right) ^{-2}\right)$ term in the Laurent series expansion of f(x, t; z) at $z=z_0$.

Proposition 14

Given $z_0\in Z$, the three symmetry relations for $A[z_0]$ and $B[z_0]$ are given as

• The first symmetry relation $A[z_0]=-A[z_0^*]^*, \quad B[z_0]=B[z_0^*]^*.$

• The second symmetry relation $A[z_0]=A[-z_0^*]^*, \quad B[z_0]=-B[-z_0^*]^*.$

• The third symmetry relation $A[z_0]=\dfrac{z_0^4\,q_-^*}{q_0^4\,q_-}\,A\left[ -\dfrac{q_0^2}{z_0}\right] ,\quad B[z_0]=\dfrac{q_0^2}{z_0^2}\,B\left[ -\dfrac{q_0^2}{z_0}\right] +\dfrac{2}{z_0}.$

Proof

According to the symmetries in the Proposition 13 and the definition for $A[z_0]$ and $B[z_0]$ given by Eq. (81) with Eq. (80), one can show that this Proposition holds. $\square$

Proposition 15

For $n=1, 2, \cdots , N_1$ and $m=1, 2, \cdots , N_2$, one derives

$$\begin{aligned} A[z_n]= & {} -A[z_n^*]^*=A[-z_n^*]^*=-A[-z_n] \nonumber \\= & {} \frac{z_n^4q_-^*}{q_0^4q_-}\,A\left[ -\frac{q_0^2}{z_n}\right] =\frac{z_n^4q_-^*}{q_0^4q_-}\,A\left[ \frac{q_0^2}{z_n^*}\right] ^* =-\frac{z_n^4q_-^*}{q_0^4q_-}\,A\left[ -\frac{q_0^2}{z_n^*}\right] ^*\nonumber \\= & {} -\frac{z_n^4q_-^*}{q_0^4q_-}\,A\left[ \frac{q_0^2}{z_n}\right] , \quad z_n\in Z_0,\\ A[w_m]= & {} -A[w_m^*]^*=A[-w_m^*]^*=-A[-w_m]=\frac{w_m^4q_-^*}{q_0^4q_-}A[w_m]^*, \quad w_m\in W_0,\nonumber \end{aligned}$$

(83)

$$\begin{aligned} B[z_n]= & {} B[z_n^*]^*=-B[-z_n^*]=-B[-z_n]=\frac{q_0^2}{z_n^2}\,B\left[ -\frac{q_0^2}{z_n}\right] +\frac{2}{z_n}\nonumber \\= & {} \frac{q_0^2}{z_n^2}\,B\left[ -\frac{q_0^2}{z_n^*}\right] ^*+\frac{2}{z_n}\nonumber \\= & {} -\frac{q_0^2}{z_n^2}\,B\left[ \frac{q_0^2}{z_n^*}\right] ^*+\frac{2}{z_n}=-\frac{q_0^2}{z_n^2}\,B\left[ \frac{q_0^2}{z_n}\right] +\frac{2}{z_n}, \quad z_n\in Z_0,\\ B[w_m]= & {} B[w_m^*]^*=-B[-w_m^*]^*=-B[-w_m]=-\frac{q_0^2}{w_m^2}B[w_m]^*+\frac{2}{w_m},\quad w_m\in W_0.\nonumber \end{aligned}$$

(84)

Proof

The proposition can be directly verified by the symmetry reductions in Propositions 13 and 14. $\square$

3.1.5 Asymptotic Behaviors

To propose and solve the matrix Riemann–Hilbert problem in the following inverse problem, one needs to give the asymptotic behaviors of the modified Jost solutions and scattering matrix as $z\rightarrow \infty$ and $z\rightarrow 0$, which differ from the case of ZBCs. The usual Wentzel–Kramers–Brillouin (WKB) expansions are used to deduce the asymptotic behaviors of the modified Jost solutions.

Proposition 16

The asymptotic behaviors for the modified Jost solutions are given as

$$\begin{aligned} \mu _{\pm }(x, t; z)=\left\{ \begin{array}{ll} \mathrm {e}^{\mathrm {i}v_{\pm }(x, t)\sigma _3}+O\left( 1/z\right) , &{} z\rightarrow \infty ,\\ \dfrac{\mathrm {i}}{z}\,\mathrm {e}^{\mathrm {i}v_{\pm }(x, t)\sigma _3}\sigma _3\,Q_{\pm }+O\left( 1\right) , &{} z\rightarrow 0, \end{array}\right. \end{aligned}$$

(85)

where

$$\begin{aligned} v_{\pm }(x, t)=\frac{1}{2}\int _{\pm \infty }^x\left( \left| q(y, t)\right| ^2-q_0^2\right) \mathrm {d}y. \end{aligned}$$

(86)

Proof

The following expansions of the modified Jost solutions $\mu _{\pm }(x, t; z)$ as $z\rightarrow \infty$ and $z\rightarrow 0$ are considered

$$\begin{aligned} \mu _{\pm }(x, t; z)=\left\{ \begin{array}{l} \displaystyle \sum _{j=0}^n\frac{\mu _{\pm }^{[j]}(x, t)}{z^j}+O\left( 1/z^{n+1}\right) , \quad \mathrm {as}\quad z\rightarrow \infty ,\\ \displaystyle \sum _{j=-1}^n\mu _{\pm }^{[j]}(x, t)\,z^{j}+O\left( z^{n+1}\right) , \quad \mathrm {as}\quad z\rightarrow 0. \end{array}\right. \end{aligned}$$

(87)

We substitute $\varPhi _{\pm }(x, t; z)=\mu _{\pm }(x, t; z)\,\mathrm {e}^{\mathrm {i}\theta (x, t; z)\sigma _3}$ with these expansions into Eq. (15). By matching the $O\left( z^2\right)$, $O\left( z\right)$ and $O\left( 1\right)$ terms as $z\rightarrow \infty$, and $O\left( z^{-3}\right)$, $O\left( z^{-2}\right)$ and $O\left( z^{-1}\right)$ terms as $z\rightarrow 0$, and combining with the asymptotic behaviors of the modified Jost solutions $\mu _{\pm }(x, t; z)$ as $x\rightarrow \pm \infty$, one deduces the asymptotic behaviors as $z\rightarrow \infty$ and $z\rightarrow 0$. $\square$

The asymptotic behaviors of the scattering matrix can be yielded by the Wronskian representations of the scattering matrix and the asymptotic behaviors of the modified Jost solutions.

Proposition 17

The asymptotic behaviors of the scattering matrix are

$$\begin{aligned} S(z)=\left\{ \begin{array}{ll} \mathrm {e}^{-\mathrm {i}v(t)\sigma _3}+O\left( 1/z\right) , &{} z\rightarrow \infty , \\ \mathrm {diag}\left( \dfrac{q_-}{q_+}, \, \dfrac{q_+}{q_-}\right) \mathrm {e}^{\mathrm {i}v\sigma _3}+O\left( z\right) , &{} z\rightarrow 0, \end{array}\right. \end{aligned}$$

(88)

where v(t) is dependent on the variable t and given by

$$\begin{aligned} v(t)=\frac{1}{2}\int _{-\infty }^{+\infty }\left( \left| q(y, t)\right| ^2-q_0^2\right) \,\mathrm {d}y. \end{aligned}$$

(89)

Proof

From the definition or Wronskian presentations of scattering matrix given by Eq. (74) and the asymptotic behaviors of the modified Jost solutions given by Eq. (87) in Proposition 16, one can yield the asymptotic behaviors (88) of the scattering matrix. Substituting $\varPhi _{\pm }(x, t; z)=\mu _{\pm }(x, t; z)\,\mathrm {e}^{\mathrm {i}\theta (x, t; z)\sigma _3}$ with these expansions into Eq. (16) and matching the $O\left( z^4\right)$, $O\left( z^3\right)$, $O\left( z^2\right)$, $O\left( z\right)$ and $O\left( 1\right)$ in order, one can yield $v_{t}\not =0$ as $x\rightarrow \mp \infty$. That is, v(t) is dependent on the variable t. $\square$

3.2 Inverse Scattering Problem with NZBCs and Double Poles

3.2.1 The Matrix Riemann–Hilbert Problem with NZBCs and Double Poles

The matrix Riemann–Hilbert problem for the case of NZBCs can also be established similarly to one of ZBCs in Sec. 2 (see, e.g., Refs. Shabat and Zakharov 1972; Ablowitz et al. 1973; Prinari et al. 2006; Demontis et al. 2013, 2014; Biondini and Kovačič 2014; Prinari 2015; Pichler and Biondini 2017; Zhang and Yan 2020a, b). To pose and solve the Riemann–Hilbert problem conveniently, we define ${{\widehat{\eta }}}_n=-\frac{q_0^2}{\eta _n}$ with

$$\begin{aligned} \eta _n=\left\{ \begin{aligned}&z_n,&n&=1, 2, \cdots , N_1,\\ -{}&z_{n-N_1},&n&=N_1+1, N_1+2, \cdots , 2N_1,\\&\frac{q_0^2}{z^*_{n-2N_1}},&n&=2N_1+1, 2N_1+2, \cdots , 3N_1,\\ -{}&\frac{q_0^2}{z^*_{n-3N_1}},&n&=3N_1+1,3N_1+2, \cdots , 4N_1,\\&w_{n-4N_1},&n&=4N_1+1, 4N_1+2, \cdots , 4N_1+N_2,\\ -{}&w_{n-4N_1-N_2},&n&=4N_1+N_2+1, 4N_1+N_2+2, \cdots , 4N_1+2N_2. \end{aligned}\right. \end{aligned}$$

(90)

Then, a matrix Riemann–Hilbert problem can be proposed as follows.

Proposition 18

Let the sectionally meromorphic matrix be

$$\begin{aligned} M(x, t; z)=\left\{ \begin{aligned} \left( \frac{\mu _{+1}(x, t; z)}{s_{11}(z)},\, \mu _{-2}(x, t; z)\right) ,\quad z\in D^+, \\ \left( \mu _{-1}(x, t; z),\, \frac{\mu _{+2}(x, t; z)}{s_{22}(z)}\right) , \quad z\in D^-, \end{aligned}\right. \end{aligned}$$

(91)

and

$$\begin{aligned} M^{\pm }(x, t; z)=\displaystyle \lim _{\begin{array}{c} z'\rightarrow z\\ z'\in D^{\pm } \end{array}}M(x, t; z'), \quad z\in \Sigma . \end{aligned}$$

(92)

Then, a multiplicative matrix Riemann–Hilbert problem is proposed:

• Analyticity: M(x, t; z) is analytic in $\left( D^+\cup D^-\right) \backslash Z$ and has the double poles in Z. The principal parts of the Laurent series of M at each double pole are determined as

  $$\begin{aligned} \begin{aligned} \displaystyle \mathop {\mathrm {L_{-2}}}\limits _{z=\eta _n}M&=\left( A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\mu _{-2}(x, t; \eta _n), 0\right) , \\ \displaystyle \mathop {\mathrm {L_{-2}}}\limits _{z={{\widehat{\eta }}}_n}M&=\left( 0, A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; {{\widehat{\eta }}}_n)}\mu _{-1}(x, t; {{\widehat{\eta }}}_n)\right) ,\\ \displaystyle \mathop {\mathrm {Res}}\limits _{z=\eta _n}M&=\left( A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\left\{ \mu _{-2}'(x, t; \eta _n)\right. \right. \\&\quad \left. \left. +\Big [B[\eta _n]-2\mathrm {i}\theta '(x, t; \eta _n)\Big ]\mu _{-2}(x, t; \eta _n)\right\} , 0\right) ,\\ \displaystyle \mathop {\mathrm {Res}}\limits _{z={{\widehat{\eta }}}_n}M&=\left( 0, A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; {{\widehat{\eta }}}_n)}\left\{ \mu _{-1}'(x, t; {{\widehat{\eta }}}_n)\right. \right. \\&\quad \left. \left. +\Big [B[{{\widehat{\eta }}}_n]+2\mathrm {i}\theta '(x, t; {{\widehat{\eta }}}_n)\Big ]\mu _{-1}(x, t; {{\widehat{\eta }}}_n)\right\} \right) , \end{aligned} \end{aligned}$$

  (93)

  where the prime denotes the partial derivative with respect to z.

• Jump condition:

  $$\begin{aligned} M^-(x, t; z)=M^+(x, t; z)\left( I-J(x, t; z)\right) , \quad z\in \Sigma , \end{aligned}$$

  (94)

  where

  $$\begin{aligned} J(x, t; z)= \mathrm {e}^{\mathrm {i}\theta (x, t; z){{\widehat{\sigma }}}_3} \begin{bmatrix} 0&{}-{{\tilde{\rho }}}(z)\\ \rho (z)&{}\rho (z)\,{{\tilde{\rho }}}(z) \end{bmatrix}. \end{aligned}$$

  (95)

• Asymptotic behaviors:

  $$\begin{aligned} M(x, t; z)=\left\{ \begin{array}{ll} \mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}+O\left( 1/z\right) , &{} z\rightarrow \infty ,\qquad \\ \dfrac{\mathrm {i}}{z}\,\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\sigma _3\,Q_-+O\left( 1\right) , &{} z\rightarrow 0. \end{array}\right. \end{aligned}$$

  (96)

Proof

The analyticity of M(x, t; z) can be verified from the analyticity of the modified Jost solutions and scattering data in Propositions 10 with Eq. (71) and Proposition 11. It follows from Eqs. (71), (82), and (91) that

$$\begin{aligned} \begin{aligned} \displaystyle \mathop {\mathrm {L_{-2}}}\limits _{z=\eta _n}\left[ \frac{\mu _{+1}(x, t; z)}{s_{11}(z)}\right]&=A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\mu _{-2}(x, t; \eta _n), \\ \displaystyle \mathop {\mathrm {L_{-2}}}\limits _{z={{\widehat{\eta }}}_n}\left[ \frac{\mu _{+2}(x, t; z)}{s_{22}(z)}\right]&=A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; {{\widehat{\eta }}}_n)}\mu _{-1}(x, t; {{\widehat{\eta }}}_n), \\ \displaystyle \mathop {\mathrm {Res}}\limits _{z=\eta _n}\left[ \frac{\mu _{+1}(x, t; z)}{s_{11}(z)}\right]&=A[\eta _n]\,\mathrm {e}^{-2\mathrm {i}\theta (x, t; \eta _n)}\left\{ \mu _{-2}'(x, t; \eta _n)\right. \\&\quad \left. +\Big [B[\eta _n]-2\mathrm {i}\theta '(x, t; \eta _n)\Big ]\mu _{-2}(x, t; \eta _n)\right\} , \\ \displaystyle \mathop {\mathrm {Res}}\limits _{z={{\widehat{\eta }}}_n}\left[ \frac{\mu _{+2}(x, t; z)}{s_{22}(z)}\right]&=A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i}\theta (x, t; {{\widehat{\eta }}}_n)}\left\{ \mu _{-1}'(x, t; {{\widehat{\eta }}}_n)\right. \\&\quad \left. +\Big [B[{{\widehat{\eta }}}_n]+2\mathrm {i}\theta '(x, t; {{\widehat{\eta }}}_n)\Big ]\mu _{-1}(x, t; {{\widehat{\eta }}}_n)\right\} , \end{aligned} \end{aligned}$$

(97)

from which we determine the principal parts of the Laurent series of M(x, t; z) at each double pole, that is, Eq. (93) holds. Similarly to the Riemann–Hilbert problem of ZBCs in Proposition 8 of Sec. 2, the proof of the jump condition (94) can also be completed. The asymptotic behaviors (96) of M(x, t; z) can be found from Propositions 16 and 17 for the asymptotic behaviors of modified Jost solutions and scattering matrix. $\square$

Proposition 19

The solution of the matrix Riemann–Hilbert problem with double poles in Proposition 18 can be expressed as

$$\begin{aligned} \begin{aligned} M(x, t; z)&=\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\left( I+\frac{\mathrm {i}}{z}\,\sigma _3\,Q_-\right) +\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{(M^+J)(x, t; \zeta )}{\zeta -z}\,\mathrm {d}\zeta \\&\quad +\sum _{n=1}^{4N_1+2N_2}\left( \!C_n(z)\left[ \mu _{-2}'(\eta _n) +\left( D_n+\frac{1}{z-\eta _n}\right) \mu _{-2}(\eta _n)\right] ,\right. \\&\quad \left. {{\widehat{C}}}_n(z)\left[ \mu _{-1}'({{\widehat{\eta }}}_n) +\left( {{\widehat{D}}}_n+\frac{1}{z-{{\widehat{\eta }}}_n}\right) \mu _{-1}({{\widehat{\eta }}}_n)\right] \right) , \end{aligned} \end{aligned}$$

(98)

where $\int _\Sigma$ stands for an integral along the oriented contour displayed in Fig. 3,

$$\begin{aligned} C_n(z)= & {} \frac{A[\eta _n]}{z-\eta _n}\,\mathrm {e}^{-2\mathrm {i}\theta (\eta _n)}, \,\, D_n=B[\eta _n]-2\,\mathrm {i}\,\theta '(\eta _n), \,\, {{\widehat{C}}}_n(z)=\frac{A[{{\widehat{\eta }}}_n]}{z-{{\widehat{\eta }}}_n}\,\mathrm {e}^{2\mathrm {i}\theta ({{\widehat{\eta }}}_n)}, \nonumber \\ {{\widehat{D}}}_n= & {} B[{{\widehat{\eta }}}_n]+2\,\mathrm {i}\,\theta '({{\widehat{\eta }}}_n), \end{aligned}$$

(99)

$\mu _{-2}(\eta _n)$ and $\mu _{-2}'(\eta _n)$ are determined by $\mu _{-1}({{\widehat{\eta }}}_n)$ and $\mu _{-1}'({{\widehat{\eta }}}_n)$ as

$$\begin{aligned} \mu _{-2}(\eta _n)=\frac{\mathrm {i}q_-}{\eta _n}\,\mu _{-1}\left( {{\widehat{\eta }}}_n\right) , \quad \mu _{-2}'(\eta _n)=-\frac{\mathrm {i}q_-}{\eta _n^2}\,\mu _{-1}({{\widehat{\eta }}}_n)+\frac{\mathrm {i}q_-q_0^2}{\eta _n^3}\,\mu _{-1}'({{\widehat{\eta }}}_n), \end{aligned}$$

(100)

and $\mu _{-1}({{\widehat{\eta }}}_n)$ and $\mu _{-1}'({{\widehat{\eta }}}_n)$ satisfy the linear system of $8N_1+4N_2$ equations

$$\begin{aligned}&\displaystyle \sum _{n=1}^{4N_1+2N_2}{{\widehat{C}}}_n(\eta _k)\,\mu _{-1}'({{\widehat{\eta }}}_n)+\left[ {{\widehat{C}}}_n(\eta _k)\left( {{\widehat{D}}}_n+\frac{1}{\eta _k-{{\widehat{\eta }}}_n}\right) -\frac{\mathrm {i}q_-}{\eta _k}\,\delta _{k, n}\right] \mu _{-1}({{\widehat{\eta }}}_n) \\&\quad \displaystyle =-\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\begin{bmatrix} \dfrac{\mathrm {i}q_-}{\eta _k} \\ 1 \end{bmatrix} -\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _2(\zeta )}{\zeta -\eta _k}\,\mathrm {d}\zeta , \\&\displaystyle \sum _{n=1}^{4N_1+2N_2}\left( \frac{{{\widehat{C}}}_n(\eta _k)}{\eta _k-{{\widehat{\eta }}}_n}+\frac{\mathrm {i}q_-q_0^2}{\eta _k^3}\, \delta _{k, n}\right) \mu _{-1}'({{\widehat{\eta }}}_n)\\&\quad +\left[ \frac{{{\widehat{C}}}_n(\eta _k)}{\eta _k-{{\widehat{\eta }}}_n} \left( {{\widehat{D}}}_n+\frac{2}{\eta _k-{{\widehat{\eta }}}_n}\right) -\frac{\mathrm {i}q_-}{\eta _k^2}\,\delta _{k, n}\right] \mu _{-1}({{\widehat{\eta }}}_n) \\&\quad \displaystyle =-\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\begin{bmatrix} \dfrac{\mathrm {i}q_-}{\eta _k^2} \\ 0 \end{bmatrix} +\frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\left( M^+J\right) _2(\zeta )}{\left( \zeta -\eta _k\right) ^2}\,\mathrm {d}\zeta \end{aligned}$$

with $k=1, 2, \cdots , 4N_1+2N_2$ and $\delta _{k,n}$ being the Kronecker $\delta$-symbol.

Proof

Similarly to the proof of Proposition 9 for the case of ZBCs, to regularize the Riemann–Hilbert problem established in Proposition 18 for the case of NZBCs, one has to subtract out the asymptotic values as $z\rightarrow \infty$ and $z\rightarrow 0$ given by Eq. (96) and the singular contributions. Then, the jump condition (94) becomes

$$\begin{aligned}&M^--\mathrm {e}^{\mathrm {i}v_-\sigma _3}-\frac{\mathrm {i}}{z} \,\mathrm {e}^{\mathrm {i}v_-\sigma _3}\sigma _3\,Q_-\\&\quad -\sum _{n=1}^{4N_1+2N_2} \left[ \frac{\mathop {\mathrm {L_{-2}}}\limits _{z=\eta _n}[M]}{\left( z-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{z=\eta _n}[M]}{z-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{z={{\widehat{\eta }}}_n}[M]}{\left( z-{{\widehat{\eta }}}_n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{z={{\widehat{\eta }}}_n}[M]}{z-{{\widehat{\eta }}}_n}\right] \\&\quad =M^+-\mathrm {e}^{\mathrm {i}v_-\sigma _3}-\frac{\mathrm {i}}{z}\, \mathrm {e}^{\mathrm {i}v_-\sigma _3}\sigma _3\,Q_-\\&\qquad -\sum _{n=1}^{4N_1+2N_2} \left[ \frac{\mathop {\mathrm {L_{-2}}}\limits _{z=\eta _n}[M]}{\left( z-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{z=\eta _n}[M]}{z-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{z={{\widehat{\eta }}}_n}[M]}{\left( z-{{\widehat{\eta }}}_n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{z={{\widehat{\eta }}}_n}[M]}{z -{{\widehat{\eta }}}_n}\right] -M^+\,J, \end{aligned}$$

where

$$\begin{aligned} \displaystyle \mathop {{\mathrm{L}}_{-2}}_{z=\eta _n}[M]= & {} \left( \mathop {{\mathrm{L}}_{-2}}_{z=\eta _n}\left[ \frac{\mu _{+1}(x,t;z)}{s_{11}(z)}\right] ,\, 0\right) ,\quad \mathop {{\mathrm{Res}}}_{z=\eta _n}[M]=\left( \mathop {{\mathrm{Res}}}_{z=\eta _n}\left[ \frac{\mu _{+1}(x,t;z)}{s_{11}(z)}\right] ,\, 0\right) , \\ \displaystyle \mathop {{\mathrm{L}}_{-2}}_{z={{\widehat{\eta }}}_n}[M]= & {} \left( 0,\, \mathop {{\mathrm{L}}_{-2}}_{z={{\widehat{\eta }}}_n}\left[ \frac{\mu _{+2}(x,t;z)}{s_{22}(z)}\right] \right) ,\quad \mathop {{\mathrm{Res}}}_{z={{\widehat{\eta }}}_n}[M]=\left( 0,\, \mathop {{\mathrm{Res}}}_{z={{\widehat{\eta }}}_n}\left[ \frac{\mu _{+2}(x,t;z)}{s_{22}(z)}\right] \right) , \end{aligned}$$

which are given by Eq. (93). By the Cauchy projectors (54) and Plemelj’s formulae (Biondini and Kovačič 2014), the proof follows. The technique of the proof is fairly standard and one can also refer to Refs. Pichler and Biondini (2017), Zhang and Yan (2020a) for more details. $\square$

3.2.2 Reconstruction Formula for the Potential

Proposition 20

The reconstruction formula for the potential of the DNLS equation (1) with NZBCs is deduced by

$$\begin{aligned} q(x, t)=\mathrm {e}^{\mathrm {i}v_-(x, t)}\left( q_-\,\mathrm {e}^{\mathrm {i}v_-(x, t)}-\mathrm {i}\,\alpha ^\mathrm {T}\gamma \right) , \end{aligned}$$

(101)

where the column vectors $\alpha =(\alpha ^{(1)},\,\alpha ^{(2)})^\mathrm {T}$ and $\gamma =(\gamma ^{(1)},\,\gamma ^{(2)})^\mathrm {T}$ are given by

$$\begin{aligned} \begin{array}{ll} \alpha ^{(1)}=\left( A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i} \theta ({{\widehat{\eta }}}_n)}{{\widehat{D}}}_n\right) _{1\times \left( 4N_1+2N_2\right) }, &{} \quad \alpha ^{(2)}=\left( A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i} \theta ({{\widehat{\eta }}}_n)}\right) _{1\times \left( 4N_1+2N_2\right) }, \\ \gamma ^{(1)}=\left( \mu _{-11}(\eta _n^*)\right) _{1\times \left( 4N_1+2N_2\right) }, &{} \quad \gamma ^{(2)}=\left( \mu _{-11}'({{\widehat{\eta }}}_n)\right) _{1\times \left( 4N_1+2N_2\right) }. \end{array}\nonumber \\ \end{aligned}$$

(102)

Proof

It follows from the solution of the matrix Riemann–Hilbert problem in Proposition 19 that one can find the asymptotic behavior of M(x, t; z):

$$\begin{aligned} M(x, t; z)=\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}+\frac{M^{[1]}(x, t)}{z}+O\left( \frac{1}{z^2}\right) , \quad z\rightarrow \infty , \end{aligned}$$

(103)

where

$$\begin{aligned}&M^{[1]}(x, t)=\mathrm {i}\,\mathrm {e}^{\mathrm {i}v_-(x, t)\sigma _3}\sigma _3\, Q_--\frac{1}{2\pi \mathrm {i}}\int _\Sigma \left( M^+J\right) (x,t;\zeta )\,\mathrm {d}\zeta \\&\quad +\sum _{n=1}^{4N_1+2N_2}\left[ A[\eta _n]\,\mathrm {e}^{-2\mathrm {i} \theta (\eta _n)}\left( \mu _{-2}'(\eta _n)+D_n\mu _{-2}(\eta _n)\right) , A[{{\widehat{\eta }}}_n]\,\mathrm {e}^{2\mathrm {i}\theta ({{\widehat{\eta }}}_n)} \left( \mu _{-1}'({{\widehat{\eta }}}_n)\right. \right. \\&\quad \left. \left. +{{\widehat{D}}}_n\mu _{-1} ({{\widehat{\eta }}}_n)\right) \right] . \end{aligned}$$

Substituting $M(x, t; z)\mathrm {e}^{-\mathrm {i}\theta (x, t; z)\sigma _3}$ into Eq. (15) and matching the $O\left( z\right)$ term, the proposition follows. $\square$

3.2.3 Trace Formulae and Theta Condition

The so-called trace formulae are that the scattering coefficients $s_{11}(z)$ and $s_{22}(z)$ are formulated in terms of the discrete spectrum Z and reflection coefficients $\rho (z)$ and ${{\tilde{\rho }}}(z)$. Recall that $s_{11}(z)$ is analytic in $D^+$ and $s_{22}(z)$ is analytic in $D^-$. The discrete spectral points $\eta _n$’s are the double zeros of $s_{11}(z)$, while ${{\widehat{\eta }}}_n$’s are the double zeros of $s_{22}(z)$. Define

$$\begin{aligned} \begin{aligned} \beta ^+(z)=s_{11}(z)\prod _{n=1}^{4N_1+2N_2}\left( \frac{z-{{\widehat{\eta }}}_n}{z-\eta _n}\right) ^2\mathrm {e}^{\mathrm {i}v}, \quad \beta ^-(z)=s_{22}(z)\prod _{n=1}^{4N_1+2N_2}\left( \frac{z-\eta _n}{z-{{\widehat{\eta }}}_n}\right) ^2\mathrm {e}^{-\mathrm {i}v}. \end{aligned} \end{aligned}$$

(104)

Then, one can know that $\beta ^+(z)$ and $\beta ^-(z)$ are analytic and have no zero in $D_+$ and $D_-$, respectively. Moreover, $\beta ^{\pm }(z)\rightarrow 1$ as $z\rightarrow \infty$. Besides, $-\log \beta ^+(z)-\log \beta ^-(z)=\log \left[ 1-\rho (z)\,{{\tilde{\rho }}}(z)\right]$. Applying the Cauchy projectors and Plemelj’s formulae (Biondini and Kovačič 2014), one has

$$\begin{aligned} \log \beta ^{\pm }(z)=\mp \frac{1}{2\pi \mathrm {i}}\int _\Sigma \frac{\log \left[ 1-\rho (\zeta )\,{{\tilde{\rho }}} (\zeta )\right] }{\zeta -z}\,\mathrm {d}\zeta , \quad z\in D^{\pm }. \end{aligned}$$

(105)

The trace formulae are given by

$$\begin{aligned} \begin{aligned} s_{11}(z)&=\exp \left( \frac{\mathrm {i}}{2\pi } \int _\Sigma \frac{\log \left[ 1-{{\tilde{\rho }}}(\zeta )\,\rho (\zeta )\right] }{\zeta -z}\,\mathrm {d}\zeta \right) \prod _{n=1}^{4N_1+2N_2} \left( \frac{z-\eta _n}{z-{{\widehat{\eta }}}_n}\right) ^2\mathrm {e}^{-\mathrm {i}v},\\ s_{22}(z)&=\exp \left( -\frac{\mathrm {i}}{2\pi } \int _\Sigma \frac{\log \left[ 1-{{\tilde{\rho }}}(\zeta )\,\rho (\zeta )\right] }{\zeta -z}\,\mathrm {d}\zeta \right) \prod _{n=1}^{4N_1+2N_2} \left( \frac{z-{{\widehat{\eta }}}_n}{z-\eta _n}\right) ^2\mathrm {e}^{\mathrm {i}v}. \end{aligned} \end{aligned}$$

(106)

As $z\rightarrow 0$, the theta condition is obtained. That is to say, there exists $j\in {\mathbb {Z}}$ such that

$$\begin{aligned} \mathrm {arg}\left( \frac{q_-}{q_+}\right) +2v= & {} 16\sum _{n=1}^{N_1} \mathrm {arg}(z_n)+8\sum _{m=1}^{N_2}\mathrm {arg}(w_m)+2j\pi \nonumber \\&+\frac{1}{2\pi }\int _\Sigma \frac{\log \left( 1-\rho (\zeta ){{\tilde{\rho }}}(\zeta )\right) }{\zeta } \,\mathrm {d}\zeta . \end{aligned}$$

(107)

3.2.4 Reflectionless Potential: Double-Pole Soliton Solutions

We consider the case of the reflectionless potential: $\rho (z)={{\widehat{\rho }}}(z)=0$, in which the part jump matrix J in Eq. (95) is simplified as $J=0_{2\times 2}$. From the Volterra integral equation (72), one can derive $\varPhi _{\pm }(x, t; q_0)=E_{\pm }(q_0)$. Combining with the definition of scattering matrix, one has $S(q_0)=I$ and $q_+=q_-$. From the theta condition, there exists $j\in {\mathbb {Z}}$ such that

$$\begin{aligned} v=8\sum _{n=1}^{N_1}\mathrm {arg}(z_n)+4\sum _{m=1}^{N_2}\mathrm {arg}(w_m)+j\pi . \end{aligned}$$

(108)

Theorem 2

The explicit formula for the double-pole solution of the DNLS Eq. (1) with NZBCs is found by

$$\begin{aligned} q(x, t)=\left( \frac{\mathrm {det}\left( {{\widehat{G}}}\right) }{\mathrm {det}\left( {{\widehat{H}}}\right) }\right) ^2\frac{\mathrm {det} \left( H\right) }{\mathrm {det}\left( G\right) }\left( 1+\frac{\mathrm {det} \left( H\right) }{\mathrm {det}\left( G\right) }\right) q_-, \end{aligned}$$

(109)

where

$$\begin{aligned} G= & {} \begin{bmatrix} H&{}\beta \\ \alpha ^T&{}0\end{bmatrix},\quad {{\widehat{G}}}=\begin{bmatrix} {{\widehat{H}}}&{}\beta \\ \alpha ^T&{}0\end{bmatrix}, \quad \beta =\begin{bmatrix} \beta ^{(1)}\\ \beta ^{(2)} \end{bmatrix},\\ \beta ^{(1)}= & {} \left( \frac{1}{\eta _j}\right) _{\left( 4N_1+2N_2\right) \times 1}, \quad \beta ^{(2)}=\left( \frac{1}{\eta _j^2}\right) _{\left( 4N_1+2N_2\right) \times 1}, \end{aligned}$$

the $\left( 8N_1+4N_2\right) \times \left( 8N_1+4N_2\right)$ matrix H is defined as

$$\begin{aligned} H&=\begin{bmatrix} H^{(1, 1)}&{} H^{(1, 2)}\\ H^{(2, 1)}&{} H^{(2, 2)} \end{bmatrix},\quad H^{(m, j)}=\left( h^{(m, j)}_{s, n}\right) _{\left( 4N_1+2N_2\right) \times \left( 4N_1+2N_2\right) },\quad m, j=1, 2, \\ \displaystyle h^{(1, 1)}_{s, n}&={{\widehat{C}}}_n(\eta _s)\left( {{\widehat{D}}}_n +\frac{1}{\eta _s-{{\widehat{\eta }}}_n}\right) -\frac{\mathrm {i}q_-}{\eta _s}\,\delta _{s,n}, \quad h^{(1, 2)}_{s, n}={{\widehat{C}}}_n(\eta _s), \\ \displaystyle h^{(2, 1)}_{s, n}&=\frac{{{\widehat{C}}}_n(\eta _s)}{\eta _s -{{\widehat{\eta }}}_n}\left( {{\widehat{D}}}_n+\frac{2}{\eta _s -{{\widehat{\eta }}}_n}\right) -\frac{\mathrm {i}q_-}{\eta _s^2}\,\delta _{s, n}, \quad h^{(2, 2)}_{s, n}=\frac{{{\widehat{C}}}_n(\eta _s)}{\eta _s-{{\widehat{\eta }}}_n} +\frac{\mathrm {i}q_-q_0^2}{\eta _s^3}\,\delta _{s, n}, \end{aligned}$$

and the $\left( 8N_1+4N_2\right) \times \left( 8N_1+4N_2\right)$ matrix ${{\widehat{H}}}$ is defined as

Proof

From the reconstruction formula (101), one can deduce the implicit formula

$$\begin{aligned} q(x, t)=\left( 1+\frac{\mathrm {det}\left( G\right) }{\mathrm {det}\left( H\right) }\right) q_-\,\mathrm {e}^{2\mathrm {i}v_-(x, t)}. \end{aligned}$$

(110)

From the Volterra integral equation (72) and trace formula (106), one has

$$\begin{aligned} M= & {} E_-+k(z)\sum _{n=1}^{4N_1+2N_2}\left( \frac{\mathop {\mathrm {L_{-2}}}\limits _{z=\eta _n} \left[ M/k(z)\right] }{\left( z-\eta _n\right) ^2} +\frac{\mathop {\mathrm {Res}}\limits _{z=\eta _n}\left[ M/k(z)\right] }{z-\eta _n} +\frac{\mathop {\mathrm {L_{-2}}}\limits _{z={{\widehat{\eta }}}_n} \left[ M/k(z)\right] }{\left( z-{{\widehat{\eta }}}_n\right) ^2}\right. \nonumber \\&\left. +\frac{\mathop {\mathrm {Res}}\limits _{z={{\widehat{\eta }}}_n} \left[ M/k(z)\right] }{z-{{\widehat{\eta }}}_n}\right) , \end{aligned}$$

(111)

with which one can solve the $\gamma$ defined by Eq. (102) explicitly. Substituting $\gamma$ into the formula for the reflectionless potential, we yield another implicit formula

$$\begin{aligned} q(x, t)=\left( \mathrm {e}^{\mathrm {i}v_-(x, t)}+\frac{\mathrm {det}\left( {{\widehat{G}}}\right) }{\mathrm {det}\left( {{\widehat{H}}}\right) }\right) q_-\,\mathrm {e}^{\mathrm {i}v_-(x, t)}. \end{aligned}$$

(112)

From Eqs. (110) and (112), the explicit formula of the double-pole solution is derived. Then, we complete the proof. $\square$

Fig. 4

Double-pole bright–dark soliton solutions of the DNLS equation with NZBCs and $N_1=0, N_2=1, q_{\pm }=1, w_1=\mathrm {e}^{\frac{\pi }{4}\mathrm {i}}, A[w_1]=\mathrm {i}, B[w_1]=1+\left( 1-\sqrt{2}\right) \mathrm {i}.$ (a) 3D profile; (b) intensity profile; (c) profiles for $t=0, \pm 2$

For example, we have the double-pole solutions of the DNLS equation with NZBCs:

• When $N_1=0,\, N_2=1,\, q_{\pm }=1,\, w_1=\mathrm {e}^{\frac{\pi }{4}\mathrm {i}},\, A[w_1]=\mathrm {i},\, B[w_1]=1+\left( 1-\sqrt{2}\right) \mathrm {i}$, we have the double-pole dark–bright solitons $q(x,t)=P_{11}(x,t)/P_{12}(x,t)$ with

  $$\begin{aligned} P_{11}(x,t)&=\Big \{2[1+\mathrm {i}-\sqrt{2}(1+(1+\mathrm {i})t)]\mathrm {e}^{4t+2x}\\&\quad +2i[t^2+t+1+\sqrt{2}(t+1/2)]\mathrm {e}^{2t+x} \\&\quad +2[1-\mathrm {i}+\sqrt{2}(\mathrm {i}+(\mathrm {i}-1)t)]\Big \}^2\\&\quad \Big \{[\sqrt{2}(1-2i+2t)+2(\mathrm {i}-t^2)+2(2i-1)t]\mathrm {e}^{4t+2x} \\&\quad +(\mathrm {i}\sqrt{2}t-\mathrm {i}+\sqrt{2})\mathrm {e}^{6t+3x}+(\mathrm {e}^{8t+4x}+1)/2\\&\quad +[\sqrt{2}(it+1+\mathrm {i})-\mathrm {i}]\mathrm {e}^{2t+x}\Big \}, \\ P_{12}(x,t)&=\Big \{[\sqrt{2}((1+\mathrm {i})t+1)-1-\mathrm {i}]\mathrm {e}^{4t+2x}+[2\sqrt{2}(1-\mathrm {i}+2t) \\&\quad -2+2i-4t^2+4(\mathrm {i}-1)t]\mathrm {e}^{2t+x} \\&\quad +\sqrt{2}(\mathrm {i}+(\mathrm {i}-1)t)+1-\mathrm {i}\Big \}^2\Big \{[t^2+t+1-\sqrt{2}(t+1/2)]\mathrm {e}^{4t+2x}\\&\quad +(1-\sqrt{2}t)/2\mathrm {e}^{6t+3x} \\&\quad +(\mathrm {e}^{8t+4x}+1)/4+[\sqrt{2}(t+1)-1]/2\mathrm {e}^{2t+x}\Big \}, \end{aligned}$$

  which is a semi-rational soliton that differs from the simple-pole solutions usually expressed by the exponential functions even if the double-pole soliton displays the interaction of dark and bright solitons (see Fig. 4a-c). Figure 4c displays the Gaussian-like profile with NZBCs when $t=0$, and the combinations of Gaussian-like and dark soliton profiles when $t\not =0$ (e.g., $t=\pm 2$).

• As $N_1=1,\, N_2=0,\, q_{\pm }=1,\, z_1=2\mathrm {e}^{\frac{\pi }{6}\mathrm {i}},\, A[w_1]=B[w_1]=\mathrm {i}$, we have the interaction of two breathers, which is complicated and omitted here (see Fig. 5).

Fig. 5

Double-pole breather–breather solutions of the DNLS equation with NZBCs and $N_1=1, N_2=0, q_{\pm }=1, z_1=2\mathrm {e}^{\frac{\pi }{6}\mathrm {i}}, A[w_1]=B[w_1]=\mathrm {i}.$ (a) 3D profile; (b) intensity profile; (c) profiles for $t=-2,\, 0,\, 4$

Remark

The obtained N double-pole solitons (109) of the DNLS equation (1) with NZBCs can be applied to the modified NLS equation (2) by the gauge transformation (Ichikawa et al. 1980).

4 Conclusions and Discussions

In conclusion, we have presented the inverse scattering transforms for the DNLS equation with double zeros of analytical scattering coefficients under ZBCs and NZBCs at infinity. A rigorous theory for direct and inverse problems was proposed. The direct scattering illustrates the analyticity, symmetries, discrete spectrum, and asymptotic behaviors. The inverse problem can be solved with the aid of a matrix Riemann–Hilbert problem, which can derive the trace formula and reflectionless potential. Moreover, the reflectionless potential with double poles is deduced explicitly by the determinants. Some representative semi-rational bright–bright solitons, dark–bright solitons, and breather–breather solutions are examined in detail. Though there exists a gauge transform (Wadati and Sogo 1983) between the NLS equation and DNLS equation (1), but it is not a trivial problem from the IST of focusing NLS equation with NZBCs to one of the DNLS equation with NZBCs by comparing Refs. Biondini and Kovačič (2014), Pichler and Biondini (2017) for the NLS equation and this paper about the DNLS equation (1).

The used idea and results for the DNLS equation (1) with ZBCs/NZBCs can also be extended to other types of DNLS equations with ZBCs/NZBCS such as the Chen–Lee–Liu equation, Gerdjikov–Ivanov equation, and Kundu equation (see them are listed in the Introduction) since they all belong to the modified Zakharov–Shabat eigenvalue problem (15,16) (Kundu 1984, 1987). Moreover, we will study the long-time asymptotic behaviors for the DNLS equation with NZBCs via the modified Deift–Zhou method (Biondini and Mantzavinos 2017) in another literature.