Inverse scattering transform for a nonlocal derivative nonlinear Schrödinger equation

Abstract

We give a detailed discussion of a nonlocal derivative nonlinear Schrödinger (NL-DNLS) equation with zero boundary conditions at infinity in terms of the inverse scattering transform. The direct scattering problem involves discussions of the analyticity, symmetries, and asymptotic behavior of the Jost solutions and scattering coefficients, and the distribution of the discrete spectrum points. Because of the symmetries of the NL-DNLS equation, the discrete spectrum is different from those for DNLS-type equations. The inverse scattering problem is solved by the method of a matrix Riemann–Hilbert problem. The reconstruction formula, the trace formula, and explicit solutions are presented. The soliton solutions with special parameters for the NL-DNLS equation with a reflectionless potential are obtained, which may have singularities.

1. Introduction

Most of the studies of integrable nonlinear evolution equations focus on local-type equations [1]–[3]. A classic example is provided by the nonlinear Schrödinger (NLS) equation, which has been thoroughly discussed from different standpoints [4]–[6]. The NLS equation describes the evolution of the complex envelope of weakly nonlinear dispersive wave trains [7]. In [8], a nonlocal nonlinear Schrödinger (NL-NLS) equation with infinitely many conservation laws was presented and its explicit solutions were derived by the inverse scattering transform (IST) method. After that, many nonlocal integrable equations have been introduced and broadly discussed [9]–[11]. Many of such nonlocal integrable equations can be turned into local equations by some variable transformations [12].

The IST is a powerful tool to deal with the initial-value problems for local or nonlocal equations [1], [13]–[24]. The inverse scattering problem is related to the Gel’fand–Levitan–Marchenko integral equations [25], which are difficult to handle in general. As a new version of the IST, the Riemann–Hilbert approach has recently become popular in studying soliton solutions and long-time asymptotics of integrable systems [16], [18], [19], [26]–[30].

The derivative nonlinear Schrödinger (DNLS) equation

$$ iq_t(x,t)=q_{xx}(x,t)+i\varepsilon(q^2(x,t)q^\ast(x,t))_x,\qquad \varepsilon=\pm 1$$

(1.1)

has important applications in plasma physics [31]. Here, the subscripts denote derivatives with respect to the corresponding variables and the star denotes complex conjugation. The IST for the DNLS equation with zero boundary conditions (ZBCs) and nonzero boundary conditions (NZBCs) was studied in [16], [32]–[36].

In this paper, we consider the NL-DNLS equation

$$ iq_t(x,t)=q_{xx}(x,t)+\varepsilon(q^2(x,t)q^\ast(-x,t))_x,\qquad \varepsilon=\pm 1,$$

(1.2)

with ZBCs at infinity:

$$ \lim_{x\to\pm\infty}q(x,t)=0.$$

(1.3)

The NL-DNLS equation was introduced and studied recently via the Darboux transformations in [37]. The NL-DNLS equation can be made into the DNLS equation by the transformations $x\to-ix$ and $t\to-t$ [12].

This paper is organized as follows. In Sec. 2, we discuss the direct scattering problem with ZBCs at infinity in detail. The Jost solutions and the scattering matrix are introduced and their analytic properties are discussed. The key symmetries for the modified Jost solutions and scattering coefficients are found using the uniqueness of solutions of ordinary differential equations. For constructing the inverse scattering problems, we also analyze the asymptotic behavior of the modified Jost solutions and the scattering matrix. To solve the inverse scattering problem, we derive the discrete spectrum, which has two completely different sets, and give the corresponding residue conditions. In Sec. 3, the matrix Riemann–Hilbert problem for the inverse scattering problem is established. Subsequently, we present a reconstruction formula for the potential and a trace formula. The explicit general solutions corresponding to reflectionless potential are obtained. In Sec. 4, we give examples of the soliton solutions in two different cases with special parameters.

2. Direct Scattering Problem

2.1. Jost solutions and analyticity

The NL-DNLS equation (1.2) is a nonlinear integrable equation, and the associated Lax pair has the form [37]

$$ \phi_x=U\phi, \qquad\phi_t=V\phi,$$

(2.1)

where

$$ \begin{aligned} \, &U(x,t,\lambda)=\lambda^2\sigma_3+\lambda P, \\ &V(x,t,\lambda)=-2i\lambda^4\sigma_3-2i\lambda^3P+i\lambda^2\sigma_3P^2+i\lambda(P^3-\sigma_3P_x) \end{aligned}$$

(2.2)

where

$$\sigma_3=\begin{pmatrix} 1& \phantom{-}0 \\ 0 & -1\end{pmatrix},\qquad P=\begin{pmatrix} 0 & q(x,t) \\ -\varepsilon q^\ast(-x,t) & 0 \end{pmatrix}.$$

Comparing with the case of the DNLS equation, we see that their Lax representations are different, which leads to the completely different spectral properties.

Solutions $\varphi_{\pm}(x,t,\lambda)$ of the asymptotic spectral problem for Lax pair (2.1) with ZBCs (1.3) can be represented as

$$ \varphi_{\pm,x}(x,t,\lambda)=U_{\pm}\varphi_{\pm}(x,t,\lambda),\qquad \varphi_{\pm,t}(x,t,\lambda)=V_{\pm}\varphi_{\pm}(x,t,\lambda),$$

(2.3)

where

$$U_{\pm}=\lambda^2\sigma_3,\qquad V_{\pm}=-2i\lambda^2U_{\pm}.$$

For simplicity, we take the basic solutions $\varphi_{\pm}(x,t,\lambda)=e^{\theta(x,t,\lambda)\sigma_3}$, where $\theta(x,t,\lambda)=\lambda^2(x-2i\lambda^2t)$. We assume that the matrix solutions of spectral problem (2.1) are Jost solutions $\phi_{\pm}(x,t,\lambda)$ satisfying the boundary conditions

$$ \phi_{\pm}(x,t,\lambda)\to e^{\theta(x,t,\lambda)\sigma_3},\qquad x\to\pm\infty,\qquad\lambda\in\Sigma,$$

(2.4)

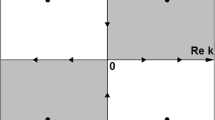
where $\Sigma:=\{\lambda\in\mathbb{C}\mid( \operatorname{Re} \lambda)^2-( \operatorname{Im} \lambda)^2=0\}$.

To eliminate the asymptotic exponential oscillations, we introduce the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ defined by

$$ \mu_{\pm}(x,t,\lambda)=\phi_{\pm}(x,t,\lambda)e^{-\theta(x,t,\lambda)\sigma_3},$$

(2.5)

and then

$$ \lim_{x\to\pm\infty}\mu_{\pm}(x,t,\lambda)=I,$$

(2.6)

where $I$ denotes the $2\times 2$ identity matrix. We use a shorthand notation $e^{-\theta\hat\sigma_3}(M)=e^{-\theta\sigma_3}Me^{\theta\sigma_3}$, where $M$ is an arbitrary $2\times 2$ matrix.

We thus obtain an equivalent Lax pair

$$\mu_{\pm,x}+\lambda^2 [\mu_{\pm},\sigma_3]=\lambda P \mu_{\pm},$$

(2.7a)

$$\mu_{\pm,t}-2i\lambda^4[\mu_{\pm},\sigma_3]=V_1 \mu_{\pm},$$

(2.7b)

which can be rewritten in the total-derivative form

$$ d(e^{-\theta(x,t,\lambda)\hat\sigma_3}\mu_{\pm})=e^{-\theta(x,t,\lambda)\hat\sigma_3}[(\lambda P\,dx+V_1\,dt)\mu_{\pm}].$$

(2.8)

Here, $[\,{\cdot}\,,\,{\cdot}\,]$ denotes the matrix commutator and $V_1=-2i\lambda^3P+i\lambda^2\sigma_3P^2+i\lambda(P^3-\sigma_3P_x)$. We can formally integrate formula (2.7a) for $\mu_{\pm}(x,t,\lambda)$ to obtain the Volterra integral equations along two special paths: $(-\infty,t)\to(x,t)$ and $(+\infty,t)\to(x,t)$

$$\mu_{-}(x,t,\lambda)=I+\lambda\int_{-\infty}^{x}e^{\lambda^2(x-y)\hat\sigma_3}[P(y,t)\mu_{-}(y,t,\lambda)]\,dy,$$

(2.9a)

$$\mu_{+}(x,t,\lambda)=I-\lambda\int_x^{+\infty}e^{\lambda^2(x-y)\hat\sigma_3}[P(y,t)\mu_{+}(y,t,\lambda)]\,dy.$$

(2.9b)

Using these integral equations, we can prove that the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ are unique solutions of the above equations and their columns have different analyticity domains in the complex $\lambda$ plane [18]. For convenience, we set

$$D^{+}=\{\lambda\in\mathbb{C}\mid( \operatorname{Re} \lambda)^2-( \operatorname{Im} \lambda)^2>0\},\qquad D^{-}=\{\lambda\in\mathbb{C}\mid( \operatorname{Re} \lambda)^2-( \operatorname{Im} \lambda)^2<0\},$$

and let $\mu_{\pm j}(x,t,\lambda)$ denote the $j$th column of the matrix $\mu_{\pm}(x,t,\lambda)$.

Proposition 1.

Let the potentials belong to the absolutely integrable space, i.e., $q(x,t),q(-x,t)\in L^1(\mathbb{R})$ . Then the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ have the following properties:

• • Volterra integral equations 2.9 have unique solutions with boundary conditions (2.6).

• • The column vectors $\mu_{-1}(x, t,\lambda)$ and $\mu_{+2}(x, t,\lambda)$ can be analytically extended to $D^{+}$ and continuously extended to $D^{+}\cup\Sigma$ .

• • The column vectors $\mu_{+1}(x, t,\lambda)$ and $\mu_{-2}(x, t,\lambda)$ can be analytically extended to $D^{-}$ and continuously extended to $D^{-}\cup\Sigma$ .

2.2. Scattering matrix

Evidently, the matrices $U$ and $V$ are traceless. Using Abel’s theorem, we conclude that the $\det\phi_{\pm}(x,t,\lambda)$ are independent of $x$ and $t$. Hence,

$$ \det\phi_{\pm}(x,t,\lambda)=\lim_{x\to\pm\infty}\det\phi_{\pm}(x,t,\lambda)=\lim_{x\to\pm\infty}\det\mu_{\pm}(x,t,\lambda)=1.$$

(2.10)

That is, the Jost solutions $\phi_{-1}(x,t,\lambda)$ and $\phi_{-2}(x,t,\lambda)$ of scattering problem (2.1) with boundary conditions (1.3) are linearly independent for all $\lambda\in\Sigma$. Similar arguments hold for the Jost solutions $\phi_{+1}(x,t,\lambda)$ and $\phi_{+2}(x,t,\lambda)$. Because scattering problem (2.1) is a $2\times 2$ linear system, the pairs $\{\phi_{-1}(x,t,\lambda),\phi_{-2}(x,t,\lambda)\}$ and $\{\phi_{+1}(x,t,\lambda),\phi_{+2}(x,t,\lambda)\}$ are linearly dependent, and we can express one basis set in terms of the other; they are two fundamental matrix solutions for the Lax pair (2.1). Therefore, there exists a $2\times 2$ matrix $S(\lambda$) (independent of $x$ and $t$) such that

$$ \phi_{-}(x,t,\lambda)= \phi_{+}(x,t,\lambda)S(\lambda),\qquad x,t\in\mathbb{R},\qquad \lambda\in\Sigma,$$

(2.11)

called the scattering matrix. After expanding formula (2.11) we arrive at

$$ \begin{aligned} \, &\phi_{-1}(\lambda)=s_{11}(\lambda)\phi_{+1}(\lambda)+s_{21}(\lambda)\phi_{+2}(\lambda), \\ &\phi_{-2}(\lambda)=s_{12}(\lambda)\phi_{+1}(\lambda)+s_{22}(\lambda)\phi_{+2}(\lambda), \end{aligned}$$

(2.12)

where the $s_{ij}$($\lambda$) are called the scattering coefficients. Moreover, Eqs. (2.10) and (2.11) imply

$$ \det S(\lambda)=1,\qquad \lambda\in\Sigma.$$

(2.13)

Proposition 2.

If $q(x,t),q(-x,t)\in L^1(\mathbb{R})$ , then the scattering coefficients $s_{11}(\lambda)$ can be analytically extended to $D^{+}$ and continuously extended to $D^{+}\cup\Sigma$ , while $s_{22}(\lambda)$ can be analytically extended to $D^{-}$ and continuously extended to $D^{-}\cup\Sigma$ . However, the rest of the scattering coefficients are nowhere analytic and are only continuous in $\Sigma$ .

Proof.

It follows from (2.12) that the $s_{ij}$($\lambda$) have the Wronskian representation

$$ \begin{alignedat}{3} &s_{11}(\lambda)= \operatorname{Wr} [\phi_{-1}(x,t,\lambda),\phi_{+2}(x,t,\lambda)],&\quad\; &s_{12}(\lambda)= \operatorname{Wr} [\phi_{-2}(x,t,\lambda),\phi_{+2}(x,t,\lambda)], \\ &s_{21}(\lambda)= \operatorname{Wr} [\phi_{+1}(x,t,\lambda),\phi_{-1}(x,t,\lambda)],&\quad\; &s_{22}(\lambda)= \operatorname{Wr} [\phi_{+1}(x,t,\lambda),\phi_{-2}(x,t,\lambda)]. \end{alignedat}$$

(2.14)

Combining with the analytic properties of the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ in Proposition 1, we prove the proposition.

The following reflection coefficients are needed in the inverse problem in what follows:

$$ \rho(\lambda)=\frac{s_{21}(\lambda)}{s_{11}(\lambda)},\qquad \tilde\rho(\lambda)=\frac{s_{12}(\lambda)}{s_{22}(\lambda)},\qquad \lambda\in\Sigma.$$

(2.15)

2.3. Symmetry conditions

Proposition 3.

Jost solutions $\phi_{\pm}(x,t,\lambda)$ satisfy two symmetry relations

$$\begin{aligned} \, &\phi_{\pm}(x,t,-\lambda)=\sigma_3\phi_{\pm}(x,t,\lambda)\sigma_3, \\ &\phi^\ast_\mp(-x,t,-\lambda^\ast)=K\phi_{\pm}(x,t,\lambda)K^{-1}, \end{aligned}$$

where

$$K=\begin{pmatrix} 0 & -\varepsilon \\ 1 & \phantom{-}0 \end{pmatrix}.$$

For individual columns,

$$\phi_{\pm 1}(x,t,-\lambda)=\sigma_3\phi_{\pm 1}(x,t,\lambda), \qquad \phi_{\pm 2}(x,t,-\lambda)=-\sigma_3\phi_{\pm 2}(x,t,\lambda),$$

(2.16)

$$\phi^\ast_{\mp 1}(-x,t,-\lambda^\ast)=K^{-1}\phi_{\pm 2}(x,t,\lambda), \qquad \phi^\ast_{\mp 2}(-x,t,-\lambda^\ast)=K\phi_{\pm 1}(x,t,\lambda).$$

(2.17)

Proof.

For the first symmetry relation, for all $\lambda\in\Sigma$, the matrices $U(\lambda)$ and $V(\lambda)$ satisfy the symmetry

$$U(-\lambda)=\sigma_3U(\lambda)\sigma_3,\qquad V(-\lambda)=\sigma_3V(\lambda)\sigma_3.$$

It is easy to see that $\phi_{\pm}(x,t,-\lambda)$ and $\sigma_3\phi_{\pm}(x,t,\lambda)\sigma_3$ satisfy the same spectral problem and have the same asymptotic form as $\phi_{\pm}(x,t,\lambda)$ (we let $\tilde\phi_{\pm}$ denote any of these function for convenience):

$$ \begin{aligned} \, &\frac{\partial}{\partial x}(\tilde\phi_{\pm}(x,t,\lambda))=U(-\lambda)\tilde\phi_{\pm}(x,t,\lambda), \\ &\frac{\partial}{\partial t}(\tilde\phi_{\pm}(x,t,\lambda))=V(-\lambda)\tilde\phi_{\pm}(x,t,\lambda), \\ &\tilde\phi_{\pm}(x,t,\lambda)\to e^{\theta(x,t,\lambda)\sigma_3},\qquad x\to\pm\infty,\qquad \lambda\in\Sigma. \end{aligned}$$

(2.18)

Hence, we obtain the desired result by the uniqueness of Jost solutions. Similar arguments hold for the second symmetry condition because

$$-U^\ast(-x,t,-\lambda^\ast)=KU(x,t,\lambda)K^{-1},\qquad V^\ast(-x,t,-\lambda^\ast)=KV(x,t,\lambda)K^{-1}.$$

Corollary 1.

The scattering matrix $S(\lambda)$ has two symmetries

$$ S(\lambda)=\sigma_3S(-\lambda)\sigma_3,\qquad S^\ast(-\lambda^\ast)=K S^{-1}(\lambda)K^{-1},$$

(2.19)

or in component form,

$$ \begin{aligned} \, &\begin{alignedat}{3} &s_{11}(\lambda)=s_{11}(-\lambda),&\qquad &s_{12}(\lambda)=-s_{12}(-\lambda), \\ &s_{21}(\lambda)=-s_{21}(-\lambda),&\qquad &s_{22}(\lambda)=s_{22}(-\lambda), \\ &s_{11}(\lambda)=s^\ast_{11}(-\lambda^\ast),&\qquad &s_{22}(\lambda)=s^\ast_{22}(-\lambda^\ast),&\qquad s_{12}(\lambda)=\varepsilon s^\ast_{21}(-\lambda^\ast).\vphantom{\Big|} \end{alignedat} \end{aligned}$$

(2.20)

Proof can be directly obtained from Proposition 3 and the scattering relation in (2.11).

2.4. Asymptotic behavior

As $\lambda\to\infty$, the asymptotic behavior of the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ and the scattering matrix $S(\lambda)$ can be derived from (2.7a) by the Wentzel–Kramers–Brillouin expansion.

Proposition 4.

The large- $\lambda$ asymptotic form of the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ is

$$ \mu_{\pm}(x,t,\lambda)=e^{\nu_{\pm}\sigma_3}+\frac{\mu_{\pm}^{[1]}(x,t)}{\lambda}+O(\lambda^{-2}),\qquad \lambda\to\infty,$$

(2.21)

where the off-diagonal part of $\mu_{\pm }^{[1]}(x,t)$ is given by

$$ \mu_{\pm\mathrm o}^{[1]}(x,t)= \frac{1}{2}P\sigma_3e^{\nu_{\pm}\sigma_3},$$

(2.22)

and

$$ \nu_{\pm}(x,t)=-\frac{\varepsilon}{2}\int_{\pm\infty}^{x}q(\xi,t)q^\ast(-\xi,t)\,d\xi.$$

(2.23)

Proof.

We suppose that the $\mu_{\pm}(x,t,\lambda)$ have the following expansions as $\lambda\to\infty$:

$$\mu_{\pm}(x,t,\lambda)=\mu_{\pm}^{[0]}(x,t)+\frac{\mu_{\pm}^{[1]}(x,t)}{\lambda}+\frac{\mu_{\pm}^{[2]}(x,t)}{\lambda^2}+O(\lambda^{-3}),\qquad \lambda\to\infty.$$

Substituting these relations in (2.7a), we find

$$\biggl(\mu_{\pm}^{[0]}+\frac{\mu_{\pm}^{[1]}}{\lambda}+\frac{\mu_{\pm}^{[2]}}{\lambda^2}+\cdots\biggr)_{\!{}^{\scriptstyle x}}+ \lambda^2\biggl[\biggl(\mu_{\pm}^{[0]}+\frac{\mu_{\pm}^{[1]}}{\lambda}+\frac{\mu_{\pm}^{[2]}}{\lambda^2}+\cdots\biggr),\sigma_3\biggr]= \lambda P\biggl(\mu_{\pm}^{[0]}+\frac{\mu_{\pm}^{[1]}}{\lambda}+\frac{\mu_{\pm}^{[2]}}{\lambda^2}+\cdots\biggr).$$

From the second-order terms in $\lambda$, we obtain

$$[\mu_{\pm}^{[0]},\sigma_3]=0,$$

which implies that $\mu_{\pm}^{[0]}(x,t)$ is a diagonal matrix. For convenience, we let $a_{ij}(x,t)$ and $b_{ij}(x,t)$ respectively denote $\mu_{\pm}^{[0]}(x,t)$ and $\mu_{\pm}^{[1]}(x,t)$. Similarly to the foregoing, from the coefficients of the first-order terms in $\lambda$, we obtain

$$a_{11}(x,t)=-\frac{2}{\epsilon}\frac{b_{21}(x,t)}{q^\ast(-x,t)},\qquad a_{22}(x,t)=-2\frac{b_{12}(x,t)}{q(x,t)}.$$

And terms of the zeroth order in $\lambda$ yield

$$a_{11 x}(x,t)=q(x,t)b_{21}(x,t),\qquad a_{22 x}(x,t)=-\epsilon q^\ast(-x,t)b_{12}(x,t).$$

Hence, using boundary conditions (2.6), we deduce that

$$\begin{alignedat}{3} &a_{11}(x,t)=e^{\nu_{\pm}},&\qquad &a_{22}(x,t)=e^{-\nu_{\pm}}, \\ &b_{12}(x,t)=-\frac{q(x,t)}{2}e^{-\nu_{\pm}},&\qquad &b_{21}(x,t)=-\frac{\varepsilon q^\ast(-x,t)}{2}e^{\nu_{\pm}}. \end{alignedat}$$

We have thus established asymptotic behavior (2.21).

Proposition 5.

The asymptotic behavior of the scattering matrix is

$$ S(\lambda)=e^{\nu \sigma_3}+O(\lambda^{-1}),\qquad \lambda\to\infty,$$

(2.24)

where

$$ \nu=-\frac{\varepsilon}{2}\int_{-\infty}^{+\infty}q(x,t)q^\ast(x,t)\,dx.$$

(2.25)

Proof.

Substituting the asymptotic forms of the modified Jost solutions $\mu_{\pm}(x,t,\lambda)$ given by (2.21) in the Wronskian representations (2.14) of the scattering coefficients, we derive the asymptotic behavior for the scattering matrix $S(\lambda)$ by simple computation.

2.5. Discrete spectrum and residue conditions

For the NL-DNLS equation, the discrete spectrum for the scattering problem is the set of all values $\lambda\in\mathbb{C}\backslash\Sigma$ such that eigenfunctions exist in $L^2(\mathbb{R})$. We show that these values are the zeros of $s_{11}(\lambda)$ in $D^{+}$ and the zeros of $s_{22}(\lambda)$ in $D^{-}$.

We suppose that $s_{11}(\lambda)$ has a finite number $N_1$ of simple zeros $k_1,\ldots,k_{N_1}$, in $D^{+}\cap\{\lambda\in\mathbb{C}\mid { \operatorname{Re} \lambda>0},\ \operatorname{Im} \lambda\geqslant 0\}$. That is, let $s_{11}(k_n)=0$ and $s_{11}'(k_n)\neq 0$, with $k_n\in D^{+}$, $\operatorname{Re} k_n>0$ and $\operatorname{Im} k_n\geqslant 0$ for $n=1,\ldots,N_1$, where the prime denotes differentiation with respect to $\lambda$. Owing to the symmetries (2.20), we have

$$s_{11}(k_n)=s_{11}(-k_n)=s_{11}^\ast(k^\ast_n)=s_{11}^\ast(-k^\ast_n)=0.$$

Similarly, if $\zeta_n$ is a simple zero of $s_{22}(\lambda)$, so are $-\zeta_n$, $\zeta^\ast_n$, $-\zeta^\ast_n$, with $\zeta_n\in D^{-}$, $\operatorname{Re} \zeta_n\geqslant 0$, and $\operatorname{Im} \zeta_n>0$ for $n=1,\ldots,N_2$. That is,

$$s_{22}(\zeta_n)=s_{22}(-\zeta_n)=s_{22}^\ast(\zeta^\ast_n)=s_{22}^\ast(-\zeta^\ast_n)=0.$$

Notably, the eigenvalues $k_n$ and $\zeta_n$ are not related, which is different from the case of the DNLS equation. Thus, the discrete spectrum is the set

$$ \Lambda=\{\pm k_n,\pm k^\ast_n\}_{n=1}^{N_1}\cup\{\pm\zeta_n,\pm\zeta^\ast_n\}^{N_2}_{n=1}.$$

(2.26)

Next, we focus on the residue conditions, which are needed for the inverse problem. Recalling the Wronskian representation of $s_{11}(\lambda)$, the Jost solutions $\phi_{-1}(x,t,\lambda)$ and $\phi_{+2}(x,t,\lambda)$ with $\lambda=k_n$ must be linearly dependent,

$$ \phi_{-1}(x,t,k_n)=b_n\phi_{+2}(x,t,k_n),$$

(2.27)

where $b_n$ is nonzero and independent of $x$, $t$, and $\lambda$. Similar arguments hold for the scattering coefficient $s_{22}(\lambda)$, and hence

$$ \phi_{-2}(x,t,\zeta_n)=d_n\phi_{+1}(x,t,\zeta_n),$$

(2.28)

where $d_n$ admits same properties as $b_n$. We can rewrite (2.27) and (2.28) equivalently as

$$\mu_{-1}(x,t,k_n)=b_ne^{-2\theta(x,t,k_n)}\mu_{+2}(x,t,k_n),$$

(2.29)

$$\mu_{-2}(x,t,\zeta_n)=d_ne^{2\theta(x,t,\zeta_n)}\mu_{+1}(x,t,\zeta_n).$$

(2.30)

For the NL-DNLS equation, we show that the eigenvalues $k_n$ and $\zeta_n$ cannot lie on the coordinate axis simultaneously. First, let the eigenvalues $k_n$ be real, i.e., $k_n=k_n^\ast$; it then follows from (2.29) and the first equation in (2.17) that

$$ \varepsilon|b_n|^2=1.$$

(2.31)

Similarly, supposing that the scattering coefficient $s_{22}(\lambda)$ has an imaginary simple zero $\zeta_n=-\zeta_n^\ast$, we can show that

$$ -\varepsilon|d_n|^2=1.$$

(2.32)

We return to the discussion of residue conditions. We now conclude that

$$ \mathop{\rm Res}\limits _{\lambda=k_n}\frac{\mu_{-1}(x,t,\lambda)}{s_{11}(\lambda)}=C_n\mu_{+2}(x,t,k_n),\qquad C_n(x)=\frac{b_n}{s'_{11}(k_n)}e^{-2\theta(x,k_n)}.$$

(2.33)

To obtain the remaining three points of the eigenvalue quartet in $D^{+}$, we apply the symmetry properties of the Jost solutions and scattering coefficient $s_{11}(\lambda)$, with the result

$$\begin{aligned} \, & \mathop{\rm Res}\limits _{\lambda=-k_n}\frac{\mu_{-1}(x,t,\lambda)}{s_{11}(\lambda)}=-C_n\sigma_3\mu_{+2}(x,t,k_n), \\ & \mathop{\rm Res}\limits _{\lambda=k^\ast_n}\frac{\mu_{-1}(x,t,\lambda)}{s_{11}(\lambda)}= \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n^{}\sigma_3^{}K^{-1}\mu_{+2}^\ast(-x,t,k_n), \\ & \mathop{\rm Res}\limits _{\lambda=-k^\ast_n}\frac{\mu_{-1}(x,t,\lambda)}{s_{11}(\lambda)}=- \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n^{}K^{-1}\mu_{+2}^\ast(-x,t,k_n),\qquad \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n=\frac{1}{[s'_{11}(k_n)]^\ast}. \end{aligned}$$

Similarly, we have

$$\begin{alignedat}{3} & \mathop{\rm Res}\limits _{\lambda=\zeta_n}\frac{\mu_{-2}(x,t,\lambda)}{s_{22}(\lambda)}=D_n\mu_{+1}(x,t,\zeta_n), \\ & \mathop{\rm Res}\limits _{\lambda=-\zeta_n}\frac{\mu_{-2}(x,t,\lambda)}{s_{22}(\lambda)}=D_n\sigma_3\mu_{+1}(x,t,\zeta_n),&\qquad &D_n(x)=\frac{d_n}{s'_{22}(\zeta_n)}e^{2\theta(x,\zeta_n)}, \\ & \mathop{\rm Res}\limits _{\lambda=\zeta^\ast_n}\frac{\mu_{-2}(x,t,\lambda)}{s_{22}(\lambda)}=- \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _n^{}\sigma_3^{}K\mu_{+1}^\ast(-x,t,\zeta_n), \\ & \mathop{\rm Res}\limits _{\lambda=-\zeta^\ast_n}\frac{\mu_{-2}(x,t,\lambda)}{s_{22}(\lambda)}=- \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _n^{}K\mu_{+1}^\ast(-x,t,\zeta_n),&\qquad & \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _n=\frac{1}{[s'_{22}(\zeta_n)]^\ast}. \end{alignedat}$$

3. Inverse Problem

3.1. Riemann–Hilbert problem

As usual, we introduce the sectionally meromorphic matrices

$$ \begin{aligned} \, &N^{+}(x,t,\lambda)=\biggl(\frac{\mu_{-1}(x,t,\lambda)}{s_{11}(\lambda)},\,\mu_{+2}(x,t,\lambda)\biggr), \\ &N^{-}(x,t,\lambda)=\biggl(\mu_{+1}(x,t,\lambda),\,\frac{\mu_{-2}(x,t,\lambda)}{s_{22}(\lambda)}\biggr). \end{aligned}$$

(3.1)

From scattering relations (2.11), we obtain the jump condition

$$ N^{+}(x,t,\lambda)=N^{-}(x,t,\lambda)(I-J(x,t,\lambda)),\qquad \lambda\in\Sigma,$$

(3.2)

where the jump matrix is

$$ J(x,t,\lambda)=e^{\theta(x,t,\lambda)\sigma_3}J_{0}(\lambda)e^{-\theta(x,t,\lambda) \sigma_3}= \begin{pmatrix} \rho(\lambda){\tilde\rho}(\lambda) & \tilde\rho(\lambda)e^{2\theta(x,t,\lambda)}\\ -\rho(\lambda)e^{-2\theta(x,t,\lambda)} & 0 \vphantom{\Big|} \end{pmatrix}.$$

(3.3)

To complete the Riemann–Hilbert problem, normalization conditions must be established. Given the asymptotic behavior of the modified Jost functions $\mu_{\pm}(x,t,\lambda)$ and scattering coefficients, it is easy to see that

$$ N^{\pm}(x,t,\lambda)=e^{\nu_{+} \sigma_3}+O(\lambda^{-1}),\qquad \lambda\to\infty.$$

(3.4)

Equations (3.1)–(3.4) define a matrix Riemann–Hilbert problem.

To solve the Riemann–Hilbert problem, we need to subtract the asymptotic behavior and the pole contributions. Hence, we rewrite the jump condition as

$$ N^{+}(x,t,\lambda)-e^{\nu_{+}\sigma_3}-\Delta=N^{-}(x,t,\lambda)-e^{\nu_{+} \sigma_3}-\Delta-N^{-}(x,t,\lambda)J(x,t,\lambda),\quad \lambda\in\Sigma,$$

(3.5)

where we introduce the pole part

$$\begin{aligned} \, \Delta={}&\sum_{n=1}^{N_1}\biggl(\frac{\operatorname{Res}_{\,k_n}N^{+}}{\lambda-k_n}+ \frac{\operatorname{Res}_{\,-k_n^{}}N^{+}}{\lambda+k_n}+ \frac{\operatorname{Res}_{\,k^\ast_n}N^{+}}{\lambda-k^\ast_n}+ \frac{\operatorname{Res}_{\,-k^\ast_n}N^{+}}{\lambda+k^\ast_n}\biggr)+{} \nonumber\\ &+\sum_{n=1}^{N_2}\biggl(\frac{\operatorname{Res}_{\,\zeta_n}N^{-}}{\lambda-\zeta_n}+ \frac{\operatorname{Res}_{\,-\zeta_n^{}}N^{-}}{\lambda+\zeta_n}+ \frac{\operatorname{Res}_{\,\zeta^\ast_n}N^{-}}{\lambda-\zeta^\ast_n}+ \frac{\operatorname{Res}_{\,-\zeta^\ast_n}N^{-}}{\lambda+\zeta^\ast_n}\biggr). \end{aligned}$$

(3.6)

We introduce the projection operators

$$\mathcal P_{\pm}[f](\lambda)=\frac{1}{2\pi i}\int_\Sigma\frac{f(\zeta)}{\zeta-(\lambda\pm i0)}\,d\zeta,$$

where the notation $\lambda\pm i 0$ indicates that when $\lambda\in\Sigma$, the limit is taken from the left/right of it. Applying the projection operators to (3.5) leads to

$$ N(x,t,\lambda)=e^{\nu_{+}\sigma_3}+\Delta- \frac{1}{2\pi i}\int_\Sigma\frac{N^{-}(x,t,\xi)J(x,t,\xi)}{\xi-\lambda}\,d\xi,\qquad\lambda\in\mathbb{C}\backslash\Sigma.$$

(3.7)

3.2. Reconstruction formula

Our last task is to reconstruct the potential for the NL-DNLS equation with ZBCs from the scattering data. We have

$$ q(x,t)=-2e^{\nu_{+}}\lim_{ \lambda\to\infty}(\lambda\mu_{+})_{12}(x,t,\lambda).$$

(3.8)

We compare the element 1,2 in expression (3.7) with (3.8). The reconstruction formula for the potential is then given by

$$\begin{aligned} \, q(x,t)=-2e^{\nu_{+}}\biggl\{\,\sum_{n=1}^{N_2} [2D_n^{}\mu_{+11}^{}(x,t,\zeta_n)&{}+2\varepsilon \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _n^{}\mu_{+21}^\ast(-x,t,\zeta_n)]+\frac{1}{2\pi i}\int_\Sigma[N^{-}(\xi)J(\xi)]_{12}\,d\xi\biggr\}. \end{aligned}$$

(3.9)

To close the system, we need to obtain expressions for the eigenfunctions appearing in (3.9). They are given by

$$\begin{aligned} \, &\mu_{+1}(x,t,w)=\binom{e^{\nu_{+}}}{0} +\sum_{n=1}^{N_1}\biggl[\biggl(\frac{1}{w-k_n}-\frac{\sigma_3}{w+k_n}\biggr)C_n\mu_{+2}(x,t,k_n)+{} \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad +\biggl(\frac{1}{w-k^\ast_n}-\frac{\sigma_3}{w+k^\ast_n}\biggr) \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n^{}\sigma_3^{}K^{-1}\mu_{+2}^\ast(-x,t,k_n^{})\biggr]-{} \nonumber\\ &\hphantom{\mu_{+1}(x,t,w)={}}-\frac{1}{2\pi i}\int_\Sigma\frac{(N^{-}(\xi)J(\xi))_1}{\xi-\lambda}\,d\xi, \end{aligned}$$

(3.10)

$$\begin{aligned} \, &\mu_{+2}(x,t,\tilde w)=\binom{0}{e^{-\nu_{+}}} +\sum_{n=1}^{N_2}\biggl[\biggl(\frac{1}{\tilde w-\zeta_n}+\frac{\sigma_3}{\tilde w+\zeta_n}\biggr)D_n\mu_{+1}(x,t,\zeta_n)-{} \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad -\biggl(\frac{1}{\tilde w-\zeta^\ast_n}+\frac{\sigma_3}{\tilde w+\zeta^\ast_n}\biggr) \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _n^{}\sigma_3^{}K\mu_{+1}^\ast( -x,t,\zeta_n^{})\biggr]-{} \nonumber\\ &\hphantom{\mu_{+2}(x,t,\tilde w)={}}-\frac{1}{2\pi i}\int_\Sigma\frac{(N^{-}(\xi)J(\xi))_2}{\xi-\lambda}\,d\xi, \end{aligned}$$

(3.11)

where $w=\pm\zeta_j^{},\pm\zeta^\ast_j$ and $\tilde w=\pm k_j^{},\pm k^\ast_j$.

3.3. Trace formula

We recall that $s_{11}(\lambda)$ is analytic in $D^{+}$ and it has simple zeros at the points $\{\pm k_n,\pm k^\ast_n\}_{n=1}^{N_1}$, while $s_{22}(\lambda)$ is analytic in $D^{-}$ with has simple zeros at the points $\{\pm\zeta_n, \pm\zeta^\ast_n\}_{n=1}^{N_2}$. We set

$$\begin{aligned} \, &\beta^{+}(\lambda)=s_{11}(\lambda)e^{-\nu} \frac{\prod_{j=1}^{N_2}(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)} {\prod_{j=1}^{N_1}(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)}, \\\ &\beta^{-}(\lambda)=s_{22}(\lambda)e^\nu \frac{\prod_{j=1}^{N_1}(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)} {\prod_{j=1}^{N_2}(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)}. \end{aligned}$$

It follows that $\beta^{\pm}(\lambda)$ is analytic in $D^{\pm}$, has no zeros, and $\beta^{\pm}(\lambda)\to 1$ as $\lambda\to\infty$. Moreover, we have the relation

$$ \beta^{+}(\lambda)\beta^{-}(\lambda)=\frac{1}{1-\rho(\lambda){\tilde\rho}(\lambda)}.$$

(3.12)

Taking the logarithms and applying the Cauchy projectors to (3.12), we have

$$ \ln\beta^{\pm}(\lambda)=\mp\frac{1}{2 \pi i}\int_\Sigma\frac{\ln(1-\rho(\xi){\tilde\rho}(\xi))}{\xi-\lambda}\,d\xi,\qquad \lambda\in D^{\pm}.$$

(3.13)

Substituting $\beta^{+}(\lambda)$ in $s_{11}(\lambda)$, we obtain the trace formula in terms of the discrete spectrum and the reflection coefficients,

$$s_{11}(\lambda)=e^\nu \frac{\prod_{j=1}^{N_1}(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)} {\prod_{j=1}^{N_2}(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)} \exp\biggl(-\frac{1}{2\pi i}\int_\Sigma\frac{\ln(1-\rho(\xi){\tilde\rho}(\xi))}{\xi-\lambda}\,d\xi\biggr),$$

where $\lambda\in D^{+}$. In the same way, substituting $\beta^{-}(\lambda)$ in $s_{22}(\lambda)$, we obtain

$$s_{22}(\lambda)=e^{-\nu} \frac{\prod_{j=1}^{N_2}(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)} {\prod_{j=1}^{N_1}(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)} \exp\biggl(\frac{1}{2 \pi i}\int_\Sigma\frac{\ln(1-\rho(\xi){\tilde\rho}(\xi))}{\xi-\lambda}\,d\xi\biggr),$$

where $\lambda\in D^{-}$.

3.4. Reflectionless potential

For simplicity, we now restrict ourself to the important case where the reflection coefficient $\rho(\lambda)$ vanishes identically and $N_1=N_2=N$. From Volterra integral equation 2.9, it then follows that $\mu_{\pm}(x,t,0)=I$.

We note that formula (3.9) is implicit because it involves $e^{\nu_{+}}$. We need to find its explicit form. For this, we substitute $\lambda=0$ in (3.10) to obtain

$$ e^{\nu_{+}}=1+2\sum_{n=1}^{N}\biggl[\frac{1}{k_n}C_n(x)\mu_{+12}(x,t,k_n)+\frac{1}{k^\ast_n} \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n\mu^\ast_{+22}(-x,t,k_n)\biggr].$$

(3.14)

Using reconstruction formula (3.9) with a reflectionless potential, we rewrite Eqs. (3.10) and (3.11) as

$$\begin{aligned} \, &\mu_{+11}^{}(x,t,\zeta_j)=e^{\nu_{+}}+\sum_{n=1}^{N} \biggl[\frac{2k_n^{}}{\zeta_j^2-k_n^2}C_n^{}(x)\mu_{+12}^{}(x,t,k_n^{})+ \frac{2k^\ast_n}{\zeta_j^2-k^{\ast 2}_n} \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _n^{}\mu^\ast_{+22}(-x,t,k_n^{})\biggr], \\ &\mu^\ast_{+21}(-x,t,\zeta_j)=\sum_{n=1}^{N} \biggl[\frac{2\zeta^\ast_j}{\zeta^{\ast2}_j-k^{\ast2}_n}C_n^\ast(-x)\mu_{+22}^\ast(-x,t,k_n^{})+ \frac{2\zeta^\ast_j}{\zeta^{\ast2}_j-k^2_n}\varepsilon \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C ^\ast_n\mu_{+12}(x,t,k_n^{})\biggr] \end{aligned}$$

where $j=1,\ldots,N$, and

$$\begin{aligned} \, &\mu_{+12}(x,t, k_n)=\sum_{j=1}^{N} \biggl[\frac{2k_n}{k_n^2-\zeta^2_j}D_j^{}(x)\mu_{+11}(x,t,\zeta_j^{})+ \frac{2k_n}{k_n^2-\zeta^{\ast2}_j}\varepsilon \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _j^{}\mu^\ast_{+21}(-x,t,\zeta_j^{})\biggr], \\ &\mu_{+22}^\ast(-x,t,k_n)=e^{\nu_{-}}{+}\sum_{j=1}^{N} \biggl[\frac{2\zeta_j^{}}{k^{\ast2}_n-\zeta^2_j} \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D ^\ast_j\mu_{+11}^{}(x,t,\zeta_j^{}){+} \frac{2\zeta^\ast_j}{k^{\ast2}_n-\zeta^{\ast2}_j}D_j^\ast(-x)\mu^\ast_{+21}(-x,t,\zeta_j^{})\biggr], \end{aligned}$$

where $n=1,\ldots,N$.

For the vanishing reflection coefficient, the trace formula becomes

$$s_{11}(\lambda) =e^\nu\prod_{j=1}^{N} \frac{(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)} {(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)}, \qquad \lambda\in D^{+},$$

(3.15)

$$s_{22}(\lambda) =e^{-\nu}\prod_{j=1}^{N} \frac{(\lambda-\zeta_j^{})(\lambda+\zeta_j^{})(\lambda-\zeta^\ast_j)(\lambda+\zeta^\ast_j)} {(\lambda-k_j^{})(\lambda+k_j^{})(\lambda-k^\ast_j)(\lambda+k^\ast_j)}, \qquad \lambda\in D^{-}.$$

(3.16)

From the reconstruction formula given by (3.9), we then have the following proposition.

Proposition 6.

The explicit solution of the NL-DNLS equation with ZBCs can be written as

$$ q(x,t)=2\frac{\det\mathbf G_1}{\det\mathbf G}\,\frac{\det\mathbf Z}{\det\mathbf G},\qquad \mathbf Z=\begin{pmatrix} 0 & \mathbf Y^{\mathrm T} \\ \mathbf B& \mathbf G \end{pmatrix},\quad \mathbf G=\mathbf I+\mathbf F,$$

(3.17)

where $\mathbf B=(B_1,\ldots,B_{4N+1})^{\mathrm T}$ , $\mathbf Y^{\mathrm T}=(Y_1,\ldots,Y_{4N+1})$ and $\mathbf G_1$ denotes the matrix $\mathbf G$ with the first column replaced by the vector $\mathbf B$ . Elements of the matrices $\mathbf B$ , $\mathbf Y$ , and $\mathbf F$ are defined as

$$\begin{aligned} \, B_i&=\begin{cases} 1, & i=1, \\ 0,& i=2,\ldots,4N+1; \end{cases}\qquad Y_i=\begin{cases} 0,& i=1,\ldots,2N+1,\\ 2D_{i-2N-1}(x),& i=2N+2,\ldots,3N+1,\\ 2\varepsilon \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _{i-3N-1}, & i=3N+2,\ldots,4N+1; \end{cases} \\[3mm] F_{ij}&=\begin{cases} -e^{\nu_{-}}, & \kern-70pt i=N+2,\ldots,2N+1,\quad j=1, \\[0.5mm] -1,& \kern-70pt i=2N+2,\ldots,3N+1,\quad j=1, \\[1mm] -\dfrac{2}{k_{j-1}}\,C_{j-1}(x), & \kern-70pt i=1,\quad j=2,\ldots,N+1, \\[4mm] -\dfrac{2}{k^\ast_{j-N-1}} \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _{j-N-1}, & \kern-70pt i=1,\quad j=N+2,\ldots,2N+1, \\[3mm] -\dfrac{2k_{i-1}}{k_{i-1}^2-\zeta_{j-2N-1}^2} D_{j-2N-1}(x),\vphantom{\Bigg|}& \\ &\kern-70pt i=2,\ldots,N+1,\quad j=2N+2,\ldots,3N+1, \\[2mm] -\dfrac{2k_{i-1}}{k_{i-1}^2-\zeta^{\ast2}_{j-3N-1}}\,\varepsilon \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D _{j-3N-1},& \\ &\kern-70pt i=2,\ldots,N+1,\quad j=3N+2,\ldots,4N+1, \\[2mm] -\dfrac{2\zeta_{j-2N-1}}{k_{i-N-1}^{\ast2}-\zeta_{j-2N-1}^2} \kern1.5pt\overline{\vphantom{D}\kern6.0pt}\kern-7.5pt D ^\ast_{j-2N-1},& \\ &\kern-70pt i=N+2,\ldots,2N+1,\quad j=2N+2,\ldots,3N+1, \\[2mm] -\dfrac{2\zeta^\ast_{j-3N-1}}{k_{i-N-1}^{\ast2}-\zeta_{j-3N-1}^{\ast2}} D^\ast_{j-3N-1}(-x),& \\ &\kern-70pt i=N+2,\ldots,2N+1,\quad j=3N+2,\ldots,4N+1, \\[2mm] -\dfrac{2k_{j-1}}{\zeta^2_{i-2N-1}-k^2_{j-1}}\,C_{j-1}(x),& \\ &\kern-70pt i=2N+2,\ldots,3N+1,\quad j=2,\ldots,N+1, \\[2mm] -\dfrac{2k^\ast_{j-N-1}}{\zeta^2_{i-2N-1}-k^{\ast2}_{j-N-1}} \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C _{j-N-1},& \\ &\kern-70pt i=2N+2,\ldots,3N+1,\quad j=N+2,\ldots,2N+1, \\[2mm] -\dfrac{2\zeta^\ast_{i-3N-1}}{\zeta^{\ast2}_{i-3N-1}-k^2_{j-1}}\,\varepsilon \kern0.9pt\overline{\vphantom{C}\kern6.3pt}\kern-7.2pt C ^\ast_{j-1},& \\ &\kern-70pt i=3N+2,\ldots,4N+1,\quad j=2,\ldots,N+1, \\[2mm] -\dfrac{2\zeta^\ast_{i-3N-1}}{\zeta^{\ast2}_{i-3N-1}-k^{\ast2}_{j-N-1}}\,C^\ast_{j-N-1}(-x),& \\ &\kern-70pt i=3N+2,\ldots,4N+1,\quad j=N+2,\ldots,2N+1, \\[2mm] 0& \kern-70pt \textit{otherwise}. \end{cases} \end{aligned}$$

4. Examples

We will give examples of soliton solutions with some special fixed parameters in two cases and present them graphically.

Case 1: $\varepsilon=1$. In this case, in accordance with Eq. (2.31), we first take $k_n= k_n^\ast$ for the discrete spectrum. Trace formula (3.15) then becomes

$$1=e^\nu\prod_{n=1}^{N}\frac{-k_n^2}{|\zeta_n|^4},$$

which is a contradiction. Hence, there is no solution for NL-DNLS equation (1.2).

We next take $k_n\neq k_n^\ast$. At $N=1$, the explicit solution is extremely complicated, and we give a two-bright-soliton solution of the NL-DNLS equation (1.2) with ZBCs for the parameters $b_1=e^{1+i}$, $d_1=e^{1+i}$, $k_1=e^{\pi i/6}$, $\zeta_1=e^{\pi i/3}$. So $q(x,t)=\frac{Q_1(x,t)}{Q_2(x,t)}$, where

$$\begin{aligned} \, &Q_1(x,t)=\{[3\cosh(2x-2i)e^{-4\sqrt{3}t+2}+(-\sqrt{3}+i)e^{-8\sqrt{3}t+4}+{} \\ &\kern70pt +e^{-4\sqrt{3}t+2}\sin(2\sqrt{3}x)-i-\sqrt{3}\,]\times{} \\ &\hphantom{Q_1(x,t)={}} \times[(-3i-\sqrt{3}\,)e^{-6\sqrt{3}t+2it+3}(e^{i-x-\sqrt{3}ix}+ie^{-i+x+\sqrt{3}ix})+{} \\ &\kern70pt +(3i-\sqrt{3}\,)e^{-2\sqrt{3}t+2it+1}( e^{i-x+\sqrt{3}ix}-ie^{-i+x-\sqrt{3}ix})]\}, \\ \vphantom{\bigg|} & Q_2(x,t)=[{}-3\cosh(2x-2i)e^{-4\sqrt{3}t+2}+(\sqrt{3}+i)e^{-8\sqrt{3}t+4}+{} \\[-2mm] &\kern70pt +e^{-4\sqrt{3}t+2}\sin(2\sqrt{3}x)-i+\sqrt{3}\,]^2. \end{aligned}$$

The two-bright-soliton solution is illustrated in Fig. 1.

Case 2: $\varepsilon=-1$. On the one hand, we can take $\zeta_n=-\zeta_n^\ast$. Trace formula (3.15) then yields

$$1=e^\nu\prod_{n=1}^{N}\frac{|k_n|^4}{|\zeta_n|^2},$$

which is valid. But the derived solution is not a soliton solution because of the appearance of the singularities.

On the other hand, if $\zeta_n\neq-\zeta_n^\ast$, the two-soliton solution of NL-DNLS (1.2) with ZBCs is made of two breathers. Choosing the parameters $b_1=1$, $d_1=1$, $k_1=e^{\pi i/6}$, and $\zeta_1=e^{\pi i/3}$, we then have $q(x,t)=\frac{Q_3(x,t)}{Q_{4}(x,t)}$ with

$$\begin{aligned} \, &Q_3(x,t)=-2i\sqrt{3}\{[e^{-4\sqrt{3}t}(-2i\sinh(2\sqrt{3}ix)-6\cosh(2x))+{} \\[-1mm] &\hphantom{Q_3(x,t)={}}\kern60pt +2(i+\sqrt{3}\,)+2e^{-8\sqrt{3}t}(\sqrt{3}-i)]\times{} \\ &\hphantom{Q_3(x,t)={}}\times[(\sqrt{3}-i)e^{2it-6\sqrt{3}t}(e^{-x-i\sqrt{3}x}-ie^{x+i\sqrt{3}x})+{} \\[-1mm] &\hphantom{Q_3(x,t)={}}\kern60pt +(\sqrt{3}+i)e^{2it-2\sqrt{3}t}(e^{-x+i\sqrt{3}x}+ie^{x-i\sqrt{3}x})]\}, \\ &\vphantom{\bigg|} Q_4(x,t)=[e^{-4\sqrt{3}t}(-2i\sinh(2\sqrt{3}ix)+6\cosh(2x))+2(i-\sqrt{3}\,)-2e^{-8\sqrt{3}t}(i+\sqrt{3}\,)]^2. \end{aligned}$$

The two-breather soliton solution is illustrated in Fig. 2.

Fig. 1.

A two-bright-soliton solution for the NL-DNLS equation (1.2) with $N=1$, $\varepsilon=1$, $b_1=e^{1+i}$, $d_1=e^{1+i}$, $k_1=e^{\pi i/6}$, and $\zeta_1=e^{\pi i/3}$: (a) the three-dimensional profile, (b) wave propagation along $x$ for $t=0,1,2$.

Fig. 2.

A two-breather soliton solution of the NL-DNLS equation with $N=1$, $\varepsilon=-1$, $b_1=1$, $d_1=1$, $k_1=e^{\pi i/6}$, and $\zeta_1=e^{\pi i/3}$: (a) the three-dimensional profile, (b) wave propagation along $x$ for $t=0,1,2$.