The general fifth-order nonlinear Schrödinger equation with nonzero boundary conditions: Inverse scattering transform and multisoliton solutions

Abstract

We study the inverse scattering transform of the general fifth-order nonlinear Schrödinger (NLS) equation with nonzero boundary conditions (NZBCs), which can be reduced to several integrable equations. First, a matrix Riemann–Hilbert problem (RHP) for the fifth-order NLS equation with NZBCs at infinity is systematically investigated. Moreover, the inverse problems are solved by studying a matrix RHP. We construct the general solutions for reflectionless potentials. The trace formulas and theta conditions are also presented. In particular, we analyze the simple-pole and double-pole solutions for the fifth-order NLS equation with NZBCs. Finally, we discuss the dynamics of the obtained solutions in terms of their plots. The results in this work should be helpful in explaining and enriching the nonlinear wave phenomena in nonlinear fields.

1. Introduction

The fundamental nonlinear Schrödinger (NLS) equation

$$iq_{t}+q_{xx}+2|q|^2q=0 $$

(1.1)

is famous as a key integrable model in the field of mathematical physics. There are many physical contexts where the NLS equation arises. For instance, the NLS equation describes weakly nonlinear surface waves in deep water. More importantly, the NLS equation models the soliton propagation in optical fibers where only the group velocity dispersion and self-phase modulation effects are taken into account. However, for ultrashort pulses in optical fibers, the effects of higher-order dispersion, self-steepening, and stimulated Raman scattering should be considered. Besides, the higher-order dispersion terms and non-Kerr nonlinearity effects have found interesting applications in optics [1]–[3]. Thus, continued research of higher-order NLS equations is inevitable and worthwhile. Due to these effects, the propagation of subpicosecond and femtosecond pulses can be described by the general integrable four-parameter $(\alpha_2,\alpha_3,\alpha_4,\alpha_5)$ fifth-order NLS (GFONLS) equation [4]–[6]

$$i\psi_t+\alpha_2K_2(\psi)-i\alpha_3K_3(\psi)+\alpha_4K_4(\psi) -i\alpha_5K_5(\psi)=0, $$

(1.2)

where

$$\begin{aligned} \, &K_2 =\psi_{xx}+2(|\psi|^2-\psi_0^2)\psi, \\ &K_3 =\psi_{xxx}+6|\psi|^2\psi_x, \\ &K_4 =\psi_{xxxx}+8|\psi|^2\psi_{xx}+6(|\psi|^4-\psi_0^4)\psi +4|\psi_x|^2\psi+6\psi^*\psi_x^2+2\psi^2\psi^*_{xx}, \\ &K_5 =\psi_{xxxxx}+10|\psi|^2\psi_{xxx}+10(\psi|\psi_x|^2)_x +20\psi^*\psi_x\psi_{xx}+30|\psi|^4\psi_x. \end{aligned} $$

(1.3)

Recently, considerable attention has been given to the inverse scattering transform (IST) to study integrable nonlinear wave equations with NZBCs using solutions of the related RHP. The approach has been extended to the focusing and defocusing NLS equation, the focusing and defocusing Hirota equations, the nonlocal modified KdV equation, the derivative NLS equation, and other equations [7]–[20]; many types of nonlinear waves have been discussed. In this paper, motivated by the work of Ablowitz [8], we extend the IST to study GFONLS equation (1.2) with the NZBCs at infinity

$$\lim_{x\to\infty}\psi(x,t)=\psi_\pm, $$

(1.4)

where $|\psi_\pm|=\psi_0\ne 0$. Equation (1.2) includes numerous important nonlinear wave equations as its special cases [21]–[32]. Here, we list some crucial cases.

Case 1. If $\alpha_3=\alpha_4=\alpha_5=0$, $\alpha_2=1$, Eq. (1.2) can be reduced to the fundamental NLS equation (1.1) with NZBCs:

$$i\psi_t+\psi_{xx}+2(|\psi|^2-\psi_0^2)\psi=0. $$

(1.5)

Case 2. If $\alpha_4=\alpha_5=0$, Eq. (1.2) can be reduced to the Hirota equation with NZBCs [21]:

$$i\psi_t+\alpha_2(\psi_{xx}+2(|\psi|^2-\psi_0^2))\psi +i\alpha_3(\psi_{xxx}+6|\psi|^2\psi_x)=0. $$

(1.6)

Case 3. If $\alpha_3=1$, $\alpha_2=\alpha_4=\alpha_5=0$, Eq. (1.2) can be reduced to the complex modified Korteweg–de Vries (mKdV) equation [22], [23]

$$\psi_t+\psi_{xxx}+6|\psi|^2\psi_x=0. $$

(1.7)

To the best of our knowledge, although many mathematical physicist have studied the particular cases of Eq. (1.2), the IST for Eq. (1.2) with NZBCs has not been reported. The GFONLS equation (1.2) is completely integrable, its Lax pair is given by [6]

$$\begin{alignedat}{2} &\phi_x =U\phi, &\qquad &U =ik\sigma_3+Q, \\ &\phi_t =V\phi, &\qquad &V =\alpha_2\Delta_{\mathrm{NLS}}+\alpha_3\Delta_{\mathrm{mKdV}} +\alpha_4\Delta_{\mathrm{LPD}}+\alpha_5\Delta_{\mathrm{FOQ}}+3i\alpha_4\sigma_3, \end{alignedat} $$

(1.8)

where the eigenfunction $\phi=\phi(x,t,\lambda)$ is a $2\times2$ matrix function, $\sigma_3=\operatorname{diag}\{1,-1\}$, and the matrices $Q$, $V_0$, $L$, $M$, and $N$ are

$$\begin{aligned} \, &\Delta_{\mathrm{NLS}} =-2kU+i\sigma_3(Q_x-Q^2-\psi_0^2), \\ &\Delta_{\mathrm{mKdV}} =-2k(\Delta_{\mathrm{NLS}}+i\psi_0^2\sigma_3)-[Q,Q_x]-Q_{xx}+2Q^3, \\ &\Delta_{\mathrm{LPD}} =2k[-(4ik^3+k^2Q+kV_0)+L_0]+M_0,\qquad \Delta_{\mathrm{FOQ}}=-2k\Delta_{\mathrm{LPD}}+N_0, \end{aligned} $$

(1.9)

with

$$\begin{aligned} \, &Q =\begin{pmatrix} 0 &\psi \\ -\psi^* &0 \end{pmatrix},\qquad V_0=\frac{1}{2}\begin{pmatrix} -i|\psi|^2 &-\psi_x \\ \psi_x^* &i|\psi|^2 \end{pmatrix},\qquad N_0=\begin{pmatrix} n_1 &-n_2^* \\ n_2 &-n_1 \end{pmatrix}, \\ &L_0 =\begin{pmatrix} \psi\psi_x^*-\psi^*\psi_x &i(\psi_{xx}+2|\psi|^2\psi) \\ i(\psi_{xx}^*+2|\psi|^2\psi^*) &\psi^*\psi_x-\psi\psi_x^* \end{pmatrix},\qquad M_0=\begin{pmatrix} m_1 &-m_2^* \\ m_2 &-m_1 \end{pmatrix}, \\ &m_1 =-i[(\psi\psi_{xx})^*-|\psi_x|^2+3|\psi|^4],\qquad m_2=\psi_{xxx}^*+6|\psi|^2\psi_x^*, \\ &n_1 =\psi_{xxx}(\psi-\psi^*)-\psi_x\psi_{xx}^*\psi_x^*\psi_{xx} +6|\psi|^2(\psi\psi_x^*-\psi^*\psi_x), \\ &n_2 =i(\psi_{xxxx}^*+2\psi^{*2}\psi_{xx}+4|\psi_x^2\psi^*| +6\psi\psi_x^{*2}+8|\psi|^2\psi_{xx}^*+6|\psi|^4\psi^*), \end{aligned} $$

(1.10)

where $\psi^*(x,t)$ is the complex conjugate of $\psi(x,t)$ and $k$ is a constant spectral parameter.

It is well known that the IST is a powerful method to construct soliton solutions [15], [33]–[49]. However, the research described in this paper, within our knowledge, has not been reported before. The main purpose of this paper is to use the IST to derive multisoliton solutions of GFONLS equation (1.2) with NZBCs (1.4). In addition, some figures are presented to discuss the behavior of solitons of GFONLS equation (1.2).

The main results in this paper are stated in the following theorems.

Theorem 1.1.

The reflectionless potential with simple poles for GFONLS equation (1.2) with NZBCs (1.4) can be represented as

$$\psi(x,t)=\psi_-+i\frac{\det\begin{pmatrix} G &v \\ w^{\mathrm T} &0 \end{pmatrix}}{\det G}, $$

(1.11)

where $w\!=\!(w_j)_{2N\times 1}$, $v\!=\!(v_j)_{2N\times 1}$, $G\!=\!(g_{sj})_{2N\times 2N}$, and $y\!=\!(y_n)_{2N\times1}\!=\!G^{-1}v$ with $w_j\!=\!A_-[\widehat\xi_j]e^{2i\theta(x,t,\widehat\xi_j)}$, $v_j=-iq_-/\xi_j$, $g_{sj}=w_j/(\xi_s-\widehat\xi_j)+v_s\delta_{sj}$, and $y_n=\mu_{-11}(x,t,\hat\xi_n)$.

Theorem 1.2.

The reflectionless potential with double poles for GFONLS equation (1.2) with NZBCs (1.4) can be written as

$$\psi(x,t)=\psi_-+i\frac{\det\begin{pmatrix} H &v \\ w^{\mathrm T} &0 \end{pmatrix}}{\det H}, $$

(1.12)

where

$$\begin{aligned} \, &H=(H^{(sj)})_{2\times 2},\quad H^{(sj)}=(h_{kn}^{(sj)})_{2N\times2N},\quad h_{kn}^{(11)}=\widehat C_n(\xi_k) \biggl(D_n+\frac{1}{\xi_k-\hat\xi_n}\biggr) -\frac{i\psi_-}{\xi_k}\delta_{kn}, \\ &h_{kn}^{(12)}=\widehat C_n(\xi_k),\qquad h_{kn}^{(21)}=\frac{\widehat C_n}{\xi_k-\hat\xi_n} (\xi_{k})\biggl(D_n+\frac{2}{\xi_k-\hat\xi_n}\biggr) -\frac{i\psi_-}{\xi_k^2}\delta_{kn}, \\ &h_{kn}^{(22)}=\frac{\widehat C_n(\xi_k)}{\xi_k-\xi_n} +\frac{i\psi_-\psi_0^2}{\xi_k^3}\delta_{kn},\qquad w_n^{(1)}=A_-[\hat\xi_n]e^{2i\theta(\xi_n)}\widehat D_n, \\ &w_n^{(2)}=A_-[\hat\xi_n]e^{2i\theta(\xi_n)},\qquad v_n^{(1)}=-\frac{\psi_-}{\xi_n},\qquad v_n^{(2)}=-\frac{\psi_-}{\xi^2_n}. \end{aligned}$$

The outline of this paper is as follows. In Sec. 2, we analyze the direct scattering problem for the GFONLS equation (1.2) with NZBCs (1.4) starting from its Lax pairs. In Sec. 3, we discuss the GFONLS equation (1.2) with NZBCs (1.4) and obtain its simple-pole solution by solving an RHP with reflectionless potentials. Similarly, in Sec. 4 we analyze the GFONLS equation (1.2) with NZBCs (1.4) and derive its double-pole solutions by solving a matrix RHP. Finally, conclusions and a discussion are presented in Sec. 5.

2. Direct scattering problem

We first discuss the first expression in (1.8) as the scattering problem of Eq. (1.4). As $x\to\pm\infty$, the scattering problem yields

$$\phi_x=U_\pm\phi,\qquad U_\pm=\lim_{x\to\pm\infty}U=ik\sigma_3+Q_\pm, $$

(2.1)

and

$$Q_\pm=\lim_{x\to\pm\infty}Q(x,t)=\begin{pmatrix} 0 &\psi_\pm \\ -\psi_\pm^* &0 \end{pmatrix}. $$

(2.2)

Consequently, the standard matrix solutions of Eq. (2.1) are defined by

$$\begin{aligned} \, \phi_{bg}^f(x,t,k)= \begin{cases} E^f_\pm(k)e^{i\theta(x,t,k)\sigma_3}, &k\ne\pm i\psi_0, \\ I+[x-2(\alpha_2k+3\alpha_3\psi_0^2+6\alpha_4i\psi_0^3 +\alpha_5(-8\psi_0^4-7\psi_0^2))t]U_\pm, &k=\pm i\psi_0, \end{cases} \end{aligned}$$

(2.3)

where $I$ is the $2\times2$ unit matrix and

$$\begin{aligned} \, \begin{aligned} \, &E^f_\pm(k)=\begin{pmatrix} 1 &\dfrac{i\psi_\pm}{k+\lambda} \\ \dfrac{i\psi^*_\pm}{k+\lambda} &1 \end{pmatrix}, \\ &\theta(x,t,k)=\lambda(k)\{x+[\alpha_5(-16k^4+8k^2-6\psi_0^2)+{} \\ &\hphantom{\theta(x,t,k)={}}+\alpha_4(8k^3-4k\psi_0^2) +\alpha_3(4k^2-2\psi_0^2)-2\alpha_2k]t\}, \end{aligned} \end{aligned}$$

(2.4)

with

$$\lambda^2=k^2+\psi_0^2. $$

(2.5)

To further study the analyticity of the Jost solutions of (1.8), we must consider the regions $\operatorname{Im}\lambda(k)>0$ $(<0)$ for the function $\theta(x,t,k)$ [9]. Taking $\psi_0\ne 0$, i.e., assuming NZBCs, the function $\lambda(k)$ satisfying (2.5) on the complex plane is a doubly branched function of $k$ with two branch points $k\ne\pm i\psi_0$ and the branch cut given by the segment $i\psi_0[-1,1]$. We take $k\pm i\psi_0=r_\pm e^{i\theta_\pm+2im_\pm\pi}$ ($r_\pm>0$, $\theta_\pm\in[-\pi/2,3\pi/2]$, $m_\pm\in\mathbb Z$). Two single-valued analytic branches of the complex $k$-plane are expressed by sheet I, $\lambda_{\mathrm I}(k)=\sqrt{r_+r_-}e^{i(\theta_++\theta_-)/2}$, and sheet II, $\lambda_{\mathrm{II}}(k)=-\lambda_{\mathrm I}(k)$. We introduce a uniformization variable $z$ given by the conformal map $z=k+\lambda$, the inverse map being

$$k(z)=\frac{1}{2}\biggl(z-\frac{\psi_0^2}{z}\biggr),\qquad \lambda(z)=\frac{1}{2}\biggl(z+\frac{\psi_0^2}{z}\biggr). $$

(2.6)

In particular, if $\psi_0=0$, the NZBCs reduce to zero boundary conditions.

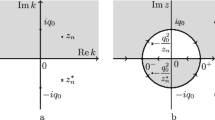
We take $\mathbb A=i\psi_0[-1,1]$ with $C_0=\{z\in\mathbb C:|z|=\psi_0\}$, and (see Fig. 1)

$$D_+^f=\{z\in\mathbb C\colon(|z|^2-\psi_0^2)\operatorname{Im}z>0\},\qquad D_-^f=\{z\in\mathbb C\colon(|z|^2-\psi_0^2)\operatorname{Im}z<0\}. $$

(2.7)

Fig. 1.

The grey (white) region for $\operatorname{Im}\lambda>0$ and $\operatorname{Im}\lambda<0$ in different spectral planes of the Lax pair with NZBCs. (a) the first sheet of the Riemann surface, showing the discrete spectrum; (b) the complex $z$ plane showing the discrete spectrum (zeros of $s_{11}(z)$ in the grey region and zeros of $s_{22}(z)$ in the white region), and the orientation of the jump contours for the related RHP.

The continuous spectrum of $U_\pm=\lim_{x\to\pm\infty}U$ is the set of all values of $z$ satisfying $\lambda(z)\in\mathbb R$, i.e., $z\in\Sigma^f=\mathbb R\cup C_0$, which are the jump contours. As mentioned in [9], it follows from $[U_\pm,V_\pm]=0$ that the Jost solutions $\phi_\pm(x,t,z)$ of both equations in (1.8) satisfy the boundary conditions

$$\phi_\pm(x,t,z)=E_\pm^f(z)e^{i\theta(x,t,z)\sigma_3}+O(1),\qquad z\in\Sigma^f,\quad x\to\pm\infty. $$

(2.8)

In view of $\phi_x=U_\pm\phi+\Delta Q_\pm\phi$, $\Delta Q_\pm(x,t)=Q(x,t)-Q_\pm$ with $Q_\pm=\lim_{x\to\pm\infty}Q$, the modified Jost solutions

$$\mu_\pm(x,t,z)=\phi_\pm(x,t,z)e^{-i\theta(x,t,z)\sigma_3}\to E_\pm^f(z),\qquad x\to\pm\infty, $$

(2.9)

take the final form

$$\mu_\pm=\begin{cases} \displaystyle{E_\pm^f(z)\biggl\{I+\int_{\pm\infty}^x e^{i\lambda(x-y)\widehat\sigma_3}[(E_\pm^f(z))^{-1}\Delta Q_\pm(y,t)\mu_\pm(y,t,z)]\,dy\biggr\}}, \\ z\ne\pm i\psi_0,\quad \psi-\psi_\pm\in L^1(\mathbb R^\pm), \\ \displaystyle{E_\pm^f(z)+\int_{\pm\infty}^x[I+(x-y)(Q_\pm\mp\psi_0\sigma_3)] \Delta Q_\pm(y,t)\mu_\pm(y,t,z)\,dy}, \\ z=\pm i\psi_0,\qquad (1+|x|)(\psi-\psi_\pm)\in L^1(\mathbb R^\pm), \end{cases} $$

(2.10)

where $e^{\widehat\sigma_3}A:=e^{\sigma_3}Ae^{-\sigma_3}$.

Let $\Sigma_0^f:=\Sigma^f\setminus\{\pm i\psi_0\}$, $\mu_\pm(x,t,z)=(\mu_{\pm,1},\mu_{\pm,2})$ and $\phi_\pm(x,t,z)=(\phi_{\pm1},\phi_{\pm2})$. Because expression (2.10) contains $e^{\pm i(x-y)}$, the following proposition follows from the properties of these functions in the different domains and the definition (2.10) of $\mu_\pm(x,t,z)$ as well as from relation (2.9) between $\mu_\pm(x,t,z)$ and $\phi(x,t,z)$ (also see [9]).

Proposition 2.1.

If $\psi-\psi_\pm\in L^1(\mathbb R^\pm)$, then the modified expressions $\mu_{\pm 2}(x,t,z)$ and the Jost functions $\phi_{\pm 2}$ given by (2.9) and (2.10) admit unique solutions in $\Sigma_0^f$. In addition, $\mu_{+1}(x,t,z)$, $\mu_{-2}(x,t,z)$, $\phi_{+1}(x,t,z)$, and $\phi_{-2}(x,t,z)$ can be continuously extended to $D_+^f\cup\Sigma_0^f$ and analytically extended to $D_+^f$, while $\mu_{-1}(x,t,z)$, $\mu_{+2}(x,t,z)$, $\phi_{-1}(x,t,z)$, and $\phi_{+2}(x,t,z)$ can be continuously extended to $D_-^f\cup\Sigma_0^f$ and analytically extended to $D_-^f$.

Because $\operatorname{tr}U(x,t,z)=\operatorname{tr}V(x,t,z)=0$, we have $(\det\phi_\pm)_x=(\det\phi_\pm)_t=0$. Besides, from Liouville’s formula, we can find

$$\det \phi_\pm=\lim_{x\to\pm\infty}\mu_\pm =\det E_\pm^f(z)=\gamma_f(z)=1+\frac{\psi_0^2}{z^2}\ne 0,\qquad z\ne\pm i\psi_0 $$

(2.11)

because both $\phi_\pm(x,t,z)$ are primary matrix solutions of spectral problem (1.8). We thus find a constant matrix $S(z)$ such that

$$\phi_+(x,t,z)=\phi_-(x,t,z)S(z),\qquad z\in\Sigma_0^f, $$

(2.12)

where $S(z)=(s_{ij}(z))_{2\times2}$ are scattering coefficients. In accordance with (2.12), we have

$$\begin{aligned} \, &s_{11}(z)=\gamma_f^{-1}(z)|\phi_{+1}(x,t,z),\phi_{-2}(x,t,z)|, \\ &s_{12}(z)=\gamma_{f}^{-1}(z)|\phi_{+1}(x,t,z),\phi_{+2}(x,t,z)|, \\ &s_{21}(z)=\gamma_f^{+2}(z)|\phi_{+1}(x,t,z),\phi_{-2}(x,t,z)|, \\ &s_{22}(z)=\gamma_f^{-1}(z)|\phi_{+1}(x,t,z),\phi_{+1}(x,t,z)|, \end{aligned} $$

(2.13)

and $\operatorname{det}S(z)=1$.

Form Proposition 2.1, it is not difficult to see that the coefficients $s_{11}(z)$ and $s_{22}(z)$ in $z\in\Sigma_0^f$ can be continuously extended to $D_+^f\cup\Sigma_0^f$ and $D_-^f\cup\Sigma_0^f$, and analytically extended to $D_+^f$ and $D_-^f$.

To discuss the matrix RHP in Sec. 3, we assume that $s_{11}(z)s_{22}(z)\ne 0$ for $z\in\Sigma^f$, and $S(z)$ is continuous for $z=i\psi_0$. We can then obtain the so-called reflection coefficients

$$\rho(z)=\frac{s_{21}(z)}{s_{11}(z)},\qquad \hat\rho(z)=\frac{s_{21}(z)}{s_{22}(z)},\qquad z\in\Sigma^f. $$

(2.14)

3. Inverse scattering problem: simple pole

In this section, to construct the residue conditions and discrete spectrum, we introduce the symmetries of the scattering matrix $S(k)$. From the results in [9], we have $k(z)=k^*(z^*)$, $k(z)=k(-\psi_0^2/z)$, ${\lambda(z)=\bar\lambda(z^*)}$, and $\lambda(z)=-\lambda(-\psi_0^2/z)$, and hence the symmetries of $U$, $V$, and $\theta$ are

$$\begin{alignedat}{2} &U(x,t,z)=\sigma_2U^*(x,t,z^*)\sigma_2,&\qquad &U(x,t,z)=U\biggl(x,t,-\frac{\psi_0^2}{z}\biggr), \\ &V(x,t,z)=\sigma_2V(x,t,z^*)^*\sigma_2,&\qquad &V(x,t,z)=V\biggl(x,t,-\frac{\psi_0^2}{z}\biggr), \\ &\theta(x,t,z)=\theta^*(x,t,z^*),&\qquad &\theta(x,t,z)=-\theta\biggl(x,t,-\frac{\psi_0^2}{z}\biggr), \end{alignedat} $$

(3.1)

where $\sigma_2=\bigl(\begin{smallmatrix} 0 &-i\\ i &\hphantom{-}0\end{smallmatrix}\bigr)$.

In view of these symmetries, Eqs. (1.8) and (2.9) yield

$$\begin{alignedat}{2} &\phi_\pm(x,t,z)=\sigma_2\phi^*_\pm(x,t,z^*)\sigma_2,&\qquad &\phi_\pm(x,t,z)=\frac{i}{z}\phi_\pm\biggl(x,t,-\frac{\psi_0^2}{z}\biggr)\sigma_3Q_\pm, \\ &\mu_\pm(x,t,z)=\sigma_2\mu^*_\pm(x,t,z^*)\sigma_2,&\qquad &\mu_\pm(x,t,z)=\frac{i}{z}\mu_\pm\biggl(x,t,-\frac{\psi_0^2}{z}\biggr)\sigma_3Q_\pm. \end{alignedat} $$

(3.2)

It follows from Eqs. (3.2) and (2.12) that

$$S(z)=\sigma_2S^*(z^*)\sigma_2,\qquad S(z)=(\sigma_3Q_-)^{-1}S\biggl(-\frac{\psi_0^2}{z}\biggr)\sigma_3Q_+, $$

(3.3)

which leads to the symmetries between $\rho(z)$ and $\hat\rho(z)$ in the form

$$\rho(z)=-\hat\rho^*(z^*),\qquad \rho(z)=\frac{q^*_-}{q_-} \rho\biggl(-\frac{\psi_0^2}{z}\biggr). $$

(3.4)

The discrete spectrum is the set of all $z\in\mathbb C\setminus\Sigma^f$ such that they admit eigenfunctions in $L^2(\mathbb R)$. According to [9], they satisfy $s_{11}(z)=0$ for $z\in D_+^f$ and $s_{22}(z)=0$ for $z\in D_-^f$, and hence the corresponding eigenfunctions are in $L^2(\mathbb R)$ in accordance with (2.13) and expression for $\phi_\pm$ in (2.9).

In what follows, we require that $s_{11}(z)$ admit $N$ simple zeros in

$$D_+^f\cap\{z\in\mathbb C\colon|z|>\psi_0,\,\operatorname{Im}z>0\}$$

given by $z_n$, $n=1,2,\dots,N$, i.e., $s_{11}(z_n)=0$ and $s'_{11}(z_n)\ne 0$, $n=1,2,\dots,N$. If $s_{11}(z_n)=0$, we have $s_{22}(z^*_n)=s_{22}(-\psi_0^2/z_n)=s_{11}(-\psi_0^2/z^*_n)=0$. Thus, the discrete spectrum is the set

$$\begin{aligned} \, &Z^f=\biggl\{z_n,-\frac{\psi_0^2}{z^*_n},z^*_n,-\frac{\psi_0^2}{z_n}\biggr\}_{n=1}^N,\qquad s_{11}(z_n)=0, \\ &z_n\in D_+^f\cap\{z\in\mathbb C\colon|z|>\psi_0,\,\operatorname{Im}z>0\}. \end{aligned} $$

(3.5)

Because $s_{11}(z_0)=0$ and $s'_{11}(z_0)\ne 0$ are taken for $z_0\in Z^f\cap D_+^f$, according to the first expression in (2.13), the normalization constant $b_+(z_0)$ is given by

$$\phi_{+1}(x,t,z_0)=b_+(z_0)\phi_{-2}(x,t,z_0). $$

(3.6)

The residue condition for $\phi_{+1}(x,t,z)/s_{11}(z)$ in $z_0\in Z^f\cap D_+^f$ yields

$$\mathop{\operatorname{Res}}\limits_{z=z^*_0} \biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}\biggr] =\frac{\phi_{+1}(x,t,z_0)}{s'_{11}(z_0)} =\frac{b_+(z_0)}{s'_{11}(z_0)}\phi_{-2}(x,t,z_0). $$

(3.7)

Similarly, from $s_{22}(z^*_0)=0$ and $s'_{22}(z^*_0)\ne 0$ for $z^*_0\in Z^f\cap D_-^f$ and the second expression in (2.13), we also see that the normalization constant $b_-(z^*_0)$ is

$$\phi_{-2}(x,t,z^*_0)=b_-(z^*_0)\phi_{-1}(x,t,z^*_0). $$

(3.8)

The residue condition $\phi_{+2}(x,t,z)/s_{22}(z)$ in $z^*_0\in Z^f\cap D_-^f$ leads to

$$\mathop{\operatorname{Res}}\limits_{z=z^*_0} \biggl[\frac{\phi_{+2}(x,t,z)}{s_{22}(z)}\biggr] =\frac{\phi_{+2}(x,t,z^*_0)}{s'_{22}(z^*_0)} =\frac{b_-(z^*_0)}{s'_{22}(z^*_0)}\phi_{-1}(x,t,z^*_0). $$

(3.9)

For simplicity, we rewrite Eqs. (3.7) and (3.9) as

$$\begin{aligned} \, &\mathop{\operatorname{Res}}\limits_{z=z_0} \biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}\biggr] =A_+[z_0]\phi_{-2}(x,t,z_0), \\ &A_+[z_0]=\frac{b_+(z_0)}{s'_{11}(z_0)},\qquad z_0\in Z^f\cap D_+^f, \\ &\mathop{\operatorname{Res}}\limits_{z=z^*_0} \biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}\biggr] =A_+[z^*_0]\phi_{-2}(x,t,z^*_0), \\ &A_+[z^*_0]=\frac{b_+(z^*_0)}{s'_{11}(z^*_0)},\qquad z^*_0\in Z^f\cap D_+^f. \end{aligned} $$

(3.10)

It follows from (3.10) that

$$A_+[z_0]=-A^*_-[z^*_0],\qquad A_+[z_0]=\frac{z_0^2}{\psi_-^2} A_-\biggl[-\frac{\psi_0^2}{z_0}\biggr],\quad z_0\in Z^f\cap D_+^f, $$

(3.11)

in terms of symmetries (3.2) and (3.3), which leads directly to

$$A_+[z_n]=-A^*_-[z^*_n] =\frac{z_n^2}{\psi_-^2}A_-\biggl[-\frac{\psi_0^2}{z_n}\biggr] =-\frac{z_n^2}{\psi_-^2}A^*_+\biggl[-\frac{\psi_0^2}{z^*_n}\biggr],\quad z_n\in Z^f\cap D_+^f. $$

(3.12)

We rewrite the relation $\phi_+(x,t,z)=\phi_-(x,t,z)S(z)$ as

$$\begin{aligned} \, &\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}=\phi_{-1}(x,t,z)+\rho(z)\phi_{-2}(x,t,z), \\ &\frac{\phi_{+2}(x,t,z)}{s_{22}(z)}=\hat\rho(z)\phi_{-1}(x,t,z)+\phi_{-2}(x,t,z), \end{aligned} $$

(3.13)

whence

$$\biggl[\phi_{-1}(x,t,z),\frac{\phi_{+2}(x,t,z)}{s_{22}(z)}\biggr] =\biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)},\phi_{-2}(x,t,z)\biggr] [I-J_0(x,t,\lambda)], $$

(3.14)

with

$$J_0=\begin{pmatrix} 0 &-\hat\rho(z) \\ \rho(z) &\rho(z)\hat\rho(z) \end{pmatrix}. $$

(3.15)

Similarly to [9], the asymptotics for the modified Jost solutions and scattering data satisfy

$$\mu_\pm(x,t,z)=\begin{cases} I+O\biggl(\dfrac{1}{z}\biggr),&z\to\infty, \\[3mm] \dfrac{i}{z}\sigma_3Q_\pm+O(1), &z\to 0, \end{cases}\qquad S(z)=\begin{cases} I+O\biggl(\dfrac{1}{z}\biggr), &z\to\infty,\\ \dfrac{\psi_+}{\psi_-}I+O(z), &z\to 0. \end{cases} $$

(3.16)

Given the modified Jost functions, we introduce the sectionally meromorphic matrix

$$\begin{aligned} \, M(x,t,z)=\begin{cases} M^+(x,t,z)=\biggl(\dfrac{\mu_{+1}(x,t,z)}{s_{11}(z)},\mu_{-2}(x,t,z)\biggr)= \\[3mm] \quad=\biggl(\dfrac{\phi_{+1}(x,t,z)}{s_{11}(z)}, \phi_{-2}(x,t,z)\biggr)e^{-i\theta(x,t,z)\sigma_3}, &z\in D_+^f, \\[3mm] M^{-}(x,t,z)=\biggl(\mu_{-1}(x,t,z),\dfrac{\mu_{+2}(x,t,z)}{s_{22}}\biggr)= \\[3mm] \quad=\biggl(\phi_{-1}(x,t,z),\dfrac{\phi_{+2}(x,t,z)}{s_{22}}\biggr) e^{-i\theta(x,t,z)\sigma_3}, &z\in D_-^f. \end{cases} \end{aligned}$$

(3.17)

Summarizing the above results, we have the following proposition.

Proposition 3.1.

The matrix function $M(x,t,z)$ has the following matrix RHP.

• • Analyticity: $M(x,t,z)$ is analytic in $(D_+^f\cup D_-^f)\setminus Z^f$ ;

• • Jump condition: $M^-(x,t,z)=M^+(x,t,z)(I-J(x,t,z))$ , $z\in\Sigma^f$ with $J(x,t,z)=e^{i\theta(x,t,z)\widehat\sigma_3}J_0$ ;

• • Asymptotic behavior: $M^\pm(x,t,z)=I+(1/z)$ for $z\to\infty$ . In addition, $M^\pm=(i/z)\sigma_3Q_-+O(1)$ for ${z\to 0}$ .

To conveniently deal with the above RHP (i.e., in Proposition 3.1), we set

$$\xi_n=\begin{cases} z_n, &n=1,2,\dots,N, \\ -\dfrac{\psi_0^2}{z^*_{n-N}}, &n=N+1,N+2,\dots,2N, \end{cases} $$

(3.18)

and $\hat\xi_n=-\psi_0^2/\xi_n$. Then $Z^f=\{\xi_n,\hat\xi_n\}_{n=1}^{2N}$ with $\xi_n\in D_+^f$ and $\hat\xi_n\in D_-^f$. Subtracting the simple pole contributions and the asymptotics, i.e.,

$$M_{sp}(x,t,z)=I+\frac{i}{z}\sigma_3Q_- +\sum_{n=1}^{2N} \biggl[\frac{\operatorname{Res}_{z=\xi_n}M^+(x,t,z)}{z-\xi_n}+ \frac{\operatorname{Res}_{z=\hat\xi_n}M^-(x,t,z)}{z-\hat\xi_n}\biggr], $$

(3.19)

from both sides of the above jump condition $M^-=M^+(I-J)$ leads to

$$M^-(x,t,z)-M_{sp}(x,t,z)=M^+(x,t,z)-M_{sp}(x,t,z)-M^+(x,t,z)J(x,t,z). $$

(3.20)

Here, $M^\pm(x,t,z)\to M_{sp}(x,t,z)$ are analytic in $D_\pm^f$. Furthermore, the asymptotics are both $O(1/z)$ as ${z\to\infty}$ and $O(1)$ as $z\to 0$, and $J(x,t,z)$ is $O(1/z)$ as $z\to\infty$ and $O(z)$ as $z\to 0$. Thus, the Cauchy projectors

$$P^\pm[f](z)=\frac{1}{2\pi i}\int_{\Sigma^f}\frac{f(\zeta)}{\zeta-(z\pm i0)}\,d\zeta $$

(3.21)

(where $z\pm i0$ is the limit taken from the left/right of $z$) and Plemelj’s formulas used to solve (3.20) give

$$M(x,t,z)=M_{sp}(x,t,z) +\frac{1}{2\pi i} \int_{\Sigma^f}\frac{M^+(x,t,\zeta)J(x,t,\zeta)}{\zeta-z}\,d\zeta,\qquad z\in\mathbb C\setminus\Sigma^f, $$

(3.22)

where $\int_{\Sigma^f}$ represents the integral along the oriented contours shown in Fig. 1.

We see from (3.17) that only its first (second) column has a simple pole at $z=\xi_n$ $(z=\hat\xi_n)$. Therefore, by using (2.9) and (3.10), we can express the residue part in (3.19) as

$$\begin{aligned} \, &\frac{\operatorname{Res}_{z=\xi_n}M^+(x,t,z)}{z-\xi_n} +\frac{\operatorname{Res}_{z=\hat\xi_n}M^-(x,t,z)}{z-\hat\xi_n}= \nonumber \\ &=\biggl(\frac{A_+[\xi_n]e^{-2i\theta(x,t,\xi_n)}}{z-\xi_n}\mu_{-2}(x,t,\xi_n), \frac{A_-[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)}}{z-\hat\xi_n} \mu_{-1}(x,t,\hat\xi_n)\biggr). \end{aligned}$$

(3.23)

For $z=\xi_s$, $s=1,2,\dots,2N$, it follows from the second column of $M(x,t,z)$ given by (3.22) and (3.23) that

$$\begin{aligned} \, \mu_{-2}(x,t,\xi_s)={}&\begin{pmatrix} \dfrac{i\psi_-}{\xi_s} \\ 1 \end{pmatrix}+\sum_{n=1}^{2N} \frac{A_-[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)}}{\xi_s-\hat\xi_n} \mu_{-1}(x,t,\hat\xi_n)+{} \nonumber \\ &+\frac{1}{2\pi i}\int_{\Sigma^f} \frac{(M^+J)_2(x,t,\zeta)}{\zeta-\xi_s}\,d\zeta,\qquad s=1,2,\dots,2N. \end{aligned}$$

(3.24)

From (3.2), we find

$$\mu_{-2}(x,t,\xi_s)=\frac{i\psi_-}{\xi_s}\mu_{-1}(x,t,\widehat\xi_s),\qquad s=1,2,\dots,2N. $$

(3.25)

Substituting (3.25) in (3.2), we have

$$\begin{aligned} \, &\sum_{n=1}^{2N}\biggl(\frac{A_-[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)}}{\xi_s-\hat\xi_n} -\frac{i\psi_-}{\xi_s}\delta_{sn}\biggr)\mu_{-1}(x,t,\hat\xi_n) +\begin{pmatrix} \dfrac{i\psi_-}{\xi_s} \\ 1 \end{pmatrix}+{} \nonumber \\ &+\frac{1}{2\pi i}\int_{\Sigma^f} \frac{(M^+J)_2(x,t,\zeta)}{\zeta-\xi_s}\,d\zeta=0,\qquad s=1,2,\dots,2N, \end{aligned}$$

(3.26)

where

$$\delta_{sn}=\begin{cases} 1, &s=n, \\ 0, &s\ne n. \end{cases}$$

System (3.26) includes $2N$ equations for $2N$ unknowns $\mu_{-1}(x,t,\hat\xi_n)$, whence the solutions for $\mu_{-1}(x,t,\widehat\xi_s)$ allows finding $\mu_{-2}(x,t,\xi_s)$ from (3.26). As a consequence, substituting $\mu_{-1}(x,t,\widehat\xi_s)$ and $\mu_{-2}(x,t,\xi_s)$ in (3.23) and then substituting (3.23) in (3.22), we express $M(x,t,z)$ in terms of the scattering data.

In view of (3.23) and (3.22), the asymptotic behavior of $M(x,t,z)$ is

$$M(x,t,z)=I+\frac{M^{(1)}(x,t)}{z}+O\biggl(\frac{1}{z^2}\biggr),\qquad z\to\infty, $$

(3.27)

where

$$\begin{aligned} \, M^{(1)}(x,t)={}&i\sigma_3Q+\sum_{n=1}^{2N} [A_+[\xi_n]e^{-2i\theta(x,t,\xi_n)}, A_-[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)}\mu_{-1}(x,t,\hat\xi_n)]-{} \nonumber \\ &-\frac{1}{2\pi i}\int_{\Sigma^f}M^+(x,t,\zeta)J(x,t,\zeta)\,d\zeta, \end{aligned}$$

(3.28)

with $\mu_{-1}(x,t,\widehat\xi_s)$ and $\mu_{-2}(x,t,\widehat\xi_s)$ given by (3.25) and (3.26).

From (3.17), we find that $M(x,t,z)e^{i\theta(x,t,z)\sigma_3}$ satisfies (1.8). Substituting $M(x,t,z)e^{i\theta(x,t,z)\sigma_3}$ given by (3.27) in the $x$-part of Lax pair (1.8) and taking the coefficients of $z^0$, we arrive at the statement of following proposition for $\psi(x,t)$.

Proposition 3.2.

The potential with simple poles of the GFONLS equation (1.2) with NZBCs (1.4) has the form

$$\psi(x,t)=\psi_--i\sum_{n=1}^{2N}A_-[\hat\xi_n] e^{2i\theta(x,t,\hat\xi_n)}\mu_{-11}(x,t,\hat\xi_n) +\frac{1}{2\pi}\int_{\Sigma^f}(M^+J)_{12}(x,t,\zeta)\,d\zeta, $$

(3.29)

where $\xi_n=z_n$, $\xi_{n+N}=-\psi_0^2/z^*_{n-N}$, $n=1,2,\dots,N$, $\hat\xi_n=-\psi_0^2/\xi_n$, and $\mu_{-11}(x,t,\hat\xi_n)$ are determined by the system of equations

$$\begin{aligned} \, &\sum_{n=1}^{2N}\biggl(\frac{A_-[\hat\xi_n] e^{2i\theta(x,t,\hat\xi_n)}}{\xi_s-\hat\xi_n} -\frac{i\psi_-}{\xi_s}\delta_{sn}\biggr)\mu_{-11}(x,t,\hat\xi_n) +\frac{i\psi_-}{\xi_s}+{} \nonumber \\ &+\frac{1}{2\pi i} \int_{\Sigma^f}\frac{(M^+J)_{12}(x,t,\zeta)}{\zeta-\xi_s}\,d\zeta=0,\qquad s=1,2,\dots,2N, \end{aligned}$$

(3.30)

which can be obtained from (3.26).

We note that $s_{11}(z)$ and $s_{22}(z)$ are respectively analytic in $D_+^f$ and $D_-^f$, and the discrete-spectrum points $\xi_n$ and $\hat\xi_n$ are respective simple zeros of $s_{11}(z)$ and $s_{22}(z)$. Following [9], we write the trace formulas for the GFONLS equation (1.2) with NZBCs as

$$\begin{alignedat}{2} &s_{11}(z)=e^{s(z)}s_0(z)&\qquad &\text{for}\quad z\in D_+^f, \\ &s_{22}(z)=\frac{e^{-s(z)}}{s_0(z)}&\qquad &\text{for}\quad z\in D_-^f, \end{alignedat} $$

(3.31)

where

$$s(z)=-\frac{1}{2\pi i} \int_{\Sigma^f}\frac{\ln[1+\rho(\zeta)\rho^*(\zeta^*)]}{\zeta-z}\,d\zeta,\qquad s_0(z)=\prod_{n=1}^N\frac{(z-z_n)(z+\psi_0^2/z^*_n)}{(z-z^*_n)(z+\psi_0^2/z_n)}. $$

(3.32)

We refer the reader to [9] for a detailed derivation.

Taking the limit $z\to 0$ of $s_{11}(z)$ in (3.32) and (3.16), we obtain the theta condition

$$\operatorname{arg}\biggl(\frac{\psi_+}{\psi_-}\biggr) =4\sum_{n=1}^N\operatorname{arg}z_n +\int_{\Sigma^f}\frac{\ln[1+\rho(\zeta)\rho^*(\zeta^*)]}{2\pi\zeta}\,d\zeta,\qquad z\to 0. $$

(3.33)

In particular, in the case of a reflectionless potential, i.e., $\rho(z)=\hat\rho(z)=0$, we have $J=(0)_{2\times2}$. As a result, Eqs. (3.30) become

$$\sum_{n=1}^{2N} \biggl(\frac{A_-[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)}}{\xi_s-\hat\xi_n} -\frac{i\psi_-}{\xi_s}\delta_{sn}\biggr)\mu_{-11}(x,t,\hat\xi_n) =\frac{i\psi_-}{\xi_s},\qquad s=1,2,\dots,2N, $$

(3.34)

which can be solved for $\mu_{-11}(x,t,\hat\xi_n)$ by using Cramer’s rule. Summarizing the above analysis, we see that Theorem 1.1 holds for the potential $\psi(x,t)$ in the case of a simple pole.

In the case of a reflectionless potential, $\rho(z)=\hat\rho(z)=0$, the trace formulas and the theta condition become

$$\begin{alignedat}{2} &s_{11}=\prod_{n=1}^N \frac{(z-z_n)(z+\psi_0^2/z^*_n)}{(z-z^*_n)(z+\psi_0^2/z_n)}&\qquad &\text{for}\quad z\in D_+^f, \\ &s_{22}=\prod_{n=1}^N\frac{(z-z^*_n)(z+\psi_0^2/z_n)}{(z-z_n)(z+\psi_0^2/z^*_n)} &\qquad &\text{for}\quad z\in D_-^f, \end{alignedat} $$

(3.35)

and

$$\operatorname{arg}\biggl(\frac{\psi_+}{\psi_-}\biggr) =\operatorname{arg}(\psi_+)-\operatorname{arg}(\psi_-) =4\sum_{n=1}^N\operatorname{arg}(z_n). $$

(3.36)

Case I. For $N=1$ and $z_{1}=1.5i$ in Theorem 1.1, Eq. (3.36) shows that the asymptotic phase difference is $2\pi$. As can be seen from Fig. 2, the solution can represent the Kuznetzov–Ma (KM) breather that is spatially localized and temporally breathing. From Figs. 2a–c, we see that as $\psi_-$ becomes smaller, the periodic behavior of the breather wave only appears in its top part, and the maximal amplitude under the background gradually decreases. In particular, as seen in Fig. 2d, as $\psi_-\to 0$, the breather wave of the GFONLS equation (1.2) with NZBCs yields a bright soliton of the GFONLS equation (1.2) with zero boundary conditions.

Fig. 2.

Breathers as solutions (1.11) with the parameters $N=1$, $z_1=1.5i$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=1$ with (a) $\psi_-=1$, (b) $\psi_-=0.6$, and (c) $\psi_-=0.3$; (d) a bright-soliton solution with ${\psi_-\to 0}$.

Case II. For $N=1$ and $z_1=ae^{\pi/4}$ in Theorem 1.1, the asymptotic phase difference is $\pi$. The GFONLS equation (1.2) with NZBCs has nonstationary solitons. The plot in Fig. 3 is for nonstationary solitons for the GFONLS equation (1.2) with NZBCs; the solitons are localized both in time and space and thus reveal the usual Akhmediev breather wave features.

Fig. 3.

Breathers as solutions (1.11) with the parameters $N=1$, $A_+[z_1]=1$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $\psi_-=1$, and (a) $z_1=e^{i\pi/4}$, (b) $z_1=0.8e^{i\pi/4}$.

Case III. For $N=2$ in Theorem 1.1, we have interactions of breather–breather solutions of the GFONLS equation (1.2) with NZBCs. As we can see from Fig. 4, the interaction is strong. In particular, as $\psi_-\to 0$, we have strongly interacting bright–bright solitons of the GFONLS equation (1.2) with zero boundary conditions. However, as shown Fig. 5, if we take two appropriate eigenvalues, then the breather–breather solutions of the GFONLS equation (1.2) with NZBCs interact weakly. Likewise, as $\psi_-\to 0$, we have weak interactions of the simple-pole bright–bright solitons of the GFONLS equation (1.2) with zero boundary conditions (see Figs. 5a–5d).

Case IV. One interesting example of the breather–breather waves is shown in Fig. 6a, where the two breather waves have different modulation frequencies. In particular, for $z_1=z_2$, they become a first-order Akhmediev breather (see Fig. 6b). In Fig. 6c, for $z_1=-z_2=0.1=1.5i$, we can see interaction of simple-pole breather–breather solutions of the GFONLS equation (1.2) with NZBCs.

Case V. For $N=2$ in Theorem 1.1, we give another interesting example of breather–breather waves. In Fig. 7, the result is a simply periodic solution. Specifically, as $\psi_-\to 0$, we have simple-pole bright–bright solitons of the GFONLS equation (1.2) with NZBCs. To our surprise, the bright–bright soliton is also a simply periodic solution (see Fig. 7d).

Fig. 4.

Breathers as solution (1.11) with the parameters $N=2$, $z_1=0.2+2i$, $z_2=1+i$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=A_+[z_2]=1$: (a) breather–breather solutions with $\psi_-=1$; (b) breather–breather solutions with $\psi_-=0.6$; (c) breather–breather solutions with $\psi_-=0.3$; (d) bright–bright solitons with $\psi_-\to 0$.

Fig. 5.

Breathers as solution (1.11) with the parameters $N=2$, $z_1=0.1+1.5i$, $z_2=-0.1+1.5i$, $\alpha_2=1$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=A_+[z_2]=1$: (a) breather–breather solutions with ${\psi_-=1}$; (b) breather–breather solutions with ${\psi_-=0.6}$; (c) breather–breather solutions with ${\psi_-=0.3}$; (d) bright–bright solitons with ${\psi_-\to 0}$.

Fig. 6.

Breathers as solution (1.11) with parameters $N=2$, $\alpha_2=1$, $\alpha_3=0.01$, $\alpha_4=\alpha_5=0.001$, $A_+[z_1]=A_+[z_2]=1$: (a) breather–breather solutions with $z_1=0.5i$, $z_2=1.5i$; (b) breather solutions with $z_1=1.5i$, $z_2=1.5i$; (c) breather–breather solutions with $z_1=0.1+1.5i$, $z_2=-0.1-1.5i$.

Fig. 7.

Breathers as solution (1.11) with the parameters $N=2$, $z_1=1/65+1.05i$, ${z_2=-1/65+1.05i}$, $\alpha_2=1$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=A_+[z_2]=1$: (a) breather–breather solutions with ${\psi_-=1}$; (b) breather–breather solutions with ${\psi_-=0.6}$; (c) breather–breather solutions with ${\psi_-=0.3}$; (d) bright–bright solitons with ${\psi_-\to 0}$.

4. The GFONLS equation with NZBCs: double poles

In what follows, we suppose that the discrete-spectrum points $Z^f$ are double zeros of the scattering coefficients $s_{11}(z)$ and $s_{22}(z)$, ($s_{11}(z_0)=s'_{11}(z_0)\ne 0$ for all $z_0\in Z^f\cap D_+^f$), and $s_{22}(z_0)=s'_{22}(z_0)=0$, $s''_{22}(z_0)\ne 0$ for all $z_0\in Z^f\cap D_-^f$. For convenience, we recall a simple proposition from [10]: if $f(z)$ and $g(z)$ are analytic in some complex domain $\Omega$, and $z_0\in\Omega$ is a double zero of $g(z)$ and $f(z_0)\ne 0$, then the function $f(z)/g(z)$ has a double pole at $z=z_0$, and the coefficient $P_{-2}[f/g]$ of $(z-z_0)^{-2}$ and its residue $\operatorname{Res}[f/g]$ in the Laurent series are given by

$$\underset{z=z_0}{P_{-2}}\biggl[\frac{f}{g}\biggr] =\frac{2f(z_0)}{g''(z_0)},\qquad \mathop{\operatorname{Res}}\limits_{z=z_0}\biggl[\frac{f}{g}\biggr] =2\biggl(\frac{f'(z_0)}{g''(z_0)} -\frac{f(z_0g'''(z_0))}{3[g''(z_0)]^2}\biggr). $$

(4.1)

According to [10], for $s_{11}(z_0)=s'_{11}(z_0)=0$, $s'_{11}(z_0)\ne 0$ for all $z_0\in Z^f\cap D_+^f$. Equation (3.6) still hold. The first equation in (2.13) then yields

$$s_{11}(z)\gamma_f(z)=|\phi_{+1}(x,t,z),\phi_{-2}(x,t,z)|, $$

(4.2)

where the first-order partial derivative with respect to $z$ is

$$[s_{11}(z)\gamma_{f}(z)]'=|\phi'_{+1}(x,t,z),\phi_{-2}(x,t,z)| +|\phi_{+1}(x,t,z),\phi'_{-2}(x,t,z)|. $$

(4.3)

Taking $z=z_0\in Z^f\cap D_+^f$ in (4.3) and using $s_{11}(z_0)=s'_{11}(z_0)=0$ and (3.6) leads to

$$|\phi'_{+1}(x,t,z_0)-b_+(z_0)\phi'_{-2}(x,t,z_0),\phi_{-2}(x,t,z_0)|=0, $$

(4.4)

which indicates that there is another constant $c_+(z_0)$ such that

$$\phi'_{+1}(x,t,z_0)=c_+(z_0)\phi_{-2}(x,t,z_0)+b_+(z_0)\phi'_{-2}(x,t,z_0). $$

(4.5)

From (3.8), (4.1), and (4.5), we find

$$\begin{aligned} \, &\underset{z=z_0}{P_{-2}}\biggl[\frac{\phi_+(x,t,z)}{s_{11}(z)}\biggr] =\frac{2\phi_{+1}(x,t,z_0)}{s''_{11}(z_0)} =\frac{2b_+(z_0)}{s''_{11}(z_0)}\phi_{-2}(x,t,z_0)= \\ &\hphantom{\underset{z=z_0}{P_{-2}}\biggl[\frac{\phi_+(x,t,z)}{s_{11}(z)}\biggr]{}}=A_+[z_0]\phi_{-2}(x,t,z_0), \\ &\mathop{\operatorname{Res}}\limits_{z=z_0}\biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}\biggr] =\frac{2\phi'_{+1}(x,t,z_0)}{s''_{11}(z_0)} -\frac{2\phi_{+1}(x,t,z_0)s'''_{11}(z_0)}{3(s''_{11}(z_0))^2}= \\ & \hphantom{\mathop{\operatorname{Res}}\limits_{z=z_0}\biggl[\frac{\phi_{+1}(x,t,z)}{s_{11}(z)}\ \biggr]}=A_+[z_0][\phi'_{-2}(x,t,z_0)+B_+[z_0]\phi_{-2}(x,t,z_0)]. \end{aligned} $$

(4.6)

Similarly, for $s_{22}(z^*_0)=s'_{22}(z^*_0)=0$ and $s''_{22}(z^*_0)\ne 0$ for all $z^*_0\in Z^f\cap D_-^f$, Eq. (3.8) holds. It follows from the second equation in (2.13) and formula (3.8) that

$$\phi'_{+2}(x,t,z^*_0)=c_-(z^*_0)\phi_{-1}(x,t,z^*_0)+b_-(z^*_0)\phi'_{-1}(x,t,z^*_0) $$

(4.7)

for $c_-(z^*_0)$.

From (3.8), (4.1), and (4.7), we obtain

$$\begin{aligned} \, &\underset{z=z^*_0}{P_{-2}}\biggl[\frac{\phi_{+2}(x,t,z)}{s_{22}(z)}\biggr] =\frac{2\phi_{+2}(x,t,z^*_0)}{s''_{22}(z^*_0)} =\frac{2b_-(z^*_0)}{s''_{22}(z^*_0)}\phi_{-1}(x,t,z^*_0)= A_-[z^*_0]\phi_{-1}(x,t,z^*_0), \\ &\mathop{\operatorname{Res}}\limits_{z=z^*_0}\biggl[\frac{\phi_{+2}(x,t,z)}{s_{22}(z)}\biggr] =A_-[z^*_0][\phi'_{-1}(x,t,z^*_0)+B_-[z^*_0]\phi_{-1}(x,t,z^*_0)]. \end{aligned} $$

(4.8)

We therefore have

$$\begin{alignedat}{3} &A_+[z_0]=\frac{2b_+[z_0]}{s''_{11}(z_0)},&\qquad &B_+[z_0]=\frac{c_+[z_0]}{b_+[z_0]}-\frac{s'''_{11}(z_0)}{3s''_{11}(z_0)},&\quad &z_0\in Z^f\cap D_+^f, \\ &A_+[z^*_0]=\frac{2b_+[z^*_0]}{s''_{11}(z^*_0)},&\qquad &B_+[z^*_0]=\frac{c_+[z^*_0]}{b_+[z^*_0]} -\frac{s'''_{11}(z^*_0)}{3s''_{11}(z^*_0)},&\quad &z^*_0\in Z^f\cap D_-^f, \end{alignedat} $$

(4.9)

whence we obtain the relations

$$\begin{aligned} \, A_+[z_0]&=-A^*_-[z^*_0] =\frac{z_0^4\psi^*_-}{\psi_0^4\psi_-}A_-\biggl[-\frac{\psi_0^2}{z_0}\biggr], \\ B_+[z_0]&=B^*_-[z^*_0]=\frac{\psi_0^2}{z_0^2} B_-\biggl[-\frac{\psi_0^2}{z_0}\biggr] +\frac{2}{z_0},\quad z_0\in Z^f\cap D_+^f, \end{aligned} $$

(4.10)

which in turn lead to

$$\begin{alignedat}{2} &A_+[z_n]=-A^*_-[z^*_n] =-\frac{z_n^4\psi^*_-}{\psi_0^4\psi_-}A_+\biggl[-\frac{\psi_0^2}{z^*_n}\biggr],&\qquad &z_n\in Z^f\cap D_+^f, \\ &B_+[z_n]=B^*_-[z^*_n]=\frac{\psi_0^2}{z_n^2} B^*_+\biggl[-\frac{\psi_0^2}{z^*_n}\biggr]+\frac{2}{z_n},&\qquad &z^*_n\in Z^f\cap D_-^f. \end{alignedat} $$

(4.11)

As a result, we have

$$\begin{aligned} \, &\underset{z=\xi_n}{P_{-2}}M_1^+(x,t,z) =P_{-2}\biggl[\frac{\mu_{+1}(x,t,z)}{s_{11}(z)}\biggr] =A[\xi_n]e^{-2i\theta(x,t,\xi_n)}\mu_{-2}(x,t,\xi_n), \\ &\underset{z=\hat\xi_n}{P_{-2}}M_2^-(x,t,z) =P_{-2}\biggl[\frac{\mu_{+2}(x,t,z)}{s_{22}(z)}\biggr] =A[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)} \mu_{-1}(x,t,\xi_n), \\ &\mathop{\operatorname{Res}}\limits_{z=\xi_n}M_1^+(x,t,z) =\mathop{\operatorname{Res}}\limits_{z=\xi_n}\biggl[\frac{\mu_{+1}(x,t,z)}{s_{11}(z)}\biggr]= \\ &\hphantom{\mathop{\operatorname{Res}}\limits_{z=\hat\xi_n}M_2^-(x,t,z){}}=A[\xi_n]e^{-2i\theta(x,t,\xi_n)}\{\mu'_{-2}(x,t,\xi_n)+ [B[\xi_n]-2i\theta'(x,t,\xi_n)]\mu_{-2}(x,t,\xi_n)\}, \\ &\mathop{\operatorname{Res}}\limits_{z=\hat\xi_n}M_2^-(x,t,z) =\mathop{\operatorname{Res}}\limits_{z=\hat\xi_n}\biggl[\frac{\mu_{+2}(x,t,z)}{s_{22}(z)}\biggr]= \\ &\hphantom{\mathop{\operatorname{Res}}\limits_{z=\hat\xi_n}M_2^-(x,t,z){}}=A[\hat\xi_n]e^{2i\theta(x,t,\hat\xi_n)} \{\mu'_{-1}(x,t,\hat\xi_n)+[B[\hat\xi_n]+2i\theta'(x,t,\hat\xi_n)]\mu_{-1}(x,t,\hat\xi_n)\}. \end{aligned} $$

(4.12)

The RHP in Proposition 3.1 still holds in the case of double poles. To solve this RHP, we have to subtract the asymptotic values as $z\to\infty$ and $z\to 0$ and the singularity contributions:

$$\begin{aligned} \, &M_{dp}(x,t,z)=I+\frac{i}{z}\sigma_3Q_-+\sum_{n=1}^{2N}M_{dp}^n, \\ &M_{dp}^n=\frac{{P_{-2}}|^{}_{z=\vphantom{\hat \xi}\xi_n}M^+}{(z-\xi_n)^2} +\frac{{P_{-2}}|^{}_{z=\hat\xi_n}M^-}{(z-\hat\xi_n)^2} +\frac{\operatorname{Res}_{z=\xi_n}M^+}{z-\xi_n} +\frac{\operatorname{Res}_{z=\hat\xi_n}M^+}{z-\hat\xi_n}. \end{aligned} $$

(4.13)

From the jump condition $M^-=M^+(I-J)$, we then obtain

$$M^-(x,t,z)-M_{dp}(x,t,z)=M^+(x,t,z)-M_{dp}(x,t,z)-M^+(x,t,z)J, $$

(4.14)

where $M^\pm(x,t,z)-M_{dp}(x,t,z)$ are analytic in $D_\pm^f$. Besides, their asymptotics are both $O(1/z)$ as $z\to\infty$ and $O(1)$ as $z\to 0$, and $J(x,t,z)$ is $O(1/z)$ as $z\to\infty$ and $O(z)$ as $z\to 0$. As a result, the Cauchy projectors and Plemelj’s formulas can be used to solve (4.14), with the result

$$M(x,t,z)=M_{dp}(x,t,z)+\frac{1}{2\pi i} \int_{\Sigma^f}\frac{M^+(x,t,\zeta)J(x,t,\zeta)}{\zeta-z}\,d\zeta,\qquad z\in\mathbb C\setminus\Sigma^f, $$

(4.15)

where $\int_{\Sigma^f}$ stands for the integral along the oriented contours shown in Fig. 1b.

Now, using (4.12), we can rewrite the parts corresponding to $P_{-2}(\,\cdot\,)$ and $\operatorname{Res}(\,\cdot\,)$ in (4.15) as

$$\begin{aligned} \, &M_{dp}^n=\biggl(C_n(z)\biggl[\mu'_{-2}(\xi_n) +\biggl(D_n+\frac{1}{z-\xi_n}\biggr)\mu_{-2}(\xi_n)\biggr], \\ &\widehat C_n(z)\biggl[\mu'_{-1}(\hat\xi_n) +\biggl(D_n+\frac{1}{z-\hat\xi_n}\biggr)\mu_{-2}(\hat\xi_n)\biggr]\biggr), \end{aligned} $$

(4.16)

where

$$C_n(z)=\frac{A_+[\xi_n]}{z-\xi_n}e^{-2i\theta(\xi_n)}, \qquad D_n=B_+[\xi_n]-2i\theta'(\xi_n),$$

(4.17)

$$\widehat C_n(z)=\frac{A_-[\hat\xi_n]}{z-\hat\xi_n}e^{2i\theta(\hat\xi_n)}, \qquad \widehat D_n=B_-(\hat\xi_n)+2i\theta'(\hat\xi_n).$$

(4.18)

We next find $\mu'_{-2}(\xi_n)$, $\mu_{-2}(\xi_n)$, $\mu'_{-1}(\xi_n)$, and $\mu_{-1}(\xi_n)$ in (4.16) for $z=\xi_s$, $s=1,2,\dots,2N$. From the second column of $M(x,t,\lambda)$ in (4.15) and (4.16), we obtain

$$\begin{aligned} \, \mu_{-2}(z)={}&\begin{pmatrix} \dfrac{i\psi_-}{z} \\ 1 \end{pmatrix}+\sum_{n=1}^{2N}\widehat C_n(z)\biggl[\mu'_{-1}(\hat\xi_n) +\biggl(\widehat D_n+\frac{1}{z-\hat\xi_n}\biggr) \mu_{-1}(\hat\xi_n)\biggr]+{} \nonumber \\ &+\frac{1}{2\pi i}\int_{\Sigma^f}\frac{(M^+J)_2(\zeta)}{\zeta-z}\,d\zeta, \end{aligned}$$

(4.19)

whose first-order derivative with respect to $z$ is given by

$$\begin{aligned} \, \mu'_{-2}(z)={}&\begin{pmatrix} -\dfrac{i\psi_-}{z^2} \\ 1 \end{pmatrix}-\sum_{n=1}^{2N}\frac{\widehat C_n(z)}{z-\hat\xi_n} \biggl[\mu'_{-1}(\hat\xi_n) +\biggl(\widehat D_n+\frac{1}{z-\hat\xi_n}\biggr)\mu_{-1}(\hat\xi_n)\biggr]+{} \nonumber \\ &+\frac{1}{2\pi i} \int_{\Sigma^f}\frac{(M^+J)_2(\zeta)}{(\zeta-z)^2}\,d\zeta. \end{aligned}$$

(4.20)

Furthermore, it follows from (3.1) that

$$\mu'_{-2}(z)=-\frac{i\psi_-}{z^2} \mu_-\biggl(\frac{-\psi_0^2}{z}\biggr) +\frac{i\psi_0^2}{z}\frac{\psi_-}{z^2} \mu'_{-1}\biggl(-\frac{\psi_0^2}{z}\biggr). $$

(4.21)

Substituting (4.21) in (4.26) and (4.27), we then have

$$\begin{aligned} \, &\sum_{n=1}^{2N}\widehat C_n(\xi_s)\mu'_{-1}(\hat\xi_n) +\biggl[\widehat C_n(\xi_{k})\biggl(\widehat D_n +\frac{1}{\xi_s-\hat\xi_n}\biggr) -\frac{i\psi_-}{\xi_s}\delta_{sn}\biggr]\mu_{-1}(\hat\xi_n)= \\ &=-\begin{pmatrix} \dfrac{iq_-}{\xi_s} \\ 1 \end{pmatrix}-\frac{1}{2\pi i} \int_{\Sigma^f}\frac{(M^+J)_2(\zeta)}{\zeta-\xi_k}\,d\zeta, \\ &\sum_{n=1}^{2N}\biggl(\frac{\widehat C_n(\xi_s)}{\xi_s-\hat\xi_n} +\frac{i\psi_0^2\psi_-}{\xi_s^3\delta_{sn}}\biggr) \mu'_{-1}(\hat\xi_n)+\biggl[\frac{\widehat C_n(\xi_s)}{\xi_s-\hat\xi_n} \biggl(\widehat D_n+\frac{2}{\xi_s-\hat\xi_n}\biggr) -\frac{i\psi_-}{\xi_s^2}\delta_{sn}\biggr]\mu_{-1}(\hat\xi_n)= \\ &=\begin{pmatrix} -\dfrac{\psi_-}{\xi_s^2} \\ 0 \end{pmatrix}+\int_{\Sigma^f}\frac{(M^+J)_2(\zeta)}{2\pi i(\zeta-\xi_k)^2}\,d\zeta, \end{aligned} $$

(4.22)

whence we find $\mu_-(x,t,\hat\xi_n)$ and $\mu'_{-1}(x,t,\hat\xi_n)$, $n=1,2,\dots,2N$, and hence also find $\mu_{-2}(x,t,\xi_n)$ and $\mu'_{-2}(x,t,\xi_n)$, $n=1,2,\dots,2N$, from (4.21). Substituting these in (4.24) and then substituting (4.24) in (4.15) gives $M(x,t,z)$ in terms of the scattering data.

We see from (4.15) and (4.24) that the asymptotic form of $M(x,t,z)$ is still given by (3.27). But we must replace $M^{(1)}(x,t)$ with

$$\begin{aligned} \, &M^{(1)}(x,t)=i\sigma_3Q_--\frac{1}{2\pi i} \int_{\Sigma^f}(M^+J)(\zeta)\,d\zeta+{} \nonumber \\ &\hphantom{M^{(1)}(x,t)={}}+\sum_{n=1}^{2N}[A_+[\xi_n] e^{-2i\theta(\xi_n)}(\mu'_{-2}(\xi_n)+D_n\mu_{-2}(\xi_n)), \nonumber \\ &A_-[\hat\xi_n]e^{2i\theta(\hat\xi_n)} (\mu'_{-2}(\hat\xi_n)+\widehat D_n\mu_{-1}(\hat\xi_n))]. \end{aligned}$$

(4.23)

Summarizing the above results, we arrive at the following proposition for the potential $u(x,t)$ in the case of double poles.

Proposition 4.1.

The potential with double poles of the GFONLS equation (1.2) with NZBCs is expressed by

$$\begin{aligned} \, \psi(x,t)={}\psi_-&-i\sum_{n=1}^{2N}A_-[\hat\xi_n]e^{2i\theta(\xi_n)} (\mu'_{-11}(\hat\xi_n)+{} \nonumber \\ &+\widehat D_n\mu_{-11}(\hat\xi_n)) +\frac{1}{2\pi}\int_{\Sigma'}(M^+J)_{12}(\zeta)\,d\zeta, \end{aligned}$$

(4.24)

where

$$\widehat C_n(z)=\frac{A[\hat\xi_n]}{z-\xi_n} e^{2i\theta(\hat\xi_n)},\qquad \widehat D_n=B[\hat\xi_n]+2i\theta'(\xi_n),$$

and $\mu_{-11}(\hat\xi_n)$ and $\mu'_{-11}(\hat\xi_n)$ are given by (4.22).

Similarly to the case of simple poles, the trace formulas in the case of double poles are

$$\begin{alignedat}{3} &s_{11}(z)=e^{s(z)}s_0(z)&\quad &\text{for}\quad z\in D_+^f, \\ &s_{22}(z)=\frac{e^{-s(z)}}{s_0(z)} &\quad &\text{for}\quad z\in D_-^f, \end{alignedat} $$

(4.25)

where

$$s(z)=-\frac{1}{2\pi i}\int_{\Sigma^f} \frac{\ln[1+\rho(\zeta)\rho^*(\zeta^*)]}{\zeta-z}\,d\zeta,\qquad s_0(z)=\prod_{n=1}^N\frac{(z-z_n)^2(z+\psi_0^2/z^*_n)^2}{(z-z^*_n)^2(z+\psi_0^2/z_n)^2}. $$

(4.26)

From the limit $z\to 0$ of $s_{11}(z)$ in (4.25), the following theta condition can be obtained:

$$\operatorname{arg}\biggl(\frac{\psi_+}{\psi_-}\biggr) =8\sum_{n=1}^N\operatorname{arg}(z_n) +\int_{\Sigma^f} \frac{\ln[1+\rho(\zeta)\rho^*(\zeta^*)]}{\zeta-z}\,d\zeta. $$

(4.27)

In particular, in the reflectionless case $\rho(z)=\hat\rho(z)=0$, Theorem 1.2 holds.

Thus, the trace formulas and the theta condition become

$$s_{11}(z)=\prod_{n=1}^N\frac{(z-z_n)^2(z+\psi_0^2/z^*_n)^2}{(z-z^*_n)^2(z+\psi_0^2/z_n)^2}, \qquad z\in D_+^f,$$

(4.28)

$$s_{22}(z)=\prod_{n=1}^N\frac{(z-z^*_n)^2(z+\psi_0^2/z_n)^2}{(z-z_n)^2(z+\psi_0^2/z^*_n)^2}, \qquad z\in D_-^f,$$

(4.29)

and

$$\operatorname{arg}\biggl(\frac{\psi_+}{\psi_-}\biggr) =\operatorname{arg}(\psi_+)-\operatorname{arg}(\psi_-) =8\sum_{n=1}^N\operatorname{arg}(z_n). $$

(4.30)

The double-pole breather–breather solutions of the GFONLS equation (1.2) with NZBCs are shown in Figs. 8–10, which are useful for understanding the propagation properties of nonlinear waves. More importantly, as $\psi_-\to 0$, we have double-pole bright–bright soliton solutions of the GFONLS equation (1.2) (see Figs. 9d and 10d).

Fig. 8.

Breather waves as solution (4.21) with the parameters $N=1$, $\psi_-=1$, $\alpha_2=1$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=B_+[z_1]=1$, and (a,d) $z_1=-0.08+1.5i$; (b,e) $z_1=-0.08+1.5i$; (c,f) $z_1=-0.06+1.5i$.

Fig. 9.

Breather waves as solution (4.21) with the parameters $N=1$, $z_1=1.5i$, $\alpha_2=1$, $\alpha_3=\alpha_4=\alpha_5=0.01$, $A_+[z_1]=B_+[z_1]=1$: (a) breather–breather solutions with $\psi_-=1$; (b) breather–breather solutions with $\psi_-=0.5$; (c) breather–breather solutions with $\psi_-=0.3$; (d) bright–bright solitons with $\psi_-\to 0$.

Fig. 10.

Contour plots corresponding to Figs. 9a–9d.

5. Conclusion and discussion

In this paper, we systematically investigated the GFONLS equation (1.2) with NZBCs, which reduces to some classical integrable equations including the NLS equation with NZBCs (1.5), mKdV equation (1.7), and Hirota equation with NZBCs (1.6). We have discussed the IST and soliton solutions of the GFONLS equation (1.2) with NZBCs. Its simple- and double-pole solutions were found by solving a matrix RHP with reflectionless potentials. Some representative solitons were constructed. Moreover, to better understand the solutions, in Figs. 2–9 we show breather-wave, bright-soliton, breather–breather wave, and bright–bright solitons, plotted with appropriate parameters chosen. The GFONLS equation (1.2) studied in this paper is much more general because it involves four real constant $\alpha_2$, $\alpha_3$, $\alpha_4$, and $\alpha_5$. The celebrated NLS equation (1.5) with NZBCs, an important model in fiber optics, is its special case. Another important reduction of (1.2) is the complex mKdV equation (1.7). Multisoliton solutions of the NLS equation (1.5) with NZBCs, mKdV equation (1.7), and Hirota equation (1.6) with NZBCs can be derived by reducing the multisoliton solutions of (1.2). We think that the proposed effective method can be helpful in understanding the diversity and integrability of nonlinear wave equations, and can be useful in studying other models in mathematical physics.