On the global attractivity for a reaction–diffusion malaria model with incubation period in the vector population

Abstract

This paper establishes the global attractivity of a positive constant equilibrium of a nonlocal and time-delayed diffusive malaria model in a homogeneous case. The same problem was achieved in a recent paper (Lou and Zhao in J Math Biol 62:543–568, 2011) by using the fluctuation method, but with a sufficient condition that the disease will become stable requires a sufficiently large basic reproduction number $\Re _0$. The present study is devoted to remove the sufficient condition by utilizing an appropriate Lyapunov functional and shows that the disease will become stable when $\Re _0$ is exactly greater than one, which remarkably improves the known results in Lou and Zhao (2011).

1 Introduction and previous results

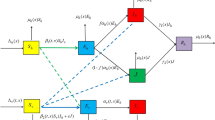
Malaria is a mosquito-borne disease caused by Plasmodium parasites, which spread in humans through the effective bite by infected female Anopheles mosquitoes. The worldwide incidence of malaria has risen significantly in recent decades. It was estimated that approximately 409,000 cases die from malaria in 2019 according to the World Health Organization (2020). Recently, a nonlocal and time-delayed diffusive malaria model in both heterogeneous and homogeneous environments was proposed and studied in Lou and Zhao (2011). Such model was obtained by introducing an infection age of mosquito populations. Denote y(t, a, x) be the density of the mosquito populations with infection age a at time t and habitat x, then the evolution of infectious mosquito populations is

$$\begin{aligned} \left( \frac{\partial }{\partial t} + \frac{\partial }{\partial a}\right) y(t,a,x) = D_m\varDelta y(t,a,x) - d_m y(t,a,x), \end{aligned}$$

where $x\in \varOmega$, and $\varOmega$ is the spatial habitat with smooth boundary $\partial \varOmega$. $D_m$ is the diffusion coefficient of mosquitoes and $d_m$ is the death rate of mosquitoes. In Lou and Zhao (2011), Lou and Zhao assumed that $\tau$ is the average incubation period (period of time during which mosquitoes can not transmit the disease to humans after taking an infected blood meal), and using the integration along characteristics (see Lou and Zhao 2011, pp. 546–548 for more details) to obtain the following nonlocal and time-delayed diffusive malaria model:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u_1}{\partial t} = D_h \varDelta u_1 + \frac{c\beta (x)}{H(x)}({H(x)}-u_1)u_3 - (d_h+\rho )u_1,\\ \displaystyle \frac{\partial u_2}{\partial t} = D_m \varDelta u_2 + \mu (x) - \frac{b\beta (x)}{H(x)}u_1u_2 - d_m u_2,\\ \displaystyle \frac{\partial u_3}{\partial t} = D_m \varDelta u_3 + e^{-d_m \tau } \int _\varOmega \varGamma (D_m\tau ,x,y)\frac{b\beta (y)}{H(y)}\\ \quad \quad \qquad \times u_1(t-\tau ,y)u_2(t-\tau ,y)\mathrm{d}y - d_m u_3,\\ \end{array}\right. \end{aligned}$$

(1.1)

with initial condition:

$$\begin{aligned} u_i(s,x) = \phi _i(0,x) \geqslant 0,\ \ \forall (s,x)\in [-\tau ,0]\times \varOmega ,\ \ i=1,2,3, \end{aligned}$$

and Neumann boundary conditions:

$$\begin{aligned} \frac{\partial u_i}{\partial \mathbf{n} } = 0,\ \ \forall (t,x)\in (0,\infty )\times \partial \varOmega ,\ \ i=1,2,3, \end{aligned}$$

where $u_1(t,x)$, $u_2(t,x)$ and $u_3(t,x)$ ($u_1$, $u_2$ and $u_3$ for short) are the spatial densities of infected humans, susceptible and infected mosquitos. $\varGamma$ is the Green function associated with $\varDelta$ and the Neumann boundary condition. $\frac{\partial }{\partial \mathbf{n} }$ denotes the outward normal derivatives on $\partial \varOmega$. The diffusion rate of human is assumed to be $D_h$; $\beta$ is the biting rate of female mosquitoes; c denotes the transmission probability of infectious mosquitoes to susceptible hosts per bite, while b denotes the transmission probability of infectious hosts to susceptible mosquitoes per bite H is the total human population; $\rho$ is the recovery rate of hosts; $d_h$ represents the mortality rate of hosts; $\mu$ is recruitment rate of adult female mosquitoes. In the rest of this section, we will give some known results proposed in Lou and Zhao (2011), and then introduce the description of the purpose for the current paper.

1.1 Heterogeneous case

Here we conclude the main results of the heterogeneous case of system (1.1) for the completeness of the current paper, we refer interested readers to the original article (Lou and Zhao 2011) for details. Denote $\mathbb {X}:=C(\overline{\varOmega },\mathbb {R}^3)$ and $\mathbb {X}^+:=C(\overline{\varOmega },\mathbb {R}^3_+)$ be two Banach spaces with supremum norms. For $\tau \geqslant 0$, define $\mathbb {Y} := C([-\tau ,0],\mathbb {X})$ with norm and further define $\mathbb {Y}^+ := C([-\tau ,0],\mathbb {X}^+)$. Clearly, it follows from Smith (1995) that $(\mathbb {X},\mathbb {X}^+)$ and $(\mathbb {Y},\mathbb {Y}^+)$ are both strongly ordered spaces. Given a function $u:[-\tau ,\sigma )\rightarrow \mathbb {X}$ for $\sigma >0$. Let

$$\begin{aligned} \mathbb {X}_H:= \left\{ \phi = (\phi _1,\phi _2,\phi _3)^{\text {T}} \in \mathbb {X}^+\ |\ {0\leqslant \phi _1(x)\leqslant H(x)},\ \forall x\in \overline{\varOmega }\right\} , \end{aligned}$$

and

$$\begin{aligned} C_H = C([ -\tau ,0],\mathbb {X}_H). \end{aligned}$$

According to Lou and Zhao (2011, pp. 549–550), for each $\phi \in C_H$, there exists a unique non-continuable mild solution $u(t,\phi )$ for system (1.1) on $(0, \sigma _\phi )$ with $u_0=\phi$ and some $\sigma _\phi >0$. Moreover, $u(t,\phi )\in \mathbb {X}_H$ for all $t\in (0,\sigma _\phi )$ and $u(t,\phi )$ is a classical solution for $t > \tau$. By proving that the solutions are bounded, Lou and Zhao obtained the solutions of system (1.1) exist globally on $[0,\infty )$ and the solution semiflow $\varPhi (t) = u_t(\cdot ): C_H \rightarrow C_H,\ t\geqslant 0$ has a global compact attractor, where $u_t\in \mathbb {Y}$ by $u_t(\theta ):=u(t+\theta )$ for $\theta \in [-\tau ,0]$. As in Lou and Zhao (2011), system (1.1) has a disease-free equilibrium $(0,m^*(x),0)$, where $m^*(x)$ is the positive steady state of

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \frac{\partial u_2}{\partial t} = D_m \varDelta u_2 + \mu (x) - d_m u_2,\ t>0,\ x\in \varOmega ,\\ \displaystyle \frac{\partial u_2}{\partial n} = 0,\ \ \ \ \ x\in \partial \varOmega .\\ \end{array}\right. \end{aligned}$$

(1.2)

Further, let $(\psi _1(x),\psi _2(x))^{\text {T}}$ be the spatial distribution of initial infective humans and mosquitoes, which are depend on x, and assume that the temporal distribution of this initial data is homogeneous. Denote $\mathbb {P}:=C(\overline{\varOmega },\mathbb {R})$ and define a positive linear operator A on $\mathbb {P}\times \mathbb {P}$ as

$$\begin{aligned} A(\psi )(x) = (A_1(\psi )(x),A_2(\psi )(x)),\ \ \forall \psi \in \mathbb {P}\times \mathbb {P},\ \ x\in \overline{\varOmega }, \end{aligned}$$

with

$$\begin{aligned} A_1(\psi )(x) = c\beta (x) \psi _2(x), \end{aligned}$$

and

$$\begin{aligned} {A_2}(\psi )(x) = e^{-d_m \tau } \int _{\varOmega } \varGamma (D_m{\tau },x,y)m^*(y)\frac{b\beta (y)}{H(y)} \psi _1(y)\mathrm{d}y. \end{aligned}$$

Then the next infection operator is defined as

$$\begin{aligned} \mathcal {L}(\psi ) := \int _0^\infty A(\mathcal {S}(t)\psi ))\mathrm{d}t, \end{aligned}$$

where $\mathcal {S}(t)\psi :=(T_1(t)\psi _1,T_2(t)\psi _2)^{\text {T}}$ with

$$\begin{aligned} T_1(t)\psi _1(x): = e^{-(d_h+\rho ){t}}\int _{\varOmega }\varGamma (D_ht,x,y)\psi _1(y)\mathrm{d}y, \end{aligned}$$

and

$$\begin{aligned} T_2(t)\psi _2(x): = e^{-d_m{t}}\int _{\varOmega }\varGamma (D_mt,x,y)\psi _2(y)\mathrm{d}y. \end{aligned}$$

By the argument in Lou and Zhao (2011), the basic reproduction ratio $\Re _0$ is defined by the spectral radius of $\mathcal {L}$, which is

$$\begin{aligned} \Re _0 : = r(\mathcal {L}). \end{aligned}$$

The threshold dynamics for the heterogeneous case of system (1.1) is the following theorem.

Theorem 1

[Lou and Zhao (2011), Theorem 2] Let $u(t,x,\phi )$ be the solution of system (1.1) with $u_0 = \phi \in C_H$. Then

• (i) If $\Re _0<1$, then the disease free equilibrium $(0,m^*,0)$ is globally attractive.

• (ii) If $\Re _0>1$, then system (1.1) admits at least one positive steady state $u^*(x)$, and there exists an $\eta > 0$ such that for any $\phi \in C_H$ with $\phi _1(0,\cdot )\not \equiv 0$ and $\phi _3(0,\cdot )\not \equiv 0$, we have

  $$\begin{aligned} \liminf _{t\rightarrow \infty }u_i(t,x)\geqslant \eta ,\ \ \forall i = 1,2,3 \end{aligned}$$

  uniformly for all $x\in \overline{\varOmega }$.

1.2 Homogeneous case

In fact, in this paper, we mainly focus on the space-independent equilibrium for system (1.1). If all coefficients are positive constants (i.e. $\beta (x)\equiv \beta$, $H(x)\equiv H$ and $\mu (x)\equiv \mu$), it follows from Lou and Zhao (2011, Sect. 4) that system (1.1) always has a disease free equilibrium $(0,\mu /d_m,0)$, which means that $m^*(x)\equiv \mu /d_m$ in this case. Moreover, define the basic reproduction number as

$$\begin{aligned} \Re _0 : = \sqrt{\frac{cb\beta ^2\mu e^{-d_m\tau }}{d_m^2 H (d_h+\rho )}}. \end{aligned}$$

Then system (1.1) has a unique constant endemic equilibrium $u^* = (u_1^*,u_2^*,u_3^*)^\text {T}$ if $\Re _0>1$ with

$$\begin{aligned} u_1^* = \frac{d_m^2 (d_h+\rho ) H^2 ({\Re _0}^2-1)}{b\beta (\mu c \beta e^{-d_m\tau }+(d_h+\rho )d_m H)}, \end{aligned}$$

and

$$\begin{aligned} u_2^* = \frac{1}{b \beta +d_m}\left( \mu +\frac{Hd_m(d_h+\rho )}{c\beta e^{-d_m\tau }}\right) ,\ u_3^* = \frac{b\beta u_1^* u_2^* e^{-d_m \tau }}{d_m H}. \end{aligned}$$

By using the fluctuation method (see Thieme and Zhao 2001) the author in (Lou and Zhao 2011) proved that $u^*$ of system (1.1) is globally attractive but under some additional conditions, which are described in the following theorem.

Theorem 2

(Lou and Zhao 2011, Theorem 3) Let $u(t,x,\phi )$ be the solution of (1.1) with $u_0=\phi \in C_H$. Then the following three statements are valid:

• (i) If $\Re _0<1$, then the disease free equilibrium $(0,\frac{\mu }{d_m},0)^{\text {T}}$ is globally attractive.

• (ii) If $\Re _0>1$, then system (1.1) admits at least one constant endemic equilibrium $u^*$, and there exists an $\eta > 0$ such that for any $\phi \in C_H$ with $\phi _i(0,\cdot )\not \equiv 0$ for $i = 1, 3$, we have $\liminf _{t\rightarrow \infty }u_i(t,x)\geqslant \eta$, $\forall i = 1, 2, 3$, uniformly for $x\in \overline{\varOmega }$.

• (iii) If

  $$\begin{aligned} \Re _0>\max \left\{ 1,\sqrt{\frac{b\beta }{d_m}}\right\} , \end{aligned}$$

  (1.3)

  then the system (1.1) admits a unique constant endemic equilibrium $u^*$ such that for any $\phi \in C_H$ with $\phi _1(0,\cdot )\not \equiv 0$ and $\phi _3(0,\cdot )\not \equiv 0$, $\lim _{t\rightarrow \infty } u(t,x,\phi ) = u^*$ uniformly for $x\in \overline{\varOmega }$.

We should mention that it is still a challenging problem (if not possible) to obtain the global attractivity of steady states in some spatial disease models that predicts whether disease will spread. In epidemic modeling, the basic reproduction number $\Re _0$ serves as a sharp threshold (Wang and Zhao 2012) in the sense that for the epidemic model with two different steady states, the disease-free steady state is global attractive if $\Re _0<1$, while the unique constant endemic equilibrium is globally attractive if $\Re _0>1$. Theorem 2 established a sufficient condition to ensure that spatially-homogeneous equilibrium will become global attractive if $\Re _0>1$ is large enough. Therefore, it comes naturally to raise a question: in model (1.1), is the constant endemic equilibrium globally attractive when $\Re _0$ is exactly greater than one? This constitutes the motivation for the present paper and we will solve this problem in Sect. 2.

2 Main results

Our goal for the current paper is to explore the global attractivity of the unique constant endemic equilibrium of (1.1) when $\Re _0>1$, which will remarkably improve statement (iii) in Theorem 2. It is widely recognized that the technique of constructing suitable Lyapunov functionals is powerful tools to achieve global attractivity of an equilibrium in epidemic models governed by, but not limited to, ordinary differential equations (Korobeinikov and Wake 2002), functional differential equations (Huang et al. 2010) or fractional order differential equations (Yang and Xu 2020).

We still focus on the same model proposed in Lou and Zhao (2011), then statements (i) and (ii) in Theorem 2 are still true for the homogeneous case of system (1.1). The next main theorem is generalized Theorem 2 by replacing the condition $\Re _0>\max \left\{ 1,\sqrt{b\beta /d_m}\right\}$ with $\Re _0>1$, and the proof idea is inspired by the a recent work (Li and Zhao 2021).

Theorem 3

Let $u(t,x,\phi )$ be the solution of (1.1) with $u_0=\phi \in C_H$, then the homogeneous case of system (1.1) has a unique constant endemic equilibrium $u^*$ such that for any $\phi \in C_H$ with $\phi _1(0,\cdot )\not \equiv 0$ and $\phi _3(0,\cdot )\not \equiv 0$, the statements (i) and (ii) in Theorem 2 are still true. Moreover, $\lim _{t\rightarrow \infty } u(t,x,\phi ) = u^*$ uniformly for all $x\in \overline{\varOmega }$ when $\Re _0>1$.

Proof

For simplicity, denote $\beta _1: = \frac{c\beta }{H}$, $\beta _2: = \frac{b\beta }{H}$ and $d_1: = d_h+\rho$. In the following of this proof, we let $u_1$, $u_2$ and $u_3$ short for $u_1(t,x)$, $u_2(t,x)$ and $u_3(t,x)$. Let $g(\varsigma )=\varsigma -1-\ln \varsigma$ for $\varsigma >0$. Clearly, $g(\varsigma )\geqslant 0$ for $\varsigma >0$. Denote a set

$$\begin{aligned} D:= \left\{ \phi \in C_H\ |\ \phi _i(0,x) > 0,\ \forall x \in \overline{\varOmega },\ i=1,2,3\right\} , \end{aligned}$$

and define the Lyapunov functional $V : D\rightarrow \mathbb {R}$ by

$$\begin{aligned} V(\phi ) = \int \limits _\varOmega \left( \sum _{i=1}^3 L_i(x,\phi ) + W(x,\phi )\right) \mathrm{d}x \end{aligned}$$

with

$$\begin{aligned} L_1(x,\phi )= \frac{\beta _2 u_1^* u_2^*}{d_1} g \left( \frac{\phi _1(0,x)}{u_1^*}\right) ,\ \ L_2(x,\phi ) = u_2^* g \left( \frac{\phi _2(0,x)}{u_2^*}\right) , \\ L_3 = e^{d_m \tau } u_3^* g \left( \frac{\phi _3(0,x)}{u_3^*}\right) , \end{aligned}$$

and

$$\begin{aligned} W(x,\phi ) = \beta _2 u_1^* u_2^* \int _{-\tau }^0 \int _\varOmega \varGamma (D_m(-s),x,y) g \left( \frac{\phi _1(s,y)\phi _2(s,y)}{u_1^*u_2^*}\right) \mathrm{d}y \mathrm{d}s. \end{aligned}$$

Fix $\phi =(\phi _1,\phi _2,\phi _3)\in D$ with $\phi _1(0,\cdot )\not \equiv 0$ and $\phi _3(0,\cdot )\not \equiv 0$. We can assume that $u_t(\phi ) \in D$ for all $t\geqslant 0$. Let $\omega (\phi )$ be the omega limit set of the orbit $\gamma ^+(\phi )$ for the semiflow $\varPhi (t)$ with $\varPhi (t)\phi = u_t(\phi )$. Hence, $\omega (\phi )\subset D$. Now, the differential of $L_1(x,u_t(\phi ))$ is calculated as follows,

$$\begin{aligned} \frac{\partial L_1(x,u_t(\phi ))}{\partial t} =&\ \frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \frac{\partial u_1(t,x)}{\partial t}\\ =&\ \frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \left( D_h \varDelta u_1 + \beta _1(H-u_1)u_3 - d_1u_1\right) \\ =&\ \frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \beta _1(H-u_1^*)u_3 + \frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \beta _1(u_1^*-u_1)u_3 \\&\ + \frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \left( D_h \varDelta u_1 - d_1u_1\right) . \end{aligned}$$

Note that $\beta _1(H-u_1^*)u_3^* = d_1 u_1^*$, one has that

$$\begin{aligned} \frac{\partial L_1(t,x)}{\partial t} =&\ D_h\frac{\beta _2 u_2^*}{d_1} \left( 1-\frac{u_1^*}{u_1}\right) \varDelta u_1 - \frac{\beta _1\beta _2u_2^*u_3}{d_1u_1}(u_1-u_1^*)^2\\&\ + \beta _2 u_1^*u_2^* \left( 1-\frac{u_1^*}{u_1}\right) \frac{u_3}{u_3^*} + \beta _2 u_1^* u_2^* - \beta _2 u_1^* u_2^* \frac{u_1}{u_1^*}. \end{aligned}$$

Using the equalities $\mu =\beta _2 u_1^* u_2^* + d_m u_2^*$ and $\beta _2 e^{-d_m\tau } u_1^*u_2^* = d_m u_3^*$, we obtain the derivatives of $L_2$ and $L_3$ as follows,

$$\begin{aligned} \frac{\partial L_2(x,u_t(\phi ))}{\partial t} =&\ \left( 1-\frac{u_2^*}{u_2}\right) \left( D_m \varDelta u_2 + \mu - \beta _2u_2u_1 - d_m u_2\right) \\ =&\ \left( 1-\frac{u_2^*}{u_2}\right) \left( D_m \varDelta u_2 + \beta _2 u_1^* u_2^* + d_m u_2^* - \beta _2 u_1u_2 - d_m u_2\right) \\ =&\ D_m \left( 1-\frac{u_2^*}{u_2}\right) \varDelta u_2 - \frac{d_m}{u_2}(u_2-u_2^*)^2\\&\ + \beta _2u_1^*u_2^* - \beta _2u_1u_2 - \beta _2u_1^*u_2^* \frac{u_2^*}{u_2} + \beta _2u_1u_2^*, \end{aligned}$$

and

$$\begin{aligned} \frac{\partial L_3(x,u_t(\phi ))}{\partial t} =&\ e^{d_m \tau }\left( 1-\frac{u_3^*}{u_3}\right) \bigg (D_m \varDelta u_3\\&\ +\left. \beta _2e^{-d_m \tau } \int _\varOmega \varGamma (D_m\tau ,x,y){(u_1u_2)}(t-\tau ,y)\mathrm{d}y - d_m u_3\right) \\ =&\ e^{d_m \tau }\left( 1-\frac{u_3^*}{u_3}\right) D_m \varDelta u_3 + \beta _2u_1^*u_2^* - \beta _2u_1^*u_2^* \frac{u_3}{u_3^*}\\&\ + \beta _2u_1^*u_2^* \left( 1-\frac{u_3^*}{u_3}\right) \int _\varOmega \varGamma (D_m\tau ,x,y)\frac{{(u_1u_2)}(t-\tau ,y)}{u_1^*u_2^*}\mathrm{d}y, \end{aligned}$$

where $(u_1u_2)(t\pm \cdot ,y): = u_1(t\pm \cdot ,y)u_2(t\pm \cdot ,y)$. Since system (1.1) subjects to Neumann boundary condition, we have $\int _\varOmega \frac{\varDelta u_i}{u_i}\mathrm{d}x = \int _\varOmega \frac{{|\nabla u_i|}^2}{u_i^2}\mathrm{d}x$ and $\int _\varOmega \varDelta u_i\mathrm{d}x = 0$, where $|\cdot |$ is the vector norm of $\nabla u_i$. Consequently,

$$\begin{aligned} \frac{\partial }{\partial t} \int _\varOmega \sum _{i=1}^3 L_i(x,u_t(\phi )) \mathrm{d}x =&\ -\frac{D_h\beta _2 u_1^*u_2^*}{d_1} \int _\varOmega \frac{{|\nabla u_1|}^2}{u_1^2}\mathrm{d}x - D_m u_2^*\int _\varOmega \frac{{|\nabla u_2|}^2}{u_2^2}\mathrm{d}x\\&\ - e^{d_m \tau }D_m u_3^* \int _\varOmega \frac{{|\nabla u_3|}^2}{u_3^2}\mathrm{d}x + \int _\varOmega \varXi (t,x) \mathrm{d}x, \end{aligned}$$

where

$$\begin{aligned} \varXi (t,x) =&\ -\frac{\beta _1\beta _2 u_2^*u_3}{d_1u_1} (u_1-u_1^*)^2 - \frac{d_m}{u_2}(u_2-u_2^*)^2\\&\ + {\beta _2 u_1^* u_2^*} \left( 3-\frac{u_1^* u_3}{u_1 u_3^*} - \frac{u_1u_2}{u_1^*u_2^*} - \frac{u_2^*}{u_2}\right) \\&\ + \beta _2u_1^*u_2^* \left( 1-\frac{u_3^*}{u_3}\right) \int _\varOmega \varGamma (D_m\tau ,x,y)\frac{{(u_1u_2)}(t-\tau ,y)}{u_1^*u_2^*}\mathrm{d}y. \end{aligned}$$

Next, we deal with W. Note that

$$\begin{aligned}&\ \frac{\partial }{\partial \theta } \left( \varGamma (D_m(-\theta ),x,y) g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \right) \\ =&\ g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \frac{\partial }{\partial \theta } \varGamma (D_m(-\theta ),x,y) \\&\ + \varGamma (D_m(-\theta ),x,y) \frac{\partial }{\partial \theta } g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) . \end{aligned}$$

Hence,

$$\begin{aligned}&\ \frac{\partial W(x,u_t(\phi ))}{\partial t}\\ =&\ \beta _2 u_1^* u_2^* \int _{-\tau }^0 \int _\varOmega \frac{\partial }{\partial \theta } \left( \varGamma (D_m(-\theta ),x,y) g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \right) \mathrm{d}y\mathrm{d}\theta \\&\ -\beta _2 u_1^* u_2^* \int _{-\tau }^0 \int _\varOmega g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \frac{\partial }{\partial \theta } \varGamma (D_m(-\theta ),x,y)\mathrm{d}y\mathrm{d}\theta \\ =&\ \beta _2 u_1^* u_2^* g\left( \frac{u_1u_2}{u_1^*u_2^*}\right) - \beta _2 u_1^* u_2^* \int _\varOmega {\varGamma (D_m\tau ,x,y)}g \left( \frac{(u_1u_2)(t-\tau ,y)}{u_1^*u_2^*}\right) \mathrm{d}y\\&\ -\beta _2 u_1^* u_2^* \int _{-\tau }^0 \int _\varOmega g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \frac{\partial }{\partial \theta } \varGamma (D_m(-\theta ),x,y)\mathrm{d}y\mathrm{d}\theta . \end{aligned}$$

Since $\varGamma$ is the Green function for the operator $\varDelta$ with the Neumann boundary condition, then it follows from Itô (1992) that $\frac{\partial }{\partial \theta } \varGamma = \varDelta \varGamma$. For the last term of the above equation, one has that

$$\begin{aligned} \beta _2 u_1^* u_2^* \int _{\varOmega }\int _{-\tau }^0 \int _\varOmega g \left( \frac{{(u_1u_2)}(t+\theta ,y)}{u_1^*u_2^*}\right) \frac{\partial }{\partial \theta } \varGamma (D_m(-\theta ),x,y)\mathrm{d}y\mathrm{d}\theta \mathrm{d}x = 0. \end{aligned}$$

Thus,

$$\begin{aligned} \frac{\mathrm{d}V(u_t(\phi ))}{\mathrm{d}t}&= \ -\frac{D_h\beta _2 {u_1^*}u_2^*}{d_1} \int _\varOmega \frac{{|\nabla u_1|}^2}{u_1^2}\mathrm{d}x - D_m {u_2^*} \int _\varOmega \frac{{|\nabla u_2|}^2}{u_2^2}\mathrm{d}x \\&\ - e^{d_m \tau }D_h{u_3^*} \int _\varOmega \frac{|{\nabla u_3|}^2}{u_3^2}\mathrm{d}x + \int _\varOmega \varXi (t,x) \mathrm{d}x\\ {}&\quad + \int _{\varOmega }\beta _2 u_1^* u_2^* g\left( \frac{u_1u_2}{u_1^*u_2^*}\right) \mathrm{d}x\\&\ - \beta _2 u_1^* u_2^* \int _\varOmega \int _\varOmega \varGamma (D_m\tau ,x,y) g\left( \frac{{(u_1u_2)}(t-\tau ,y)}{u_1^*u_2^*}\right) \mathrm{d}y \mathrm{d}x. \end{aligned}$$

Using another property of function $\varGamma$, which is $\int _{\varOmega } \varGamma (t,x,y) \mathrm{d}x =1$ (see Itô 1992), we have

$$\begin{aligned}&\ \varXi (t,x) + \beta _2 u_1^* u_2^* g\left( \frac{u_1u_2}{u_1^*u_2^*}\right) - \beta _2 u_1^* u_2^* \int _\varOmega \varGamma (D_m\tau ,x,y) g\left( \frac{(u_1u_2)(t-\tau ,y)}{u_1^*u_2^*}\right) \mathrm{d}y\\&\quad = \ -\frac{\beta _1\beta _2 u_2^*u_3}{d_1u_1} (u_1-u_1^*)^2 - \frac{d_m}{u_2}(u_2-u_2^*)^2 \\&\qquad + \beta _2 {u_1^*} u_2^* \left( 3-\frac{u_1^* u_3}{u_1 u_3^*} - \frac{u_1u_2}{u_1^*u_2^*} - \frac{u_2^*}{u_2}\right) \\&\qquad + \beta _2u_1^*u_2^* \left( 1-\frac{u_3^*}{u_3}\right) \int _\varOmega \varGamma (D_m\tau ,x,y)\frac{{(u_1u_2)}(t-\tau ,y)}{u_1^*u_2^*}\mathrm{d}y\\&\qquad + \beta _2 u_1^* u_2^* g\left( \frac{u_1u_2}{u_1^*u_2^*}\right) - \beta _2 u_1^* u_2^* \int _\varOmega \varGamma (D_m\tau ,x,y) g\left( \frac{(u_1u_2)(t-\tau ,y)}{u_1^*u_2^*}\right) \mathrm{d}y\\&\quad = \ -\frac{\beta _1\beta _2 u_2^*u_3}{d_1u_1} (u_1-u_1^*)^2 - \frac{d_m}{u_2}(u_2-u_2^*)^2 + \beta _2 {u_1^*} u_2^* \left( 3-\frac{u_1^* u_3}{u_1 u_3^*} - \frac{u_2^*}{u_2}\right) \\&\qquad - \beta _2u_1^*u_2^* \int _\varOmega \varGamma (D_m\tau ,x,y)\frac{(u_1u_2)(t-\tau ,y)u_3^*}{u_1^*u_2^*u_3}\mathrm{d}y + \beta _2u_1^*u_2^* \left( \ln \frac{u_3}{u_3^*} - \ln \frac{u_3}{u_3^*}\right) \\&\qquad - \beta _2u_1^*u_2^* \ln \frac{u_1u_2}{u_1^*u_2^*} + \beta _2u_1^*u_2^* \int _\varOmega \varGamma (D_m\tau ,x,y) \ln \left( \frac{(u_1u_2)(t-\tau ,y)}{u_1^*u_2^*}\right) \mathrm{d}y\\&\quad = - \frac{\beta _1\beta _2 u_2^*u_3}{d_1u_1} (u_1-u_1^*)^2 - \frac{d_m}{u_2}(u_2-u_2^*)^2 \\&\qquad - \beta _2 u_1^* u_2^*\int _\varOmega \varGamma (D_m\tau ,x,y)g\left( \frac{{(u_1u_2)}(t-\tau ,y)u_3^*}{u_1^* u_2^*u_3}\right) \mathrm{d}y\\&\qquad - \beta _2 u_1^* u_2^* \left[ g\left( \frac{u_1^*u_3}{u_1u_3^*}\right) + g\left( \frac{u_2^*}{u_2}\right) \right] . \end{aligned}$$

Hence, we obtain the derivative of $V(u_t(\phi ))$ as following

$$\begin{aligned} \frac{\mathrm{d}V(u_t(\phi ))}{\mathrm{d}t}&= \ -\frac{D_h\beta _2{u_1^*} u_2^*}{d_1} \int _\varOmega \frac{{|\nabla u_1|}^2}{u_1^2}\mathrm{d}x - D_m {u_2^*}\int _\varOmega \frac{{|\nabla u_2|}^2}{u_2^2}\mathrm{d}x\\ {}&\quad - e^{d_m \tau }D_h{u_3^*} \int _\varOmega \frac{{|\nabla u_3|}^2}{u_3^2}\mathrm{d}x\\&\quad - \int _\varOmega \frac{\beta _1\beta _2 u_2^*{u_3^*}}{d_1u_1} (u_1-u_1^*)^2\mathrm{d}x - \int _\varOmega \frac{d_m}{u_2}(u_2-u_2^*)^2 \mathrm{d}x\\&\quad - \int _\varOmega \beta _2 u_1^* u_2^*\int _\varOmega \varGamma (D_m\tau ,x,y)g\left( \frac{{(u_1u_2)}(t-\tau ,y)u_3^*}{u_1^* u_2^*u_3}\right) \mathrm{d}y\mathrm{d}x\\&\quad -\int _\varOmega \beta _2 u_1^* u_2^* \left[ g\left( \frac{u_1^*u_3}{u_1u_3^*}\right) + g\left( \frac{u_2^*}{u_2}\right) \right] \mathrm{d}x\\ \leqslant&\ \mathcal {L}_{\phi }(t), \end{aligned}$$

where

$$\begin{aligned} \mathcal {L}_{\phi }(t) : =&\ - \int _\varOmega \frac{\beta _1\beta _2 u_2^*u_3^*}{d_1u_1} (u_1-u_1^*)^2\mathrm{d}x - \int _\varOmega \frac{d_m}{u_2}(u_2-u_2^*)^2 \mathrm{d}x\nonumber \\&\ - \int _\varOmega \beta _2 u_1^* u_2^*\int _\varOmega \varGamma (D_m\tau ,x,y)g\left( \frac{{(u_1u_2)}(t-\tau ,y)u_3^*}{u_1^* u_2^*u_3}\right) \mathrm{d}y\mathrm{d}x\nonumber \\&\ -\int _\varOmega \beta _2 u_1^* u_2^* \left[ g\left( \frac{u_1^*u_3}{u_1u_3^*}\right) + g\left( \frac{u_2^*}{u_2}\right) \right] \mathrm{d}x. \end{aligned}$$

(2.1)

Recall that the map $t\rightarrow V(u_t(\phi ))$ is non-increasing and it is bounded from below, then there is some constant $V_\infty >0$ such that $\lim _{t\rightarrow \infty } V(u_t(\phi ))= V_\infty$. It follows from (Lou and Zhao 2011, pp. 562) that $\omega (\phi )$ is invariant for $\varPhi (t)$ and the solution semiflow $\varPhi (t)$ has a global compact attractor, then $\omega (\phi )\subset D$ and it is non-empty. For any $\chi \in \omega (\phi )$, choose a sequence $t_n$ with $t_n\rightarrow \infty$ as $n\rightarrow \infty$ such that $\lim _{n\rightarrow \infty } u_{t_n} (\phi )= \chi$ in D, which means that $V(\chi ) = V_\infty$ for $\chi \in \omega (\phi )$. Since $u_t(\chi )\in \omega (\phi )$, one has that $V(u_t(\chi )) = V_\infty$ for all $t>0$, which means that $\frac{\mathrm{d}V(u_t(\chi ))}{\mathrm{d}t} = 0$. Using $\chi$ instead of $\phi$ in (2.1), we have $0 = \frac{\mathrm{d}V(u_t(\chi ))}{\mathrm{d}t} \leqslant \mathcal {L}_{\chi }(t)\leqslant 0$. As a consequence, $\mathcal {L}_{\chi }(t) = 0$. Together with system (1.1), we obtain that $u_t(\chi ) = u^*$ for all $t\geqslant \tau$. Note that $\chi$ is arbitrary selected in $\omega (\phi )$ and this lead to $u_t(\omega (\phi )) = u^*$ for all $t\geqslant \tau$. Thanks to the invariance of omega limit sets, we arrive at $\omega (\phi ) = u_\tau (\omega (\phi )) = u^*$. Thus, we have $\lim _{t\rightarrow \infty }u_t(\phi )=u^*$. This completes the proof. $\square$

3 Discussions

In this paper, we construct a Lyapunov functional to guarantee the global attractivity for a reaction-diffusion malaria model with incubation period when $\Re _0>1$, which improves the known results proposed in Lou and Zhao (2011). We think this method is also applicable to other epidemic models with nonlocal delay reaction terms. As mentioned in Hattaf and Yousfi (2013), the approach to construct Lyapunov functionals for partial differential equations with or without delays could be inspired by the Lyapunov functions for ordinary differential equations (ODEs). Actually, the Lyapunov functional for the systems with nonlocal delayed reaction term could be also constructed with the help to the corresponding ODEs. In our case, the terms $\sum _{i=1}^3 L_i$ in Lyapunov functional V is the Lyapunov function for the corresponding ODEs to system (1.1). However, the computation requires some properties of Green function $\varGamma$.

Biologically, the basic reproduction number $\Re _0$ is frequently used as a predictor of whether or not an epidemic will spread, and the quantity of $\Re _0$ can be used to measure the epidemic or pandemic risk of emerging infectious diseases (Heffernan et al. 2005). Due to some mathematical difficulties, as in Lou and Zhao (2011), Lou and Zhao have shown that the disease will become established and stabilize at a unique constant endemic equilibrium when $\Re _0>\max \left\{ 1,\sqrt{b\beta /d_m}\right\}$. But in some realistic circumstances, this condition may underestimate the risk of malaria transmission. Imagine such a situation, real data satisfy $\sqrt{b\beta /d_m}>1$, which means we just need to control some parameters so that $\Re _0>\sqrt{b\beta /d_m}$ to control the malaria spread. Clearly, this $\Re _0$ is still greater than unit and the malaria spread can not be controlled due to the current study. Our result shows that $\Re _0 = 1$ defines a threshold for the spatially-homogeneous case. On the other hand, $\Re _0>\sqrt{b\beta /d_m}$ is equivalent to the condition

$$\begin{aligned} \sqrt{\frac{c\beta \mu e^{-d_m\tau }}{{d_m} H (d_h+\rho )}} >1, \end{aligned}$$

this condition is independent of the parameter b. But we can not ignore the impact on b in the real world application in our case since $\Re _0>1$ is depend on b. Indeed, our results remarkably improve the known results in Lou and Zhao (2011), and it can provide more accurate theoretical support for disease prevention and control.